Moving Charges and Magnetism

Multiple Choice Questions

Single Correct Answer Type
Question 1. Two charged particles traverse identical helical paths in a completely oppo-site sense in a uniform magnetic field B = B₀k
(a) They have equal z-components of momenta
(b) They must have equal charges
(c) They necessarily represent a particle, anti-particle pair
(d) The charge to mass ratio satisfy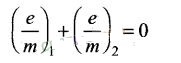

Solution: (d)
Key concept: In this situation if the particle is thrown in x-y plane (as shown in figure) at some angle θ with velocity v, then we have to resolve the velocity of the particle in rectangular components, such that one component is along the field (v cosθ) and other one is perpendicular to the field (v sinθ). We find that the particle moves with constant velocity v cosθ along the field. The distance covered by the particle along the magnetic field is called pitch.

Here in this case, charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field B, LHS for two particles should be same and of opposite sign. Therefore,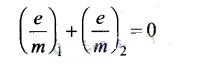

Question 2. Biot-Savart law indicates that the moving electrons (velocity v) produce a magnetic field B such that
(a) B is perpendicular to v.
(b) B is parallel to v.
(c) it obeys inverse cube law.
(d) it is along the line joining the electron and point of observation.
Solution:

where is a proportionality constant, V’ is the magnitude of position vector from charge to that point at which we have to find the magnetic field and <f) is the angle between v and F .
Where h is the direction of B which is in the direction of cross product of v and F . Or we can say that B _L to both v and F .

Question 3. A current carrying circular loop of radius R is placed in the x-y plane with centre at the origin. Half of the loop with x >0 is now bent so that it now lies in the y-z plane.
(a) The magnitude of magnetic moment now diminishes.
(b) The magnetic moment does not change.
(c) The magnitude ofB at (0,0, z), z>>R increases.
(d) The magnitude ofB at (0,0,z), z>>R is unchanged.
Solution: (a)
Key concept: Direction of magnetic moment (M= 14) of circular loop (in figure (a)) is perpendicular to the loop by right hand thumb rule.
So to compare these magnetic moments, we have to analyse them vectorically.
Now let us first analyse the situation: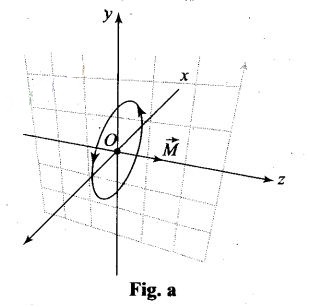

The direction of magnetic moment of circular loop of radius R is placed in the x-y plane is along z-direction and given by M = InR , (as shown in above figure-a). When half of the loop with x > 0 is now bent so that it now lies in the y-z plane as shown in the figure below.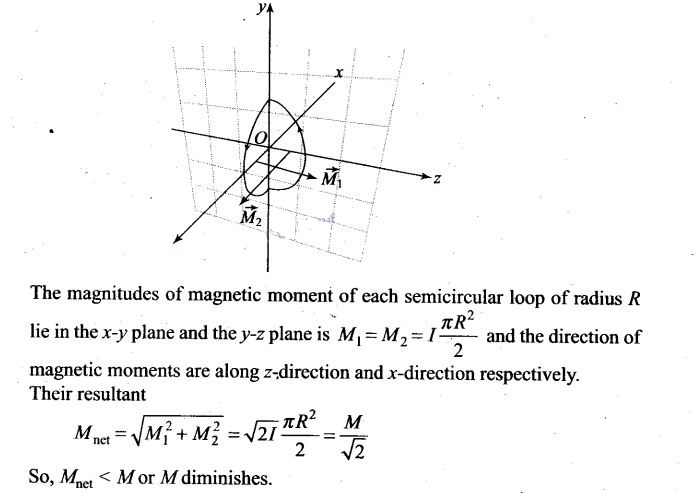

Question 4. An electron is projected with uniform velocity along the axis of a current carrying long solenoid. Which of the following is true?
(a) The electron will be accelerated along the axis
(b) The electron path will be circular about the axis
(c) The electron will experience a force at 45° to the axis and hence execute a helical path
(d) The electron will continue to move with uniform velocity along the axis of the solenoid
Solution: (d)
Key concept: A solenoid consists of a helical winding of wire on a cylinder, usually circular in cross-section. There can be hundreds or thousands of closely spaced turns, each of which can be regarded as a circular loop. There may be several layers of windings.
Magnetic field due to solenoid B = μ₀nl Direction of the field inside the solenoid is parallel to the axis, obtained by right hand thumb rule as shown in figure.

Now, here an electron is moving in magnetic field of solenoid, so the concept of magnetic force comes into existence.
When an electron is projected with uniform velocity along the axis of a current carrying long solenoid, then the magnetic force due to magnetic field acts on the electron will be F= -evB sin 180° = 0 (either velocity is parallel to magnetic field or anti-parallel or 0= 0°or 180° in both cases F = 0). The electron will continue to move with uniform velocity or will go undeflected along the axis of the solenoid.

Question 5. In a cyclotron, a charged particle
(a) undergoes acceleration all the time
(b) speeds up between the dees because of the magnetic field
(c) speeds up in a dee
(d) slows down within a dee and speeds up between dees
Solution: (a) Cyclotron is a device used to accelerate positively charged particles (like a-particles, deutrons etc.)
It is based on the fact that the electric field accelerates a charged particle and the perpendicular magnetic field keeps it revolving in circular orbits of constant frequency. Thus a small potential difference would impart enormously large velocities if the particle is made to traverse the potential difference a number of times.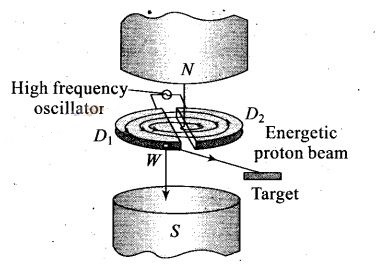

Question 6. A circular current loop of magnetic moment Mis in an arbitrary orientation in an external magnetic field B. The work done to rotate the loop by 30° about an axis perpendicular to its plane is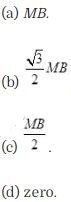

Solution: (d)

One or More Than One Correct Answer Type

Question 7. The gyro-magnetic ratio of an electron in an H-atom, according to Bohr model, is .
(a) independent of which orbit it is in.
(b) negative
(c) positive
(d) increases with the quantum number n.
Solution: (a, b) .

Question 8. Consider a wire carrying a steady current, I placed in a uniform magnetic field B perpendicular to its length. Consider the charges inside the wire. It is known that magnetic forces do not work. This implies that,
(a) motion of charges inside the conductor is unaffected by B, since they do not absorb energy.
(b) some charges inside the wire move to the surface as a result of B.
(c) if the wire moves under the influence of B, no work is done by the force.
(d) if the wire moves under die influence of B, no work is done by the magnetic force on the ions, assumed fixed within the wire.
Solution: (b, d)
Key concept: If a current carrying straight conductor (length l) is placed in a uniform magnetic field (B) such that it makes an angle θ with the direction of field, then force experienced by it is F_max= Bil sin θ. Direction of this force is obtained by right hand palm rule.
Right-hand palm rule: Stretch the fingers and thumb of right hand at right angles to each other. Then if the fingers point in the direction of field B and thumb in the direction of current z, then normal to the palm will point in the direction of force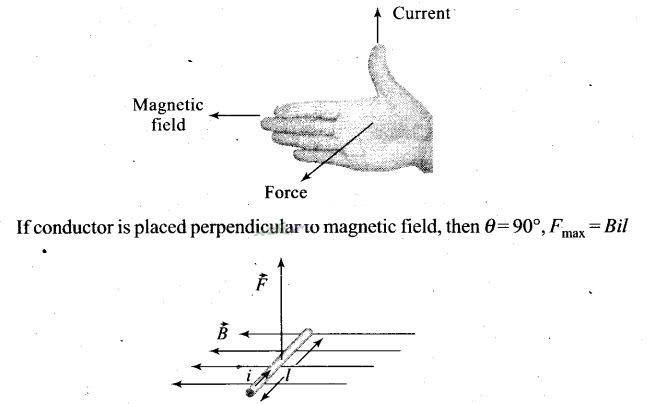

Question 9. Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C,
(a) ФBdl =mμ₀I
(b) the value of  ФB.dl = ±2μ₀I is independent of sense of C
(c) there may be a point on C where, B and dl are perpendicular
(d) B vanishes everywhere on C
Solution: (b, c)
Key concept: Ampere’s law gives another method to calculate the magnetic field due to a given current distribution.

Question 10. A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters thq cube across one of its faces with velocity v and a positron enters via opposite face with velocity -v. At this instant,
(a) the electric forces on both the particles cause identical accelerations.
(b) the magnetic forces on both the particles cause equal accelerations.
(c) both particles gain or loose energy at the same rate.
(d) the motion of the Centre of Mass (CM) is determined by B alone.
Solution: (b, c, d)
Key concept: This problem is based upon the single moving charge placed with some uniform electric and magnetic fields in space. Then they experiences a force called Lorentz force is given by the relation F_net  =qE + q(v x B).
(i) The magnetic forces (F_m =q(v x B)), on charge particle is either zero or Fm is perpendicular to v (or component of v) which in turn revolves particles on circular path with uniform speed. In both the cases particles have equal accelerations.
(ii) Due to same electric force (F_e = qE) which is in opposite direction (because of sign of charge) both the particles gain or loss energy at the same rate.
(iii) There is no change of the Centre of Mass (CM) of the particles, therefore the motion of the Centre of Mass (CM) is determined by B alone.

Question 11. A charged particle would continue to move with a constant velocity in a region wherein,
(a) E = 0,B≠0 (b) E≠0,B≠0
(c) E≠0,B = 0 (d) E = 0, B = 0
Solution: (a, b, d)
Key concept: This problem is based upon the single moving charge placed with some uniform electric and magnetic fields in space. Then they experiences a force called Lorentz force is given by the relation F_net =qE + q(v x B).
Force experience by the charged particle due to electric field F_e = qE
Force experience by the charged particle due to magnetic field, F_m = q(v x B)
According to the problem, particle is moving with constant velocity means acceleration of particle is zero and also it is not changing its direction of motion.
This will happen when net force on particle is zero.
(i) if E = 0, and v || B, thenF_net = 0.
(ii) if E ≠ 0, B ≠ 0 and E, v and B are mutually perpendicular.
And (iii) when both E and B are absent.

Very Short Answer Type Questions

Question 12. Verify that the cyclotron frequency ω = eB/m has the correct dimensions of [T]^-1       .
Solution: In cyclotron, charge particle describes the circular path where magnetic force acts as centripetal force.

Question 13. Show that a force that does no Work must be a velocity dependent force.
Solution: To show that a force that does no work must be a velocity dependent force, then we have to assume that work done by force is zero. As shown by the equation below: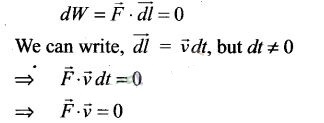

So we can say that force F must be velocity dependent, this implies that angle between F and v is 90°. If the direction of velocity changes, then direction of force will also change.

Question 14. The magnetic force depends on v which depends on the inertial frame of reference. Does then the magnetic force differ from inertial frame to frame? Is it reasonable that-the net acceleration has a different value indifferent frames of reference?
Solution: As F = q(v x B),velocity depends on frame of reference. Hence The magnetic force is frame dependent. So, yes the magnetic force differ from inertial frame to frame.
The net acceleration which a rising from this is however, frame independent for inertial frames (non-relativistic physics).

Question 15. Describe the motion of a charged particle in a cyclotron if the frequency of the radio frequency (rf) field were doubled.
Solution: The frequency va of the applied voltage (radio frequency) is adjusted so that the polarity of the dees is reversed in the same time that it takes the ions to complete one half of the revolution. The requirement v_a = v_c is called the resonance condition.
When the frequency of the radio frequency (rf) field were doubled, then the resonance condition are violated and the time period of the radio frequency (rf) field were halved. Therefore, the duration in which particle completes half revolution inside the dees, radio frequency completes the cycle.
So, particle will accelerate and decelerate alternatively. So, the radius of path in the dees will remain same.

Question 16. Two long wires carrying current I₁, and I₂ are arranged as shown in figure. The one carrying current I₁ is along the x-axis. The other carrying current I₂ is along a line parallel to the y-axis given by x = 0 and z = d. Find the force exerted at O₂ because of the wire along the x-axis.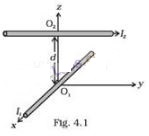

Solution:
Key concept: In this problem first we have to find the direction of magnetic field due to one wire at the point on other wire, then the magnetic force on that current carrying wire.
In Biot-Savart law, magnetic field B is parallel to ; dl x r and idl have its direction along the direction of flow of current, or we can find the direction of B with the help of right hand thumb rule.

Short Answer Type Questions

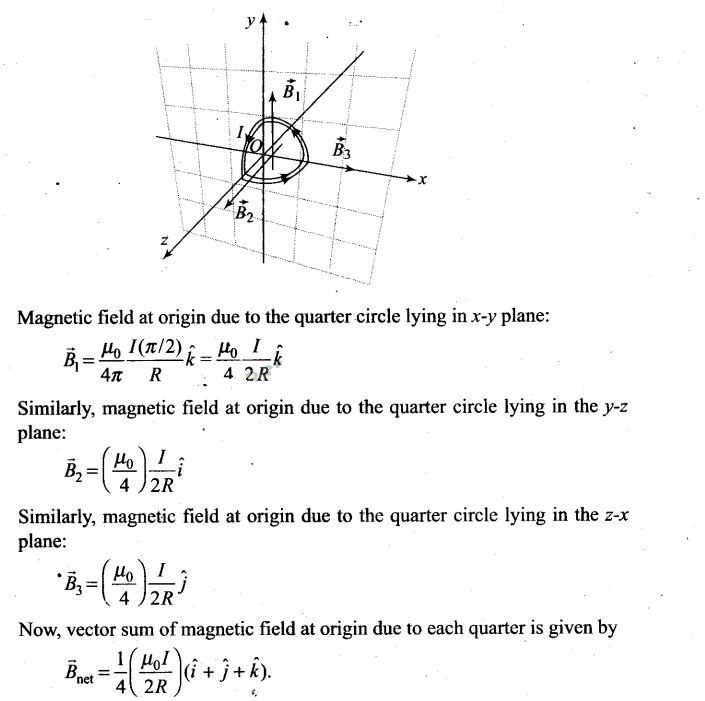
Question 17. A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.
Solution:
Key concept: From Biot-Savart law we find the relation of magnetic field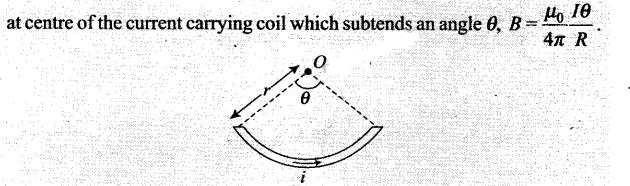

Question 18. A charged particle of charge e and mass m is moving in an electric field E and magnetic field B. Construct dimensionless quantities and quantities of dimension [T]^-1  .
Solution: If a charged particle is moving in electric and magnetic field, we cannot construct any dimensionless quantity with these physical quantities.
For a charged particle moving perpendicular to the magnetic field, the magnetic Lorentz forces provides necessary centripetal force for revolution.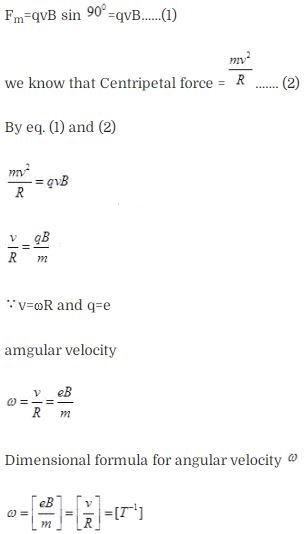

Question 19. An electron enters with a velocity v = v₀i into a cubical region (face parallel to coordinate planes) in which there are uniform electric and magnetic fields. The orbit of the electron is found to spiral down inside the cube in a plane parallel to the x-y plane. Suggest a configuration to fields E and B that can lead to it.
Solution:
Key concept: Due to magnetic force charge particle revolves in uniform circular motion in x-y plane and due to electric field charge particle increases the speed along x-directi on, which in turn increases the radius of circular path and hence, particle traversed on spiral path.
Let us consider a magnetic field B = B₀ present in the region and an electron enters with a velocity into cubical region (faces parallel to coordinate planes). The force on electron, using magnetic Lorentz force, is given by

which revolves the electron in x-y plane.
The electric force F = eE₀j accelerates e along z-axis which in turn increases the radius of circular path and hence particle traversed on spiral path.

Question 20. Do magnetic forces obey Newton’s third law. Verify for two current elements dl₁ = dl i located at the origin and dl₂ = dl j located at(0, R, 0). Both carry current I.
Solution:
Key concept: In this problem first we have to find the direction of magnetic field due to one wire at the point on other wire, then the magnetic force on that current carrying wire.
According to Biot-Savart’s law, magnetic field B is parallel to idl x r and idl is the current carrying element having its direction along the direction of flow of current.
Here, for the direction of magnetic field, at dl2, located at (0, R, 0) due to wire dlx is given by B || idl x r or i xj (because point (0, R, 0) lies ony-axis), but i x j = k.
So, the direction of magnetic field at dl2 is along z-direction.
The direction of magnetic force exerted at dl2 due to the magnetic field of first wire is along the x-axis.
F-i(l X B), i.e., F||(i x k) or along – j direction.
Therefore, force due to dl[ on dl2 is non-zero.
Now, for the direction of magnetic field, at dx, located at (0, 0, 0) due to wire d2 is given by B||idl x r or j x – j (because origin lies on y-direction w.r.t. point (0, R, 0), but j x – j = 0.
So, the magnetic field at dx does not exist.
Force due to dl₂ on dl₁, is zero.
So, magnetic forces do not obey Newton’s third law. But they obey Newton’s third law if current carrying element are placed parallel to each other.

Question 21.

A multirange voltmeter can be constructed by using a galvanometer circuit as shown in figure. We want to construct a voltmeter that can measure 2 V, 20 V and 200 V using a galvanometer of resistance 10 Ω and that produces maximum deflection for current of 1 mA. Find R₁, R₂ and R₃ that have to be used,
Solution:
Key concept: The galvanometer can also be used as a voltmeter to measure the voltage across a given section of the circuit. For this a very high resistance wire is to be connected in series with galvanometer. The relationship is given by I_g (G + R) – V where I_g is the range of galvanometer, G is the resistance of galvanometer and R is the resistance of wire connected in series with galvanometer.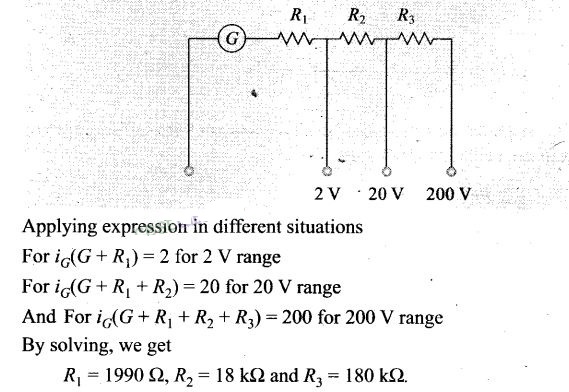

Question 22. A long straight wire carrying current of 25 A rests on a table as shown in figure. Another wire PQ of length 1 m, mass 2.5 g carries the same current but in the opposite direction. The wire PQ is free to slide up and down. To what height will PQ rise?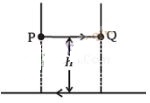

Solution:
Key concept: The force applied on PQ by a long straight wire carrying current of 25 A which rests on a table. And the forces which other are repulsive if two straight wires are placed parallel to each other carrying current in opposite direction. Now if the wire PQ is in equilibrium then that repulsive force onPQ must balance its weight.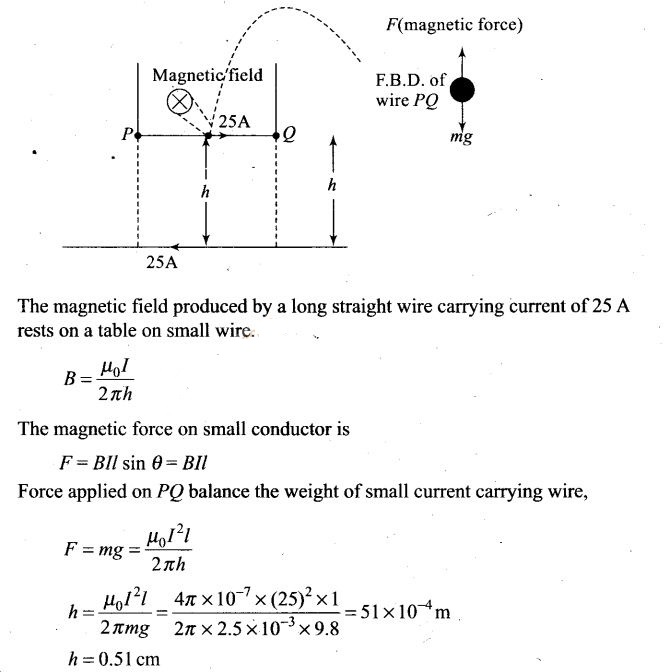

Long Answer Type Questions

Question 23.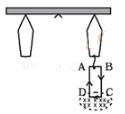

A 100 turn rectangular coil ABCD (in X-Y plane) is hung from one arm of a balance (shown in figure). A mass 500 g is added to the other arm to balance the weight of the coil. A current 4.9 A passes through the coil and a constant magnetic field of 0.2 T acting inward (in x-z plane) is switched on such that only arm CD of length 1 cm lies in the field. How much additional mass m must be added to regain the balance?
Solution:
Key concept: Here we use the concept of magnetic force on straight current carrying conductor placed in the region of external uniform magnetic field. The magnetic force exerted on CD due to external magnetic field must balance its weight.
And spring balance to be in equilibrium net torque should also be equal to zero.

Question 24. A rectangular conducting loop consists of two wires on two opposite sides of length l joined together by rods of length d. The wires each are of the same material but with cross-sections differing by a factor of 2. The thicker wire has a resistance R and the rods are of low resistance, which in turn are connected to a constant voltage source V₀. The loop is placed in a uniform magnetic field B at 45° to its plane. Find T, the torque exerted by the magnetic field on the loop about an axis through the centres of rods.
Solution: After analyzing the direction of current in both wires, magnetic forces and torques need to be calculated for finding the net torque.

Question 25. An electron and a positron are released from (0, 0, 0) and (0, 0, 1.5R) respectively, in a uniform magnetic field B = B₀i, each with an equal momentum of magnitude p = eBR. Under what conditions on the direction of momentum will the orbits be non-intersecting circles?
Solution: The magnetic field B is along the x-axis, hence for a circular orbit the momenta of the two particles are in the y-z plane. Let p₁ and p₂ be the momentum of the electron (e^– ) and positron (e⁺), respectively. Both traverse a circle of radius R of opposite sense. Let p, make an angle θ with they-axis p₂ must make the same angle withy axis.
The centres of the respective circles must be perpendicular to the momenta and at a distance R. Let the centre of the electron be at C_e and of the positron at C_p.
The coordinates of C_e is C_e = (0, -R sin θ, R cos θ)
The coordinates of C_p is C_p = [0, -R sin θ, (1.5R – R cos θ)]

Question 26. A uniform conducting wire of length 12a and resistance R is wound up as a current carrying coil in the shape of (i) an equilateral triangle of side a, (ii) a square of sides a, and (iii) a regular hexagon of sides a. The coil is connected to a voltage source V₀. Find the magnetic moment of the coils in each case.
Solution:
Key concept: In this problem different shapes form figures of different area and the number of loops in each case is different and hence, there magnetic moments varies.
Magnetic moment is m = nlA.
Since, the same wire is used in three cases with same potentials, therefore, same current flows in three cases.

Question 27. Consider a circular current-carrying loop of radius R in the x-y plane with centre at origin. Consider the line integral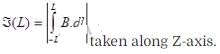

Solution: (a) Magnetic field due to a circular current-carrying loop lying in the xy- plane acts along z-axis as shown in figure.

Question 28. A multirange current meter can be constructed by using a galvanometer circuit as shown in figure. We want a current meter that can measure 10 mA, 100 mA and 1 mA using a galvanometer of resistance 10 Ω and that produces maximum deflection for current of 1 mA. Find S₁ ,S₂ and S₃ that have to be used.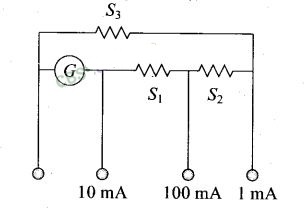

Solution:
Key concept: A galvanometer can be converted into ammeter by connecting a very low resistance wire (shunt S) connected in parallel with galvanometer. The relationship is given by I_gG = (I – I_g) S, whereI_g is the range of galvanometer, G is the resistance of galvanometer.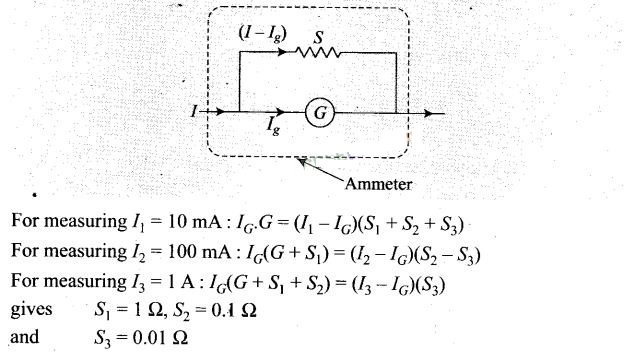

Question 29.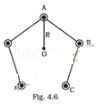

Five long wires A, B, C, D and E, each carrying current I are arranged to form edges of a pentagonal prism as shown in figure. Each carries current out of the plane of paper.
(a) What will be magnetic induction at a point on the axis 0? Axis is at a distance R from each wire.
(b) What will be the field if current in one of the wires (say A) is switched off?
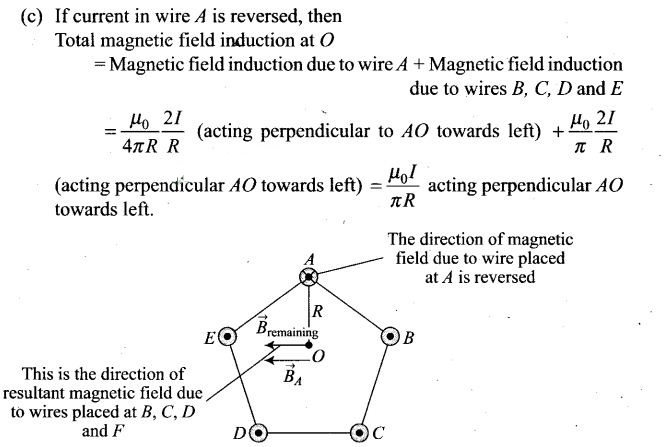
(c) What if current in one of the wire (say A) is reversed?
Solution: (a)
Key concept: The wires shown in this problem carrying current outwards to the plane. And we know that direction of magnetic field is perpendicular to both current and position vector r. So, the vector sum of magnetic field produced by each wire at O is equal to 0.
Suppose the five wires A, B, C, D and E be perpendicular to the plane of paper at locations as shown in figure.
Thus, magnetic field induction due to five wires will be represented by various sides of closed pentagon in one order, lying in the plane of paper. So, its value is zero.