Electrostatic Potential and Capacitance

Multiple Choice Questions

Single Correct Answer Type

Question 1.
A capacitor of 4 μF is connected as shown in the circuit. The internal resistance of the battery is 0.5 Ω. The amount of charge on the capacitor plates will be

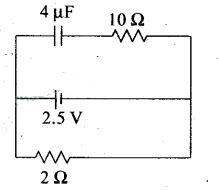
(a) 0 (b) 4 μC
(c) 16 μC (d) 8 μC
Solution: (d)
Key concept: A capacitor offers zero resistance in a circuit when it is uncharged, i.e., it can be assumed as short circuited and it offers infinite resistance when it is fully charged.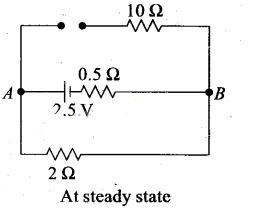

At steady state the capacitor offers infinite resistance in DC circuit and acts as open circuit as shown in figure, therefore no current flows through the capacitor and 10 Ω resistance, leaving zero potential difference across 10 Ω resistance. Hence potential difference across capacitor will be the potential difference across A and B.
The potential difference across lower and middle branch of circuit is equal to the potential difference across capacitor of upper branch of circuit.
Current flows through 2 Ω resistance from left to right, is given by I=v/R+r=1A.The potential difference across 2Ω resistance, V=IR= 1 x 2 = 2V Hence potential difference across capacitor is also 2 V.
The charge on capacitor is q = CV= (2 μF) x 2 V = 8 μC.

Question 2.  A positively charged particle is released from rest in an uniform electric field. The electric potential energy of the charge
(a) remains a constant because the electric field is uniform
(b) increases because the charge moves along the electric field
(c) decreases because the charge moves along the electric field
(d) decreases because the charge moves opposite to the electric field
Solution: (c)
Key concept: Electric potential decreases in the direction of electric field. The direction of electric field is always perpendicular to one equipotential surface maintained at high electrostatic potential to other equipotential surface maintained at low electrostatic potential.
The positively charged particle experiences electrostatic force along the direction of electric field, hence moves in the direction of electric field. Thus, positive work is done by the electric field on the charge .We know

Hence electrostatic potential energy of the positive charge decreases.

Question 3. Figure shows some equipotential lines distributed in space. A charged object is moved from point A to point B.
(a) The work done in Fig. (i) is the greatest.
(b) The work done in Fig. (ii) is least.
(c) The work done is the same in Fig. (i), Fig.(ii) and Fig. (iii).
(d) The work done in Fig. (iii) is greater than Fig. (ii) but equal to that in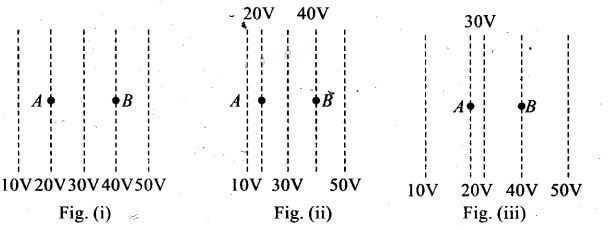

Solution: (c)
Key concept: For a given charge distribution, locus of all points or regions for which the electric potential has a constant value are called equipotential regions. Such equipotential can be surfaces, volumes or lines. Regarding equipotential surface the following points should be kept in mind:
• The density of the equipotential lines gives an idea about the magnitude of electric field. Higher the density, larger the field strength.
• The direction of electric field is perpendicular to the equipotential surfaces or lines.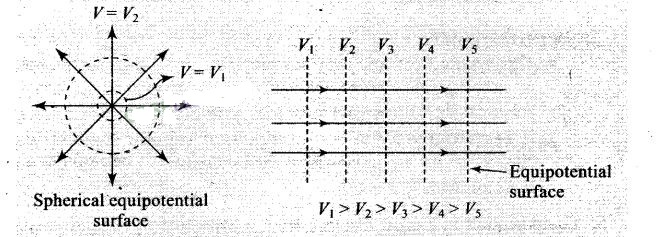

• The equipotential surfaces produced by a point charge or a spherically charge distribution are a family of concentric spheres.
• For a uniform electric field, the equipotential surfaces are a family of plane perpendicular to the field lines.
• A metallic surface ofany shape is an equipotential surface.
• Equipotential surfaces can never cross each other.
• The work done in moving a charge along an equipotential surface is always zero.
As the direction of electric field is always perpendicular to one equipotential surface maintained at high electrostatic potential than other equipotential surface maintained at low electrostatic potential. Hence direction of electric field is from B to A in all three cases.
The positively charged particle experiences electrostatic force along the direction of electric field, hence moves in the direction opposite to electric field. Thus, the work done by the electric field on the charge will be negative. We know

Here initial and final potentials are same in all three cases and same charge is moved, so work done is same in all three cases.

Question 4. The electrostatic potentiaLon the surface of a charged conducting sphere is 100 V. Two statements are made in this regard.
S₁ : At any point inside the sphere, electric intensity is zero.
S₂: At any point inside the sphere, the electrostatic potential is 100 V.
Which of the following is a correct statement?
(a) S₁ is true but S₂ is false
(b) Both S₁ and S₂ are false
(c) S₁ is true, S₂ is also true and 5, is the cause of S₂
(d) S₂ is true, S₂ is also true but the statements are independent
Solution: (c) We know, the electric field intensity E and electric potential V are related
E=dV/dr
If electric field intensity  E= 0, then  dV/dr = 0.  It means, E = 0 inside the charged conducting sphere causes uniform potential inside the sphere. Hence uniform electrostatic potential 100 V will be at any point inside the sphere.
Important points:
• The electric field zero does not necessary imply that electric potential is zero. E.g., the electric field intensity at any point inside the charged spherical shell is zero but there may exist non-zero electric potential.
• If two charged particles of same magnitude but opposite sign are
placed, the electric potential at the midpoint will be zero but electric field is not equal to zero. *

Question 5. Equipotentials at a great distance from a collection of charges whose total sum is not zero are approximately
(a) spheres (b) planes
(c) paraboloids (d) ellipsoids
Solution: (a) The collection of charges, whose total sum is not zero, with regard to great distance can be considered as a single point charge. The equipotential surfaces due to a point charge are spherical.
Important point:
The electric potential due to point charge q is given by V=q/4πϵ₀r
It means electric potential due to point charge is same for all equidistant points. The locus of these equidistant points, which are at same potential, form spherical surface.

Question 6. A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d₁ and dielectric constant K₁ and the other has thickness d₂ and dielectric constant K₂ as shown in figure. This arrangement can be thought as a dielectric slab of thickness d (= d₁ + d₂) and effective dielectric constant K. Then K is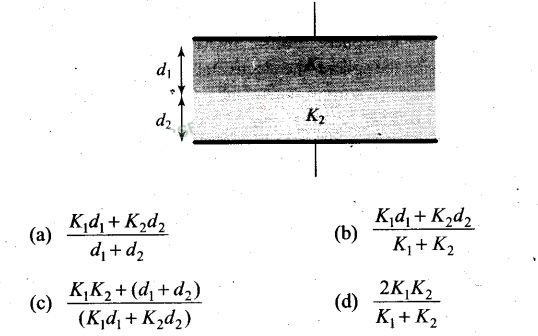

Solution: (c) Here the system can be considered as two capacitors C₁ and C₂ connected in series as shown in figure.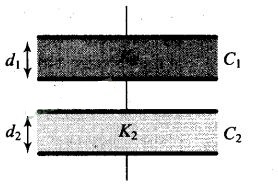

The capacitance of parallel plate capacitor filled with dielectric block has thickness d₁ and dielectric constant K₂ is given by

One or More Than One Correct Answer Type

Question 7. Consider a uniform electric field in the z -direction. The potential is a constant
(a) in all space (b) for any x for a given z
(c) for any y for a given z (d) on the x-y plane for a given z
Solution: (b c, d) We know, the electric field intensity E and electric potential V are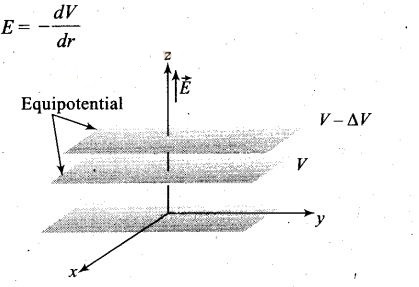

Electric potential decreases inf the direction of electric field. The direction of electric field is always perpendicular to one equipotential surface maintained at high electrostatic potential to other equipotential surface maintained at low electrostatic potential.
The electric field in z-direction suggest that equipotential surfaces are in x-y plane. Therefore the potential is a constant for any x for a given z, for any y for a given z and on the x-y plane for a given z.

Question 8. Equipotential surfaces
(a) are closer in regions of large electric fields compared to regions of lower electric fields
(b) will be more crowded near sharp edges of a conductor
(c) will be more crowded near regions of large charge densities
(d) will always be equally spaced
Solution: (a, b, c)
Key concept: The density of the equipotential lines gives an idea about the magnitude of electric field. Higher the density, larger the field strength.
We know, the electric field intensity E and electric potential V are related as

Hence the electric field intensity E is inversely proportional to the separation between equipotential surfaces. So, equipotential surfaces are closer in regions of large electric fields.
As electric field intensities is large near sharp edges of charged conductor and near regions of large charge densities. Therefore, equipotential surfaces are closer at such places.

Question 9. The work done to move a charge along an equipotential from A to B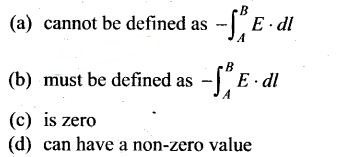

Solution: (b, c)
Key concept: The work done by the external agent in shifting the test charge along the dashed line from 1 to 2 is

Question 10. In a region of constant potential
(a) the electric field is uniform
(b) the electric field is zero
(c) there can be no charge inside the region
(d) the electric field shall necessarily change if a charge is placed outside the region
Solution: (b, c) We know, the electric field intensity E and electric potential V are dV
related as E =- dV/dr
or we can write |E|=ΔV/Δr
The electric field intensity E and electric potential V are related as E = 0 and for V = constant,dV/dr=0 this imply that electric field intensity E = 0.
If some charge is present inside the region then electric field cannot be zero at that region, for this V = constant is not valid.

Question 11.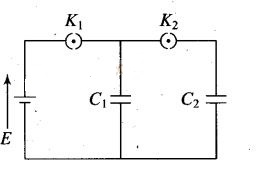

In the circuit shown in figure initially key K₁ is closed and key K₂ is open. Then K₁ is opened and K₂ is closed (order is important).
[Take Q’₁ and Q’₂ as charges on C₁ and C₂ and V₁ and V₂ as voltage respectively.]
Then, E
(a) charge on C, gets redistributed such that V₁ = V₂
(b) charge on C₁ gets redistributed such that Q’₁ = Q’₂
(c) charge on C₁ gets redistributed such that C₁V₁ + C₂V₂ = C₁E
(d) charge on C₁ gets redistributed such that Q’₁ + Q’₂=Q
Solution: (a, d) Initially key K₁ is closed and key K₂ is open, the capacitor C₁ is charged by battery and capacitor C₂ is still uncharged. Now K₁ is opened and K₂ is closed, the capacitors C₁ and C₂ both are connected in parallel. The charge stored by capacitor C₁, gets redistributed between C₁ and C₂ till their potentials become same, i.e., V₂ = V₁.
By law of conservation of charge, the charge stored in capacitor Cx is equal to sum of charges on capacitors C₁ and C₂ when K₁ is opened and K₂ is closed, i.e.,
Q’₁+Q’₂=Q

Question 12. If a conductor has a potential V≠0 and there are no charges anywhere else outside, then 
(a) there must be charges on the surface or inside itself
(b) there cannot be any charge in the body of the conductor
(c) there must be charges only on the surface
(d) there must be charges inside the surface
Solution: (a, b) The potential of a body is due to charge of the body and due to the charge of surrounding. If tfiere are no charges anywhere else outside, then the potential of the body will be due to its own charge. If there is a cavity inside a conducting body, then charge can be placed inside the body. Hence there must be charges on its surface or inside itself. Hence option (a) is correct. The charge resides on the outer surface of a closed charged conductor. Hence there cannot be any charge in the body of the conductor. Hence option (b) is correct.

Question 13.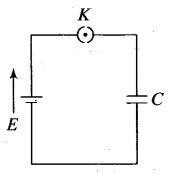

A parallel plate capacitor is connected to a battery as shown in figure. Consider two situations.
A. Key K is kept closed and plates of capacitors are moved apart using insulating handle.
B. Key K is opened and plates of capacitors are moved apart using insulating handle.
Choose the correct option(s).
(a) In A, Q remains the same but G changes
(b) In B, V remains the same but C changes
(c) In A, V remains the same hence Q changes
(d) In B ,Q remains the same hence V changes
Solution: (c, d) The battery maintains the potential difference across connected capacitor in every circumstance. However, charge stored by disconnected charged capacitor remains conserved.
Case A: When key K is kept closed and plates of capacitors are moved apart using insulating handle.
The battery maintains the potential difference across connected capacitor in every circumstance. The separation between two plates increases which in turn decreases its capacitance (C=ϵ₀A/d)and potential difference across
connected capacitor continue to be the same as capacitor is still connected with battery. Hence, the charge stored decreases as Q = CV.
Case B: When key K is opened and plates of capacitors are moved apart using insulating handle.
The charge stored by isolated charged capacitor remains conserved. The separation between two plates is increasing which in turn decreases its capacitance with the decrease of capacitance, potential difference V increases as V=Q/C.

Very Short Answer Type Questions

Question 14. Consider two conducting spheres of radii R₁ and R₂ with R₁ > R₂. If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whether the charge density of the smaller sphere is more or less than that of the larger one.
Solution: Since, the two spheres are at the same potential, therefore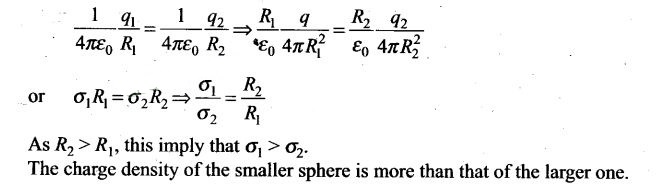

Question 15. Do free electrons travel to region of higher potential or lower potential?
Solution: The force on a charge particle in electric field F = qE
The free electrons (negative charge) experience electrostatic force in a direction opposite to the direction of electric field.
Thedirection of electric field is always from higher potential tolower. Hence direction of travel of electrons is from lower potential to region of higher potential.

Question 16. Can there be a potential difference between two adjacent conductors carrying the same charge?
Solution: Yes, if the sizes are different.
Explanation: We define capacitance of a conductor C = Q/V is the charge
of conductor and V is the potential of the conductor. For given charge potential V ∝ 1/C. The capacity of conductor depends on its geometry, so two adjacent conductors carrying the same charge of different dimensions may have different potentials.

Question 17. Can the potential function have a maximum or minimum in free space?
Solution: No, the potential function does not have a maximum or minimum in free
space, it is because the absence of atmosphere around conductor prevents the phenomenon of electric discharge or potential leakage.

Question 18.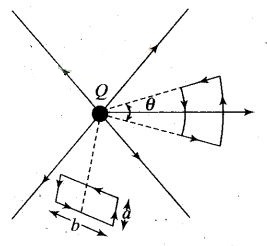

A test charge q is made to move in the electric field of a point charge Q along two different closed paths [figure first path has sections along and perpendicular to lines of electric field]. Second path is a rectangular loop of the same area as the first loop. How does the work done compare in the two cases?
Solution: Work done will be zero in both the cases.
Explanation: The electrostatic field is conservative, and in this field work done by electric force on the charge in a closed loop is zero. In this question both are closed paths, hence the work done in both the cases will be zero.

Short Answer Type Questions

Question 19. Prove that a closed equipptential surface with no charge within itself must enclose an equipotential volume.
Solution: Let us assume that in a closed equipotential surface with no charge the potential is changing from position to position. Let the potential just inside the surface is different to that of the surface causing in a potential gradient (dV/dr)
It means E ≠ 0 electric field comes into existence, which is given by as E=-dV/dr
It means there will be field lines pointing inwards or outwards from the surface. These lines cannot be again on the surface, as the surface is equipotential. It is possible only when the other end of the field lines are originated from the charges inside. This contradicts the original assumption. Hence, the entire volume inside must be equipotential.

Question 20. A capacitor has some dielectric between its plates and the capacitor is connected to a DC source. The battery is now disconnected and then the dielectric is removed. State whether the capacitance, the energy stored in it, electric field, charge stored and the voltage will increase, decrease or remain constant.
Solution: The capacitance of the parallel plate capacitor, filled with dielectric medium of dielectric constant K is given by     C=K ϵ₀A/d
The capacitance of the parallel plate capacitor decreases with the removal of dielectric medium as for air or vacuum K = 1 and for dielectric K > 1.
If we disconnect the battery from capacitor, then the charge stored will remain the same due to conservation of charge.
The energy stored in an isolated charge capacitor  U =q²/2C  as q is constant, energy stored U ∝ 1/C .As C decreases with the removal of dielectric medium, therefore energy stored increases.
The potential difference across the plates of the capacitor is given by V =q/C
Since q is constant and C decreases which in turn increases V and therefore E increases as E = V/d.
Important point: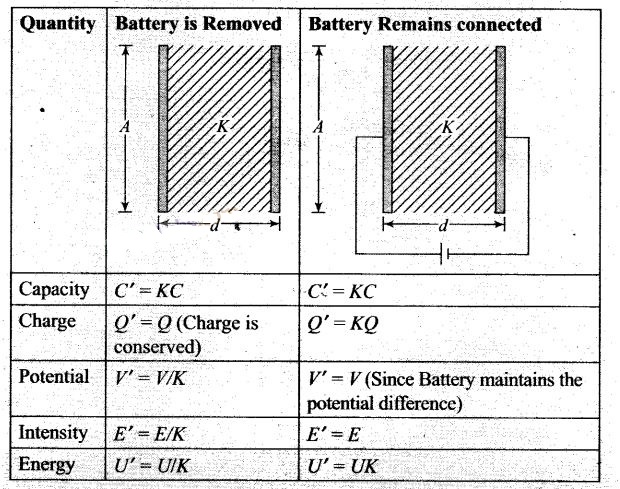

Question 21. Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must intermediate in potential between that of the charged body and that of infinity. 
Solution: The electric field E = dV/dr suggests that electric potential decreases along the direction of electric field.
Let us take any path from the eharged’conductor to the uncharged conductor along the direction of electric field. Therefore, the electric potential decrease along this path.
Now, another path from the uncharged conductor to infinity will again continually lower the potential further. This ensures that the uncharged body must be intermediate in potential between that of the charged body and that of infinity.

Question 22. Calculate potential energy of a point charge -q placed along the axis due to a charge +Q uniformly distributed along a ring of radius R. Sketch PE, as a function of axial distance z from the centre of the ring. Looking at graph, can you see what would happen if -q is displaced slightly from the centre of the ring (along the axis)?
Solution: The potential energy (U) of a point charge q placed at-potential V,U=qV In our case a negative charged particle is placed at the axis of a ring having charge Q. Let the ring has radius a,the electric potential at an axial distance z from the centre of the ring is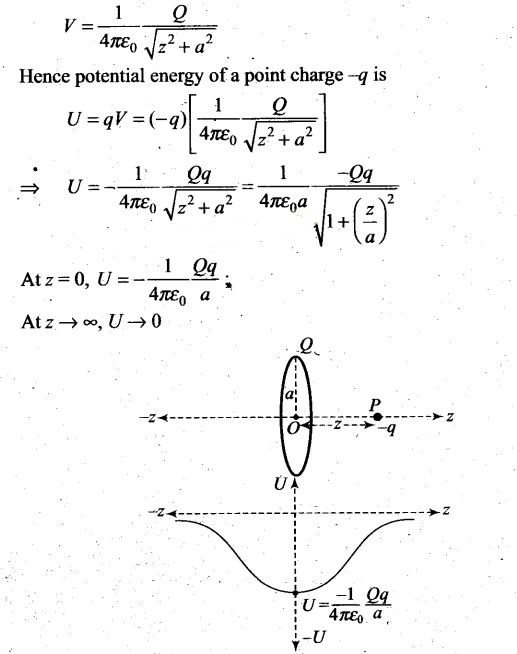

The variation of potential energy with z is shown in the figure.
The charge -q displaced would perform oscillations. Nothing can be concluded just by looking at the graph.

Question 23. Calculate the potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
Solution:

Long Answer Type Questions

Question 24. Find the equation of the equipotentials for an infinite cylinder of radius r0 carrying charge of linear density A.
Solution: We know the integral relation between electric field gives potential difference between two points.
The electric field due to line charge need to be obtained in order to find the potential at distance r from the line chaige. For this we need to apply Gauss’ theorem.
Let the field lines must be radically outward. Draw a cylindrical Gaussian surface of radius r and length l.

>

Question 25. Two point charges of magnitude +q and -q are placed at (-d/2, 0, 0) and (d/2, 2, 0), respectively. Find the equation of the equipotential surface where the potential is zero.
Solution: Let the required plane lies at a distance x from the origin as shown in figure.

Question 26. A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as ε= αU where α = 2V^-1. A similar capacitor with no dielectric is charged to U₀ = 78 V. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.
Solution: Both capacitors will be connected in parallel, hence the potential difference across both capacitors should be same. Assuming the required final voltage. be U. If C is the capacitance of the capacitor without the dielectric, then the charge on the capacitor is given by Q₁ = CU.
As the capacitor with the dielectric has a capacitance εC. Hence, the charge on the capacitor is given by

Question 27. A capacitor is made of two circular plates of radius R each, separated by a , distance d << R. The capacitor is connected to a constant voltage. A thin
conducting disc of radius r << R and thickness t << r is placed at the centre of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m.
Solution: Initially the thin conducting’disc is placed at the centre of the bottom plate, the potential of the disc will be equal to potential of the disc. The disc will be lifted if weight is balanced by electrostatic force.
The electric field on the disc, when potential difference V is applied across it

Question 28. (a) In a quark model of elementary particles, a neutron is made of one up quarks [charge (2/3)e] and two down quarks [charges (-l/3)e]. Assume that they have a triangle configuration with side length of the order of 10^-15 m. Calculate electrostatic potential energy of neutron and compare it with its mass 939 MeV.
(b) Repeat above exercise for a proton which is made of two up and one down quark.
Solution: This system is made up of three charges. The potential energy of the system is equal to the algebraic sum of PE of each pair. So,

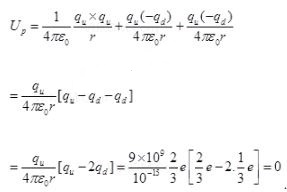
Question 29. Two metal spheres, one of radius R and the other of radius 2R, both have same surface charge density σ. They are brought in contact and separated. What will be the new surface charge densities on them?
Solution: The charges on metal spheres before contact, are

Question 30. In the circuit shown in figure, initially K₁ is closed and K₂ is open. What are the charges on each capacitors?
Then K₁ was opened and K₂ was closed (order is important), what will be the charge on each capacitor now? [C = 1 μF]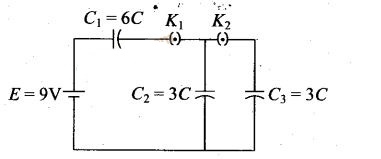

Solution: In the circuit, when initially K₁ is closed and K₂ is open, the capacitors C₁ and C₂ connected in series with battery acquire equal charge.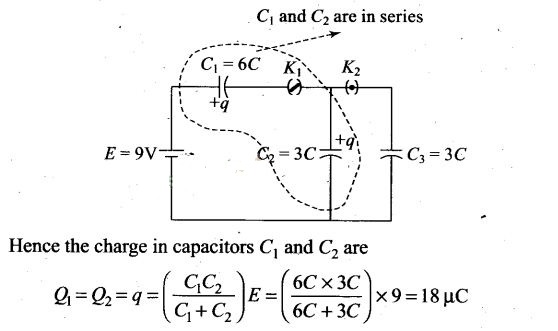

Hence the charge in capacitors C₁ and C₂ are
Henee Q₁ = Q₂ = 18 μC and Q₃ = 0
Now K₁ was opened and K₂ was closed, the battery and capacitor C, are disconnected from the circuit .The charge in capacitor C, will remain constant equal to Q₁ – Q₂ = 18 μC . The charged capacitor C₂ now connects in parallel with uncharged capacitor C₃, considering common potential of parallel combination as V.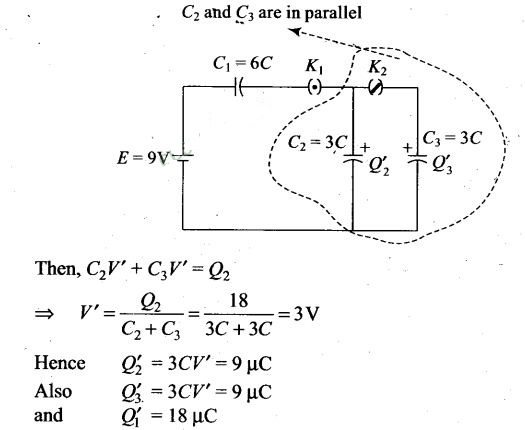

Question 31. Calculate potential on the axis of a disc of radius R due to a charge Q uniformly distributed on its surface.
Solution:

Question 32. Two charges q₁ and q₂ are placed at (0, 0, d) and (0, 0, -d) respectively. Find
the locus of points where the potential is zero.
Solution:
Key concept: Following the principle of superposition of potentials as
described in last section, let us find the potential V due to a collection of
discrete point charges q₁, q₂, …,q_n, at a point P.

Question 33.

Solution: