Nuclei

Multiple Choice Questions (MCQs)

Single Correct Answer Type

Question 1. Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year,
(a) all the containers will have 5000 atoms of the material
(b) all the containers will contain the same number of atoms of the material but that number will only be approximately 5000
(c) the containers will in general have different numbers of the atoms of the material but their average will be close to 5000
(d) none of the containers can have more than 5000 atoms
Solution: (c)
Key concept: Half life ( T_1/2):
Radioactivity is a process due to which a radioactive material spontaneously decays. Time interval in which the mass of a radioactive substance or the number of its atom reduces to half of its initial value is called the half life of the substance.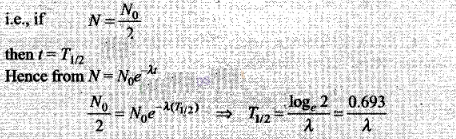

In half-life (t= 1 yr) of the material on the average half the number of atoms will decay. Therefore, the containers will in general have different number of atoms of the material, but their average will be approx 5000.

Question 2. The gravitational force between a H-atom and another particle of mass m will

Solution: (b)
Key concept: The gravitational force between a H-atom and another
particle of mass m will be given by Newton’s law, F = G M.m/r²
Here M is the effective mass of Hydrogen atom.
Let us learn how to find the effective mass of a Hydrogen atom.
Suppose you start with a proton and an electron separated by a large distance. The mass of this system is just m_proton + m_electron.
Now let the proton and electron fall towards each other under their mutual electrostatic attraction. As they fall they will speed up, so by the time the  proton and electron are about one hydrogen atom radius apart they are moving with a high speed. Note that we haven’t added or removed any energy, so the mass/energy of the system is still  m_proton + m_electron.
The trouble is that this would not form a hydrogen atom because the proton and electron will just speed past each other and fly away again. To form a hydrogen atom we have to take the kinetic energy of the electron and proton out of the system so we can bring them to a stop. Let’s call the kinetic energy E_k. This energy has a mass given by Einstein’s famous equation E = mc², so die mass of our atom is the mass we started with less the energy we’ve taken out:

Question 3. When a nucleus in an atom undergoes a radioactive decay, the electronic energy levels of the atom
(a) do not change for any type of radioactivity
(b) change for α and β-radioactivity but not for γ-radioactivity
(c) change for α -radioactivity but not for others
(d) change for β-radioactivity but not for others
Solution: (b)
Key concept:

A /3-particle carries one unit of negative charge (-e), an α-particle carries 2 units of positive charge (+ 2e ) and γ (particle) carries no charge. Hence electronic energy levels of the atom charges for α and β decay, but not for γ-decay.

Question 4. M_x and M_y denote the atomic masses of the parent and the daughter nuclei respectively in a radioactive decay. The Q-value for a β^– decay is Q₁ and that for a β⁺decay is Q₂. If me denotes the mass of an electron, then which of the following statements is correct?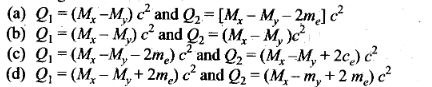

Solution: (a)
Key concept: Q value or energy of nuclear reaction: The energy absorbed or released during a nuclear reaction is known as Q-value of nuclear reaction.
Q-value = (Mass of reactants – mass of products)c² Joules
= (Mass of reactants – mass of products) amu
If Q < 0, the nuclear reaction is known as endothermic. (The energy is absorbed in the reaction)
If Q > 0, the nuclear reaction is known as exothermic. (The energy is released in the reaction)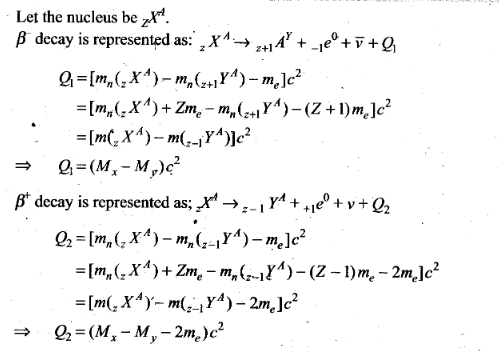

Question 5. Tritium is an isotope of hydrogen whose nucleus triton contains 2 neutrons and 1 proton. Free neutrons decay into p + e + n . If one of the neutrons in Triton decays, it would transform into He³ nucleus. This does not happen. This is because
(a) Triton energy is less than that of a He³ nucleus
(b) The electron created in the beta decay process cannot remain in the nucleus
(c) Both the neutrons in triton have to decay simultaneously resulting in a nucleus with 3 protons, which is not a He³ nucleus.
(d) Free neutrons decay due to external perturbations which is absent in triton nucleus .
Solution: (a)

Question 6. Heavy stable nuclei have more neutrons than protons. This is because of the fact that .
(a) neutrons are heavier than protons
(b) electrostatic foree between protons are repulsive
(c) neutrons decay into protons through beta decay
(d) nuclear forces between neutrons are weaker than that between protons
Solution: (b)

Question 7. In a nuclear reactor, moderators slow down the neutrons which come out in a fission process. The moderator used have light nuclei. Heavy nuclei will not serve the purpose, because
(a) they will break up
(b) elastic collision of neutrons with heavy nuclei will not slow them down
(c) the net weight of the reactor would be unbearably high
(d) substances with heavy nuclei do not occur in liquid or gaseous state at room temperature
Solution: (b)
Key concept: A moderator is a material used in a nuclear reactor to slow down the neutrons produced from fission. By slowing the neutrons down the probability of a neutron interacting with Uranium-235 nuclei is greatly increased thereby maintaining the chain reaction. Moderators are made from materials with light nuclei which do not absorb the neutrons but rather slow them down by a series of collisions.
The moderator only slows neutrons down in order to increase the interaction with Uranium nuclei. They do not give any protection if the reaction goes out of control. 1 fa chain reaction is heading out of control the reactors needs to be able to reduce the concentration of neutrons. For this the reactor uses control rods. Control rods are matte from material with the ability to absorb neutrons. Cadmium and Boron are examples of suitable materials. By inserting.control rods between the fuel rods the chain reaction can be slowed dowp-or shut down. Withdrawing the control rods can restart or speed up the reaction.
In our given question, the moderator used have light nuclei (like proton). When protons undergo perfectly elastic collision with the neutron emitted their velocities are exchanged, i.e., neutrons come to rest and protons move with the velocity of neutrons.
Heavy nuclei will not serve the purpose because elastic collisions of neutrons with heavy nuclei will not slow them down.

One or More Than One Correct Answer Type

Question 8. Fusion processes, like combining two deuterons to form a He nucleus are impossible at ordinary temperatures and pressure. The reasons for this can be traced to the fact
(a) nuclear forces have short range
(b) nuclei are positively charged
(c) the original nuclei must be completely ionized before fusion can take place
(d) the original nuclei must first break up before combining with each other
Solution: (a, b)
Key coneept:
Nuclear Fusion: In nuclear fusion two or more than two lighter nuclei combine to form a single heavy nucleus. The mass of a single nucleus so formed is less than the sum of the masses of parent nuclei. This difference in mass results in the release of tremendous amount of energy To achieve fusion, you need to create special conditions to overcome this tendency.
Here are the conditions that make fusion possible:
High Temperature: The high temperature gives the hydrogen atoms enough energy to overcome the electrical repulsion between the protons.
• Fusion requires temperatures about 100 million Kelvin (approximately six times hotter titan the sun’s core).
• At these temperatures, hydrogen is a plasma, not a gas. Plasma is a high-energy state of matter in which all the electrons are stripped from atoms and move freely about.
• The sun achieves these temperatures by its large mass and the force of gravity compressing this mass in the core. We must use energy from microwaves, lasers and ion particles to achieve these temperatures.
High pressure: Pressure squeezes the hydrogen atoms together. They must be within 1 x 10^-15 metres of each other to fuse.
• The sun uses its mass and the force of gravity to squeeze hydrogen atoms together in its core.
• We must squeeze hydrogen atoms together by using intense magnetic fields, powerful lasers or ion beams.
Fusion processes are impossible at ordinary temperatures and pressures. The reason is that nuclei are positively charged and nuclear forces are short range strongest forces. In order to force two hydrogen nuclei together, we need to have a very high pressure, or a very high temperature, or both. A high pressure helps because it causes all the hydrogen nuclei in the sun to squeeze into a smaller space. Then there is more chance of one hydrogen bumping into another. A high temperature helps because it makes the hydrogen nuclei move faster. They need this extra speed so that they can get close together and join. It is as if the nucleus has to break through a barrier, and so the faster it is moving, the greater chance it has.
So, at the “normal” temperature and pressure on earth, a hydrogen nucleus has basically no chance of ever joining with another hydrogen nucleus.
Important point: We know that in the middle of the sun, where the temperature is about 16 million degrees, and the pressure is 250 billion atmospheres, hydrogen nuclei will sometimes have enough energy to join together. (An atmosphere is the “normal”, pressure of the air here on earth. A pressure of 250 billion atmospheres is like having a large mountain piled on top of you!)

Question 9. Samples of two radioactive nuclides A and B are taken. λ_A and λ_B are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
(a) Initial rate of decay of A is twice the initial rate of decay of B and λ_A = λ_B
(b) Initial rate of decay of A is twice the initial rate of decay of B and λ_A > λ_B
(c) Initial rate of decay of B is twice the initial rate of decay of A and  λ_A > λ_B
(d) Initial rate of decay of B is same as the rate of decay of A at t = 2h and  λ_A < λ_B
Solution: (b, d)
Key concept:
Law of radioactive disintegration : According to Rutherford and Soddy law for radioactive decay is as follows:
“At any instant the rate of decay of radioactive atoms is proportional to the number of atoms present at that instant.” i.e.
dN/dt ∞ N => dN/dt = -λN
it can be proved that N=N₀e^-λ1          
In terms of mass M— M₀e^-λ1   
where N = Number of atoms remains undecayed after time t,
N₀ = Number of atoms present initially (i.e., at t = 0),
M = Mass of radioactive nuclei at time t,
M₀ = Mass ofradioactive nuclei at time t = 0,
N₀-N= Number of disintegrated nucleus in time t,
dN/dt= rate of decay, λ = Decay constant or disintegration constant or radioactivity constant or Rutherford Soddy’s constant or the probability of decay per unit time of a nucleus.
The samples of the two radioactive nuclides A and B can simultaneously have the same decay rate at any time if initial rate of decay of A is twice the initial rate of decay of B and λ_A > λ_B.
Also, when initial rate of decay of B is the same as rate of decay of A at t = 2h and λ_B < λ_A.

Question 10.

Solution:

Hence at point P, rate of decay for both A and B is the same.

Very Short Answer Type Questions

Question 11. He₂³ and He₁³ nuclei have the same mass number. Do they have the same binding energy?
Solution: The nuclei He₂³ and He₁³ have the same mass number. He₂³ has two protons and one neutron. He₂³ has one proton and two neutrons. As He3 has only one proton hence the repulsive force between protons is missing in ₁He³, so the binding energy of ₁He³ is greater than that of ₂He³.

Question 12. Draw a graph showing the variation of decay rate with number of active nuclei.
Solution:

Question 13. Which sample AoxB shown in figure has shorter mean-life?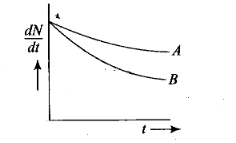

Solution:
Key concept:
Mean (or average) life (ґ) : The time for which a radioactive material remains active is defined as mean (average) life of that material.
• It is defined as the sum of lives of all atoms divided by the total number of atoms.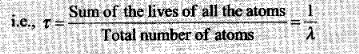



Question 14. Which one of the following cannot emit radiation and why? Excited nucleus, excited electron.
Solution:
Key concept: The energy of internal motion of a nucleus is quantized. A typical nucleus has a set of allowed energy levels, including a ground state (state of lowest energy) and several excited states. Because of the great strength of nuclear interactions, excitation energies of nuclei are typically of the order of the order of 1 MeV, compared with a few eV for atomic energy levels. In ordinary physical and chemical transformations the nucleus always remains in its ground state. When a nucleus is placed in an excited state, either by bombardment with high-energy particles or by a radioactive transformation, it can decay to the ground state by emission of one or more photons called gamma rays or gamma-ray photons, with typical energies of 10 keV to 5 MeV. This proceks is called gamma (γ) decay.
Excited electron cannot emit radiation because energy of electronic energy levels is in the range of eV and not MeV ( mega electron volt), y-radiations have energy of the order of MeV.

Question 15. In pair annihilation, an electron and a positron destroy each other to produce gamma radiations. How is the momentum conserved?
Solution: In pair annihilation, an electron and a positron destroy each other to produce 2yphotons which move in.opposite directions to conserve linear momentum. The annihilation is shown below: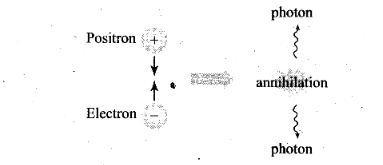

Short Answer Type Questions

Question 16. Why do stable nuclei never have more protons than neutrons?
Solution: The reason is that protons, being charged particles, repel each other. This repulsion becomes so great in nuclei with more than 10 protons or so, that an excess of neutrons which produce only attractive forces, is required for stability.
Important point: As you get to heavier elements, with each new proton you add, there is a larger repulsive force. The nuclear force is attractive and stronger than the electrostatic force, but it has a finite range. So you need to add extra neutrons, which do not repel each other, to add extra attractive force. You eventually reach a point where the nucleus is just too big, and tends to decay via alpha decay or spontaneous fission.
To view this in quantum mechanical terms, the proton potential well is not as deep as the neutron well due to the electrostatic repulsion. [Due to the Pauli exclusion principle, you only get two particles per level (spin up and spin down)]. If one well is filled higher than the other, you tend to get a beta decay to even them out. As the nuclei get larger, the neutron well gels deeper as compared to the proton well and you get more neutrons than protons.

Question 17. Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
                                               A -> B -> C
Here B is an intermediate nuclei which is also radioactive. Considering that there are N₀ atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
Solution: Consider radioactive nucleus A have N₀ atoms of A initially; or at t = 0, N_A = N₀ (maximum) whole N_B = 0. As time increases, N_A decreases exponentially and the number of atoms of B increases. After some time N_B becomes maximum. As B is an intermediate nuclei which is also radioactive, it also start decaying and finally drop to zero exponentially by radioactive decay law. We can represent the situation as shown in the graph.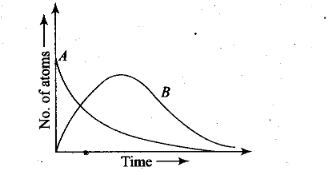

Question 18. A piece of wood from the ruins of an ancient building was found to have a ¹⁴ C activity of 12 disintegrations per minute per gram of its carbon content. The ¹⁴ C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of  ¹⁴ C is 5760 yr.
Solution:
Key concept:
Carbon dating: Radiocarbon dating (also referred to as carbon dating or carbon-14 dating) is a method tor determining the age of an object containing organic material by using the properties of radiocarbon -14(¹⁴ C), a radioactive isotope of carbon.
Radiocarbon, or carbon 14, is an isotope of the element carbon that is unstable and weakly radioactive. The stable isotopes are carbon 12 and carbon 13.
Carbon 14 is continually being formed in the upper atmosphere by the effect of cosmic ray neutrons on nitrogen 14 atoms. It is rapidly oxidized in air to form carbon dioxide and enters the global carbon cycle.
Plants and animals assimilate carbon 14 from carbon dioxide throughout their lifetimes. When they die, they stop exchanging carbon with the biosphere and their carbon 14 content then starts to decrease at a rate determined by the law of radioactive decay.
Radiocarbon dating is essentially a method designed to measure residual radioactivity. By knowing how much carbon 14 is left in a sample, the age of the organism when it died can be known. It must be noted though that radiocarbon dating results indicate when the organism was alive but not when a material from that organism was used.

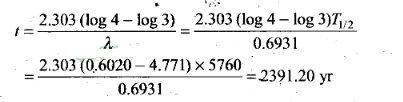
Question 19. Are the nucleons fundamental particles, or do they consist of still smaller parts? One way to find out is to probe a nucleon just as Rutherford probed an atom. What should be the kinetic energy of an electron for it to be able to probe a nucleon? Assume the diameter of a nucleon to be approximately 10^-15 m. 
Solution:
Key concept: A nucleon is one of the particles that makes up the atomic nucleus. Each atomic nucleus consists of one or more nucleons, and each atom in turn consists of a cluster of nucleons surrounded by one of more electrons. There are two known kinds of nucleon: the neutron and the proton. The mass number of a given atomic isotope is identical to its number of nucleons. Thus the term nucleon number may be used in place of the more common terms mass number or atomic mass number.
For resolving two objects separated by distance d, the wavelength A of the proving signal must be less than d. Therefore, to detect separate parts inside a nucleon, the electron must have a wavelength less than 10^-15 m.

Important point: Until the 1960s, nucleons were thought to be elementary particles, each of which would not then have been made up of smaller parts. Now they are known to be composite particles, made of three quarks bound together by the so-called strong interaction. The interaction between two or more nucleons is called intemucleon interactions or nuclear force, which is also ultimately caused by the strong interaction. (Before the discovery of quarks, the term “strong interaction” referred to just intemucleon interactions.)

Question 20. A nuclide 1 is said to be the mirror isobar of nuclide 2 if Z₁=N₂ and Z₂ = N₁ (a) What nuclide is a mirror isobar of ₁₁²³Na ? (b) Which nuclide out of the two mirror isobars have greater binding energy and why?
Solution:
Key concept: Mirror nuclei are nuclei where the number of protons of element one (Z₁) equals the number of neutrons of element two (N₂), the number of protons of element two (Z₂) equal the number of neutrons in element one (N₁) and the mass number is the same.
Pairs of mirror nuclei have the same spin and parity. If we constrain to odd number of nuclcons(A), then w find mirror nuclei that differ one another by exchanging a proton by a neutron. Interesting to observe is their binding energy which is mainly due to the strong interaction and also due to Coulomb interaction. Since the strong interaction is invariant to protons and neutrons one can expect these mirror nuclei to have very similar binding energies.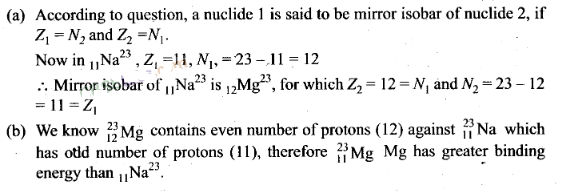

Long Answer Type Questions

Question 21. Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is

Assume that we start with 1000 ³⁸ S nuclei at time t = 0. The number of ³⁸ Cl is of count zero at t = 0 and will again be zero at t =∞, At what value of t, would the number of counts be a maximum?
Solution:

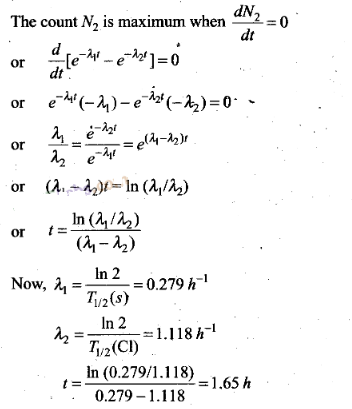
Question 22. Deuteron is a bound state of a neutron and a proton with a binding energy B = 2.2 MeV. A γ-ray of energy E is aimed at a deuteron nucleus to try to break it into a (neutron + proton) such that the n and p move in the direction of the incident γ-ray. If  E = B, show that this cannot happen. Hence, calculate how much bigger than B must be E be for such a process to happen.
Solution: Given the binding energy of a deuteron, B = 2.2 MeV Let kinetic energy and momentum of neutron and proton be K_n, K_P and p_n, p_p respectively.
From conservation of energy,

Question 23. The deuteron is bound by nuclear forces just as H-atom is made up of p and e bound by electrostatic forces. If we consider the force between neutron and proton in a deuteron as given in the form a coulomb potential but with an effective charge e’.

Solution:

Question 24. Before the neutrino hypothesis, the beta decay process was thought to be the transition.
n —> p + e
If this was true, show that if the neutron was at rest, the proton and electron would emerge with fixed energies and calculate them. Experimentally, the electron energy was found to have a large range.
Solution:

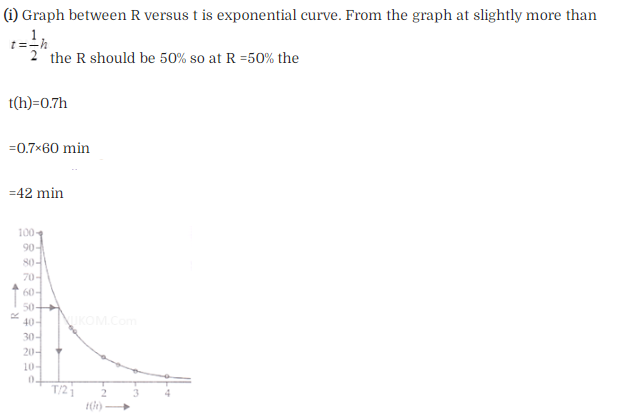
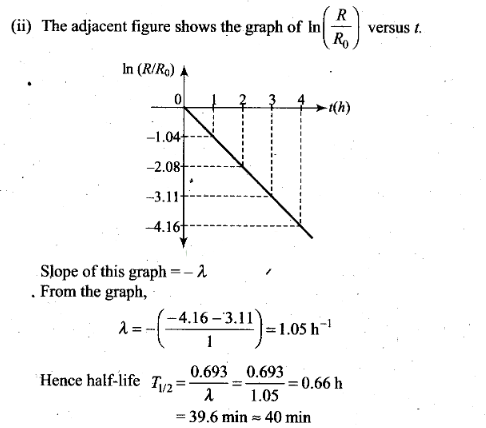
Question 25. The activity R of an unknown radioactive nuclide is measured at hourly intervals. The result found are tabulated as follows:

Solution:

Question 26. Nuclei with magic number of proton Z = 2, 8, 20, 28, 50, 52 and magic number of neutrons N = 2, 8, 20, 28, 50, 82 and 126 are found to be very stable. 
(i) Verify this by calculating the proton, separation energy S_P for ¹²⁰ Sn (Z= 50) and ¹²¹ Sb(Z= 51).
The proton separation energy for a nuclide is the minimum energy required to separate the least tightly bound proton from a nucleus of that nuclide. It is given by

Solution:

Important point: “Magic Numbers” in Nuclear Structure Careful observation of the nuclear properties of elements, showed certain patterns that seemed to change abruptly at specific key elements. Mayer noticed that magic numbers applied whether one counts the number of neutrons (A). the atomic number (Z), or the sum of the two, known as mass number (A). I-xamples are Helium Z = 2, Lead Z = 82, Helium A = 2, Oxygen N = 8, Lead A = 126, Neon A = 20, Silicon A = 28.
Magic numbers in the nuclear structure have been coming up during all this time, but no plausible explanation for their existence has ever been given. Interestingly, there are peaks and dips for binding energy, repeating every fourth nucleon. This periodicity is one clear indication of a geometrical structure within the nucleus. In particular, those nuclei that can be thought of as containing an exact number of alpha particles (2P + 2A), are more tightly bound than their neighbours. This effect is more pronounced for the lightest nuclei, but is still perceptible up to A – 28. For those nuclei with A > 20, the number of neutrons exceeds the number of protons, so some sort of distortion occurs wi thin the cluster.
It is found that nuclei with even numbers of protons and neutrons are more stable than those with odd numbers. This comes from the fact that the physical structure must have an even number of vertices. A type of regular polyhedron would satisfy this condition, since no regular polyhedron exists with an odd number of vertices. These specific “magic numbers” of neutrons or protons which seem to be particularly favoured in terms of nuclear stability are:
2, 8. 20. 28, 50, 82, 126
. Note that the structure must apply to both protons and neutrons individually, so that we can speak of “magic nuclei” where any one nucleon type, or their sum, is at a magic number. .
The existence of these magic numbers suggests closed shell configurations, like the shells in atomic structure. They represent one line of reasoning which led to the development of a shell model of the nucleus. Other forms – of evidence suggesting shell structure include the following.

1.  Enhanced abundance of those elements for which Z or N is a magic number.
2. The stable elements at the end of the naturally occurring radioactive series all have a “magic number” of neutrons or protons.
3.  The neutron absorption cross-sections for isotopes where N = magic number are much lower than surrounding isotopes.
4.  The binding energy for the last neutron is a maximum for a magic neutron number and drops sharply for the next neutron added.
5.  Electric quadrupole moments are near zero for magic number nuclei.
6.  The excitation energy from the ground nuclear state to the first excited state is greater for closed shells.

Visualizing the densely packed nucleus in terms of orbits and shells seems much less plausible than the corresponding shell model for atomic electrons. You can easily believe that an atomic electron can complete many orbits without running into anything, but you expect protons and neutrons in a nucleus to be in a continuous process of collision with each other. But dense-gas type models of nuclei with multiple collisions between particles didn’t fit the data, and remarkable patterns like the “magic numbers” in the stability of nuclei suggested the seemingly improbable shell structure.