CBSE Sample Papers for Class 12 Maths Set-9

CBSE Sample Papers for Class 12 Maths Set 9 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case/passage based/intergrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

Question 1.
The value of projection of the line joining the points (3, 4, 5) and (4, 6, 3) on the line joining the points (-1, 2, 4) and (1, 0, 5) is
(a) \(\frac{4}{3}\)
(b) \(\frac{3}{4}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{2}{3}\)
Solution:
(a) The direction ratios of the line joining P(-1, 2, 4) and 0(1, 0, 5) are proportional to (2, -2, 1), i.e. \(2\hat{i}-2\hat{j}+\hat{k}\).
and the direction ratio of the line joining 4(3, 4, 5) and 6(4, 3 3)are proportional to (1, 2, -2), i.e.\(\hat{i}+2\hat{j}-2\hat{k}\).

Thus, the projection of line \(\vec{AB}\) on \(\vec{PQ}\) is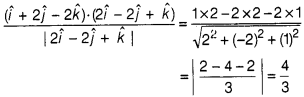

Question 2.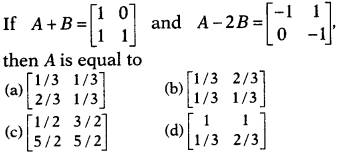

Solution: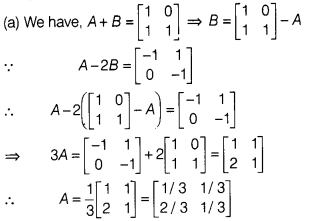

Question 3.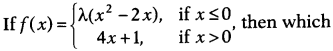

one of the following is correct
(a) f(x) is continuous at x = 0 for any value of X
(b) f(x) is discontinuous at* =0 for any value of X
(c) f(x) is discontinuous atx = 1 for any value of X
(d) None of the above
Solution:

⇒ f(x) is discontinuous at x = 0 for any value of λ.

Question 4.
The function f(x) = 4sin x-6sin2 x + 12 sin x +100 is strictly.

Solution:
(b) We have, f(x) = 4sin³x – 6sin²x + 12sinx + 100
∴ f'(x) = 12sin² x.cos x – 12sin x.cos x + 12cosx
= 12 [sin²x . cosx – sin x .cos x + cos x]
= 12cos x [sin² x – sin x + 1]
⇒ f'(x) = 12cos x [sin²x + (1 – sin x)] ∵ 1-sin x ≥ 0 and sin2 x ≥ 0
∴ sin²x + 1 – sin x ≥ 0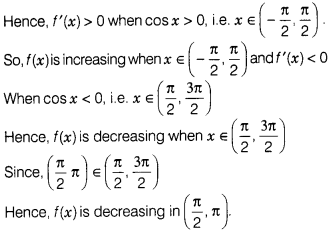

Question 5.
The magnitude of greater diagonal of parallelogram whose sides are \(\hat{i}+\hat{j}-2\hat{k}\) and \(-2\hat{i}+3\hat{j}+4\hat{k}\), is
(a) √21
(b) √31
(c) 21
(d) 31
Solution: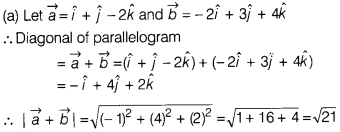

Question 6.

Solution: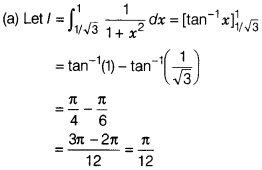

Question 7.
The area of the region bounded by the curve x = 2y + 5 and the lines y = 2, y = -2 is
(a) 10 sq units
(b) 15 sq units
(c) 25 sq units
(d) 20 sq units
Solution: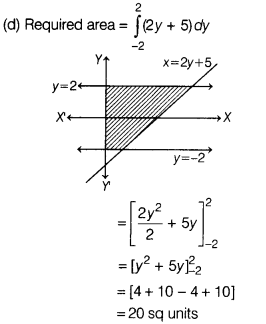

Question 8.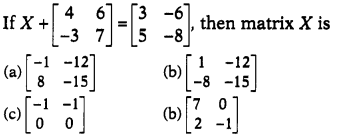

Solution: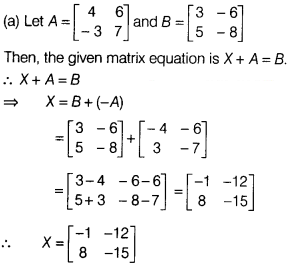

Question 9.
If \(\vec{a}=4\hat{i}-\hat{j}+\hat{k}\) and \(\vec{b}=2\hat{i}-2\hat{j}+\hat{k}\), then |\(\vec{a}-\vec{b}\)| is equal to
(a) √3
(b) √5
(c) 5
(d) 3
Solution: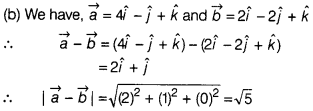

Question 10.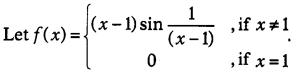

Then, which of the following is true?
(a) f is differentiable at x = 1 but not at x = 0
(b) f is neither differentiable at x = 0 nor at x = 1
(c) f is differentiable at x = 0 and at x = 1
(d) f is differentiable at x = 0 but not at x = 1
Solution:
(d) We observe that,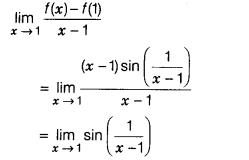

An oscillating number between -1 and 1

∴ f(x) differentiable at x = 0

Question 11.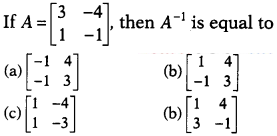

Solution:

Question 12.
If A_ij is the cofactor of the element a_ij, of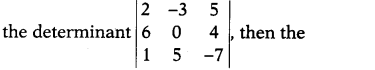

value of a₃₂. A₃₂ is
(a) 100
(b) 225
(c) 110
(d) 150
Solution:

Question 13.
The family y = Ax + A³ of curves is represented by differential equation of degree
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(a) Given that, y = Ax + A³
Here, equation has only one arbitrary constant.
Therefore, the order of differential equation is 1.

Question 14.
The function f(x) = x^x has a stationary point at
(a) x = e
(b) x = \(\frac{1}{e}\)
(c) x = 1
(d) x = √e
Solution:
(b) We have, f(x) = x^x
Let y = x^x
and log y = xlog x
∴ \(\frac{1}{y}.\frac{dy}{dx}\) = x.\(\frac{1}{x}\) + log x . 1
⇒ \(\frac{dy}{dx}\) = (1 + log x).x^x
∴ \(\frac{dy}{dx}\) = 0
⇒ (1 + logx).x^x = 0 ⇒ log x = -1
⇒ log x = log e^-1 ⇒ x = e^-1
⇒ x = \(\frac{1}{e}\)
Hence, f(x) has a stationary point at x = \(\frac{1}{e}\)

Question 15.
If \(\vec{a}\) is a unit vector such that \(\vec{a}\times\hat{i}=\hat{j}\), then \(\vec{a}.\hat{i}\) is equal to
(a) 1
(b) 0
(c) -1
(d) \(\hat{i}\)
Solution: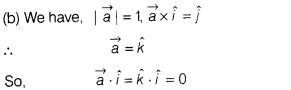

Question 16.
The angle between the vectors \(\vec{a}\times\vec{a}\) and \(\vec{b}\times\vec{a}\) is
(a) –\(\frac{\pi}{2}\)
(b) π
(c) \(\frac{\pi}{2}\)
(d) \(\frac{3\pi}{2}\)
Solution:
(b) We know that \(\vec{b}\times\vec{a}\) = -(\(\vec{a}\times\vec{b}\))
So, angle between \(\vec{a}\times\vec{b}\) and \(\vec{b}\times\vec{a}\) is π.

Question 17.
The function = \(\frac{4-x^2}{4x-x^3}\)
(a) discontinuous at only one point
(b) discontinuous at exactly two points
(c) discontinuous at .exactly three points
(d) None of the above
Solution: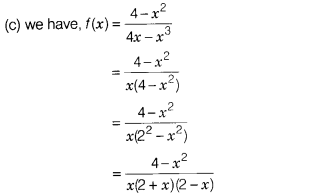

Clearly, f(x) is discontinuous at exactly three points
x = 0, x = -2 and x = 2.

Question 18.
If \(\vec{b}\) is a unit vector such that
(\((\vec{a}+\vec{b}).(\vec{a}-\vec{b})\) = 8, then |\(\vec{a}\)| is equal to
(a) 1
(b) 2
(c) 3
(d) 4
Solution: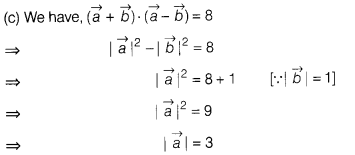

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true

Question 19.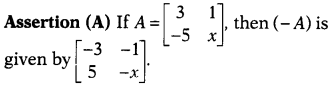

Reason (R) The negative of a matrix is given by – A and is defined as -A = (-1)A.
Solution:
(a) We define -A = (-1)A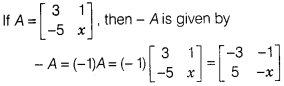

Question 20.
The solution of the differential equation \(\frac{d^2y}{dx^2}\) + y = 0 is y = Φ(x) a sin(x + b).
Assertion (A) The function y = Φ(x) is called general solution.
Reason (R) The solution which contains arbitrary constants, is called general solution.
Solution:
(a) The solution which contains arbitrary constants is called the general solution (primitive) of the differential equation.
Here, function Φ consists of two arbitrary constants (parameters) a and b and it is called general solution of the given differential equation,

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
Show that the function
f(x) = 4x³ – 18x² + 27x – 7 has neither maxima nor minima.
Or
Show that the function f(x) = \(\frac{x}{3}+\frac{3}{x}\) decreases in the intervals (-3, 0) ∪ (0, 3).
Solution:
We have, f(x) = 4x³ – 18x² + 27x – 7
f'(x) = 12x² – 36x + 27
f'(x) = 3(4x² – 12x + 9) = 3(2x – 3)²
On putting f'(x) = 0 ⇒ 3(2x – 3)² = 0
⇒ (2x – 3)² = 0
⇒ x = \(\frac{3}{2}\)(critical point)
Since, f'(x) > 0 for all x < \(\frac{3}{2}\) and x > \(\frac{3}{2}\).
Hence, x = \(\frac{3}{2}\) is a point of inflexion.
i.e. f(x) has neither a point of maxima nor a point of minima.
Or
When, x ∈ (-3, 0) ∪ (0, 3)
f'(x) < 0
∴ f(x) is decreasing function in (-3, 0) ∪ (0, 3).

Question 22.
If cosec^-1x + cosec^-1y + cosec^-1z = \(\frac{-3\pi}{2}\),
find the value of \(\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\).
Solution:

Question 23.
knd [P(B / A) + P( A / B)l if P( A) = \(\frac{3}{10}\), P(B) = \(\frac{2}{5}\) and P(A ∪ B) = \(\frac{3}{5}\).
Or
Three distinct numbers are chosen randomly from the first 50 natural numbers. Find the probability that all the three numbers are divisible by both 2 and 3.
Solution: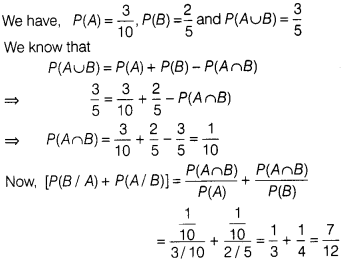

Or
Three distinct numbers can be chosen from first 50 natural numbers in ⁵⁰C₃ ways.
Total numbers which is divisible by 2 and 3 from first 50 natural numbers is
{6, 12, 18, 24, 30,36, 42, 48} = 8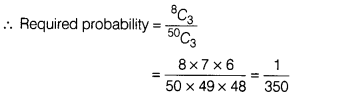

Question 24.
Find the angle between vectors \(\vec{a}=\hat{i}-\hat{j}+\hat{k}\) and \(\vec{b}=\hat{i}+\hat{j}-\hat{k}\).
Solution: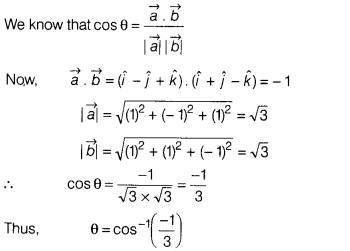

Question 25.
Three cards are drawn successively without replacement from a pack of 52 well-shuffled cards. What is the probability that first two cards are king and the third card drawn is an ace?
Solution:
Since, there are 52 cards in a pack.
∴ n(S) = 52
Let A = event that the card drawn is king and B = event that the card drawn is an ace.
Now, P(A) = \(\frac{4}{52}\)

P(\(\frac{A}{A}\)) = Probability of drawing second king when one king has already been drawn
= \(\frac{3}{51}\) [∵ remaining cards are (52 – 1) = 51]
P(B/ AA) = Probability of drawing third card to be an ace when two kings have already been drawn = \(\frac{4}{50}\)

Now, probability of getting first two cards are king and third card is an ace
= P(A ∩ A ∩ B) = P(A).P(\(\frac{A}{A}\)).P(\(\frac{B}{AA}\))
[by multiplication theorem]
= \(\frac{4}{52}\times\frac{3}{51}\times\frac{4}{50}\)
= \(\frac{2}{5525}\)

Section C
This section comoprises of short answer type questions (SA) of 3 marks each

Question 26.
If x, y, z ∈ [-1, 1] such that sin^-1 x + sin^-1 y + sin^-1 z = \(\frac{3\pi}{2}\), find the value of x² + y² + z².
Solution:
We know that, the minimum value of sin^-1 x for x ∈ [-1, 1] is – π/2.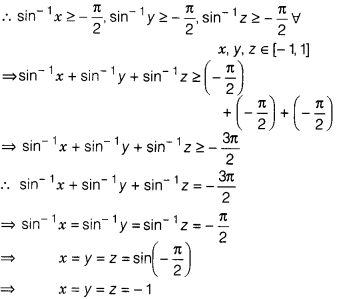

Hence, x² + y² + z² = (-1)² + (-1)² + (-1)² = 3

Question 27.
Show that the function f : R → R defined by f(x) = 2x³ – 5, is a bijective function.
Or
If R₁ and R₂ be two equivalence relations on a set A, prove that R₁ ∩ R₂ is also an equivalence relation on A.
Solution:
Given, f : R → R defined by f (x) = 2x³ – 5
For one-one (injective)
Let f(x₁) = f(x₂), ∀ x₁, x₂ ∈ R
⇒ 2x³₁ – 5 = 2x³₂ – 5
⇒ 2x³₁ = 2x³₂
⇒ x³₁ = x³₂ ⇒ x₁ = x₂
Thus, f(x₁) = f(x₂) ⇒ x₁ = x₂
So, f is one-one (injective).
For onto (surjective)
Let y be an arbitrary element of R (codomain), then
f(x) = y
⇒ 2x³ – 5 = y
⇒ 2x³ = y + 5
⇒ x³ = \(\frac{y+5}{2}\)
⇒ x = (\(\frac{y+5}{2}\))^1/3

Clearly, x ∈ R (domain), ∀ y ∈ R (codomain).
Thus, for each y ∈ R (codomain) there exists

This shows that every element in the codomain has its pre-image in the domain.
So, f is onto (or f is surjective).
Thus, f is both one-one and onto (or both injective and surjective). Hence, f is bijective.
Hence proved.
Or
Let R₁ and R₂ be two equivalence relations on a set A.
Then, R₁ ⊆ A × A, R₂ ⊆ A × A ⇒ (R₁ ∩ R₂) ⊆ A × A.
So, (R₁, ∩ R₂) is a relation on A
This relation on A satisfies the following properties

(i) Reflexivity R₁ is reflexive and R₂ is reflexive
⇒ (a, a) ∈ R₁ and (a, a) ∈ R₂ for all a ∈ A
⇒ (a, a) ∈ R₁ ∩ R₂ for all a ∈ A
⇒ R₁ ∩ R₂ is reflexive.

(ii) Symmetry Let (a, b) be an arbitrary element of R₁ ∩ R₂ .
Then, (a, b) ∈ R₁ ∩ R₂
⇒ (a, b) ∈ R₁, and (a, b) ∈ R₂
⇒ (b, a) ∈ R₁, and (b, a) ∈ R₂ [∵ R₁, is symmetric and R₂ is symmetric]
⇒ (b, a) ∈ R₁ ∩ R₂
This shows that R₁, ∩ R₂ is symmetric.

(iii) Transitivity Let (a, b) ∈ R₁, ∩ R₂ and (b, c) ∈ R₁, ∩ R₂
⇒ (a, b) ∈ R₁, (a, b) ∈ R₂ and
⇒ (b, c) ∈ R₁, (b, c) ∈ R₂
⇒ {(a, b) ∈ R₁, (b, c) ∈ R₁},
and {(a, b) ∈ R₂, (b, c) ∈ R₂}
⇒ {a, c} ∈ R₁ and (a, c) ∈ R₂ [∵ R₁ is transitive and R₂ is transitive]
⇒ (a, c) ∈ R₁ ∩ R₂
This shows that (R₁, ∩ R₂) is transitive.
Thus, R₁, ∩ R₂ is reflexive, symmetric and transitive.
Hence, R₁, ∩ R₂ is an equivalence relation.

Question 28.
If \(x\sqrt{1+y}+y\sqrt{1+x}\) = 0, (x ≠ y), then prove that \(\frac{dy}{dx}=\frac{1}{(1+x)^2}\)
Or
If y = e^x sin x, then prove that
\(\frac{d^2y}{dx^2}-2\frac{dy}{dx}\) + 2y = 0
Solution:
To prove \(\frac{dy}{dx}=\frac{1}{(1+x)^2}\)
Given equation is \(x\sqrt{1+y}+y\sqrt{1+x}\) = 0,
where x ≠ y, we first convert the given equation into
y = f(x) form.
Clearly, \(x\sqrt{1+y}=-y\sqrt{1+x}\)
On squaring both sides, we get
⇒ x²(1 + y) = y² (1 + x)
⇒ x² + x² y = y² + y²x
⇒ x² – y² = y²x – x²y
⇒ (x – y)(x + y) = -xy (x – y) [∵ a² – b² = (a – b)(a + b)]
⇒ (x – y) (x + y) + xy (x – y) = 0
⇒ (x – y) (x + y + xy) = 0
Either x – y = 0 or x + y + xy = 0
Now, x – y = 0 ⇒ x = y
But it is given that x ≠ y.
So, it is a contradiction.
∴ x – y = 0 is rejected.
Now consider, y + xy + x = 0
y (1 + x) = -x ⇒ y = \(\frac{-x}{1+x}\)
On differentiating both sides w.r.t. x, we get

Question 29.
Evaluate ∫\(\frac{1}{3x^2+5x+7}\)dx.
Or
Evaluate ∫\(\frac{xe^x}{(x+1)^2}\)dx.
Solution: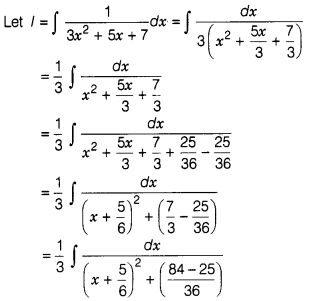

Question 30.
If \(\vec{a}\) and \(\vec{b}\) are unit vectors, then find the angle between \(\vec{a}\) and \(\vec{b}\), given that (√3\(\vec{a}-\vec{b}\) – b) is a unit vector.
Solution: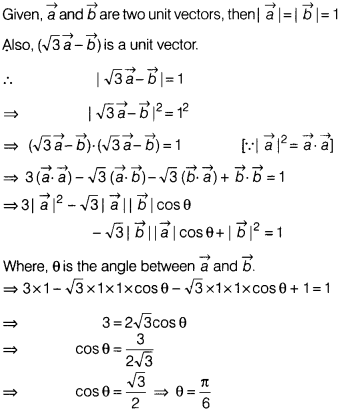

Hence, the required angle between \(\vec{a}\) and \(\vec{b}\) is \(\frac{\pi}{6}\).

Question 31.
Find the angle between the lines whose direction cosines are given by the equations 3l + m + 5n = 0,
6mn – 2nl + 5lm = 0.
Solution:
The given equations are
3l + m + 5n = 0 … (i)
and 6mn – 2nl + 5lm = 0 …(ii)
Now, from Eq. (i), wegetm = – 3l – 5n … (iii)
On substituting m = -3l – 5n in Eq. (ii), we get
6(-3l – 5n)n – 2nl + 5l(-3l – 5n) = 0
⇒ 30n² + 45ln + 15l² = 0
⇒ 2n² + 2ln + nl + l² = 0
⇒ 2n(n + l)+ l(n + l) = 0
⇒ (n + l)(2n + l) = 0
⇒ Either l = -n or l = – 2n
If l = -n,then m = -2n [using Eq. (iii)]
and if l = — 2n, then m = n [using Eq. (iii)]
Thus, the direction ratio of two lines are proportional to (- n, -2n, n) and (-2n, n, n) i.e. (-1, -2, 1) and (-2, 1, 1) respectively.

Now, let 0be the acute angle between the lines, then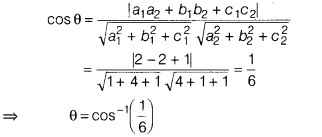

Section D
This section comprises of long answer type questions (LA) of 5 marks each

Question 32.
Two schools P and Q want to award their selected students on the values of Discipline, Politeness and Punctuality.
The school P wants to award ₹ x each, ₹ y each and t z each for the three respective values of its 3, 2 and 1 students with a total award money of ₹ 1,000. School Q wants to spend ₹ 1,500 to award its 4, 1 and 3 students on the respective values (by giving the same award money for the three values as before). If the total amount of award for one prize on each value is ₹ 600. Using matrices, find the award money for each value. Apart from the above three values, suggest one more value of awards.
Solution:
₹x. ₹y and ₹z each are award to the selected students on the values of Discipline, Politeness and Punctuality.
According to the given conditions,
3x + 2y + z = 1000
4x + y + 3z = 1500
and x + y + z = 600
On representing the obtained equations in the matrix form, we get

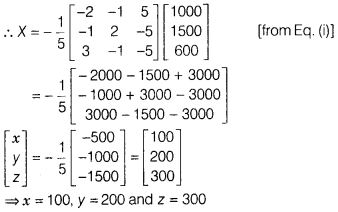
Question 33.
Find the particular solution of the differential equation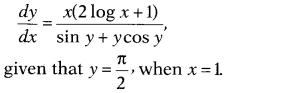

Or
Solve the following differential equation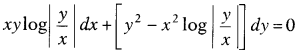

Solution:
Given, differential equation is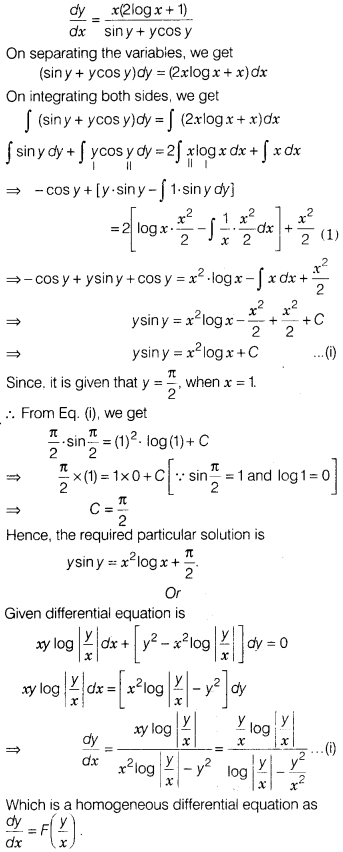


Using integration by parts, we get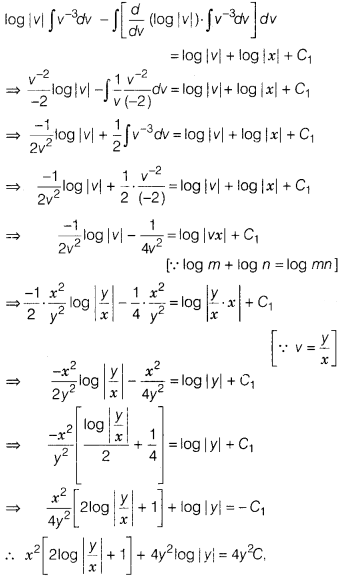

where C = – C₁,
which is the required solution.

Question 34.
Solve the LPP, maximise, Z = 0.08x + 0.10y
Subject to the constraints, x + y ≤ 12000, x ≥ 2000, y ≥ 4000, x ≥ 0, y ≥ 0.
Or
Solve the following LPP graphically: Minimise and maximise Z = 5x + 2y
Subject to constraints
-2x – 3y ≤ -6, x – 2y ≤ 2, 3x + 2y ≤ 12, -3x + 2y ≤ 3, x, y ≥ 0
Solution:
The linear programming problem is
Maximise Z = 0.08x + 0.10y
Subject to the constraints
x + y ≤ 12000, x ≥ 2000, y ≥ 4000
and x ≥ 0, y ≥ 0
Consider the constraints as equations, we get

So, line passes through the points (0, 12000) and (12000, 0).
Oh putting (0, 0) in the inequality x + y ≤ 12000, we get
0 + 0 ≤ 12000
⇒ 0 ≤ 12000 [true]
∴ The shaded region is towards the origin.
∵ Line x = 2000 is parallel to Y-axis.
On putting (1000,0) in the inequality x ≥ 2000, we get
1000 ≥ 2000 [false]
∴ The shaded region is at the right side of the line,
∵ Line y = 4000 is parallel to X-axis.
On putting (0,6000) in the inequality y ≥ 4000, we get
6000 ≥ 4000 [true]
∴ The shaded region is above the line.
The intersection point of lines (ii) and (iii), (i) and (iii),
(i) and (ii) are respectively,
4(2000, 4000), 6(8000, 4000) and C (2000, 10000)

Now, plot the graph of the system of inequalities. The shaded portion ABC represents the feasible region which is bounded.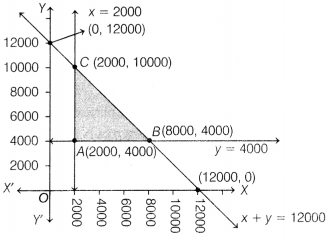

and the coordinates of the corner points are
A(2000, 4000), B(8000, 4000) and C(2000, 10000), respectively.
Now, the values of Z at each corner point are given below

Corner points	Z = 0.08x + 0.10y
A(2000, 4000)	Z = 0.08 (2000) + 0.10(4000) = 160 + 400= 560
B(8000, 4000)	Z = 0.08 (8000) + 0.10(4000) = 640 + 400 = 1040
C(2000,10000)	Z = 0.08 (2000) + 0.10(10000) = 160 + 1000 = 1160 (maximum)

∴ Maximum value of Z is 1160 at (2000, 10000).

Or

Converting the given inequations into equations, we get
2x + 3y = 6, x – 2y = 2, 3x + 2y = 12, -3x + 2y = 3, x = 0 and y = 0
Region represented by – 2x – 3y ≤ -6:
The line – 2x – 3y = – 6 or 2x + 3y = 6 cuts OX and OY at A₁(3, 0) and B₁(0, 2) respectively.
Join these points to obtain the line 2x + 3y = 6. Since, 0(0, 0) does not satisfy the inequation – 2x – 3y ≤ – 6.
So, the region represented by – 2x – 3y ≤ -6 is that part of XOY-plane which does not contain the origin.

Region represented by x – 2y ≤ 2: The line x – 2y = 2 meets the coordinate axes at A₂(2, 0) and B₂(0, -1). Join these points to obtain x – 2y = 2. Since, (0, 0) satisfies the inequation x – 2y ≤ 2, so the region containing the origin represents the solution set of this inequation.

Region represented by 3x + 2y ≤ 12: The line 3x + 2y = 12 intersects OX and OY at A₃(4, 0) and B₃(0, 6). Join these points to obtain the line 3x + 2y = 12.
Clearly, (0, 0) satisfies the inequation 3x + 2y ≤ 12. So, the region containing the origin represents the solution set of the given inequation.

Region represented by -3x + 2y ≤ 3: The line -3x + 2y = 3 intersects OX and OY at A₄(-1, 0) and B₄( 0, \(\frac{3}{2}\)). Join these points to obtain the line -3x + 2y = 3. Clearly, (0, 0) satisfies the inequation. So, the region containing the origin represents the solution set of the given inequation.

Region represented by x ≥ 0 , y ≥ 0. Clearly, XOY quadrant represents the solution set of these two inequations.

The shaded region shown in figure represents the common solution set of the above inequations. This region is the feasible region of the given LPP.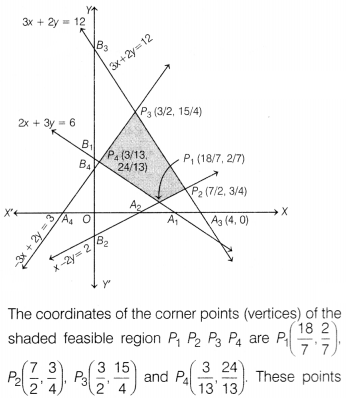

These points have been obtained by solving the equations of the corresponding intersecting lines, simultaneously. The values of the objective function at these points are given in the following table

Question 35.
Show that \(\int_0^{\frac{\pi}{2}}\) f (sin 2x)sin xdx
= √2 \(\int_0^{\frac{\pi}{4}}\) f (cos 2x)cos xdx.
Solution: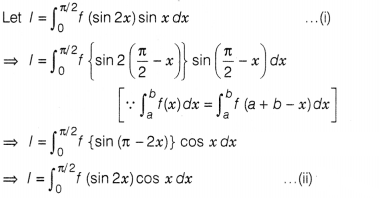

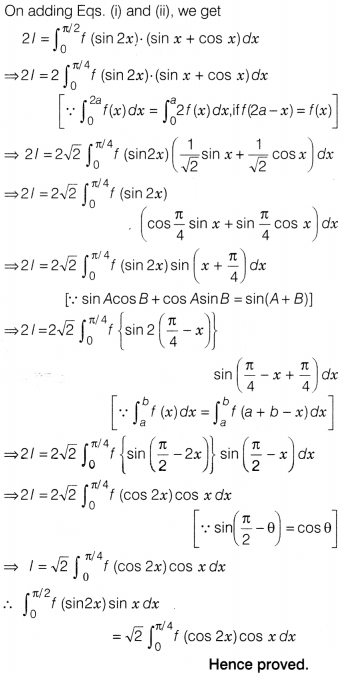
Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
A square piece of tin of side 24 cm is to be made into a box without top by cutting a square from each corner and folding up the flaps to form a box.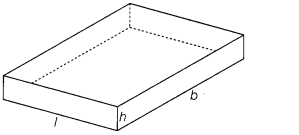

On the basis of above information, answer the following questions
(i) Write the length, breadth and height of the box formed in terms of x.
(ii) Express volume V of the box in terms of x.
(iii) Show that volume of the box is maximum, when x = 4 cm.
Or
If volume of the box is maximum at x = 4, then find the maximum value of volume of box. If rate of making the box is ₹5/cm², then find the cost of box when volume is maximum.
Solution: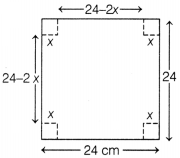

(i) From figure it is clear that
Length of box = 24 – 2x
Breadth of box = 24 – 2x
Height of box = x

(ii) Volume of box, V = length × breadth × height
= (24 – 2x)(24 – 2x) (x) = x(24 – 2x)²

(iii) We have, V = x(24-2x)²
∴ \(\frac{dV}{dx}\) = (24 – 2x)² + 2x(24 – 2x)(- 2) dx
= (24 – 2x) [24 – 2x – 4x]
= (24 – 2x) (24 – 6x) = 6 (24 – 2x)(4 – x)
For maximum,
\(\frac{dV}{dx}\) = 0
⇒ 6(24 – 2x)(4 – x) = 0
⇒ x = 4 and x = 12
Again, \(\frac{d^2V}{dx^2}\) = 6[-2(4 – x) + (24 – 2x)(- 1)]
= 6 [-8 + 2x – 24 + 2x] = 6[4x – 32]
∴ \(\frac{d^2V}{dx^2}\)|_x=4 < 0 and \(\frac{d^2V}{dx^2}\)|_x=12 >0
So, V is maximum at x = 4

Or

∵ Volume of box, V = x(24 – 2x)²
∴ V_max = x(24 – 2x)²
= 4(24 – 8)² = 4 × 16² = 1024cm³
Length of box = 24 – 2x = 24 – 2 × 4 = 16cm,
Breadth of box = 24 – 2x = 24 – 2 × 4 = 16 cm
and height of box = 4 cm
∴ Surface area of box = 2(l + b)h + lb
= 2(16 + 16) × 4 + 16 × 16 = 256 + 256 = 512 cm²
∴ Total cost of making the box = 512 × 5
= ₹2560

Question 37.
If f(x) is a continuous function defined on [-a, a], then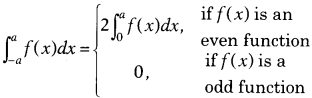

A function f(x) is even , when f(-x) = f(x) and odd when f(-x) = -f(x).
On the basis of above information, answer the following questions
(i) If f(x) is an even function, then evaluate \(\int_{-1}^1\)f(x) -f(-x))dx.
(ii) If g(x) is an odd function, then evaluate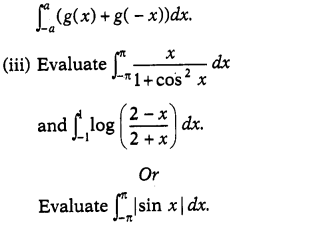

Solution: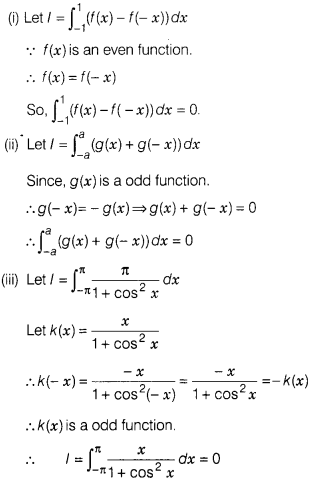

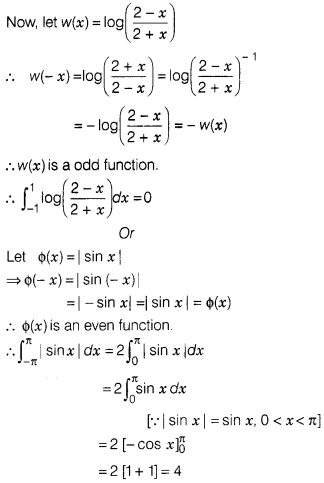
Question 38.
A can hit a target 4 times in 5 shots, B hit 3 times in 4 shots and C hit 2 times in 3 shots.

On the basis of above information, answer the following questions
(i) Find P(any two of A, B and C will hit the target).
(ii) Find P(none of them will hit the target) and P (B and C may hit and A may not).
Solution:
Consider the following events,
E = A hits the target,
F = B hits the target
and G = C hits the target
(i) ∴ Required probability = P (any two of A, B and C will hit the target)