CBSE Sample Papers for Class 12 Maths Set-7

CBSE Sample Papers for Class 12 Maths Set 7 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case/passage based/intergrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

Question 1.
The cartesian equation of the line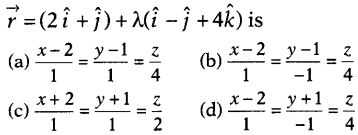

Solution:
(b) Given, vector equation of line is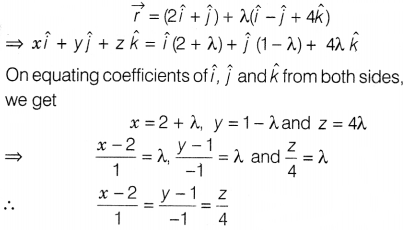

Which is the required cartesian equation of line.

Question 2.
If P(A) = \(\frac{1}{2}\) and P(B) = 0, then P(\(\frac{A}{B}\)) is equal to
(a) 1
(b) 0
(c) not defined
(d) 0.5
Solution:
(c) It is given that

Question 3.
If A and B are two independent events, then P( A ∩ \(\overline{\mathrm{B}}\)) is equal to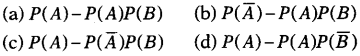

Solution:
(a) We have, P(A ∩ \(\overline{\mathrm{B}}\)) = P(A) – P(\(\overline{\mathrm{B}}\))
[∵ A and 6 are independent events]
⇒ P(A ∩ \(\overline{\mathrm{B}}\)) = P(A) . [1 – P(B)] = P(A) – P(A) . P(B)

Question 4.
\(\int_0^\pi\frac{xdx}{1+sinx}\)
(a) π
(b) 2π
(c) 3π
(d) π/2
Solution: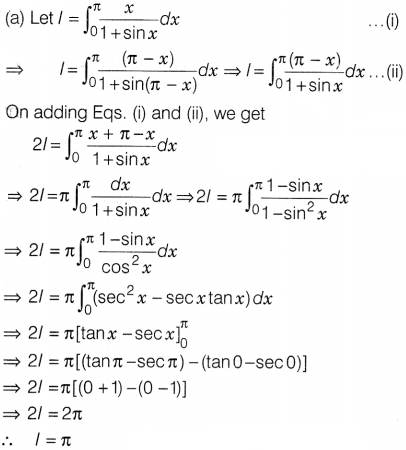

Question 5.
If I be any interval disjoint from [-1, 1], then the function f given by f(x) = x + \(\frac{1}{x}\) is
(a) strictly decreasing on I
(b) strictly increasing on I
(c) decreasing on I
(d) Only (a) and (c) are true
Solution:
(b) Given, f(x) = x + \(\frac{1}{x}\) ⇒ f'(x) = 1 – \(\frac{1}{x^2}=\frac{x^2+1}{x^2}\)
[on differentiating w.r.t. x we get]
If x< -1, then f'(x) > 0. If x > 1, then f'(x) > 0
∴ f(x) is strictly increasing on interval / disjoint from [-1, 1]

Question 6.
Direction cosines of the vector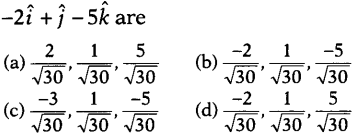

Solution:

Question 7.
The least value of a, such the function f given by f(x) = x² + ax + 1 is strictly increasing on (1, 2) is
(a) -1
(b) -2
(c) 0
(d) 1
Solution:
(b) We find f'(x), then for 1 < x < 2, put f'(x) > 0 and find the required least value of a.
Given, f(x) = x² + ax + 1 ⇒ f'(x) = 2x + a
In interval (1, 2), 1 < x < 2 ⇒ 2 < 2x < 4
⇒ (2 + a) < (2x + a) < (4 + a) Since, f(x) is strictly increasing function, then (2 + a) > 0 [for this f'(x) > 0 and (2x + a) > (2 + a)]
∴ (2 + a) > 0
⇒ a > -2
Hence, the least value of a = – 2.

Question 8.
If \((\hat{i}+3\hat{j}+9\hat{k})\times(3\hat{i}-\lambda\hat{j}+\mu\hat{k})\) = 0, then λ + µ is equal to
(a) 10
(b) 18
(c) 0
(d) 1
Solution: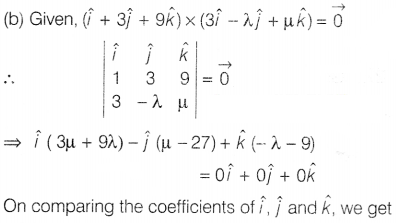

3µ + 9λ = 0, – µ + 27 = 0 and -λ – 9 = 0
⇒ µ = 27 and λ = -9
Also, the values of µ and λ satisfy the equation 3µ + 9λ = 0.
∴ λ + µ = -9 + 27 = 18

Question 9.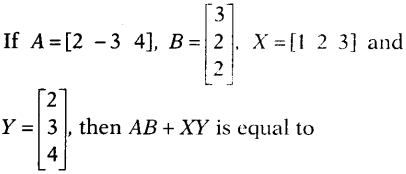

(a) [28]
(b) [24]
(c) 28
(d) 24
Solution: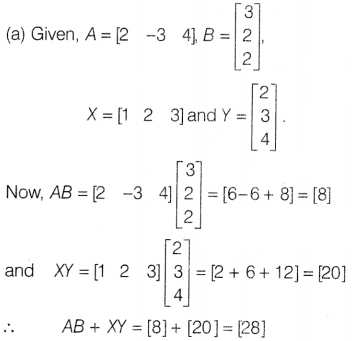

Question 10.
A bag contains 5 red and 3 blue balls. If 3 balls are drawn at random without replacement, then the probability of getting exactly one red ball is
(a) \(\frac{15}{36}\)
(b) \(\frac{15}{46}\)
(c) \(\frac{15}{56}\)
(d) \(\frac{1}{2}\)
Solution:
(c) We have, 5 red and 3 blue balls.
Probability of getting exactly one red ball, when 3 balls are drawn is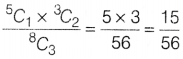

Question 11.
\((\hat{k}\times\hat{j}).\hat{i}+\hat{j}.\hat{k}\) is equal to
(a) -1
(b) 1
(c) 0
(d) -2
Solution: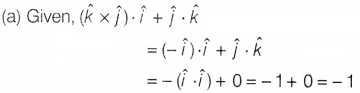

Question 12.
\(\int_0^{\pi}\)|sin x| dx is equal to
(a) 1
(b)2
(c) 3
(d) 4
Solution: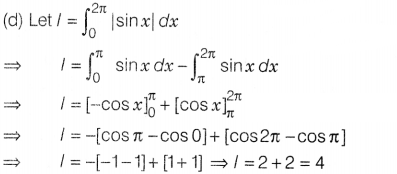

Question 13.
If y = Ae^5x + Be^-5x, then \(\frac{d^2y}{dx^2}\) is equal to
(a) 25y
(b) 5y
(c) -25y
(d) 15y
Solution: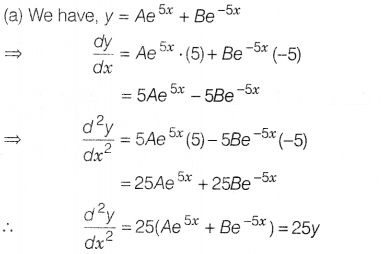

Question 14.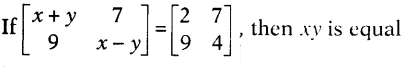

to
(a) 1
(b) 2
(c) -3
(d) -5
Solution: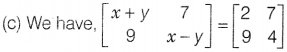

⇒ x + y = 2 and x – y = 4
Since (x + y)² – (x – y)² = 4xy
∴ 2² – 4² = 4xy
⇒ 4xy = 4 – 16 = -12 ⇒ xy = -3

Question 15.
Let A and B be the events associated with the sample space S, then the value of P(A/B) lies in the interval
(a) (0, 1)
(b) [0, 1]
(c) (0, 1]
(d) [0, 1)
Solution:
(b) 0 ≤ P(A/B) ≤ 1

Question 16.
Write the number of vectors of unit length perpendicular to both the vectors
\(\vec{a}=2\hat{i}+\hat{j}+2\hat{k}\) and \(\vec{b}=\hat{j}+\hat{k}\)
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) We know that unit vectors perpendicular to \(\vec{a}\) and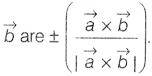

So, there are two unit vectors perpendicular to the given vectors.

Question 17.
Area of the region bounded by the curve y² = 4V, F-axis and the line y = 3 is
(a) 2 sq units
(b) \(\frac{9}{4}\) sq units
(c) \(\frac{9}{3}\) sq units
(d) \(\frac{9}{2}\) sq units
Solution:
(b) The area bounded by the curve y² = 4x. Y-axis and y = 3 is represented in the figure by shaded region.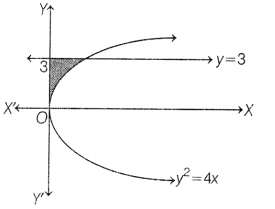

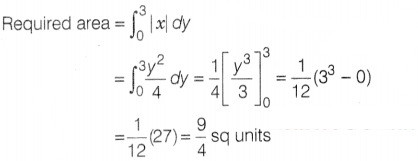
Question 18.
A unit vector in the direction of vector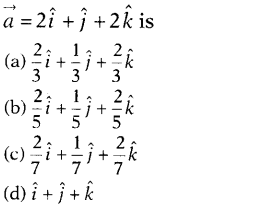

Solution:
(a) We know that unit vector in the direction of \(\vec{a}\) is

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true.

Question 19.
Assertion (A) Scalar matrix

an identity matrix when k = 1.
Reason (R) Every identity matrix is not a scalar matrix.
Solution: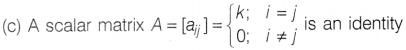

matrix, when k =1.
But every identity matrix is clearly a scalar matrix as identity matrix is a diagonal matrix in which all the diagonal elements are equal.
Hence, Assertion is true but Reason is false.

Question 20.
Assertion (A) The relation R on the set N × N defined by (a, b)R(c, d) ⇔ a + d = b + c, for all (a, b), (c, d) ∈ N × N is an equivalence relation.
Reason (R) Any relation is an equivalence relation, if it is reflexive, symmetric and transitive.
Solution:
(a) Let (a, b) be an arbitrary element of N × N.
Then, (a, b) ∈ N × N
⇒ a, b ∈ N
⇒ a + b = b + a [by commutative of addition in N]
⇒ (a, b)R(a, b)
⇒ R is reflexive on N × N.
Let (a, b), (c, d) ∈ N × N be such that (a, b) R(c, d).
⇒ a + d = b + c
⇒ b + c = a + d
⇒ c + b = d + a
⇒ (c, d)R(a, b)
⇒ R is symmetric on N × N.
Now, let (a, b), (c, d), (e, f) ∈ N × N, such that (a, b)R(c,d) and (c, d)R(e, f).
∵ (a, b)R(c,d)
⇒ a + d= to + c …(i)
∵ (c, d)R(e, f)
⇒ c + f = d + e …(ii)
On adding Eqs. (i) and (ii), we get (a + d) + (c + f) = (b + c) + (d + e)
⇒ a + f = b + e
⇒ (a, b)R(e, f)
Thus, (a, b) R(c, d) and (c, d) R(e, f).
⇒ (a, b)R(e, f)for all (a, b),(c, d), (e, f) ∈ N × N
⇒ R is transitive on N × N.
⇒ R is an equivalence relation on N × N

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
If AB = BA for any two square matrices, then prove by mathematical induction that (AB)ⁿ = AⁿBⁿ.
Or
Solution:
Let P(n): (AB)ⁿ = AⁿBⁿ
∴ P(1) : (AB)¹ = A¹B¹ ⇒ AB = AB
So, P(1) is true.
Now, P(k): (AB)^k = A^kB^k, k ∈ N
So, P(k) is true, whenever P(k +1) is true.
∴ P(AB)^k+1 = A^k+1B^k+1
⇒ A^kB^k.BA = A^kB^k+1 ⇒ A^k . A . B^k+1 = A^k+1B^k+1
⇒ (A.B)^k+1 = A^k+1B^k+1
So, P(k + 1)is true for all n ∈ N, whenever P(/r)is true. By mathematical induction, (AB) = AⁿBⁿ
is true for all a ∈ N. Hence proved.
Or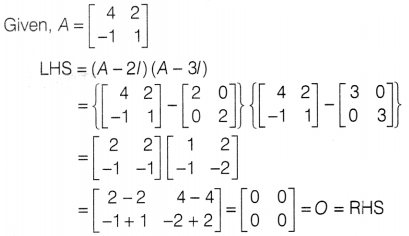

Hence proved.

Question 22.
Find the position vector of a point R which divides the line joining the points
P\((\hat{i}+2\hat{j}-\hat{k})\) andQ\((-\hat{i}+\hat{j}+\hat{k})\) in the ratio 2 : 1
(i) internally.
(ii) externally.
Solution:

Question 23.
Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
Or
II (a, b), (a’, b’) and (a – a’, b – b’) are collinear, then prove that ab’ = a’b.
Solution:
Given points are (a + 5, a – 4), (a -2, a + 3) and (a, a).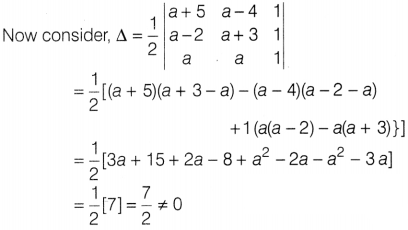

which is also independent of a.
Hence, the given points form a triangle i.e. given points do not lie on a straight line for any value of a.
Hence proved.
Or
If given points are collinear, then

Question 24.
Find the general solution of the differential equation \(\frac{dy}{dx}\) = e^{x +y}.
Solution:
The given differential equation is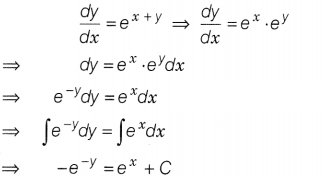

which is the required solution.

Question 25.
The x-coordinate of a point on the line joining the points P(2, 2, 1) and Q(5, 1, -2) is 4. Find its z-coordinate.
Solution:
The equation of line joining the points
P(2, 2, 1) and Q(5, 1, -2) is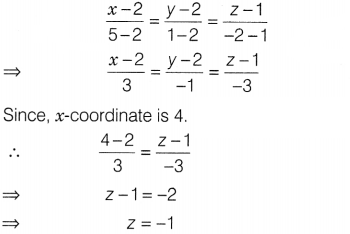

Section C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.
Find the inverse of the matrix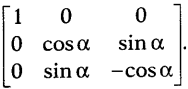

Solution: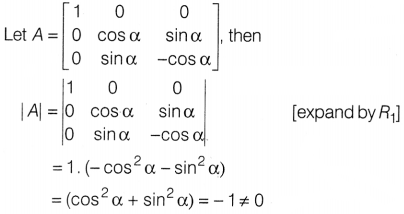

⇒ A^-1 exists.
To find adj A,
A₁₁ = -1, A₁₂ = 0, A₁₃ = 0; A₂₁ = 0, A₂₂ = -cos α, A₂₃ = -sin α.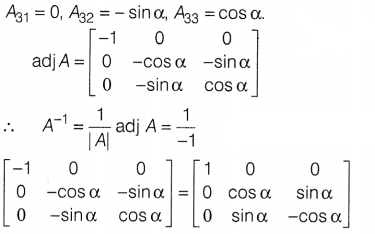

Question 27.
Using integration, find the area of the region bounded by the curves y = |x + 1| + 1, x = -3, A = 3 and y = 0.
Solution:
Given curves are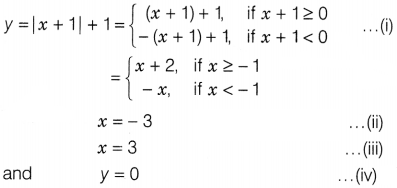

Eq. (ii) represents the line parallel to V-axis and passes through the point (- 3, 0).
Eq. (iii) represents the line parallel to Y-axis and passes through the point (3, 0).
Eq. (iv) represents X-axis.
Now, Eqs. (i), (ii), (iii) and (iv) can be represented in graph as shown below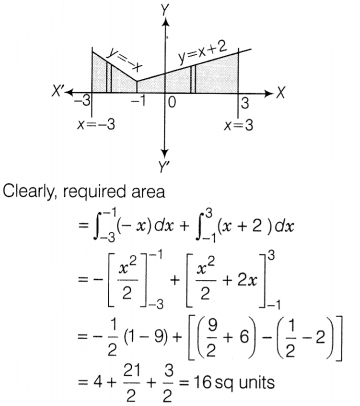

Hence, the required area is 16 sq units.

Question 28.
If the sum of two unit vectors \(\hat{a}\) and \(\hat{b}\) is a unit vector, then show that the magnitude of their difference is √3.
Or
If |\(\vec{a}\)| = 10, |\(\vec{b}\)| = 2 and \(\vec{a}.\vec{b}\) = 12, then find the value of |\(\vec{a}\times\vec{b}\)|.
Solution:
Let \(\vec{c}=\hat{a}+\hat{b}\) = a + b. Then, according to given condition c is a unit vector i. e.|\(\vec{c}\)| = 1 …(i)
To show |\(\hat{a}-\hat{b}\)| = √3

Question 29.
Find ∫\(\frac{x^2+x+1}{(x+1)^2(x+2)}\)dx.
Or
Evaluate ∫\(\frac{sin(x-\alpha)}{sin(x+\alpha)}\)dx
Solution: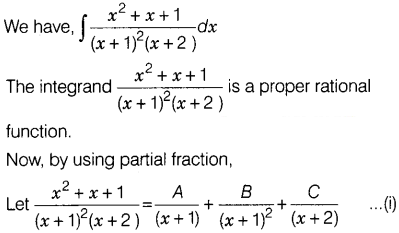

⇒ x² + x + 1 = A(x + 1)(x + 2) + B (x + 2) + C(x + 1)²
⇒ x² + x + 1 = A(x² + 3x + 2) + B(x + 2 ) + C(x² + 2x + 1)
⇒ x² + x + 1 = (A + C)x² + (3A + B + 2C)x + (2A + 2B + C)
On comparing the coefficients of like powers from both sides, we get
A + C = 1
3A + B + 2C = 1 and 2A + 2B + C = 1
On solving these equations, we get
A = -2, B = 1 and C = 3
From Eq.(i), we get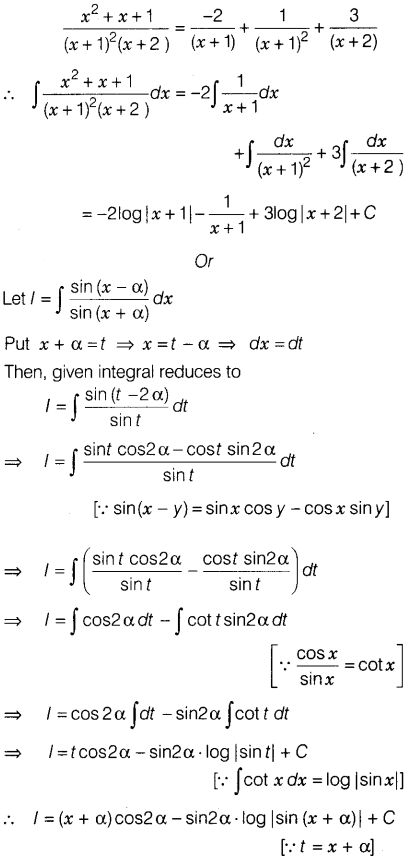

Question 30.
Find the value of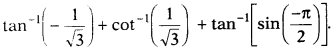

Solution: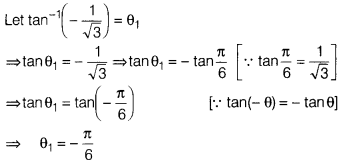

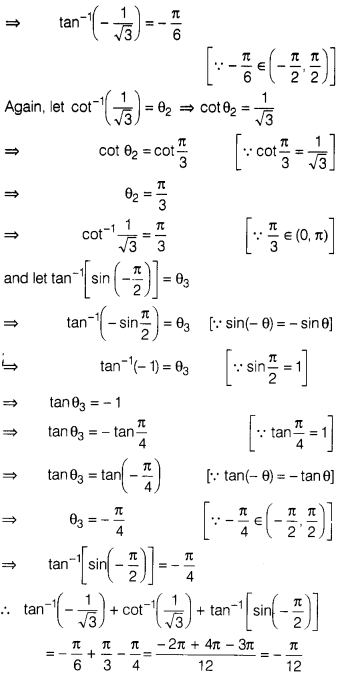
Question 31.
Find the value of a, for which the function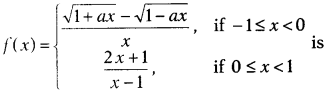

continuous at x = 0.
Or
If x = a(2t – sint) and y = a(1 – cost), then find \(\frac{dy}{dx}\) when θ = \(\frac{\pi}{6}\)
Solution:

Section D
(This section comprises of long answer type questions (LA) of 5 marks each)

Question 32.
Solve the following differential equation
Solution:
Given differential equation is


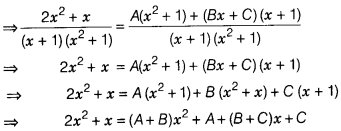
On comparing the coefficients of x², x and constant terms from both sides, we get
A + B = 2, B + C = 1
and A + C = 0 ⇒ A = -C
On solving above equations, we get
A = \(\frac{1}{2}\), B = \(\frac{3}{2}\) and C = – \(\frac{1}{2}\)
On substituting the values of A, B and C in Eq. (ii), we get

which is the required solution.

Question 33.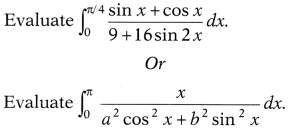

Solution:

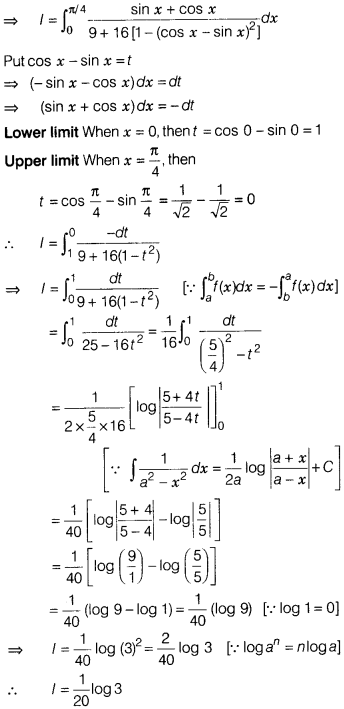
Question 34.
Determine graphically the minimum value of the objective function
Z = – 50x + 20y, subject to constraints are
2x – y ≥ – 5, 3x + y ≥ 3, 2 x – 3y ≤ 12 and x ≥ 0, y ≥ 0.
Or
Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below
2 x + 4y ≤ 8, 3x + y ≤ 6,
x + y ≤ 4, x > 0, y≥0.
Solution:
Given objective function is
Minimise Z = – 50x + 20y
Subject to constraints, 2x – y ≥ – 5 …..(i)
3x + y ≥ 3 …..(ii)
2x – 3y ≤ 12 …..(iii)
and x ≥ 0, y ≥ 0 …..(iv)
Table for line 2x – y = -5 is

x	-5/2	0
y	0	5

So, the line passes through the points (\(\frac{-5}{2}\), 0) and (0, 5).
On putting (0, 0) in the inequality 2x – y ≥ -5, we get
0 – 0 ≥ -5
⇒ 0 ≥ -5, which is true.
So, the half plane is towards the origin.
Table for line 3x + y = 3 is

x	0	1
y	3	0

So, the line passes through the points (0, 3)and(1, 0). On putting (0, 0) in the inequality 3x + y ≥ 3, we get
0 + 0 ≥ 3
⇒ 0 ≥ 3, which is not true.
So, the half plane is away from the origin.
Table for line 2x – 3y = 12 is

x	0	6
y	-4	0

So, the line passes through the points (0, -4) and (6, 0).
On putting (0, 0)in the inequality 2x – 3y ≤ 12, we get
0 – 0 ≤ 12
⇒ 0 ≤ 12, which is true.
So, the half plane is towards the origin.
Also, x ≥ 0 and y ≥ 0, so the region lies in the 1st quadrant.
On drawing the graph of each linear equation, we get the following graph. In first quadrant, these equations has no intersection point.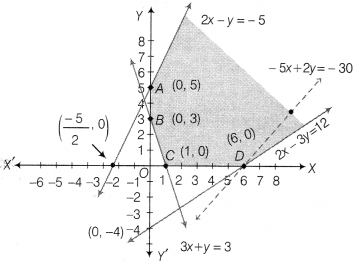

which gives the feasible region and it is unbounded. The corner points of feasible region are A(0, 5), B(0, 3), C(1, 0)and D(6, 0).
The value of Z at corner points are given below

Corner points	Z = -50x + 20y
A(0, 5)	Z = – 50(0)+ 20(5) = 100
B(0, 3)	Z = – 50(0) + 20(3) = 60
C(1, 0)	Z = – 50(1) + 20(0) = – 50
D( 6, 0)	Z = – 50(6) + 20(0) = – 300

Here, feasible region is unbounded so the minimum and maximum value may or may not exist.
Now, we draw a dotted line of inequation
– 50x + 20y < -300 or – 5x + 2y < -30

Here, we see that half plane determined by – 5x + 2y < – 30 has a point in common with the feasible region.
Hence, no minimum value exists.
Or
We have the following LPR,
Maximise, Z = 2x + 5y
Subject to constraints,
2x + 4y < 8 or x + 2y ≤ 4
3x + y ≤ 6
x + y ≤ 4
and x ≥ 0, y ≥ 0
Now, considering the inequations as equations, we
get x + 2y = 4 …(i)
3x + y = 6 …(ii)
and x + y = 4 …(iii)
Table for line x + 2y = 4 is

x	4	0
y	0	2

So, the line passes through (4, 0) and (0, 2).
On putting (0, 0) in the inequality x + 2y ≤ 4, we get
0 + 0 ≤ 4 [which is true]
So, the half plane is towards the origin.
Table for line 3x + y = 6 is

x	2	0
y	0	6

So, the line passes through (2, 0) and (0, 6).
On putting (0, 0) in the inequality 3x + y ≤ 6, we get
0 + 0 ≤ 6 [which is true]
So, the half plane is towards the origin.
Table for line x + y = 4 is

x	4	0
y	0	4

On putting (0, 0) in the inequality x + y ≤ 4, we get
0 + 0 ≤ 4 [which is true]
So, the half plane is towards the origin.
Also, x ≥ 0, y ≥ 0 , so the region lies in the 1st quadrant.
The graphical representation of the above system of inequations is given below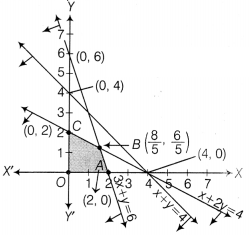

Clearly, the feasible region is OABCO.
The intersection point of lines (i) and (ii) is B(\(\frac{8}{5}\), \(\frac{6}{5}\))
Thus, the corner points are
O(0, 0), A(2, 0), B(\(\frac{8}{5}\), \(\frac{6}{5}\)), C(0, 2).
The values of Z at corner points are as follows

Hence, the maximum value of Z is 10.

Question 35.
If y = (log x)^x + x^{log x}, then find \(\frac{dy}{dx}\).
Solution:
We have, y = (logx)^x+ x^{log x}
Let u = (log x)^x and v = x^{log x}
Then, y = u + v
⇒ \(\frac{dy}{dx}=\frac{du}{dx}+\frac{dy}{dv}\) …….(i)
Consider, u = (logx)^x
On taking log both sides, we get
log u = log(logx)^x = xlog(log x)
On differentiating both sides w.r.t. x, we get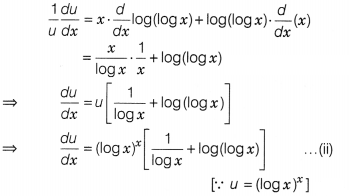

Now, v = x^{log x}
On taking log both sides, we get
log v = log(x^{log x})
= (log x) (log x)
= (log x)²
On differentiating both sides w.r.t. x, we get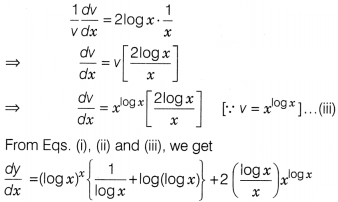

Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
If a real valued function f(x) is finitely derivable at any point of its domain, it is necessarily continuous at that point. But its converse need not be true.
e.g. Every polynomial, constant functions are both continuous as well as differentiable and inverse trigonometric functions are continuous and ‘ differentiable in their domain etc.
Based on the above information, answer the following questions,
(i) Write the interval in which the function f(x) = cos^-1 x is always continuous.

(iii) Show that the function f(x) = |x – 2|, x ∈ R, is continuous at x = 2.
Or Show that the function f(x) = |cos 2x| is continuous at x = \(\frac{\pi}{4}\)
Solution:
(i) cos^-1 x is always continuous in its domain, x ∈ [-1, 1].

Question 37.
In a classroom, a teacher teaches a topic ‘Relation on a set’, which is defined below.

A relation Ron a set A is said to be an equivalence relation on A iff it is
I. Reflexive i.e. aRa or (a, a) ∈ R,∀ a ∈ A.
II. Symmetric i.e. aRb ⇒ bRa
or(a, b) ∈ R ⇒ (b, a) ∈ R, where a,b ∈ A.
III. Transitive i.e. if aRb and bRc, then aRc
or (a, b) ∈ R and (b, c) ∈ R
⇒ (a, c) ∈ R, where a, b, c ∈ A.
Based on the above information, answer the following questions.
(i) If the relation R = {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)} defined on the set A = {1, 2, 3}, then show that R is reflexive but neither symmetric nor transitive.
(ii) If the relation R = {(1, 2), (2, 1), (1, 3), (3, 1)} defined on the set A = {1, 2, 3}, then show that R is symmetric but neither reflexive nor transitive.
(iii) If the relation R on the set N of all natural numbers defined as R = {(x, y): y – x + 5 and x < 4}, then show that R is neither reflexive, nor symmetric nor transitive.
Or
The relation R in the set Z of integers given by R = {(a, b): 2 divides (a – b)}, show that R is an equivalence relation.
Solution:
(i) ∵ (1, 1), (2, 2), (3, 3) ∈ R
⇒ R is reflexive on A.
Now, (1, 2) efl but (2, 1) ∈ R
⇒ R is not symmetric on A.
Now, (2, 3) eRand (3, 1) eRbut (2, 1) ∈ R
⇒ R is not transitive on A.

(ii) ∵ j(d, .1) (2, 2) and (3, 3) are not in R.
⇒ R is not reflexive on A.
∵ (1, 2) ∈ R ⇒ (2, 1) eR and (1, 3) ∈ R.
⇒ (3, 1) ∈ R fl is symmetric.
∵ (1, 2) ∈ R and (2, 1) ∈ R but (1, 1) ∉ R
∴ R is not transitive on A.

(iii) Given, R={(x, y):y = x + 5 and x < 4}, where x, y ∈ N
R = {( 1,6), (2, 7), (3, 8)}
∵ (1, 1), (2, 2) and (3, 3) are not in R.
So, R is not reflexive.
Now, (1, 6) ∈ R but (6, 1) ∉ R
⇒ R is not symmetric.
Now, (1, 6) ∈ R and there is no order pair in R which has 6 as the first element.
Similar is the case for (2, 7) and (3, 8).
⇒ R is not transitive.
Or
Given, R={(a,b) : 2 divides(a – d)}
and Z = Set of integers
Reflexive Let aeZ be any arbitrary element.
Now, if (a, a) ∈ R, then 2 divides a-a, which is true.
So, R is reflexive.
Symmetric Let a.b ∈ Z, such that (a, b) ∈ R.
2 divides (a – b).
⇒ 2 divides [-(a – b)]
⇒ 2 divides (b – a) ⇒ (b, a) ∈ R
So, R is symmetric.
Transitive Let a,b,c ∈ Z, such that (a, b) ∈ R and (b.c) ∈ R.
⇒ a – b and b – c both are divisible by 2.
⇒ a-b + to -c is divisible by 2.
⇒ (a – c) is divisible by 2 ⇒ (a, c) ∈ R
So, R is transitive.
Thus, R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation.

Question 38.
In a school, teacher asks a question to three students Ravi, Mohit and Sonia.
The probability of solving the question by Ravi, Mohit and Sonia are 30%, 25% and 45%, respectively. The probability of making error by Ravi, Mohit and Sonia are 1%, 1.2% and 2%, respectively.

Based on the above information, answer the following questions.
(i) Find the total probability of committing an error in solving the question.
(ii) If the solution of question is checked by teacher and has some error, then find the probability that the question is not solved by Ravi.
Solution:
Let
A = The event that question has some error
E₁ = The event that question is solved by Ravi
E₂ = The event that question is solved by Mohit
E₃ = The event that question is solved by Sonia
Then, we have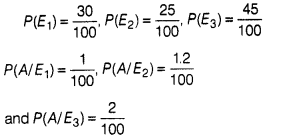

(i) Required probability = P(A)