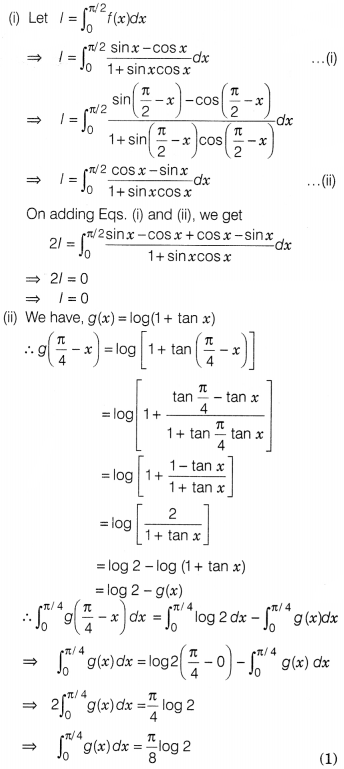CBSE Sample Papers for Class 12 Maths Set-6

CBSE Sample Papers for Class 12 Maths Set 6 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case/passage based/intergrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

Questions 1.
If a line makes angles 90°, 135° and 45° with the positive directions of X, Y and Z-axes, then its direction cosines are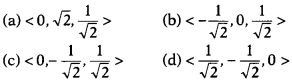

Solution:
(c) Let the direction cosines of the line be l, m, and n, then
l = cos 90° = 0, m = cos 135° = –\({\frac{1}{\sqrt2}}\)
and n = cos 45° = \({\frac{1}{\sqrt2}}\)

Hence, the direction cosines of the line are
<0, –\({\frac{1}{\sqrt2}}\), \({\frac{1}{\sqrt2}}\)>

Questions 2.
The projection of the vector \(\hat{i}-\hat{j}\) on the vector \(\hat{i}+\hat{j}\) is
(a) 1
(b) 0
(c) 2
(d) 5
Solution:

Question 3.
If a matrix has 8 elements, then which of the following will not be a possible order of the matrix?
(a) 1 × 8
(b) 2 × 4
(c) 4 × 2
(d) 4 × 4
Solution:
(d) We know that if a matrix of order mxn, then it has mn elements. Thus, to find all the possible order of a matrix with 8 elements, we will find all the ordered pairs of natural numbers, whose product is 8. Thus, all possible ordered pairs are (1, 8), (8, 1), (2, 4), (4, 2).

Question 4.
The probability distribution of a random variable x is given as under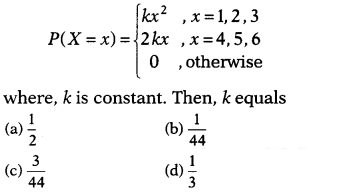

Solution:
(b)The probability distribution is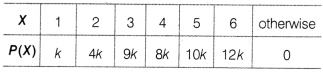

We know that ∑ P_l = 1
∴ k + 4k + 9k + 8k + 10k + 12k = 1
⇒ 44k = 1
⇒ k = \({\frac{1}{44}}\)

Question 5.

not invertible?
Solution:
(c) The given matrix is not invertible, if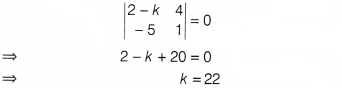

Question 6.
A vector in the direction of a vector \(\vec{a}=\hat{i}-\hat{j}+\hat{k}\), which has magnitude 8 units is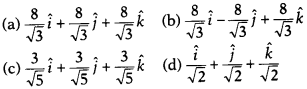

Solution:

Question 7.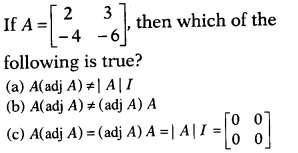

(d) None of the above
Solution:
(c) We know that, if A is any square matrix of order n, then A(adj A) = (adj A) . A = |A| . l.

Question 8.
If the area of a triangle with vertices (-3, 0), (3, 0) and (0, k) is 9 sq units, then the value of k is
(a) ±4
(b) ± 2
(c) ±3
(d) ± 1
Solution:
(c) Given area of a triangle with vertices (-3, 0), (3, 0) and (0, k) is 9 sq units.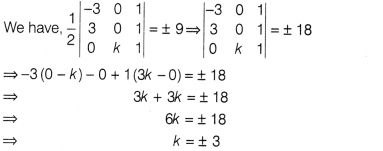

Question 9.
If two events A and B are mutually exclusive, then P( A/B) equals
(a) 0
(b) 1
(c) 0.5
(d) 0.25
Solution:
(a) We know that if A and B are mutually exclusive, then P(A ∩ B) = 0.

Question 10.
The direction cosines of a line are k, k, k, then
(a) k > 0
(b) 0 < k < 1
(c) k = 1
(d) k = ± \({\frac{1}{\sqrt3}}\)
Solution:
(d) We have, l = m = n = k
We know that l² + m² + n² = 1
⇒ k² + k² + k² = 1 ⇒ 3k² = 1
⇒ k² = \(\frac{1}{3}\)
⇒ k = ±\({\frac{1}{\sqrt3}}\)

Question 11.
The order and degree of the differential equation \(\frac{d^2y}{dx^2}+(\frac{dy}{dx})^{\frac{1}{4}}\) + x^1/5 = 0 respectively, are
(a) 2 and 4
(b) 2 and 2
(c) 2 and 3
(d) 3 and 3
Solution:

Question 12.
The direction ratios of the line \(\frac{x+2}{2}=\frac{2y-5}{-3}\), z = 2 are
(a) 1, 1, 5
(b) 2, 1, 3
(c) 4, 3, 0
(d) 4, -3, 0
Solution:
(d) Given, equation of line can be written as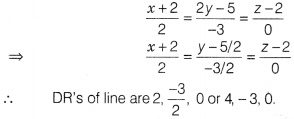

Question 13.
Which of the following is not a homogeneous function of x and y ?
(a) x² + 2xy
(b) 2x – y
(c) cos²(\(\frac{y}{x}\) + \(\frac{y}{x}\)
(d) sin x – cos y
Solution:
(d) Since, sin x-cos y can’t expressed in the form xⁿ(\(\frac{y}{x}\)) or yⁿh(\(\frac{x}{y}\)), therefore, it is not a homogeneous function.

Question 14.
The derivative of \(\frac{x^3}{cos x}\) is, when x = 0
(a) \(\frac{x^3}{sin x}\)
(b) 1
(c) 0
(d) \(\frac{x^2}{cos^2 x}\)
Solution: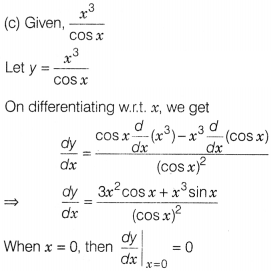

Question 15.
If y = x(x – 3)² decreases for the values of x given by
(a) 1 < x < 3
(b) x < 0
(c) x > 0
(d) 0 < x < \(\frac{3}{2}\)
Solution:
(a) We have, y = x(x – 3)²
∴ \(\frac{dx}{dy}\) = x . 2(x – 3) . 1 + (x – 3)² . 1
= 2x² – 6x + x² + 9 – 6x = 3x² – 12x + 9
= 3(x² – x + 3)= 3(x – 3)(x – 1)

So, y = x(x – 3)² decreases from (1, 3).
[since, y’ < 0 for all x ∈ (1, 3), hence y is decreasing on (1, 3)]

Question 16.
If a die is thrown and a card is selected at random from a deck of 52 playing cards, then the probability of getting an even number on the die and a spade card equals
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{8}\)
(d) \(\frac{1}{3}\)
Solution:
(c) Let the event A and B are getting an even number on die and getting spade card, respectively.

Question 17.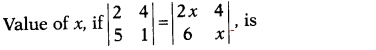

(a) ± √3
(b) 2
(c) ± 3
(d) ± √2
Solution: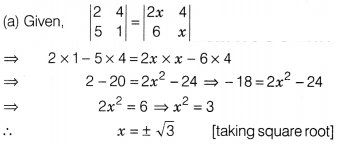

Question 18.
The interval in which y = x² e^-x is increasing, is
(a) (-∞, ∞)
(b) (-2, 0)
(c) (2, ∞)
(d) (0, 2)
Solution:
(d) Given, y = x²e^-x
On differentiating w.r.t. x, we get
\(\frac{dy}{dx}\) = x² e^-x (-1) + e^-x (2x)
= xe^-x(-x + 2) = xe^-x (2 – x)
For increasing function, \(\frac{dy}{dx}\) > 0
⇒ xe^-x (2 – x) > 0

Case I
⇒ x > 0 and 2 – x > 0
⇒ x > 0 and x < 2
⇒ 0 < x < 2

Case II
⇒ x < 0 and 2 – x < 0
⇒ x < 0 and x > 2
Hence, there is no value of x exist.
Clearly, it is increasing in (0, 2).

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true

Question 19.
Assertion (A) Let A = {2, 4, 6} and B = {3, 5, 7, 9} and defined a function f = {(2, 3), (4, 5), (6, 7)} from A to B. Then, f is not onto.
Reason (R) A function f: A → B is said to be onto, if every element of B is the image of some elements of A under f.
Solution:
(b) Assertion Given that,
A = {2, 4, 6},
B = {3, 5, 7,9}
and R = {(2, 3), (4, 5), (6, 7)}
Here, f(2) = 3, f(4) = 5 and f(6) = 7
It can be seen that the images of distinct elements of A under f are distinct.

Hence, function f is one-one but f is not onto, as 9 e 8 does not have a pre-image in A.
Hence, both Assertion and Reason are true, but Reason is not the correct explanation of Assertion.

Question 20.
Assertion (A) Consider the linear programming problem.
Maximize Z = 4x + y, subject to constraints are x + y ≤ 50, x + y ≥ 100, and x, y ≥ 0. Then, maximum value of Z is 50.
Reason (R) If the shaded region is not bounded, then maximum value cannot be determined.
Solution:
(d) Assertion Given, maximize Z = 4x + y
and x + y < 50, x + y > 100; x, y > 0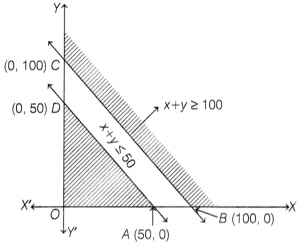

Hence, it is clear from the graph that it is not bounded region. So, maximum value cannot be determined.
Hence, Assertion is false but Reason is true.

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
Show that the area of a parallelogram having diagonals \(3\hat{i}+\hat{j}-2\hat{k}\) and \(\hat{i}-3\hat{j}+4\hat{k}\) is 5√3 sq units.
Solution:

Question 22.
If two vectors \(\vec{a}\) and \(\vec{b}\) are such that |\(\vec{a}\)| = 2, |\(\vec{b}\)| = 3 and \(\vec{a}.\vec{b}\) = 4, then find |\(\vec{a}-\vec{b}\)|.
Solution: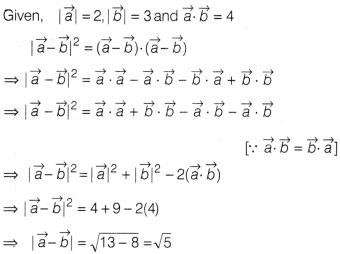

Question 23.
Evaluate ∫e^x (cos x – sin x)dx.
Or
Evaluate ∫xe^x dx.
Solution:
Let l = ∫e^x(cos x-s\nx)dx
⇒ I = ∫e^x{cos x + (-sin x)}dx
Let f(x) = cos x ⇒ f'(x) = -sin x
We know that ∫e^x{f{x)+ f'(x)}dx = e^x f(x) + C
∴ From Eq, (i), we get
l = e^x cos x + C
Or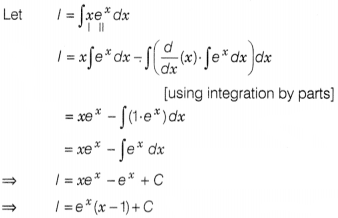

Question 24.
Let A and B be two events of the same sample space S of an experiment, then prove that 0 ≤ P (A/B) ≤ 1, B ≠ Φ.
Solution:

Question 25.
Evaluate \(\int_{-1}^1\)|1 – x|.
Or
Evaluate \(\int_0^3\)[x] dx, where [x] is the greatest integer function.
Solution: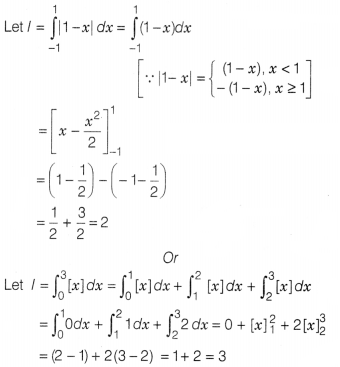

Section C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.
Determine f (0), so that the function f(x)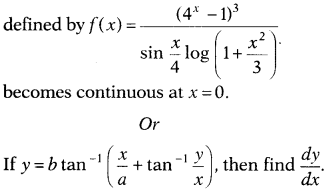

Solution:
For f(x) to be continuous at x = 0, we must have

Question 27.
Show that the relation S in set
A = {x ∈ Z : 0 ≤ x ≤ 12} given by
S = {(a, b): a, b ∈ A, |a – b| is divisible by 4}
is an equivalence relation. Find the set of all elements related to 1.
Solution:
Given relation is
S = {(a, b): |a – b| is divisible by 4 and a, b ∈ A} and A = {x : x ∈ Z and 0 < x < 12}
Now, A can be written as
A = {0, 1, 2, 3 12}
Reflexive As for any x ∈ A, we get
|x – x| = 0, which is divisible by 4.
⇒ (x, x) ∈ S, ∀ x ∈ A
Therefore, S is reflexive.
Symmetric As for any (x, y) ∈ S, we get | x – y| is divisible by 4. [by using definition of given relation]
⇒ | x – y| = 4λ., for some λ ∈ Z
⇒ |y – x| = 4λ, for some λ ∈ Z
⇒ (y, x) ∈ S
Thus, (x, y) ∈ S
⇒ (y, x) ∈ S, ∀ x, y ∈ A
Therefore, S is symmetric.

Transitive For any (x, y) ∈ S and (y, z) ∈ S, we get |x – y| is divisible by 4 and |y – z| is divisible by 4.
[by using definition of given relation]
⇒ | x – y| = 4λ and |y – z| = 4µ, for some λ, µ ∈ Z.
Now, x – z = (x – y) + (y – z)
= ± 4λ ± 4µ = ± 4 (λ + µ)
⇒ |x – z| is divisible by 4.
⇒ (x, z) ∈ S
Thus, (x, y) ∈ S and (y, z) ∈ S
⇒ (x, z) ∈ S, ∀ x, y, z ∈ A
Therefore, S is transitive.
Since, S is reflexive, symmetric and transitive, so it is an equivalence relation.
Now, set of all elements related to 1 is {1, 5, 9}.

Question 28.
Evaluate ∫tan(x – θ)tan(x + θ) tan 2xdx.
Or
Evaluate \(\frac{sin x – xcos x}{x(x+sin x)}\)dx
Solution:
We know that

Question 29.
Sketch the region {(x, y) : x = \(\sqrt{4-y^2}\)} and F-axis. Find the area of the region using integration.
Solution:
Given region is {(x, y): x = \({\sqrt{4-y^2}}\)} and Y-axis.
We have, x = \({\sqrt{4-y^2}}\) ⇒ x² = 4 – y² ⇒ x² + y² = 4
This represents the equation of circle having centre (0, 0) and radius 2.
But original equation isx = \({\sqrt{4-y^2}}\), so x is positive. It means that we have to take a curve to the right side of the Y-axis.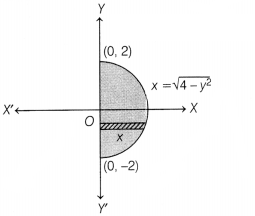

Thus, only semi-circle is formed to the right side of the Y-axis.
Since, the region is symmetrical about X-axis.
∴ Area of shaded region,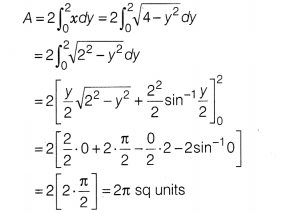

Question 30.
Find the intervals in which the function f (x) = 20 – 9x + 6x² – x³ is
(i) strictly increasing.
(ii) strictly decreasing.
Solution:
Given function is f(x) = 20 – 9x + 6x² -x³.
On differentiating both sides w.r.t. x, we get
f'(x) = – 9 + 12x – 3x²
On putting f(x) = 0, we get
-9+ 12x – 3x² = 0
⇒ -3 (x² – 4x + 3) = 0
⇒ -3 (x – 1)(x – 3) = 0
⇒ (x – 1)(x – 3) = 0
⇒ x – 1 = 0 or x – 3 = 0
⇒ x = 1 or 3
Now, we find intervals in which f(x) is strictly increasing or strictly decreasing.

Interval	f'(x) = -3 (x – 1) (x- 3)	Sign of f'(x)
x < 1	(-)(-)(-)	– ve
1 < x < 3	(-)(+)(-)	+ ve
x > 3	(-)(+)(+)	– ve

We know that a function f{x) is said to be strictly increasing when f’(x) > 0 and it is said to be strictly decreasing, if f'(x) < 0. So, the given function f(x) is
(i) strictly increasing on the interval (1, 3).
(ii) strictly decreasing on the intervals (-∞, 1) and (3, ∞).

Question 31.
Three cards are drawn successively without replacement from a pack of 52 well-shuffled cards. What is the probability that first two cards are king and the third card drawn is an ace?
Or
A and B are independent events. The probability that both A and B occur is \(\frac{1}{8}\) and the probability that neither occurs is \(\frac{3}{8}\). Find P(A) and P(B).
Solution:
There are 52 cards in a pack.
∴ n(S) = 52
Let A = Event that the card drawn is king
and B = Event that the card drawn is an ace.
Now, P(A) = \(\frac{4}{52}\)
P(\(\frac{A}{A}\)) = Probability of drawing second king when one king has already been drawn
= \(\frac{3}{51}\) [∵ remaining cards are (52 – 1) = 51]

P(\(\frac{B}{AA}\)) = Probability of drawing third card to be an A ace when two kings have already been drawn
\(\frac{4}{50}\)

Now, probability of getting first two cards are king and third card is an ace = P(A ∩ A ∩ B)

Section D
This section comprises of long answer type questions (LA) of 5 marks each

Question 32.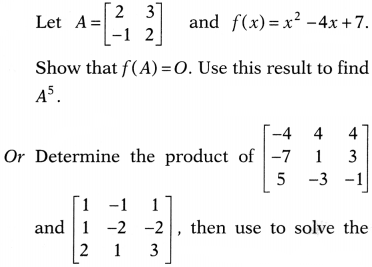

system of equations
x – y + z = 4, x – 2y – 2z = 9
and 2x + y + 3z = 1.
Solution:
We have, f(x) = x² – 4x + 7
∴ f(A) = A² – 4A + 7l₂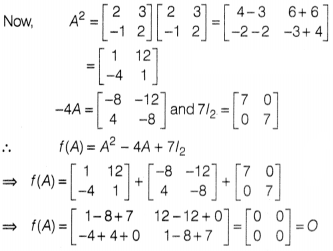

Hence proved
Now, f'(A) = 0
⇒ A² = 4A + 7l₂ =0 =
⇒ A² = 4A – 7l₂
⇒ A³ = A²A = (4A – 7l₂)A = 4A² – 7l₂A
⇒ A³ = 4(4A – 7l₂) – 7A [using A² = 4A – 7l₂]
⇒ A³ = 9A – 28l₂
⇒ A⁴ = A³A = (9A – 28l₂)A
⇒ A⁴ = 9A² – 28A = 9(4A – 7l₂) – 28A [using A² = 4A – 7l₂]
⇒ A⁴ = 36A – 63l₂ – 28A = 8A – 63l₂
⇒ A⁵ = A⁴A = (84 – 63l₂)A = 8A² – 63l₂A
⇒ A⁵ = 8(4A – 7l₂) – 63A = -31A – 56l₂ [using A² = 4A – 7l₂]


On comparing corresponding elements, we get
x = 3, y = -2 and z = -1

Question 33.
Solve \(\frac{dy}{dx}+\frac{1}{x}=\frac{e^y}{x}\).
Or
Solve x\(\frac{dy}{dx}\) + v – x + xy cot x = 0
Solution: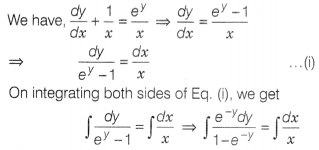

⇒ log(1 – e^-y) = log x + log C
⇒ log(1 – e^-y) = (log Cx) ⇒ 1 – e^-y = Cx
⇒ e^-y = 1 – Cx ⇒ -y = log(1 – Cx)
⇒ y + log(1 – Cx) = 0
Or
x\(\frac{dy}{dx}\) + y(1 + x cot x) = x dx
⇒ \(\frac{dy}{dx}\) + y(\(\frac{1}{x}\) + cot x) = 1 ….(i)
The given differential equation is a linear differential equation of the form \(\frac{dy}{dx}\) + Py = Q …(ii)
On comparing Eqs. (i) and (ii), we get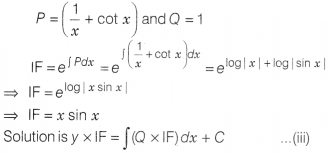

On putting values of IF and 0 in Eq. (iii), we get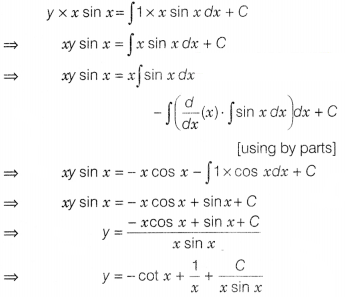

It is the required solution.

Question 34.
Vertices B and C of AABC lie along the line \(\frac{x+2}{2}=\frac{y-1}{1}=\frac{z-0}{4}\). Find the area of the triangle given that A has coordinates (1, -1, 2) and line segment BC has length 5 units.
Solution:
Let h be the height of ∆ABC. Then, h is the length of perpendicular from A(1, -1, 2) to the line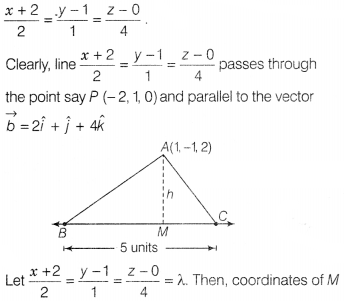

are (2λ – 2, λ + 1, 4λ).
Now, DR’s of AM are 2λ – 3, λ + 2 and 4λ – 2.
Since, AM ⊥ BC. therefore
2(2λ – 3) + 1(λ + 2) + 4(4λ – 2) = 0 [∵ DR’s of line BC are 2, 1, 4]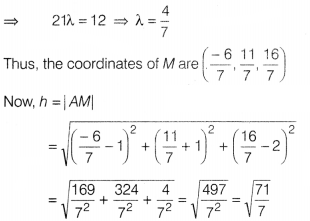

It is given that the length of BC is 5 units.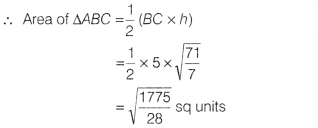

Question 35.
If (tan^-1 x)^y + y^{cot x} = 1, then find dy/dx.
Solution:
Letu = (tan^-1 x)^y and v = y^{cot x}
Then, given equation becomes u + v = 1
On differentiating both sides w.r.t. x, we get

Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
Ronit and Aman, two friends are standing on either side of a tower of 30 m high. They observe its top at the angle of elevation a and (3 respectively, (as shown in the figure below).
The distance between Ronit and Aman is 40 √3 m and distance between Ronit and tower is 30√3 m.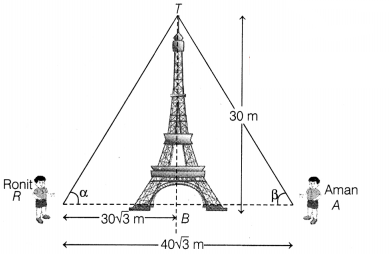

Based on the above information, answer the following questions.
(i) Find sin α.
(ii) Find ∠TAR.
(iii) If α = cos^-1(\(\frac{k_1}{k_2}\)), then find k₁ + k₂.
Or
Find ∠ATR.
Solution:
(i) In ∆RTB,

Question 37.
Suppose a dealer in rural area wishes to purchase a number of sewing machines. He has some money to invest and has space for few items for storage. Let x denotes the number of electronic sewing machines and y denotes the number of manually operated sewing machines purchased by the dealer.
For the same, constraint related to investment is given by 3x + 2y ≤ 48 and objective function is Z = 22x + 18y and other constraints consists the following x + y ≤ 20, x, y ≥ 0.

Based on the above information, answer the following questions.
(i) Find Z_{(3, 4)}.
(ii) Evaluate Z_{(\(\frac{1}{2},\frac{1}{3}\))}.
(iii) Find the number of corner points of the feasible region.
Or
Find Z_(max).
Solution: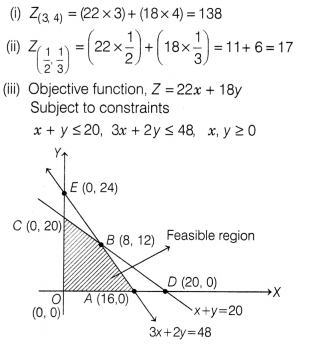

∴ Number of corner points are 4.
The coordinates of the corner points A, B, C and 0 are (16, 0), (8, 12), (0, 20) and (0, 0), respectively.

Corner points	Z = 22x + 18y
(0, 0)	0 (Minimum)
(16, 0)	352
(8, 12)	392 (Maximum)
(0, 20)	360

Z is maximum at the point (8, 12).
∴ To get maximum profit 8 electronic sewing machines and 12 manually operated sewing machines should be purchased by the dealer. Hence,
Hence Z_(max) = 392

Question 38.
If f(x) is a continuous function defined on [0, a], then \(\int_0^a\)d(x) dx = \(\int_0^a\)f(a – x) dx.
On the basis of above information, answer the following questions.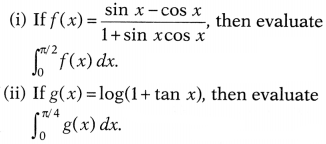

Solution: