CBSE Sample Papers for Class 12 Maths Set-5

CBSE Sample Papers for Class 12 Maths Set 5 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case/passage based/intergrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

Question 1.
The sum of order and degree of the differential equation (\(\frac{dy}{dx}\))² + 3y(\(\frac{d^2y}{dx^2}\)) = 0 is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(c) We have,
(\(\frac{dy}{dx}\))² + 3y(\(\frac{d^2y}{dx^2}\)) = 0
Here, order = 2 and degree = 1
∴ Required sum = 2 + 1 = 3

Question 2.
If y = x³ + tan x, then y” – 2 sec² x tan x equals
(a) 6
(b) 6x
(c) 3
(d) 3x
Solution:
(b) Given that
y = x³ + tan x
On differentiating both sides w.r.t. x, we get
y’ = 3x² + sec² x
Again, on differentiating both sides w.r.t. x, we get
y” = 6x + 2sec² x tan x
⇒ y” = -2sec² x tan x = 6x

Question 3.
If P(A) = \(\frac{7}{13}\), P(B) = \(\frac{9}{13}\) and P(A ∩ B) = \(\frac{4}{13}\), then P(\(\frac{A}{B}\)) equal
(a) \(\frac{1}{9}\)
(b) \(\frac{2}{9}\)
(c) \(\frac{3}{9}\)
(d) \(\frac{4}{9}\)
Solution:
(d) We know that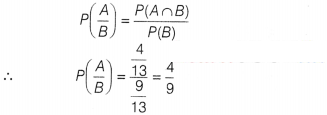

Question 4.
If x is real, then the minimum value of x² – 8x + 17 is
(a) -1
(b) 0
(c) 1
(d) 12
Solution:
(c) Let f(x) = x² – 8x + 17
∴ f'(x) = 2x – 8
So, f (x) = 0, gives x = 4
Now, f” (x) = 2 > 0 , ∀ x
So, x = 4 is the point of local minimum.
∴ Minimum value of f (x) at x = 4
f (4) = 4 × 4 – 8 × 4 + 17
= 1

Question 5.
The feasible region for an LPP is shown in the following figure.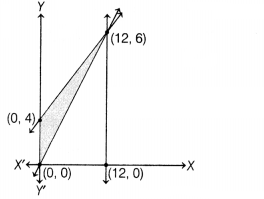

Let F = 3x – 4y be the objective function. Maximum value of F is
(a) 0
(b) 8
(c) 12
(d) -18
Solution:
(c) The feasible region as shown in the figure, has objective function F = 3x – 4y.

Corner points	Corresponding value of F = 3x – 4y
(0, 0)	0
(12, 6)	12 ← Maximum
(0, 4)	-16

Hence, the maximum value of F is 12.

Question 6.
If a leap year is selected at random, then what is the chance that it will contain 53 Tuesday?
(a) \(\frac{1}{7}\)
(b) \(\frac{2}{7}\)
(c) \(\frac{3}{7}\)
(d) \(\frac{5}{7}\)
Solution:
(b) In a leap year, there are 366 days i.e, 52 weeks and 2 days.
The two days can be
(1) Sunday and Monday
(2) Monday and Tuesday
(3) Tuesday and Wednesday
(4) Wednesday and Thursday
(5) Thursday and Friday
(6) Friday and Saturday
(7) Saturday and Sunday
∴ Total number of cases = 7
Number of favourable cases = 2
∴ Required probability = \(\frac{2}{7}\)

Question 7.
The value of λ, so that the vectors \(\vec{a}=3\hat{i}+2\hat{j}+9\hat{k}\) and \(\vec{b}=\hat{i}+\lambda\hat{j}+3\hat{k}\) are perpendicular to each other is
(a) 15
(b) -15
(c) 12
(d) -12
Solution:

Hence, the required value of λ is -15.

Question 8.
Solve x³y dx = dy, given that y = 1 when x = 1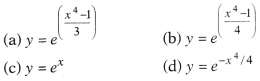

Solution:
(b) We have, x³y dx = dy ⇒ x³dx = \(\frac{dy}{y}\)
On integrating both sides, we get
∫x³dx = ∫\(\frac{dy}{y}\) ⇒ \(\frac{x^4}{4}\) = logy + C …(i)
which is a general solution of the given differential equation.
Also, given y = 1, when x = 1
∴ From Eq. (i), we get C = \(\frac{1}{4}\)
On putting the value of C in Eq. (i), we get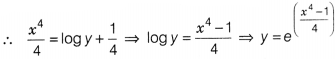

Question 9.
If y = log_a x, then \(\frac{dy}{dx}\) equal to

Solution:
(a) We have,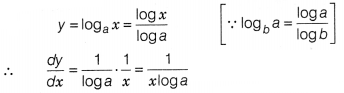

Question 10.
Which of the following statements is true for f(x) = 4x³ – 6x² – 72x + 30 ?
I. f is strictly increasing in the interval (-∞, -2).
II. f is strictly increasing in the interval (3, ∞).
III. f is strictly decreasing in the interval (-2, 3).
IV. f is neither increasing nor decreasing in R.
(a) I and II are true
(b) II and III are true
(c) II and IV are true
(d) All are true
Solution:
(d) We have, f(x) = 4x³ – 6x² – 72x + 30
On differentiating w.r.t. x, we get
f'(x) = 12x² – 12x – 72
= 12(x² – x – 6) = 12(x – 3) (x + 2)
Therefore, f'(x)= 0 gives x = – 2, 3.
The points x = – 2 and x = 3 divides the real line into three disjoint intervals, namely, (-∞, -2), (-2, 3) and (3, ∞).

In the intervals (-∞, – 2) and (3, ∞), f'(x)is positive while in the interval (- 2, 3), f'(x) is negative.
Consequently, the function f is strictly increasing in the intervals (-∞, – 2) and (3, ∞) while the function is strictly decreasing in the interval (-2, 3).
However, f is neither increasing nor decreasing in R.

Interval	Sign of f'(x)	Nature of function f
(-∞, -2)	(-)(-) > 0	f is strictly increasing
(-2, 3)	(-)(+) < 0	f is strictly decreasing
(3, ∞)	(+)(+) > 0	f is strictly increasing

Question 11.
If A and B are two independent events with P(A) = \(\frac{3}{5}\) and P(B) = \(\frac{4}{9}\), then P(A’ ∩ B’) equal to
(a) \(\frac{4}{15}\)
(b) \(\frac{8}{45}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{2}{9}\)
Solution:
(d)P{A’ ∩ B’) = -1 – P(A ∪ B)
= 1 -[P(A)+ P(B)-P(A ∩ B)]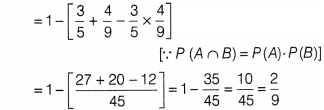

Question 12.
If A ⊂ B, then P(B / A) equals
(a) 1
(b) 0
(c) 0.5
(d) 0.25
Solution: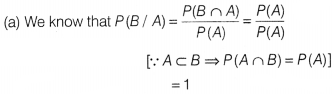

Question 13.
Evaluate \(\int_0^{2 \pi}\frac{3^{sin x}}{1+3^{sin x}}\)
(a) 2π
(b) \(\frac{\pi}{2}\)
(c) 3π
(d) π
Solution:

Question 14.
If y = tan x \(\frac{1}{3}\) log x – \(\frac{2}{x}\), then \(\frac{dy}{dx}\) is equal to
(a) sec x – \(\frac{1}{3x}+\frac{2}{x^2}\)
(a) sec² x – \(\frac{1}{3x}+\frac{2}{x^2}\)
(c) sec x – 3x + x²
(d) None of these
Solution:
(b) We have, y = tanx – \(\frac{1}{3}\) logx – \(\frac{2}{x}\)
On differentiating both the sides w.r.t. x, we get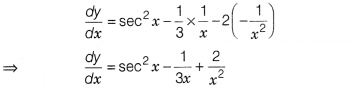

Question 15.
The equation of a line passing through the point (-3, 2, -4) and equally inclined to the axes are
(a) x – 3 = y + 2 = z – 4
(b) x + 3 = y – 2 = z + 4
(c) \(\frac{x+3}{1}=\frac{y-2}{2}=\frac{z+4}{3}\)
(d) None of these
Solution:
(b) Here, l = m = n, therefore required equation of line is

∴ x + 3 = y – 2 = z + 4

Question 16.
Evaluate \(\int_{-1}^1\frac{3x^2}{1+4^{tan x}}\) dx.
(a) 1
(b) 2
(c) 3
(d) 0
Solution: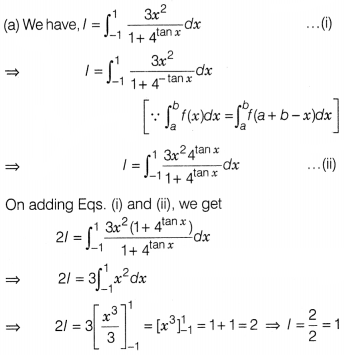

Question 17.
If |\(\vec{a}\)| = 20, |\(\vec{b}\)| = 4 and \(\vec{a}.\vec{b}\) = 24, then |\(\vec{a}\times\vec{b}\)| is equal to
(a) 30
(b) 32
(c) 0
(d) 24
Solution:

Question 18.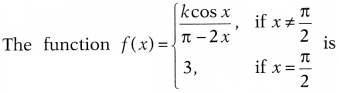

continuous at x = \(\frac{\pi}{2}\), when k equals
(a) -6
(b) 6
(c) 5
(d) -5
Solution: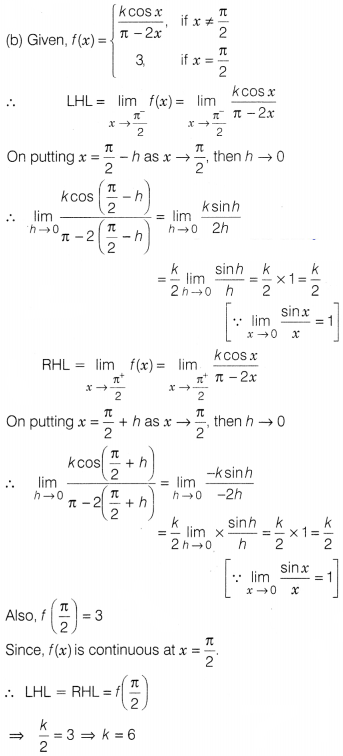

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true

Question 19.
Assertion (A) Let a relation R defined from set A = {1, 2, 5, 6} to A is
R = {(1, 1), (1, 6), (6, 1)}, then R is symmetric relation.
Reason (R) A relation R in set A is called symmetric, if (a, b) ∈ R
⇒ (b, a) ∈ R for every a, b ∈ A.
Solution:
(a) Assertion We have, A = { 1,2, 5, 6}
and R = {(1, 1), (1, 6), (6, 1)}
Here, (1, 6) ∈ R ⇒ (6, 1) ∈ R
So, R is symmetric relation.
Hence, Assertion is true and Reason is also true and Reason is the correct explanation of Assertion.

Question 20.
Assertion (A) The inverse of sine function is define in the interval [-π, 0], [0, π] etc.
Reason (R) The inverse of sine function is denoted by sin^-1.
Solution:
(d) Assertion Sine function is one-one and onto in the

range is [-1, 1],
So, inverse of sine function is define in each of these intervals.
Reason We denote the inverse of sine function by sin^-1 (arc sine function).
Hence, we can say that the Reason is true and Assertion is false.

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
Evaluate ∫sin x sin 2 x sin 3x dx.
Or Evaluate ∫ tan⁴ x dx
Solution:
Let l = ∫sinx sin2x sin3xdx
= \(\frac{1}{2}\)∫(2sinx sin2x)sin3x dx
= \(\frac{1}{2}\)∫(cosx – cos3x)sin3x dx
= \(\frac{1}{4}\)∫(2sin3xcosx – 2sin3xcos3x)dx
= \(\frac{1}{4}\)∫(sin4x + sin2x – sin6x)dx
= \(\frac{1}{4}\)[-\(\frac{cos 4x}{4}-\frac{cos 2x}{2}+\frac{cos 6x}{6}\)] + C
Or
Let l = ∫tan⁴xdx
= ∫tan²x(sec²x -1)dx
= ∫tan² xsec² xdx – ∫tan²xdx
= ∫tan² xsec² xdx – ∫(sec²x -1)dx

On putting tan x=t and sec² xdx =dt in first integral, we get
= ∫ t²dt- ∫(sec²x – 1)dx
= ∫t²dt – ∫sec²xdx + ∫1dx
= \(\frac{r^3}{3}\) – tan x + C = \(\frac{tan^{3}}{3}\) – (tan x – x) + C

Question 22.
If the points A(-1, 3, 2), B(-4, 2, -2) and C(5, 5, λ) are collinear, find the value of λ.
Solution:
The equations of line passing through A(-1, 3, 2) and 8(-4, 2, -2) is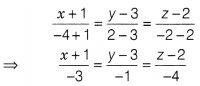

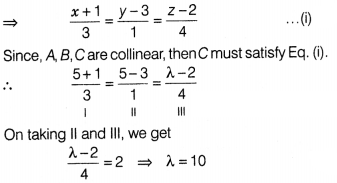
Question 23.
Show that the function f(x) = (x³ – 6x² + 12x -18) is an increasing function on R.
Or
Prove that the function f given by f(x) = log cos x is strictly decreasing x ∈ (0, \(\frac{\pi}{2}\)).
Solution:
We have, f(x) = x³ – 6x² + 12x – 18
∴ f'(x) = 3x² – 12x + 12 = 3(x² – 4x + 4)
= 3(x – 2)² ≥ ∀ x ∈ R
∴ f'(x) ≥ 0 ∀ x ∈ R
Hence, f(x) is increasing function on R.
Or
Given, f(x) = log cos x
On differentiating both sides w.r.t. x, we get
∴ f'(x) = – tan x < 0
Hence, f(x) is strictly decreasing. Hence proved.

Question 24.
Solve \(\frac{dy}{dx}\) + 2 y = e^3x.
Solution:
We have, \(\frac{dy}{dx}\) + 2y = e^3x
This is of the form \(\frac{dy}{dx}\) + Py = Q.
Here, P = 2 and Q = e^3x
∴ IF =e^∫2dx = e^2x
The solution is given by
y × IF = ∫(Q × IF)dx + C
⇒ y e^2x =∫e^2x . e^3xdx + C
⇒ ye^2x = ∫e^5xdx + C
⇒ ye^2x = \(\frac{1}{5}\)e^5x + C
⇒ y = \(\frac{1}{5}\)e^3x + Ce^-2x

Question 25.
Solve \(\frac{dy}{dx}=\frac{3e^{2x}+3e^{4x}}{e^x+e^{-x}}\)
Solution: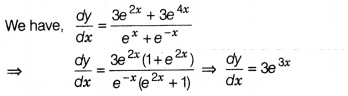

⇒ dy = 3e^3x dx
On integrating both sides, we get
∫ldy = 3∫e^3xdx ⇒ y = e^3x + C

Section C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.
If y = (x)^x + (sin x)^x, then find \(\frac{dy}{dx}\).
Solution:
Given, y = (x)^x +(sin x)^x
Let u = (x)^x and v = (sin x)^x
Then, given equation becomes, y = u + v
On differentiating both sides w.r.t. x, we get
\(\frac{dy}{dx}=\frac{du}{dx}+\frac{dv}{dx}\) …..(i)
Consider, u = x^x
On taking log both sides, we get
log u = log x^x
⇒ log u = x log x [∵ log mⁿ = n log m]

On differentiating both sides w.r.t. x, we get
dy_du dv dx dx dx [by using product rule of derivative]
Consider, u = xx On taking log both sides, we get log u = log xx => log u = x log x
[v log mt – n log m]
On differentiating both sides w.r.t. x, we get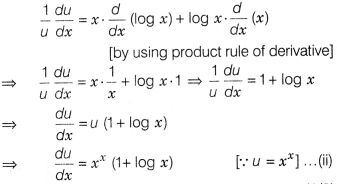

Now consider, v = (sin x)^x
On taking log both sides, we get
log v = log (sin x)^x
⇒ log v = x log (sin x) [∵ log mⁿ = n log m]
On differentiating both sides w.r.t. x, we get

Now, from Eqs. (i), (ii) and (iii), we get
\(\frac{dy}{dx}\)= x^x (1 + log x)+ (sin x)^x (x cot x + log sin x)dx

Question 27.
Let A = {1, 2, 3, ….,9} and R be the relation in A × A defined by (a, b) R(c, d), if a + d = b + c for (a, b),(c, d) in A × A. Prove that R is an equivalence relation.
Or
Prove that the relation R in set A = {1, 2, 3, 4, 5} given by R = {(a, b) : |a – b| is even} is an equivalence relation.
Solution:
Given, A = {1,2, 3,…,9} and a relation ft in A × A defined by (a, b)R(c, d), if a + d =b + c.
Reflexivity Let (a, b) ∈ A × A be any arbitrary element. Now, a + to = to + a
[∵ addition is commutative on the set of real numbers]
Therefore, (a, b)R(a, b).
∵ (a, b) ∈ A × A was arbitrary.
∴ R is reflexive.

Symmetricity Let (a, b),(c, d) ∈ A × A
such that (a, b)R(c, d).
∵ (a, b)R(c, d)
∴ a + d=b + c
⇒ c + b = d + a
[∵ addition is commutative on the set of real numbers]
⇒ (c, d)R(a, b)
So, R is symmetric.
Transitivity Let (a, b),(c, d),(e, f) ∈ A × A such that (a, b)R(c, d) and (c, d)R(e, f).
Since, (a, b)R(c, d) and (c, d)R(e, f).
So. we have a + d = b + c …(i)
and c + f = d + e …(ii)
On adding Eqs. (i) and (ii), we get
(a + d)+(c + f) = (b + c)+(d + e)
⇒ a + f = b + e ⇒ (a, b)R(e, f)
So, R is transitive.
Thus, R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation.
Or
The given relation is R = {(a, b):|a – b| is even} defined on set A = {1,2, 3, 4, 5}.
To show that R is an equivalence relation, we show that it is reflexive, symmetric and transitive.

(i) Reflexive As |x – x| = 0 is even, ∀ x ∈ A
⇒ (x, x) ∈ R, ∀ x ∈ A
Hence, R is reflexive.

(ii) Symmetric As, (x, y) ∈ R ⇒ |x – y| is even
[by the definition of given relation]
⇒ |y – x| is also even [∵ |a| =|-a|, ∀ a ∈ R]
⇒ (y, x) ∈ R, ∀ x, y ∈ A
We have shown that (x, y) ∈ R ⇒ (y, x) ∈ R, ∀ x, y ∈ A
Hence, R is symmetric.

(iii) Transitive As (x, y) ∈ R and (y, z) ∈ R
⇒ | x – y| is even and | y – z| is even.
[by using definition of given relation]
Now, |x – y| is even
⇒ x and y both are even or odd. and |y – x|iseven
⇒ y and x both are even or odd.
There are two cases arise.

Case I When y is even.
Now, (x, y)&R and (y, z) ∈ R.
⇒ |x – y| is even and |y – z|iseven.
⇒ x is even and z is even ⇒ | x – z| is even [∵ difference of two even numbers is also even]
⇒ (x, z) ∈ R

Case II When y is odd.
Now, (x, y) ∈ R and (y, z) ∈ R
⇒ |x – y| is even and |y – z| is even
⇒ x is odd and z is odd ⇒ |x – z| is even [∵ difference of two odd numbers is even]
⇒ (x, z) ∈ R
So. we have shown that (x, y ) ∈ R and (y. z) ∈ R
⇒ (x. z) ∈ R. ∀ ,v. y, z ∈ A
∴ R is transitive.
Since, R is reflexive, symmetric and transitive. So, it is an equivalence relation.

Question 28.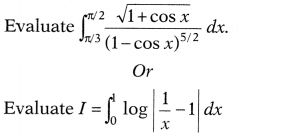

Solution: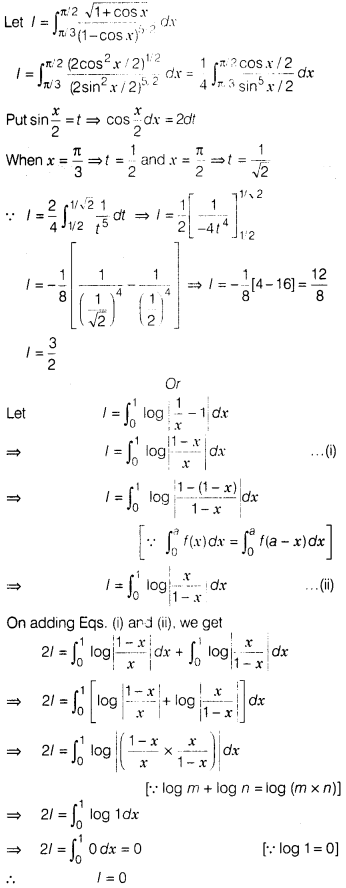

Question 29.
Find the area bounded by the curve y = cos x between x = 0 and x = 2 π.
Or
Find the area bounded by the curve y² = 4a²(x – 1) and the lines x = 1 and y = 4a.
Solution:
The graph of y = cos x between 0 to 2π is the curve shown in given figure.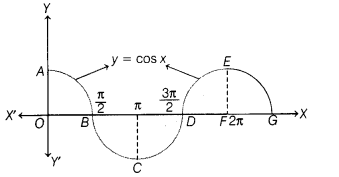

∴ Required area = Area of region OABO + Area of region BCDB + Area of region DEFD

[∵ in region BCDB, the curve is below the X-axis, where yalue comes out to be negative, so we take the absolute value]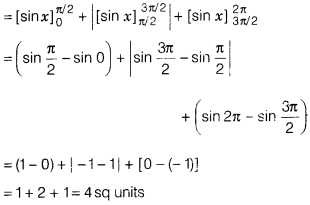

Therefore, the required area is 4 sq units
Or
The equation of the given cur e is y² = 4a²(x – 1) or (y – 0)² – 4a²(x – 1).

Clearly, this equation represents a parabola with vertex at (1, 0) as shown in figure.

The region encloser by y² = 4a²(x – 1), x = 1 and y = 4a is the area of s. iaded portion in figure.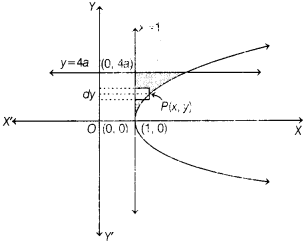

When we slice the area of the shaded portion in horizontal strips, we observe that each strip has left end on the line x = 1 and the right end on the parabola y² = 4a²(x – 1).

So, the approximating rectangle shown in figure has, length = x – 1, width = dy and area = (x -1 )dy.
Since, the approximating rectangle can move from y = 0 to y = 4a.
So, required area A is given by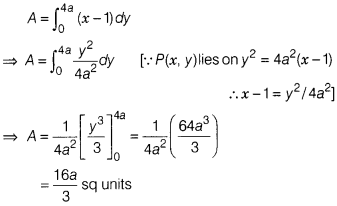

Question 30.
Let A = R – {3}, F = R – {1}. If f : A → B be defined by f(x) = \(\frac{x-2}{x-3}\), ∀ x ∈ A, then show that f is bijective.
Solution:
Given, A = B – {3}, B = R – {1} and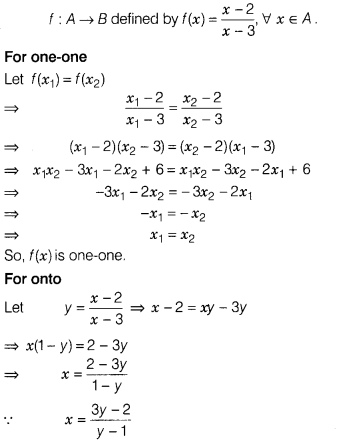

Clearly, x ∈ R – {3}, ∀ y ∈ R – {1}
So, range of f(x) = R – {1}
∴ Range = Ccdomain
So, f(x) is onto.
Thus, f(x) is bijective.

Question 31.
Find the position vector of a point C which divides the line segment joining A and B, whose position vectors are \(2\vec{a}+\vec{b}\) and \(\vec{a}-3\vec{b}\), externally in the ratio 1 : 2. Also, show that A is the mid-point of the line segment BC.
Solution:
Given, \(\vec{OA}=2\vec{a}+\vec{b}\) and \(\vec{OB}=\vec{a}-3\vec{b}\) …(i)
Also, it is given that C is the point which divides the line joining A and B externally in the ratio 1:2.
Then, by using section formula of external division, we get

Hence, A is mid-point of line segment BC.

Section D
This section comprises of long answer type questions (LA) of 5 marks each

Question 32.
By computing shortest distance, determine whether the following pair of lines intersect or not \(\vec{r}=(4\hat{i}+5\hat{j})+\lambda(\hat{i}+2\hat{j}-3\hat{k})\) and \(\vec{r}=(\hat{i}-\hat{j}+2\hat{k})+\mu(2\hat{i}+4\hat{j}-5\hat{k})\).
Solution:
Given equations of lines are

Hence, the two lines intersect each other.

Question 33.
Find a vector of magnitude 5 units, perpendicular to each of the vectors
(\(\vec{a}+\vec{b}\)) and (\(\vec{a}-\vec{b}\)), where \(\vec{a}=(\hat{i}+\hat{j}+\hat{k})\) and \(\vec{b}=(\hat{i}+2\hat{j}+3\hat{k})\).
Solution: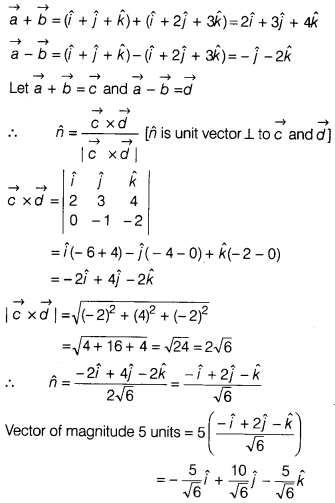

Question 34.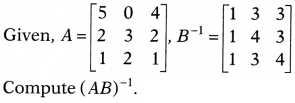

Or
Determine the product of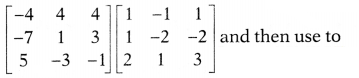

solve the system of equations x – y + z = 4, x – 2y – 2z = 9 and 2x + y + 3z = 1.
Solution:


Given system of equations can be written in matrix form as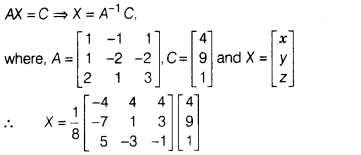


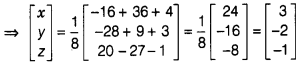
On comparing corresponding elements, we get
x = 3, y = 2 and z = -1

Question 35.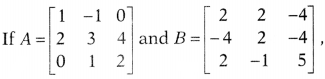

then find AB. Use this to solve the system of equations
x – y = 3, 2x + 3y + 4z = 17 and y + 2z =7.
Or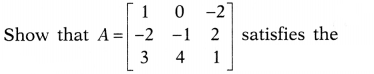

equation A³ – A² – 3A – 1 = 0.
Solution: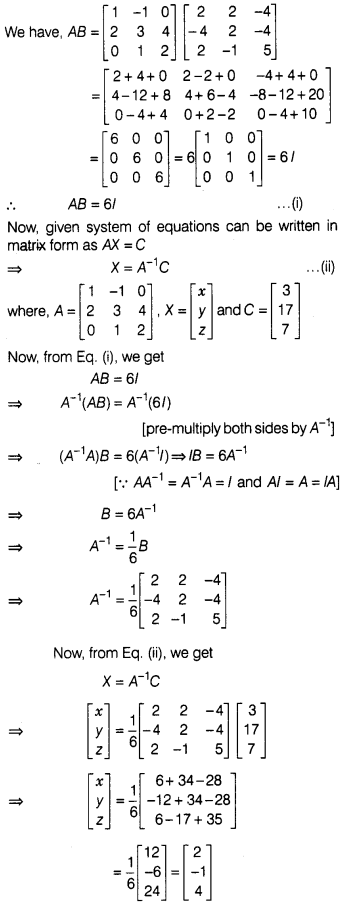

On comparing corresponding elements, we get
x = 2, y = -1 and z = 4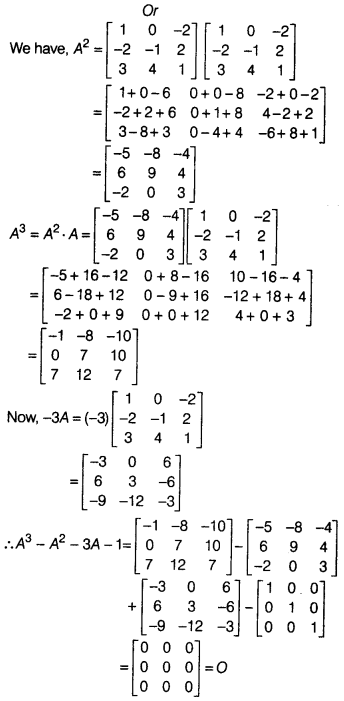

Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
Sometimes, x and y are given as functions of one another variable, say x = Φ(t), y = Ψ(t) are two functions and t is a variable. In such a case, x and y are called parametric functions or parametric equations and t is called the parameter.
To find the derivatives of parametric functions, we use following steps
I. First, write the given parametric functions, suppose x = f(t) and y = g(t), where t is a parameter.
II. Differentiate both functions separately w.r.t. parameter t by using suitable formula i.e. find \(\frac{dx}{dt}\) and \(\frac{dy}{dt}\).
III. Divide the derivative of one function w.r.t. parameter by the derivative of second function w.r.t. parameter, to get required value i.e. \(\frac{dy}{dx}\).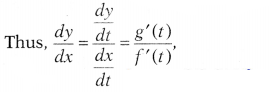

where f'(t) = 0.
On the basis of above information, answer the following questions.
(i) If x = log t and v = cos t, then find \(\frac{dy}{dx}\).
(ii) If x = at³ and y = t² + 1, then find \(\frac{dy}{dx}\) at t = \(\frac{2}{3}\)
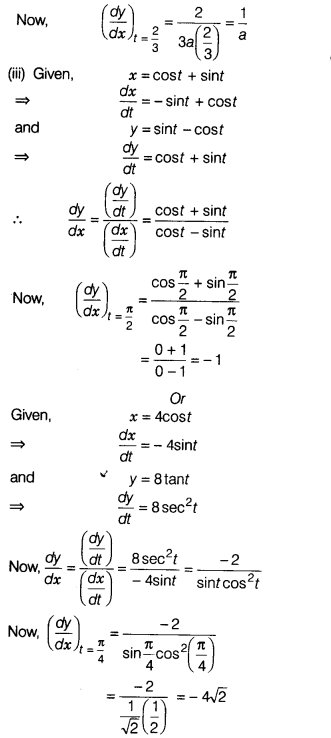
(iii) If x = cos t + sin t and y = sin t – cos t, then find \(\frac{dy}{dx}\) at t = \(\frac{\pi}{2}\).
Or
If x = 4 cos t and y = 8 tan t, then find \(\frac{dy}{dx}\) at t = \(\frac{\pi}{4}\)
Solution: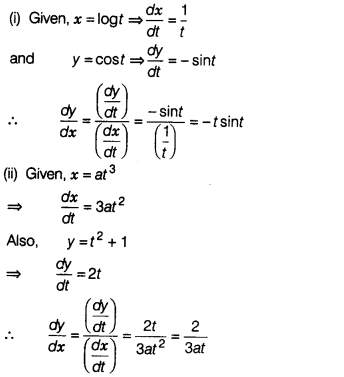

Question 37.
If feasible solution of a LPP is given as follows: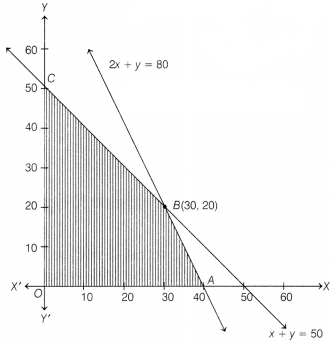

And the objective function is Z = 10500x + 9000y.
On the basis of above information, answer the following question.
(i) If n is the number of corner points, then find the value of (n + 2 )³.
(ii) Find the value of Z_{(1, 1)}
(iii) Find the point where objective function is maximum.
Or Evaluate Z|_{(20, 20)}– Z|_{(10, 10)}.
Solution:
(i) We have, n = 4
∴ (n + 2)³ = (4+ 2)³ = 6³ = 216 ….(i)
(ii) Z_{(1, 1)} = (10500 × 1) + (9000 × 1) = 19500
(iii) To know the maximum value of Z, we need coordinates of all the corner points.
We have, equation of lines x + y = 50 … (i)
and 2x + y = 80 …(ii)
For point A, on putting y = 0 into Eq. (ii), we get
2x + 0 = 80 –
⇒ x = 40
⇒ A(40, 0)
For point C, on putting x = 0 into Eq. (i), we get 0 + y = 50
⇒ y = 50 ⇒ C(0, 50)
Now,

Comer points	Value of Z = 10500x + 9000y
0(0, 0)	10500 × 0+ 9000 × 0 = 0
A(40, 0)	10500 × 40 + 9000 × 0 = 420000
B (30, 20)	10500 × 30 + 9000 × 20 = 495000 (Maximum)
C (0, 50)	10500 × 0 + 9000 × 50 = 450000

Hence, Z is maximum at B(30, 20).
Or
Z|_{(20, 20)} – Z|_{(10, 10)}
= (10500 × 20 + 9000 × 20) – (10500 × 10 + 9000 × 10)
= 1000 [(105 × 2 + 90 × 2) – (105 + 90)]
= 1000 [(210 + 180) – (195)]
= 1000 [390 – 195] = 195000

Question 38.
Given three identical boxes I, II and III, each containing two coins. In Box I both
coins are gold coins, in Box II both are silver coins and in Box III there is one gold and one silver coin. A person choose a box at random and takes out a coin.
On the basis of above information, answer the following questions.
(i) Find the total probability of drawing gold coin.
(ii) If drawn coin is of gold, then find the probability that other coin in box is also of gold.
Solution:
Consider the following events,
E₁ = Box I is choosen,
E₂ = Box II is choosen,
E₃ = Box III is choosen.
A = The coin drawn is of gold.
Clearly, P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\)
Then, P(A/E₁) = Probability of drawing a gold coin from Box I
= \(\frac{2}{2}\) = 1,
P(A/ E₂) = Probability of drawing a gold coin from Box II
= 0
and P(A/E₃) = Probability of drawing a gold coin from Box I
= \(\frac{1}{2}\)
(i) ∴ Required probability