CBSE Sample Papers for Class 12 Maths Set-3

CBSE Sample Papers for Class 12 Maths Set 3 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case/passage based/intergrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

Question 1.
P is a point on the line joining the points A(0, 5, -2) and 5(3, -1, 2). If the x-coordinate of P is 6, then its Z-coordinate is
(a) 10
(b) 6
(c) -6
(d) -10
Solution:
(b) The line through the points 4(0, 5, -2) and B(3, -1, 2) is given by
\(\frac{x}{3}=\frac{y-5}{-6}=\frac{z+2}{4}\) = λ
Here, x-coordinate is 6.
∴ \(\frac{6}{3}\) = λ, λ = 2
Now, for z-coordinate z + 2
\(\frac{z+2}{4}\) = 2 ⇒ z = 8 – 2 = 6

Question 2.
If \(\int_0^a\frac{dx}{1+4x^2}=\frac{\pi}{8}\), then the value of a is
(a) 1
(b) \(\frac{1}{2}\)
(c) 3
(d) 0
Solution: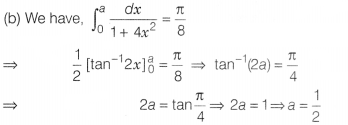

Question 3.
The projection of the vector \(\hat{i}+3\hat{j}+7\hat{k}\) on the vector \(2\hat{i}-3\hat{j}+6\hat{k}\) is
(a) 4
(b) 5
(c) 1
(d) 0
Solution: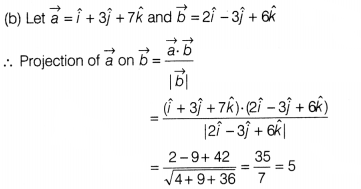

Question 4.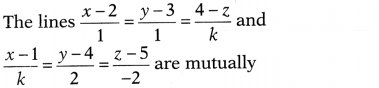

perpendicular, if the value of k is
(a) –\(\frac{2}{3}\)
(b) \(\frac{2}{3}\)
(c) -2
(d) 2
Solution:
(a) We have,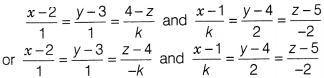

Since, the given lines are perpendicular.
∴ (1)(k) + (1)(2) + (-k)(-2) = 0
⇒ k + 2 + 2k = 0
⇒ 3k +2 = 0 ⇒ k = –\(\frac{2}{3}\)

Question 5.
The value of determinant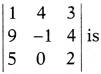

(a) 21
(b) 166
(c) 64
(d) None of these
Solution: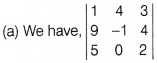

On expanding along fl3, we get
= 5(16 + 3) + 2(-1 – 36) = 95 – 74 = 21

Question 6.
\(\int\frac{dx}{\sqrt{x}+x}\) is equal to
(a) 2log|√x + 1| + C
(b) log|x + 1| + C
(c) log |x – 1| + C
(d) 2log |x + 1| + C
Solution: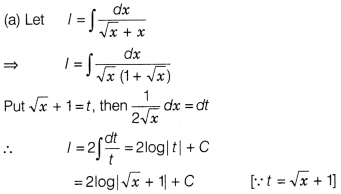

Question 7.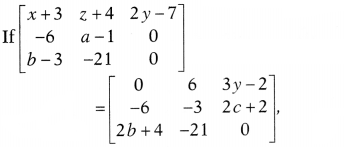

then the values of x, y,z, a, b and c are
(a) x = -3, y = -5, z = 2 a = -2, b = -7 and c = -1
(b) x = -2, y = -7, z = -1, a = -3, b = -5 and c = 2
(c) x = -3, y = -5, z = 2, a = 2, b = 7 and c = 1
(d) x = 3, y = 5, z = 2, a = 2, b = 7 and c = 1
Solution:
(a) The given matrices are equal, therefore their corresponding elements must be equal.
On comparing the corresponding elements, we get
x + 3 = 0 , z + 4 = 6, 2y – 7 = 3y – 2,
a – 1 = -3, 0 = 2c + 2 and b – 3 = 2b + 4
On simplifying, we get
a = -2, b = -7, c = -1,
x = -3, y = -5 and z = 2

Question 8.
A card is picked at random from a pack of 52 playing cards. Given that the picked card is a queen, the probability of this card to be a card of spade is
(a) \(\frac{1}{3}\)
(b) \(\frac{4}{13}\)
(c) \(\frac{1}{4}\)
(d) \(\frac{1}{2}\)
Solution:
(c) Let A be the event that card drawn is a spade and 6 be the event that card drawn is a queen. We have a total of 13 spades and 4 queen and one queen is from spade.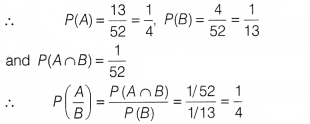

Question 9.
General solution of \(\frac{dy}{dx}=\frac{y}{x}\) is
(a) y = kx²
(b) y =kx
(c) y = \(\frac{k}{x}\)
(d) yx = k
Solution:
(b) We have, \(\frac{dy}{dx}=\frac{y}{x}\) ⇒ \(\frac{1}{y}\)dy = \(\frac{1}{x}\) dx
On integrating both sides, we get
∫latex]\frac{1}{y}[/latex]dy = ∫\(\frac{1}{x}\)
⇒ log y = log x + log k
⇒ log y = log kx
⇒ y = kx

Question 10.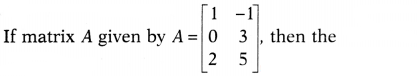

order of the matrix A is
(a) 1 × 2
(b) 2 × 3
(c) 3 × 2
(d) 2 × 2
Solution: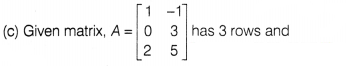

2 columns.
∴ Order of matrix A is 3 × 2.

Question 11.
If \(|\vec{a}\times\vec{b}|\) = 1, |\(\vec{a}\)| = 2 and |\(\vec{b}\)| = 1, then angle between \(\vec{a}\) and \(\vec{b}\) is equal to
(a) \(\frac{\pi}{3}\)
(b) \(\frac{\pi}{6}\)
(c) \(\frac{\pi}{4}\)
(d) \(\frac{\pi}{2}\)
Solution: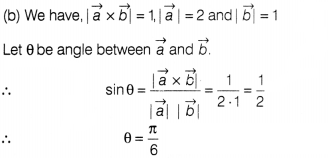

Question 12.
Direction cosines of the vector \(2\hat{i}-\hat{j}+3\hat{k}\) are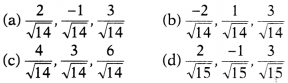

Solution:
(a) Direction cosines of the vector \(2\hat{i}-\hat{j}+3\hat{k}\) are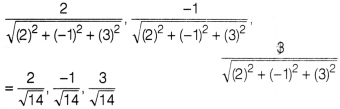

Question 13.
All the points of discontinuity of f defined by f(x) = |x| – |x + 1| is/are
(a) 0, 1
(b) 1, 0, 2
(c) no point of discontinuity
(d) None of the above
Solution:
(c) Let g(x) = |x| and h(x) = |x + 1|
Now, g(x) = |x| is the absolute value function, so it is a continuous function for all x ∈ R
h(x) = |x + 1| is the absolute value function, so it is a continuous function for all x ∈ R.
Since, g(x)and h(x) are both continuous functions for all x e R, so difference of two continuous function is a continuous function for all x ∈ R
Thus, f(x) = |x| – |x + 1| is a continuous function at all points.
Hence, there is no point at which f(x) is discontinuous.

Question 14.
The function f given by f(x) = 3x + 17, is
(a) strictly increasing on R
(b) strictly decreasing on R
(c) decreasing on R
(d) Both (b) and (c) are correct
Solution:
(a) Given. f(x) = 3x 1 17
On differentiating w.r.t. x, we get
f'(x) = 3 > 0, in every interval of R.
Thus, the function is strictly increasing on R.

Question 15.
If Radha has 15 notebooks and 6 pens, Fauzia has 10 notebooks and 2 pens and Simran has 13 notebooks and 5 pens, then the above information is expressed as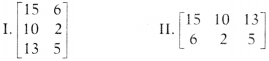

(a) Only I
(b) Only II
(c) Both I and II
(d) None of these
Solution:
(c) If Radha has 15 notebooks and 6 pens. Fauzia has 10 notebooks and 2 pens and Simran has 13 notebooks and 5 pens, then this could oe arranged in tabular form as

Name	Notebooks	Pens
Radha	15	6
Fauzia	10	2
Simran	13	5

This can be expressed as “15 6” 10 2 13 5
The above information can also be arranged in tabular form as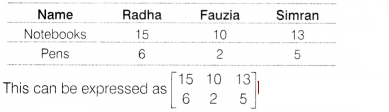

Question 16.
If f(x) = \({\frac{\sqrt{4+x}-2}{x}}\) x ≠ 0 be continuous at x = 0, then 4f(0) is equal to
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) 1
(d) \(\frac{3}{2}\)
Solution:

Question 17.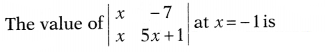

(a) -1
(b) -3
(c) 2
(d) -5
Solution: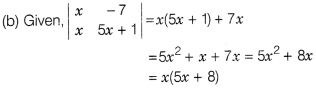

Now at x = -1,
Required result = (-1)(-5 + 8)
= (-1) (3) = – 3

Question 18.
Degree of differential equation \(\frac{d^2y}{dx^2}\) + e^dy/dx = 0 is
(a) 1
(b) 2
(c) 3
(d) not defined
Solution:
(d) Given, \(\frac{d^2y}{dx^2}\) + e^dy/dx = 0
Since, the differential equation is not a polynomial equation.
So, degree of the equation is not defined.

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true

Question 19.
Assertion (A) If R is the relation defined in set {1, 2, 3, 4, 5, 6} and
R = {(a, b):b = a +1}, then R is reflexive.
Reason (R) The relation R in the set {1, 2, 3} given by R= {(1, 2), (2, 1)} is symmetric.
Solution:
(d) Assertion Let A = {1,2, 3, 4, 5, 6}
A relation ft is defined on set A as
R = {(a, b): to = a + 1}
∴ R = {(1,2), (2, 3), (3, 4), (4, 5), (5, 6)}
Now, (1, 1 ) ∈ R
∴ R is not reflexive.
Hence, Assertion is false.
Reason Given set A = {1,2, 3}
A relation R on A is defined as
R = {(1, 2), (2, 1)}
∴ (1, 2) ∈ R and (2, 1) ∈ R
So, R is symmetric.
Hence, Reason is true.

Question 20.
Assertion (A) The acute angle between the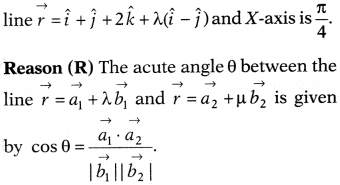

Solution:

∴ Assertion is true.

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
Solve the following LPP graphically :
Maximise Z = 4x + 6y,
Subject to constraints
x + y ≤ 8, x ≥ 0, y ≥ 0
Solution:
Let us draw the graph of x + y = 8 as shown below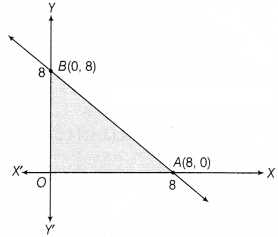

OABO is the feasible region determined by the system of constraints x ≥ 0, y ≥ 0 and x + y ≤ 8.

So, the corner points are O(0, 0), A(8, 0)and B(0, 8).
On evaluating Z at each corner points, we have

Corner points	Z = 4x + 6y
O(0, 0)	Z = 4 × 0 + 6 × 0 = 0
A(8, 0)	Z = 4 × 8 + 6 × 0 = 32
B(0, 8)	Z = 4 × 0 + 6 × 8 = 48 (Maximum)

Hence, the maximum value of Z is 48, which occurs at the point (0, 8).

Question 22.
Find the derivative of log(1 + x²) w.r.t. tan^-1x.
Solution:
Let y = log (1 + x²)
On differentiating both sides w.r.t. x, we get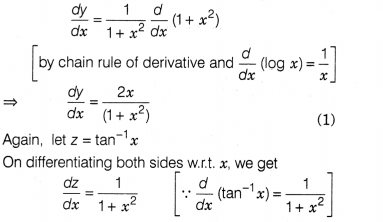

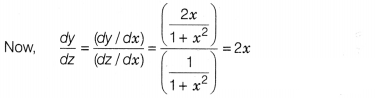
Question 23.
One card is drawn at random from a pack of well-shuffled deck of cards.
Let E : The card drawn is a spade
F : The card drawn is an ace
Are the events E and F independent?
Solution:
Lets be the sample space.
Given, E = The event that the card drawn is a spade
and F = The event that the card drawn is an ace
Then, E ∩ F =The event that the card drawn is an ace and spade

Total number of cards = 52,
number of spade cards = 13,
number of ace cards = 4
and number of ace of spade card = 1

Hence, the events E and F are independent.

Question 24.
Evaluate \(\int_0^\frac{\pi}{2}\) sin² x dx.
Or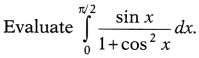

Solution: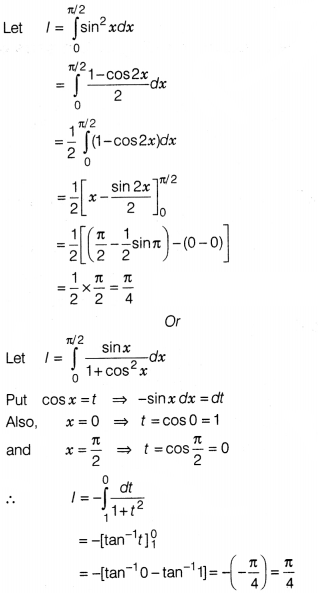

Question 25.
If x = cos t + sin t and y = sin t – cos t, then find \(\frac{dy}{dx}\) at t = \(\frac{\pi}{2}\).
Or
If x = at² and y = 2 at, then find \(\frac{dy}{dx}\) at t = 1.
Solution:

Section C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.
Evaluate ∫\(\frac{x^2+1}{(x^2+2)(2x^2+1)}\) dx.
Solution:
Let x² = y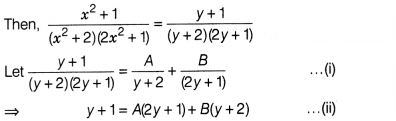

On putting 2y + 1 = 0 i.e. y = -2 in Eq. (ii), we get
-1 = -3A
⇒ A = \(\frac{1}{3}\)
On putting 2y + 1 = 0 i.e y = –\(\frac{1}{2}\) in Eq. (ii), we get
\(\frac{1}{2}\) = B(\(\frac{3}{2}\))
⇒ B = \(\frac{1}{3}\)
On substituting the values of A and 6 in Eq. (i), we obtain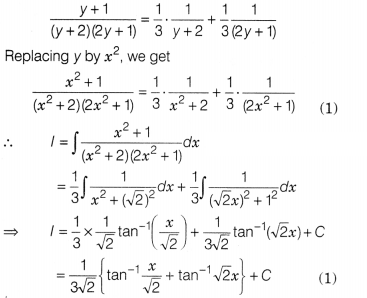

Question 27.
Find the particular solution of the differential equation (1 + e^2x) dy +(1 + y²) e^x dx = 0, given that y = 1 when x = 0.
Or
Solve the following differential equation y²dx + (x² – xy + y²)dy = 0
Solution:
Given, differential equation is
(l + e^2x)dy + (1 + y²) e^x dx = 0
⇒ (1 + e^2x)dy = -(1 + y²)e^x dx

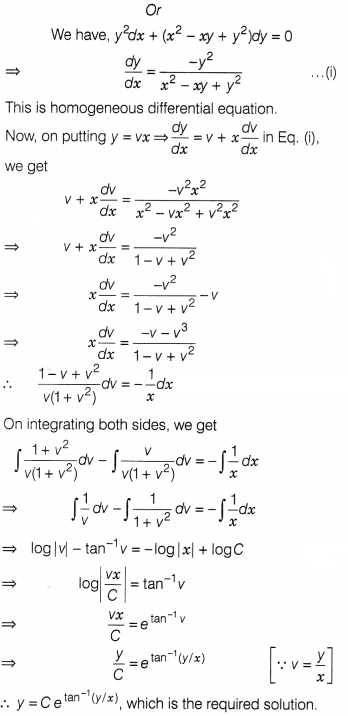
Question 28.
Let R be the relation in the set A of all books in a library of a college given by R= {{x, y): x and y have same number of pages}. Then, show that R is an equivalence relation.
Or
Show that the relation R = {(a, b): a and b work at the same place}, is an equivalence relation.
Solution:
Here, A is the set of all books in the library of a college and R – {(x, y): x and y have the same number of pages}
Now, R is reflexive, since (x, x) ∈ R ∀ x ∈ A, as x and x has the same number of pages.

Let (x, y) ∈ R.
⇒ x and y have the same number of pages.
⇒ y and x have the same number of pages.
⇒ (y, x) ∈ R. So, R is symmetric.
Now, let (x, y) ∈ R and (y, z) ∈ R.
⇒ x and y have the same number of pages and y and z have the same number of pages.
⇒ x and z have the same number of pages.
⇒ (x, z) ∈ R
Therefore, ft is transitive.
Hence, R is an equivalence relation.
Or
Here, R = {(a, b): a and b work at the same place}.
Then, ft is reflexive as a works at same place of a.
⇒ (a, a) ∈ R ∀ a ∈ A
If a and b work at same place, then b and a also work at same place
i.e. if (a, b) ∈ R ⇒ (b, a) ∈ R
⇒ R is symmetric.
Let (a, b) ∈ R, (b, c) ∈ R
⇒ a and b work at same place and b and c work at same place.
Since, all three work at same place.
⇒ a and c work at same place.
⇒ (a, c) ∈ R
⇒ R is transitive.
⇒ R is an equivalence relation.

Question 29.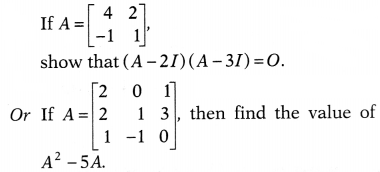

Solution: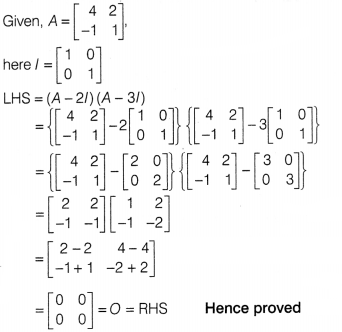

Question 30.
Find the shortest distance between lines

Solution:
Given equations of lines are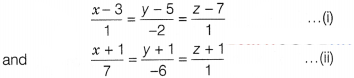

On comparing above equations with one point form of equation of line which is
\(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\), we get
a₁ = 1, b₁ = -2, c₁ = 1, x₁ = 3, y₁ = 5, z₁ = 7
and a₂ = 7, b₂ = 6, c₂ = 1, x₂ = -1, y₂= -1, z₂ = -1
We know that the shortest distance between two lines is given by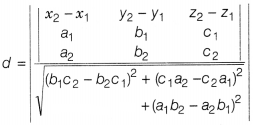


Hence, the required shortest distance is √116 units.

Question 31.
The minimum value of Z, where
Z = 2x + 3y, subject to constraints
2x + y ≥ 23, x + 3y ≤ 24 and x, y ≥ 0, is
Solution:
Given, objective function is minimise Z = 2x + 3y
Subject to constraints,
2x + y ≥ 23, x + 3y ≤ 24 and x, y ≥ 0
Now, table for line 2x + y = 23

X	0	11.5
y	23	0

At (0, 0), 2 – 0 + 0 ≥ 23
⇒ 0 ≥ 23, which is false.
So, the shaded portion is away from the origin.

Table for line x + 3y = 24

X	0	24
y	8	0

On putting (0, 0) in x + 3y ≤ 24, we get
0 + 3.0 ≤ 24
⇒ 0 ≤ 24, which is true
So, the shaded portion is towards the origin.
Also, x, y ≥ 0.
On drawing the graph of each linear equation, we get the following graph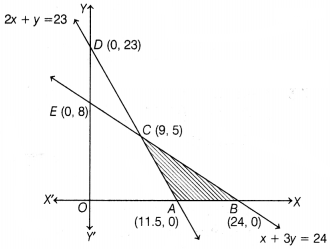

The feasible region is ABC and corner points are A(11.5, 0), 6(24, 0) and C(9, 5).

Corner points	Value of Z = 2x + 3y
A( 11.5, 0)	23 (Minimum)
8(24, 0)	48
C (9, 5)	33

Hence, the minimum value of Z is 23 at A(11.5, 0).

Section D
This section comprises of long answer type questions (I.A) of 5 marks each

Question 32.
Find the area of the region bounded by the curves x = 4y – y² and the Y-axis.
Solution:
Given, curve is x = 4y – y²
⇒ x = -(y² – 4y)
⇒ x = – (y² – 4y + 4) + 4
⇒ x = – (y – 2)² + 4
(y – 2)² = – (x – 4)
Let y – 2 = Y and (x – 4) = X
Then, Y² = – X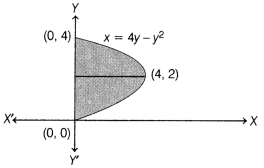

which represents a parabola whose axis is parallel to X-axis.
Vertex X = 0, Y = 0
i.e. x – 4 = 0 and y – 2 = 0
⇒ x = 4 and y = 2
Also, at Y-axis,
(y – 2)² = 4 – 0 [∵ x = 0]
⇒ y – 2 = + 2 ⇒ y = 4, 0
Area bounded between parabola and Y-axis.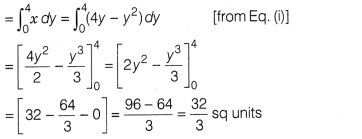

Question 33.
Find the intervals on which the function f(x) = (x – 1)³ (x – 2)² is strictly increasing and strictly decreasing.
Or
Find the dimensions of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible, when revolved about one of its side. Also, find the maximum volume.
Solution:
Given, function is f(x) = (x – 1)³ (x – 2)².
On differentiating w.r.t. x, we get
f'(x) = 3(x -1)²(x – 2)² + 2(x – 2)(x -1)³
= (x – 1)²(x – 2)[3(x -2) + 2(x -1)]
= (x – 1)²(x – 2)(5x – 8)
= (x – 1)²(2 – x)(8 – 5x)

For strictly increasing f'(x) > 0, we get positive f'(x) in the interval (-∞, \(\frac{5}{8}\)) ∪ (2, ∞).
And for strictly decreasing f'(x) < 0, we get negative f'(x) in the interval (\(\frac{5}{8}\), 2).
Or
Here, ABCD is a rectangle with length AD = y cm and breadth AB = x cm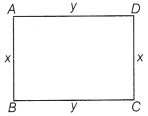

The rectangle is rotated about AD. Let V be the volume of the cylinder so formed
∴ V = πx²y [∵ r = x and h = y] ….(i)
Perimeter of rectangle = 2(x + y)
⇒ 36 = 2(x + y)
⇒ y = 18 – x
From Eq. (i), V = πx²(18 – x)
⇒ V = π(18x² – x³)
⇒ \(\frac{dV}{dx}\) = π(36x – 3x²)

For maxima or minima, put \(\frac{dV}{dx}\) = 0
π(36x – 3x²) = 0
⇒ x = 12, x ≠ 0
Now, \(\frac{d^2V}{dx^2}\) = π(36 – 6x)
(\(\frac{d^2V}{dx^2}\))_x=12 = π(36 – 72)
∴ Volume is maximum, when x = 12 cm
∴ y = 18 – x = 18 – 12 = 6cm
Hence, the dimensions of rectangle, which have maximum volume, when revolved about of its side are 12 × 6.

Question 34.
If \(\vec{a}=\hat{i}+2\hat{j}+3\hat{k}\) and \(\vec{b}=2\hat{i}+4\hat{j}-5\hat{k}\) represent two adjacent sides of a parallelogram, find unit vectors parallel to the diagonals of the parallelogram.
Or
Using vectors, find the area of the ∆ABC with vertices A(1, 2, 3), B(2, -1, 4) and C(4, 5, -1).
Solution:
We have, \(\vec{a}=\hat{i}+2\hat{j}+3\hat{k}\) and \(\vec{b}=2\hat{i}+4\hat{j}-5\hat{k}\)
So, the diagonals of the parallelogram whose adjacent sides are \(\vec{a}\) and \(\vec{b}\) are given by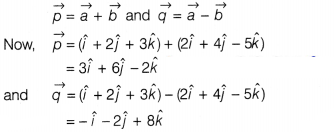

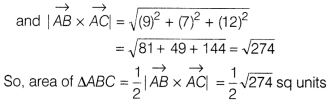
Question 35.
Evaluate \(\int_{-1}^2\)|x³ – x|
Solution:
Let l = \(\int_{-1}^2\)|x³ – x|dx
Again, let f(x) = x³ – x = x(x² – 1) = x(x – 1)(x + 1)
Now, break the given limit at x = 0, 1
[putting f(x) = 0, we get x = 0, 1, -1]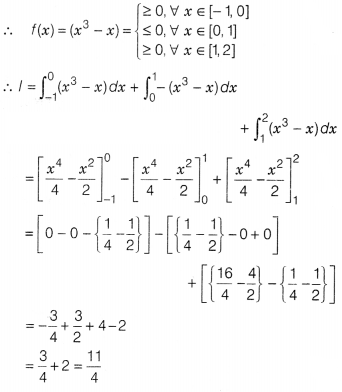

Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
Area of a triangle whose vertices are (x₁, y₁), (x₂, y₂) and (x₃, y₃) is given by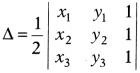

Since, area is position quantity, so always we take the absolute value of the determinant ∆. Also, the area of the triangle formed by three collinear points is zero.
Based on above information, answer the following questions.
(i) Find the area of the triangle whose vertices are (- 2, 6), (3, – 6) and (1, 5).
(ii) Find the equation of the line joining the points (1, 2) and (3, 6).
(iii) Find the value of k, if area of a AABC with vertices A(1, 3), 5(0, 0) and C(k, 0) is 3 sq units.
Or
Find the value of k, if the points (2, -3), (k, -1) and (0, 4) are collinear.
Solution:

Question 37.
For awareness on Covid-19 protocol, Indian Government planned to fix a hoarding board at the face of a building on the r oad of a busy market. Sagar, Roy and Asif are the three engineers who are working on the project, P and P’ are considered to be two person viewing the hoarding board 40 m and 50 m respectively, away from the building. All three engineers suggested to the firm to place the hoarding board at three different locations namely R, S and T. R is at the height of 20 m from the ground level. For the viewer P, the angle of elevation of S is double the angle of elevation of R. The angle of elevation of T is triple the angle of elevation of R for the same viewer. Look at the given figure.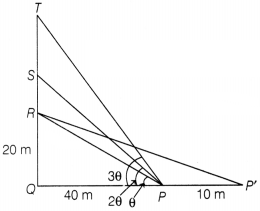

On the basis of above information, answer the following questions.
(i) Write the domain and range of tan x.
(ii) Find ∠RPQ.
(iii) Find ∠SPQ.
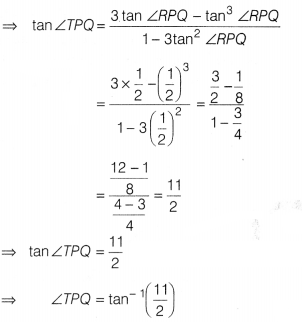
Or
Find ∠TPQ.
Solution:
(i) Domain of tan^-1 x = R

Question 38.
A doctor is to visit a patient. From the post experience, it is known that the probabilities that he will come by train, bus, scooter and by other means of transport are respectively \(\frac{3}{10},\frac{1}{5},\frac{1}{10}\) and \(\frac{2}{5}\). The probability that he will be late are \(\frac{1}{4},\frac{1}{3}\) and \(\frac{1}{12}\), if he comes by train, bus and scooter respectively, but if he comes by other means of transport, then he will not be late.
On the basis of above information, answer the following questions.
(i) Find the probability that he is late.
(ii) Find the probability that he come by scooter given that he is late and also find the probability that he comes late given that he comes by other means of transport.
Solution:
Let E₁, E₂, E₃ and E₄ be the events that the doctor comes by train, bus, scooter and other means of transport, respectively.
It is given that
P(E₁) = \(\frac{3}{10}\), P(E₂) = \(\frac{1}{5}\)
P(E₃) = \(\frac{1}{10}\) and P(E₄) = \(\frac{2}{5}\)
Let A denotes the event that the doctor visits the patient late, It is given that