CBSE Sample Papers for Class 12 Maths Set-12

CBSE Sample Papers for Class 12 Maths Set 12 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This questions paper contains – five sections, A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case based/passage based/integrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

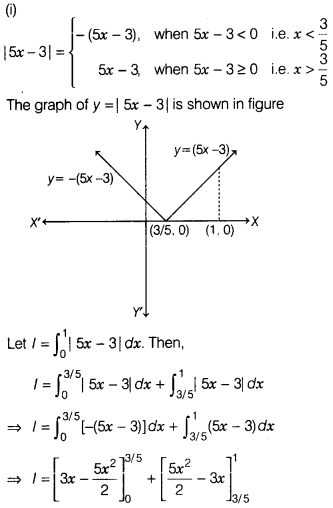
Question 1.
The magnitude of \(\vec{a}\) given by \(\vec{a}=(\hat{i}+3\hat{j}-2\hat{k})\times(-\hat{i}+3\hat{k})\) is equal to
(a) 91
(b) √91
(c) 90
(d) √90
Solution:
(b) We have,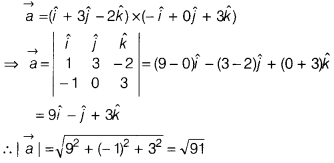

Question 2.
The maximum slope of curve
y = -x³ + 3x² + 9x – 27 is
(a) 0
(b) 12
(c) 16
(d) 32
Solution:
(b) We have,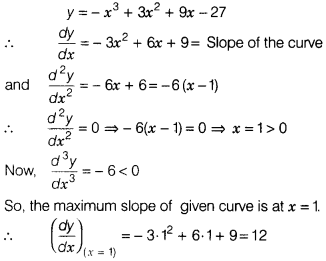

Question 3.

equal to
(a) y
(b) \(\frac{y}{2}\)
(c) \(\frac{y}{3}\)
(d) -y
Solution:

Question 4.
The domain of f(x) = sin^-1 (-x²)is
(a) (-1, 1)
(b) [-1, 1]
(c) (-1, 1]
(d) [-1, 1)
Solution:
(b) We know that domain of sin^-1 x is [-1, 1]
Therefore, f(x) = sin^-1(-x²) is defined for all x satisfying
-1 ≤ -x² ≤ 1
⇒ 1 ≥ x² ≥ -1
⇒ 0 ≤ x² ≤ 1
⇒ x² ≤ 1 ⇒ x² – 1 ≤ 0
⇒ (x – 1)(x + 1) ≤ 0
⇒ -1 ≤ x ≤ 1
Hence, the domain of f(x) is [-1, 1].

Question 5.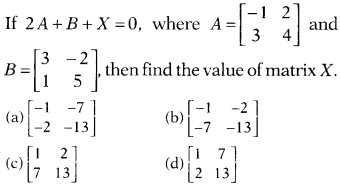

Solution:
(b) We have, 2A + B + X = 0
⇒ X = -(2A + B)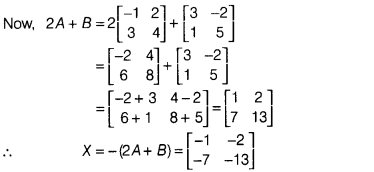

Question 6.
The value of cos^-1(sin\(\frac{\pi}{6}\)) is
(a) \(\frac{\pi}{2}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{\pi}{6}\)
(d) \(\frac{\pi}{4}\)
Solution:
(b) We have, cos^-1(sin\(\frac{\pi}{6}\)) = cos^-1(\(\frac{1}{2}\)) = \(\frac{\pi}{3}\)

Question 7.
The function f(x) = x² + 2 is
(a) one-one
(b) not one-one
(c) one-one and onto
(d) None of these
Solution:
(b) We have, f(x) = x² + 2
Let x₁, x₂ ∈ R such that
f(x₁) = f(x₂)
⇒ x²₁ + 2 = x²₂ + 2
⇒ x²₁ = x²₂
⇒ x₁ = ±x₂
∴ f(x) is not one-one.

Question 8.
The principal value of
sec^-1(-√2) + cosec^-1(-√2) is
(a) \(\frac{\pi}{2}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{2\pi}{3}\)
(d) \(\frac{-\pi}{2}\)
Solution:
(a) We have, sec^-1(-√2) + cosec^-1 (-√2)
= (π – \(\frac{\pi}{4}\)) + (\(\frac{\pi}{4}\))
= π – \(\frac{\pi}{2}\) = \(\frac{\pi}{2}\)

Question 9.
If A is a matrix of order 3 × 3 such that |A| = 4, then |A^-1| is equal to
(a) 4
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{2}\)
(d) 2
Solution:
(b) We have, |A| = 4
Now, |A^-11 = \(\frac{1}{|A|}=\frac{1}{4}\)

Question 10.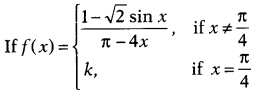

is continuous at \(\frac{\pi}{4}\), then k is equal to
(a) 4
(b) 3
(c) –\(\frac{1}{2}\)
(d) \(\frac{1}{4}\)
Solution:

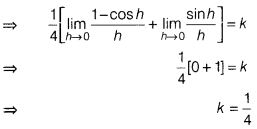
Question 11.
If y = 2x + |x|, then \(\frac{dy}{dx}\) at x = -1 is equal to
(a) 1
(b) -1
(c) 0
(d) 2
Solution:
(a) We have, y = 2x + |x|
⇒ y = 2x – x
⇒ y = x
∴ \(\frac{dy}{dx}\) = 1

Question 12.
The radius of the base of a cone is increasing at the rate of 3 cm/min and the altitude is decreasing at the rate of 4 cm/min. The rate of change of lateral surface when the radius is 7 cm and altitude 24 cm, is
(a) 54n cm²/min
(b) 7 n cm²/min
(c) 27 cm²/min
(d) None of the above
Solution:
(a) Let r, l and h denote respectively the radius, slant height and height of the cone at any time t. Then,

Question 13.
The degree of the differential equation
(a) 3
(b) 2
(c) not defined
(d) 1
Solution:
(c) The given differential equation is not a polynomial equation in \(\frac{dy}{dx}\). Therefore, its degree is not defined, dx

Question 14.
If \(\vec{a}\) and \(\vec{b}\) are two vectors, then \((\vec{a}\times\vec{b})^2+(\vec{a}.\vec{a})^2\) is equal to
(a) ab
(b) a²b
(c) ab²
(d) a²b²
Solution: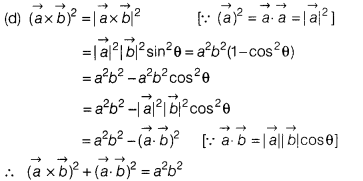

Question 15.
The angle between the lines through the points (4, 7, 8), (2, 3, 4) and (-1, -2, 1), (1, 2, 5) is
(a) 0
(b) \(\frac{\pi}{2}\)
(c) \(\frac{2\pi}{4}\)
(d) \(\frac{-\pi}{6}\)
Solution:
(a) DR’s of given line are -2, -4, -4 and 2, 4, 4.
Since, DR’s are proportional, therefore given lines are parallel to each other.
Hence, the angle between them is zero.

Question 16.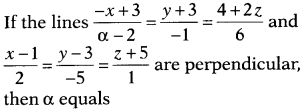

(a) 1
(b) 2
(c) 6
(d) 8
Solution:
(c) Given, lines can be rewritten as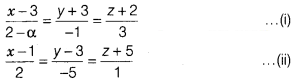

∵ Lines of Eqs. (i) and (ii) are perpendicular.
∴ 2(2 – α) + (-1)(-5) + 3(1) = 0
4 – 2α + 5 + 3 = 0
⇒ 2α = 12 ⇒ α = 6

Question 17.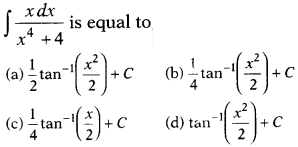

Solution: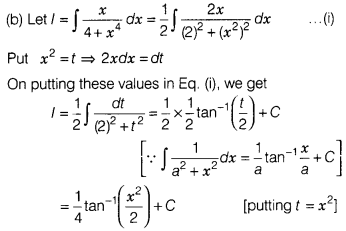

Question 18.
In ∆ABC, which of the following is not true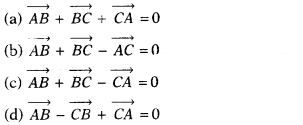

Solution:
(c) By triangle law of vector addition,

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true

Question 19.
Assertion (A) If R is the relation defined in set {1, 2, 3, 4, 5, 6} as R = {{a, b): b = a + 1}, then R is reflexive
Reason (R) The relation R in the set {1, 2, 3 } given by R = {(1, 2), (2, 1)} is symmetric.
Solution:
(d) Assertion Let A = {1,2, 3, 4, 5, 6}
A relation R is defined on set A is
R = {(a, b):b = a + 1}
∴ R = {(1, 2,), (2, 3), (3, 4), (4, 5), (5, 6)}
Now, 6 ∈ A but (6, 6) ∉ R
∴ R is not reflexive.
Hence, Assertion is false.
Reason Given, set A = {1,2, 3}
A relation ft on A is defined as R = {(1,2), (2,1)}
∵ (1, 2) ∈ R and (2, 1) ∈ R.
So, R is symmetric,
Hence, Reason is true.

Question 20.
Assertion (A) The equation of the line joining A(1, 3) and B(0, 0) is given by y = 3x.
Reason (R) The area of triangle with vertices (x₁, y₁) (x₂, y₃) and (x₃, y₃) in

Solution:
(a) Assertion Let P(x, y) be any point on AS.
Then, area of ∆ABP is zero.
[since, the three points are collinear]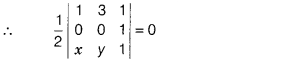

This gives \(\frac{1}{2}\)(3x – y) = 0 or y = 3x
which is the equation of required line AS.
Hence, Assertion is true.
Reason The area of triangle with vertices (x₁ + y₁), (x₂, y₂)and (x₃, y₃) is given by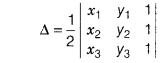

Hence, Reason is also true and it is the correct explanation of Assertion.

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
Given two independent events A and B such that P(A) = 0.3 and P(B) = 0.6, find P(A’ ∩ B’).
Solution:
Given, P(A) = 0.3 and P(B) = 0.6
Now, P(A’ ∩ B’)=P(A ∪ B)’ = 1 – P[A ∪ B]
= 1 – [P(A) + P(B) – P(A ∩ B)]
= 1 – { 0.3 + 0.6 – 0.3 x 0.6}
[∵ A and S are independent events
∴ P(A n B) = P(A)P(B)]
= 1 – {0.9 – 0.18} = 1 – {0.72} = 0.28

Question 22.
If \(\vec{a}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{b}=3\hat{i}+5\hat{j}-2\hat{k}\), then find |\(\vec{a}\times\vec{b}\)|.
Solution: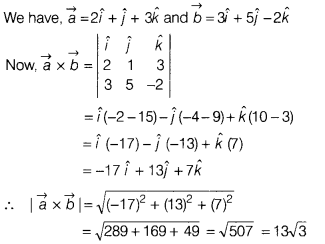

Question 23.
The probability of two students A and B coming to the school in time are \(\frac{3}{7}\) and \(\frac{5}{7}\), respectively. Assuming that the events ‘A coming in time’ and ‘B coming in time’ are independent. Find the probability of only one of them coming to the school in time.
Or
A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy.
(ii) the older child is a boy.
Solution:
Given, probability of student A coming in time,

Or
Let B represents the boy and G represents the girl. Then, the sample space of given problem is
S = {BB, GB, BG, GG}
∴ n(S) = 4
Now, let E be the event that both children are boys,
i.e. E = {BB}

(i) Let Fi be the event that one of the children is boy.
Then, F₁ = {BB, GB, BG}
∴ Required probability

Question 24.
Find the direction cosines of the following line \(\frac{3-x}{-1}=\frac{2y-1}{2}=\frac{z}{4}\)
Solution:

Question 25.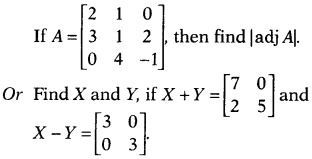

Solution: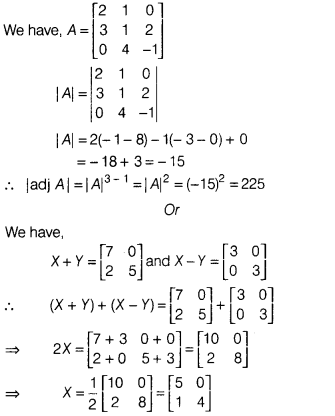

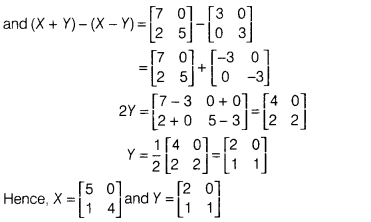
Section C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.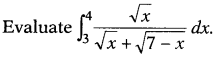

Solution:

Question 27.
Solve [xsin² (\(\frac{y}{x}\)) – y]dx + x dy = 0
such that y = \(\frac{\pi}{4}\), at x = 1.
Or
Solve x²dy + y(x + y)dx = 0.
Solution:
Given, differential equation is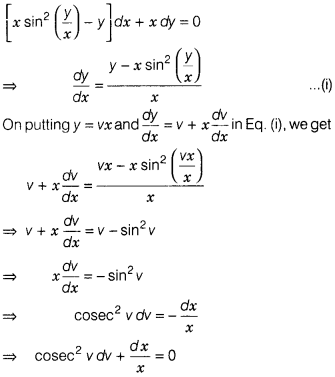

On integrating both sides, we get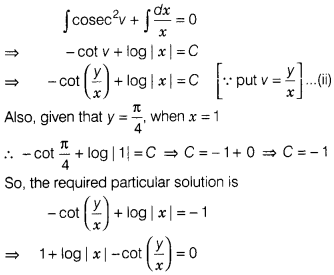

Or
Given differential equation x²dy + y(x + y)dx = O can be written as x²dy + (xy + y²)dx = 0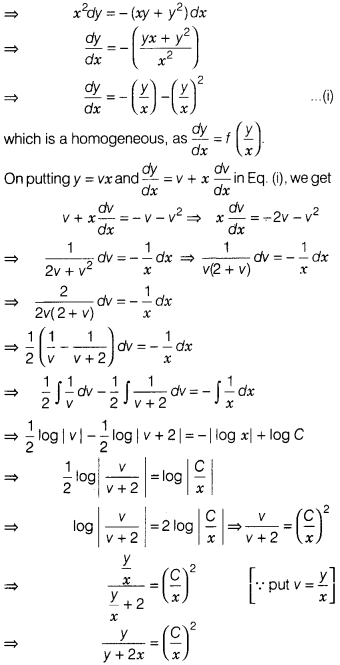

Question 28.
If x^y – y^x = a^b, then find \(\frac{dy}{dx}\)
Or
Discuss the continuity of the function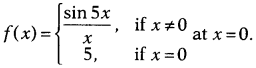

Solution: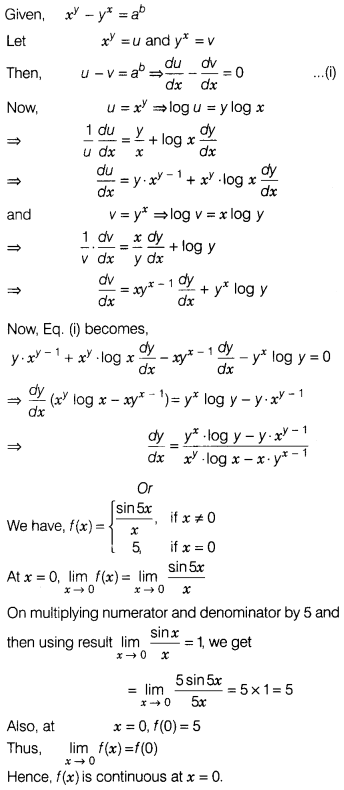

Question 29.
Solve the differential equation
(tan^-1 x – y)dx = (1 + x²)dy.
Or
Find the particular solution of the differential equation \(\frac{dy}{dx}\) + 2y tan x = sin x, dx given that y = 0, when x = \(\frac{\pi}{3}\)
Solution:
Given, (tan^-1 x – y)dx = (1 + x²)dy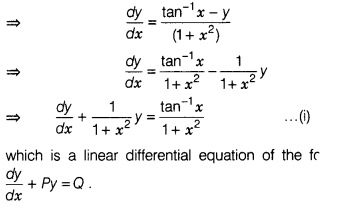


Or
Given, differential equation is
\(\frac{dy}{dx}\) + 2y tan x = sin x dx
which is a linear differential equation of the form

⇒ 0 = 2 + C ⇒ C = – 2
On putting the value of C in Eq. (ii), we get
y sec² x = sec x – 2
∴ y = cos x – 2 cos²x
which is the required particular solution of the given differential equation.

Question 30.
Sketch the region bounded by the curve y = 2x – x² and the X-axis and find its area using integration.
Solution:
Given,
y = 2x – xy
= -(x² – 2x)
= – (x² – 2x + 1 -1)
⇒ y = – (x – 1)² + 1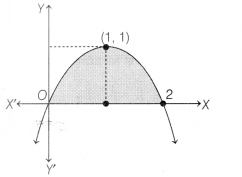

⇒ y – 1 = – (x – 1)²
⇒ (x – 1)² = -(y – 1)
Clearly, it Is downward parabola with vertex (1, 1)
Also, y = 2x – x² meets X-axis when y = 0
⇒ 0 = 2x – x²
⇒ 0 = x(2 – x) ⇒ x = 0, 2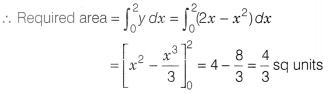

Question 31.
Consider the function f : R⁺ → [4, ∞) defined by f(x) = x² +4, where R⁺ is the set of all non-negative real numbers. Show that f is bijective.
Solution:
We have a mapping f : R⁺ → [4, ∞) given by
f(x) = x² + 4.
To prove f is invertible.
For f to be one-one.
Let x₁, x₂ ∈ R⁺ be any arbitrary elements, such that
f(x₁) = f(x₂)
⇒ x²₁ + 4 = x²₂ + 4 ⇒ x²₁ – x²₂ = 0
⇒ (x₁ – x₂) (x₁ + x₂) = 0
⇒ x₁ – x₂ = 0 [∵ x₁ + x₂ ≠ 0 as x₁, x₂ ∈ R⁺]
⇒ x₁ = x₂
So, f is one-one.
For f to be onto
Let y ∈ [4, ∞) be any arbitrary element and let y = f (x)

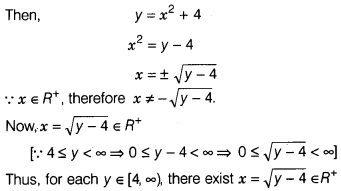
such that f(x) = y
So, f is onto.
Hence, f is bijective. Hence proved.

Section D
This section comprises of long answer type questions (LA) of 5 marks each

Question 32.
If with reference to a right handed system of mutually perpendicular unit vectors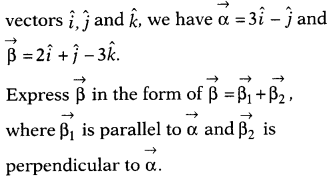

Solution:

Question 33.
Using matrices, solve the following system of equations
x – y + 2z = 7
3x + 4y – 5z = -5
and 2x -y + 3z = 12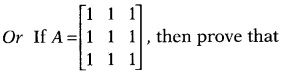


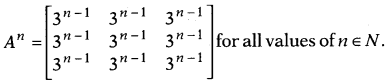
Solution:
Given, system of equations is
x – y + 2z = 7
3x + 4y – 5z = – 5
and 2x – y + 3z = 12
In matrix form, it can be written as


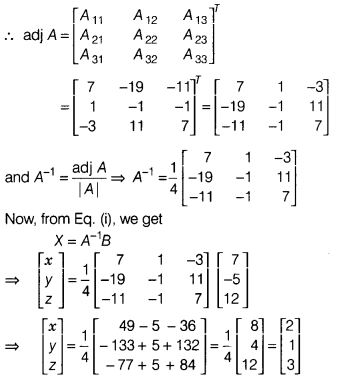
On comparing corresponding elements, we get
x = 2, y = 1 and z = 3
Or
We shall prove that result by using the principle of mathematical induction.
When n = 1, we have

Question 34.
Solve the following LPP graphically maximize Z = 2x + 3y
Subject to constraints
x + 2y ≤ 10, 2x + y ≤ 14 and x, y ≥ 0.
Or
Solve the LPP graphically Maximize Z = 60x + 40y
Subject to constraints
5x + 6y ≤ 45
3x + 2y ≤ 18
and x, y ≥ 0
Solution:
Given, maximize Z = 2x + 3y
Subject to constraints
x + 2y ≤ 10
2x + y ≤ 14
and x ≥ 0, y ≥ 0
Shade the region to the right of Y-axis to show x ≥ 0 and above X-axis to show y ≥ 0.
Table for line x + 2y = 10 is

So, the line is passing through the points (0, 5), (4, 3) and (10, 0).

On putting (0, 0) in the inequality x + 2y ≤ 10, we get 0 + 0 ≤ 10, which is true.
So, the half plane is towards the origin.
Table for line 2x + y = 14 is

So, the line is passing through the points (4, 6), (6, 2) and (7, 0).
On putting (0, 0) in the inequality 2x + y ≤ 14, we get 0 + 0 ≤ 14, which is true.
So, the half plane is towards the origin.
The intersection point of lines corresponding to Eqs. (i) and (ii) is B(6, 2).
On shading the common region, we get the feasible region OABD.

The values of Z at corner points are given below

Corner points	Value of Z = 2x + 3y
O(0, 0)	Z = 2 × 0 + 3 × 0 = 0
A(7, 0)	Z = 2 × 7 + 3 × 0 = 14
B(6, 2)	Z = 2 × 6 + 3 × 2 = 18
D(0, 5)	Z = 2 × 0 + 3 × 5 = 15

Hence, the maximum value of Z is 18 which occurs at the point (6, 2).
Or
We have to maximize Z = 60x + 40y,
Subject to the constraints
5x + 6y ≤ 45,
3x + 2y ≤ 18,
and x, y ≥ 0
Now 5x + 6y = 45
⇒ \(\frac{x}{9}=\frac{y}{15/2}\) = 1
This line meets the axes at A(9, 0) and D(0, \(\frac{15}{2}\)).

Plot these points and join them to obtain the line 5x + 6y = 45.
Clearly, (0, 0) satisfies 5x + 6y ≤ 45.
So, the region below AB represents 5x + 6y ≤ 45.
Again, 3x + 2y = 18 ⇒ \(\frac{x}{6}+\frac{y}{9}\)= 1.
This line meets the axes at C(6, 0) and D(0, 9).
Plot these points and join them to obtain the line 3x + 2y = 18.
Clearly, (0, 0) satisfies 3x + 2y ≤ 18.
So, the region below CD represents 3x + 2y ≤ 18.
x ≥ 0 is the region to the right of the Y-axis,
and y ≥ 0 is the region above the X-axis.
On solving 5x + 6y = 45 and 3x + 2y = 18, we get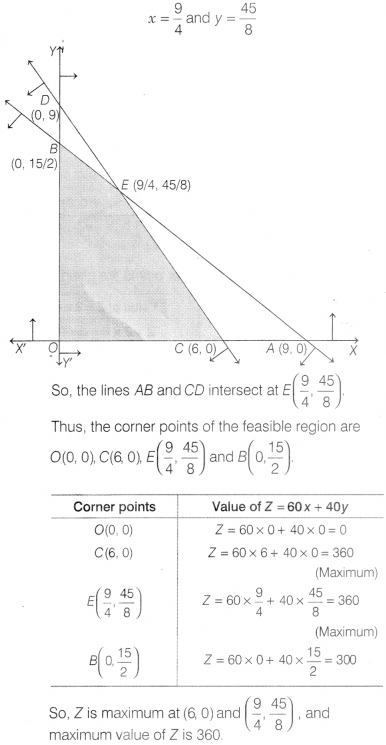

Question 35.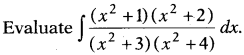

Solution:

On comparing the coefficients of t and constant terms from both sides, we get
A + B = 4 ,..(i)
and 34 + 46 = 10 … (ii)
On multiplying Eq, (i) by 3 and then subtracting Eq. (ii) from obtained equation, we get
-B = 2 ⇒ 8 = -2
Then, from Eq. (i), we get A = 6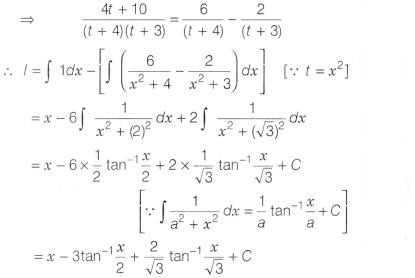

Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
Let a cone is inscribed in a sphere of radius R. The height and radius of cone are h and r, respectively.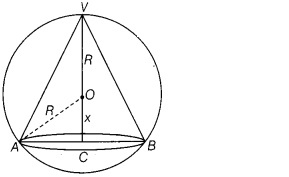

On the basis of above information, answer the following questions.
(i) Write the relation between r and R in terms of x.
(ii) Write the volume V of the cone in terms of R and x.
(iii) Show that volume V of the cone is maximum, when x = \(\frac{R}{3}\).
Or
If volume V of the cone is maximum at x = \(\frac{R}{3}\), then find the maximum value of V and find the ratio of volume of cone and volume of sphere, when volume of cone is maximum,
Solution:
(i) In ∆OAC, we have
OC² + AC² = OA²
⇒ x² + r² = R²
⇒ r = \(\sqrt{R^2-x^2}\)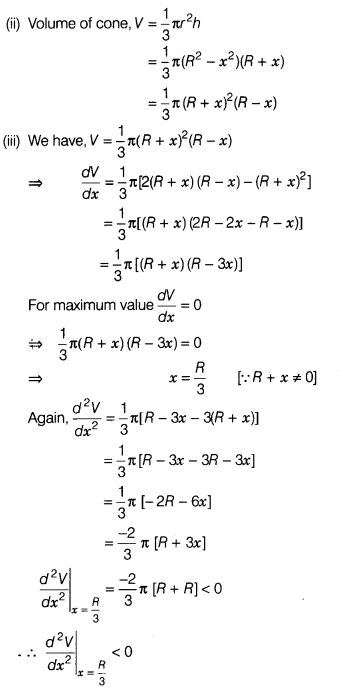

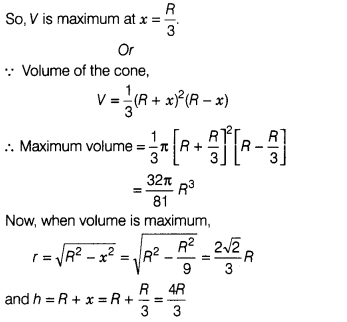
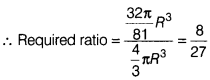
Question 37.
By examine the test, the probability that a person is diagnosed with CORONA when he is actually suffering from it, is 0.99.
The probability that the doctor incorrectly diagnosed a person to be having CORONA, on the basis of test reports, is 0.001. In a certain city, 1 in 1000 persons suffers from CORONA. A person is selected at random and is diagnosed to have CORONA.
On the basis of above information, answer the following questions.
(i) Find the probability P(person suffering from CORONA).
(ii) Find the probability P(CORONA is diagnosed, when the person actually has CORONA).
(iii) Find the probability P(CORONA is diagnosed).
Or
Find the probability P(person has CORONA given CORONA is diagnosed).
Solution:
(i) Let E = Event that the doctor diagnoses CORONA.
E₁ = Event that the person selected is suffering from CORONA.
E₂ = Event that the person selected is not suffering from CORONA.
We have,

Question 38.
For any function f(x), we have

Solution: