CBSE Sample Papers for Class 12 Maths Set-11

CBSE Sample Papers for Class 12 Maths Set 11 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case/passage based/intergrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

Question 1.
If order and degree of the differential equation (\(\frac{dy}{dx}\))⁴ + 3x\(\frac{d^2y}{dx^2}\)= 0 is m and n respectively, then m – n is equal to
(a) 1
(b) 2
(c) 3
(d) 0
Solution:
(a) We have, (\(\frac{dy}{dx}\))⁴ + 3x\(\frac{d^2y}{dx^2}\) = 0
∴ Order = 2 ⇒ m = 2
and degree = 1 ⇒ n = 1
∴ m – n = 2 – 1 = 1

Question 2.
The angle between the unit vectors \(\hat{a}\) and \(\hat{b}\), given that |\(\hat{a}+\hat{b}\)| = 1, is
(a) \(\frac{\pi}{3}\)
(b) \(\frac{\pi}{2}\)
(c) \(\frac{2\pi}{3}\)
(d) –\(\frac{\pi}{3}\)
Solution:
(c) We have, |\(\hat{a}+\hat{b}\)| = 1
Let θ be the angle between a\(\hat{a}\) and \(\hat{b}\).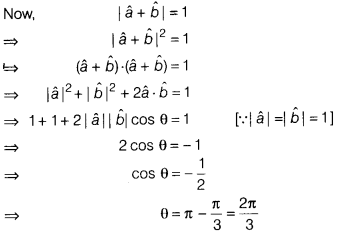

Question 3.
The function f : R → R given by f (x) = cos x ∀ x ∈ R, is
(a) one-one
(b) not one-one
(c) bijective
(d) None of these
Solution:
(b) We know that
f(0) = cos 0 = 1 and f(2π) = cos2π = 1
So, different elements in R may have the same image.
Hence, f is not one-one.

Question 4.
If f(x) = x|x|, then f'(x) is equal to
(a) x²
(b) 2x
(c) 2|x|
(d) 1
Solution:
(c) Given, f(x) = x|x|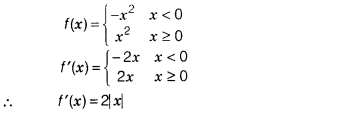

Question 5.
The value of xdy + (x – 1)dx = 0 is
(a) y = logx – x +C
(B) y = logx + x + C
(c) y = -logx + C
(d) y = -logx – x + C
Solution:
(a) We have, xdy + (x – 1)dx = 0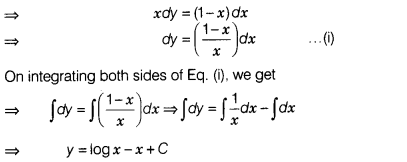

Question 6.
If f(x) = 2|x| + 3|sin x| + 6, then the right hand derivative of f (x) at x – 0, is
(a) 1
(b) 5
(c) 3
(d) 4
Solution: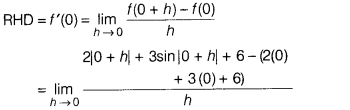

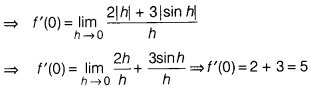
Question 7.
Let R – {(a, a³): a is the prime number less than5} be a relation, then the range of R is
(a) {2, 3}
(b) {8, 27}
(c) {2}
(d) {2, 3, 8, 27}
Solution:
(b) Given, R = {(a, a³): a is prime number less than 5}
⇒ R = {(2, 8), (3, 27)}
Hence, range of R = {8, 27}

Question 8.
If a matrix A is both symmetric and skew-symmetric, then A is
(a) null matrix
(b) identity matrix
(c) diagonal matrix
(d) None of these
Solution:
(a) Null matrix

Question 9.
The value of tan [\(\frac{1}{2}\) cos^-1(\(\frac{\sqrt5}{3}\))]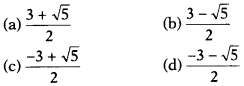

Solution: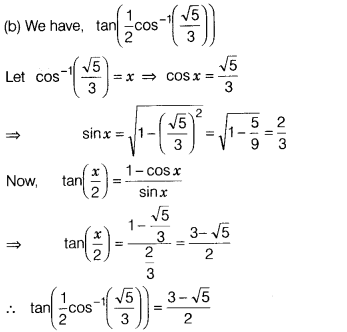

Question 10.
If A ≡ (2, 3, 1) and B ≡ (5, 4, 2), then the direction ratios of \(\vec{AB}\) are
(a) -3, 1, 1
(b) 3, 1, 1
(c) 5, 4, 2
(d) 3, 0, 1
Solution:
(b) Given, A ≡ (2, 3, 1) and B ≡ (5, 4, 2)
∴ Direction ratios of \(\vec{AB}\) are
(5 – 2), (4 – 3), (2 – 1) i.e. 3, 1, 1

Question 11.
A kite is moving horizontally at a height of 151.5 m. If the speed of kite is 10 m/sec, then the rate at which the string is being let out when the kite is 250 m away from tjie boy who is flying the kite and the height of the boy 1.5 m is
(a) 4 m/sec
(b) 6 m/sec
(c) 7 m/sec
(d) 8 m/sec
Solution:
(d) Let AB be the height of kite and DE be the height of the boy.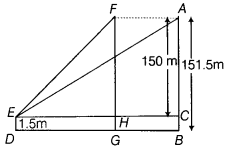

Let DB = x = EC
∴ \(\frac{dx}{dt}\) = 10 m/sec
Let AE = y
∵ AB = 151.5 m
∴ AC = AB – BC = 151.5 – 1.5m = 150 m
AC² + EC² = AE² [by Pythagoras theorem]
⇒ 150² + x² = y²
On differentiating both sides w.r.t. x, we have

Question 12.
The value of ∫sin⁵(\(\frac{x}{2}\)).cos(\(\frac{x}{2}\)) dx is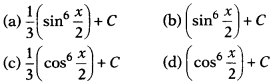

Solution: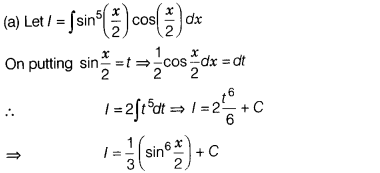

Question 13.
A right circular cylinder which is open at the top and has a given surface area, will have the greatest volume, if its height h and radius r are related by
(a) 2h = r
(b) h = 4r
(c) h = 2r
(d) h = r
Solution:
(d) Surface area, S = 2πrh + πr² …….(i)
and V = nπ²h …….(ii)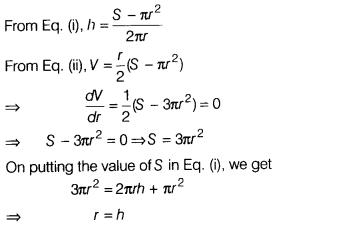

Question 14.
The value of tan^-1{tan\(\frac{15\pi}{4}\)} is
(a) \(\frac{\pi}{4}\)
(b) \(\frac{3\pi}{4}\)
(c) –\(\frac{\pi}{4}\)
(d) π
Solution:
(c) We have,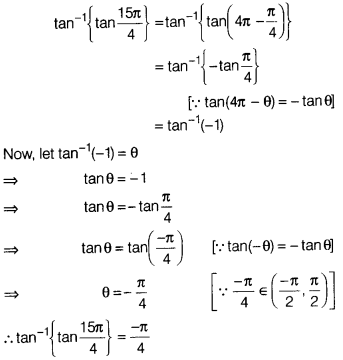

Question 15.
If [x] denotes the greatest integer function, then \(\int_0^{3/2}\) [x²] dx is equal to
(a) √2 – 2
(b) 2 – √2
(c) √2
(d) √2 + 2
Solution: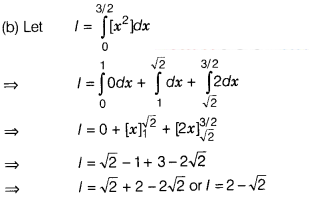

Question 16.
If A is symmetric matrix, then B’ AB is
(a) symmetric matrix
(b) skew symmetric matrix
(c) scalar matrix
(d) None of the above
Solution:
(a) (B’AB)’ = (AB)'(B’)’ = B’A’B = B’AB [∵ A’ = A]

Question 17.
The direction ratios of the line segment joining P(x₁, y₁, z₁) andQ(x₂, y₂, z₂) are
(a) x₁ – x₂, y₁ – y₂, z₁ – z₂
(b) x₂ – x₁, y₂ – y₁, z₂ – z₁
(c) Both (a) and (b)
(d) None of the above
Solution:
(c) The direction ratios of the line segment joining
P(x₁, y₁, z₁ and Q(x₂, y₂, z₂)may be taken as
x₂ – x₁ > y₂ – y₁ z₂ – z₁ or x₁ – x₂, y₁ – y₂, z₁ – z₂.

Question 18.
The area of the triangle whose two sides are represented by the vectors 2\(\hat{i}\) and – 3\(\hat{j}\) is
(a) 6 sq units
(b) 3 sq units
(c) 2 sq units
(d) 1 sq unit
Solution: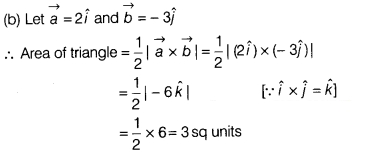

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true

Question 19.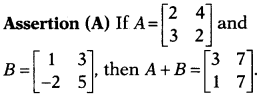

Reason (R) Two different matrices can be added only if they are of same order.
Solution: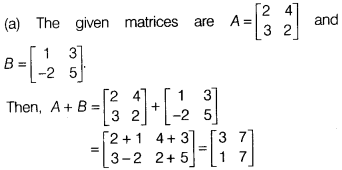

Hence, Assertion (A) is true. Reason (R) is also true and it is the correct explanation of Assertion (A).

Question 20.
Assertion (A) Let f : R → R be defined by f(x) = x² + L Then, pre-images of 17 are ± 4.
Reason (R) A function f : A → B is called a one-one function, if distinct elements of A have distinct images in B.
Solution:
(b) Assertion Consider, x² +1 = 17
⇒ x² = 16 ⇒ x = ±4
Hence, pre-images of 17 are ± 4.
Hence, both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
Find |\(\vec{a}\times\vec{b}\)|, if \(\vec{a}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{b}=3\hat{i}+5\hat{j}-2\hat{k}\).
Solution: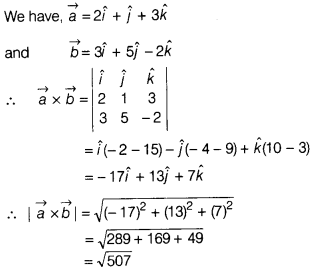

Question 22.
Find the area of the region bounded by the curve y = cos x between \(\frac{\pi}{2}\) to \(\frac{3\pi}{2}\).
Solution:
We have, y = cos x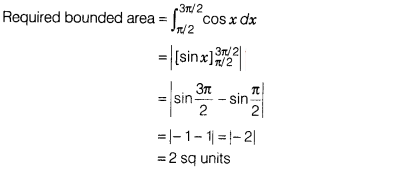

Here. -2 represents that the area of the required region is below the X-axis.

Question 23.
Evaluate ∫\(\frac{1}{\sqrt{9+8x-x^2}}\)
Or
Evaluate ∫x log x dx
Solution:

Question 24.
Show that the function x + \(\frac{1}{x}\) is increasing for x > 1.
Solution: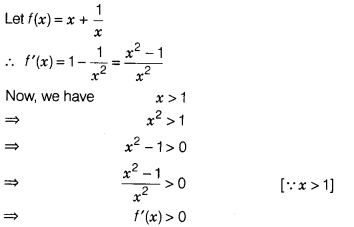

Hence, f(x) is increasing for x > 1.

Question 25.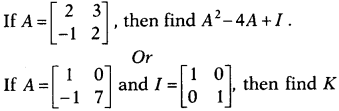

so that A² = 8A + KI
Solution: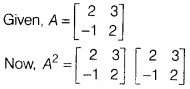

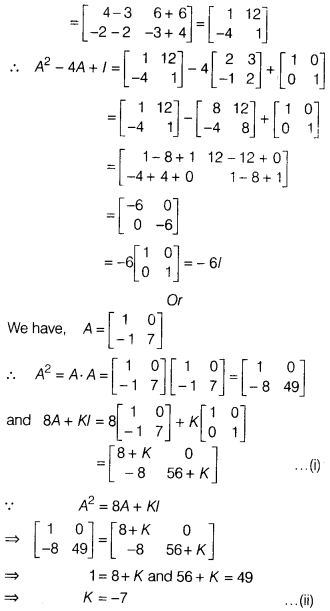
Section C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.
Find the value of c, for which the vectors
\(\vec{a}=(c log_2 x)\hat{i}-6\hat{j}+3\hat{k}\) and
\(\vec{b}=(log_2 x)\hat{i}+2\hat{j}+(2c log_2 x)\hat{k}\) make an obtuse angle for any x ∈ (0, ∞).
Solution:

⇒ c(log₂ x)² – 12 + 6c(log₂ x) < 0 ∀ x ∈ (0, ∞)
⇒ cy² + 6cy -12 < 0 ∀ y ∈ R,
where y = log₂x [∵ x > 0 ⇒ y = log₂ x ∈ R]
⇒ c <0 and 36c² + 48c <0
[∵ ax² + bx + c <0 ∀ x ⇒ a < 0 and discriminant < 0]
⇒ c < 0 and c (3c + 4) < 0
⇒ c < 0 and –\(\frac{-4}{3}\) < c < 0
⇒ c ∈ (\(\frac{-4}{3}\), 0

Question 27.
If y = x^x, then prove that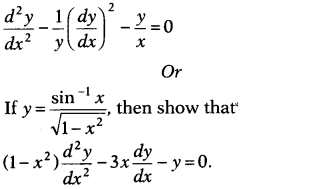

Solution:
Given, y = x^x
On taking log both sides, we get log y = log x^x
⇒ logy = xlog x
On differentiating both sides w.r.t. x, we get

On differentiating both sides w.r.t. x, we get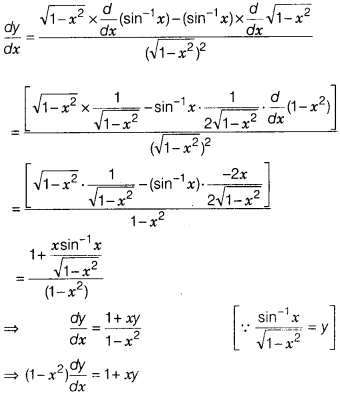

On differentiating both sides of above equation w.r.t. x, get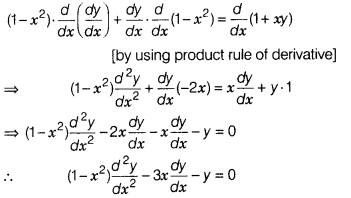

Question 28.
Show that the function f : R → R defined by f(x) = \(\frac{3x-1}{2}\), x ∈ R is one-one and onto functions.
Solution:
Given, f(x) = \(\frac{3x – 1}{2}\), x ∈ R
For one-one Let x₁, x₂ ∈ R such that f(x₁) = f(x₂)

Hence, f is onto.
So, f is one-one and onto. Hence proved.

Question 29.
Find the particular solution of the differential equation (1 + e^2x) dy + (1 + y²) e^xdx = 0, given that y = 1, when x = 0.
Or
Solve the following differential equation y²dx + (x² – xy + y²) dy = 0.
Solution:
Given, differential equation is
(1 + e^2x)dy + (1 + y²) e^xdx = 0
⇒ (1 + e^2x)dy = -(1 + y²)e^xdx


which is the required solution.

Question 30.
Find whether the following function is differentiable at x = 1 and x = 2 or not.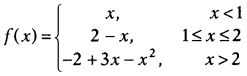

Solution: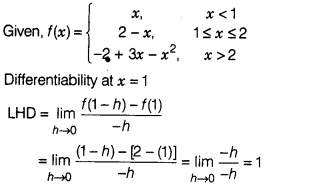


∵ LHD = RHD
So, f (x) is differentiable at x = 2.
Hence, f(x) is not differentiable at x = 1, but it differentiable at x = 2.

Question 31.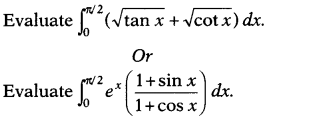

Solution:

Section D
This section comprises of long answer type questions (LA) of 5 marks each

Question 32.
Show that area of the parallelogram, whose diagonals are given by \(\vec{a}\) and \(\vec{b}\) is \(\frac{|\vec{a}\times\vec{b}|}{2}\).
Or
Find the area of the parallelogram, whose diagonals are \(2\hat{i}-\hat{j}+\hat{k}\) and \(\hat{i}+3\hat{j}-\hat{k}\).
Solution:

Question 33.
Find the equation of line joining P(11, 7) and Q(5, 5) using determinants. Also, find the value of k, if R(-1, k) is the point such that area of ∆PQR is 9 sq m.
Solution:
Let A(x, y) be any point on line PC.
Then, the points P, Q and A are collinear.


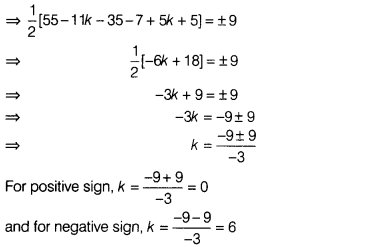
Hence, the required values of k are 0 and 6.

Question 34.
Maximise Z = 8x + 9y subject to the constraints given below
2x + 3y ≤ 6, 3x – 2y ≤ 6, y ≤ 1, x, y ≥ 0.
Or
Solve minimise Z = 5x+ 7y
Subject to constraints
2x + y ≥ 8; x + 2y ≥ 10, x, y ≥ 0
Solution:
We have the following LPP
Maximise Z = 8x + 9y
Subject to the constraints
2x + 3y ≤ 6
3x – 2y ≤ 6
y ≤ 1 and x, y ≥ 0
Now, considering the inequations as equations, we get
2x + 3y = 6 ….(i)
3x – 2y = 6 …(ii)
and y = 1 …(iii)
Table for line 2x + 3y = 6 is

x	3	0
y	0	2

So, it passes through the points, (3, 0) and (0, 2).
On putting (0, 0) in the inequality 2x + 3y ≤ 6, we get
0 ≤ 6 [which is true]
So, the half plane is towards the origin.
Table for line 3x – 2 y = 6 is

x	2	0
y	0	-3

So, it passes through the points (2, 0) and (0, -3). On putting (0,0) in the inequality 3x – 2y ≤ 6, we get
0 ≤ 6 [which is true]

So, the half plane is towards the origin.
The line y = 1 is perpendicular to Y-axis.
On putting (0,0) in the inequality y < 1, we get
0 < 1 [which is true]
So, the half plane is towards the origin.
Also, x ≥ 0, y ≥ 0, so the feasible region lies in the first quadrant.
The point of intersection of Eqs. (i) and (ii) is (\(\frac{30}{13}\), \(\frac{6}{13}\))
Eqs. (ii) and (iii) is (\(\frac{8}{3}\), 1) and Eqs.(i) and (iii) is (\(\frac{3}{2}\), 1)

The graphical representation of the above system of inequations is given below

To solve the LPP graphically, we first convert the inequations into equations to obtain the following lines.
2x + y = 8,
x +2 y = 10.
x = 0. y = 0
The line 2x + y = 8 meets the coordinate axes at A₁(4, 0)and B₁(0, 8), join these points to obtain the line represented by 2x + y = 8.
Clearly, 0(0,0) does not satisfy the inequation 2x + y ≥ 8.

So, the region not containing the origin is represented by this inequation.

The line x + 2y = 10 meets the coordinate axes at A₂(10, 0)and S₂(0, 5). Join these points to obtain the line represented by x + 2y = 10.
Clearly, 0(0, 0) does not satisfy the inequation x + 2y ≥ 10.

So, the region not containing the origin is represented by this inequation. Clearly.x ≥ 0 and y ≥ 0 resprcsent the first quadrant.

Thus, the shaded region in figure is the feasible region of the LPP The coordinates of the corner points of this region are A₂(10, 0), P(2, 4) and B₁(0, 8).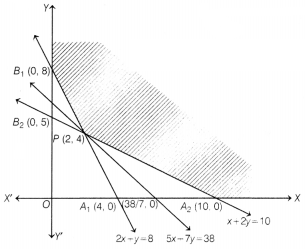

The,point P(2, 4) is obtained by solving 2x + y = 8 and x + 2y = 10 simultaneously. The values of the objective function Z = 5x + 7y at the corner points of the feasible region are given in the following table

Point (x, y)	Value of the objective function Z = 5x + 7y
A2(10, 0)	Z = 5 × 10 + 7 × 0 = 50
P(2, 4)	Z = 5 × 2 + 7 × 4 = 36
B1(0, 8)	Z = 5 × 0 + 7 × 8 = 56

Clearly, Z is minimum at x = 2 and y = 4.

Question 35.
Find the area under the curve y = \(\sqrt{3x+4}\) between x = 0, x = 4 and the X-axis.
Solution:
Given, curve is y = \(\sqrt{3x+4}\)
On squaring both sides, we get

As, y = \(\sqrt{3x+4}\) is a positive square root, so we take a upper part of the parabola, y² = 3x + 4

The area of the region bounded by the curve y = \(\sqrt{3x+4}\) between x = 0, x = 4 and the X-axis, is the area shown in the figure given below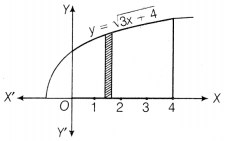


Hence, the required area is \(\frac{112}{9}\)sq units.

Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
A school wants to form a poster for advertisement purpose. The top and bottom margins of poster should be 10 cm and the side margins should be 6 cm. Also, the area for printing the advertisement should be 1200 cm².
Based on the above information, answer the following questions.
(i) If b cm be the width and h cm be the height of poster, then find the ai ea of poster, expressed in terms of b and h.
(ii) Find the relation between b and h.
(iii) Find the value of h, so that the area of the poster is minimised.
Or
Find the value of b, so that area of the poster is minimised.
Solution:
(i) Let the area of the poster be A, then
A = 1200 + 2(b . 10) + 2(h . 6) – 4(6 . 10)
= 1200 + 20b + 12h – 240
= 960 + 20b + 12b

(ii) The relation between b and h


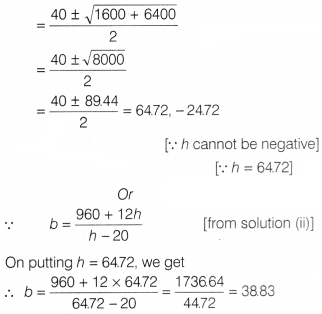
Hence, the required value of b is 38.83 cm.

Question 37.
Integration is the process of finding the antiderivative of a function. In this process, we are provided with the derivative of a function and asked to find out the function (i.e. primitive) integration is the inverse process of differentiation.
Let f(x) be a function of x. If there is a function g(x), such that \(\frac{d}{dx}\)[g(x)] = f(x), then g(x) is called an integral of f(x) w.r.t.x and is denoted by ∫f(x)dx = g(x) + C, where C is constant of integration.
Based on the above information, answer the following questions.
(i) ∫(3x + 4)³dx is equal to
(ii) ∫\(\frac{(x+1)^2}{x(x^2+1)}\)dx is equal to
(iii) ∫sin² x dx is equal to
Or
∫tan² x dx is equal to
Solution:
(i) We know that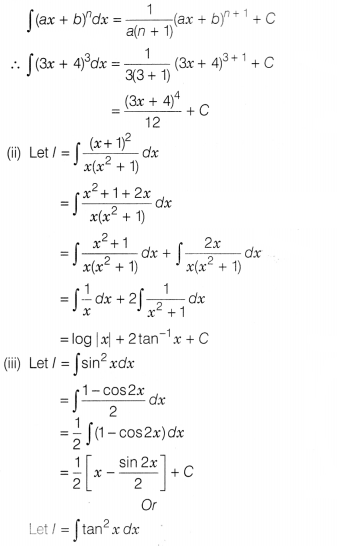

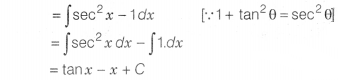
Question 38.
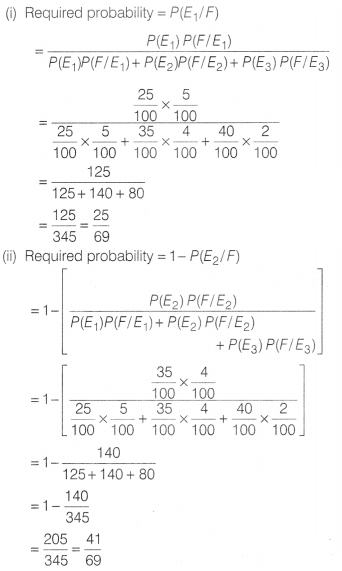
In a bolt factory, machines A, B and C manufactured respectively, 25%, 35% and 40% of the total bolts. Of their output 5%, 4% and 2% are respectively, defective bolts.
Based on the above information, answer the following questions.
(i) Find the probability, if drawn bolt is defective, then it is manufactured by A.
(ii) If drawn bolt is defective, then find the probability that it is not manufactured by B.
Solution:
Consider the following events
E₁ = Bolt is manufactured by machine A
E₂ = Bolt is manufactured by machine B
E₃ = Bolt is manufactured by machine C
F = Drawn bolt is defective
We have,