Ray Optics and Optical Instruments

Class 12 Physics Chapter 9 Important Extra Questions Ray Optics and Optical Instruments

Very Short Answer

Question 1.
When light undergoes refraction at the surface of separation of two media, what happens to its frequency/wavelength?
Answer:
There is no change in its frequency, but its wavelength changes.

Question 2.
Define the refractive index.
Answer:
The Refractive index of a medium is defined as the ratio of the speed of light in a vacuum to the speed of light in the given medium.

Question 3.
What is the distance between the objective and eyepiece of an astronomical telescope in its normal adjustment?
Answer:
Distance between objective and eyepiece of telescope = f_o + f_e

Question 4.
Name the phenomenon responsible for the reddish appearance of the sun at sunrise and sunset.
Answer:
Atmospheric refraction.

Question 5.
What are the two main considerations that have to be kept in mind while designing the ‘objective’ of an astronomical telescope?
Answer:
Two main considerations are

1. Large light gathering power
2. Higher resolution (or resolving power)

Question 6.
Under what condition does a biconvex lens of glass having a certain refractive index act as a plane glass sheet when immersed in a liquid? (CBSE Delhi 2012)
Answer:
When the refractive index of the liquid is equal to the refractive index of a glass of which the lens is made.

Question 7.
Write the relationship between the angle of incidence ‘i’, angle of prism ‘A’ and angle of minimum deviation for a triangular prism. (CBSE Delhi 2013)
Answer:
2i = A + δ_m

Question 8.
Why can’t we see clearly through the fog? Name the phenomenon responsible for it. (CBSE Al 2016)
Answer:
Because it scatters light. Scattering of light.

Question 9.
How does the angle of minimum deviation of a glass prism vary if the incident violet light is replaced by red light? Give reason. (CBSE AI 2017)
Answer:
It decreases as δ_m ∝ \(\frac{1}{λ}\)

Question 10.
The objective lenses of two telescopes have the same apertures but their focal lengths are in the ratio 1: 2. Compare the resolving powers of the two telescopes. (CBSE AI 2017C)
Answer:
Same as resolving power does not depend upon the focal length of lenses.

Question 11.
An object is kept in front of a concave lens. What is the nature of the image formed? (CBSE Delhi 2017C)
Answer:
Virtual and erect.

Question 12.
Aglasslensof refractive index 1.5 is placed in a trough of liquid. What must be the refractive index of the liquid in order to mark the lens disappear? (Delhi 2008)
Answer:
In order to make the lens disappear the refractive index of liquid must be equal to 1.5 i.e. equal to that of glass lens.

Question 13.
A converging lens of refractive index 1.5 is kept in a liquid medium having same refractive index. What would be the focal length of the lens in this medium? (Delhi 2008)
Answer:
The lens in the liquid will act like a plane sheet of glass
∴ Its focal length will be infinite (∞)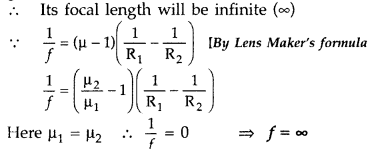

Question 14.
How does the power of a convex lens vary, if the incident red light is replaced by violet light? (Delhi 2008)
Answer:
According to Lens Maker’s formula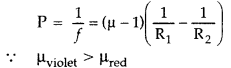

∴ power of the lens will be increased.

Question 15.
How does the angle of minimum deviation of a glass prism vary, if the incident violet light is replaced with red light? (All India 2008)
Answer:
We know that λ red > λ violet, therefore µ red < µ violet and hence δ red < δ violet.
When incident violet light is replaced with red light, the angle of minimum deviation of a glass decreases.

Question 16.
Why does the bluish colour predominate in a clear sky? (All India 2008)
Answer:
Blue colour of the sky : The scattering of light by the atmosphere is a colour dependent. According to Rayleigh’s law, the intensity of scattered light \(\mathrm{I} \propto \frac{1}{\lambda^{4}}\), blue light is scattered much more strongly than red light. Therefore, the colour of sky becomes blue. The blue component of light is proportionately more in the light coming from different parts of the sky. This gives the impression of the blue sky.

Question 17.
How does the angle of minimum deviation of a glass prism of refractive index 1.5 change, if it is immersed in a liquid of refractive index 1.3? (All India 2008)
Answer: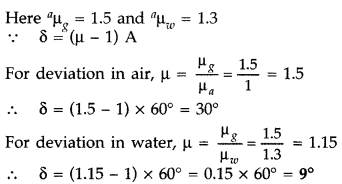

Hence angle of deviation is decreased.

Question 18.
You are given following three lenses. Which two lenses will you use as an eyepiece and as an objective to construct an astronomical telescope? (Delhi 2009)

Lenses	Power (P)	Aperture
L1	3D	8 cm
L2	6D	1 cm
L3	10D	1 cm

Answer:
Objective – Less power and more aperture. So L₁
Eyepiece – More power and less aperture. So L₃.

Question 19.
Two thin lenses of power + 4D and – 2D are in contact. What is the focal length of the combination? (All India 2009)
Answer: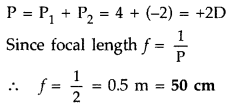

Question 20.
Two thin lenses of power + 6D and – 2D are in contact. What is the focal length of the combination? (All India 2009)
Answer: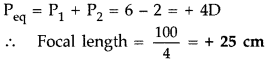

Question 21.
A glass lens of refractive index 1.45 disappears when immersed in a liquid. What is the value of refractive index of the liquid? (Delhi 2010)
Answer:
The value of refractive index of the liquid should be 1.45 so that the glass lens of refractive index 1.45 disappears when immersed in a liquid.

Question 22.
State the conditions for the phenomenon of total internal reflection to occur. (Delhi 2010)
Answer:
Two essential conditions for total internal reflection are :

1. Light should travel from an optically denser medium to an optically rarer medium.
2. The angle of incidence in the denser medium must be greater than the critical angle for the two media.

Question 23.
Calculate the speed of light in a medium whose critical angle is 30°. (Delhi 2010)
Answer: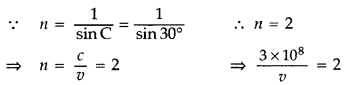

∴ Speed of light, v = 1.5 × 10⁸ ms^-1

Question 24.
A converging lens is kept coaxially in contact with a diverging lens — both the lenses being of equal focal lengths. What is the focal length of the combination? (Delhi 2010)
Answer:
Focal length of the combination is Infinity.

Question 25.
When light travels from a rarer to a denser medium, the speed decreases. Does this decrease in speed imply a decrease in the energy carried by the light wave? Justify your answer. (All India 2010)
Answer:
No, the energy carried by the lightwave remains the same.
Reason : As energy E = hv

Here frequency remains same.

Question 26.
When monochromatic light travels from one medium to another its wavelength changes but frequency remains the same. Explain. (Delhi 2011)
Answer:
If v₁ and v₂ denote the velocity of light in medium 1 and medium 2 respectively and λ₁ and λ₂ denote the wavelength of light in medium 1 and medium 2. Thus

The above equation implies that when a wave gets refracted into denser medium (v₁ > v₂) the wavelength and the speed of propagation decreases but the frequency v (\(=v / \lambda\)) remains the same.

Question 27.
Under what condition does a biconvex lens of glass having a certain refractive index act as a plane glass sheet when immersed in a liquid? (Delhi 2012)
Answer:
When the refractive index of glass of biconvex lens is equal to the refractive index of the liquid in which lens is immersed
or µ₁ = µ_g

Question 28.
For the same value of angle of incidence, the angles of refraction in three media A, B and C are 15°, 25° and 35° respectively. In which medium would the velocity of light be minimum? (All India 2012)
Answer: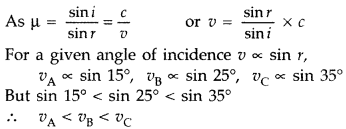

∴ Velocity of light is minimum in medium A.

Question 29.
How would a biconvex lens appear when placed in a trough of liquid having the same refractive index as that of the lens? (Comptt. Delhi 2011)
Answer:
A biconvex lens appears plane glass when placed in a trough of liquid having the same refractive index as that of the lens.

Question 30.
Two thin lenses of power -4D and 2D are placed in contact coaxially. Find the focal length of the combination. (Comptt. All India 2011)
Answer:
Power of combination = – 4D + 2D = – 2D

∴ Focal length, f = – 50 cm

Question 31.
Two thin lenses of power -2D and 2D are placed in contact coaxially. What is the focal length of the combination? (Comptt. All India 2011)
Answer:
Power of combination = -2D + 2D = 0

Question 32.
Write the relationship between angle of incidence ‘i’, angle of prism ‘A’ and angle of minimum deviation for a triangular prism. (Delhi 2013)
Answer:

where [δ_m is angle of minimum deviation]

Question 33.
When red light passing through a convex lens is replaced by light of blue colour, how will the focal length of the lens change? (Comptt. All India 2013)
Answer:
Focal length of lens will decrease \(\mu_{v}>\mu_{r}\)

Question 34.
If the wavelength of light incident on a convex lens is increased, how will its focal length change? (Comptt. All India 2013)
Answer: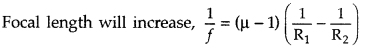

Question 35.
A convex lens is placed in contact with a plane mirror. A point object at a distance of 20 cm on the axis of this combination has its image coinciding with itself. What is the focal length of the lens? ‘ (Delhi 2014)
Answer:
Focal length of lens = 20 cm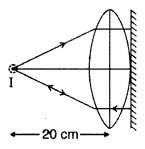

(Hint: Rays coming out of lens are incident normally on plain mirror and hence reflected rays will trace the path of incident ray, hence forming image on the object itself, thus object and image overlapping each other at F of convex lens.)

Question 36.
A biconvex lens made of a transparent material of refractive index 1.25 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Give reason. (All India 2014)
Answer:
The lens will behave as a diverging lens, because -1)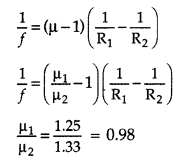

The value of (µ – 1) is negative and ‘f’ will be negative.

Question 37.
A biconvex lens made of a transparent material of refractive index 1.5 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Give reason. (All India 2014)
Answer:
The lens will behave as a converging lens because

Hence value of ‘f’ will be positive.

Question 38.
A concave lens of refractive index 1.5 is immersed in a medium of refractive index 1.65. What is the nature of the lens? (Delhi 2015)
Answer:
Converging.

Question 39.
Why does bluish colour predominate in a clear sky? (All India 2015)
Answer:
Blue colour of the sky : The scattering of light by the atmosphere is a colour dependent. According to Rayleigh’s law, the intensity of scattered light \(\mathrm{I} \propto \frac{1}{\lambda^{4}}\), blue light is scattered much more strongly than red light. Therefore, the colour of sky becomes blue. The blue component of light is proportionately more in the light coming from different parts of the sky. This gives the impression of the blue sky.

Question 40.
When an object is placed between f and 2f of a concave mirror, would the image formed be
(i) real or virtual and
(ii) diminished or magnified? (Comptt. Delhi 2015)
Answer:
(i) Real
(ii) magnified

Question 41.
How does the angle of minimum deviation of a glass prism vary, if the incident violet light is replaced by red light? Give reason. (Delhi 2017)
Answer:
The angle of minimum deviation decreases, when violet light is replaced by red light because refractive index for violet light is more than that for red light.

Question 42.
An object is kept in front of a concave lens. What is the nature of the image formed? (Comptt. Delhi 2017)
Answer:
When an object is kept in front of a concave lens, the nature of image formed is virtual, erect and diminished.

Question 43.
When light travels from a rarer medium to denser medium, the speed of light decreases. Does the reduction in speed imply a reduction in the energy? (Comptt. Delhi 2017)
Answer:
The reduction in speed, due to light travelling from a rarer to denser medium does not imply reduction in the energy.

Question 44.
The objective lenses of two telescopes have the same apertures but their focal lengths are in the ratio 1: 2. Compare the resolving powers of the two telescopes. (Comptt. All India 2017)
Answer:
Ratio of resolving power = 1 : 1
Resolving power is same because it does not depend on focal length of the objective.

Question 45.
Why must both the objective and the eye piece of a compound microscope have short focal lengths? (Comptt. All India 2017)
Answer:
For getting higher magnification in compound microscope, both objective and eyepiece must have short focal length, because

Question 46.
The refractive index of the material of a concave lens is n₁. It is immersed in a medium of refractive index n₂. A parallel beam of tight is incident on the lens. Trace the path of the emergent rays when n₂ > n₁.
Answer:
The path of rays is as shown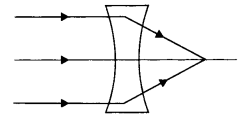

Question 47.
A convex lens made of glass of refractive index μ_L is immersed in a medium of refractive index μ_m. How will the lens behave when μ_L < μ_m?
Answer:
The lens will continue to behave as a convex lens.

Question 48.
The image of an object formed by a lens on the screen is not in sharp focus. Suggest a method to get clear focusing of the image on the screen without disturbing the position of the object, the lens or the screen.
Answer:
Limit the field of view of the lens by using a blackened glass having a small circular hole in the middle.

Question 49.
In the figure given below, the path of a parallel beam of light passing through a convex lens of refractive index ng kept in a medium of refractive index nm is shown. Is (i) n_g = n_m or (ii) n_g > n_m, or (iii) n_g < n_m?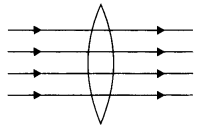

Answer:
As the rays of light do not suffer any deviation, therefore n_g = n_m.

Question 50.
In the figure path of a parallel beam of light passing through a convex lens of refractive index ng kept in a medium of refractive index, nm is shown. Is (i) n_g = n_m or (ii) n_g > n_m, or (iii) n_g < n_m?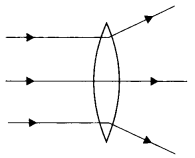

Answer:
As the rays of light diverge, therefore n_g < n_m.

Question 51.
The refractive index of the material of a concave lens is μ₁. It is immersed in a medium of refractive index μ₂. A parallel beam of light is incident on the lens. Trace the path of emergent rays when μ₂ < μ₁.
Answer:
The path of rays is as shown below.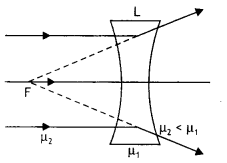

Question 52.
Suppose that the lower half of the concave mirror’s reflecting surface is covered with an opaque (non-reflective) material. What effect will this have on the image of an object placed in front of the mirror?
Answer:
The image of the whole object will be formed. However, as the area of the reflecting surface has been reduced the intensity of the image will below (in this case, half).

Question 53.
For the same value of angle of incidence, the angles of refraction in three media A, B and C are 15°, 25° and 35° respectively. In which medium would the velocity of light be minimum? (CBSE Al 2012)
Answer:
Medium A.

Question 54.
When red light passing through a convex lens is replaced by the light of blue colour, how will the focal length of the lens change? (CBSE AI 2013C)
Answer:
It will decrease.

Question 55.
A biconvex lens made of a transparent material of refractive index 1.25 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Give reason. (CBSE AI 2014)
Answer:
The diverging lens as its focal length will become negative.

Question 56.
A concave lens of refractive index 1.5 is immersed in a medium of refractive index 1.65. What is the nature of the lens? (CBSE Delhi 2015)
Answer:
It will behave as a convex lens.

Question 57.
Why can’t we see clearly through a fog? Name the phenomenon responsible for it. (CBSE AI 2016)
Answer:
Because it scatters light. Scattering of light.

Question 58.
How does the angle of minimum deviation of a glass prism vary if the incident violet light is replaced by red light? Give reason. (CBSE AI 2017)
Answer:
It decreases as δ_m ∝ \(\frac{1}{λ}\)

Question 59.
The objective lenses of two telescopes have the same apertures but their focal lengths are in the ratio 1: 2. Compare the resolving powers of the two telescopes. (CBSE AI 2017C)
Answer:
Same as resolving power does not depend upon the focal length of lenses.

Question 60.
An object is kept in front of a concave lens. What is the nature of the image formed? (CBSE Delhi 2017C)
Answer:
Virtual and erect.

Question 61.
A convex lens is held in water. What change, if any, do you expect In its focal length?
Answer:
Focal Length of the given Lens increases in accordance with tens maker’s formula
\(\frac{1}{f}\) = (μ – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)

This is because _wμ_{g a}μ_g

Question 62.
Violet light is incident on a converging lens of focal length f. State with reason, how the focal length of the lens will change 1f the violet light is replaced by a red light.
Answer:
As μ_r < μ_v hence in accordance with the relation
\(\frac{1}{f}\) = (μ – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) focal Length of Lens for red colour will be more.

Question 63.
What is the minimum value of the refractive index of the prism shown in the figure below?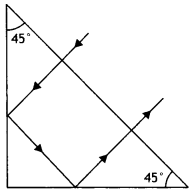

Answer:
μ = \(\frac{1}{\sin i_{c}}=\frac{1}{\sin 45^{\circ}}=\frac{1}{\sqrt{2}}\)

Question 64.
How does the resolving power of a telescope change on decreasing the aperture of its objective lens? Justify your answer.
Answer:
As the resolving power of a telescope is \(\frac{D}{1.22λ}\) hence on decreasing the aperture of its objective lens, the resolving power of the telescope decreases in the same ratio.

Question 65.
What will happen to a ray of light incident normally on the interface of air and glass?
Answer:
It will pass un-deviated into the glass.

Question 66.
What is the speed of light in glass having a refractive index of 1.5?
Answer:
Speed of light in glass v = c/n = 3 × 10⁸ / 1.5 = 2 × 10⁸ m s^-1

Question 67.
Light of wavelength 600 nm in air enters a medium of refractive index 1.5. What will be its frequency in the medium?
Answer:
Frequency does not change when light moves from one medium into another. Therefore frequency of light
v = \(\frac{c}{\lambda}=\frac{3 \times 10^{8}}{600 \times 10^{-9}}\) = 5 × 10¹⁴ Hz

Question 68.
How does the focal length of a convex lens change if monochromatic red light Is used instead of monochromatic blue
light?
Answer:
Focal Length increases, i.e. f_r > f_v.

Question 69.
Two thin lenses of power + 5 D and – 3 D are in contact. What Is the focal length of the combination?
Answer:
Here P = P₁ + P₂ = + 5 – 3 = + 2 D
Hence f = 1/P = ½ m = + 50 cm.

Question 70.
Use the maker’s formula to write an expression for the (relative) refractive index, μ, of the material in terms of its focal length, f and the radii of curvature, r₁ and r₂, of Its two surfaces.
Answer:
The formula is \(\frac{1}{f}\) = (μ – 1)\(\left(\frac{1}{r_{1}}-\frac{1}{r_{2}}\right)\)

Question 71.
Two thin lenses of power – 4 D and 2 D are placed in contact coaxially. Find the focal length of the combination. (CBSE Ai 2012C)
Answer:
Total power P = – 4 + 2 = – 2 D
Now f = 1/P = 1/ -2 = – 0.5 m

Question 72.
A convex lens is placed In contact with a plane mirror. A point object at a distance of 20 cm on the axis of this combination has its image coinciding with itself. What is the focal length of the lens? (CBSE Delhi 2014)
Answer:
20 cm

Question 73.
The focal length of a biconvex lens is equal to the radius of curvature of either face. What is the refractive index of the material of the lens? (CBSEAI 2015)
Answer:
1.5
Using \(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)

Given R₁ = R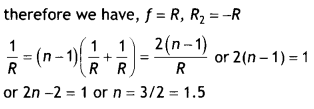

Question 74.
An unsymmetrical double convex thin lens forms the image of a point object on its axis. Will the position of the image change if the ens are reversed? (NCERT Exemplar)
Answer:
No, the reversibility of the Lens does not change the lens formula.

Short Answer Type

Question 1.
The aperture of the objective lens of an astronomical telescope is doubled. How does it affect
(i) the resolving power of the telescope and
(ii) the intensity of the image? (CBSE Sample Paper 2018-19)
Answer:
The resolving power of a telescope is given by the expression \(\frac{D}{1.22λ}\).

(i) When the aperture of the objective lens is increased, the resolving power of the telescope increases in the same ratio.
(ii) The intensity of the image is given by the expression β ∝ D₂, thus when the aperture is doubled, the intensity of the image becomes four times.

Question 2.
How does the resolving power of a compound microscope change on (a) decreasing the wavelength of light used, and (b) decreasing the diameter of the objective lens?
Answer:
The resolving power of a microscope is given by the expression RP = \(\frac{2 n \sin \theta}{\lambda}\)

(a) If the wavelength of the incident tight is decreased, the resolving power of the microscope increases.
(b)There is no effect of the decrease in the diameter of the objective on the resolving power of the microscope.

Question 3.
The layered lens shown in the figure is made of two kinds of glass. How many and what kinds of images will be produced by this lens with a point source placed on the optic axis? Neglect the reflection of light at the boundaries between the layers.

Answer:
Two images will be formed as the lens may be thought of, as two separate lenses of different focal lengths. The images will be surrounded by bright halos.

Question 4.
Monochromatic light is refracted from air into a glass of refractive index n. Find the ratio of wavelengths of the incident and refracted light.
Answer:
Using the relation λ₁n₁ = λ₂n₂ we have
\(\frac{\lambda_{1}}{\lambda_{2}}\) = n

Question 5.
Draw a labelled ray diagram to show the image formation in a compound microscope.
Answer:
The labelled diagram is as shown.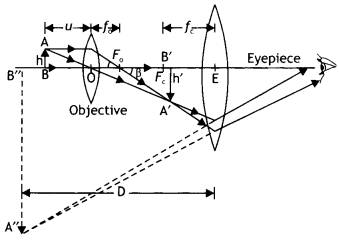

Question 6.
A ray of light while travelling from a denser to a rarer medium undergoes total internal reflection. Derive the expression for the critical angle in terms of the speed of light in the two media.
Answer:
Snell’s law can be used to find the critical angle. Now Snell’s law, when the ray moves from denser medium ‘b’ to rarer medium ‘a’, is given by


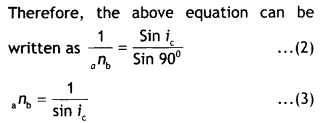
Now we know that n = \(\frac{c}{v}\) , substituting in the above relation we have
\(\frac{c}{v}=\frac{1}{\sin i_{c}}\) or sin i_c = \(\frac{v}{c}\)

Question 7.
Draw a ray diagram of a reflecting type telescope. State two advantages of this telescope over a refracting telescope. (Delhi 2008)
Answer: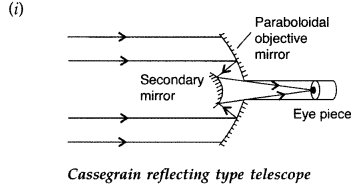

(ii) Advantages of reflecting telescope over a refracting telescope:

1. Due to large aperture of the mirror used, the reflecting telescopes have high resolving power.
2. This type of telescope is free from chromatic aberration (formation of coloured image of a white object).
3. The use of paraboloidal mirror reduces the spherical aberration (formation of non-point, blurred image of a point object).
4. Image formed by reflecting telescope is brighter than refracting telescope.
5. A lens of large aperture tends to be very heavy and therefore difficult to make and support by its edges. On the other hand, a mirror of equivalent optical quality weights less and can be supported over its entire back surface.

Question 8.
Draw a ray diagram of an astronomical telescope in the normal adjustment position. State two drawbacks of this type of telescope. (Delhi 2008)
Answer:
(i) Magnifying power m = \(-\frac{f_{0}}{f_{e}}\). It does not change with increase of aperature of objective lens, because focal length of a lens has no concern with the aperature of lens.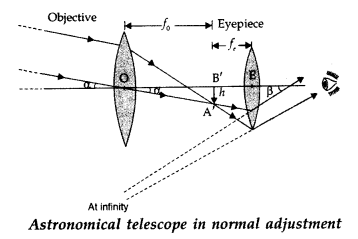

(ii) Drawbacks :

• Images formed by these telescopes have chromatic aberrations.
• Lesser resolving power.
• The image formed is inverted and faintes.

Question 9.
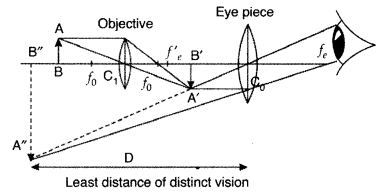
Draw a ray diagram of a compound microscope. Write the expression for its magnifying power.
(Delhi 2008)
Answer: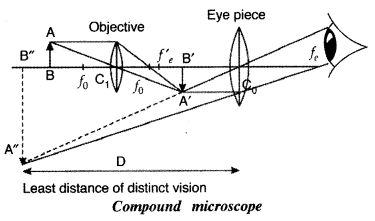

When the final image is formed at the least distance of distinct vision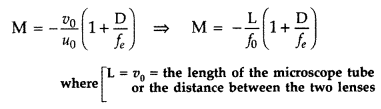

Question 10.
Draw a labelled ray diagram of an astronomical telescope in the near point position. Write the expression for its magnifying power. (All India 2008)
Answer: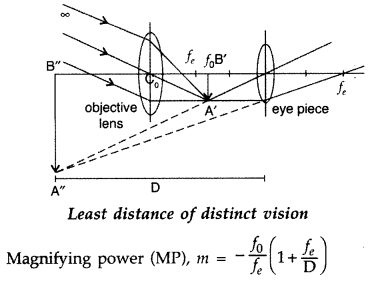

Question 11.
Draw a labelled ray diagram, showing the image formation of an astronomical telescope in the normal adjustment position. Write the expression for its magnifying power.(All India 2008)
Answer:
(i) Magnifying power m = \(-\frac{f_{0}}{f_{e}}\). It does not change with increase of aperature of objective lens, because focal length of a lens has no concern with the aperature of lens.

(ii) Drawbacks :

• Images formed by these telescopes have chromatic aberrations.
• Lesser resolving power.
• The image formed is inverted and faintes.

Question 12.
Draw a ray diagram for the formation of image in a compound microscope. Write the expression for its magnifying power. (All India 2008)
Answer:

When the final image is formed at the least distance of distinct vision

Question 13.
A ray of light passing through an equilateral triangular glass prism from air undergoes minimum deviation when angle of incidence is 3/4^th of the angle of prism. Calculate the speed of light in the prism. (Delhi 2008)
Answer: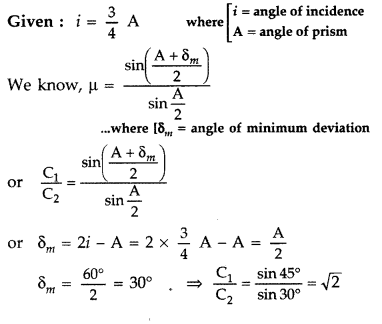

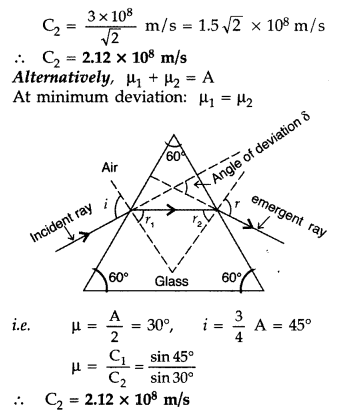
Question 14.
Calculate the distance of an object of height h from a concave mirror of focal length 10 cm, so as to obtain a real image of magnification 2. (Delhi 2008)
Answer:
Given : f = -10 cm; Magnification, m = 2
To calculate : u = ?

Question 15.
Define refractive index of a transparent medium. A ray of light passes through a triangular prism. Plot a graph showing the variation of the angle of deviation with the angle of incidence. (All India 2009)
Answer:
Refractive index of a transparent medium is the ratio of the speed of light in free space to the speed in the given medium.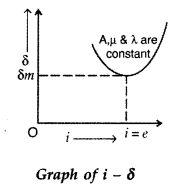

Question 16.
(i) What is the relation between critical angle and refractive index of a material?
(ii) Does critical angle depend on the colour of light? Explain. (All India 2009)
Answer: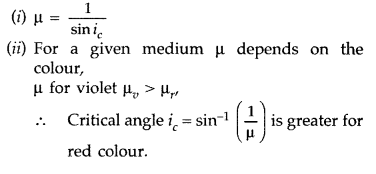

Question 17.
The radii of curvature of the faces of a double convex lens are 10 cm and 15 cm. If focal length of the lens is 12 cm, find the refractive index of the material of the lens. (Delhi 2010)
Answer:
Given : R₁ = 10 cm,
R₂ = -15 cm,
f = 12 cm
Using lens maker’s formula, we have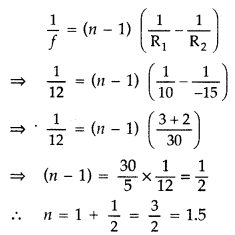

Refractive index of the material of the lens :

Question 18.
(a) The bluish colour predominates in clear sky.
(b) Violet colour is seen at the bottom of the spectrum when white light is dispersed by a prism.
State reasons to explain these observations. (Delhi 2010)
Answer:
(a) The scattering of light by the atmosphere is colour dependent. According to Rayleigh’s law, the intensity of scattered light, \(I \propto \frac{1}{\lambda_{4}}\)

Blue light is scattered much more strongly than red light. The blue component of light is proportionately more in the light coming from different parts of the sky. This gives the impression of the blue sky.

(b) As refractive index of prism is different for different colours, therefore, different colours deviate through different angles on passing through the prism. As λ_violet < λ_red therefore µ_violet > µ_red. Hence δ_violet > δ_red maximum deviation is of violet colour. That is why violet colour, is seen at the bottom of the spectrum when white light is dispersed by a prism.

Question 19.
A biconvex lens has a focal length 2/3 times the radius of curvature of either surface. Calculate the refractive index of lens material.
Answer: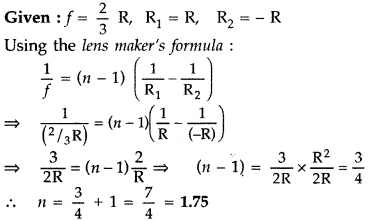

Question 20.
(i) Why does the Sun appear reddish at sun-set or sun-rise?
(ii) For which colour the refractive index of prism material is maximum and minimum? (Delhi 2009).
Answer:
(i) During Sunrise or sunset, the Sun is near the horizon. Sunlight has to travel a greater distance. So shorter waves of blue region are scattered away by the atmosphere. Red waves of longer wavelength are least scattered and reach the observer. So the Sun appears reddish.
(ii) Refractive index of prism material is maximum for violet colour and refractive index of prism material is minimum for red colour.

Question 21.
Find the radius of curvature of the convex surface of a plano-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5. (Delhi 2009)
Answer: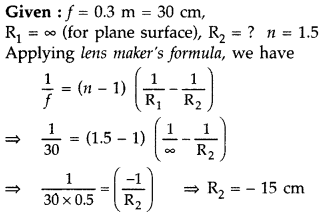

∴ Radius of curvature = -15 cm.

Question 22.
(i) Out of blue and red light which is deviated more by a prism? Give reason.
(ii) Give the formula that can be used to determine refractive index of material of a prism in minimum deviation condition. (Delhi 2009)
Answer: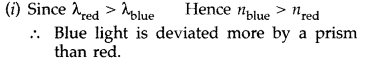

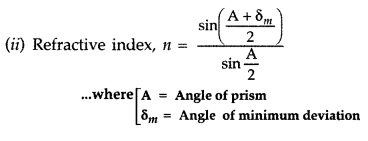
Question 23.
Two convex lenses of same focal length but of aperture Ar and A2 (A2 < A-,), are used as the objective lenses in two astronomical telescopes having identical eyepieces. What is the ratio of their resolving power? Which telescope will you prefer and why? Give reason. (Delhi 2009)
Answer:
Resolving power of a telescope is given by R.P.

From the given condition, the ratio of resolving power of two astronomical telescopes will be R.P, A,

Telescope with large aperture (A₁) should be preferred as it increases the resolution by collecting more light.

Question 24.
A ray of light, incident on an equilateral glass prism (µ_g = \(\sqrt{3}\) ) moves parallel to the base line of the prism inside it. Find the angle of incidence for this ray.
Answer: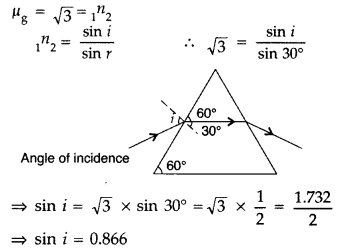

∴ Angle of incidence, i = 60°

Question 25.
An object AB is kept in front of a concave mirror as shown in the figure.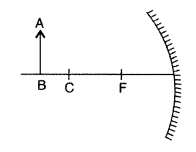

(i) Complete the ray diagram showing the image formation of the object.
(ii) How will the position and intensity of the image be affected if the lower half of the mirror’s reflecting surface is painted black? (All India 2012)
Answer: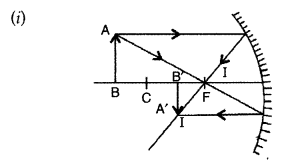

(ii) When the lower half of the mirror is painted black, the image formed is still of the same size as that with unpainted mirror but the intensity of the image has now reduced.

Question 26.
Draw a labelled ray diagram of a reflecting telescope. Mention its two advantages over the refracting telescope. (All India 2012)
Answer: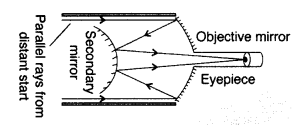

Two advantages over the refracting telescope :

1. There is no chromatic aberration as the objective is a mirror.
2. Spherical aberration is reduced using mirror objective in the form of a paraboloid.
3. Image is brighter compared to that in a refracting type telescope.
4. Higher resolving power. (any two)

Question 27.
(a) Plane and convex mirrors are known to produce virtual images of the objects. Draw a ray diagram to show how, in the case of convex mirrors, virtual objects can produce real images.
(b) Why are convex mirrors used as side view mirrors in vehicles? (Comptt. Delhi 2012)
Answer:
(a) When rays incident on a plane. mirror or convex mirror are tendmg to converge to a point behind the mirror, they are reflected ‘ to a point on a screen in front of the mirror. Hence, a real image is formed (when the object is virtual).

(b) A convex mirror is used as side view mirror in vehicles because it has larger field of view as compared to other mirror. The image formed is small and erect.

Question 28.
(a) Draw a ray diagram for a convex minor showing the image formation of an object placed anywhere in front of the minor.
(b) Use this ray diagram to obtain the expression for its linear magnification. (Comptt. All India 2012)
Answer:
(a) Ray diagram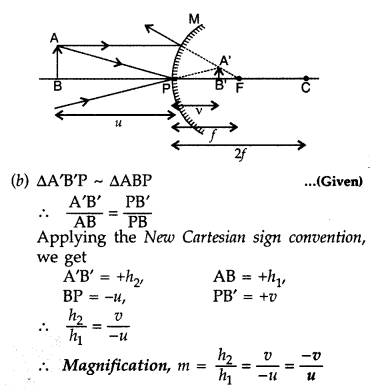

Question 29.
(a) Draw a ray diagram for a concave minor showing the image formation of an object placed anywhere in front of a minor.
(b) Using the ray diagram, obtain the expression for its linear magnification. (Comptt. All India 2012)
Answer:
(a) Ray diagram :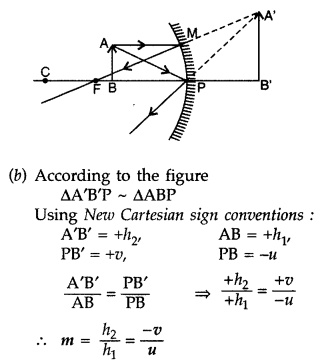

Question 30.
Deduce, with the help of ray diagram, the expression for the mirror equation in the case of convex minor. ‘ (Comptt All India 2012)
Answer:

Question 31.
A convex lens of focal length 25 cm is placed coaxially in contact with a concave lens of focal length 20 cm. Determine the power of the combination. Will the system be converging or diverging in nature? (Delhi 2013)
Answer:

The system will be a diverging lens as it has negative power.

Question 32.
Draw a ray diagram showing the image formation by a compound microscope. Hence obtain the expression for total magnification when the image is formed at infinity. (Delhi 2013)
Answer:
Ray Diagram:
(a) Ray diagram of a compound microscope : A schematic diagram of a compound microscope is shown in the figure. The lens nearest the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece, which functions essentially like a simple microscope or magnifier, produces the final image, which is enlarged and virtual. The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image formation at infinity, or a little closer for image formation at the near point. Clearly, the final image is inverted with respect to the original object.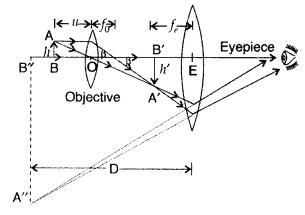

Magnification due to a compound microscope.
The ray diagram shows that the (linear) magnification due to the objective, namely h’/h, equals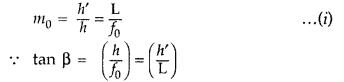

Here h’ is the size of the first image, the object size being h and f₀ being the focal length of the objective. The first image is formed near the focal point of the eyepiece. The distance L, i.e., the distance between the second focal point of the objective and the first focal point of the eyepiece (focal length f_e) is called the tube length of the compound microscope.

As the first inverted image is near the focal point of the eyepiece, we use for the simple microscope to obtain the (angular) magnification me due to it when the final image is formed at the near point, is

When the final image is formed at infinity, the angular magnification due to the eyepiece, me = (D//e)

Thus, the total magnification from equation (i) and (iii), when the image is formed at infinity, is

(b) Resolving power of a microscope :

(i) The focal length of the objective lens has no effect on the resolving power of microscope.
(ii) When the wavelength of light is increased, the resolving power of a microscope

Expression for total magnification when image is formed at infinity:
Magnification of object,

Angular magnification due to eye piece,

Total magnification when image is formed at infinity

Question 33.
A convex lens of focal length 30 cm is placed coaxially in contact with a concave lens of focal length 40 cm. Determine the power of the combination. Will the system be converging or diverging in nature? (Delhi 2013)
Answer: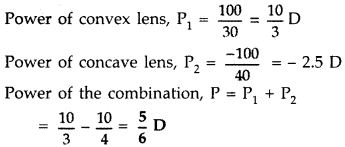

The system is converging in nature.

Question 34.
A convex lens of focal length f₁ is kept in contact with a concave lens of focal length fr Find the focal length of the combination. (All India 2013)
Answer:
f₁ ➝ is focal length of convex lens
f₁ ➝ is focal length of concave lens.
f_net ➝ be the focal length of the combination. The power of the combination is the sum of the two powers.
So, net focal length of combined lens is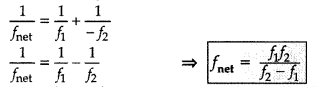

Question 35.
Draw a schematic arrangement of a reflecting telescope (Cassegrain) showing how rays coming from a distant object are received at the eye-piece. Write its two important advantages over a refracting telescope. (Comptt. Delhi 2013)
Answer:
Reflecting telescope. Telescope with mirror objectives is called reflecting telescope. This is also known as Cassegrain telescope / Newtonian telescope. The ray diagram of reflecting type telescope is shown in figure.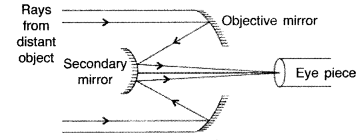

Advantage over refracting telescope :

1. Since reflecting telescope has mirror objective, so the image formed is free from chromatic aberration.
2. Since the spherical mirrors are parabolic mirrors, free from spherical aberration, they produce a very sharp and distinct image.

Question 36.
Draw a labelled ray diagram of refracting type telescope in normal adjustment. Write two main considerations required of an astronomical telescope. (Comptt. Delhi 2013)
Answer:
Refracting telescope :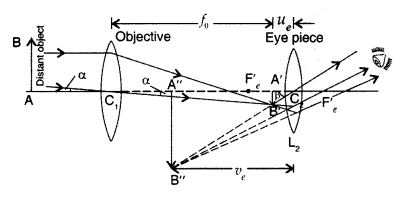

Magnifying power. It is defined as the ratio of angle (β) subtended by the final image on the eye to the angle (α) subtended by object on eye.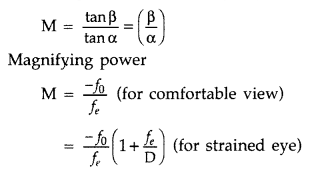

Limitations of refracting telescope over a a reflecting type telescope :

1. It suffers from chromatic aberration due to refraction and hence the image obtained is multicoloured and blurred.
2. As a lens of large apparatus can’t be manufactured easily, its light gathering power is low and hence can’t be used to see faint stars.

Question 37.
Draw a labelled ray diagram of a compound microscope. Why are the objective and the eye-piece chosen to have small focal length? (Comptt. Delhi 2013)
Answer: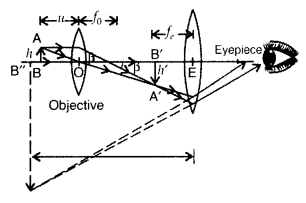

1. If the focal lengths are less, then their magnifying power will be more.
2. To avoid any aberration in refraction due to larger bend on passing through the eyepiece.

Question 38.
A ray of light passes through an equilateral prism in such a way that the angle of incidence is equal to the angle of emergence and each of these angles is 3/4 times the angle of the prism. Determine
(i) the angle of deviation and
(ii) the refractive index of the prism. (Comptt. All India 2013)
Answer: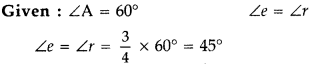

We know, that δ + A = i + e
=> δ = z + e – A
∴ 8 = 45° + 45° – 60° = 30°
(i) angle of deviation = 30°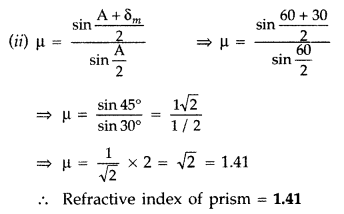

Question 39.
Two monochromatic rays of light are incident normally on the face AB of an isosceles right angled prism ABC. The refractive indices of the glass prism for the two rays ‘1’ and ‘2’ are respectively 1.35 and 1.45. Trace the path of these rays entering through the prism. (All India 2014)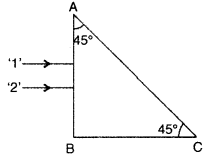

Answer: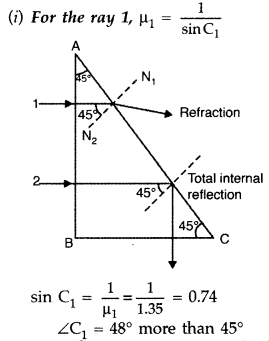

Since the angle of incidence (45°) is less than the critical angle (48°), the ray will be refracted.
(ii) For the ray 2,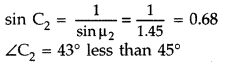

Since the angle of incidence (45°) is more than the critical angle (43°), the ray will be total internally reflected.

Question 40.
Two monochromatic rays of light are incident normally on the face AB of an isosceles right-angled prism ABC. The refractive indices of the glass prism for the two rays ‘T and ‘2’ are respectively 1.3 and 1.5. Trace the path of these rays after entering through the prism. (All India 2014)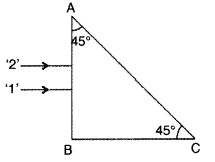

Answer: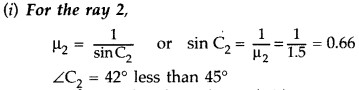

Since the angle of incidence (45°) is more than the critical angle (42°), the ray will be total internally reflected.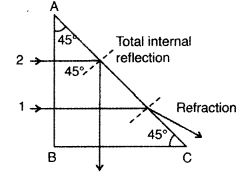

(ii) For the ray 1,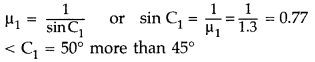

Since the angle of incidence (45°) is less than the critical angle (50°) the ray will be total refracted.

Question 41.
Draw a schematic diagram of a reflecting telescope (Cassegrain). Write its two advantages over a refracting telescope. (Comptt. Delhi 2014)
Answer:
Reflecting telescope. Telescope with mirror objectives is called reflecting telescope. This is also known as Cassegrain telescope / Newtonian telescope. The ray diagram of reflecting type telescope is shown in figure.

Advantage over refracting telescope :

1. Since reflecting telescope has mirror objective, so the image formed is free from chromatic aberration.
2. Since the spherical mirrors are parabolic mirrors, free from spherical aberration, they produce a very sharp and distinct image.

Question 42.
Draw a ray diagram for the formation of image by a compound microscope. Write the expression for total magnification when the image is formed at infinity. (Comptt. Delhi 2014)
Answer:
Compound Microscope :

Magnifying power : The magnifying power of a compound microscope is defined as the ratio of the angle subtended at the eye by the final virtual image to the angle subtended at the eye by the object, when both are at the least distance of distinct vision from the eye.

Numerical: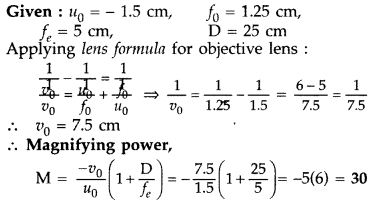

The -ve sign shows that the final image is an inverted image.

The expression magnifying power of compound microscope when the final image is formed at infinity is :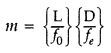

Question 43.
Write the conditions for observing a rainbow. Show, by drawing suitable diagrams, how one understands the formation of a rainbow. (Comptt. All India 2014)
Answer:
The conditions for observing a rainbow are:

1. The Sun comes out after a rainfall.
2. The observer stands with the Sun towards his/her back.

Formation of a rainbow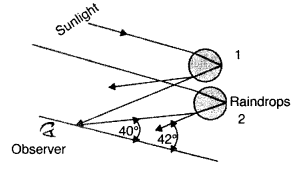

• The rays of light reach the observer through a refraction, followed by a reflection followed by a refraction.
• Figure shows red light from drop 1 and violet light from drop 2, reaching the observer’s eye.

Question 44.
Use the mirror equation to show that an object placed between f and 2f of a concave mirror produces a real image beyond 2f. (Delhi 2014)
Answer: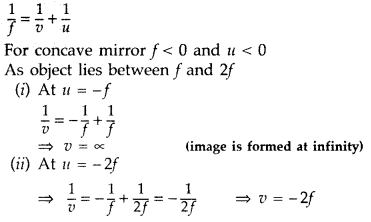

Hence, image distance v ≥ -2f
Since, v is negative therefore the image is real.

Question 45.
You are given two converging lenses of focal lengths 1.25 cm and 5 cm to design a compound microscope. If it is desired to have a magnification of 30, find out the separation between the objective and the eyepiece. (All India 2014)
Answer:
(a) When the image lies at infinity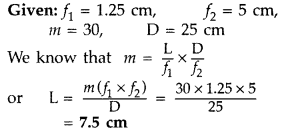

(b) When the image is formed at the near point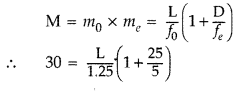

30 × 1.25 = L × 6
L = 5 × 1.25 = 6.25 cm

Question 45 a.
A small telescope has an objective lens of focal length 150 cm and eyepiece of focal length 5 cm. What is the magnifying power of the telescope for viewing distant objects in normal adjustment?
If this telescope is used to view a 100 m tall tower 3 km away, what is the height of the image of the tower formed by the objective lens? (All India 2014)
Answer:

Question 46.
Why does white light disperse when passed through a glass prism?
Using lens maker’s formula, show how the focal length of a given lens depends upon the colour of light incident on it. (Comptt. Delhi 2014)
Answer:
(i) The white light disperses when passed through a prism, because the refractive index of the glass of the prism is different for different wavelengths (colours). Hence, different colours get bent along different directions.

(ii) Using lens maker’s formula,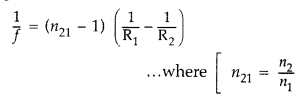

As the refractive index of the medium (n₂) (glass) with respect to air (n₁) depends on the wavelength or colour of light, therefore focal length of the lens would change with colour.

Question 47.
A ray PQ incident normally on the refracting face BA is refracted in the prism BAC made of material of refractive index 1.5. Complete the path of ray through the prism. From which face will the ray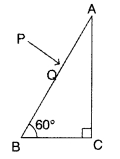

Answer:
(i) The ray will emerge from the face AC as shown. A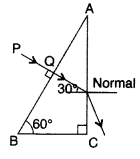


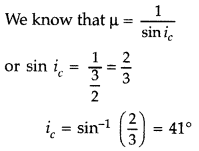
The angle of incidence (i) on the face AC is 30°, which is < i_c, hence the ray will emerge as shown in the diagram, and will NOT be reflected back.

Question 48.
Draw a ray diagram to show how a right angled isosceles prism may be used to “bend the path of light rays by 90°”.
Write the necessary condition in terms of the refractive index of the material of this prism for the ray to bend to 90°. (Comptt. Delhi 2014)
Answer:
(a) Ray diagram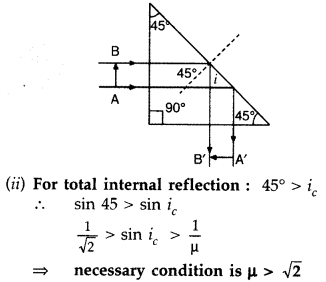

Question 49.
The image of an object, formed by a combination of a convex lens (of focal length f) and a convex mirror (of radius of curvature R), set up, as shown is observed to coincide with the object.
Redraw this diagram to mark on it the position of the centre of curvature of the mirror.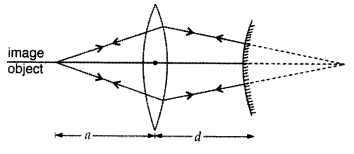

Obtain the expression for R in terms of the distances, marked as a and d, and the focal length, l, of the convex lens. (Comptt. Delhi 2014)
Answer: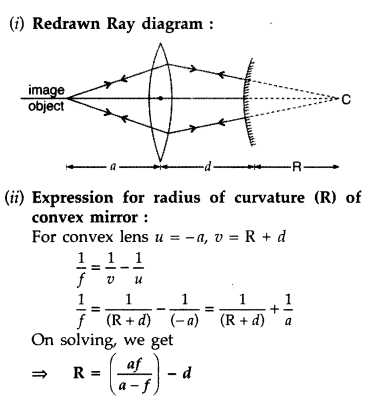

Question 50.
Define the magnifying power of a compound microscope when the final image is formed at infinity. Why must both the objective and the eyepiece of a compound microscope have short focal lengths? Explain. (Delhi 2016)
Answer:
Definition : Magnifying power of a compound microscope is defined as “the angle subtended at the eye by the image to the angle subtended (at the unaided eye) by the object”.
Reason : To increase the magnifying power, both the objective and the eyepiece must have short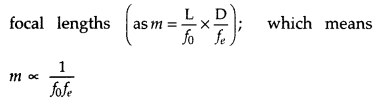

Question 51.
Why should the objective of a telescope have large focal length and large aperture? Justify your answer.
Answer:
Large focal length : to increasing magnifying power.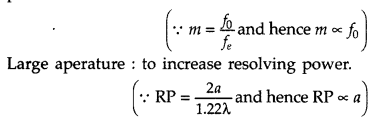

Question 52.
A small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index upto a height H. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut-off the light from the bulb. (Comptt. Delhi 2016)
Answer:
It is only the light coming out from a cone of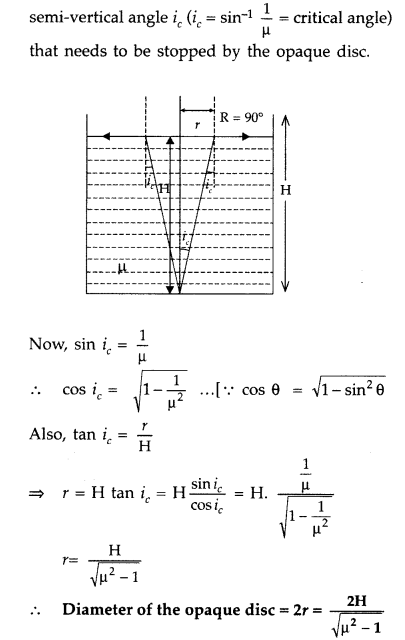

Question 53.
A ray of light is incident on a glass prism of refractive index and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence, angle of prism and critical angle. (Comptt. Delhi 2017)
Answer: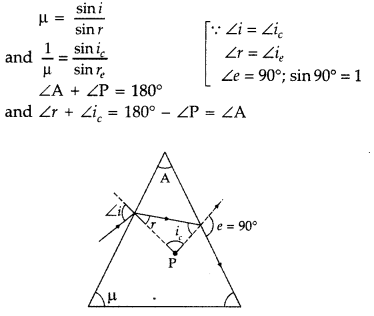

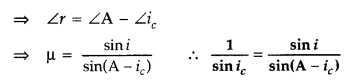
Question 54.
(i) Define refractive index of a medium.
(ii) In the following ray diagram, calculate the speed of light in the liquid of unknown refractive index. (Comptt. All India 2017)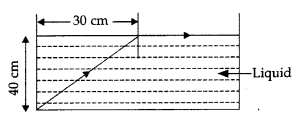

Answer:
(i) The refractive index of a medium is defined as the ratio of speed of light in vacuum (c) to the speed of light in the medium (v)

(ii) Given : Width of liquid surface (w) = 30 cm
Depth of liquid (d) = 40 cm
Since it is a critical case of total internal reflection, when refracted ray gazes along the liquid surface.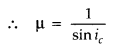

From the given ray diagram, the length of ray inside liquid is 50 cm

Question 55.
Draw a labelled diagram for a refracting type astronomical telescope. How will its magnifying power be affected by increasing for its eyepiece (a) the focal length and (,b) the aperture? Justify your answer. Write two drawbacks of refracting type telescopes. (CBSE Sample Paper 2018-19)
Answer:
The labelled diagram of the telescope is as shown in the figure.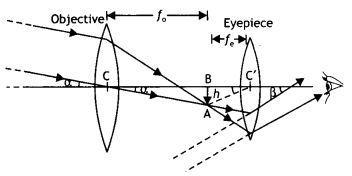

(a) The magnifying power of a telescope is given by M = \(\frac{f_{0}}{f_{\mathrm{e}}}\). If the focal length of the eyepiece is increased, it will decrease the magnifying power of the telescope.

(b) Magnifying power does not depend upon the aperture of the eyepiece. Therefore there is no change in the magnifying power if the aperture of the eyepiece is increased.

Drawbacks:

• Large-sized lenses are heavy and difficult to support.
• Large-sized lenses suffer from chromatic and spherical aberration.

Question 56.
Draw a labelled ray diagram of a Newtonian type reflecting telescope. Write any one advantage over refracting type telescope.
Answer:
The labelled diagram is shown below.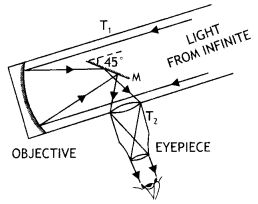

Due to the large aperture of the mirror as compared to a lens the image formed is much brighter than that formed by a refracting type telescope.

Question 57.
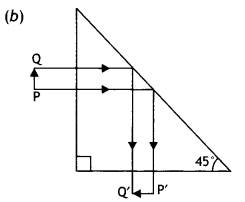
A right-angle crown glass prism with a critical angle of 41° is placed between the object PQ in two positions as shown in figures (a) and (b). Trace the path of rays from P and Q passing through the prisms in the two cases.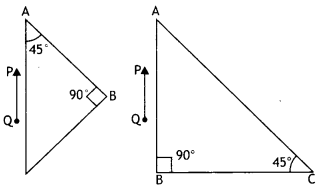

Answer:
The path of rays is as shown.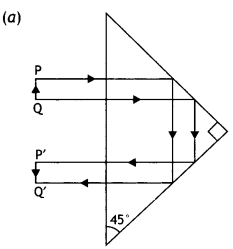


Question 58.
Write two conditions necessary for total internal reflection to take place.
Answer:
(a) The incident ray should travel from the denser to the rarer medium.
(b) The angle of incidence, in the denser medium, should be greater than the critical angle for the given pair of media.

Question 59.
(a) Explain the working of a compound microscope with the help of a labelled diagram.
Answer:
A compound microscope is an instrument used to see highly magnified images of tiny objects.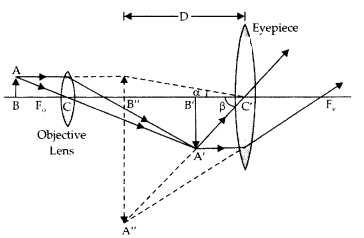

Working:
Let a tiny object AB be placed in front of the objective lens at a distance more than F₀. Its real and enlarged image is formed at A ‘ B ‘. The image A’ B’ acts as an object for the eyepiece and forms the final image at A” B “,

i.e. at a distance D, the least distance of distinct vision.

(b) Write the considerations that you keep in mind while choosing lenses to be used as eyepiece and objective in a compound microscope. (CBSE 2019C)
Answer:
The objective and eyepiece should have a short focal length for large magnification.

Question 60.
Explain the working of a refracting telescope with the help of a labelled diagram. What are the main limitations of this type of telescope and how are these overcome in a reflecting telescope? (CBSE 2019C)
Answer:
Refracting telescope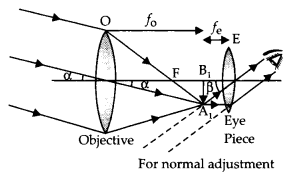

Working:
When the rays of light are made to incident on the objective from a distant object, the objective forms the real and inverted image at its focal plane. The lens is so adjusted that the final image is formed at least distance of distinct vision or at infinity.

Limitations:

• Large-sized lenses are needed which are expensive.
• Large-sized lenses suffer from spherical aberration and distortions.

Reflecting telescope (To overcome limitations):

• Reflecting telescopes are free from chromatic aberration and spherical aberration is very small.
• They are less heavy and easier to support.

Question 61.
Explain why the colour of the sky is blue.
Answer:
As sunlight travels through the earth’s atmosphere, it gets scattered (changes its direction) by the atmospheric particles. Light of shorter wavelengths is scattered much more than light of longer wavelengths. (The amount of scattering is inversely proportional to the fourth power of the wavelength. This is known as Rayleigh scattering.)

Hence, the bluish colour predominates in a clear sky, since blue has a shorter wavelength than red and is scattered much more strongly. In fact, violet gets scattered even more than blue, having a shorter wavelength. But since our eyes are more sensitive to blue than violet, we see the sky blue.

Question 62.
Why does the sun look reddish during sunrise and sunset?
Answer:
At sunset or sunrise, the sun’s rays have to pass through a larger distance in the atmosphere (Figure). Most of the blue and other shorter wavelengths are removed by scattering. The least scattered light reaching our eyes, therefore, the sun looks reddish. This explains the reddish appearance of the sun near the horizon.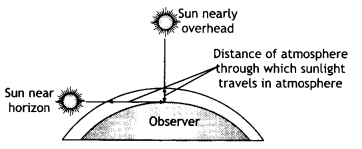

Question 63.
What are the two ways of adjusting the position of the eyepiece while observing the final image in a compound microscope? Which of these is usually preferred and why?
Answer:
The two ways
(a) Final image formed at least distance of distinct vision.
(b) Final image formed at infinity.

The second one is usually preferred as it helps the observer to observe the final image with his/her eye in a relaxed position.

Question 64.
Write the relation between the angle of incidence (i), the angle of emergence (e), the angle of the prism (A) and the angle of deviation (δ) for rays undergoing refraction through a prism. What is the relation between ‘i’ and ‘e’ for rays undergoing minimum deviation? Using this relation obtain an expression for the refractive index (μ) of the material of the prism in terms of ‘A’ and angle of minimum deviation.
Answer:
The relation is i + e = A + δ_m
In the minimum deviation position ∠i = ∠e
In the minimum deviation position we have A = r₁ + r₂ = r + r = 2r
or
r = A / 2
and i + i = A + δ_m
or
2i = A + δ_m
or
i = \(\frac{A+\delta_{m}}{2}\)

substituting for i and r in the expression for Snell’s law we have
μ = \(\frac{\sin i}{\sin r}=\frac{\sin \left[\frac{A+\delta_{m}}{2}\right]}{\sin \left(\frac{A}{2}\right)}\)

Question 65.
Draw a ray diagram showing the formation of the image by a concave mirror of an object placed beyond its centre of curvature. If the lower half of the mirror’s reflecting surface is covered, what effect will it have on the image? (CBSE AI 2011C)
Answer:
The required ray diagram is shown below.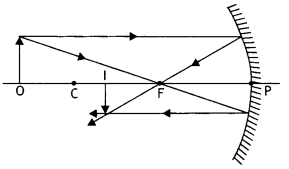

When the lower half of the mirror’s reflecting surface is covered, the intensity of the image will be reduced.

Question 66.
An object AB is kept in front of a concave mirror as shown in the figure.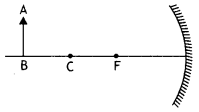

(a) Complete the ray diagram showing the image formation of the object.
(b) How will the position and intensity of the image be affected if the lower half of the mirror’s reflecting surface is painted black? (CBSE AI 2012)
Answer:
The completed ray diagram is as shown.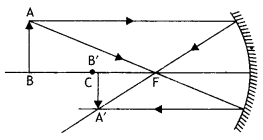

No change in the position of the image, but the intensity will decrease.

Question 67.
Draw a ray diagram to show the formation of the image by an astronomical telescope when the final image is formed at the near point. Answer the following, giving reasons
(a) Why the objective has a larger focal length and a larger aperture than the eyepiece?
(b) What would be the effect on the resolving power of the telescope if its objective lens is immersed in a transparent medium of the higher refractive index? (CBSE AI 2012C)
Answer:
The ray diagram is as shown.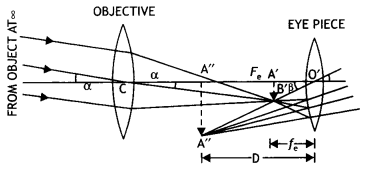

(a) The objective lens has a large focal length and large aperture for large magnification and resolving power.
(b) The resolving power will increase as the wavelength of light used will decrease.

Question 68.
Two convex lenses of the same focal length but of aperture A₁ and A, (A, < A₁), are used as the objective lenses in two astronomical telescopes having identical eyepieces. What is the ratio of their resolving power? Which telescope will you prefer and why? Give reason. (CBSE Delhi 2011)
Answer:
The resolving power is directly proportional to the aperture. Therefore the ratio of their resolving power is RP = \(\frac{A_{1}}{A}\).

Since A₁ > A therefore we will prefer the telescope with aperture A1 as it will gather a larger amount of light than the telescope of aperture A.

Question 69.
Which two of the following lens L₁ L₂ and L₃ will you select as objective and eyepiece for constructing the best possible (a) telescope and (b) microscope. Give a reason to support your answer. (CBSE Delhi 2015C)

Lens	Power	Aperture
L1	6 D	1 cm
L2	3 D	8 cm
L3	10 D	1 cm

Answer:
(a) For telescope

• Objective lens L₂: Because it has a large focal length and large aperture
• Eye lens L₃: Because it has a small focal length and small aperture

(b) For Microscope

• Objective lens L₃: Because it has a small aperture and small focal length
• Eye lens L₃: because it has a large aperture and large focal length

Question 70.
Draw a ray diagram to show how a right-angled isosceles prism may be used to bend the path of light by 90°.
Write the necessary condition in terms of the refractive index of the material of this prism for the ray to bend by 90°. (CBSE Delhi 2016C)
Answer:
The ray diagram is as shown.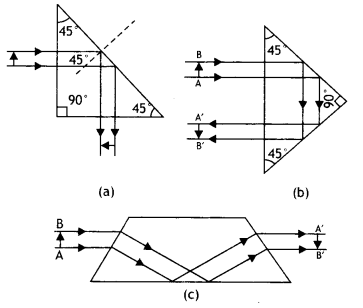

The angle of incidence in the denser medium should be greater than the critical angle for the given pair of media, i.e.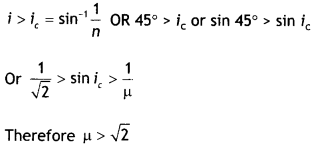

Question 71.
The image of a candle is formed by a convex lens on a screen. The lower half of the lens is painted black to make it completely opaque. Draw the ray diagram to show the image formation. How will this image be different from the one obtained when the lens is not painted black?
Answer:
The ray diagram depicting the image is shown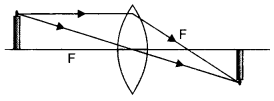

The image formed will be less bright as compared to that when half of the lens is not painted black. This is because every part of the lens forms the image. When the lower half is blackened, light from this portion will be blocked, hence the intensity of light in the image will be less.

Question 72.
A magician during a show makes a glass lens with n = 1.47 disappear in a trough of liquid. What is the refractive index of the liquid? Could the liquid be water?
Answer:
The refractive index of the liquid must be equal to 1.47 in order to make the lens disappear. This means n₁ = n₂. This gives 1 /f = 0 or f = ∞. The lens in the liquid will act as a plain sheet of glass. No, the liquid is not water, it could be glycerine.

Question 73.
Explain with reason, how the resolving power of an astronomical telescope will change, when
(a) frequency of the incident light on the objective lens is increased,
(b) the focal length of the objective lens is increased, and
(c) the aperture of the objective lens is halved?
Answer:
Resolving power of a telescope = \(\frac{D}{1.22 \lambda}\) hence
(a) on increasing the frequency of incident light, wavelength X decreases and consequently resolving power is increased.
(b) increase in focal length of the objective lens will have no effect on the resolving power, and
(c) if the aperture of the objective lens is halved, then resolving power is also halved.

Question 74.
With the help of a suitable ray diagram, derive the mirror formula for a concave mirror. (All India 2009)
Answer:
Consider a concave mirror of focal length/, radius of curvature R receiving light from an object AB placed between F and C as shown in the figure. The image will be formed as shown in the ray diagram.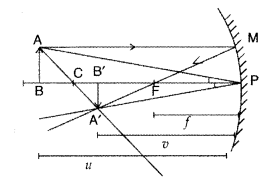

Using Cartesian sign convention, we find
Object distance, BP = – u
Image distance B’P = – v
Focal length, FP = – l
Radius of curvature, CP = -R = -2f

This proves the mirror formula for a concave mirror.

Question 75.
Three light rays red (R), green (G) and blue (B) are incident on a right B angled prism ‘abc’ Q at face ‘ab’. The R refractive indices of the material of the prism for red, green and blue wavelengths are 1.39, 1.44 and 1.47 respectively. Out of the three which colour ray will emerge out of face ‘ac’? Justify your answer. Trace the path of these rays after passing through face ‘ab’. (Delhi 2009)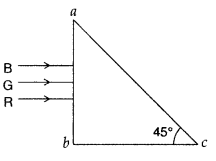

Answer:
Critical angle i_c for total internal reflection is related to refractive index µ as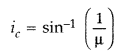

Critical angle for :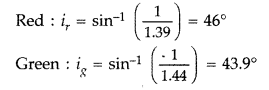


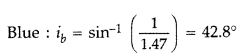
Incident angle in the surface ac is 45° for all the three colours. So red colour will undergo refraction while the other two colours will undergo total internal reflection in a.c. It is indicated in the figure. All the three colours will undergo total internal reflection if they are incident normally on one of the faces of an equilateral prism as shown in Figure 3. This is due to the reason that the incident angle on the second surface will be greater than critical angle for all the colours.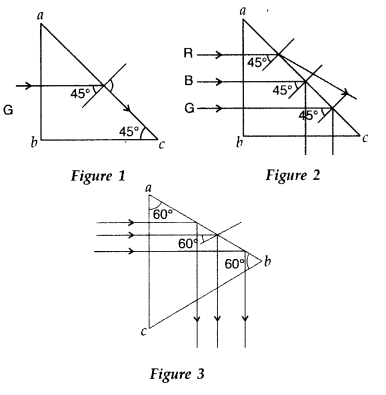

Question 76.
(i) Draw a neat labelled ray diagram of an astronomical telescope in normal adjustment. Explain briefly its working.
(ii) An astronomical telescope uses two lenses of powers 10 D and 1 D. What is its magnifying power in normal adjustment? (All India 2009)
Answer:
(i) Magnifying power m = \(-\frac{f_{0}}{f_{e}}\). It does not change with increase of aperature of objective lens, because focal length of a lens has no concern with the aperature of lens.

(ii) Drawbacks :

• Images formed by these telescopes have chromatic aberrations.
• Lesser resolving power.
• The image formed is inverted and faintes.

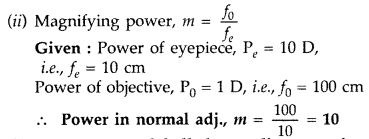
Question 77.
(i) Draw a neat labelled ray diagram of a compound microscope. Explain briefly its working.
(ii) Why must both the objective and the eye-piece of a compound microscope have short focal lengths? (All India 2010)
Answer:
(i)
(a) Ray diagram of a compound microscope : A schematic diagram of a compound microscope is shown in the figure. The lens nearest the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece, which functions essentially like a simple microscope or magnifier, produces the final image, which is enlarged and virtual. The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image formation at infinity, or a little closer for image formation at the near point. Clearly, the final image is inverted with respect to the original object.

Magnification due to a compound microscope.
The ray diagram shows that the (linear) magnification due to the objective, namely h’/h, equals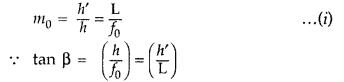

Here h’ is the size of the first image, the object size being h and f₀ being the focal length of the objective. The first image is formed near the focal point of the eyepiece. The distance L, i.e., the distance between the second focal point of the objective and the first focal point of the eyepiece (focal length f_e) is called the tube length of the compound microscope.

As the first inverted image is near the focal point of the eyepiece, we use for the simple microscope to obtain the (angular) magnification me due to it when the final image is formed at the near point, is

When the final image is formed at infinity, the angular magnification due to the eyepiece, me = (D//e)

Thus, the total magnification from equation (i) and (iii), when the image is formed at infinity, is

(b) Resolving power of a microscope :

(i) The focal length of the objective lens has no effect on the resolving power of microscope.
(ii) When the wavelength of light is increased, the resolving power of a microscope

(ii) The magnifying power of a compound microscope is given by,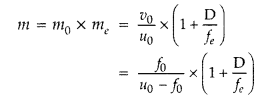

Angular magnification (m₀) of objective will be large when u₀ is slightly greater than f₀. Since microscope is used for viewing very close objects, so u0 is small. Consequently f₀ has to be small.
Moreover, the angular magnification (m_e) of the eyepiece will be large if f₀ is small.

Question 78.
An illuminated object and a screen are placed 90 cm apart. Determine the focal length and nature of the lens required to produce a clear image on the screen, twice the size of the object. (All India 2010)
Answer:
According to the question,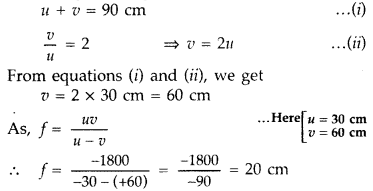

Nature of lens : Convex lens of focal length 20 cm is required.

Question 79.
The image obtained with a convex lens is erect and its length is four times the length of the object. If the focal length of the lens is 20 cm, calculate the object and image distances. (All India 2010)
Answer: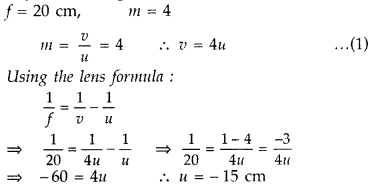

Putting the value of u in eqn (i), we get v = – 60 cm
∴ Object distance, u = 15 cm and
Image distance, v = 60 cm.

Question 80.
A convex lens is used to obtain a magnified image of an object on a screen 10 m from the lens. If the magnification is 19, find the focal length of the lens. (All India 2010)
Answer:
Given : u = -10 m, m = 19
For real image m = -19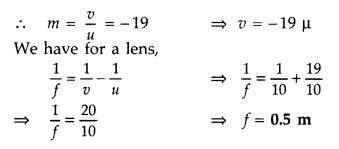

Question 81.
Draw a ray diagram to show refraction of a ray of monochromatic light passing through a glass prism.
Deduce the expression for the refractive index of glass in terms of angle of prism and angle of minimum deviation. (Delhi 2011)
Answer:
Ray diagram : The minimum deviation Dm, the refracted ray inside the prism becomes parallel to its base, we have

Question 82.
Use the mirror equation to show that
(a) an object placed between / and 2/ of a concave mirror produces a real image beyond 2f.
(b) a convex mirror always produces a virtual image independent of the location of the object.
(c) an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image. (All India 2011)
Answer: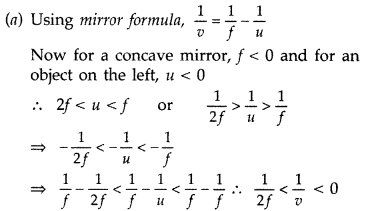

This implies that v < 0, formed on left. Also the above inequality implies 2f > v

i.e., the real image is formed beyond 2f.
(b) For a convex mirror, f > 0 and for an object on left, u < 0. From the mirror formula, \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\) This implies that \(\frac{1}{v}\) > 0 or v > 0 v
This shows that whatever be the value of u, a convex mirror forms a virtual image on the right.
(c) From mirror formula : \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
For a concave mirror, f < 0 and for an object located between the pole and focus of a concave mirror, f < u < 0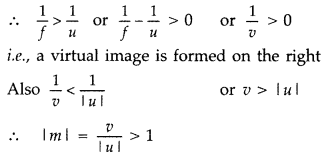

i.e., image is enlarged

Question 83.
A compound microscope uses an objective lens of focal length 4 cm and eyepiece lens of focal length 10 cm. An object is placed at 6 cm from the objective lens. Calculate the magnifying power of the compound microscope. Also calculate the length of the microscope. (All India 2011)
Answer:
Given f₀ = 4 cm, f_e = 10 cm, u₀ = -6 cm
Magnifying power of microscope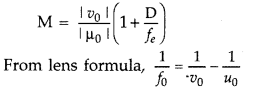

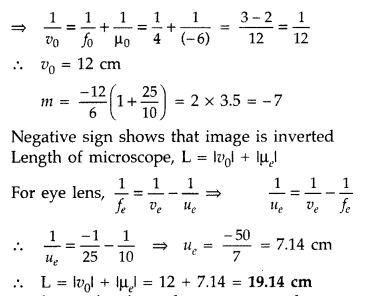
Question 84.
A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece lens of focal length 1.0 cm is used, find the angular magnification of the telescope.
If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is 3.42 × 10⁶ m and the radius of the lunar orbit is 3.8 × 10⁶ m. (All India 2011)
Answer:
Given : f₀ = 15 m, f_e = 1.0 cm = 0.01 m

(ii) Let d be the diameter of the image in metres Then angle subtended by the moon will be

Angle subtended by the image formed by the objective will also be equal to a and is given by

Question 85.
A convex lens made up of glass of refractive index 1.5 is dipped, in turn,
(i) a medium of refractive index 1.6,
(ii) a medium of refractive index 1.3.
(a) Will it behave as a converging or a diverging lens in the two cases?
(b) How will its focal length change in the two media? (All India 2011)
Answer:

Let f_air be the focal length of the lens in air
According to lens maker formula :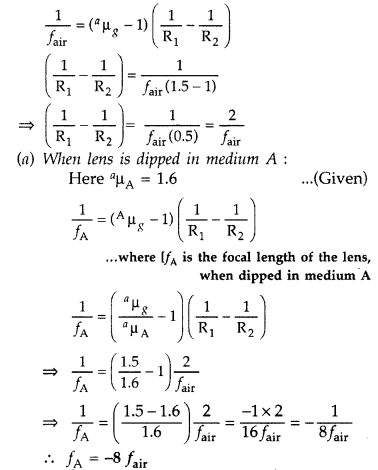

As the sign of f_B is opposite to that of f_air, the lens will behave as a diverging lens.
(b) When lens is dipped in medium B :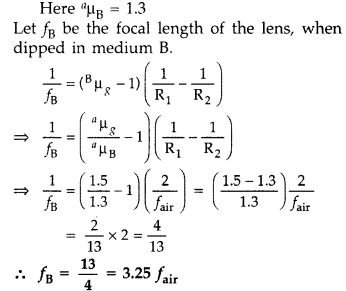

As the sign of f_B is same as that of /air, the lens will behave as a converging lens.

Question 86.
A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1.6. It is immersed in a liquid of refractive index 1.3. Calculate its new focal length. (All India 2011)
Answer:
According to lens maker formula :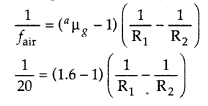


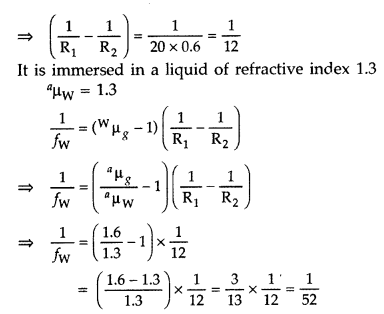
New focal length, f_w = 52 cm

Question 87.
A convex lens made up of glass of refractive index 1.5 is dipped, in turn, in
(i) a medium of refractive index 1.65,
(ii) a medium of refractive index 1.33.
(a) Will it behave as a converging or a diverging lens in the two cases?
(b) How will its focal length change in the two media? (All India 2011)
Answer: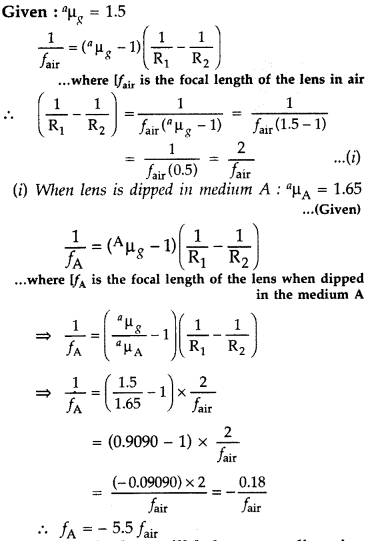

Hence the lens will behave as a diverging lens.
(ii) When lens is dipped in medium B : \(a_{\mu_{\mathrm{B}}}=1.33\)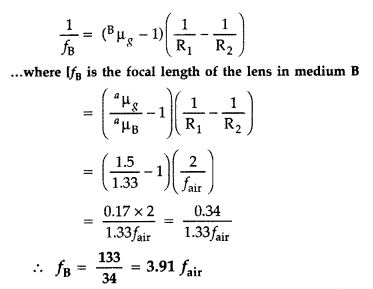

Hence the lens will behave as a converging lens.

Question 88.
You are given three lenses L₁ L₂ and L₃ each of focal length 20 cm. An object is kept at 40 cm in front of L₁, as shown. The final real image is formed at the focus T of L₃. Find the separations between L₁, L₂ and L₃.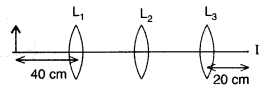

Answer: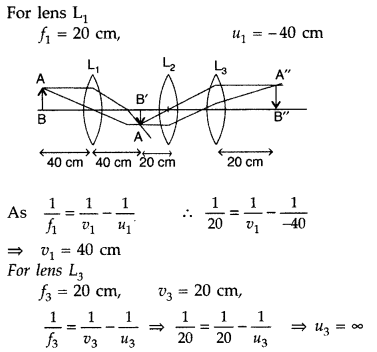

This shows that for lens L₂ the object should be at focus of that lens.
Hence the distance between L₁ and L₂ = v₁ + f₂ = 40 + 20 = 60 cm
It clearly indicates that the distance between L₂ and L₃ can have any value.

Question 89.
You are given three lenses L₁ L₂ and L₃ each of focal length 15 cm. An object is kept at 20 cm in front of L₁, as shown. The final real image is formed at the focus ‘I’ of L₃. Find the separations between L₁, L₂ and L₃.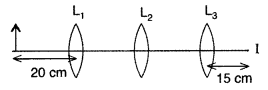

Answer:
Let f₁ f₂ and f₃ be the focal length of three lenses.
For lens L₁ : u = 20 cm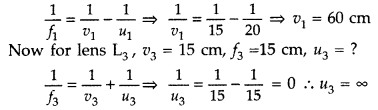

It shows that lens infinite.
Hence for lens L₁, image is formed at a distance of 15 cm from L₂
∴ the focus of L₂ i.e. u₂ = 15 cm
Now, to calculate the distance between L₁ and L₂,
u₁ + H₂ = 60 + 15 = 75 cm
Distance between L₂ and L₃ = v₂ + v₃ = ∞ or can be any value.

Question 90.
A fish in a water tank sees the outside world as if it (the fish) is at the vertex of a cone such that the circular base of the cone coincides with the surface of water. Given the depth of water, where fish is located, being ‘h’ and the critical angle for water-air interface being ‘i_c‘, find out by drawing a suitable ray diagram the relationship between the radius of the cone and the height ‘h’. (Comptt. Delhi 2012)
Answer:
Let the fish beat point B, and OA is the base of the water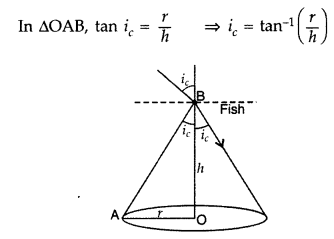

Question 91.
Draw a ray diagram to show the formation of the image of an object placed on the axis of a convex refracting surface, of radius of curvature ‘R’, separating the two media of refractive indices “n₁ and ‘n₂‘ (n₂ > n₁). Use this diagram to
deduce the relation \(\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{n_{2}-n_{1}}{\mathbf{R}}\), where u and v represent respectively the distance of the object and the image formed. (Comptt. Delhi 2012)
Answer: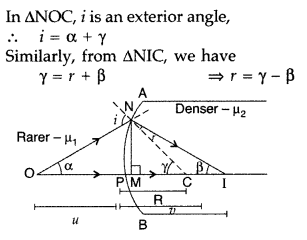

Suppose all the rays are paraxial
Then the angles i, r, a, P and y will be small

Using new Cartesian sign convention, we find
Object distance, OP = – u,
Image distance, PI = tv
Radius of curvature, PC = + R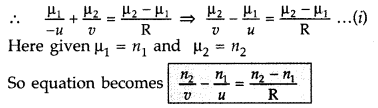

Question 92.
Answer the following:
(i) Do the frequency and wavelength change when light passes from a rarer to a denser medium?
(ii) Why is the value of the angle of deviation for a ray of light undergoing refraction through a glass prism different for different colours of light? (Comptt. Delhi 2012)
Answer:
(i) Frequency remains same.
While wavelength changes by λ/m
(ii) Deviation produced by small angles prism,

Question 93.
Define power of a lens. Write its S.L units. Two thin convex lenses of focal lengths f₁ and f₂ are placed in contact coaxially. Derive the expression for the effective focal length of the combination. (Comptt. Delhi 2012)
Answer:
Power of a lens is defined as the ability to converge a beam of light facing on the lens

Its S.I. unit is dioptre (D)
Let C₁, C₂ be the optical centres of two thin convex lenses L₁ and L₂ held co-axially in contact with each other in air.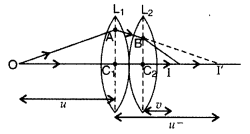

Suppose f₁ and f₂ are their respective focal lengths Let a point object O be placed on the common principal axis at a distance OC₁ = u
The lens L₁ alone would form its image at I’ where C₁I’ = v’
From the lens formula for L₁,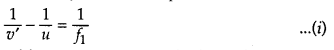

I’ would serve as a virtual object for lens L₂, which forms a final image I at a distance of
C₁I = v
As the lenses are thin, therefore, for the lens L₂,
u = i₂I’ = C₁I’ = v’
From the lens formula for L₂,

Adding equations (i) and {ii), we get

Let the two lenses be replaced by a single lens of focal length f which forms image I at distance v, of an object at distance u from the lens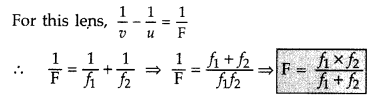

Question 94.
Draw a ray diagram showing the path of a ray of light entering through a triangular glass prism. Deduce the expression for the refractive index of glass prism in terms of the angle of minimum deviation and angle of the prism. (Comptt. All India 2012)
Answer:
A ray PQ is incident on the face AB of prism at ∠i and effected along QR at ∠r. The angle of incidence (from glass to air) to the second face is Y and the angle of refraction or emergence is i’.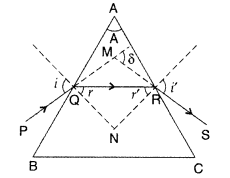

The angle between the emergent ray RS and incident ray in the direction PQ is called the angle of deviation δ.
In the quadrilateral AQNR,

Question 95.
Draw a ray diagram showing the image formation by a compound microscope when the final image is formed at the near point.
Define the resolving power of a microscope. Write two factors by which resolving power can be increased. (Comptt. All India 2012)
Answer:
(a) Ray diagram of a compound microscope : A schematic diagram of a compound microscope is shown in the figure. The lens nearest the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece, which functions essentially like a simple microscope or magnifier, produces the final image, which is enlarged and virtual. The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image formation at infinity, or a little closer for image formation at the near point. Clearly, the final image is inverted with respect to the original object.

Magnification due to a compound microscope.
The ray diagram shows that the (linear) magnification due to the objective, namely h’/h, equals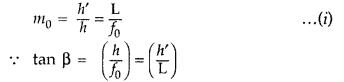

Here h’ is the size of the first image, the object size being h and f₀ being the focal length of the objective. The first image is formed near the focal point of the eyepiece. The distance L, i.e., the distance between the second focal point of the objective and the first focal point of the eyepiece (focal length f_e) is called the tube length of the compound microscope.

As the first inverted image is near the focal point of the eyepiece, we use for the simple microscope to obtain the (angular) magnification me due to it when the final image is formed at the near point, is

When the final image is formed at infinity, the angular magnification due to the eyepiece, me = (D//e)

Thus, the total magnification from equation (i) and (iii), when the image is formed at infinity, is

(b) Resolving power of a microscope :

(i) The focal length of the objective lens has no effect on the resolving power of microscope.
(ii) When the wavelength of light is increased, the resolving power of a microscope

Definition of resolving power: Resolving power of compound microscope is defined as reciprocal of the smallest distance between two point objects at which they can be just resolved when seen through microscope.

It can be increased by

• increasing the diameter of objective lens upto a certain limit; “
• using light of smaller wavelength.
• having a medium of higher refractive index.

Question 96.
Draw a ray diagram to show the formation of image by an astronomical telescope when the final image is formed at the near point. Answer the following, giving reasons:
(i) Why the objective has a larger focal length and a larger aperture than the eyepiece?
(ii) What would be the effect on the resolving power of the telescope if its objective lens is immersed in a transparent medium of higher refractive index?(Comptt. All India 2012)
Answer:

1. Objective of larger focal length and large aperture gives higher magnification.
2. Resolving power will increase.

Question 97.
Draw a labelled ray diagram of a refracting telescope. Define its magnifying power and write the expression for it.
Write two important limitations of a refracting telescope over a reflecting type telescope. (All India 2013)
Answer:
Refracting telescope :

Magnifying power. It is defined as the ratio of angle (β) subtended by the final image on the eye to the angle (α) subtended by object on eye.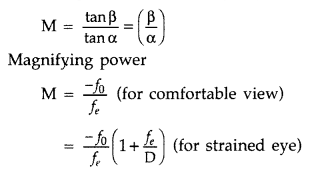

Limitations of refracting telescope over a a reflecting type telescope :

1. It suffers from chromatic aberration due to refraction and hence the image obtained is multicoloured and blurred.
2. As a lens of large apparatus can’t be manufactured easily, its light gathering power is low and hence can’t be used to see faint stars.

Question 98.
A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80 cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of the refractive index of water to be 4/3. (Comptt. Delhi 2013)
Answer: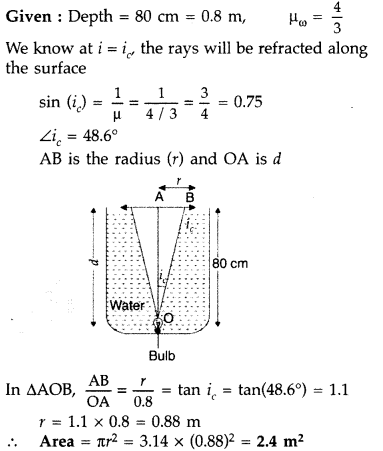

Question 99.
(a) A small telescope has an objective lens of focal length 140 cm and an eye-piece of focal length 5.0 cm. Find the magnifying power of the telescope for viewing distant objects when
(i) the telescope is in normal adjustment,
(ii) the final image is formed at the least distance of distinct vision.
(b) Also find the separation between the objective lens and the eye-piece. (Comptt. All India 2013) Answer:
(a) (i) For normal adjustment :

(ii) When the final image is formed at the least distance of distinct vision,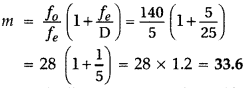

(b)
(i) For normal adjustment separation = (f₀ + f_e)
(ii) For least distance of distinct vision

Question 100.
An equiconvex lens of refractive index µ₁, focal length ‘f’ and radius of curvature ‘R’ is immersed in a liquid of refractive index µ₂. For
(i) µ₂ µ₁, and
(ii) µ₂ < µ₁, draw the ray diagrams in the two cases when a beam of light coming parallel to the principal axis is incident on the lens. Also find the focal length of the lens in terms of the original focal length and the refractive index of the glass of the lens and that of the medium.
(Comptt. All India 2013)
Answer:
(i) The ray diagrams are as shown below: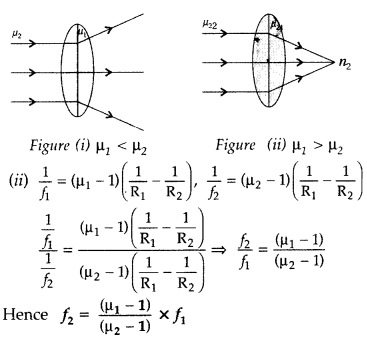

Question 101.
(a) Draw a labelled ray diagram showing the formation of a final image by a compound microscope at least distance of distinct vision.
(b) The total magnification produced by a compound microscope is 20. The magnification produced by the eye piece is 5. The microscope is focussed on a certain object. The distance between the objective and the eyepiece is observed to be 14 cm. If least distance of distinct vision is 20 cm, calculate the focal length of the objective and the eye piece. (Delhi 2014)
Answer:
(a) Ray diagram of a compound microscope : A schematic diagram of a compound microscope is shown in the figure. The lens nearest the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece, which functions essentially like a simple microscope or magnifier, produces the final image, which is enlarged and virtual. The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image formation at infinity, or a little closer for image formation at the near point. Clearly, the final image is inverted with respect to the original object.

Magnification due to a compound microscope.
The ray diagram shows that the (linear) magnification due to the objective, namely h’/h, equals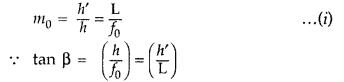

Here h’ is the size of the first image, the object size being h and f₀ being the focal length of the objective. The first image is formed near the focal point of the eyepiece. The distance L, i.e., the distance between the second focal point of the objective and the first focal point of the eyepiece (focal length f_e) is called the tube length of the compound microscope.

As the first inverted image is near the focal point of the eyepiece, we use for the simple microscope to obtain the (angular) magnification me due to it when the final image is formed at the near point, is

When the final image is formed at infinity, the angular magnification due to the eyepiece, me = (D//e)

Thus, the total magnification from equation (i) and (iii), when the image is formed at infinity, is

(b) Resolving power of a microscope :

(i) The focal length of the objective lens has no effect on the resolving power of microscope.
(ii) When the wavelength of light is increased, the resolving power of a microscope


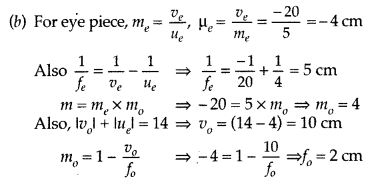
Hence Focal length of objective = 3.5 cm and Focal length of eyepiece = 5 cm

Question 102.
(a) A mobile phone lies along the principal axis of a concave mirror. Show, with the help of a suitable diagram, the formation of its image. Explain why magnification is not uniform.
(b) Suppose the lower half of the concave mirror’s reflecting surface is covered with an opaque material. What effect will this have on the image of the object? Explain (Delhi 2014)
Answer:
(a) The formation of image is shown in the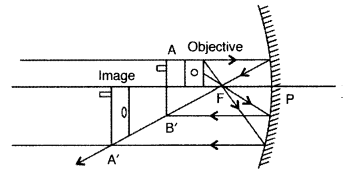

The magnification is not uniform and image is distorted because of the reason that the parts of mobile are situated at different distances from the mirror.
(b) When lower half of the concave mirror’s reflecting surface is covered with an opaque material, the image will be of the whole object, i.e. mobile. However, as the area of the reflecting surface has been reduced, the intensity of image (brightness) will be reduced to half.

Question 103.
A convex lens of focal length 20 cm is placed coaxially with a convex mirror of radius of curvature 20 cm. The two are kept at 15 cm from each other. A point object lies 60 cm in front of the convex lens. Draw a ray diagram to show the formation of the image by the combination. Determine the nature and position of the image formed.
Answer: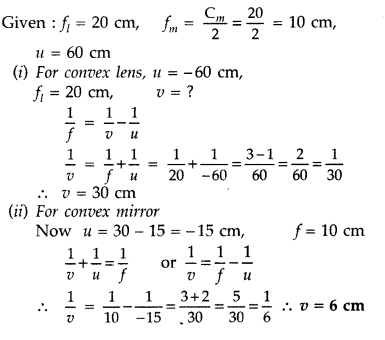

The image I₁ is formed behind the mirror and acts as a virtual object for the convex mirror; and finally image I₂ is formed, which is virtual between focus and pole of mirror.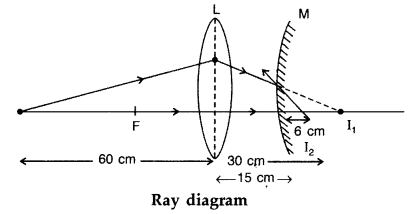

Question 104.
A convex lens of focal length 20 cm is placed coaxially with a concave mirror of focal length 10 cm at a distance of 50 cm apart from each other. A beam of light coming parallel to the principal axis is incident on the convex lens. Find the position of the final image formed by this combination. Draw the ray diagram showing the formation of the image. (All India 2014)
Answer: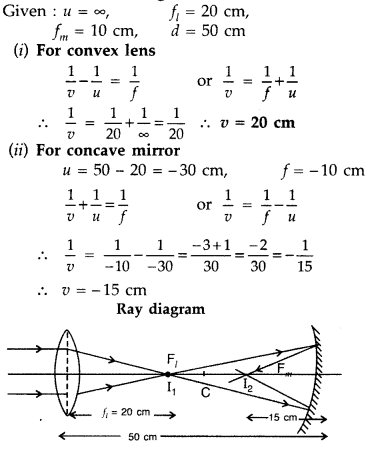

Final image is real and lies between F and C of concave mirror.

Question 105.
A convex lens of focal length 20 cm is placed coaxially with a convex mirror of radius of curvature 20 cm. The two are kept 15 cm apart. A point object is placed 40 cm in front of the convex lens. Find the position of the image formed by this combination. Draw the ray diagram showing the image formation. (All India 2014)
Answer: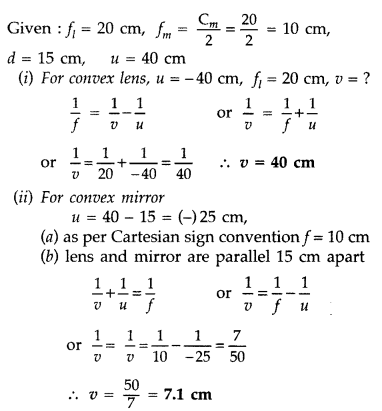

The final image is virtual and lies between pole and focus of convex mirror.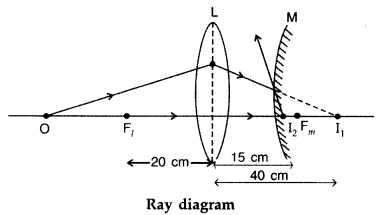

Question 106.
A ray PQ is incident normally on the face AB of a triangular prism of refracting angle of 60°, made of a transparent material of refractive index \(2 / \sqrt{3}\), as shown in the figure. Trace the path of the ray as it passes through the prism. Also calculate the angle of emergence and angle of deviation. (Comptt. Delhi 2014)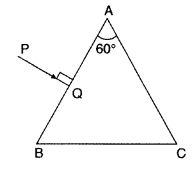

Answer: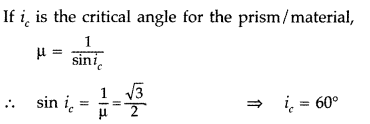

Angle of incidence at face AC of the prism = 60°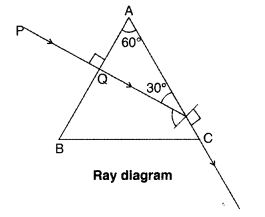

Hence, refracted ray grazes the surface AC as i_c = i
∴ Angle of emergence = 90°
and Angle of deviation = 30°

Question 107.
(i) A giant refracting telescope has an objective lens of focal length 15 m. If an eye piece of focal length 1.0 cm is used, what is the angular magnification of the telescope?
(ii) If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is 3.48 × 10⁶ m and the radius of lunar orbit is 3.8 × 10⁸ m. (Delhi 2015)
Answer:
(i) Let : f₀ = focal length of objective lens = 15 cm
f_e = focal length of eye lens = 1.0 cm
Angular magnification (m)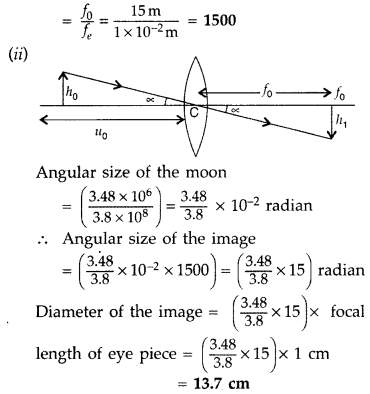

Question 108.
Define the term ‘critical angle’ for a pair of media.
A point source of monochromatic light ‘S’ is kept at the centre of the bottom of a cylinder of radius 15.0 cm. The cylinder contains water (refractive index 4/3) to a height of 7.0 cm. Draw the ray diagram and calculate the area of water surface through which the light emerges in air.
Answer:
(a) Critical Angle : For an incident ray, travelling from an optically denser medium to optically rarer medium, the angle of incidence, for which angle of refraction is \(90^{\circ}\), is called the critical Angle.

∴ The Area of water surface through which the light emerges in air is 63π m²

Question 109.
Which two of the following L₁, L₂ and L₃ will you select as objective and eyepiece for constructing best possible
(i) telescope
(ii) microscope? Give reason to support your answer. (Comptt. Delhi 2015)

Answer:
(i) Telescope : L₂ : objective, L₃ = eyepiece
Reason : Light gathering power magnifying power will be larger.

(ii) Microscope : L₃ : objective, L₁ = eyepiece
Reason : Angular magnification is more for short focal length of objective and eyepiece.

Question 110.
(a) Write the factors by which the resolving power of a telescope can be increased.
(b) Estimate the angular separation between first order maximum and third order minimum of the diffraction pattern due to a single slit of width 1 mm, when light of wavelength 600 nm is incident normal on it. (Comptt. All India 2015)
Answer:
(a) Factors for increasing the resolving power of telescope : The resolving power of a telescope is given by,

(iii) Resolving power is independent of focal length of objective lens.

(b) Given : a = 1 mm = 1 × 10^-3m,
λ = 600 nm = 600 × 10^-9m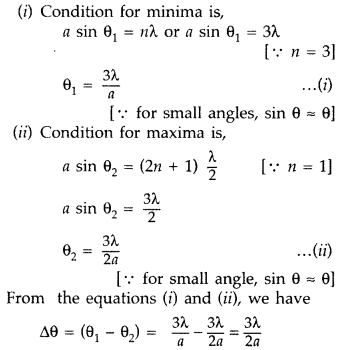

Putting the value of λ and a, we have

Question 111.
(a) Calculate the distance of an object of height ‘h’ from a concave mirror of radius of curvature 20 cm, so as to obtain a real image of magnification 2. Find the location of image also.
(b) Using mirror formula, explain why does a convex mirror always produce a virtual image. (Delhi 2016)
Answer:
(a) Given : R = -20 cm and magnification
m = -2
Focal length of the mirror f = \(\frac{\mathrm{R}}{2}\) = -10 cm
Magnification (m) = \(-\frac{v}{u}\)

∴ f is positive and u is negative,
⇒ v is always positive, hence image is always virtual.

Question 112.
Draw a schematic ray diagram of reflecting telescope showing how rays coming from a distant object are received at the eye-piece. Write its two important advantages over a refracting telescope. (Delhi 2016)
Answer:
Reflecting telescope. Telescope with mirror objectives is called reflecting telescope. This is also known as Cassegrain telescope / Newtonian telescope. The ray diagram of reflecting type telescope is shown in figure.

Advantage over refracting telescope :

1. Since reflecting telescope has mirror objective, so the image formed is free from chromatic aberration.
2. Since the spherical mirrors are parabolic mirrors, free from spherical aberration, they produce a very sharp and distinct image.

Question 113.
Explain the following, giving reasons :
(i) When monochromatic light is incident on a surface separating two media, the reflected and refracted light both have the same frequency as the incident frequency.
(ii) When light travels from a rarer to a denser medium, the speed decreases. Does this decrease in speed imply a reduction in the energy carried by the wave?
(iii) In the wave picture of light, intensity of light is determined by the square of the amplitude of the wave. What determines the intensity in the photon picture of light? (All India 2016)
Answer:
(i) Reflection and refraction arise through interaction of incident light with atomic constituents of matter which vibrate with the same frequency as that of the incident light. Hence frequency of reflected and refracted light both have the same frequency as the incident frequency.

(ii) No, energy carried by a wave depends on the amplitude of the wave and not on the speed of wave propagation.

(iii) For a given frequency, intensity of light in the photon picture is determined by the number of photons incident normally on crossing a unit area per unit time.

Question 114.
A convex lens, of focal length 25 cm, and a convex mirror, of radius of curvature 20 cm, are placed co-axially 40 cm apart from each other. An incident beam, parallel to the principal axis, is incident on the convex lens. Find the position and nature of the image formed by this combination. (Comptt. All India 2016)
Answer:
The given ‘setup’ is as shown
The object, being at infinity, the image formed by the convex lens, is at its focus, i.e. 25 cm from the lens. This image becomes the ‘object’ for convex mirror.
Now, for the convex mirror
Object distance = (40 – 25) cm = 15 cm
Radius of curvature, R = 20 cm
u = -15 cm, R = +20 cm
Using the mirror formula :

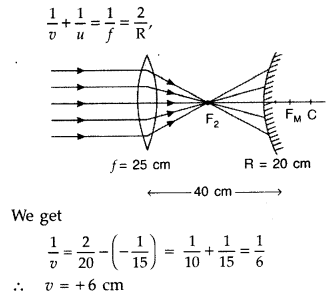
The final image is, therefore, a vitrual image that appears to be formed (behind the convex mirror) at a distance of 6 cm from it.

Question 115.
(i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30°. Calculate the speed of light through the prism.

(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC. (Delhi 2016)
Answer:
(i) Given : For equilateral glass prism ∠A = 60°, ∠δm = 30°
We know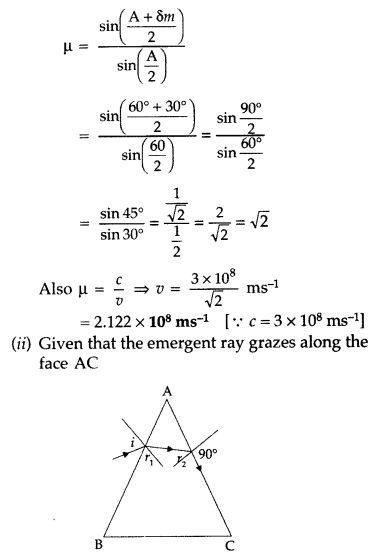

At face AC, let the angle of incidence be r₂ For grazing ray e = 90°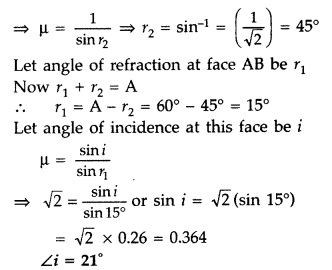

Question 116.
(a) Monochromatic light of wavelength 589 nm is incident from air on a water surface. If p for water is 1.33, find the wavelength, frequency and speed of the refracted light.
(b) A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is 20 cm. (All India 2017)
Answer:
(a) Given : Wavelength of monochromatic
light, λ = 589 nm = 589 × 10^-9m,
Refractive index of water, µ = 1.33,
Speed of light in air, c = 3 × 10⁸ ms^-1
Frequency of light does not depend on the property of the medium in which it is travelling. Hence, the frequency of the emergent ray in water will be equal to the frequency of the incident or emergent light in air.

Speed of light in water is related to the refractive index of water, as :

Wavelength of light in water is given by the relation,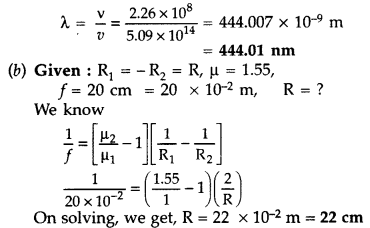

Question 117.
(a) Draw a ray diagram depecting the formation of the image by an astronomical telescope in normal adjustment.
(b) You are given the following three lenses. Which two lenses will you use as an eyepiece and as an objective to construct an astronomical telescope? Give reason. (All India 2017)

Lenses	Power (D)	Aperture (cm)
L1	3	8
L2	6	1
L3	10	1

Answer: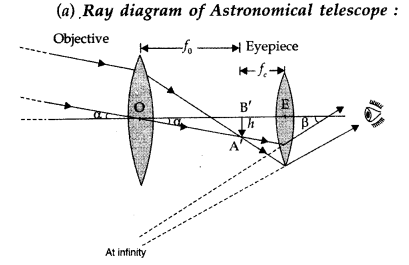

(b) Objective Lens : Lens L₁
Eyepiece Lens : Lens L₂
Reason : The objective should have large aperture and large focal length; while the eyepiece should have small aperture and small focal length.

Question 118.
(a) Draw a ray diagram showing the formation of image by a reflecting telescope.
(b) Write two advantages of a reflecting telescope over a refracting telescope. (All India 2017)
Answer:
Reflecting telescope. Telescope with mirror objectives is called reflecting telescope. This is also known as Cassegrain telescope / Newtonian telescope. The ray diagram of reflecting type telescope is shown in figure.

Advantage over refracting telescope :

1. Since reflecting telescope has mirror objective, so the image formed is free from chromatic aberration.
2. Since the spherical mirrors are parabolic mirrors, free from spherical aberration, they produce a very sharp and distinct image.

Question 119.
(a) Draw a ray diagram for the formation of image by a compound microscope.

Lenses	Power (D)	Aperture (cm)
L1	3	8
L2	6	1
L3	10	1

(b) You are given the following three lenses. Which two lenses will you use as an eyepiece and as an objective to construct a compound microscope?
(c) Define resolving power of a microscope and write one factor on which it depends.
(All India)
Answer:
(a) Compound microscope :

(a) Ray diagram of a compound microscope : A schematic diagram of a compound microscope is shown in the figure. The lens nearest the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece, which functions essentially like a simple microscope or magnifier, produces the final image, which is enlarged and virtual. The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image formation at infinity, or a little closer for image formation at the near point. Clearly, the final image is inverted with respect to the original object.

Magnification due to a compound microscope.
The ray diagram shows that the (linear) magnification due to the objective, namely h’/h, equals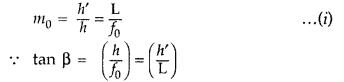

Here h’ is the size of the first image, the object size being h and f₀ being the focal length of the objective. The first image is formed near the focal point of the eyepiece. The distance L, i.e., the distance between the second focal point of the objective and the first focal point of the eyepiece (focal length f_e) is called the tube length of the compound microscope.

As the first inverted image is near the focal point of the eyepiece, we use for the simple microscope to obtain the (angular) magnification me due to it when the final image is formed at the near point, is

When the final image is formed at infinity, the angular magnification due to the eyepiece, me = (D//e)

Thus, the total magnification from equation (i) and (iii), when the image is formed at infinity, is

(b) Objective : Lens L₃ Eyepiece : Lens L₂

(c)
Resolving power of a microscope :

1. The focal length of the objective lens has no effect on the resolving power of microscope.
2. When the wavelength of light is increased, the resolving power of a microscope
   

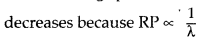
Question 120.
An optical instrument uses eye-lens of power 16 D and objective lens of power 50 D and has a tube length of 16.25 cm. Name the optical instrument and calculate its magnifying power if it forms the final image at infinity. (Comptt. Delhi 2017)
Answer:
The optical instrument is Compound Microscope.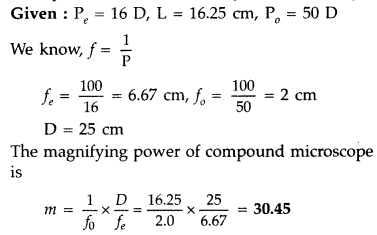

Question 121.
Answer the following questions:
(a) Plane and convex mirrors produce virtual images of objects. Can they produce real images under some circumstances? Explain
(b) A virtual image, we always say, cannot be caught on a screen. Yet when we ‘see’ a vitrual image, we are obviously bringing it on to the ‘screen’ (i.e. the retina) of our eye. Is there a contradiction?
(c) A diver under water, looks obliquely at a fisherman standing on the bank of a lake. Would the fisherman look taller or shorter to the diver than what he actually is?
(d) Does the apparatus depth of a tank of water change if viewed obliquely? If so, does the apparatus depth increase or decrease?
(e) The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter? (Comptt. Delhi 2017)
Answer:
(a) Rays converging to a point ‘behind’ a plane or convex mirror are reflected to a point in front of the mirror on a screen. In other words, a plane or convex mirror can produce a real image if the object is virtual. Convince yourself by drawing an appropriate ray diagram.

(b) When the reflected or refracted rays are divergent, the image is virtual. The divergent rays can be converged on to a screen by means of an appropriate converging lens. The convex lens of the eye does just that. The virtual image here serves as an object for the lens to produce a real image. Note, the screen here is not located at the position of the virtual image. There is no contradiction.

(c) Taller

(d) The apparent depth for oblique viewing decreases from its value for near-normal viewing. Convince yourself of this fact by drawing ray diagrams for different positions of the observer.

(e) Refractive index of a diamond is about 2.42, much larger than that of ordinary glass (about 1.5). The critical angle of diamond is about 24°, much less than that of glass. A skilled diamond-cutter exploits the larger range of angles of incidence (in the diamond), 24° to 90°, to ensure that light entering the diamond is totally reflected from many faces before getting out, thus producing a sparkling effect.

Question 122.
An optical instrument uses eye-lens of power 20 D and the objective lens of power 50 D. It has a tube length of 15 cm. Name the optical instrument and calculate its magnifying power if it forms the final image at infinity. (Comptt. Delhi 2017)
Answer:
The optical instrument is Compound Microscope.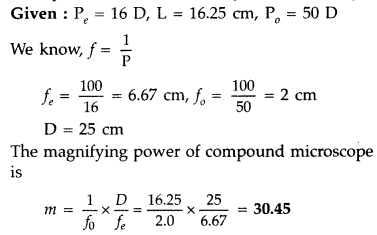

Hint  : Compound microscope, m = 37.5

Question 123.
An optical instrument uses eye-lens of power 12.5 D and object lens of power 50 D and has a tube length of 20 cm. Name the optical instrument and calculate its magnifying power, if it forms the final image at infinity. (Comptt. Delhi 2017)
Answer:
The optical instrument is Compound Microscope.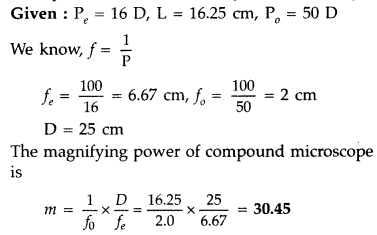

Hint : Compound microscope, m = 31.25

Question 124.
Explain with reason, how the resolving power of a compound microscope will change when
(a) frequency of the incident light on the objective lens is increased,
(b) the focal length of the objective lens is increased, and
(c) the aperture of the objective lens is increased.
Answer:
Resolving power of a compound microscope RP = \(\frac{2 \mu \sin \theta}{\lambda}\), hence
(a) on increasing the frequency of incident light, its wavelength X decreases and consequently resolving power increases.
(b) on increasing the focal length of the objective lens, the value of sine and hence resolving power decreases.
(c) on increasing the aperture of the objective lens, the value of sin 0 and hence resolving power increases.

Question 125.
A convex lens of the focal length is kept in contact with a concave lens of focal length f₂. Find the focal length of the combination. (CBSE AI 2013)
Answer:
For a convex lens +f₁ and for a concave lens – f₂, using the expression
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
or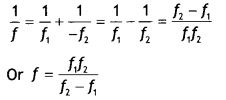

Question 126.
(a) The relation between the angle of incidence ‘i’ and the corresponding angle of deviation (δ), for a certain optical device, is represented by the graph shown in the figure. Identify this device. Draw a ray diagram for this device and use it for obtaining an expression for the refractive index of the material of this device in terms of an angle characteristic of the device and the angle, marked as δ_m, in the graph. (CBSE Al 2016C)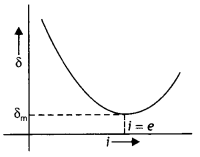

Answer:
(a) The device is a prism.
The relation is i + e = A + δ_m
In the minimum deviation position ∠i = ∠e
In the minimum deviation position we have A = r₁ + r₂ = r + r = 2r
or
r = A / 2
and i + i = A + δ_m
or
2i = A + δ_m
or
i = \(\frac{A+\delta_{m}}{2}\)

substituting for i and r in the expression for Snell’s law we have
μ = \(\frac{\sin i}{\sin r}=\frac{\sin \left[\frac{A+\delta_{m}}{2}\right]}{\sin \left(\frac{A}{2}\right)}\)

(b) The diagram is as shown.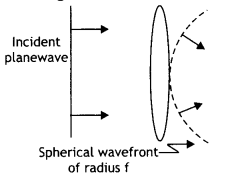

Long Answer Type

Question 1.
Draw a labelled ray diagram to show the image formation in a refracting type astronomical telescope. Obtain an expression for the angular magnifying power and the length of the tube of an astronomical telescope in its ‘normal adjustment’ position. Why should the diameter of the objective of a telescope be large?
Answer:
A labelled diagram of the telescope is shown in the figure.

The object subtends an angle at the objective and would subtend essentially the same angle at the unaided eye. Also, since the observers’ eye is placed just to the right of the focal point f’₂, the angle subtended at the eye by the final image is very nearly equal to the angle β.

Therefore, M = \(\frac{\beta}{\alpha}=\frac{\tan \beta}{\tan \alpha}\) …(1)

From right triangles ABC and ABC’ as shown in figure, we have
tan α = \(\frac{\mathrm{AB}}{\mathrm{CB}}=\frac{-h}{f_{0}}\) and
tan β = \(\frac{\mathrm{AB}}{\mathrm{C}^{\prime} \mathrm{A}}=\frac{-h}{f_{\mathrm{e}}}\)

substituting the above two equations in equation (1), we have
M = \(\frac{\beta}{\alpha}=\frac{-h^{\prime}}{f_{e}} \times \frac{f_{0}}{-h^{\prime}}=\frac{f_{0}}{f_{e}}\)

The length of the telescope is the distance between the two lenses which is L = f_o + f_e The diameter of the objective of a telescope should be large so that it can collect more light and image of distant objects is formed clear.

Question 2.
Draw a ray diagram to show the formation of an erect image of an object kept in front of a concave mirror. Hence deduce the mirror formula. (CBSE 2019C)
Answer:
An object AB is placed between P and F. The course of rays for obtaining erect image A₁B₁ of object AB is shown in the figure.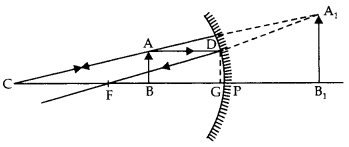

Draw DG ⊥ on the principal axis.
Triangles DGF and A₁ B₁C are similar

Since Point G is close to P, so GF = PF

Multiplying and dividing both sides by uvf, we get
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)

Question 3.
(a) Define the term power of a lens. Write its SI units.
Answer:
The power of a lens is the reciprocal of its focal length in the metre.
i.e. P = \(\frac{1}{f(\text { in } m)}\)

S.I. unit of power of a lens is dioptre (D).

(b) Derive the expression for the power of two thin lenses placed coaxially in contact with each other. (CBSE 2019C)
Answer:
Power of two thin lenses in contact. Consider an object O placed at a distance u on the principal axis of the lens A. Rays of light starting from O forms, the image at I₁
∴ \(\frac{1}{v_{1}}-\frac{1}{u}=\frac{1}{f_{1}}\) …(1)

Place lens B in contact with A. The image I₁ will serve as a virtual object and forms a real image I.
∴ Again apply lens formula
\(-\frac{1}{v_{1}}+\frac{1}{v}=\frac{1}{f_{2}}\) …(2)

Adding (1) and (2), we have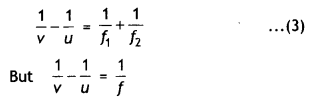

where f is the focal length of the combination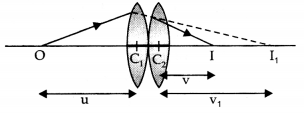

From (3), \(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)

The total power of the lens combination is given by
P = P₁ + P₂

Question 4.
(a) For a ray of light travelling from a denser medium of refractive index n₁ to a rarer medium of refractive index n₂, prove that \(\frac{n_{2}}{n_{1}}\), where i_c is the critical angle of incidence for the media.
(b) Explain with the help of a diagram, how the above principle is used for transmission of video signals using optical fibres. (Delhi 2008)
Answer:
(a) When i = i_c, r = 90°
Using Snell’s law of refraction : n_x sin ic = n₂ sin 90°

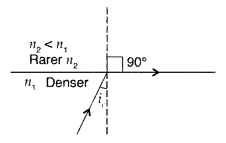
(b) When a video signal is directed into an optical fibre at a suitable angle, it undergoes internal reflections repeatedly along the length of the optical fibre and comes out of it with almost neglible loss of intensity.

Question 5.
Derive the lens formula, \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) for a concave lens, using the necessary ray diagram. Two lenses of powers 10 D and – 5 D are placed in contact.
(a) Calculate the power of the new lens.
(b) Where should an object be held from the lens, so as to obtain a virtual image of magnification 2?
Answer:

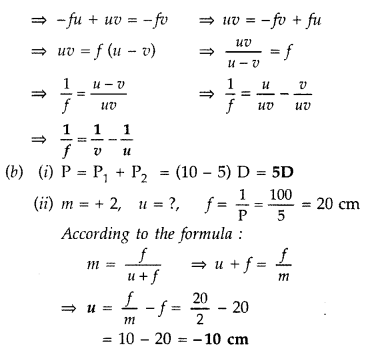
Question 6.
Trace the rays of light showing the formation of an image due to a point object placed on the axis of a spherical surface separating the two media of refractive indices n₁ and n₂. Establish the relation between the distances of the object, the image and the radius of curvature from the central point of the spherical surface.
Hence derive the expression of the lens maker’s formula. (Delhi 2009)
Answer: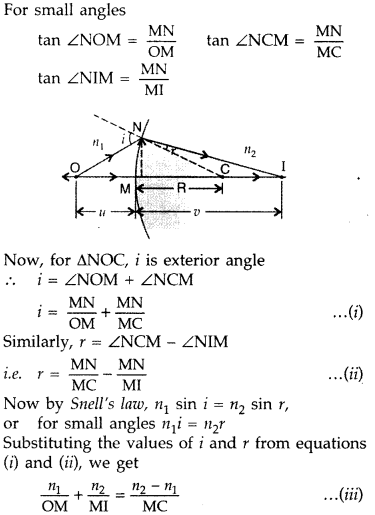

By applying Cartesian sign convention,
OM = -M, MI = -v, MC = +R
Substituting these values in (iii), we get

This equation gives us a relation between object and image distance in terms of refractive index of the medium and the radius of the curvature of the curved spherical surface. It holds for any curved spherical surface.
Lens maker’s formula:

(a) Lens maker’s formula : Consider a thin double convex lens of refractive index n₂ placed in a medium of refractive index n₁. Here, n₁ < n₂. Let B and D be the poles, C₁ and C₂ be the centres of curvature and R₁ and R₂ be the radii of curvature of the two lens surfaces ABC and ADC, respectively. For refraction at surface ABC, we can write the relation between the object distance u, image distance v₁ and radius of curvature R₁ as

For refraction at surface ADC, we can write the relation between the object distance v₁, image distance v and radius of curvature R₂, as

Question 7.
Draw the labelled ray diagram for the formation of image by a compound microscope.
Derive the expression for the total magnification of a compound microscope. Explain why both the objective and the eyepiece of a compound microscope must have short focal lengths.(Delhi 2009) Answer:
Compound Microscope :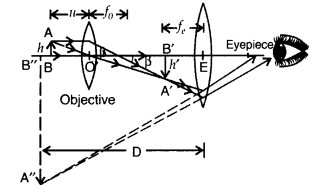

Magnifying power : The magnifying power of a compound microscope is defined as the ratio of the angle subtended at the eye by the final virtual image to the angle subtended at the eye by the object, when both are at the least distance of distinct vision from the eye.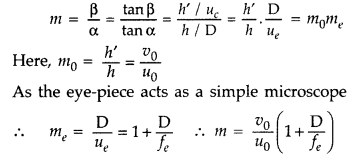

As the object AB is placed close to the focus f₀ of the objective
∴ u₀ = -f_o
Also image A’B’ is formed close to the eyelens whose focal length is short, therefore v₀ = L = the length of the microscope tube or the distance between the two lenses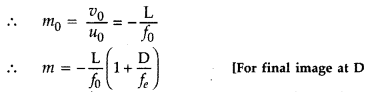

(i) If the focal lengths are less, then their magnifying power will be more.
(ii) To avoid any aberrations in refraction due to larger bend on passing through the eye-piece.

Question 8.
(i) Draw a labelled ray diagram to show the formation of image in an astronomical telescope for a distant object.
(ii) Write three distinct advantages of a reflecting type telescope over a refracting type telescope.
(b) A convex lens of focal length 10 cm is placed coaxially 5 cm away from a concave lens of focal length 10 cm. If an object is placed 30 cm in front of the convex lens, find the position of the final image formed by the combined system. (All India 2009)
Answer:
(a)
(i) Magnifying power m = \(-\frac{f_{0}}{f_{e}}\). It does not change with increase of aperature of objective lens, because focal length of a lens has no concern with the aperature of lens.

(ii) Drawbacks :

• Images formed by these telescopes have chromatic aberrations.
• Lesser resolving power.
• The image formed is inverted and faintes.

(ii)

(ii) Advantages of reflecting telescope over a refracting telescope:

1. Due to large aperture of the mirror used, the reflecting telescopes have high resolving power.
2. This type of telescope is free from chromatic aberration (formation of coloured image of a white object).
3. The use of paraboloidal mirror reduces the spherical aberration (formation of non-point, blurred image of a point object).
4. Image formed by reflecting telescope is brighter than refracting telescope.
5. A lens of large aperture tends to be very heavy and therefore difficult to make and support by its edges. On the other hand, a mirror of equivalent optical quality weights less and can be supported over its entire back surface.

(b) For convex lens :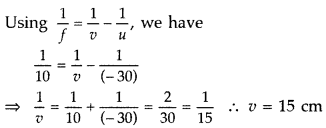

Since concave lens is at 5 cm distance, a virtual object for concave lens is said to be at a distance of 10 cm.
For concave lens :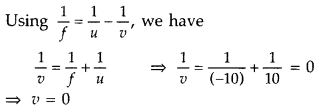

∴ Image will be at infinite distance or the ray will emerge parallel to the axis.

Question 9.
Draw a ray diagram to show the working of a compound microscope. Deduce an expression for the total magnification when the final image is formed at the near point.
In a compound microscope, an object is placed at a distance of 1.5 cm from the objective of focal length 1.25 cm. If the eye piece has a focal length of 5 cm and the final image is formed at the near point, estimate the magnifying power of the microscope. (Delhi 2010)
Answer:
Compound Microscope :

Magnifying power : The magnifying power of a compound microscope is defined as the ratio of the angle subtended at the eye by the final virtual image to the angle subtended at the eye by the object, when both are at the least distance of distinct vision from the eye.

Numerical: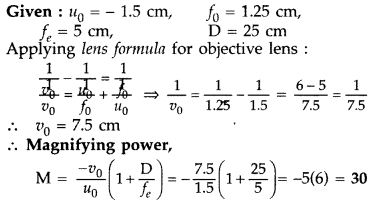

The -ve sign shows that the final image is an inverted image.

Question 10.
(a) Obtain lens makers formula using the expression

Here the ray of light propagating from a rarer medium of refractive index (n₁) to a denser medium of refractive index (n₂) is incident on the convex side of spherical refracting surface of radius of curvature R.
(b) Draw a ray diagram to show the image formation by a concave mirror when the object is kept between its focus and the pole. Using this diagram, derive the magnification formula for the image formed. (Delhi 2011)
Answer:
(a) Lens maker’s formula : Consider a thin double convex lens of refractive index n₂ placed in a medium of refractive index n₁. Here, n₁ < n₂. Let B and D be the poles, C₁ and C₂ be the centres of curvature and R₁ and R₂ be the radii of curvature of the two lens surfaces ABC and ADC, respectively. For refraction at surface ABC, we can write the relation between the object distance u, image distance v₁ and radius of curvature R₁ as

For refraction at surface ADC, we can write the relation between the object distance v₁, image distance v and radius of curvature R₂, as

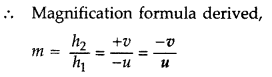
Question 11.
Define magnifying power of a telescope. Write its expression.
A small telescope has an objective lens of focal length 150 cm and an eyepiece of focal length 5 cm. If this telescope is used to view a 100 m high tower 3 km away, find the height of the final image when it is formed 25 cm away from the eyepiece. (Delhi 2012)
Answer:
The magnifying power of a telescope is defined as the ratio of the angle subtended at the eye by the final image formed at the least distance of distance vision to the angle subtended at the eye by the object at infinity, when seen directly

Angle substended by the 100 m tall tower at 3 km aways is,

Let h be the height of the image of tower formed by the objective.
Then angle subtended by the image produced by the objective will also be equal to h and is given by ‘

Magnification produced by the eyepiece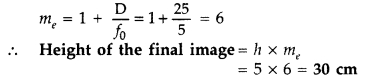

Question 12.
How is the working of a telescope different from that of a microscope?
The focal lengths of the objective and eyepiece of a microscope are 1.25 cm and 5 cm respectively. Find the position of the object relative to the objective in order to obtain an angular magnification of 30 in normal adjustment. (Delhi 2012)
Answer:

	Telescope	Microscope
1.	Resolving power should be higher for certain magni­fication.	Resolving power is not so large but the magnification should be higher.
2.	Focal length of objective should be kept larger while eyepiece focal length should be small for better magni­fication.	Both objective and eyepiece should have less focal length for better magnification.
3.	Objective should be of large aperture.	Eyepiece should be of large aperture.
4.	Distance between objective and eyepiece is adjusted to focus the object at infinity.	Distance between objective and eyepiece is fixed, for focusing an object the distance of the objective is changed.

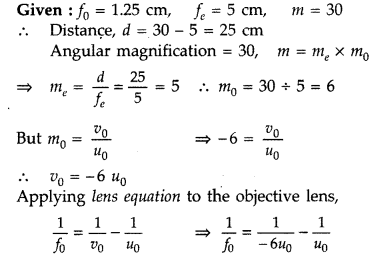
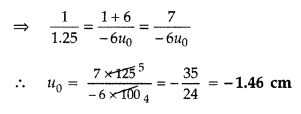
Question 13.
Draw a ray diagram showing the formation of the image by a point object on the principal axis of a spherical convex surface separating two media of refractive indices n₁ and n₂, when a point source is kept in rarer medium of refractive index nv Derive the relation between object and image distance in terms of refractive index of the medium and radius of curvature of the surface.
Hence obtain the expression for Lens-maker’s formula in the case of thin convex lens. (Comptt. Delhi 2014)
Answer:

By applying Cartesian sign convention,
OM = -M, MI = -v, MC = +R
Substituting these values in (iii), we get

This equation gives us a relation between object and image distance in terms of refractive index of the medium and the radius of the curvature of the curved spherical surface. It holds for any curved spherical surface.
Lens maker’s formula:

(a) Lens maker’s formula : Consider a thin double convex lens of refractive index n₂ placed in a medium of refractive index n₁. Here, n₁ < n₂. Let B and D be the poles, C₁ and C₂ be the centres of curvature and R₁ and R₂ be the radii of curvature of the two lens surfaces ABC and ADC, respectively. For refraction at surface ABC, we can write the relation between the object distance u, image distance v₁ and radius of curvature R₁ as

For refraction at surface ADC, we can write the relation between the object distance v₁, image distance v and radius of curvature R₂, as
>

Question 14.
(a) A point object is placed in front of a double convex lens (of refractive index n = n2/n1 with respect to air) with its spherical faces of radii of curvature R₁ and R₂. Show the path of rays due to refraction at first and subsequently at the second surface to obtain the formation of the real image of the object.
Hence obtain the Lens-maker’s formula for a thin lens.
(b) A double convex lens having both faces of the same radius of curvature has refractive index 1-55. Find out the radius of curvature of the lens required to get the focal length of 20 cm. (Comptt. All India)
Answer:
(a) Lens-maker’s formula. The image of point object O is formed in two steps. The first reflecting surface ‘c₁ forms the image I₁ of the object O. The image I₁ acts as a virtual object for formation of image I by the second surface ‘c₂‘.
For the first surface ABC ‘c₁‘,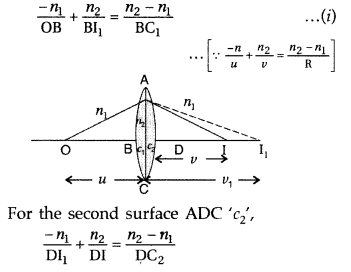

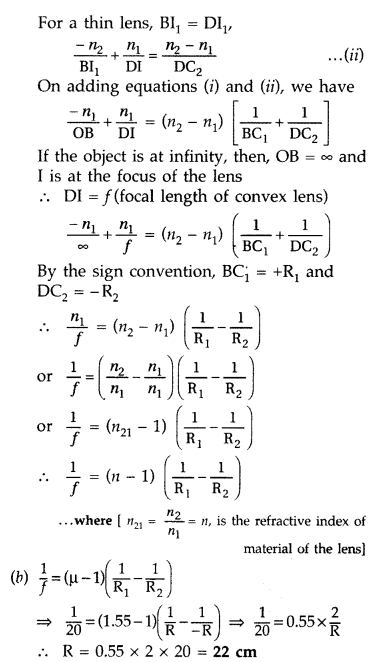
Question 15.
(a) Draw a labelled ray diagram showing the image formation of a distant object by a refracting telescope.
Deduce the expression for its magnifying power when the final image is formed at infinity.
(b) The sum of focal lengths of the two lenses of a refracting telescope is 105 cm. The focal length of one lens is 20 times that of the other. Determine the total magnification of the telescope when the final image is formed at infinity. (Comptt. All India 2015)
Answer:
(a) Refracting telescope :

Magnifying power. It is defined as the ratio of angle (β) subtended by the final image on the eye to the angle (α) subtended by object on eye.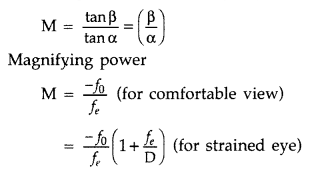

Limitations of refracting telescope over a a reflecting type telescope :

1. It suffers from chromatic aberration due to refraction and hence the image obtained is multicoloured and blurred.
2. As a lens of large apparatus can’t be manufactured easily, its light gathering power is low and hence can’t be used to see faint stars.

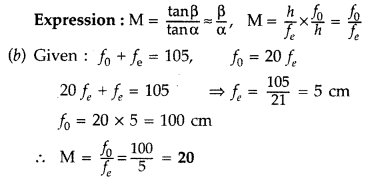
Question 16.
(a) A ray ‘PQ’ of light is incident on the face AB of a glass prism ABC (as shown in the figure) and emerges out of the face AC. Trace the path of the ray. Show that
∠i + ∠e = ∠A + ∠δ

where δ and e denote the angle of deviation and angle of emergence respectively.
Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. State the condition under which ∠δ is minimum.
(b) Find out the relation between the refractive index (µ) of the glass prism and ∠A for the case when the angle of prism (A) is equal to the angle of minimum deviation (δ_m). Hence obtain the value of the refractive index for angle of prism A = 60°. (All India 2015)
Answer:
(a) The figure shows the passage of light through a triangular prism ABC. The angles of incidence and refraction at the first face AB are i and rv while the angle of incidence (from glass to air) at the second face AC is r₂ and the angle of refraction or emergence e. The angle between the emergent ray RS and the direction of the incident ray PQ is called the angle of deviation δ.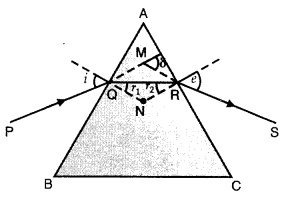

In the quadrilateral AQNR, two of the angles (at the vertices Q and R) are right angles. Therefore, the sum of the other angles of the quadrilateral is 180°.

From the triangle

Comparing these two equations, we get
r₁ + r₂ = A
The total deviation 8 is the sum of deviations at the two faces,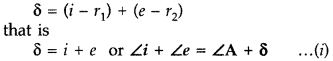

A plot between the angle of deviation and angle of incidence is shown in the figure. In general, any given value of δ, except for i = e, corresponds to two values i and hence of e. This, in fact, is expected from the symmetry of i and e in equation (i) above, i.e., δ remains the same if i and e are. interchanged. Physically, this is related to the fact that the path of ray in the diagram above can be traced back, resulting in the same angle of deviation. At the minimum deviation dm, the refracted ray inside the prism becomes parallel to its base. We have,

When angle of incidence (i) and angle of emergence (e) are equal, ie,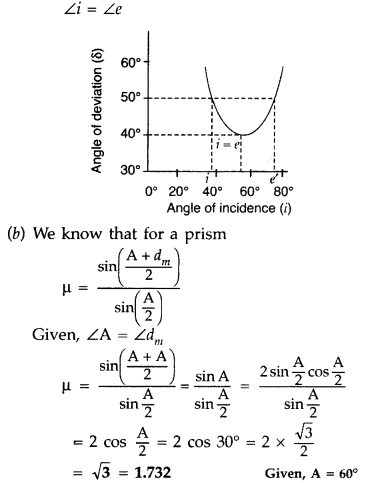

Question 17.
(a) Draw a ray diagram showing the image formation by a compound microscope. Obtain expression for total magnification when the images is formed at infinity.
(b) How does the resolving power of a compound microscope get affected, when
(i) focal length of the objective is decreased.
(ii) the wavelength of light is increased? Give reasons to justify your answer.
Answer:
(a) Ray diagram of a compound microscope : A schematic diagram of a compound microscope is shown in the figure. The lens nearest the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece, which functions essentially like a simple microscope or magnifier, produces the final image, which is enlarged and virtual. The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image formation at infinity, or a little closer for image formation at the near point. Clearly, the final image is inverted with respect to the original object.

Magnification due to a compound microscope.
The ray diagram shows that the (linear) magnification due to the objective, namely h’/h, equals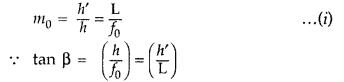

Here h’ is the size of the first image, the object size being h and f₀ being the focal length of the objective. The first image is formed near the focal point of the eyepiece. The distance L, i.e., the distance between the second focal point of the objective and the first focal point of the eyepiece (focal length f_e) is called the tube length of the compound microscope.

As the first inverted image is near the focal point of the eyepiece, we use for the simple microscope to obtain the (angular) magnification me due to it when the final image is formed at the near point, is

When the final image is formed at infinity, the angular magnification due to the eyepiece, me = (D//e)

Thus, the total magnification from equation (i) and (iii), when the image is formed at infinity, is

(b) Resolving power of a microscope :

(i) The focal length of the objective lens has no effect on the resolving power of microscope.
(ii) When the wavelength of light is increased, the resolving power of a microscope

Question 18.
(a) A point object ‘O’ is kept in a medium of refractive index n₁ in front of a convex spherical surface of radius of curvature R which separates the second medium of refractive index n₂ from the first one, as shown in the figure.
Draw the ray diagram showing the image formation and deduce the relationship between the object distance and the image distance in terms of n₁ n₂ and R.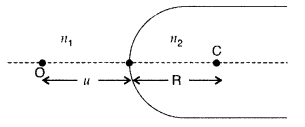

(b) When the image formed above acts as a virtual object for a concave spherical surface separating the medium n₂ from n₂ (n₂ > n₁), draw this ray diagram and write the similar [similar to (a)] relation. Hence obtain the expression for the lens maker’s formula. (Delhi 2015)
Answer:
(a) For small angles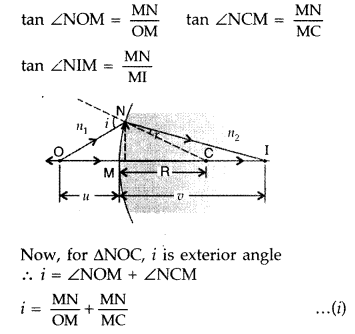


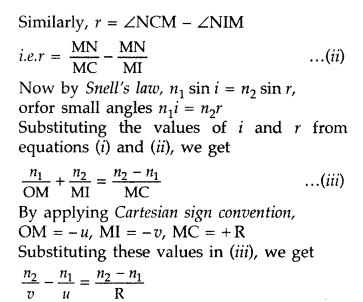
This equation gives us a relation between object and image distance interms of refractive index of the medium and the radius of the curvature of the curved Spherical surface. It holds for any curved Spherical surface.

(b) Len’s maker’s formula : Consider a thin double convex lens of refractive index n₂ placed in a medium of refractive index n₁.

Here n₁ < n₂. Let B and D be the poles, C₁ and C₂ be the centres of curvature R₁and R₂ be the radii of curvature of the two lens surfaces ABC and ADC, respectively.

For refraction at surface ABC, we can write the relation between the object distance u, image distance v₁ and radius of curvature R₁ as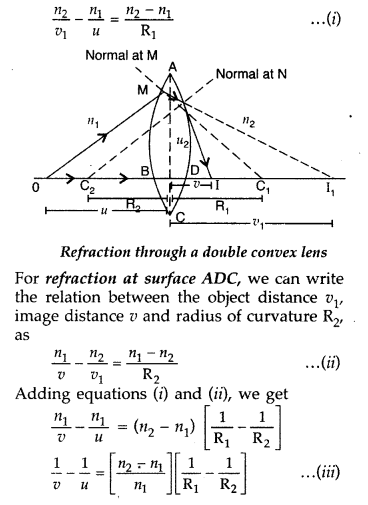

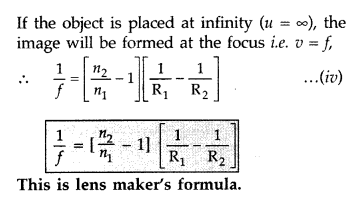
Question 19.
(i) Plot a graph to show variation of the angle of deviation as a function of angle of incidence for light passing through a prism. Derive an expression for refractive index of the prism in terms of angle of minimum deviation and angle of prism.
(ii) What is dispersion of light? What is its cause?
(iii) A ray of light incident normally on one face of a right isosceles prism is totally reflected as shown in figure. What must be the minimum value of refractive index of glass? calculations.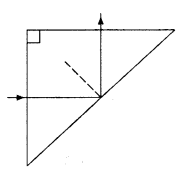

Answer:
(i)
(a) The figure shows the passage of light through a triangular prism ABC. The angles of incidence and refraction at the first face AB are i and rv while the angle of incidence (from glass to air) at the second face AC is r2 and the angle of refraction or emergence e. The angle between the emergent ray RS and the direction of the incident ray PQ is called the angle of deviation δ.

In the quadrilateral AQNR, two of the angles (at the vertices Q and R) are right angles. Therefore, the sum of the other angles of the quadrilateral is 180°.

From the triangle

Comparing these two equations, we get
r₁ + r₂ = A
The total deviation 8 is the sum of deviations at the two faces,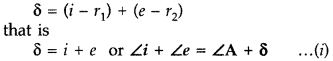

A plot between the angle of deviation and angle of incidence is shown in the figure. In general, any given value of δ, except for i = e, corresponds to two values i and hence of e. This, in fact, is expected from the symmetry of i and e in equation (i) above, i.e., δ remains the same if i and e are. interchanged. Physically, this is related to the fact that the path of ray in the diagram above can be traced back, resulting in the same angle of deviation. At the minimum deviation dm, the refracted ray inside the prism becomes parallel to its base. We have,

When angle of incidence (i) and angle of emergence (e) are equal, ie,

(ii) The white light disperses when passed through a prism, because the refractive index of the glass of the prism is different for different wavelength (colours). Hence, different colours get bent along different directions.

(iii) For total internal reflection, Zi > Zi (critical angle)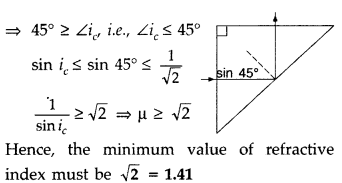

Hence, the minimum value of refractive index must be \(\sqrt{2}\) = 1.41

Question 20.
(i) Derive the mathematical relation between refractive indices n₁ and n₂ of two radii and radius of curvature R for refraction at a convex spherical surface. Consider the object to be a point since lying on the principle axis in rarer medium of refractive index n₁ and a real image formed in the denser medium of refractive index n₂.
Hence, derive lens maker’s formula.
(ii) Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20 cm. The distance of light source from the glass surface is 100 cm. At what position is the image formed?
Answer:
(a) For small angles


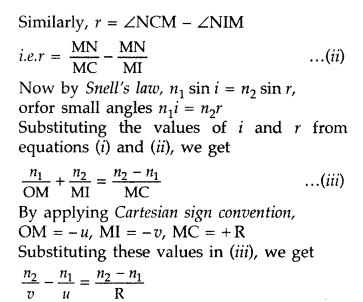
This equation gives us a relation between object and image distance interms of refractive index of the medium and the radius of the curvature of the curved Spherical surface. It holds for any curved Spherical surface.

(b) Len’s maker’s formula : Consider a thin double convex lens of refractive index n₂ placed in a medium of refractive index n₁.

Here n₁ < n₂. Let B and D be the poles, C₁ and C₂ be the centres of curvature R₁and R₂ be the radii of curvature of the two lens surfaces ABC and ADC, respectively.

For refraction at surface ABC, we can write the relation between the object distance u, image distance v₁ and radius of curvature R₁ as

⇒ v = 100 cm a real image on the other side, 100 cm away from the surface.

Question 21.
(a) Draw a labelled ray diagram to obtain the real image formed by an astronomical telescope in normal adjustment position. Define its magnifying power.
(b) You are given three lenses of power 0.5 D, 4 D and 10 D to design a telescope.
(i) Which lenses should be used as objective and eyepiece? Justify your answer.
(ii) Why is the aperture of the objective preferred to be large? (All India 2016)
Answer:
(a)
(i) Magnifying power m = \(-\frac{f_{0}}{f_{e}}\). It does not change with increase of aperature of objective lens, because focal length of a lens has no concern with the aperature of lens.

(ii) Drawbacks :

• Images formed by these telescopes have chromatic aberrations.
• Lesser resolving power.
• The image formed is inverted and faintes.

(b) Definition : It is the ratio of the angle subtended at the eye, by the final image, to the angle which the object subtends at the lens, or the eye.
(i) Objective = 0.5 D and eye lens = 10 D
∵ This choice would give higher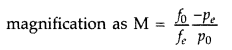

(ii) High resolving power/Brighter image/ lower limit of resolution.

Question 22.
(a) A point object, O is on the principal axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indices of the media and the radius of curvature of the spherical surface.
(b) Write the Lens Maker’s formula and use it to obtain the range of values of µ (the refractive index of the material of the lens) for which the focal length of an equiconvex lens, kept in air, would have a greater magnitude than that of the radius of curvature of its two surfaces. (Comptt. Delhi 2016)
Answer:
(a) For small angles


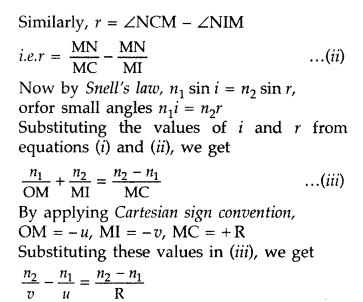
This equation gives us a relation between object and image distance interms of refractive index of the medium and the radius of the curvature of the curved Spherical surface. It holds for any curved Spherical surface.

(b) Len’s maker’s formula : Consider a thin double convex lens of refractive index n₂ placed in a medium of refractive index n₁.

Here n₁ < n₂. Let B and D be the poles, C₁ and C₂ be the centres of curvature R₁and R₂ be the radii of curvature of the two lens surfaces ABC and ADC, respectively.

For refraction at surface ABC, we can write the relation between the object distance u, image distance v₁ and radius of curvature R₁ as

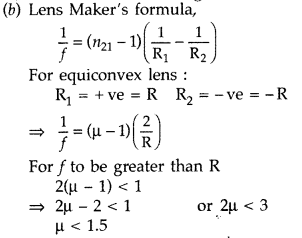
Hence required range is 1.0 < µ < 1.5

Question 23.
The relation, between the angle of incidence
(i) and the corresponding, angle of deviation (δ), for a certain optical device, is represented by the graph shown in the figure. Identify this device. Draw a ray diagram for this device and use it for obtaining an expression for the refractive index of the material of this device in terms of an angle characteristic of the device and the angle, marked an 8m, in the graph.(Comptt. All India 2016)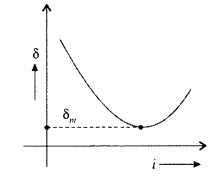

Answer:

1. The device identified is a ‘PRISM’.
2. For ray diagram and derivation :

(a) The figure shows the passage of light through a triangular prism ABC. The angles of incidence and refraction at the first face AB are i and rv while the angle of incidence (from glass to air) at the second face AC is r₂ and the angle of refraction or emergence e. The angle between the emergent ray RS and the direction of the incident ray PQ is called the angle of deviation δ.

In the quadrilateral AQNR, two of the angles (at the vertices Q and R) are right angles. Therefore, the sum of the other angles of the quadrilateral is 180°.

From the triangle

Comparing these two equations, we get
r₁ + r₂ = A
The total deviation 8 is the sum of deviations at the two faces,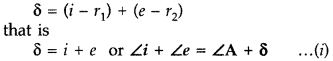

A plot between the angle of deviation and angle of incidence is shown in the figure. In general, any given value of δ, except for i = e, corresponds to two values i and hence of e. This, in fact, is expected from the symmetry of i and e in equation (i) above, i.e., δ remains the same if i and e are. interchanged. Physically, this is related to the fact that the path of ray in the diagram above can be traced back, resulting in the same angle of deviation. At the minimum deviation dm, the refracted ray inside the prism becomes parallel to its base. We have,

When angle of incidence (i) and angle of emergence (e) are equal, ie,

Question 24.
(a) Draw a ray diagram to show the image formation by a combination of two thin convex lenses in contact. Obtain the expression for the power of this combination in terms of focal lengths of the lenses.
(b) A ray of light passing from air through an equilateral glass prism undergoes minimum deviation when the angle of incidence is \(\frac{3}{4}\)th of the angle prism. Calculate the speed of light in the prism. (All India 2017)
Answer:
(a) Two thin lenses in contact: Two thin lenses, of focal length f₁ and f₂ are kept in contact. Let O be the position of object and let u be the object distance. The distance of the image (which is at I₁), for the first lens is v₁.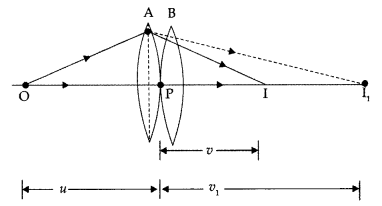

This image serves as object for the second lens.
Let the final image be at I, We then have

Question 25.
(a) Explain with reason, how the power of a diverging lens changes when
(i) it is kept in a medium of refractive index greater than that of the lens,
(ii) incident red light is replaced by violet light.
(b) Three lenses L₁ L₂, L₃ each of focal length 30 cm are placed co-axially as shown in the figure. An object is held at 60 cm from the optic centre of Lens L₁. The final real image is formed at the focus of L₃. Calculate the separation between
(i) (L₃ and L₂) and
(ii) (L₂ and L₃). (Comptt. All India 2017)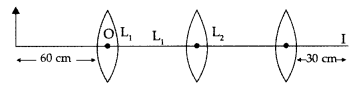

Answer:
(a) The power of a lens is the reciprocal of its focal length.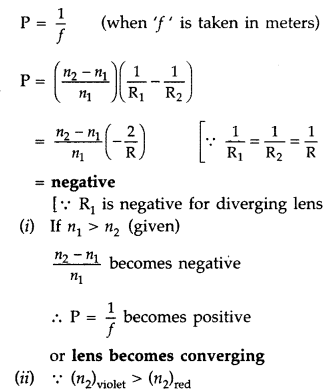

which means that the power of lens increases on changing to violet light from red light.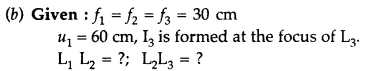

Since final image (I₃) is formed at the focus of L₃, the rays emerging from L₂ and incident on L₃ have to be parallel to principal axis.
Since the object is placed at a distance of 60 cm from L₁ i.e., at 2F; the image will be formed at 2F on the other side of L₁ (60 cm).
This image I₁ will be at the focus of L₂, because rays emerging out from L₂ are parallel to principal axis.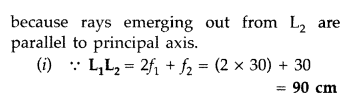

(ii) L₂L₃ can be any distance.

Question 26.
(a) Deduce the expression, by drawing a suitable ray diagram, for the refractive index of triangular glass prism in terms of the angle of minimum deviation (D) and the angle of prism (A).
Draw a plot showing the variation of the angle of deviation with the angle of incidence.
(b) Calculate the value of the angle of incidence when a ray of light incident on one face of an equilateral glass prism produces the emergent ray, which just grazes along the adjacent face. Refractive index of the prism is \(\sqrt{2}\). (Comptt. All India 2017)
Answer:
(a) The figure shows the passage of light through a triangular prism ABC. The angles of incidence and refraction at the first face AB are i and rv while the angle of incidence (from glass to air) at the second face AC is r2 and the angle of refraction or emergence e. The angle between the emergent ray RS and the direction of the incident ray PQ is called the angle of deviation δ.

In the quadrilateral AQNR, two of the angles (at the vertices Q and R) are right angles. Therefore, the sum of the other angles of the quadrilateral is 180°.

From the triangle

Comparing these two equations, we get
r₁ + r₂ = A
The total deviation 8 is the sum of deviations at the two faces,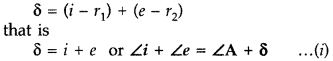

A plot between the angle of deviation and angle of incidence is shown in the figure. In general, any given value of δ, except for i = e, corresponds to two values i and hence of e. This, in fact, is expected from the symmetry of i and e in equation (i) above, i.e., δ remains the same if i and e are. interchanged. Physically, this is related to the fact that the path of ray in the diagram above can be traced back, resulting in the same angle of deviation. At the minimum deviation dm, the refracted ray inside the prism becomes parallel to its base. We have,

When angle of incidence (i) and angle of emergence (e) are equal, ie,

(b) Given µ = \(\sqrt{2}\), ∠i = ?
Since the emergent ray just grazes along the adjacent face of an equilateral glass prism,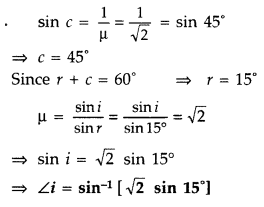

Question 27.
A biconvex lens of refractive index μ1 focal length ‘f and radius of curvature R is immersed in a liquid of refractive index μ₂. For (i) μ₂ > μ₁, and (ii) μ₂ < μ₁, draw the ray diagrams in the two cases when a beam of light coming parallel to the principal axis is incident on the lens. Also, find the focal length of the lens in terms of the original focal length and the refractive index of the glass of the lens and that of the medium. (CBSE AI 2013C)
Answer: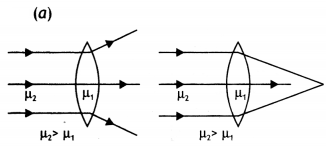

(b) Given: As the lens is equiconvex therefore R₁ = R₂ = R, _aμ_g = μ₁; _aμ₁ = μ₂ f_a = f, f_L = ?

Using the expression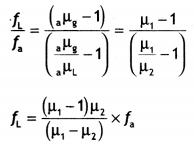

Question 28.
Write the conditions for observing a rainbow. Show, by drawing suitable diagrams, how one understands the formation of a rainbow. (CBSE AI 2014C)
Answer:
The conditions for observing a rainbow are that the sun should be shining in one part of the sky (say near the western horizon) while it is raining in the opposite part of the sky (say the eastern horizon). An observer can therefore see a rainbow only when his back is towards the sun.

Sunlight is first refracted as it enters a raindrop, which causes the different wavelengths (colours) of white light to separate. The longer wavelength of light (red) is bent the least while the shorter wavelength (violet) are bent the most. Next, these component rays strike the inner surface of the water drop and get internally reflected if the angle between the refracted ray and normal to the drop surface is greater than the critical angle (48°, in this case).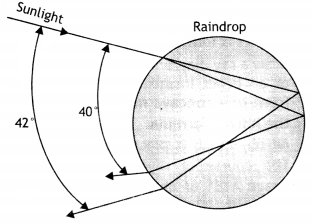

The reflected light is refracted again as it comes out of the drop as shown in the figure. It is found that the violet light, emerges at an angle of 40° related to the incoming sunlight and red light emerges at an angle of 42°. For other colours, angles lie in between these two values.

Question 29.
Explain the basic differences between the construction and working of a telescope and a microscope. (CBSE AI 2015)
Answer:
(a) In a telescope the objective has a large aperture and a large focal length, while in a microscope both the aperture and focal length of the objects are small (f_e > f_o). In a telescope, the eyepiece has a small aperture as compared to the objective, while in a microscope the eyepiece has a bigger aperture than the objective (f_e < f_o).

(b) A telescope increases the angle the object subtends at the eye thereby increasing its clarity by bringing it closer, while a microscope actually magnifies the object or a telescope magnifies distant objects, while a microscope magnifies nearby objects.

Question 30.
Why does white light disperse when passed through a glass prism?
Using the lens maker’s formula show how the focal length of a given lens depends upon the wavelength of light incident on it. (CBSE Delhi 2015C)
Answer:
It is because a glass prism offers a different refractive index to different wavelengths of light.
Lens maker’s formula is \(\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\).

The refractive index depends upon wavelength as n ∝ \(\frac{1}{λ}\), therefore f ∝ λ.

Hence the focal length of a lens increases with the increase in the wavelength of light.

Question 31.
A thin converging lens has a focal length f in air. If it is completely immersed in a liquid, briefly explain, how the focal length of the lens will vary?
Answer:
The focal length of a converging lens is given by
\(\frac{1}{f}\) = (_an_g – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
where ang = refractive index of Lens with respect to air.

And In a given liquid medium the focal Length of the Lens is given by
\(\frac{1}{f_{m}}\) = (_mn_g – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)

Therefore the ratio of the totaL focal Length is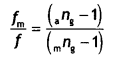

(a) If _mn_g < _an_g then f is +ve and has a value greater than f, i.e. focal length of the lens increases when immersed in a given liquid medium.

(b) If _mn_g >_an_g, then f is -ve, i.e. the lens will begin to behave as a diverging lens.

Question 32.
When monochromatic light is incident on a surface separating two media, the reflected and refracted light both have the same frequency as the incident frequency. Explain why?
Answer:
Reflection and refraction arise through the interaction of incident light with the atomic constituents of matter. Atoms may be viewed as oscillators that take up the frequency of the external agency (light) causing forced oscillations. The frequency of light emitted by a charged oscillator equals its frequency of oscillation. Thus the frequency of scattered light equals the frequency of incident light.

Question 33.
The image of an object formed by the combination of a convex lens (of focal length f) and a convex mirror (of the radius of curvature R), set up as shown is observed to coincide with the object. Redraw this diagram to mark on it the position of the centre of curvature of the mirror. Obtain the expression for R in terms of the distances marked as ‘a’ and ‘d’ and focal length f of the convex lens. (CBSE Delhi 2016C)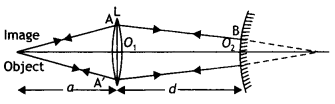

Answer:
The final image, formed by the combination, is coinciding with the object itself. This implies that the rays, from the object, are retracing their path, after refraction from the tens and reflection from the mirror. The (refracted) rays are, therefore, fatling normally on the mirror. It follows that the rays A B, and A’ B’, when produced, are meeting at the centre of curvature C of the mirror. Hence C is the centre of curvature of the mirror.

From the figure, we then see that for the convex lens we have

u = – a and v = + (d + R). If f is the focal length of the lens, we have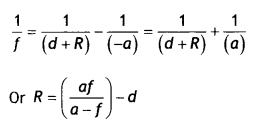


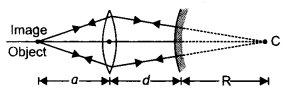
Question 34.
Define the magnifying power of a compound microscope when the final image is formed at infinity. Why must both the objective and the eyepiece of a compound microscope have short focal lengths? Explain. (CBSE Delhi 2017)
Answer:
It is defined as the ratio of the angle subtended on the eye by the final image when it lies at infinity to the angle subtended on the eye by the object when it lies at the least distance of distinct vision from the eye or the near point of the eye. The magnifying power of a microscope is given by
M = M_e × M_o = \(\frac{L}{f_{0}} \times\left(1+\frac{D}{f_{e}}\right)\)

Since it depends inversely on the focal lengths of the objective and the eyepiece, therefore both have to be small to get a large magnification.

Question 35.
(a) Draw a ray diagram for the formation of the image by a compound microscope.
Answer:
The ray diagram is as shown.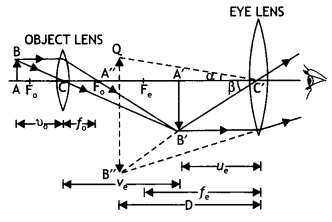

(b) You are given the following three lenses. Which two lenses will you use as an eyepiece and as an objective to construct a compound microscope?

Lenses	Power(D)	Aperture(cm)
L1	3	8
L2	6	1
L3	10	1

Answer:
The objective should have a short focal length and large aperture while the eyepiece should have a short focal length and small aperture. Thus for objective lens L₃ should be used and for eyepiece lens, L₂ should be used.

(c) Define the resolving power of a microscope and write one factor on which it depends. (CBSE AI 2017)
Answer:
The resolving power of a microscope is given by the expression
RP = \(\frac{2 \mu \sin \theta}{1.22 \lambda}=\frac{2 \mu v \sin \theta}{1.22 c}\)

It depends upon the wavelength/ frequency of the incident light.

Question 36.
Draw a labelled ray diagram of an astronomical telescope in the near point adjustment position. (CBSE Delhi 2019)
A giant refracting telescope at an observatory has an objective lens of focal length 15 m and an eyepiece of focal length 1.0 cm. If this telescope is used to view the Moon, find the diameter of the image of the Moon formed by the objective lens. The diameter of the Moon is 3.48 × 10⁶ m, and the radius of the lunar orbit is 3.8 × 10⁸ m.
Answer:
A Labelled ray diagram is as shown.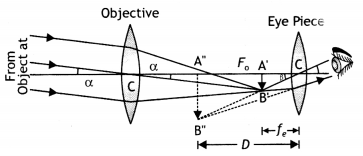

Given f_o = 15 m, f_e = 1.0 cm = 0.01 m, M = ? D_m = 3.48 × 10⁶ m, r = 3.8 × 10⁸ m,
Using M = \(\frac{f_{0}}{f_{e}}=\frac{15}{0.01}\) = 1500

The angle subtended by the moon at the objective of the telescope

Question 37.
(a) Amobilephoneliesalongtheprincipal axis of a concave mirror. Show with the help of a suitable diagram the formation of its image. Explain why magnification is not uniform.
Answer:
The image of the mobile phone formed by the concave mirror is shown in the below figure.

The part of the mobile phone that is at C will form an image of the same size only at C. In the figure, we can see that B’C = BC. The part of the mobile phone that lies between C and F will form an enlarged image beyond C as shown in the figure. It can be observed that the magnification of each part of the mobile phone cannot be uniform on account of different locations. That is why the image formed is not uniform.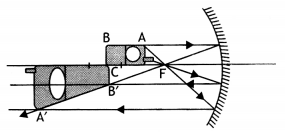

(b) Suppose the lower half of the concave mirrors reflecting surface is covered with an opaque material. What effect this will have on the image of the object. Explain. (CBSE Delhi 2014)
Answer:
The intensity of the image will decrease while the whole image will be for.

Question 38.
(a) Draw a labelled ray diagram of a compound microscope, when the final image forms at the least distance of distinct vision.
(b) Why is its objective of short focal length and of short aperture compared to its eyepiece? Explain.
(c) The focal length of the objective is 4 cm while that of the eyepiece is 10 cm. The object is placed at a distance of 6 cm from the objective lens.
(i) Calculate the magnifying power of the compound microscope, if its final image is formed at the near point.
(ii) Also calculate the length of the compound microscope. (CBSE AI 2019)
Or
(a) With the help of a labelled ray diagram, explain the construction and working of a Cassegrain reflecting telescope.
(b) An amateur astronomer wishes to estimate roughly the size of the sun using his crude telescope consisting of an objective lens of focal length 200 cm and an eyepiece of focal length 10 cm. By adjusting the distance of the eyepiece from the objective, he obtains an image of the sun on a screen 40 cm behind the eyepiece. The diameter of the sun’s image is measured to be 6-0 cm. Estimate the sun’s size, given that the average earth-sun distance is 1.5 × 10¹¹ m.
Answer:
(a) The diagram is as shown.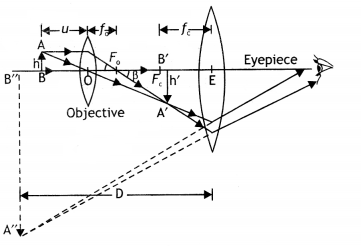

(b) The magnifying power of compound microscope m = m₀ × m_e = \(\frac{L}{f_{o}}\left(1+\frac{D}{f_{e}}\right)\)

To have high magnifying power and high resolution, the focal length of the objective and its aperture should be short.

The focal length of the eyepiece is comparatively greater than the objective so an image formed by the objective lens may form within the focal length of the eyepiece and the final magnified image may be formed.

Aperture is short for higher resolution,

(c) Given u_o = – 6 cm
For objective lens we have

(i) For magnifying power of compound microscope we have
m = \(\frac{v_{o}}{u_{o}}\left(1+\frac{D}{f_{e}}\right)=\frac{12}{6}\left(1+\frac{25}{10}\right)\) = 7

(ii) Length of the compound microscope L = v₀ + u_e = 12 + 7.14 = 19.14 cm
Or
(a) Cassegrain reflecting telescope consists of a large concave (primary) parabolic mirror having a hole in its centre. There is a small convex (secondary) mirror near the focus of the concave mirror. The eyepiece is placed near the hole of the concave mirror. The parallel rays from a distant object are reflected by the large concave mirror. These rays fall on the convex mirror which reflects these rays outside the hole. The final magnified image is formed at infinity.

The diagram is as shown.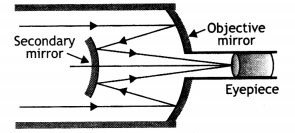

(b)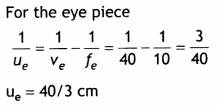

Magnification produced by the eye piece is
me = \(\frac{v_{e}}{u_{e}}=\frac{40}{40 / 3}\) = 3

Diameter of the image formed by the objective is
D = 6/3 = 2 cm

If D is the diameter of the sun then the angle subtended by it on the objective will be
α = \(\frac{D}{1.5 \times 10^{11}}\) rad

Now, angle subtended by the image at the objective = angle subtended by the sun
α = \(\frac{\text { size of image }}{f_{0}}=\frac{2}{200}=\frac{1}{100}\) rad

Therefore,
\(\frac{D}{1.5 \times 10^{11}}=\frac{1}{100}\)
D = 1.5 × 10⁹

Question 39.
A convex lens is placed in contact with a plane mirror. An axial point object, at a distance of 20 cm from this combination, has its image coinciding with itself. What is the focal length of the convex lens?
Answer:
Figure (a) shows a convex lens L in contact with a plane mirror M. P is the point object, kept in front of this combination at a distance of 20 cm, from it. Since the image of the object is coinciding with the object itself, the rays from the object, after refraction from the lens, should fall normally on the mirror M, so that they retrace their path and form an image coinciding with the object itself.

This will be so, if the incident rays from P form a parallel beam perpendicular to M, after refraction from the lens. For clarity, M has been shown at a finite distance from L, in figure (b). For lens L, since the rays from P form a parallel beam after refraction, P must be at the focus of the lens. Hence the focal length of the lens is 20 cm.


Question 40.
A convex lens and a convex mirror (of the radius of curvature 20 cm) are placed co-axially with the convex mirror placed at a distance of 30 cm from the lens. For a point object, at a distance of 25 cm from the lens, the final image, due to this combination, coincides with the object itself. What is the focal length of the convex lens?
Answer:
The ray diagram is as shown.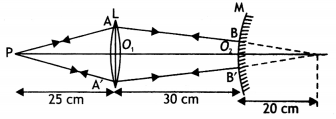

The final image, formed by the combination, is coinciding with the object itself. This implies that the rays, from the object, are retracing their path, after refraction from the lens and reflection from the mirror. The (refracted) rays are, therefore, falling normally on the mirror. It follows that the rays A B, and A’ B’, when produced, are meeting at the centre of curvature C of the mirror. Hence O₂C = 20 cm, the radius of curvature of the mirror. From the figure, we then see that for the convex lens u = – 25 cm and v = + (30 + 20) cm = + 50 cm. If f is the focal length of the lens, we have
\(\frac{1}{50}-\frac{1}{(-25)}=\frac{1}{f}\)
or
f = 16.67 cm

Question 41.
Derive a relation between focal length, image distance and object distance for a
concave mirror.
Answer:
Consider a concave mirror of small aperture, image distance and object distance for a Figure below shows two rays of light leaving the tip of the object. One of these rays passes through the centre of curvature C of the mirror, hitting the mirror head-on and reflecting back on itself. The second ray BP strikes the mirror at its pole P and reflects as shown obeying the laws of reflection. The image of the tip of the arrow is located at the point where these two rays intersect. Thus the image is formed between the focus and centre of curvature.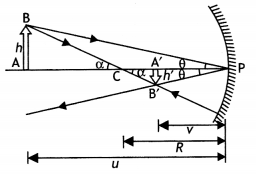

Consider the two right-angled triangles BAP and B’A’P

Now from triangle BAP using trigonometry, we have
tan θ = \(\frac{AB}{PA}\) …(1)

Therefore equation (7) becomes
\(\frac{\mathrm{PA}}{\mathrm{PA}^{\prime}}=\frac{\mathrm{PA}-\mathrm{PC}}{\mathrm{PC}-\mathrm{PA}^{\prime}}\)

By Cartesian sign conventions we have PA = -u, PA’ = -v and PC = – R, substituting in equation (8), we have

simplifying we have 2uv = vR + uR dividing both sides by uvR we have
\(\frac{1}{u}+\frac{1}{v}=\frac{2}{R}\) …(11)

but R = 2 f, where f is the focal length of the mirror. Therefore the above equation
reduces to \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
which is the required mirror formula.

Question 42.
With the help of a suitable ray diagram, derive a relation between the object distance (u) image distance v and radius of curvature (R) for a convex spherical surface, when a ray of light travels from rarer to denser medium. (CBSE Delhi 2011C)
Answer:
Let a convex spherical surface XPY separate a rarer medium of refractive index (n₁) from a denser medium of refractive (n2). The real image of object 0 is formed by refraction from the convex spherical surface of radius of curvature R. The angle α β γ are shown in the figure.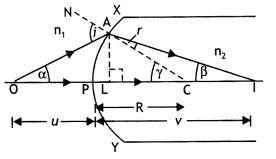

Let ∠AOP = α, ∠AIP = β and ∠ACP = γ.

From point A, drop AN perpendicular to the principal axis of the spherical refracting surface. From triangle AOC, we have
i = α + γ

Since the aperture of the spherical refracting surface is small, point A will be close to point P and hence angles α, β and γ will be small. As such, these angles may be replaced by their tangents.

Therefore, equation (1) may be written as
i = tanα + tanγ …(2)

From right angled triangles ΔALO and ΔALC, we have

tan α = \(\frac{AL}{LO}\) and tan γ = \(\frac{AL}{LC}\)

Substituting for tan α and tan γ in equation (2), we have

i = \(\frac{AL}{LO}\) + \(\frac{AL}{LC}\) …(3)

Again, as aperture of the refracting surface is small, point L will be close to point P, the pole of the refracting surface.
Therefore,
LO ≈ PO and LC ≈ PC

Therefore, equation (3) becomes
i = \(\frac{AL}{PO}\) + \(\frac{AL}{PC}\) …(4)

Now, from triangle ΔACI, γ = r + β
or
r = γ— β

Since angles γ and β are small, we have
r = tan γ— tan β …(5)

From right angled triangles ΔALC and ΔALI,
we have
tan γ = \(\frac{A L}{L C} \approx \frac{A L}{P C}\) and tan β = \(\frac{A L}{L I} \approx \frac{A L}{P I}\)

Substituting for tan β and tan γ in equation (5) we have
r = \(\frac{\mathrm{AL}}{\mathrm{PC}}-\frac{\mathrm{AL}}{\mathrm{PI}}\) …(6)

Now by Snell’s Law at point A we have
n₁ sin i = n₂ sin r

Since angles are small, therefore the above relation becomes
n₁ i = n₂ r …(7)

Substituting the values of i and r from equations (4) and (6) we have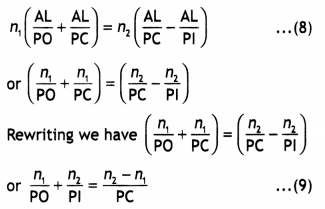

Applying new Cartesian sign conventions:
PO = – u (a distance of the object is against incident Light)

PI = + v (distance of image Is along incident Light)
PC = + R (a distance of the centre of curvature is along with incident Light) we have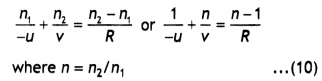

The above equation connects u, V and R to the absolute refractive indices of the material of the refracting surface and that of the rarer medium.

Question 43.
A ray of light Is an Incident on one face of a glass prism and emerges out from the other face. Trace the path of the ray and derive an expression for the refractive index of the glass prism. Also, plot a graph between the Angle of incidence and angle of deviation. (CBSE Delhi 201 IC)
Answer:
The graph is as shown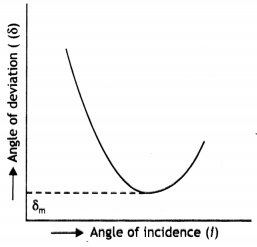

Consider a cross-section XYZ of a prism as shown in the figure. Let A be the angle of the prism. A ray PQ of monochromatic light is incident on face XY of the prism at an angle i. The ray is called the incident ray and the angle is called the angle of incidence. This ray is refracted towards the normal NQE and travels in the prism along QR. This ray is called the refracted ray at the face XY.

Let r₁ be the angle of refraction at this surface. The refracted ray QR is incident at an angle r₂ on the surface XZ. The ray QR again suffers refraction and emerges out of face XZ at an angle e along with RS. The ray is called the emergent ray and the angle e is called the angle of emergence. When the ray SR is extended backwards it meets the extended ray PQ at point D such that δ is the angle of deviation of the ray.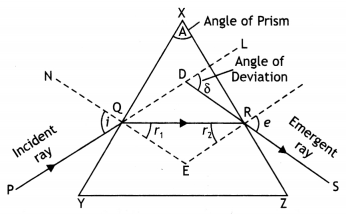

As seen from figure we have in triangle QDR that ∠DQR = i – r₁ and
∠DRQ = e – r₂. Therefore from triangle QDR we have
δ = ∠DQR + ∠DRQ = (i – r₁) + (e – r₂)
or
δ = (i + e) – (r₁ + r₂) …(1)

Now from the quadrilateral XQER, we have
A + E = 180° …(2)

In triangle QER we have r₁ + r₂ + e – 180° …(3)

From equations (2) and (3) we have
A = r₁ + r₂ …(4)

Substituting in equation (1) we have
δ = i + e – A
or
i + e = A + δ … (5)

The deviation produced by a prism depends upon (i) the angle of incidence (ii) the angle of prism and (Hi) the refractive index of the material of the prism. It is found that as the angle of incidence changes, the angle of deviation also changes.

A graph between the angle of incidence and the angle of deviation is shown in the figure above. As the angle of incidence increases, the angle of deviation first decreases becomes a minimum for a particular angle of incidence and then increases. The minimum value of the angle of deviation is called the angle of minimum deviation. It is denoted by δ_m. In this position the ray of light passes symmetrically through the prism, i.e. the refracted ray QR is parallel to the base of the prism. In this position, the angle of incidence is equal to the angle of emergence, i.e. i = e. Also in this position, the angle of refraction at the faces of the prism are equal, i.e. r₁ = r₂.

Substituting these values in equations (4) and (5) we have
A = r₁ + r₂ = r + r = 2r
or
r = A/2 …(6)
and i + i = A + δm
or
2i = A + δm
or
i = \(\frac{A+\delta_{m}}{2}\) …(7)

substituting for i and r in the expression for Snell’s law we have
μ = \(\frac{\sin i}{\sin r}=\frac{\sin \left[\frac{A+\delta_{m}}{2}\right]}{\sin \left(\frac{A}{2}\right)}\)

Question 44.
(a) Draw a ray diagram showing the image formation by a compound microscope. Obtain an expression for total magnification when the image is formed at infinity.
Answer:
The ray diagram is as shown.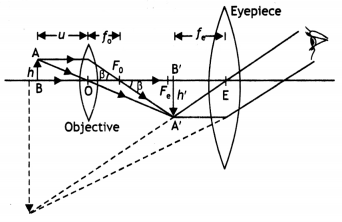


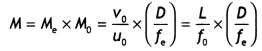
(b) How does the resolving power of a compound microscope get affected, when
(i) the focal length of the objective is decreased.
(ii) the wavelength of light is increased? Give reasons to justify your answer. (CBSE AI 2015C)
Answer:
The resolving power of a microscope is given by the expression RP = \(\frac{2 n \sin \theta}{\lambda}\)
(i) There is no effect of the increase in the focal length of the objective on the resolving power of the microscope.
(ii) If the wavelength of the incident light is increased, the resolving power of the microscope also decreases.

Question 45.
An optical instrument uses eye-lens of power 12.5 0 and an object lens of power 50 D and has a tube length of 20 cm. Name the optical instrument and calculate its magnifying power, if it forms the final image at infinity. (CBSE Delhi 2017C)
Answer:
It is a compound microscope.
The ray diagram is as shown.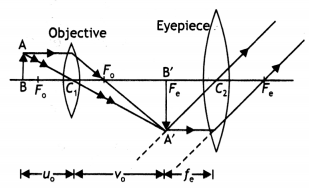

Let m_o and me be the magnifications produced by the objective lens and eye lens respectively, the total magnifying power of the microscope
M = m_o x m_e

Now m_o = – \(\frac{v_{0}}{u_{0}}\)

Also, the magnifying power of the eyepiece when the final image is formed at infinity
m_e = \(\frac{D}{f_{e}}\)

Thus magnifying power of the microscope is
M = \(\frac{-v_{0}}{u_{0}} \times \frac{D}{f_{e}}\)

As a first approximation, u_e ≈ f_e and v_e ≈ L = distance between objective and eyepiece (or length of microscope tube), then we have
M = \(\frac{-L}{f_{0}} \times \frac{D}{f_{e}}\)

Question 46.
Use the mirror equation to show that
(i) an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
Answer:
By mirror formula we have \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
Therefore \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\) and for concave mirror u and f both are having negative sign, i.e. f < 0 and u < 0.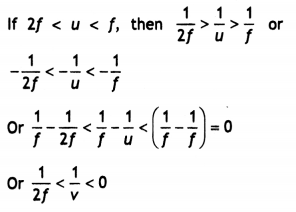

It means that v > 2f, having a negative sign. Thus, the image is real and lies beyond 2f.

(ii) a convex mirror always produces a virtual image independent of the location of the object.
Answer:
(Ii) For a convex mirror \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\) but f is positive and u is negative, i.e. f >0 but u < 0.

Therefore, it is self-evident from the above relation that irrespective of the value of u, the value of v is aLways +ve. It means that the Imaged formed by the convex mirror is always virtual independent of the location of the object.

(iii) an object placed between the pole and the focus of a concave mirror produces a virtual and enlarged image. (CBSE AI 2011)
Answer:
As for a concave mirror f and u, both are negative, hence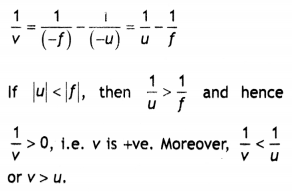

It means that for an object placed between the pole and principal focus of a concave mirror the image formed (as v is +ve) is virtual and magnification

m = \(\frac{1}{O}=\frac{|v|}{|u|}\) > 1, i.e. the image is an enlarged image.

Question 46.
(i) Obtain Lens makers formula using the expression \(\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{\left(n_{2}-n_{1}\right)}{R}\), here the ray of light propagating from a rarer medium of refractive index (n₁) to a denser medium of refractive index (n₂) is incident on the convex side of spherical refracting surface of radius of curvature R.
(ii) Draw a ray diagram to show the image formation by a concave mirror when the object is kept between its focus and the pole. Using this diagram, derive the magnification formula for the Image formed. (CBSE DelhI 2011)
Answer:
(i) The course of rays through the Lens Is as shown. For refraction at the spherical surface XP₁Y, we have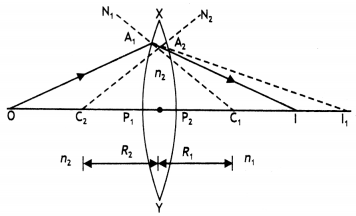


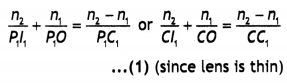
Consider the second surface XP₂Y. Actually, the materiaL of the Lens does not extend beyond XP₁Y. Therefore, before the refracted ray from A₁ could meet the principal axis, it will suffer refraction at point A₂ on the second face XP₂Y and the Lightray will finally meet the principal axial. Such that l is the final image. Thus point lies the real Image of the virtual object I. Hence for refraction at the surface XP₂Y we have

The above equation becomes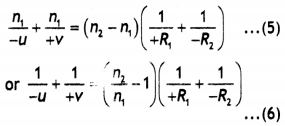

But n₂/n₁ = n, the absolute refractive index of the material of the lens, therefore the above equation takes the form
\(\frac{1}{v}-\frac{1}{u}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)

But by lens formula we have \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
Therefore, from the above two equations we have
\(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) …(7)

This is the Lens maker’s equation or formula.

(ii) The ray diagram is as shown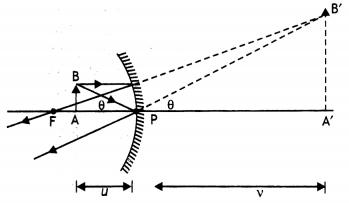

Now from triangle BAP we have
tan θ = \(\frac{AB}{PA}\) …(1)

Also from triangle B’A’P, we have A’B’
tan θ = \(\frac{A^{\prime} B^{\prime}}{P A^{\prime}}\) …(2)

Comparing equations (1) and (2), we have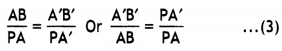

By Cartesian sign convention AB = h, A’B’ = h’, PA = – u and PA’= v . Substituting in equations (3) we have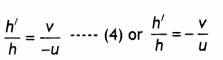

But \(\frac{h^{\prime}}{h}\) = m ( Linear magnification),
therefore
m = – \(\frac{\text { image distance }}{\text { object distance }}\)

Question 47.
(a) Two thin convex lenses L₁ and L₂ of focal lengths f₁ and f₂ respectively, are placed coaxially in contact. An object is placed at a point beyond the focus of lens L₁. Draw a ray diagram to show the image formation by the combination and hence derive the expression for the focal length of the combined system.
Answer:
Consider two lenses A and B of focal length f₁ and f₂ placed in contact with each other. Let the object be placed at a point O beyond the focus of the first lens L₁ as shown.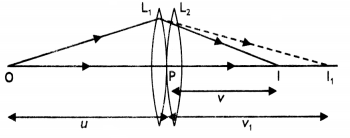

The first lens L₁ produces an image at l₁ Since image l₂ is real, it serves as a virtual object for the second lens L₂, producing the final image at l. Since the lenses are thin, we assume the optical centres of the lenses to be coincident. Let this central point be denoted by P.

For the image formed by the first lens L₁, we get
\(\frac{1}{v_{1}}-\frac{1}{u}=\frac{1}{f_{1}}\) …(i)

For the image formed by the second lens L₂, we get
\(\frac{1}{v}-\frac{1}{v_{1}}=\frac{1}{f_{2}}\) …(ii)

Adding equations (i) and (ii) we have
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\) …(iii)

If the two lens-system is regarded as equivalent to a single lens of focal length f, we have
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) …(iv)

Therefore from equations (iii) and (iv) we get
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)

(b) A ray PQ incident on the face AB of a prism ABC, as shown in the figure, emerges from the face AC such that AQ = AR.

Draw the ray diagram showing the passage of the ray through the prism. If the angle of the prism is 60° and the refractive index of the material of the prism is \(\sqrt{3}\), determine the values of angle of incidence and angle of deviation. (CBSE AI 2015)
Answer:
The ray diagram is as shown

The prism, in this situation, is in the minimum deviation position, therefore we have
r = \(\frac{A}{2}=\frac{60}{2}\) = 30°

Hence n = \(\frac{\sin i}{\sin r}=\frac{\sin i}{\sin 30^{\circ}}\) = \(\sqrt{3}\)

This gives, i = 60°
Hence from
i = \(\frac{A+\delta_{m}}{2}\) we have
δ_m = 2i – A = 2 × 60° – 60° = 60°

Question 48.
(a) Plot a graph to show the variation of the angle of deviation as a function of the angle of incidence for light passing through a prism. Derive an expression for the refractive index of the prism in terms of angle of minimum deviation and angle of prism.
(b) What is the dispersion of light? What is its cause?
(c) A ray of light incident normally on one face of a right isosceles prism is totally reflected as shown in the figure. What must be the minimum value of the refractive index of glass? Give relevant calculations.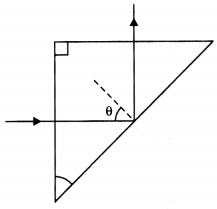

Answer: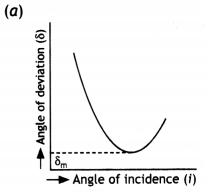

For a prism we have
i + e = A + δ …(1)

From the graph between the angle of incidence and the angle of deviation it follows that as the angle of incidence increases, the angle of deviation first decreases becomes a minimum for a particular angle of incidence and then again increases. The minimum value of the angle of deviation is called the angle of minimum deviation. It is denoted by 5m. In this position the ray of light passes symmetrically through the prism, i.e. the refracted ray QR is parallel to the base of. the prism. In this position, the angle of incidence is equal to the angle of emergence, i.e. i = e. Also in this position, the angle of refraction at the faces of the prism are equal, i.e. r₁ = r₂. Substituting these values in equations (4) and (5) we have
A = r₁ + r₂ = r + r = 2r
or
r = A/2 …(2)
and
i + i = A + δ_m
or
2i = A + δ_m
or
i = \(\frac{A+\delta_{m}}{2}\) …(3)

Substituting for i and r in the expression for Snell’s law we have a speed of light in a vacuum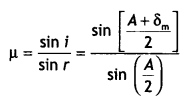

(b) The phenomenon of splitting a ray of white tight into its constituent colours (wavelengths) is catted dispersion.
Cause: It is because different wavelengths travel at different speeds In a medium other than vacuum.

(C) The diagram of the path of rays through the prism is as shown.
Here θ = 45° > i_c

Now n = \(\frac{1}{\sin i_{c}}=\frac{1}{\sin 45^{\circ}}=\frac{1}{1 / \sqrt{2}}=\sqrt{2}\)
Therefore n > \(\sqrt{2}\)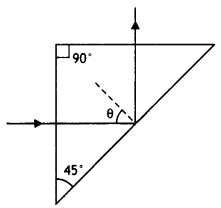

Numerical Problems :

Formulae for solving numerical problems

• When Light travels from an optically denser medium to an optically rarer medium It bends away from the normal.
• When light travels from an optically rarer medium to an optically denser medium It bends towards from the normal. speed of Light in vacuum
• μ = \(\frac{\text { speed of light in vacuum }}{\text { speed of light in the medium }}\)
• μ = \(\frac{1}{\sin \theta_{c}}\)
• In minimum deviation position A = 2r or
  
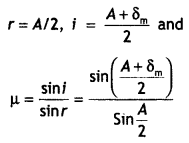
• Lens maker’s formula
  \(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
• MagnifyIng power of a compound microscope
  M = M_e × M_o = \(\frac{L}{f_{0}} \times\left(1+\frac{D}{f_{e}}\right)\)

Question 1.
A convex lens made up of a glass of refractive index 1.5 is dipped, In turn, In
(a) a medium of refractive index 1.65,
Answer:
When dipped in the medium of refractive index 1.65, it will behave as a concave lens and when dipped in the medium of refractive index 1.33, it will behave as a convex lens.

(b) a medium of refractive index 1.33.
(i) Will it behave as a converging or a diverging lens in the two cases?
Answer:
Its focal length in another medium is given by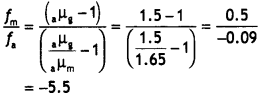

Thus f_m = -5.5 f_a, i.e. focal length increases and becomes negative.

(ii) How will Its focal length change In the two media? (CBSE AI 2011)
Answer:
Similarly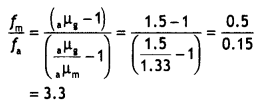

Thus f_m = 3.3 f_a, i.e. focal length increases.

Question 2.
A compound microscope uses an objective lens of focal length 4 cm and an eyepiece lens of focal length 10 cm. An object is placed at 6 cm from the objective lens. Calculate the magnifying power of the compound microscope. Also, calculate the length of the microscope. (CBSE Al 2011)
Answer:
f_o = 4 cm, f_e = 10 cm, u_o = – 6 cm, M = ?, L = ?
Using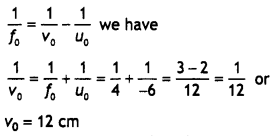

Hence angular magnification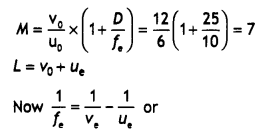


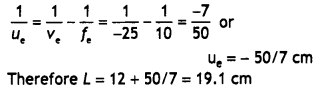
Question 3.
A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece lens of focal length 1 cm is used, find the angular magnification of the telescope.
If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is 3.42 × 10⁶ m and the radius of the lunar orbit is 3.8 × 10⁸ m. (CBSE AI 2011, Delhi 2015)
Answer:
Given f_o = 15 m, f_e = 1.0 cm = 0.01 m, M = ?
Dm = 3.48 × 10⁶ m, r = 3.8 × 10⁸ m,

Using M = \(\frac{f_{0}}{f_{\mathrm{e}}}=\frac{15}{0.01}\) = 1500

The angle subtended by the moon at the objective of the telescope

Question 4.
A beam of light converges at a point P. A concave lens of focal length 16 cm is placed in the path of this beam 12 cm from P. Draw a ray diagram and find the location of the point at which the beam would now converge. (CBSE Delhi 2011C)
Answer:
The ray diagram is shown in the figure. In the absence of the concave lens the beam converges at point P. When the concave lens is introduced, the incident beam of light is diverged and now comes to focus at point Q. Thus for the concave lens P serves as a virtual object giving rise to a real Image at Q.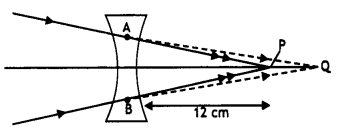

Here u = + 12 cm, f = – 16 cm, v = ?, Now for a lens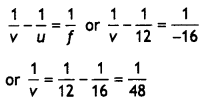

Hence v = 48 cm
i. e. the point at which the beam is focused is 48 cm from the lens.

Question 5.
Two convex lenses of focal length 20 cm and 1 cm constitute a telescope. The telescope is focused on a point that is 1 m away from the objective. Calculate the magnification produced and the length of the tube, if the final image Is formed at a distance of 25 cm from the eyepiece. (CBSE Delhi 2011 C)
Answer:
Given f_o = 2o cm, f_e = 1 cm, u = – 100 cm, M =?, y =?

Fora lens \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
or
\(\frac{1}{v}-\frac{1}{-100}=\frac{1}{20}\)
or
v = 25cm

Since the eye lens forms the image of the virtual object at the distance of distinct vision for the eye lens
v = – 25 cm, f_e = 1 cm,

Now \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
or
\(\frac{1}{-25}-\frac{1}{u}\) = 1
or
u = – \(\frac{25}{26}\)cm

Now magnification produced by the object lens
m_o = \(\frac{v}{u}=-\frac{25}{100}=-\frac{1}{4}\)

Magnification produced by the eye Lens
m_e = \(\frac{v}{u}=\frac{-25}{-25}\) × 26 = 26

Hence total magnification
M = m_o × m_e = -1 /4 × 26 = – 6.5

Question 6.
(a) Under what conditions are the phenomenon of total internal reflection of light observed? Obtain the relation between the critical angle of incidence and the refractive index of the medium.
(b) Three lenses of focal lengths +10 cm, -10 cm and +30 cm are arranged coaxially as in the figure given below. Find the position of the final image formed by the combination. (CBSE Delhi 2019 C)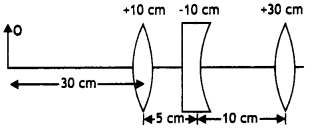

Answer:
(a) (i) Light travels from a denser medium to a rarer medium.
(ii) Angle of Incidence in the denser medium is more than the critical angle for a given pair of media.
For the grazing incidence n sin i_C = l sin 90°
n = \(\frac{1}{\sin i_{c}}\)

(b) For convex lens f = + 10 cm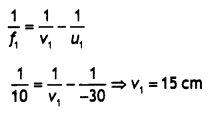

Object distance for concave lens u₂ = 15 – 5 = 10 cm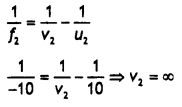

For third lens
\(\frac{1}{f_{3}}=\frac{1}{v_{3}}-\frac{1}{\infty}\) ⇒ v₃ = 30 cm

Question 7.
A ray of light incident on an equilateral glass prism (μ_g = \(\sqrt{3}\)) moves parallel to the baseline of the prism inside it. Find the angle of Incidence for this ray. (CBSE Delhi 2012)
Answer:
Given A = 60°, μ_g = \(\sqrt{3}\), i = ?

Using the expression μ = \(\frac{\sin i}{\sin A / 2}\)
or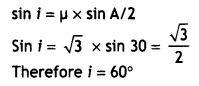

Question 8.
Two monochromatic rays of light are incident normally on the face AB of an isosceles right-angled prism ABC. The refractive indices of the glass prism for the two rays ‘1’ and ‘2’ are respectively 1.35 and 1.45. Trace the path of these rays after entering through the prism. (CBSE AI 2014)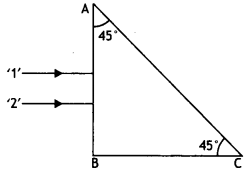

Answer:
The critical angle for the two rays is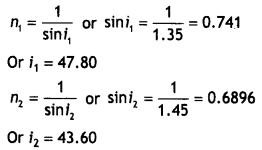

This shows that the angle of Incidence for ray ‘2’ Is greater than the critical angle. Hence it suffers total internal reflection, white ray ‘1’ does not. Hence the path of rays is as shown.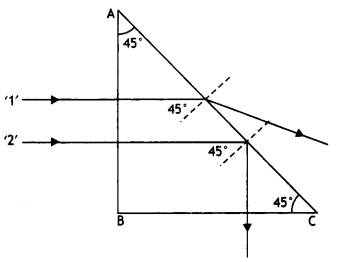

Question 9.
A convex lens of focal length 20 cm is placed coaxially with a convex mirror of radius of curvature 20 cm. The two are kept at 15 cm from each other. A point object lies 60 cm in front of the convex lens. Draw a ray diagram to show the formation of the image by the combination. Determine the nature and position of the image formed. (CBSE AI 2014)
Answer:
The ray diagram is as shown.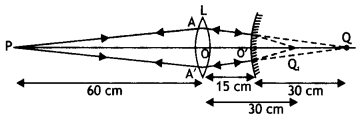

For the convex lens, we have
u₁ = – 60 cm, f = + 20 cm, v = ?

Using lens formula we have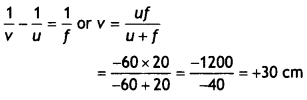

Had there been only the Lens, the image would have been formed at Q₁, which acts as a virtual object for the convex mirror.
Therefore u₂ = OQ₁ – OO’ = 30 – 15 = 15 cm

Using mirror formuLa we have
\(\frac{1}{v_{2}}+\frac{1}{u_{2}}=\frac{2}{R}\)
or
\(\frac{1}{v_{2}}+\frac{1}{u_{15}}=\frac{2}{20}\)

Solving for v₂ we have
v₂ = 30cm

Hence the final image is formed at (Point Q) a distance of 30 cm behind the mirror.

Question 10.
A ray PQ is an incident normally on the face AB of a triangular prism refracting angle of 60°, made of a transparent material of refractive index 2 / \(\sqrt{3}\), as shown in the figure. Trace the path of the ray as it passes through the prism. Also, calculate the angle of emergence and angle deviation. (CBSE Delhi 2014C)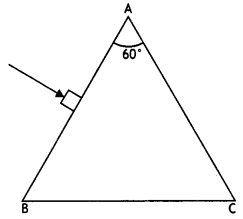

Answer:
Critical angle for glass
µ = \(\frac{1}{\sin i_{c}}\)
or
sin i_c = \(\frac{1}{\mu}=\frac{\sqrt{3}}{2}\)= 0.866
or
i_c = 60°

Now the ray is incident at an angle of 60° which is equal to the critical angle, therefore the ray graces the other edge of the prism

Therefore the angle of emergence is = 90°
Hence δ = 30°

This is as shown.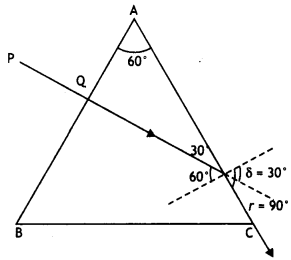

Question 11.
An object Is placed 15 cm In front of a convex lens of focal length 10 cm. Find the nature and position of the image formed. Where should a concave mirror of radius of curvature 20 cm be placed so that the final image is formed at the position of the object itself? (CBSE AI 2015)
Answer:
Given u = -15 cm, f = + 10 cm, v = ?
For lens we have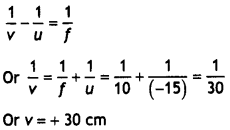

Nature of image-real, magnified Final image formed will be at the object itself only if the image formed by the lens is at the position of the centre of curvature of the mirror
∴ Distance of mirror from lens, D = 30 + R = 30 + 20 cm = 50 cm

Question 12.
Define the critical angle for a pair of media. A point source of monochromatic light ‘S’ is kept at the centre of the bottom of a cylinder with the radius of 15 cm. The cylinder contains water (refractive index 4/3) to a height of 7.0 cm. Draw the ray diagram and calculate the area of the water surface through which the light emerges in the air. (CBSE Delhi 2015C)
Answer:
It the angle of incidence in the denser medium for which the angle of refraction in the rare medium is 90°.
Given h = 7 cm, A = πr² = ?, μ = 4/3 = 1.33

Due to total internal reflection light from the bulb will not come out of the entire surface of the water as shown.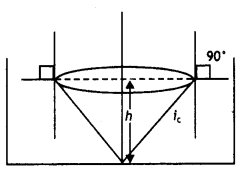

The angle of the cone through which tight will spread out is twice the critical angle.

Therefore the radius of the circular patch will be
Using the relation r= \(\frac{h}{\sqrt{\mu^{2}-1}}\) we have
r = \(\frac{7}{\sqrt{(1.33)^{2}-1}}\) = 7.98 cm

Therefore area of the surface of water through which light comes out
A = πr² = 3.14 × (7.98)² = 199.95 cm²

Question 13.
A ray PQ incident on the refracting face BA Is refracted in the prism BAC as shown In the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60° and refractive Index of the material of prism is \(\sqrt{3}\), calculate angle θ. (CBSE AI 2016)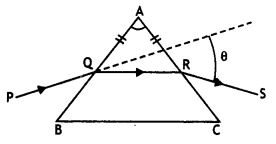

Answer:
Here As AQ = AR, therefore QR is parallel to BC, hence prism is in minimum deviation position
A = 60°, θ = δ_m = ?, n = \(\sqrt{3}\)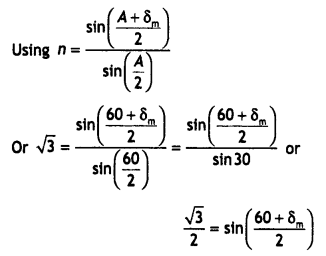

Solving θ = 60°

Question 14.
(i) A ray of light incident on face AB of an equilateral glass prism shows a minimum deviation of 30°. Calculate the speed of light through the prism.

(ii) Find the angle of incidence at face AB so that the emergent ray grazes along with the face AC. (CBSE Delhi 2017)
Answer:
(i) Given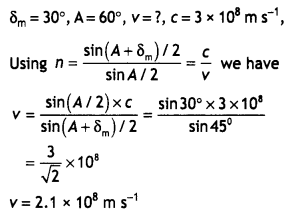


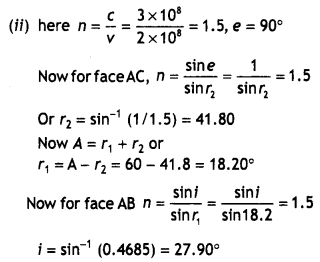
Question 15.
A small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index p up to a height h. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut off light from the bulb. (CBSE Sample Paper 2018-19)
Answer:
Let d be the diameter of the disc. The bulb shall be invisible if the incident rays from the bulb at 0 to the surface at d/2 are at the critical angle.
Let l be the angle of incidence
Then sin i = \(\frac{1}{μ}\) = tan i.
Now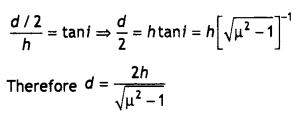

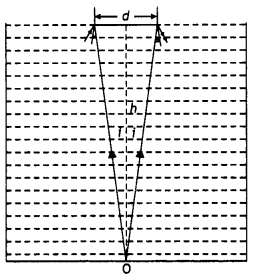
Question 16.
A ray of light is incident on a glass prism of refractive index μ and refracting angle A. If it just suffers total internal reflection at the other face, obtain an expression relating to the angle of incidence, angle of prism and critical angle.
Answer:
For a ray to just suffer total internal reflection at the second face of the prism r₂ = i_c
Now A = r₁ + i_c, therefore r₁ = A – i_c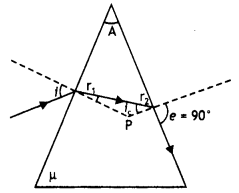

Now by Snells Law, we have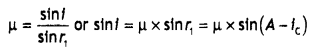

or
μ = \(\frac{\sin i}{\sin \left(A-1_{c}\right)}=\frac{1}{\sin i_{c}}\)

Question 17.
(a) Define, the refractive index of a medium.
(b) In the following ray diagram, calculate the speed of light In the liquid of unknown refractive index. (CBSE AI 2017C)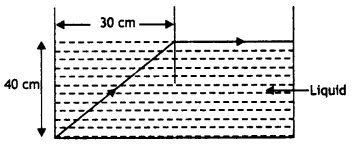

Answer:
(a) It is defined as the ratio of the speed of light in a vacuum to the speed of light in the given medium.
(b) The speed of Light can be found by using the formula
\(\frac{v}{c}=\frac{\sin 1}{\sin r}\)
or
v = \(\frac{\sin i}{\sin r}\) × c

From the diagram, we find that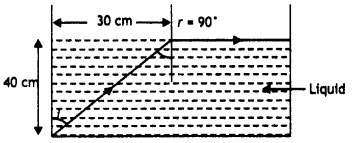

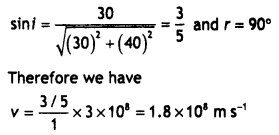
Question 18.
A concave lens made of material of refractive index n₁ is kept In a medium of refractive index n2. A parallel beam of light is incident on the lens. Complete the path of the rays of light emerging from the concave lens If (i) n₁ > n₂ (ii) n₁ < n₂ and (iii) n₁ n₂
Answer:
The path of rays in the three cases is as shown.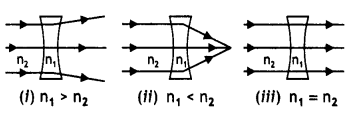

Question 19.
A convex ten made of a material of refractive index n₁ is kept in a medium of refractive index n₂. A parallel beam of light is incident on the lens. Complete the path of rays of light emerging from the convex lens if (i) n₁ > n₂, (ii) n₁ = n₂, and (iii) n₁ < n₂.
Answer:
The path of the rays in the three cases is as shown.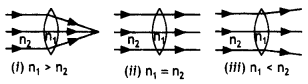

Question 20.
Write the Lens Maker’s formula and use it to obtain the range of values of μ (the refractive index of the material of the lens) for which the focal length of an equi-convex lens, kept in air, would have a greater magnitude than that of the radius of curvature of its two surface. (CBSE Delhi 2016C)
Answer:
Lens maker’s formula is given by
\(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)

For equiconvex Lens we have R₁ = + R and
R₂ = – R
Therefore we have
\(\frac{1}{f}\) = (n – 1)\(\frac{2}{R}\)

For f to be greater than R
2(n – 1) < 1
2n – 2 < 1
2n < 3
n < 1.5
Hence range is 1.0< n < 1.5

Question 21.
A ray of light passing from the air through an equilateral glass prism undergoes minimum deviation when the angle of Incidence is 3/4th of the angle of the prism. Calculate the sp..d of light In the prism. (CBSE AI 2017)
Answer:
Given A = 60°, i = 3/4 × 60 = 45°,
c = 3 × 10⁸ m s^-1,

Now δ_m = 2i – A
= 90 – 60 = 30°

Using the formula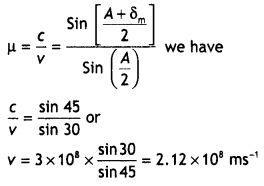

Question 22.
Calculate the value of the angle of Incidence when a ray of light incident on one face of an equilateral glass prism produces the emergent ray, which just grazes along the adjacent face. Refractive index of the prism is \(\sqrt{2}\). (CBSE 2017C)
Answer:
The diagram is as shown.


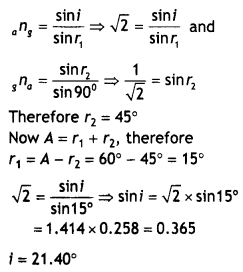
Question 23.
How is the working of a telescope different from that of a microscope?
The focal lengths of the objective and eyepiece of a microscope are 1.25 cm and 5 cm respectively. Find the position of the object relative to the objective in order to obtain an angular magnification of 30 in normal adjustment. (CBSE Delhi 2012)
Answer:
A microscope increases the size of the object whereas a telescope brings the object closer for better vision.
Given f_o = 1.25 cm, f_e = 5 cm, M = 30 cm, u = l
In normal adjustment final image is formed at infinity, therefore we have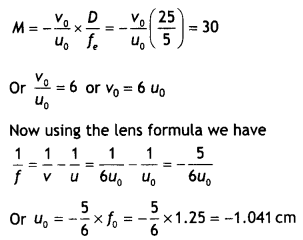

Question 24.
(a) Draw a labelled ray diagram showing the image formation of a distant object by a refracting telescope. Deduce the expression for its magnifying power when the final image is formed at infinity.
(b) The sum of focal lengths of the two lenses of a refracting telescope is 105 cm. The focal length of one lens is 20 times that of the other. Determine the total magnification of the telescope when the final image is formed at infinity. (CBSE AI 2014C)
Answer:
(a) For the diagram

From right triangles ABC and ABC’ as shown in figure, we have
tan α = \(\frac{\mathrm{AB}}{\mathrm{CB}}=\frac{-h}{f_{0}}\) and
tan β = \(\frac{\mathrm{AB}}{\mathrm{C}^{\prime} \mathrm{A}}=\frac{-h}{f_{\mathrm{e}}}\)

From the above we have we have
M = \(\frac{\beta}{\alpha}=\frac{-h}{f_{e}} \times \frac{f_{0}}{-h}=\frac{f_{0}}{f_{e}}\)

(b) L = 105 cm, f_o = 20f_e,

Now L = f_o + f_e = 21f_e
Or
fe = 105/21 = 5 cm
Hence f_o = 20 × f_e 20 × 5 = 100 cm
Hence M = f_o/f_e = 100/ 5 = 20

Question 25.
(a) Explain with reason, how the power of a diverging lens changes when
(i) it is kept in a medium of refractive index greater than that of the lens.
(ii) Incident red light is replaced by violet light.
(b) Three lenses L₁, L₂, and L₃ each of focal length 30 cm are placed coaxially as shown in the figure. An object is held at 60 cm from the optic centre of L₁. The final image is formed at the focus of L₃. Calculate the separation between (i) L₁ and L₂ and (ii) L₂ and L₃ (CBSE AI 2017C)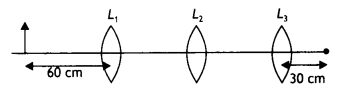

Answer:
(a) (i) The power of is given by the expression P = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) medium changes the power of the lens decreases as its focal length increases.
(ii) We know that f ∝ X, therefore a decrease in the wavelength from red to violet decreases the focal length and increases the power of the lens.

(b) Given f₁ = f₂ = f₃ = 30 cm
For lens L1, u₁ = 60 cm = 2f₁, therefore the image will be formed at If on the other side of the lens L₁.

Since the final image for lens L₃ is formed at the focus, therefore the rays of light falling on lens L₃ should come from infinity. This is possible if the image of L₁ lies at the focus of L₂.

Thus distance L₁L₂ = 60 + 30 = 90 cm

Also, distance L₂L₃ can have any value as the rays between L₂ and L₃ will be parallel.

Question 26.
Calculate the radius of curvature of an equi-concave lens of refractive Index 1.5, when It Is kept In a medium of refractive index 1.4, to have a power of -5 D?
OR
An equilateral glass prism has a refractive Index of 1.6 In the air. Calculate the angle of minimum deviation of the prism, when kept In a medium of refractive Index \(\frac{4 \sqrt{2}}{5}\). (CBSE Delhi 2019)
Answer:
Given n_L = 1.5, n_M = 1.4, P = -5 D
Focal length f \(\frac{1}{P}=\frac{1}{-5}=\frac{-100}{5}\) = 20 cm

Using the lens makers formula and putting
R₁ = – R and
R₂ = +R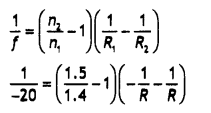

Solving for R, we get
R = 20/7 = 2.86cm
or
Given A = 60, n = 1.6, δm =?,n_M = \(\frac{4 \sqrt{2}}{5}\)

Using the prism formula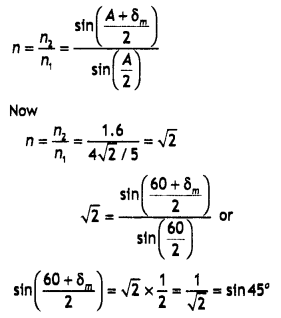

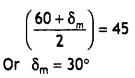
Question 27.
A ray of light passes through an equilateral glass prism, such that the angle of Incidence Is equal to the angle of emergence. If the angle of emergence is v times the angle of the prism, calculate the refractive index of the glass prism.
Answer:
Given the angle of prism A = 60°,
the angle of incidence i = angle of emergence ‘e’ and under this condition angle of deviation is minimum.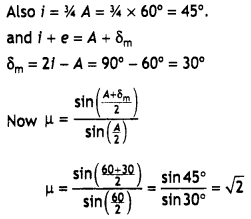

Question 28.
The magnifying power of an astronomical telescope In the normal adjustment position is 100. The distance between the objective and the eyepiece is 101 cm. Calculate the focal length of the objective and the eyepiece.
Answer: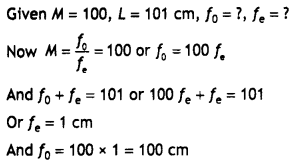

Question 29.
A double convex lens made of glass of refractive Index 1.5 has both radii of curvature of magnItude 20 cm. An object 2 cm high is placed at 10 cm from the lens. Find the position, nature and size of the image.
Answer:
Given n = 1.5 and for a double convex Lens R₁ = + 20 cm and R₂ = – 20 cm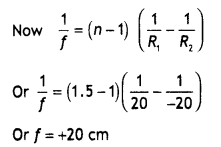

Now size of the object O = + 2 cm and u = – 1o cm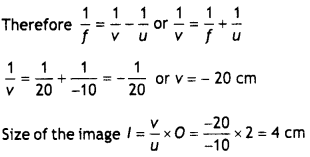

The image ¡s virtual and erect.

Question 30.
Three rays of light-red (R), green (G) and blue (B) are Incident on the face AB of a right-angled prism ABC. The refractive indices of the material of the prism for red, green and blue wavelengths are 1.39, 1.44 and 1.47, respectively. Trace the path of the rays through the prism. How will the situation change if these rays were incident normally on one of the faces of an equilateral prism?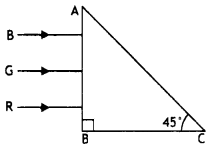

Answer:
The course of rays through the prism is as shown below.
Critical angle for a light ray is given by
sin i_c = \(\frac{1}{n}\)
or
i_c = sin^-1\(\left(\frac{1}{n}\right)\)

Now critical angle for red ray (R)
i_R = sin^-1\(\left(\frac{1}{n}\right)\) = sin-1\(\left(\frac{1}{1.39}\right)\) = 46°

Critical angle for green ray (G)
i_G = sin^-1\(\left(\frac{1}{n}\right)\) = sin-1\(\left(\frac{1}{1.44}\right)\) = 44°

and Cnticat angLe for bLue ray (B)
i_B = sin^-1\(\left(\frac{1}{n}\right)\) = sin-1\(\left(\frac{1}{1.47}\right)\) = 42°52′

Thus the angle of incidence for blue and green rays inside the prism will be greater than the critical angle for these two colours. Therefore blue and green rays undergo total internal reflection. The angle of incidence for red colour is smaller than its critical angle; therefore it does not undergo total internal reflection. This is depicted in the figure below.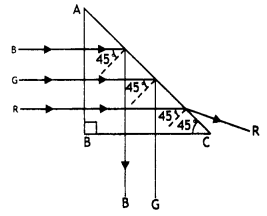

For an equilateral prism, the light rays pass through the prism suffering deviation. The angle of deviation δ = (n – 1) A. Hence, the deviation for red coloured ray will be the least and that for blue ray maximum. Paths of rays are shown in the figure below.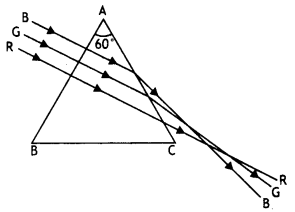

Question 31.
You are given three lenses of powers 0.5 D, 4 D, 10 D. State, with reason, which two lenses will you select for constructing a good astronomical telescope.
Calculate the resolving power of this telescope, assuming the diameter of the objective lens to be 6 cm and the wavelength of light used to be 540 nm.
Answer:
The focal lengths of the three lenses are
f₁ = 1 /P₁ = 1 / 0.5 = 2 m = 200 cm,
f₂ = 1 /P₂ = 1 / 4 = 0.25 m = 25 cm,
f₃ = 1 /P₃ = 1 /10 = 0. 1 m = 10 cm,

For an astronomical telescope, the objective should have a large focal length and the eyepiece should have a small focal length. Therefore for the objective, we will use the lenses of power 0.5 D and for the eyepiece the lens of power 10 D.

Given D = 6 cm = 0.06 m, λ = 540 nm = 540 × 10^-9 m

Now resolving power
R.P. = \(\frac{D}{1.22 \lambda}=\frac{0.06}{1.22 \times 540 \times 10^{-9}}\) = 91074.6

Question 32.
A screen is placed 90 cm from an object. The image of the object on the screen is formed by a convex lens at two different positions separated by 20 cm. Calculate the focal length of the lens.
OR
A convex lens of focal length 20 cm and a concave lens of focal length 15 cm are kept 30 cm apart with their principal axes coincident. When an object is placed 30 cm in front of the convex lens, calculate the position of the final image formed by the combination. Would this result change if the object were placed 30 cm In front of the concave tens? Give reason. (CBSE AI 2019)
Answer:
The image of an object can be obtained at two different positions of a convex lens for a fixed value of the distance between the object and the screen if values of u and v are interchanged in these two positions. This situation is as shown below.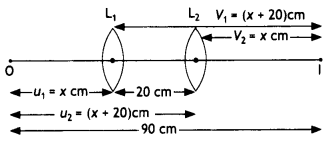

Here x + 20 + x = 90 cm or x = 35cm
Therefore, u = -35 cm, v = + 55 cm, f = ?

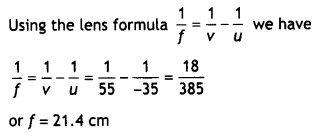
or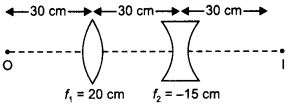

For image formed by a convex Lens
f₁ = + 20 cm, u = – 30 cm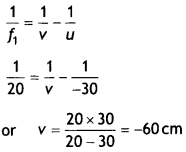

Therefore, u for concave Lens = 60 – 30 = + 30 cm and f₂ = – 15 cm

Now for concave lens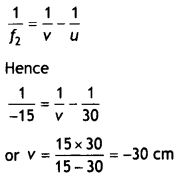

No, the result will not change as per the principle of reversibility.

Question 33.
For an equilateral glass prism, the minimum angle of deviation, for a parallel beam of monochromatic Incident light, is measured to be 30°. What is the refractive index of the glass used for making this prism?
If this prism were to be placed in a medium of refractive Index 1.414, how would a ray of light incident on one of its refracting faces pass through it? Draw the ray diagram for the same.
Answer:
Given A = 60°, δ_m = 30°, μ = ?
Using the relation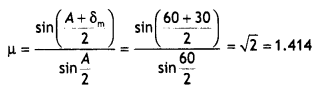

When this prism is placed in a medium of refractive index 1.414, it will behave like a plane glass piece as both the prism and the medium have the same refractive index.

The ray diagram is as shown.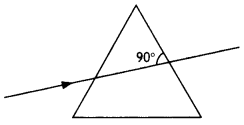

Question 34.
Find the position of the image formed by the lens shown in the figure.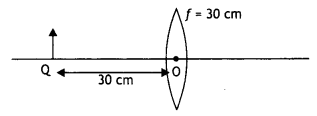

Another lens is placed in contact with this lens to shift the image further away from the lens. What is the nature of the second lens?
Answer:
f = + 10 cm, u = – 30 cm, v =?
Using the lens equation we have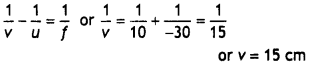

The second lens Is concave.

Question 35.
A beam of light of wavelength 400 nm is incident normally on a right-angled prism as shown. It is observed that the light just grazes along with the surface AC after falling on it. Given that the refractive index of the material of the prism varies with the wavelength as per the relation
μ = 1.2 + \(\frac{b}{\lambda^{2}}\) calculate the value of b and the refractive index of the prism material for a wavelength λ = 500 nm. [(Given θ = Sin^-1 (0.625)]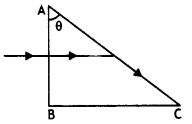

Answer:
The figure can be redrawn as shown below.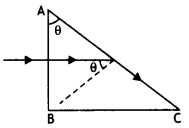

By symmetry angle, θ will be the critical angle.
Therefore
μ = \(\frac{1}{\sin \theta}=\frac{1}{0.625}\) = 1.6

Now the value of the constant b is obtained as follows:
μ_A = 1.2 + \(\frac{b}{\lambda^{2}}\)
or
1.6 = 1.2 + \(\frac{b}{(400)^{2}}\)

Solving for b we have b = 64000 nm²
Now for a wavelength λ = 500 nm the refractive index of the material of the prism is
μ = 1.2 + \(\frac{(64000)^{2}}{(500)^{2}}\) = 1.456

Question 36.
A convex lens, of focal length 20 cm, has a point object placed on its principal axis at a distance of 40 cm from It. A plane mirror Is placed 30 cm behind the convex lens. Locate the position of the image formed by this combination.
Answer:
We first consider the effect of the lens. For the Lens, we have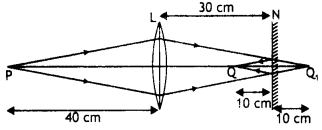

u = – 40 cm and f = + 20 cm
Using the lens formula, we get
\(\frac{1}{v}-\frac{1}{(-40)}=\frac{1}{20}\)
or
v = + 40 cm

Had there been the lens only the image would have been formed at Q₁. The plane mirror M is at a distance of 30 cm from the lens L. We can, therefore, think of a Q₁ as a virtual object, located at a distance of 10 cm, behind the plane mirror M. The plane mirror, therefore, forms a real image (of this virtual object Q₁) at Q₁, 10 cm in front of it. This is shown in the figure.

Question 37.
(i) Calculate the distance of an object of height h from a concave mirror of radius of curvature 20 cm, so as to obtain a real image of magnification 2. Find the location of the image also.
(ii) Using the mirror formula, explain why does a convex mirror always produce a virtual image. (CBSE Delhi 2016) Answer:
Given R = – 20 cm or f = – 10 cm, m = + 2 (real image), u = ?, v = ?
Using the relation m = \(\frac{f}{f-u}\) we have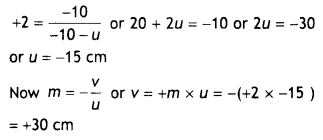

(b) For a convex mirror \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\) but f is positive and u is negative i.e., f > 0 but u < 0.
Therefore, it is self-evident from the above relation that irrespective of the value of u, the value of v is always +ve. It means that the image formed by a convex mirror is always virtual Independent of the location of the object.

Question 38.
A convex lens of focal length 20 cm and a concave mirror of focal length 10 cm are placed co-axially 50 cm apart from each other. An incident beam parallel to its principal axis is incident on the convex lens. Locate the position of the (final) image formed due to this combination.
Answer:
The incident beam, on lens L_, is parallel to its principal axis. Hence the lens forms an image Q₁ at its focal point, i.e. at a distance OQ₁ (= 20 cm) from the lens. This image, Q₁, now acts as a real object for the concave mirror. For the mirror, we then have: u = – 30 cm, and f = – 10 cm,

Hence using the mirror formula, we get
\(\frac{1}{v}+\frac{1}{(-30)}=\frac{1}{(-10)}\)
or
v = – 15 cm

The lens-mirror combination, therefore, forms a real image Q at a distance of 15 cm from M. The ray diagram is as shown in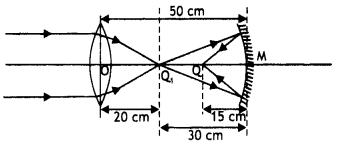

Question 39.
A convex lens of focal length 25 cm and a concave mirror of radius of curvature 20 cm are placed coaxially 40 cm apart from each other. An incident beam parallel to the principal axis is incident on the convex lens. Find the position and nature of the image formed by the combination. (CBSE Al 2016)
Answer:
The image of the object is formed at the focus of the convex lens, i.e. 25 cm. This image acts as an object for the concave mirror and ties at a distance (40 – 25) = 15 cm from the mirror.

Hence for the mirror
u = – 15 cm, v =? f = R/2 = 20/2 = 10 cm

Using mirror formula we have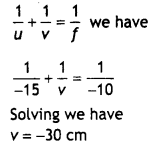

The image is formed in front of the mirror.

Question 40.
(i) A screen is placed at a distance of 100 cm from an object. The image of the object is formed on the screen by a convex lens for two different locations of the lens separated by 20 cm. Calculate the focal length of the lens used.
(ii) A converging lens is kept coaxially in contact with a diverging lens both the lenses being of equal focal length. What is the focal length of the combination? (CBSE AI 2016)
Answer:
(i) Given u + v= 100 or v= 100 – u
Using lens formula From lens first \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) we have

Or
f = 24 cm

(ii) f = infinity. \(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{-f_{2}}\) = 0

Question 41.
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on the face of the prism. By rotating the prism, the angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism? If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light. The refracting angle of the prism is 60°. (NCERT)
Answer:
Given δ_m = 40°, aμg = ?, _aμ_w = 1.33, A = 60°

Solving for δ_m we have δ_m = 100°

Question 42.
A beam of light converges to a point P. A lens is placed in the path of the convergent beams 12 cm from P. At what point does the beam converge if the lens is
(i) a convex lens of focal length 20 cm,
Answer:
(i) Here u = 12 cm, f = + 20 cm and v = ?
Using the formula \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) we have
\(\frac{1}{v}=\frac{1}{12}+\frac{1}{20}=\frac{3+5}{60}=\frac{8}{60}\)
or
v = 7.5 cm

(ii) a concave lens of focal length 16 cm? (NCERT)
Answer:
Here u = 12 cm, f = – 16 cm and v =?
Using the formula \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)we have
\(\frac{1}{v}=\frac{1}{12}+\frac{1}{-16}=\frac{-3+4}{48}=\frac{1}{48}\)
or
v = 48 cm

Question 43.
A compound microscope consists of an objective lens of focal length 2.0 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15 cm. How far from the objective should an object be placed in order to obtain the final image at (i) the least distance of distinct vision (25 cm), (ii) infinity? What is the magnifying power of the microscope in each case? (NCERT)
Answer:
Given f0 = 2.0 cm, fe = 6.25 cm, L = 15 cm, u0 = ?,

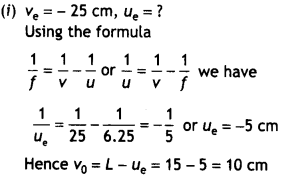
Now applying Lens formula for objective Lens we have \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u} \text { or } \frac{1}{u_{0}}=\frac{1}{v_{0}}-\frac{1}{f_{0}}\)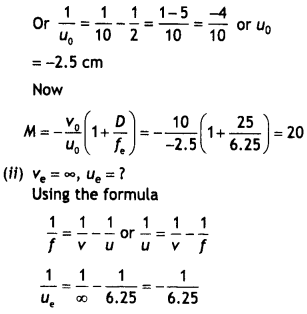

Question 44.
A small telescope has an objective lens of a focal length of 144 cm and an eyepiece of a focal length of 6.0 cm. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece? (NCERT)
Answer:
Given f_o = 144 cm, f_e = 6.0 cm, M = ?,
L = f_o + f_e = ?

Using the formula M = \(\frac{f_{0}}{f_{e}}=\frac{144}{6}\) = 24 and
L = f_o + f_e = 144 + 6 = 150 cm

Question 45.
(a) A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece of focal length 1.0 cm is used, what is the angular magnification of the telescope?
(b) If this telescope Is used to view the moon, what is the diameter of the Image of the moon formed by the objective lens? The diameter of the moon is 3.48 × 10⁶ m, and the radius of lunar orbit Is 3.8 × 10⁸ m. (NCERT)
Answer:
Given f_o = 15 m, f_e = 1.0 cm = 0.01 m, M = ?
D_m = 3.48 × 10⁶ m, r = 3.8 × 10⁸m,
(a) Using M = \(\frac{f_{0}}{f_{e}}=\frac{15}{0.01}\) = 1500
(b) AngLe subtended by moon at the objective of the teLescope
α = \(\frac{D_{m}}{r}=\frac{3.48 \times 10^{6}}{3.8 \times 10^{8}}\)

Therefore angLe subtended by the image
β = M × α = 1500 × \(\frac{3.48 \times 10^{6}}{3.8 \times 10^{8}}\)

If I be the Linear size of the image then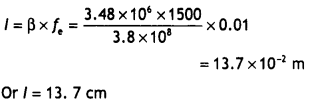

Question 46.
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524. (NCERT)
Answer:
Given A = 60°, i = ?, μ = 1.524
For a ray to just suffer total internal reflection at the second face of the prism r₂ = i_c
Now sin ic = \(\frac{1}{\mu}=\frac{1}{1.524}\) = 0.6562
or
i_c = 41°

Now A = r₁ + r₂, therefore r₁ = A – r2
r₁ = 60 – 41 = 19°

Now by Snell’s law we have
μ = \(\frac{\sin i}{\sin r_{1}}\)
or
sin i = μ × sinr₁ = 1.524 × sin 19°
or
i = 29.75° = 30°

Question 47.
A small telescope has an objective lens of a focal length of 140 cm and an eyepiece of a focal length of 5.0 cm. What is the magnifying power of the telescope for viewing distant objects when
(a) the telescope is in normal adjustment (i.e. when the final image is at infinity.
Answer:
Given f_o = 140 cm, f_e = 5.0 cm, M = ?
For normal adjustment we have
M = \(\frac{f_{0}}{f_{e}}=\frac{140}{5}\) = 28

(b) the final image is formed at the least distance of distinct vision (25 cm) (NCERT)
Answer:
When the final image is formed at the least distance of distinct vision we have
M = \(\frac{f_{0}}{f_{e}}\left(1+\frac{f_{e}}{D}\right)=\frac{140}{5}\left(1+\frac{5}{25}\right)\) = 33.6

Question 48.
(a) The refractive index of glass is 1.5. What is the speed of light In a glass? (Speed of light in a vacuum is 3.0 × 10⁸ ms^-11 )
(b) Is the speed of light in glass independent of the colour of light? If not, which of the two colours red and violet travels slower in a glass prism?
Answer:
(a) Given μ = 1.5, c = 3.0 × 10⁸ m s^-1
v = \(\frac{c}{\mu}=\frac{3 \times 10^{8}}{1.5}\) = 2.0 × 10⁸ ms^-1

(b) No. The refractive index, and hence the speed of light in a medium, depends on wavelength. When no particular wavelength or colour of light is specified, we may take the given refractive index to refer to yellow colour or mean light. Now we know violet colour deviates more than red in a glass prism, i.e. μ_v > μ_R. Therefore, the violet component of white light travels slower than the red component.

Question 49.
Three immiscible liquids of densities d₁ > d₂ > d₃ and refractive indices μ₁ > μ₂ > μ₃ are put in a beaker. The height of each liquid column is d₃. A dot is made at the bottom of the beaker. For near-normal vision, find the apparent depth of the dot. (NCERT Exemplar)
Answer:
The situation is as shown.

Let the apparent depth be O₁ for the object as seen from μ2, then
Apparent depth = real depth/μ
O₁ = \(\frac{h / 3}{\mu_{1} / \mu_{2}}=\frac{\mu_{2} h}{3 \mu_{1}}\)

If seen from O₃ the apparent depth O₂ is
Apparent depth = real depth/μ
O₂ = \(\frac{\left(h / 3+O_{1}\right)}{\mu_{2} / \mu_{3}}=\frac{\mu_{3}}{\mu_{2}}\left(\frac{h}{3}+\frac{\mu_{2}}{\mu_{1}} \frac{h}{3}\right)\)

Seen from outside the apparent height is
Apparent depth = real depth/μ

Question 50.
For a glass prism (μ = \(\sqrt{3}\)) the angle of minimum deviation Is equal to the angle of the prism. Find the angle of the prism. (NCERT Exemplar)
Answer: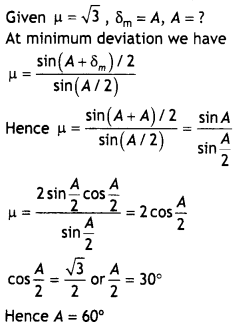

Question 51.
In many experimental set-ups, the source and screen are fixed at a distance say D and the lens Is movable. Show that there are two positions for the lens for which an image Is formed on the screen. Find the distance between these points and the ratio of the Image sizes for these two points. (NCERT Exemplar)
Answer:
The situation is shown.

If there was no cut then the object would have been at a height of 0.5 cm from the principal axis OO’. Consider the image for this case by lens formuLa we have
\(\frac{1}{v}=\frac{1}{u}+\frac{1}{f}=\frac{1}{-50}+\frac{1}{25}=\frac{1}{50}\)
Or
v = 50 cm
Hence magnification of the image is.
m = \(\frac{v}{u}=\frac{-50}{50}\) = -1

Thus the image would have been formed at 50 cm from the pole and 0.5 cm below the principal axis. Hence with respect to the X-axis passing through the edge of the cut lens, the co-ordinates of the image are (50 cm, -1 cm)