Moving Charges And Magnetism

Class 12 Physics Chapter 4 Important Questions Moving Charges and Magnetism

Very Short Answer

Question 1.
What is the direction of the force acting on a charged particle q, moving with a velocity \(\overrightarrow{\mathbf{v}}\) in a uniform magnetic field B? (Delhi)
Answer:
The direction of the force acting on a charged particle q, moving with a velocity \(\overrightarrow{\mathbf{v}}\) in a uniform
magnetic field \(\overrightarrow{\mathbf{B}}\) is perpendicular to the plane of vectors \(\overrightarrow{\mathbf{v}}\) and \(\overrightarrow{\mathbf{B}}\)

So, force is perpendicular to both \(\overrightarrow{\mathbf{v}}\) and \(\overrightarrow{\mathbf{B}}\). From equation (i), we can also say that the force \(\overrightarrow{\mathbf{F}}\) acts in the direction of the vectors \(\overrightarrow{\mathbf{v}}\) and \(\overrightarrow{\mathbf{B}}\)

Question 2.
Why should the spring/suspension wire in a moving coil galvanometer have low torsional constant? (All India 2008)
Answer:
Low torsional constant is basically required to increase the current/charge sensitivity in a moving coil ballistic galvanometer.

Question 3.
Magnetic field lines can be entirely confined within the core of a toroid, but not within a straight solenoid. Why? (Delhi 2008)
Answer:
At the edges of the solenoid, the field lines get diverged due to other fields and/or non-availability of dipole loops, while in toroids the dipoles (in loops) orient continuously.

Question 4.
An electron does not suffer any deflection while passing through a region of uniform magnetic field. What is the direction of the magnetic field? (All India 2009)
Answer:

∴Magnetic field will be in the line of the velocity of electron.

Question 5.
A beam of a particles projected along +x-axis, experiences a force due to a magnetic field along the +y-axis. What is the direction of the magnetic field? (All India 2009)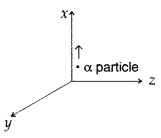

Answer:

Direction of the magnetic field is towards negative direction of z-axis.

Question 6.
A beam of electrons projected along +x-axis, experiences a force due to a magnetic field along the +y/-axis. What is the direction of the magnetic field? (All India 2010)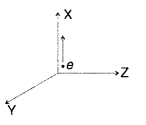

Answer:
Direction of the magnetic field is F = q (v × B) towards positive direction of z-axis.

Question 7.
A beam of protons, projected along + x-axis, experiences a force due to a magnetic field along the – y-axis. What is the direction of the magnetic field? (All India 2010)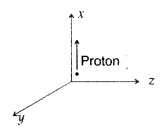

Answer:
The direction of the magnetic field is towards positive direction of z-axis.

Question 8.
Depict the trajectory of a charged particle moving with velocity v as it enters a uniform magnetic field perpendicular to the direction of its motion. (Comptt. All India 2012)
Answer: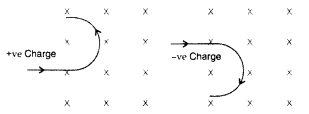

The force acting on the charge particle will be perpendicular to both v and S and therefore will describe a circular path.

Question 9.
Write the expression in vector form, for the magnetic force \(\overrightarrow{\mathrm{F}}\) acting on a charged particle moving with velocity \(\overrightarrow{\mathrm{V}}\) in the presence of a magnetic field B. (Comptt. All India 2012)
Answer: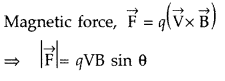

Question 10.
An ammeter of resistance 0.6 Ω can measure current upto 1.0 A. Calculate
(i) The shunt resistance required to enable the ammeter to measure current upto 5.0 A
(ii) The combined resistance of the ammeter and the shunt. (Delhi 2013)
Answer: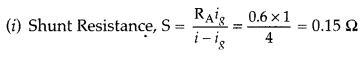

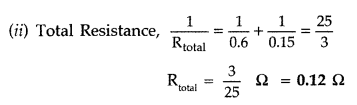
Question 11.
Write the expression, in a vector form, for the Lorentz magnetic force \(\overrightarrow{\mathrm{F}}\) due to a charge moving with velocity \(\overrightarrow{\mathrm{V}}\) in a magnetic field \(\overrightarrow{\mathrm{B}}\). What is the direction of the magnetic force? (Delhi 2013)
Answer:

… [q is the magnitude of the moving charges)
This force is normal to both the directions of velocity \(\overrightarrow{\mathrm{V}}\) and magnetic field \(\overrightarrow{\mathrm{B}}\) .

Question 12.
Using the concept of force between two infinitely long parallel current carrying conductors, define one ampere of current. (All India 2013)
Answer:

“One ampere of current is the value of steady current, which when maintained in each of the two very long, straight, parallel conductors of negligible cross-section; and placed one metre apart in vacuum, would produce on each of these conductors a force of equal to 2 × 10^-7 newtons per metre (Nm^-1) of length. ”

Question 13.
Write the condition under which an electron will move undeflected in the presence of crossed electric and magnetic fields.(Comptt. All India 2013)
Answer:

and electric and magnetic fields are mutually perpendicular.

Question 14.
Why do the electrostatic field lines not form closed loops? (All India 2015)
Answer:
Electric field lines do not form closed loops because the direction of an electric field is from positive to negative charge. So one can regard a line of force starting from a positive charge and ending on a negative charge. This indicates that electric field lines do not form closed loops.

Question 15.
A particle of mass ‘m’ and charge ‘q’ moving with velocity V enters the region of uniform magnetic field at right angle to the direction of its motion. How does its kinetic energy get affected? (Comptt. Delhi 2015)
Answer:
Kinetic energy will NOT be affected.
*(When \(\vec{v}\) is perpendicular to \(\vec{B}\), then magnetic field provides necessary centripetal force)

Question 16.
Write the underlying principle of a moving coil galvanometer. (Delhi 2015)
Answer:
Principle of a galvanometer : “A current carrying coil, in the presence of magnetic field, experiences a torque which produces proportionate deflection”.

Question 17.
A coil, of area A, carrying a steady current I, has a magnetic moment, \(\vec{m}\), associated with it. Write the relation between \(\vec{m}\), I and A in vector form. (Comptt Delhi 2015)
Answer:
Relation for magnetic moment = \(\vec{m}\) = I\(\vec{A}\)

Question 18.
Under what condition is the force acting on a charge moving through a uniform magnetic field minimum?
Answer:
When the charge moves parallel to the direction of the magnetic field.

Question 19.
What Is the nature of the magnetic field in a moving coil galvanometer?
Answer:
Radial magnetic field.

Question 20.
State two properties of the material of the wire used for suspension of the coil in a moving coil galvanometer.
Answer:

1. High tensile strength.
2. SmalL vaLue of torque per unit twist.

Question 21.
Write one condition under which an electric charge does not experience a force in a magnetic field.
Answer:
When it moves parallel to the direction of the magnetic field.

Question 22.
Mention the two characteristic properties of the material suitable for making the core of a transformer. (CBSE AI 2012)
Answer:

1. Low retentivity
2. High permeability

Question 23.
Write the expression, in a vector form, for the Lorentz magnetic force due to a charge moving with velocity \(\vec{V}\) in a magnetic field \(\vec{B}\). What is the direction of the magnetic force? (CBSE Delhi 2014)
Answer:
The expresion is \(\vec{F}\) = q(\(\vec{V}\) × \(\vec{B}\)). The force is perpendicular to both the velcoity and the magentic field vector.

Question 24.
Write the condition under which an electron will move undeflected in the presence of crossed electric and magnetic fields. (CBSE Al 2014C)
Answer:
An electron moves perpendicular to both fields.

Question 25.
What can be the cause of the helical motion of a charged particle?
Answer:
The charge enters the magnetic field at any angle except 0°, 180°, and 90°.

Question 26.
Write the underlying principle of a moving coil galvanometer.
Answer:
A current-carrying loop placed in a magnetic field experiences a torque.

Question 27.
A proton and an electron traveling along parallel paths enter a region of the uniform magnetic field, acting perpendicular to their paths. Which of them will move in a circular path with a higher frequency? (CBSEAI and Delhi 2018)
Answer:
The frequency of revolution is given by
v = \(\frac{B q}{2 \pi m}\) ⇒ v ∝ \(\frac{1}{m}\) .

As for m_e < m_p
therefore v_e >v_p

Question 28.
Two protons of equal kinetic energies enter a region of the uniform magnetic field. The first proton enters normal to the field direction while the second enters at 30° to the field direction. Name the trajectories followed by them. (CBSEAI and Delhi 2018C)
Answer:
Normal: circular
At an angle of 30°, it will follow a helical path.

Question 29.
Consider the circuit shown here where APB and AQB are semi-circles. What will be the magnetic field at the center C of the circular loop?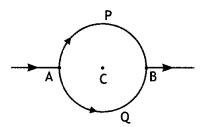

Answer:
Zero, because magnetic fields due to APB and AQB are equal in magnitudes but opposite in directions.

Question 30.
Which one of the following will have a minimum frequency of revolution,
when projected with the same velocity v perpendicular to the magnetic field B: (i) α – particle and (ii) β – particle.
Answer:
Frequency of revolution v = \(\frac{q B}{2 \pi m}\) and \(\frac{q}{m}\) of α – particle is less, hence α – particle will have minimum frequency of revolution.

Question 31.
An ammeter and a milli-ammeter are converted from the same galvanometer. Out of the two, which current-measuring instrument has higher resistance?
Answer:
A milli-ammeter has higher resistance.

Question 32.
Equal currents I and I are flowing through two infinitely long parallel wires. What will be the magnetic field at a point mid-way when the currents are flowing in the same direction?
Answer:
Zero, because fields due to two wires will be equal but opposite.

Question 33.
The figure shows a circular loop carrying current l. Show the direction of the magnetic field with the help of lines of

Answer:
The magnetic field lines are as shown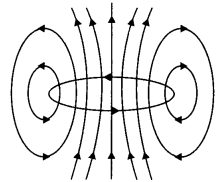

Question 34.
An electron is moving with velocity v along the axis of a long straight solenoid carrying current I. What will be the force acting on the electron due to the magnetic field of the solenoid?
Answer:
Zero, as a force on a charged particle moving in a magnetic field, is F= Bqv sin θ
Here both v and B are along the axis of – solenoid, so θ = 0° between them. Hence F= qvB sin θ = 0.

Short Answer Type

Question 1.
Using Ampere’s circuital law, obtain an expression for the magnetic field along the axis of a current carrying solenoid of length l and having N number of turns.
Answer:
Magnetic field due to Solenoid Let length of solenoid = L
Total number of turns in solenoid = N
No. of turns per unit length = \(\frac{N}{L}\) = n
ABCD is an Ampere’s loop
AB, DC are very large
BC is in a region of \(\overrightarrow{\mathrm{B}}\) = 0
AD is a long axis
Length of AD = x
Current in one turn = I₀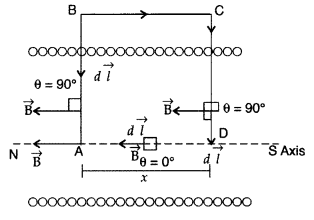

Applying Ampere’s circuital loop — | B .dl = go I ’

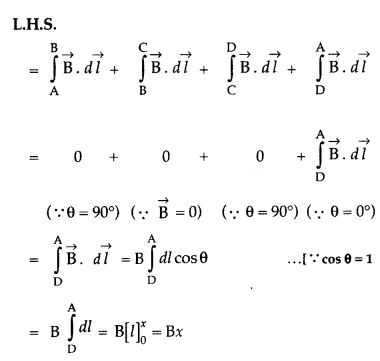
No. of turns in x length = nx,
Current in turns nx, I = nx I₀
According to Ampere’s circuital law
Bx = µ₀ I => Bx = µ₀ nx I₀
∴ B = µ₀nI₀

Question 2.
A charge ‘q’ moving B along the X-axis with a velocity v is subjected to a uniform magnetic field B acting along the Z-axis as it crosses the origin O. (Delhi 2009)
(i) Trace its trajectory.
(ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify your answer.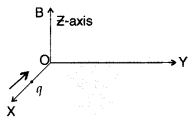

Answer: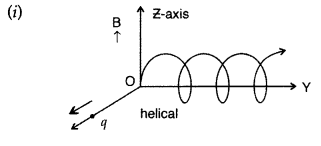

(ii) K.E does not change irrespective of the direction of the charge as

Question 3.
State Biot-Savart law.
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element \(\overrightarrow{d \vec{l}}\) at point P situated at a distance \(\vec{r}\) from the element as shown in the figure.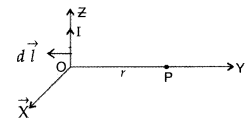

Answer:
Biot-Savart law and its applications :
Biot-Savart law states that “the magnitude of the magnetic field dB at any point due to a small current element dl is given by

Question 4.
(a) In what respect is a toroid different from a solenoid? Draw and compare the pattern of the magnetic field lines in the two cases.
(b) How is the magnetic field inside a given’ solenoid made strong? (All India 2011)
Answer:
(a) Solenoid consists of a long wire wound in the form of a helix where the neighbouring turns are closely spaced, whereas, the toroid is a hollow circular ring on which a large number of turns of a wire is closely wound.
(b) Magnetic field inside a given solenoid is made strong by putting a soft iron core inside it. It is strengthened by increasing the amount of current through it.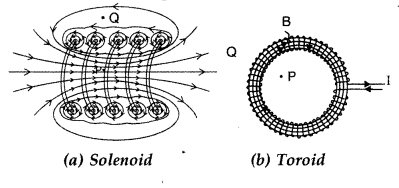

Question 5.
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity \(\vec{v}\) in a magnetic field \(\vec{B}\). Show that no work is done by this force on the charged particle. (All India 2011)
Answer:
Expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity \(\vec{v}\) in a magnetic field \(\vec{B}\) is \(\vec{F}\) = q(\(\vec{E}\) + \(\vec{v}\) × \(\vec{B}\))
Work done by a magnetic force on a charged particle :
The magnetic force \(\overrightarrow{\mathrm{F}}=q(\overrightarrow{\mathrm{E}}+\vec{v} \times \overrightarrow{\mathrm{B}})\) always acts perpendicular to the velocity \(\vec{v}\) on the direction of motion of charge q.

Question 6.
A steady current (I₁) flows through a long straight wire. Another wire carrying steady current (I₂) in the same direction is kept close and parallel to the first wire. Show with the help of a diagram how the magnetic field due to the current I₁ exerts a magnetic force on the second wire. Write the expression for this force. (All India 2011)
Answer:
Consider two infinitely long parallel conductors carrying current I₁ and I₂ in the same direction.
Let d be the distance of separation between these two conductors.

Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10^-7 N on each metre of the other wire.
Then current flowing is 1A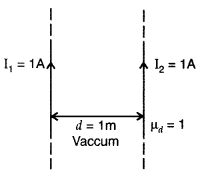

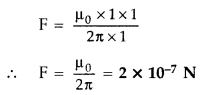
Question 7.
Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis.
Answer:
Magnetic field due to Solenoid Let length of solenoid = L
Total number of turns in solenoid = N
No. of turns per unit length = \(\frac{N}{L}\) = n
ABCD is an Ampere’s loop
AB, DC are very large
BC is in a region of \(\overrightarrow{\mathrm{B}}\) = 0
AD is a long axis
Length of AD = x
Current in one turn = I₀
Applying Ampere’s circuital loop — | B .dl = go I ’


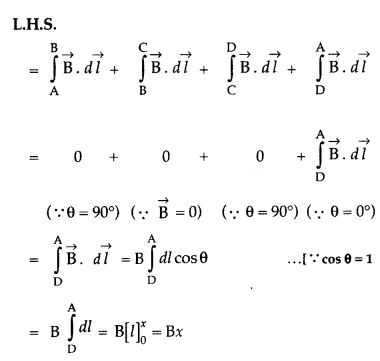
No. of turns in x length = nx,
Current in turns nx, I = nx I₀
According to Ampere’s circuital law
Bx = µ₀ I => Bx = µ₀ nx I₀
∴ B = µ₀nI₀

Question 8.
Two identical circular wires P and Q each of radius R and carrying current ‘I’ are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils. (Delhi 2011)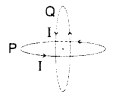

Answer:
Magnetic field produced by the two coils at their common centre are: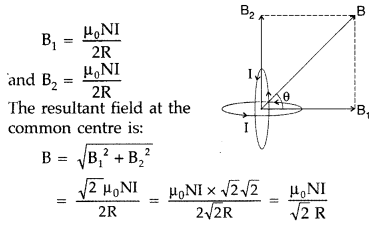


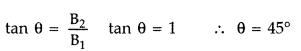
The net magnetic field is directed at an angle of 45° with either of the fields.

Question 9.
Two identical circular loops, P and Q, each of radius r and carrying current I and 21 respectively are lying in parallel planes such that they have a common axis. The direction of current in both the loops is clockwise as seen from O which is equidistant from both the loops. Find the magnitude of the net magnetic field at point O. (Delhi 2011)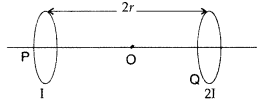

Answer:
When the currents are in the same direction, the resultant field at point O is,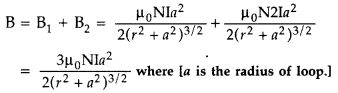

Question 10.
Two identical circular loops, P and Q, each of radius r and carrying equal currents are kept in the parallel planes having a common axis passing through O. The direction of current in P is clockwise and in Q is anti-clockwise as seen from O which is equidistant from the loops P and Q. Find the magnitude of the net magnetic field at O.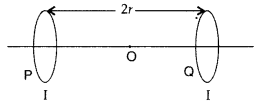

Answer: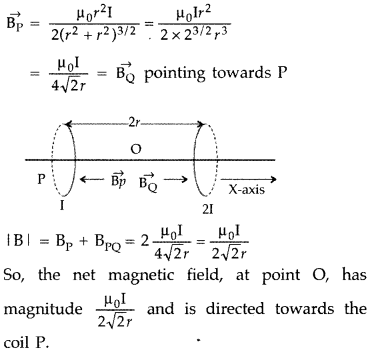

Question 11.
A circular coil of closely wound N turns and radius r carries a current I. Write the expressions for the following :
(i) the magnetic field at its centre
(ii) the magnetic moment of this coil
Answer:
(i) The magnetic field at the centre of a circular coil of N turns and radius r carrying a current, I is

(iii) Magnetic moment, M = NIA = NIπr²

Question 12.
A proton and a deuteron, each moving with velocity \(\vec{v}\) enter simultaneously in the region of magnetic field \(\vec{B}\) acting normal to the direction of velocity. Trace their trajectories establishing the relationship between the two. (Comptt. Delhi 2011)
Answer: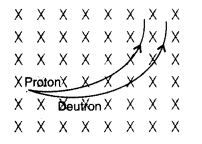

Question 13.
A particle of mass 10^-3 kg and charge 5 pC enters into a uniform electric field of 2 × 10⁵ NC^-1, moving with a velocity of 20 ms^-1 in a direction opposite to that of the field. Calculate the distance it would travel before coming to rest. (Comptt. Delhi 2011)
Answer: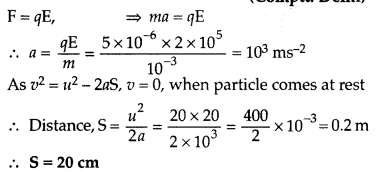

Question 14.
A particle of mass 2 x 10^-3 kg and charge 2 µC enters into a uniform electric field of 5 × 10⁵ NC^-1, moving with a velocity of 10 ms^-1 in a direction opposite to that of the field. Calculate the distance it would travel before coming to rest. (Comptt. Delhi 2011)
Answer:
Force applied on the charged particle, f = qE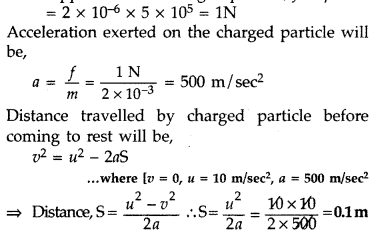

Question 15.
A particle of mass 5 × 10^-3 kg and charge 4 µC enters into a uniform electric field of 2 × 10⁵ NC^-1, moving with a velocity of 30 ms^-1 in a direction opposite to that of the field. Calculate the distance it would travel before coming to rest.
Answer:
Force applied on the charged particle,

Acceleration exerted on the charged particle when it enters in electric field.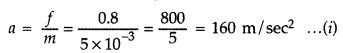

Distance travelled by charged particle before coming to rest will be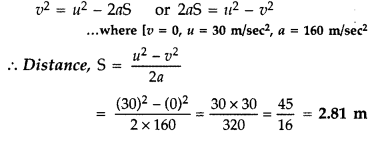

Question 16.
An ammeter of resistance 0.80 Ω can measure current upto 1.0 A.
(i) What must be the value of shunt resistance to enable the ammeter to measure current upto 5.0A?
(ii) What is the combined resistance of the ammeter and the shunt? (Delhi 2013)
Answer:

Question 17.
(a) How is a toroid different from a solenoid?
(b) Use Ampere’s circuital law to obtain the magnetic field inside a toroid.
(c) Show that in an ideal toroid, the magnetic field
(i) inside the toroid and
(ii) outside the toroid at any point in the open space is zero. (Comptt. All India 2014)
Answer:
(a) A toroid is essentially a solenoid which has been bent into a circular shape to close on itself.
(b)

(b) A toroid is a solenoid bent to form a ring shape.
Let N number of turns per unit length of toroid and I be current flowing in it.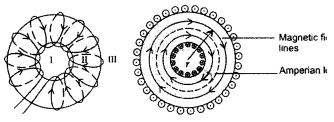

Consider a loop (region II) of radius r passes through the centre of the toroid.
Let (region II) \(\overrightarrow{\mathrm{B}}\) be magnetic field along the loop is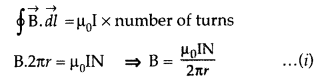

Let (region I) B₁ be magnetic field outside toroid in open space. Draw an amperian loop L₂ of radius r₂ through point Q.
Now applying ampere’s law :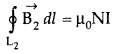

As I = 0, because the circular turn current coming out of plane of paper is cancelled exactly by current going into it, so net I = 0, equation (i) becomes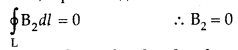

(c) For the loop 1, Ampere’s circuital law gives,

Thus the magnetic field, in the open space inside the toroid is zero.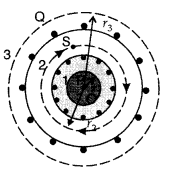

Also at point Q, we have

But from the sectional cut, we refer to that the current coming out of the plane of the paper is cancelled exactly by the current going into it
Hence I_enclosed = 0
∴ B₃ = 0

Question 18.
Derive an expression for the magnetic moment (\(\vec{\mu}\)) of an electron revolving around the nucleus in terms of its angular momentum  . What is the direction of* the magnetic moment of the electron with respect to its angular momentum? (Comptt. All India 2014)
Answer: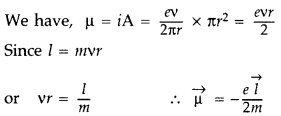

[ ∴ electron has a negative charge
The direction of (\(\vec{\mu}\)) is opposite to that of , because of the negative charge of the electron.

Question 19.
State the underlying principle of a cyclotron. Write briefly how this machine is used to accelerate charged particles to high energies.
(Delhi 2014)
Answer:
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.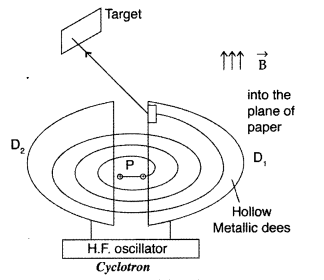

Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D₁ to be negative. It gets accelerated towards dee D₁. As it enters the dee D₁, it does not experience any electric field due to shielding
effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.

At the instant the proton comes out of dee D₁. It finds dee D₁ positive and dee D₂ negative. It now gets accelerated towards dee D₂. It moves faster through dee D₂ describing a larger semicircle than
before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.

Question 20.
Draw the magnetic field lines due to a current passing through a long solenoid. Use Ampere’s circuital law, to obtain the expression for the magnetic field due to the current I in a long solenoid having n number of turns per unit length. (Comptt. Delhi 2014)
Answer: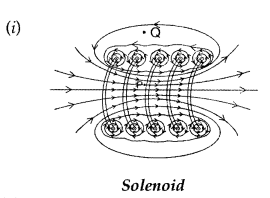

(ii) Expression for magnetic field :
Magnetic field due to Solenoid Let length of solenoid = L
Total number of turns in solenoid = N
No. of turns per unit length = \(\frac{N}{L}\) = n
ABCD is an Ampere’s loop
AB, DC are very large
BC is in a region of \(\overrightarrow{\mathrm{B}}\) = 0
AD is a long axis
Length of AD = x
Current in one turn = I₀

Applying Ampere’s circuital loop — | B .dl = go I ’


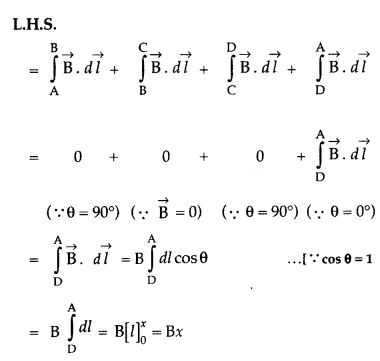
No. of turns in x length = nx,
Current in turns nx, I = nx I₀
According to Ampere’s circuital law
Bx = µ₀ I => Bx = µ₀ nx I₀
∴ B = µ₀nI₀

Question 21.
A rectangular coil of sides ‘V and ‘b’ carrying a current I is subjected to a uniform magnetic field \(\overrightarrow{\mathbf{B}}\) acting perpendicular to its plane. Obtain the expression for the torque acting on it.

Answer:
(a) Torque on a rectangular current loop in a uniform magnetic field:
Let I = current through the coil
a, b – sides of the rectangular loop
A = ab = area of the loop
n = Number of turns in the loop
B = Magnetic field
θ = angle between magnetic field
\(\overrightarrow{\mathrm{B}}\) and area vector \(\overrightarrow{\mathrm{A}}\)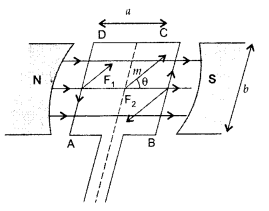

Force exerted on the arm DA inward
F₁ = I b B …[∵ F = ILB]
Force exerted on the arm BC outward
F₂ = I b B ∴ F₂ = F₁
Thus net force on the loop is zero
∴ Two equal and opposite forces form a couple which exerts a torque
∴ Magnitude of the torque on the loop is,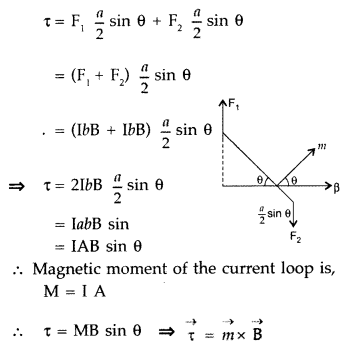

If loop has n turns then M = n I A
∴ τ = nIAB sin θ
When θ = 90° then \(\tau_{\max }=n I A B\)
When θ = 0° then τ = 0
(b) Since the momentum and the charge on both the proton and deutron are the same, the particle will follow a circular path with radius 1:1.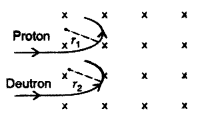

Question 22.
(i) State Biot – Savart law in vector form expressing the magnetic field due to an \(\overrightarrow{\mathbf{B}}\) element \(\overrightarrow{\mathbf{dl}}\) carrying current I at a distance \(\overrightarrow{\mathbf{r}}\) from the element.
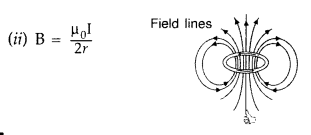
(ii) Write the expression for the magnitude of the magnetic field at the centre of a circular loop of radius r carrying a steady current I. Draw the field lines due to the current loop. (Comptt. All India 2014)
Answer:
(i) According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.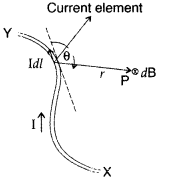


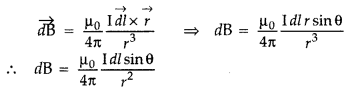
Magnetic field on the axis of circular current loop :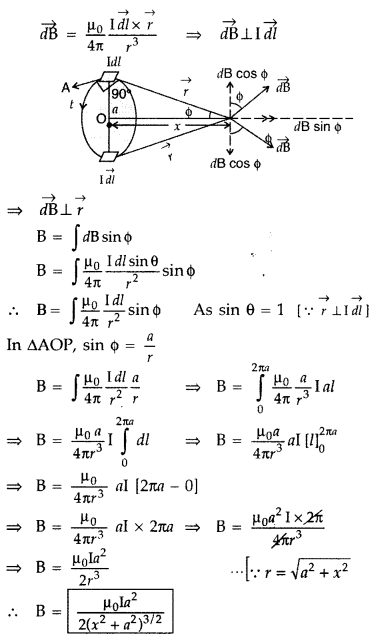

As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain

In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.

Question 23.
A square loop of side 20 cm carrying current of 1A is kept near an infinite long straight wire carrying a current of 2A in the same plane as shown in the figure.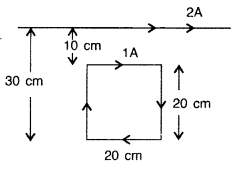

Calculate the magnitude and direction of the net force exerted on the loop due to the current carrying conductor. (Comptt. All India)
Answer: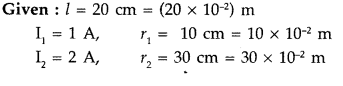


The direction of force is towards the infinitely long straight wire.

Question 24.
A square shaped plane coil of area 100 cm2 of 200 turns carries a steady current of 5A. It is placed in a uniform magnetic field of 0.2 T acting perpendicular to the plane of the coil. Calculate the torque on the coil when its plane makes an angle of 60° with the direction of the field. In which orientation will the coil be in stable equilibrium? (Comptt. All India 2014)
Answer: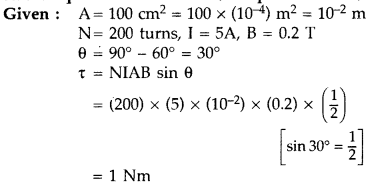

The coil will be in stable equilibrium when it is parallel to the magnetic field.

Question 25.
Find the condition under which the charged particles moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speed. (All India 2015)
Answer:
Condition: The velocity \(\vec{v}\) of the charged particles, and the \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{B}}\) vectors, should be mutually perpendicular

It means that the forces on q, due to \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{B}}\) must be oppositely directed.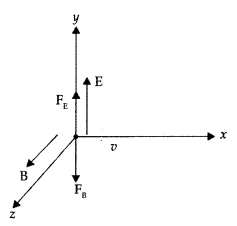

Question 26.
A charge q of mass m is moving with a velocity of v, at right angles to a uniform magnetic field B. Deduce the expression for the radius of the circular path it describes. (Comptt. Delhi 2015)
Answer:
Force experienced by charged particle in magnetic field.

As v and B are perpendicular, F = qvB
This force is perpendicular to the direction of velocity and hence acts as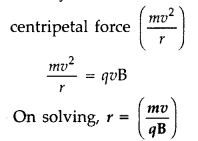

Question 27.
A proton and an alpha particle having the same kinetic energy are, in turn, passed through a region of uniform magnetic field, acting normal to the plane of the paper and travel in circular paths. Deduce the ratio of the radii of the circular paths described by them. (Comptt. Delhi 2015)
Answer: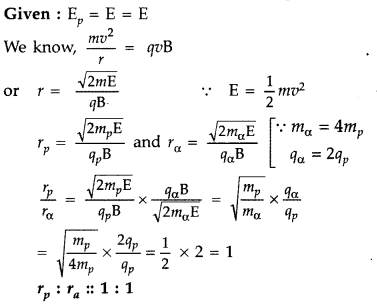

Question 28.
A charged particle having a charge q is moving with a speed of v along the X-axis. It enters a region of space where the electric field is \(\overrightarrow{\boldsymbol{E}}(\boldsymbol{E} \hat{\boldsymbol{j}})\) and a magnetic field \(\vec{B}\) are both present. The particle, on emerging from the region, is observed to be moving, along the X-axis only. Obtain an expression for the magnitude of \(\vec{B}\) in terms of v and E. Give the direction of \(\vec{B}\).
Answer:
Since the particle continues to move along the X-axis, therefore, the magnetic force acting on it should be completely balanced by the electric force. Since the electric force acts along the Y-axis, therefore, the magnetic force must be along the Z-axis.
Thus is equilibrium q E = B q v or v = E/B

Question 29.
A stream of electrons traveling with speed v m s^-1 at right angles to a uniform magnetic field ‘B’ is reflected in a circular path of radius ‘r’ . Prove that \(\frac{e}{m}=\frac{v}{r B}\)
Answer:
Let a stream of electrons be traveling with speed v at right angles to a uniform magnetic field B then force due to magnetic field provides the required centripetal force which deflects the electron beam along a circular path of radius ‘r’ such that
Bev = \(\frac{m v^{2}}{r}\)
or
\(\frac{e}{m}=\frac{v}{r B}\)
where e = electronic charge and m = mass of the electron.

Question 30.
Which one of the two, an ammeter or a milliammeter, has a higher resistance and why?
Answer:
The shunt resistance connected to convert a galvanometer into an ammeter or a milliammeter is given by the expression S = \(\frac{I_{g} G}{I-l_{g}}\) where S is shunt resistance, G galvanometer resistance, l total current through G and S, and l_g galvanometer current. In the case of milliammeter, l is small.

Therefore S_milliammeter > S_ammeter . Hence the resistance of a milliammeter is greater than that of an ammeter.

Question 31.
A straight wire of length L carrying a current l stays suspended horizontally in mid-air in a region where there is a uniform magnetic field \(\vec{B}\). The linear mass density of the wire is l. Obtain the magnitude and direction of the magnetic field.
Answer:
The magnetic force acting on the straight wire balances the weight of the wire.
Therefore, in equilibrium we have Mg = BIL, here M = L l, therefore we have L l g = BlL or B = l/ l g
This field acts vertically upwards.

Question 32.
In the figure below, the straight wire AB Is fixed while the loop Is free to move under the influence of the electric currents flowing in them. In which direction does the loop begin to move? Give a reason for your answer.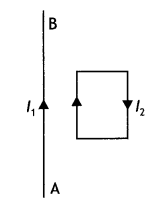

Answer:
The loop moves towards the straight wire AB. In the loop in the side nearer to the wire AB current l₂ is in the same direction as l₁ and hence attractive force acts. However, on the side farther away from the wire AB current l₂ is in the opposite direction and the force is repulsive. But as the magnitude of attractive force is greater than the repulsive force, the net force is attractive in nature and hence, the loop moves towards the wire AB.

Question 33.
A coil of ‘N’ turns and radius ‘R’ carries a current ‘l’. It is unwound and rewound to make a square coil of side ‘a’ having the same number of turns (N). Keeping the current ‘l’ same, find the ratio of the magnetic moments of the square coil and the circular coil. (CBSE Delhi 2013C)
Answer:
The magnetic moment of a current loop is given by the relation M = nlA
For the circular loop M_c = NlπR² …(1)

Now when the coil is unwound and rewound to make a square coil, then
2 πR = 4a or a = πR/2

Hence magnetic moment of the square coil is
M_s = Nl a² = Nl (πR/2)² = Nl π²R²/4 …(2)

From (1) and (2) we have
\(\frac{M_{S}}{M_{C}}=\frac{N l \pi^{2} R^{2} / 4}{N l \pi R^{2}}=\frac{\pi}{4}\)

Question 34.
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity v in a magnetic field B. Show that no work is done by this force on the charged particle. (CBSE Al 2011)
Answer:
The expression is \(\vec{F}\) = q(\(\vec{v}\) × \(\vec{B}\)). This force always acts perpendicular to the direction of motion of the charged particle. Therefore the angle between \(\vec{F}\) and \(\vec{r}\) is 90°. Hence work done is W = \(\vec{F}\). r = Fr cos 90° = 0

Question 35.
(a) State Biot-Savart law in vector form expressing the magnetic field due to an element \(\vec{dl}\) carrying current l at a distance \(\vec{r}\) from the element.
Answer:
It states that for a small current element dl the magnetic field at a distance r is given by
\(\overrightarrow{d B}=\frac{\mu_{0}}{4 \pi} \frac{I \overline{(d L} \times \hat{r})}{r^{2}}\).

(b) Write the expression for the magnitude of the magnetic field at the center of a circular loop of radius r carrying a steady current l. Draw the field lines due to the current loop. (CBSE Al 2014C)
Answer:
The magnetic field at the center of a circular loop is given by
B = \(\frac{\mu_{0} l}{2 r}\)

The field lines are as shown.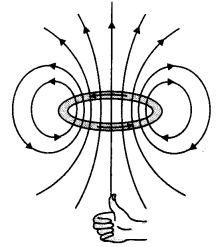

Question 36.
Draw the magnetic field lines due to current passing through a long solenoid. Use Ampere’s circuital law, to obtain the expression for the magnetic field due to the current l in a long solenoid having n number of turns per unit length. (CBSE Delhi 2014C)
Answer:
The diagram is as shown.

Consider a rectangular path abed of length L as shown in the figure below. Let us apply Ampere’s circuital law to this rectangular path so that we have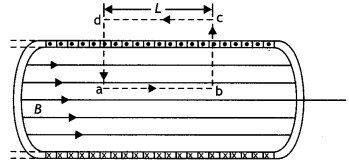



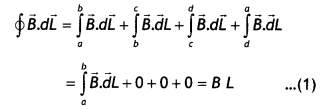
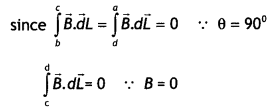
But by Ampere’s circuital law we have
\(\oint \vec{B} \cdot \vec{d} L\) = μ₀Nl = μ0(nL)l …(2)

From equations (1) and (2) we have
BL = μ₀nLl
or
B = μ₀ n l

But n = N/L, therefore we have
B = μ₀ \(\frac{N l}{L}\)

This gives the value of a magnetic field inside a solenoid.

Question 37.
(a) Why do we use a shunt to convert a galvanometer into an ammeter?
Answer:
Since an ammeter is an instrument used to measure the current in the circuit, so it has to be connected in series in the circuit to measure the whole current. Hence its resistance must below. A low shunt resistance makes it suitable for measuring current.

(b) A galvanometer of resistance 15 Ω shows a full-scale deflection on the meter scale for a current of 6 mA. Calculate the value of the shunt resistance required to convert the galvanometer into an ammeter of range 0-6 A. (CBSE 2019C)
Answer:
Given G = 15 Ω, l_g = 6 mA = 6 × 10^-3 A, l = 6 A, S = ?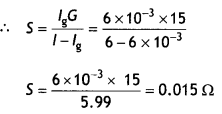

Question 38.
An electron beam projected along + X-axis experiences a force due to a magnetic field along the + Y-axis. What is the direction of the magnetic field?
Answer:
The direction of the magnetic field is along  Z-axis. This is because the direction of motion, the magnetic field, and the force are perpendicular to one other as an electron carries a negative charge.

Question 39.
A current is set up in a long copper pipe. Is there a magnetic field
(i) inside,
Answer:
There is no magnetic field inside the pipe.

(ii) outside the pipe?
Answer:
There is a magnetic field outside the pipe.

Question 40.
Which one of the following will experience a maximum force, when projected with the same velocity V perpendicular to the magnetic field (i) alpha particle and (ii) beta particle?
Answer:
The force experienced by a charged particle is given by the expression F = B q v. Since an alpha particle has a moving charge than the beta particle, therefore the alpha particle will experience more force.

Question 41.
An electron and a proton moving parallel to each other in the same direction with equal momenta enter into a uniform magnetic field which is at right angles to their velocities. Trace their trajectories in the magnetic field.
Answer:
Because both electron and proton have the same charge and momentum, therefore they will describe circles of equal radii as shown.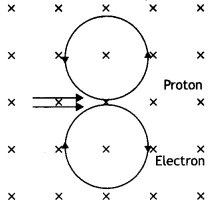

Question 42.
Is the steady electric current the only source of the magnetic field? Justify your answer. (CBSE Delhi 2013C)
Answer:
No, the magnetic field is also produced by alternating current.

Question 42 a.
A deuteron and an alpha particle having the same momentum is in turn allowed to pass through a magnetic field B, acting normal to the direction of motion of the particles. Calculate the ratio of the radii of the circular paths described by them. (CBSE Delhi 2019)
Answer:
P_d = P_α
Now r = \(\frac{mv}{Bq}\) ⇒ r ∝ \(\frac{1}{q}\)

Therefore, \(\frac{r_{d}}{r_{\alpha}}=\frac{q_{\alpha}}{q_{d}}=\frac{2 e}{e}\) = 2

Question 43.
Two wires of equal length are bent in the form of two loops. One of the loops is square-shaped and the other is circular. These are suspended in a uniform magnetic field and the same current is passed through them. Which loop will experience a greater torque? Give reasons.
Answer:
Torque experienced by a current-carrying loop placed in a uniform magnetic field is given by the expression τ = BlnA. In other words, torque is directly proportional to the area of the loop. Since a circular wire has more area than a square wire for the same dimension, therefore the circular wire experiences more torque than the square wire.

Question 44.
Which one of the following will have a minimum frequency of revolution, when projected with the same velocity v perpendicular to the magnetic field B: (i) alpha particle and (ii) beta particle?
Answer:
The frequency of revolution of a charged particle in a magnetic field is given by Bq
v = \(\frac{Bq}{2πm}\).

The ratio of q/m for an alpha particle is less than that for a beta particle; therefore, the alpha particle will have a minimum frequency of revolution.

Question 45.
Using the concept of force between two infinitely long parallel current-carrying conductors, define one ampere of current. (CBSE AI 2014)
Answer:
One ampere is that much current which when flowing through each of the two infinitely long straight conductors held 1 meter apart in space, produce a force of F= 2 × 10^-7 N per meter of their length.

Question 46.
(a) Write the expression for the force \(\vec{F}\) , acting on a charged particle of charge ‘q’, moving with a velocity v in the presence of both electric field \(\vec{E}\) and magnetic field \(\vec{B}\) . Obtain the condition under which the particle moves undeflected through the fields.
Answer:
(a) The required expression is \(\vec{F}=q \vec{E}+q(\vec{v} \times \vec{B})\)

The particle will move undeflected if the force acting on it due to the electric field balances the force acting on it due to the magnetic field. Thus qE = Bqv or v=E/B

(b) A rectangular loop of size l × b carrying a steady current I is placed in a uniform magnetic field \(\vec{B}\) . Prove that the torque τ acting on the loop is given by \(\vec{τ}\) = \(\vec{m}\) × \(\vec{B}\) , where m is the magnetic moment of the loop. (CBSE AI 2012, Delhi 2013)
Answer:
The figure below shows a rectangular loop of wire with length ‘a’ and breadth ‘b’. A line perpendicular to the plane of the loop (i.e. a normal to the plane) makes an angle Φ with the direction of the magnetic field B, and the loop carries a current / as shown. Let the forces acting on the various sides of the loop be \(\vec{F}_{1}\), \(\vec{F}_{2}\), \(\vec{F}_{3}\) and \(\vec{F}_{4}\) as shown.

It follows from the expression for the force experienced by a conductor in a magnetic field that force on arm AB is
\(\vec{F}_{1}=I(\overrightarrow{\mathrm{AB}} \times \vec{B})\) …(1)
(in the plane of the paper and is directed upwards as shown).

The force on arm CD is given by \(\vec{F}_{2}=l(\overrightarrow{\mathrm{CD}} \times \vec{B})\) …(2)
(in the plane of the paper and is directed downwards as shown.)

Since these two forces are equal and opposite and have the same line of action therefore they cancel out each other’s effect and their resultant effect on the coil is zero.

Now the force on arm BC is
\(\vec{F}_{3}=l(\overrightarrow{\mathrm{BC}} \times \vec{B})\) …(3)
(acts perpendicular to the plane of the paper and is directed outwards as shown) Finally the force on arm DA is
\(\vec{F}_{4}=I(\overrightarrow{\mathrm{DA}} \times \vec{B})\) …(4)
(acts perpendicular to the plane of the paper and is directed inwards as shown in figure).

Both forces F₃ and F₄ make an angle of 90° with the direction of the magnetic field. Therefore, in magnitude, these forces are given by
F₃ = F₄ = laB sin90° = laB …(5)

The lines of action of both these forces are perpendicular to the plane of the paper. The two forces F3 and F4 lie along different lines and each give rise to a torque about the X-axis. The two torques produce a resultant torque in + X direction. The arm of the couple (perpendicular distance between the lines of action of the two forces) from the figure below is given by
An arm of couple = b Sin Φ …(6)

Therefore, by the definition of torque we have
Torque = either force × arm of couple Using equations (5) and (6) we have
Torque = l B a × b Sin Φ
But a b = A, area of the coil, therefore τ = l B A Sin Φ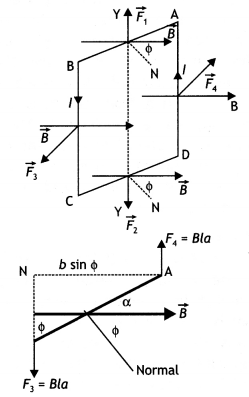

Question 47.
Show that a force that does no work must be a velocity-dependent force. (NCERT Exemplar)
Answer:
We know that work is the dot product of force and displacement, therefore
dW = \(\vec{F} \cdot d \vec{l}\) = 0
Or
dW = \(\vec{F}\) .\(\vec{v}\)dt = 0
Or
\(\vec{F} \cdot \vec{v}\) = 0

Thus F must be velocity dependent which implies that the angle between F and v is 90°. If v changes direction then the direction of F should also change so that the above condition is satisfied.

Question 48.
Five long wires A, B, C, D, and E, each carrying current l is arranged to form edges of a pentagonal prism as shown in the figure. Each carries current out of the plane of the paper.
(a) What will be magnetic induction at a point on axis 0? Axis is at a distance R from each wire.
(b) What will be the field if the current in one of the wires (say A) is switched off?
(c) What if the current in one of the wires (say) A is reversed? (NCERT Exemplar)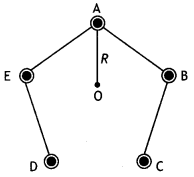

Answer:
(a) Zero Mn I
(b) \(\frac{\mu_{0}}{2 \pi} \frac{1}{R}\) perpendicular to AO towards left
(c) \(\frac{\mu_{0}}{\pi} \frac{1}{R}\) perpendicular to AO towards left

Question 49.
A circular coil of 200 turns and radius 10 cm is placed in a uniform magnetic field of 0.5 T, normal to the plane of the coil. If the current in the coil is 3.0 A, calculate the
(a) total torque on the coil.
(b) total force on the coil.
(c) average force on each electron in the coil, due to the magnetic field.
Assume the area of cross-section of the wire to be 10^-5 m² and the free electron density is 10²⁹/m³. (All India 2015)
Answer: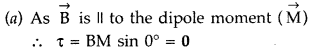

(b) As the forces on different parts of the coil appears in pairs, equal in magnitude and opposite in direction, net force on the coil is zero.i.e., F = 0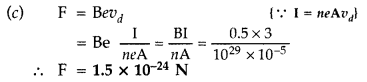

Question 50.
An electron moves around the nucleus in a hydrogen atom of radius 0.51 A, with a velocity of 2 × 10⁵ m/s. Calculate the following :
(i) the equivalent current due to orbital motion of electron
(ii) the magnetic field produced at the centre of the nucleus
(iii) the magnetic moment associated with the electron. (All India 2015)
Answer: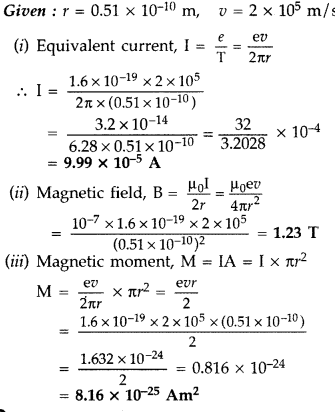

Question 51.
Derive the expression for force per unit length between two long straight parallel current carrying conductors. Hence define one ampere. (Delhi 2015)
Answer:
Consider two infinitely long parallel conductors carrying current I₁ and I₂ in the same direction.
Let d be the distance of separation between these two conductors.

Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10^-7 N on each metre of the other wire.
Then current flowing is 1A

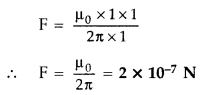
Question 52.
Explain the principle and working of a cyclotron with the help of a schematic diagram. Write the expression for cyclotron frequency. (Delhi 2015)
Answer:
Cyclotron :
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.

Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D₁ to be negative. It gets accelerated towards dee D₁. As it enters the dee D₁, it does not experience any electric field due to shielding
effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.

At the instant the proton comes out of dee D₁. It finds dee D₁ positive and dee D₂ negative. It now gets accelerated towards dee D₂. It moves faster through dee D₂ describing a larger semicircle than before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.

Question 53.
Find the magnetic field at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of the circular coil carrying current.
Answer:
Magnetic field at a point on the axis of a circular coil carrying current
Consider a circular coil of radius ‘a’ with centre ‘O’, carrying current I. Its plane is perpendicular to the plane of the loop. Suppose P is any point on the axis of the circular coil at a distance x from the centre, such that
OP = x
Consider two small elements of length dl at C and D at diametrically opposite current elements of the coil
PC = PD = r = \(\sqrt{a^{2}+x^{2}}\)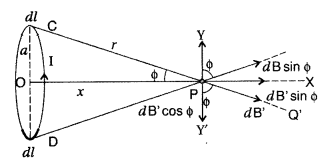

According to Biot Savart’s law, the magnitude of magnetic field at P due to current element dl at C is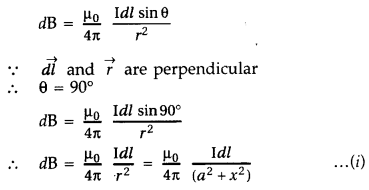

The direction of \(\overrightarrow{d \overrightarrow{\mathrm{B}}}\) is perpendicular to \(\vec{r}\) in the plane paper i.e., along PQ.
Similarly, the magnitude of magnetic field at P due to current element dl at D is

Its direction is along PQ’
From (i) an (ii), we get, dB = dB’ = \(\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} d l}{\left(a^{2}+x^{2}\right)}\)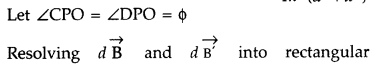

components :
(i) dB cos ϕ along PY and dB’ sin ϕ along PX
(ii) dB cos ϕ along PY and dB’ sin ϕ along PX
Since the components of the magnetic field along Y-axis are equal and opposite and cancel each other, the components along X-axis are in the same direction and are added up.
Hence the total magnetic field at point P is,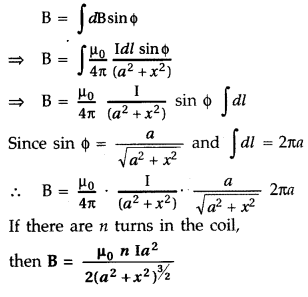

Question 54.
Deduce the expression for the magnetic dipole moment of an electron orbiting around the central nucleus. (All India 2010)
Answer:
Consider an electron revolving around the nucleus of an atom. Electron is in uniform circular motion around the nucleus of charge + Ze. This constitutes a current.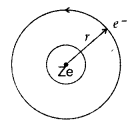


If ‘r’ is orbital radius of the electron and ‘V’ is orbital speed, then the time period is

Now putting the value of T in (i), we get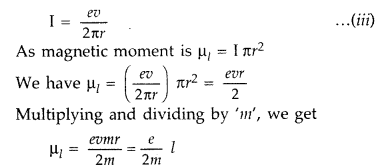

…where [Z is angular momentum of the electron.
According to Bohr hypothesis angular momentum we can have discrete values only.

Question 55.
A long straight wire of a circular cross-section of radius ‘a’ carries a steady current ‘I’. The current is uniformly distributed across the cross-section. Apply Ampere’s circuital law to calculate the magnetic field at a point V in the region for
(i) r < a and (ii) r > a.
Answer:
Consider an infinite long thick wire of radius V with axis XY. Let I be the current flowing through the wire.
When the point P lies outside the wire :

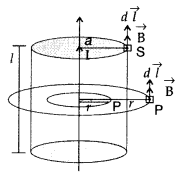
Let r be the perpendicular distance of point P from the axis of the cylinder, where r > a.
Here \(\overrightarrow{\mathrm{B}}\) and d \(\overrightarrow{\mathrm{l}}\) are acting in the same direction.
Applying Ampere’s circuital law, we have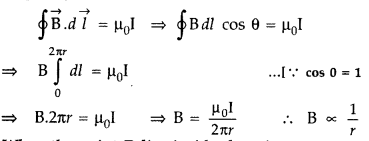

When the point P lies inside the wire :
Here r ≤ a. We have two possibilities:
According to Ampere circuital law,
(i) “Whenever the current floras only through the surface of the wire, B = 0 as current in the closed path will be zero.”
(ii) “Wherever in the case when current is uniformly distributed through the cross-section of conductor, current through the closed path will be :
I’ = Current per unit area of the wire × area of the circle of radius r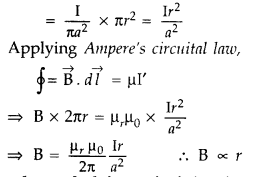

Question 56.
State the underlying principle of working of a moving coil galvanometer. Write two reasons why a galvanometer can not be used as such to measure current in a given circuit. Name any two factors on which the current sensitivity of a galvanometer depends. (Delhi 2010)
Answer:
(i) Moving coil galvanometer works on the principle of a torque experienced by a current carrying coil placed in a magnetic field, whose magnitude is a function of current passing through the coil.
(ii) The galvanometer cannot be used to measure the value of the current in a given circuit due to the following two reasons:
(a) Galvanometer is a very sensitive device. It gives a full scale deflection for a small value of current.
(b) The galvanometer has to be connected in series for measuring currents and as it has a large resistance, this will change the value of the current in the circuit.
(iii)

It depends on the number of turns N of the coil, torsion constant and the area A of the coil.

Question 57.
Write the expression for the magnetic moment (\(\overrightarrow{\mathbf{M}}\)) due to a planar square loop of side ‘l’ carrying a steady current I in a vector form. In the given figure this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I, at a distance l as shown. Give reasons to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop. (Delhi 2010)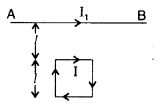

Answer:
(i) The magnetic moment \((\overrightarrow{\mathrm{M}})\) due to a planar square loop of side ‘l’ carrying a steady current I in a vector form is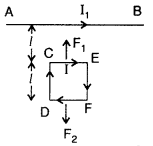


(ii) CE will be attracted towards AB with a force F₁ given by

Question 58.
Write the expression for the magnetic moment (\(\overrightarrow{\mathbf{M}}\)) due to a planar square loop of side ‘l’ carrying a steady current I in a vector form. In the given figure this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I, at a distance l as shown. Give reasons to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop. (Delhi 2010)

Answer:
(i) The magnetic moment \((\overrightarrow{\mathrm{M}})\) due to a planar square loop of side ‘l’ carrying a steady current I in a vector form is


(ii) CE will be attracted towards AB with a force F₁ given by

Question 59.
A rectangular loop of wire of size 4 cm × 10 cm carries a steady current of 2 A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the loop and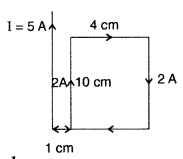

(ii) the magnitude and direction of the force on the loop due to the current carrying wire. (Delhi 2012)
Answer:
τ = IAB sin θ => τ = IAB sin θ (as θ = 0)

(ii) Force acting on the loop on |F|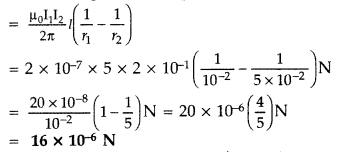

Direction : Towards conductor/Attractive Net force on the loop will act towards the long conductor (attractive) if the current in its closer side is in the same direction as the current in the long conductor, otherwise it will be repulsive.

Question 60.
A rectangular loop of wire of size 2 cm × 5 cm carries a steady current of 1 A. A straight long wire carrying 4 A current is kept near the loop as shown in the figure.
If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire. (Delhi 2010)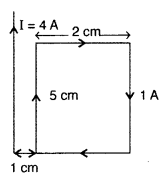

Answer:
(i) τ (Torque on the loop) = MB sin θ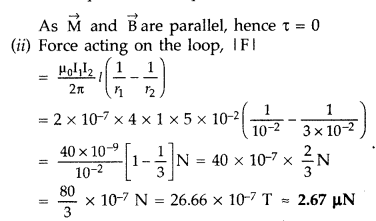

Direction : Towards the conductor/Attractive
Net force on the loop will act towards the long conductor (attractive) if the current in its closer side is in the same direction as the
current in the long conductor, otherwise it will be repulsive.

Question 61.
Two identical coils, each of radius ‘R’ and number of turns ‘N’ are lying in perpendicular planes such that their centres coincide. Find the magnitude and direction of the resultant magnetic field at the centre of the coils, if they are carrying currents ‘I’ and √3I respectively.
(Comptt. Delhi 2010)
Answer: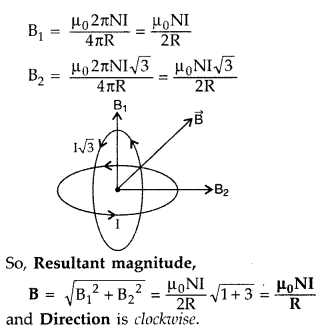

Question 62.
Two identical coils, each of radius ‘R’ and number of turns ‘N’ are lying in perpendicular planes such that their centres coincide. Find the magnitude and direction of the resultant magnetic field at the centre of the coils, if they are carrying currents ‘I’ and √2I respectively.
(Comptt. Delhi 2010)
Answer: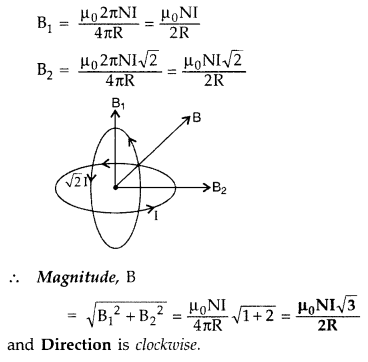

Question 63.
Figure shows a rectangular loop conducting PQRS in which the arm PQ is free to move. A uniform magnetic field acts in the direction perpendicular to the plane of the loop. Arm PQ is moved with a velocity v towards the arm RS. Assuming that the arms QR, RS and SP have negligible resistances and the moving arm PQ has the resistance r, obtain the expression for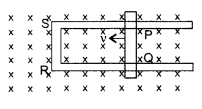

(i) the current in the loop
(ii) the force and
(iii) the power required to move the arm PQ. (Delhi 2010)
Answer:
Let the magnetic field acting on the loop be B and length of the rod PQ be l
The induced e.m.f. ε = Blv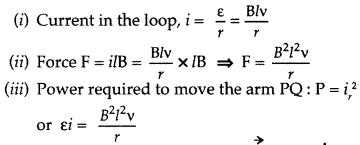

Question 64.
A rectangular conductor LMNO is placed in a uniform magnetic field of 0.5 T. The field is directed perpendicular to the plane of the conductor. When the arm MN of length of 20 cm is moved towards left with a velocity of 10 ms^-1, calculate the emf induced in the arm. Given the resistance of the arm to be 5Ω (assuming that other arms are of negligible resistance) find the value of the current in the arm. (All India 2010)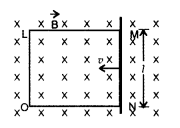

Answer: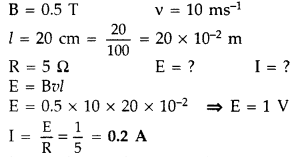

Question 65.
A wire AB is carrying a steady current of 12A and is lying on the table. Another wire CD carrying 5A is held directly above AB at a height of 1 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms^-2] (All India 2010)
Answer:
Given :
Current in the wire AB (I₁) = 12 A,
Current in wire CD (I₂) = 5 A
Separation between two wires (d) = 1 mm
= 10^-3 m
Let ‘m’ be the mass of wire CD of length (L),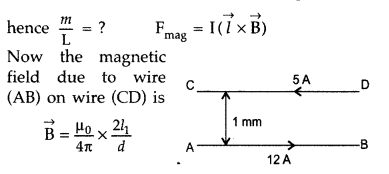


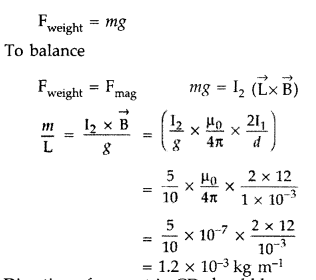
Direction of current in CD should be opposite to that of AB.

Question 66.
A wire AB is carrying a steady current of 10 A and is lying on the table. Another wire CD carrying 6 A is held directly above AB at a height of 2 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms^-2] (All India 2010)
Answer:
Let AB has current in +ve x-direction
(I₁) Current in wire AB = 10 A,
(I₂) Current in wire CD = 6 A
Separation between the two wires = 2 mm
= 2 × 10^-3m
To keep the wire CD suspended in its vertical position when left free. For this magnetic force on CD due to AB should balance mg due to its own weight.
Let m be the mass of the wire CD and L be its length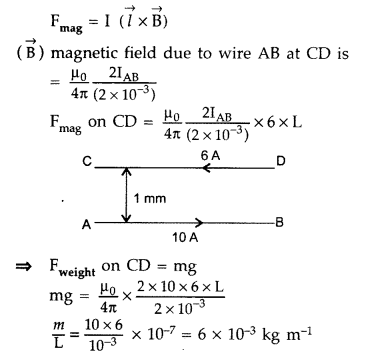

Direction of current in CD should be opposite to that AB.

Question 67.
(a) Define the current sensitivity of a galvanometer.
(b) The coil area of a galvanometer is 16 × 10^-4 m². It consists of 200 turns of a wire and is in a magnetic field of 0.2 T. The restoring torque constant of the suspension fibre is 10^-6 Nm per degree. Assuming the magnetic field to be radial, calculate the maximum current that can be measured by the galva-nometer if the scale can accommodate 30° deflection. (Comptt. All India 2010)
Answer:
Sensitivity of a galvanometer: A galvanometer is said to be sensitive, if it gives a large deflection, even when a small current passes through it.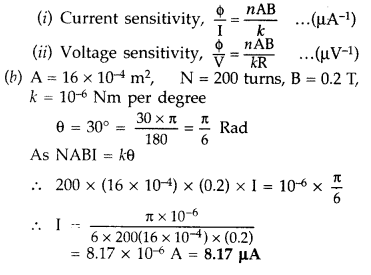

Question 68.
(a) State Ampere’s circuital law, expressing it in the integral form.
(b) Two long coaxial insulated solenoids, S₁ and S₂ of equal lengths are wound one over the other as shown in the figure. A steady current “I” flows through the inner solenoid S₁ to the other end B, which is connected to the outer solenoid S₂ through which the same current “l” flows in the opposite direction so as to come out at end A. If n₁ and n₂ are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point
(i) inside on the axis and
(ii) outside the combined system. (Delhi 2014)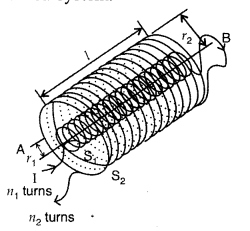

Answer:
(a) According to Ampere’s Circuital law, the magnetic field B is related to steady current

(i) Inside the combined system : Magnetic field at a point on the axis.
Using Ampere’s Circuital law, the magnetic field due to inner solenoid S₁ is given by

Similarly due to outer solenoid S₂,

Since these two magnetic fields are opposite in direction,

in the upward direction.
(ii) Outside the combined system : At such a point, magnetic field is zero, because corresponding turns of the two halves of the solenoid produce equal and opposite magnetic fields.

Question 69.
Consider the motion of a charged particle of mass ‘m’ and charge ‘q’ moving with velocity \(\vec{v}\) in a magnetic field \(\vec{B}\).
(a) If \(\vec{v}\) is perpendicular to \(\vec{B}\), show that it describes a circular path having angular frequency ω = qB/m.
(b) If the velocity \(\vec{v}\) has a component parallel to the magnetic field \(\vec{B}\), trace the path described by the particle. Justify your answer. (Comptt. Delhi 2014)
Answer:
(a) When a charged particle with charge q moves inside a magnetic field \(\overrightarrow{\mathrm{B}}\) with velocity v, it experiences a force, which is given by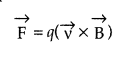

Here, \(\overrightarrow{\mathrm{v}}\) is perpendicular to \(\overrightarrow{\mathrm{B}}\), \(\overrightarrow{\mathrm{F}}\) is the force on the charged particle which acts as the centripetal force and makes it move along a circular path.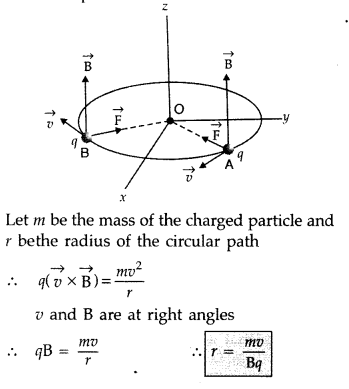

Let m be the mass of the charged particle and r be the radius of the circular path.
Time period of circular motion of the charged particle can be calculated as shown below:

Therefore, the frequency of the revolution of the charged particle is independent of the velocity or the energy of tire particle.
(b)

Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.

Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D₁ to be negative. It gets accelerated towards dee D₁. As it enters the dee D₁, it does not experience any electric field due to shielding effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.

At the instant the proton comes out of dee D₁. It finds dee D₁ positive and dee D₂ negative. It now gets accelerated towards dee D₂. It moves faster through dee D₂ describing a larger semicircle than
before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.

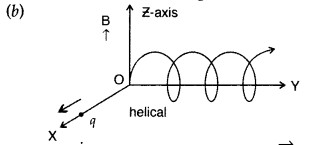
Justification : Component of velocity \(\vec{v}\), parallel to magnetic field, will make the particle move along the field.

Perpendicular component of velocity \(\vec{v}\) will cause the particle to move along a circular path in the plane perpendicular to the magnetic field Hence, the particle will follow a helical path, as shown above.

Question 70.
(a) Draw a schematic sketch of a moving coil galvanometer and describe briefly its working.
(b) “Increasing the current sensitivity of a galvanometer does not necessarily increase the voltage sensitivity.” Justify this statement. (Comptt. Delhi 2014)
Answer:
(a)
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB

The spring S_p attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring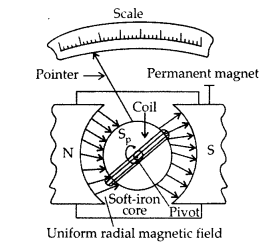

In equilibrium state,

Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.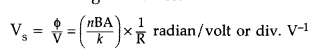

…where [R = Resistance of the coil

does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

(b) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

may not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

Question 71.
A uniform magnetic field \(\overrightarrow{\mathrm{B}}\) is set up along the positive x-axis. A particle of charge ‘q’ and mass ‘m’ moving with a velocity v enters the field at the origin in X-Y plane such that it has velocity components both along and perpendicular to the magnetic field \(\overrightarrow{\mathrm{B}}\). Trace, giving reason, the trajectory followed by the particle. Find out the expression for the distance moved by the particle along the magnetic field in one rotation. (All India 2014)
Answer:
Since the velocity of the particle is inclined to x-axis, thererfore, the velocity has a component along B, this component remains unchanged as the motion along the magnetic field will not be affected by the magnetic field. The motion in a plane perpendicular to B is as before a circular one, thereby producing a helical motion, which is its trajectory.

If r is the radius of the circular path of a particle, then a force of mv²/r, acts perpendicular to the path towards the centre of the circle and is called the centripetal force. If the velocity v is perpendicular to the magnetic field B, the magnetic force is perpendicular to both v and B and acts like a centripetal force. It has a magnitude qvB. Equating the two expressions (for centripetal force)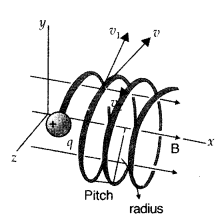

mv²/r = qvB, which gives r = mv/qB …(i) for the radius of the circle described by the charged particle.

There is a component of the velocity parallel to the magnetic field (denoted by v₁₁), it will make the particle move along the field and the path of the particle would be a helical one.

The distance moved along the magnetic field in one rotation is called pitch p.
Using equation (ii), we have

Question 72.
Write the expression for the generalized form of Ampere’s circuital law. Discuss its significance and describe briefly how the concept of displacement current is explained through charging/discharging of a capacitor in an electric circuit. (All India 2014)
Answer:
Maxwell’s displacement current : According to Ampere’s circuital law, the magnetic field \(\overrightarrow{\mathrm{B}}\) is related to steady current I as,

Maxwell showed that this relation is logically inconsistent. He accounted this inconsistency as follows :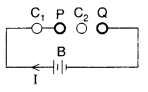

Ampere’s circuital laic for loop C, gives

Loop C₂ lies in the region between the plates


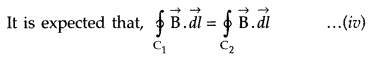
which is logically inconsistent. So, Maxwell gave idea of displacement current.

Thus displacement current is that current which comes into play in the region in which the electric

where [I_D is displacement current and

It is now called Ampere-Maxwell law. This is the generalization of Ampere’s Circuital law.

Question 73.
(a) Why is the magnetic field radial in a moving coil galvanometer? Explain how it is achieved.
(b) A galvanometer of resistance ‘G’ can be converted into a voltmeter of range (0 – V) volts by connecting a resistance ‘R’ in series with it. How much resistance will be required to change its range from 0 to V/2? (Comptt. All India 2014)
Answer:
(a) The magnetic field in a moving coil galvanometer is made ‘radial’ to keep the magnetic field ‘normal’ to the area vector of the coil. It is done by taking the cylindrical soft iron core. The torque acting on the coil is maximum (sin θ = 1, when, θ = 90°)
(b) Given : resistance of galvanomter = G Ω
Range of voltmeter (R_L) = (0 – V) volts
Resistance to be connected in parallel = R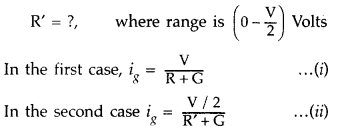

[i_g is the maximum current which can flow through galvanometer]
From equation (i) and (ii), on solving we get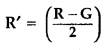

Question 74.
A closely wound solenoid of 2000 turns and cross sectional area 1.6 × 10^-4 m² carrying a current of 4.0 A is suspended through its centre allowing it to turn in a horizontal plane. Find
(i) the magnetic moment associated with the solenoid,
(ii) magnitude and direction of the torque on the solenoid if a horizontal magnetic field of 7.5 × 10^-2 T is set up at an angle of 30° with the axis of the solenoid. (Comptt. All India 2014)
Answer: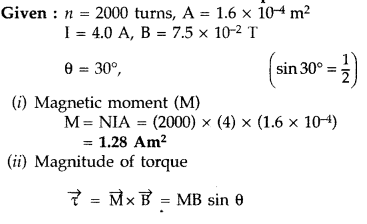


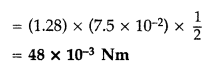
(iii) Direction of torque is perpendicular to both the planes of the solenoid and the magnetic field.

Question 75.
(a) Write the expression for the magnetic force acting on a charged particle moving with velocity v in the presence of magnetic field B.
(b) A neutron, an electron and an alpha particle moving with equal velocities, enter a uniform magnetic field going into the plane of the paper as shown. Trace their paths in the field and justify your answer. (Delhi 2016)

Answer:
(a) Expression for magnetic force :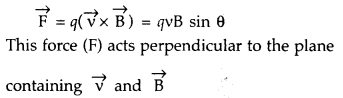

(b) Justification : Direction of force experienced by 01 the particle will be n according to Fleming’s Left hand rule.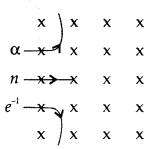

Question 76.
Two long straight parallel conductors carry steady current I₁ and I₂ separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other. Obtain the expression for this force. Hence define one ampere. (Delhi 2014)
Answer:
Consider two infinitely long parallel conductors carrying current I₁ and I₂ in the same direction.
Let d be the distance of separation between these two conductors.

Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10^-7 N on each metre of the other wire.
Then current flowing is 1A

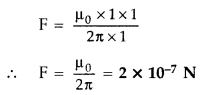
Question 77.
Use Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to a circular . wire carrying current I. (All India 2014)
Answer:
(i) According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.


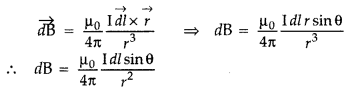
Magnetic field on the axis of circular current loop :

As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain

In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.
(ii)
(a) Magnetic field lines :

(b) Moving coil galvanometer. It is a device used for the detection and measurement of small electric current.
Principle. The working is based on the fact that a current carrying coil suspended in a magnetic field experiences a torque.
Construction. It consists of a coil having a large number of turns of insulated copper wire wound on a metallic frame. The coil is suspended by means of a phosphor-bronze strip and is surrounded by a horse-shoe magnet NS. A hair spring is attached to lower end of the coil. The other end of the spring is attached to the scale through a pointer.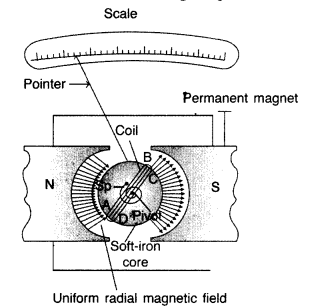

Working. When current is passed, say along ABCD, the couple acts on it. Since the plane remains always parallel to the magnetic field in all positions of the coil (radial field), the force on the vertical arms always remains perpendicular to the place of the coil.

Let, I be the current flowing through coil,
B be magnetic field supposed to be uniform and always parallel to the coil, A be area of the coil
Deflecting torque acting on the coil is,
τ = nI BA sin 900

Due to deflecting torque, the coil rotates and suspension wire gets twisted. A restoring torque is set up in the suspension fibre. If <|) is angle through which the coil rotates and k is the restoring torque per unit angular twist, then restoring torque, τ = kϕ
In equilibrium,
Deflecting torque = Restoring torque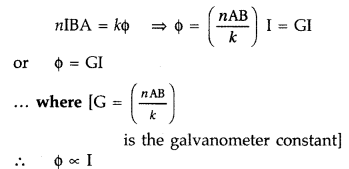

This provide a linear scale for the galvanometer.
Function of a radial magnetic field : Radial magnetic field being normal in all directions is formed to get maximum torque.
Function of Soft iron core, which not only makes the field radial but also increases the strength of the magnetic field.
(c) One uses a shunt resistance in parallel with the galvanometer, so that most of the current passes through the shunt. In the case of a voltmeter, a resistance of large value is used in series because it must draw a very small current, otherwise the voltage measurement will disturb the original set up by an amount which is very large.

Question 78.
Three long straight parallel wires are kept as shown in the figure. The wire (3) carries a current I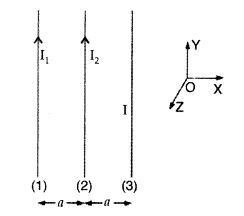

(i) The direction of flow of current I in wire (3), is such that the net force, on wire (1), due to the other two wires, is zero.
(ii) By reversing the direction of I, the net force, on wire (2), due to the other two wires, becomes zero. What will be the directions of current I, in the two cases? Also obtain the relation between the magnitudes of currents I₁ I₂ and I.
Answer: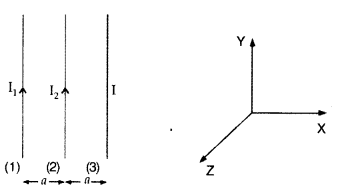

(i) Net force experienced by wire (1) can be zero only, when the current in wire (3) flows along – \(\hat{\mathrm{j}}\) i.e. downwards, it means that the forces acting on wire (1) due to wire (3) and wire (2) are equal and opposite.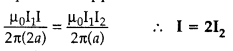

(ii) When direction of current in wire (3) is reversed then current should be along + \(\hat{\mathrm{j}}\) i.e. upwards.
For this case net force on wire (2) becomes zero, which means that the forces due to wire (1) and wire (3) are equal and opposite.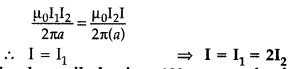

Question 79.
A circular coil, having 100 turns of wire, of radius (nearly) 20 cm each, lies in the XY plane with its centre at the origin of co-ordinates. Find the magnetic field, at the point (0, 0, 20√3 cm), when this coil carries a current of (Comptt. Delhi 2016)
Answer: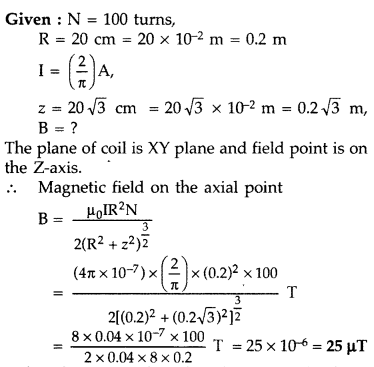

Question 80.
Write the expression for the magnetic force \(\overrightarrow{\mathbf{F}}\) acting on a charged particle q moving with velocity \(\overrightarrow{\mathbf{F}}\) in the presence of the magnetic field \(\overrightarrow{\mathbf{B}}\) in a vector form. Show that no work is done and no change in the magnitude of the velocity of the particle is produced by this force. Hence define the unit of magnetic field. (Comptt. All India 2016)
Answer:
(i) The required expression is \([latex]\overrightarrow{\mathbf{F}}=q(\vec{v} \times \overrightarrow{\mathbf{B}})\)
(ii) The magnetic force, at all instants, is, therefore, perpendicular to the instantaneous direction of \(\vec{v}\), which is also the instantaneous direction of displacement (\(\overrightarrow{d s}\)).
Since, \(\overrightarrow{\mathrm{F}}\) is perpendicular to (\(\overrightarrow{d s}\)), at all instants, work done \((=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{d s})\) is zero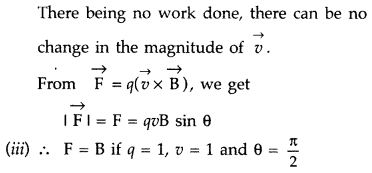

Hence, the magnetic field \(\overrightarrow{\mathrm{B}}\), at a point equals one tesla if a charge of one coulomb, moving with a velocity 1/sec, along a direction perpendicular to the direction of \(\overrightarrow{\mathrm{B}}\), experience a force of one newton.

Question 81.
A long straight wire, of circular cross section (radius = a) carries a current I which is uniformly distributed across the cross section of the wire.
Use Ampere’s circuital law to calculate the magnetic field B(r), due to this wire, at a point distance r < a and r > a from its axis. Draw a graph showing the dependence of B(r) on r. (Comptt. All India 2016)
Answer: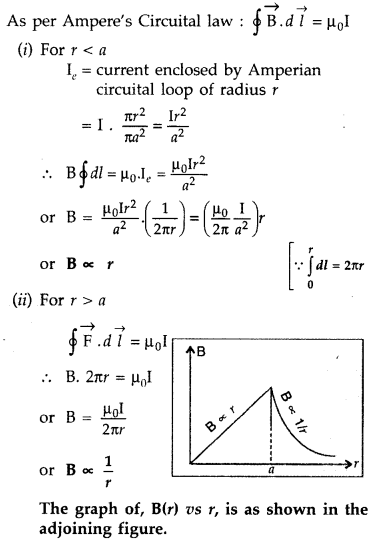

Question 82.
Derive the expression for the torque τ acting on a rectangular current loop of area A placed in a uniform magnetic field B. Show that \(\vec{\tau}=\vec{m} \times \overrightarrow{\mathbf{B}}\) where \(\vec{m}\) is the magnetic moment of the current loop given by \(\vec{m}=\overrightarrow{\mathbf{I}} \overrightarrow{\mathbf{A}}\). (Comptt. All India)
Answer:
(a) Torque on a rectangular current loop in a uniform magnetic field:
Let I = current through the coil
a, b – sides of the rectangular loop
A = ab = area of the loop
n = Number of turns in the loop
B = Magnetic field
θ = angle between magnetic field
\(\overrightarrow{\mathrm{B}}\) and area vector \(\overrightarrow{\mathrm{A}}\)

Force exerted on the arm DA inward
F₁ = I b B …[∵ F = ILB]
Force exerted on the arm BC outward
F₂ = I b B ∴ F₂ = F₁
Thus net force on the loop is zero
∴ Two equal and opposite forces form a couple which exerts a torque
∴ Magnitude of the torque on the loop is,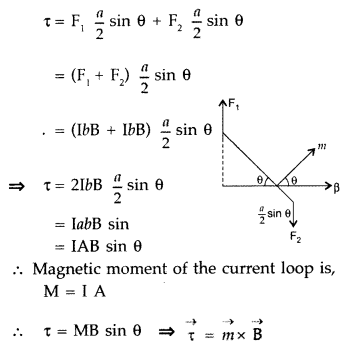

If loop has n turns then M = n I A
∴ τ = nIAB sin θ
When θ = 90° then \(\tau_{\max }=n I A B\)
When θ = 0° then τ = 0
(b) Since the momentum and the charge on both the proton and deutron are the same, the particle will follow a circular path with radius 1:1.

Question 83.
(i) Obtain the expression for the cyclotron frequency.
(ii) A deuteron and a proton are accelerated by the cyclotron. Can both be accelerated with the same oscillator frequency? Give reason to justify your answer. (Delhi 2017)
Answer:
(i) Expression for cyclotron frequency : The magnetic field provides necessary centripetal force needed by the charged particle to move in a circular path.
m = mass of the charged particle,
v = velocity,
r = radius of the circular path
q = charge,
B = Magnetic field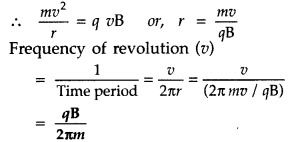

Therefore, the frequency of revolution is independent of energy of the particle.
(ii) The mass of the two particles, i.e. deuteron and proton, is different. Since cyclotron frequency depends inversely on the mass, they cannot be accelerated by the same oscillator frequency.

Question 84.
Describe the working principle of a moving coil galvanometer. Why is it necessary to use
(i) a radial magnetic field and
(ii) a cylindrical soft iron core in a galvanometer? Write the expression for current sensitivity of the galvanometer.
Can a galvanometer as such be used for measuring the current? Explain. (Delhi 2017)
Answer:
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB

The spring S_p attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring

In equilibrium state,

Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.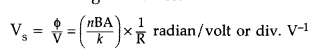

…where [R = Resistance of the coil

does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
No, the galvanometer cannot be used to measure current. It can only detect current but cannot measure as it is not calibrated. The galvanometer coil is likely to be damaged by currents in the (mA/A) range.

Question 85.
An electron of mass m_e revolves around a nucleus of charge +Ze. Show that it behaves like a tiny magnetic dipole. Hence prove that the magnetic moment associated with it is expressed as \(\vec{\mu}=-\frac{e}{2 m_{e}} \overrightarrow{\mathbf{L}}\) where L is the orbital angular momentum of the electron. Give the significance of negative sign. (Delhi 2017)
Answer:
(i) Electron, in circular motion around the nucleus, constitutes a current loop which behaves like a tiny magnetic dipole.
Current associated with the revolving electron :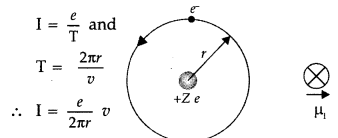

Magnetic moment of the loop, µ = IA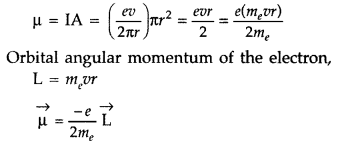

Negative sign signifies that the angular momentum of the revolving electron is opposite in direction to the magnetic moment associated with it.

Question 86.
(a) Write the expression for the force \(\overrightarrow{\mathbf{F}}\) acting on a particle of mass m and charge q moving with velocity \(\overrightarrow{\mathbf{v}}\) in a magnetic field \(\overrightarrow{\mathbf{B}}\). Under what conditions will it move in
(i) a circular path and
(ii) a helical path?
(b) Show that the kinetic energy of the particle moving in magnetic field remains constant. (Delhi 2017)
Answer:

(i) When velocity of charged particle and magnetic field are perpendicular to each other, it will move in a circular path.
(ii) When velocity is neither parallel nor perpendicular to the magnetic field, it will move in helical path.
(b) The force experienced by the charged particle, is perpendicular to the instantaneous velocity \(\vec{v}\), at all instants.
Hence the magnetic force cannot bring any change in the speed of the charged particle. Since speed remains constant, the kinetic energy also stays constant.

Question 87.
(a) State Biot-Savart law and express this law in vector form.
(b) Two identical circular coils, P and Q each of radius R, carrying currents 1 A and √3 A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils. (All India 2017)
Answer:
(a) Biot-Savart law : It states that “the magnetic field dB due to a current element d l at any point P is:
(i) directly proportional to current dB ∝ I.
(ii) directly proportional to the length dl of the element \(d \vec{B}\) ∝ dl.
(iii) directly proportional to sin θ, where θ is the angle between d\(\overrightarrow{l}\) and \(\overrightarrow{r}\),
Therefore \(d \vec{B}\) ∝ sin θ
(iv) inversely proportional to the square of the distance r from the current element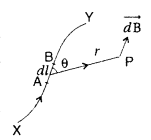

Combining (i), (ii), (iii) and (iv), we get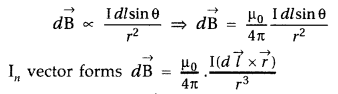

The direction of \(\overrightarrow{d \mathrm{B}}\) is perpendicular to the plane of the vector d \(\vec{l}\) and \(\vec{r}\) given by Right Handed Screw Rule.
(b) Consider a circular coil of radis r, carrying current I. It consists of a large number of small current elements of length dl. According to Biot-Savart law, magnetic field at the centre O due to current element dl is,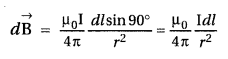

Magnetic field due to all such current elements will point into the plane of paper.
Hence total field at O is,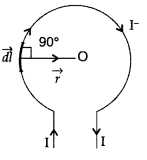


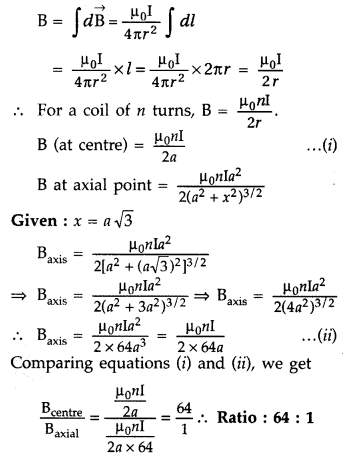
(b) Given : R_P = R_Q = R, I_p = 1 A, I_Q = √3 A
B = ? (Magnitude and direction)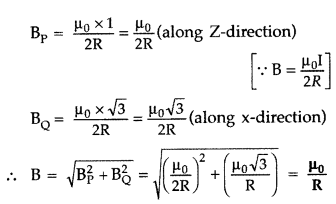

This net magnetic field B, is inclined to the field B_P, at an angle θ, where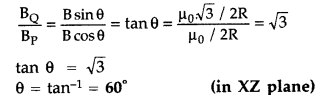

Question 88.
Two identical loops P and Q each of radius 5 cm are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils, if they carry currents equal to 3 A and 4 A respectively. (All India 2017)

Answer:

Question 89.
State the Lorentz’s force and express it in vector form. Which pair of vectors are always perpendicular to each other? Derive the expression for the force acting on a current carrying conductor of length L in a uniform magnetic field ‘B’. (Comptt. Delhi 2017)
Answer:
Lorentz’s magnetic force is force experienced by a charged particle of charge ‘q’ moving in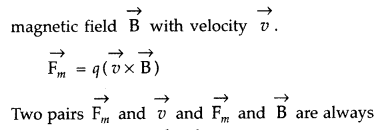

perpendicular to each other Let us consider a conductor of uniform cross-sectional area A and length ‘U having number density of electrons as V Total force on charge carriers in the conductor,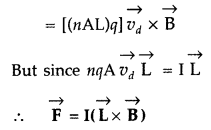

Question 90.
Define the term magnetic moment of a current loop. Derive an expression for the magnetic field at any point along the axis of a solenoid of length 21, and radius «, and number of terms per unit length n. (Comptt. Delhi 2017)
Answer:
(i) Definition of magnetic moment: Magnetic moment of a current loop is equal to the product of current flowing in the loop and its area; and its direction is along area vector as per the right handed screw rule.
(ii) Magnetic field for solenoid :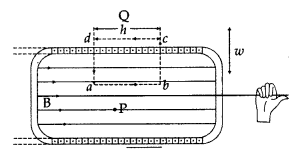

Using Ampere’s circuital law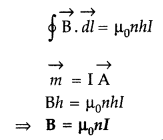

Question 91.
(a) Draw the pattern of magnetic field lines for a circular coil carrying current.
(b) Two identical circular loops X and Y of radius R and carrying the same current are kept in perpendicular planes such that they have a common centre at P as shown in the figure. Find the magnitude and direction of the net magnetic field at the point P due to the loops. (Comptt. All India 2017)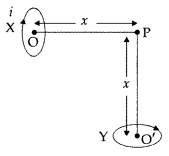

Answer:
(a) Pattern of magnetic field lines for a circular coil carrying current :
(a) Magnetic field lines :

(b) The magnetic field due to a circular coil at a point carrying current is given by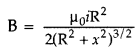

Since these two circular coils are identical and carrying the same current,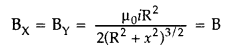

Resultant magnetic field (B_R)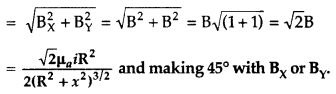

Question 92.
Define the term current sensitivity of a galvanometer. Write its SI unit. (Comptt. All India 2017)
Answer:
• Current sensitivity of a galvanometer is “deflection per unit current”. It is defined as the ratio of deflection produced in the galvanometer to the current flowing through it.

SI unit is radian per ampere.

Question 93.
A toroidal solenoid of mean radius 20 cm has 4000 turns of wire wound on a ferromagnetic core of relative permeability 800. Calculate the magnetic field in the core for a current of 3A , passing through the coil. How does the field change, when this core is replaced by a core of Bismuth? (Comptt. All India 2017)
Answer: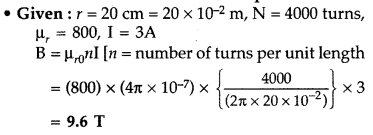

Since bismuth is diamagnetic, its μ_r < 1, therefore the magnetic field in the core will be very much reduced.

Long Answer Type

Question 1.
(a) A particle of charge ‘q’ and mass ‘m’, moving with velocity \(\vec{v}\) is subjected to a uniform magnetic field \(\vec{B}\) perpendicular to its velocity. Show that the particle describes a circular path. Obtain an expression for the radius of the circular path of the particle.
Answer:
Let a charged particle of charge q and mass m be moving with velocity \(\vec{v}\) right angle to the field (i.e. in the plane of the paper), then magnetic force \(\vec{F}\) acting on the charge q will be
\(\vec{F}=q(\vec{v} \times \vec{B})\)
or
F = qvB sin 90°
or
F = qvB … (1)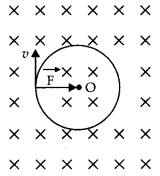

As this forces fact at a right angle to the velocity V of the charged particle, the slot is unable to change the velocity but can make the charged particle move In a circular path.

If r is the radius of the circle, then the centripetal force required by the charged particle will be
\(F_{c}=\frac{m v^{2}}{r}\)

This centripetal force Is provided by the magnetic force acting on the charged particle.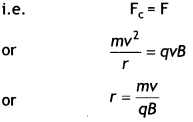

(b) Explain, how its path will be affected if the velocity \(\vec{v}\) makes an angle (θ ≠ 90°) with the direction of the magnetic field. (CBSE 2019C)
Answer:
If (θ ≠ 90°), the velocity \(\vec{v}\) of the moving charge can be resolved into two components v cos θ, in the direction of the magnetic field and make it v sin θ, in the direction perpendicular to the magnetic field. The charged particle under the combined effect of the two components of velocities wilt cover linear as well as a circular path, i.e. helical path whose axis is parallel to the magnetic field.

Question 2.
(a) Obtain the conditions under which an electron does not suffer any deflection while passing through a magnetic field.
Answer:
No deflection suffered by the electron if it moves parallel or anti-parallel to the magnetic field.

(b) Two protons P and Q moving with the same speed pass through the magnetic fields \(\vec{B}_{1}\) and \(\vec{B}_{2}\) respectively, at right angles to the field directions. If \(\left|\vec{B}_{2}\right|>\left|\vec{B}_{1}\right|\), which of the two protons will describe the circular path of smaller radius? Explain. (CBSEAI 2019)
Answer:
The radius of the circular path traveled by a charged particle in a magnetic field is given by
r = \(\frac{mv}{Bq}\)

Therefore, \(\frac{r_{1}}{r_{2}}=\frac{B_{2}}{B_{1}}\)

As \(\left|\vec{B}_{2}\right|>\left|\vec{B}_{1}\right|\) therefore, r₂ < r₁

Question 3.
A straight wire of length L is bent into a semi-circular loop. Use Biot-Savart law to deduce an expression for the magnetic field at its center due to the current l passing through it. (CBSE Delhi 2011C)
Answer:
Consider a straight wire of length L. Let it be bent into a semicircular arc of radius r as shown,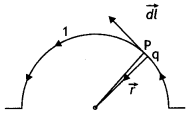

Then πr = L or r = L/π

Let a current I be passed through it. Divide the semi-circular loop into a large number of elements; consider one such element PQ of length dl. Then the small magnetic field cfB produced at the point O is

dB = \(\frac{\mu_{0}}{4 \pi} \frac{l d l \sin 90^{\circ}}{r^{2}}=\frac{\mu_{0}}{4 \pi} \frac{l d l}{r^{2}}\) outwards at point O.

Therefore total magnetic field at point O is
B = \(\int_{0}^{\pi r} \frac{\mu_{0}}{4 \pi} \frac{l d l}{r^{2}}=\frac{\mu_{0} l}{4 r}=\frac{\mu_{0} l \pi}{4 L}\)

Question 4.
A circular coil of N turns and radius R carries a current l. It is unwound and rewound to make another coil of radius R/2, current l remaining the same. Calculate the ratio of the magnetic moments of the new coil and the original coil. (CBSE AI 2012)
Answer:
The magnetic moment of a current-carrying coil is given by
M = n lA = n l πR²

When the coil is unwound and wound into another coil of radius R/2, the number of turns will double, i.e. n = 2
Therefore, n₁ = 1, n₂ = 2, R₁ = R, R₂ = R/2, hence

Therefore \(\frac{M_{2}}{M_{1}}=\frac{n_{2} / \pi R_{2}^{2}}{n_{1} / \pi R_{1}^{2}}=\frac{2}{4}=\frac{1}{2}\)

Question 5.
Two identical coils P and Q each of radius R are lying in perpendicular planes such that they have a common center. Find the magnitude and direction of the magnetic field at the common center when they carry currents equal to l and \(\sqrt{3}\) l respectively. (CBSE Al 2019)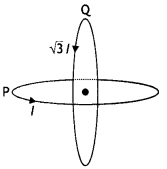

Answer:
Magnetic field at the common centre due to coil P
\(B_{1}=\frac{\mu_{o} l}{2 R}\)

Magnetic field at the common centre due to coil Q
\(B_{2}=\frac{\mu_{0} \sqrt{3} l}{2 R}\)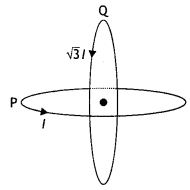

The two fields are mutually perpendicular, therefore, the resultant field at the common centre is
B = \(\sqrt{B_{1}^{2}+B_{2}^{2}}=\sqrt{\left(\frac{\mu_{o} l}{2 R}\right)^{2}+\left(\frac{\mu_{0} \sqrt{3} 1}{2 R}\right)^{2}}\)
= \(\frac{\mu_{o} l}{R}\)

Let the resultant field make an angle θ with magnetic field B₂ as shown
tan θ = \(\frac{B_{1}}{B_{2}}=\frac{1}{\sqrt{3}}\) ⇒ θ = 30°

Question 6.
Find the condition under which the charged particles moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speed. (CBSE A! 2017)
Answer:
Consider crossed electric and magnetic fields. Let the particle enter perpendicular to both these fields. Due to this, the electric and magnetic forces are in opposite directions. Suppose, we adjust the value of E and B such that the magnitudes of the two forces are equal. Then, the total force on the charge is zero and the charge will move in the fields undeflected.

This happens when, or qE = qvB or v = E/B

This condition can be used to select charged particles of a particular velocity out of a beam containing charges moving at different speeds (irrespective of their charge and mass). The crossed E and B fields, therefore, serve as a velocity selector. Only particles with speed E/B pass undeflected through the region of crossed fields.

Question 7.
(a) Define the SI unit of current in terms of the force between two parallel current-carrying conductors.
Answer:
One ampere is that much current which when flowing through each of the two infinitely long straight conductors held 1 meter apart in space, produces a force of F = 2 × 10^-7 N per meter of their length.

(b) Two long straight parallel conductors carrying steady currents l_a and l_b along the same direction are separated by a distance d. How does one explain the force of attraction between them? If a third conductor carrying a current l in the opposite direction is placed just in the middle of these conductors, find the resultant force acting on the third conductor. (CBSE AI, Delhi 2018C)
Answer:
The magnetic field produced by one current applies a force on the other current-carrying conductor. By Fleming’s left-hand rule the forces acting on each due to other is directed towards each other. This shows attraction.

Force on C conductor due to conductor A
F_ca = \(\frac{\mu_{0} l_{a} l_{c}}{\pi d}\) repulsive

Force on C conductor due to conductor B
F_cb = \(\frac{\mu_{0} l_{b} l_{c}}{\pi d}\)

\(F_{\mathrm{ac}}-F_{\mathrm{bc}}=\frac{\mu_{0} l_{\mathrm{c}}}{\pi d}\left(l_{a}-l_{b}\right)\)

Question 8.
ExplaIn how will you convert a galvanometer into a voltmeter to read a maximum potential of ‘V’ volt. Can one use a voltmeter to measure the emf of a cell? Justify your answer.
Answer:
Suppose a galvanometer having resistance G is to be converted into a voltmeter, which can measure the potential difference from O to V volt. Let a high resistance R be joined in senes with the galvanometer for this purpose. Its value is so chosen that when the galvanometer with the resistance is connected between two points having a potential difference of V volt, the gaLvanometer gives full-scale deflection. It is clear from the figure below that
V = l_g (R + G)
or
R = \(\frac{v}{l_{g}}\) – G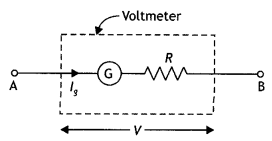

On connecting the above high resistance in series with a galvanometer, the galvanometer is converted into a voltmeter of range V volt.

A voltmeter cannot measure the emf of the cell as it draws current from the cell while measuring the potential differences.

Question 9.
Explain how will you convert a galvanometer into an ammeter to read a maximum current of ‘l’ ampere. An ammeter is always connected in series with a circuit. Why? (CBSE AI 2019)
Answer:
Suppose a galvanometer of resistance G is to be converted into an ammeter having range 0 to l ampere. Let lg be the current,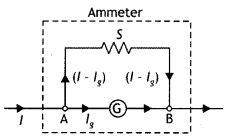

which gives full-scale deflection in the galvanometer. Suppose S is the appropriate shunt required for this purpose, i.e. when shunt S Is used, current ‘g passes through the galvanometer and the remaining (l – l_g) passes through the shunt as shown in the figure below. Since the shunt and the galvanometer are connected In parallel therefore the potential differences across both wilL be the same. Hence
l_g G = (l – l_g) S ….(1)

S = \(\frac{l_{s} G}{l-l_{s}}\) ….(2)

An ammeter is used to measure current; therefore, it is connected in senes so that the entire current passes through it. Moreover, an ammeter is a low resistance device.

Question 10.
A steady current (l₁) flows through a long straight wire. Another wlrè carrying steady current (l₂) In the same direction is kept close and parallel to the first wire. Show with the help of a diagram how the magnetic field due to the current l₁ exerts a magnetic force on the second wire. Write the expression for this force. (CBSE AI 2011)
Answer:
The diagram is as shown below.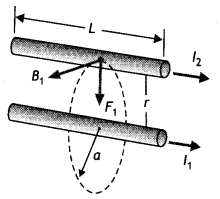

Magnetic field B1 is produced by the wire carrying current l₁ on a wire carrying current l₂. Thus the second current-carrying wire is placed in the magnetic field produced by the first as a result it experiences a force is given by F = \(\frac{\mu_{0} l_{1} l_{2}}{2 \pi r}\) per unit length.

Question 11.
(a) Using Biot-Savart’s law, derive an expression for the magnetic field at the centre of a circular coil of radius R, number of turns N, carrying current i.
(b) Two small identical circular coils marked 1, 2 carry equal currents and are placed with their geometric axes perpendicular to each other as shown in the figure. Derive an expression for the resultant magnetic field at O. (Delhi 2017)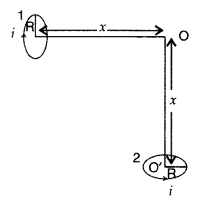

Answer:
(a) Consider a circular loop of wire of radius R carrying current I. The entire loop can be divided into a large number of small current elements.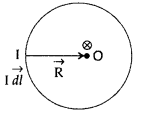

According to Biot-Savart’s law, magnetic field due to current element ‘Idl’ at the centre O of a coil is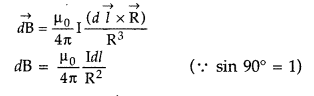

The direction of d \(\vec{l}\) is along the tangent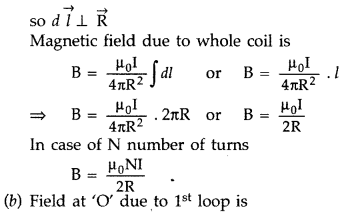

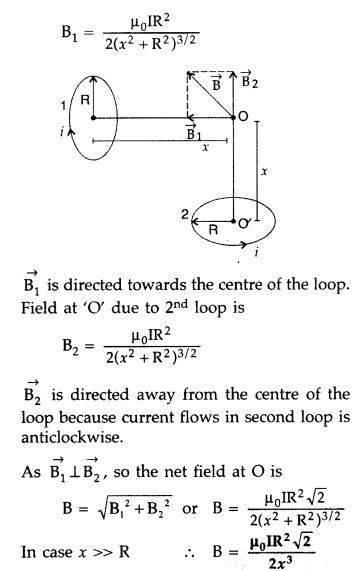
Question 12.
Draw a schematic diagram of a cyclotron. Explain its underlying principle and working, stating clearly the function of the electric and magnetic field applied on a charged particle. Deduce an expression for the period of revolution and show that it does not depend on the speed of the charged particle. (Delhi 2017)
Answer:
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.

Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D₁ to be negative. It gets accelerated towards dee D₁. As it enters the dee D₁, it does not experience any electric field due to shielding
effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.

At the instant the proton comes out of dee D₁. It finds dee D₁ positive and dee D₂ negative. It now gets accelerated towards dee D₂. It moves faster through dee D₂ describing a larger semicircle than before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.

Question 13.
Draw a schematic sketch of a cyclotron. Explain briefly how it works and how it is used to accelerate the charged particles.
(i) Show that time period of ions in a cyclotron is independent of both the speed and radius of circular path.
(ii) What is resonance condition? How is it used to accelerate the charged particles? (All India 2017)
Answer:
(i) Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.

Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D₁ to be negative. It gets accelerated towards dee D₁. As it enters the dee D₁, it does not experience any electric field due to shielding effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.

At the instant the proton comes out of dee D₁. It finds dee D₁ positive and dee D₂ negative. It now gets accelerated towards dee D₂. It moves faster through dee D₂ describing a larger semicircle than before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.

(ii) The frequency v_a of the applied voltage is adjusted so that the polarity of the dees is reversed in the same time that it takes the ions to complete one-half of the revolution. The requirement v_a = v_c is called the resonance condition.
The phase of the supply is adjusted so that when the positive ions arrive at the edge of D₁, D₂ is at a lower potential and the ions are accelerated across the gap.

Question 14.
(a) Two straight long parallel conductors carry currents I₁ and I₂ in the same direction. Deduce the expression for the force per unit length between them.
Depict the pattern of magnetic field lines around them.
(b) A rectangular current carrying loop EFGH is kept in a uniform magnetic field as shown in the figure.
(i) What is the direction of the magnetic moment of the current loop?
(ii) When is the torque acting on the loop
(A) maximum,
(B) zero? (All India 2017)

Answer:
Consider two infinitely long parallel conductors carrying current I₁ and I₂ in the same direction.
Let d be the distance of separation between these two conductors.

Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10^-7 N on each metre of the other wire.
Then current flowing is 1A


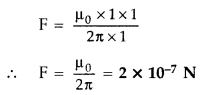
(i) Magnetic moment will be out of the plane from the surface HEFG.
(ii) Torque
(A) Torque is maximum when MII B i.e., when it gets rotated by 90°.
(B) Torque is minimum when M and B are at 270° to each other.

Question 15.
(a) With the help of a diagram, explain the principle and working of a moving coil galvanometer.
(b) What is the importance of a radial magnetic field and how is it produced?
(c) Why is it that while using a moving coil galvanometer as a voltmeter a high resistance in series is required whereas in an ammeter a shunt is used? (All India)
Answer:
(a) Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB

The spring S_p attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring

In equilibrium state,

Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.

(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.

…where [R = Resistance of the coil

does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

(b) For radial magnetic field, sin θ = 1,
so torque τ = NIAB.
Thus when radial magnetic field is used, the deflection of the coil is proportional to the current flowing through it. Hence a linear scale can be used to determine the deflection of the coil.

(c) A high resistance is joined in series with a galvanometer so that when the arrangement (voltmeter) is used in parallel with the selected section of the circuit, it should draw least amount of current. In case voltmeter draws appreciable amount of current, it will disturb the original value of potential difference by a good amount.

To convert a galvanometer into ammeter, a shunt is used in parallel with it so that when the arrangement is joined in series, the maximum current flows through the shunt, and thus the galvanometer is saved from its damage, when the current is passed through ammeter.

Question 16.
(a) Derive an expression for the force between two long parallel current carrying conductors.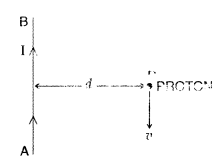

(b) Use this expression to define S.I. unit of current.
(c) A long straight wire AB carries a current I. A proton P travels with a speed v, parallel to the wire, at a distance d from it in a direction opposite to the current as shown in the figure. What is the force experienced by the proton and what is its direction? (All India)
Answer:
(a) For (a) and (b) :
Consider two infinitely long parallel conductors carrying current I₁ and I₂ in the same direction.
Let d be the distance of separation between these two conductors.

Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10^-7 N on each metre of the other wire.
Then current flowing is 1A


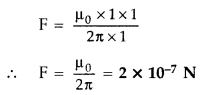
(c) Force experienced by the proton,

As magnetic field due to the current carrying wire is directed into the plane of the paper (θ = 90°)

Force is directed away from the current carrying wire or in the right direction of observer.

Question 17.
State Biot-Savart law, giving the mathematical expression for it.
Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis.
How does a circular loop carrying current behave as a magnet? (Delhi 2011)
Answer:
According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.


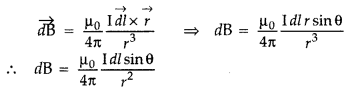
Magnetic field on the axis of circular current loop :

As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain

In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.

Question 18.
With the help of a labelled diagram, state the underlying principle of a cyclotron. Explain clearly how it works to accelerate the charged particles. Show that cyclotron frequency is independent of energy of the particle. Is there an upper limit on the energy acquired by the particle? Give reason. (Delhi 2011)
Answer:
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.

Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D₁ to be negative. It gets accelerated towards dee D₁. As it enters the dee D₁, it does not experience any electric field due to shielding effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.

At the instant the proton comes out of dee D₁. It finds dee D₁ positive and dee D₂ negative. It now gets accelerated towards dee D₂. It moves faster through dee D₂ describing a larger semicircle than before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.

Yes, there is an upper limit. The increase in the kinetic energy of particles is qv. Therefore, the radius of their path goes on increasing each time, their kinetic energy increases. The lines are repeatedly accelerated across the dees, untill they have the required energy to have a radius approximately that of the dees. Hence, this is the upper limit on the energy required by the particles due to definite size of dees.

Question 19.
(a) State the principle of the working of a moving coil galvanometer, giving its labelled diagram.
(b) “Increasing the current sensitivity of a galvanometer may not necessarily increase its voltage sensitivity.” Justify this statement
(c) Outline the necessary steps to convert a galvanometer of resistance RG into an ammeter of a given range. (All India 2011)
Answer:
(a)
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB

The spring S_p attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring

In equilibrium state,

Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.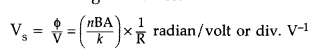

…where [R = Resistance of the coil

does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

(b) Since \(\mathrm{v}_{\mathrm{s}}=\frac{\mathrm{I}_{\mathrm{s}}}{\mathrm{R}}\) increase in current sensitivity may not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

(c) Conversion of galvanometer into ammeter: By just connecting a low resistance known as shunt in parallel to the galvanometer, it can be converted into an ammeter.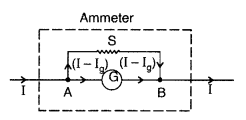

Let G = resistance of the galvanometer.
I_g = the current with which galvanometer gives full scale deflection.
S = shunt resistance
I – I_g = current through the shunt.
As the galvanometer and shunt are connected in parallel,
Potential difference across the galvanometer = Potential difference across the shunt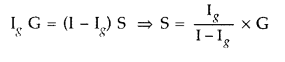

Question 20.
(a) Write the expression for the force, \(\overrightarrow{\mathbf{F}}\), acting on a charged particle of charge ‘q’, moving with a velocity latex]\overrightarrow{\mathbf{v}}[/latex] in the presence of both electric field \(\overrightarrow{\mathrm{E}}\) and magnetic field \(\overrightarrow{\mathrm{B}}\). Obtain the condition under which the particle moves undeflected through the fields.
(b) A rectangular loop of size l × b carrying a steady current I is placed in a uniform magnetic field \(\overrightarrow{\mathrm{B}}\). Prove that the torque \(\vec{\tau}\) acting on the loop is given by \(\vec{\tau}=\vec{m} \times \overrightarrow{\mathrm{B}}\), where \(\overrightarrow{\mathrm{m}}\) is the magnetic moment of the loop. (All India 2011)
Answer:
(a) A charge q in an electric field \(\overrightarrow{\mathrm{E}}\) experiences the electric force, \(\overrightarrow{\mathrm{F}}_{e}=q \overrightarrow{\mathrm{E}}\)

This force acts in the direction of field \(\overrightarrow{\mathrm{E}}\) and is independent of the velocity of the charge.

The magnetic force experienced by the charge q moving with velocity \(\overrightarrow{\mathrm{v}}\) in the magnetic field B is given by

This force acts perpendicular to the plane of \(\overrightarrow{\mathrm{V}}\) and \(\overrightarrow{\mathrm{B}}\) and depends on the velocity \(\overrightarrow{\mathrm{v}}\) of the charge.

The total force, or the Lorentz force, experienced by the charge q due to both electric and magnetic field is given by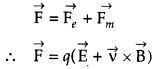

Hence, A stationary charged particle does not experience any force in a magnetic field. (b) Torque on a current loop in a uniform magnetic field.
Let I = Current flowing through the coil PQRS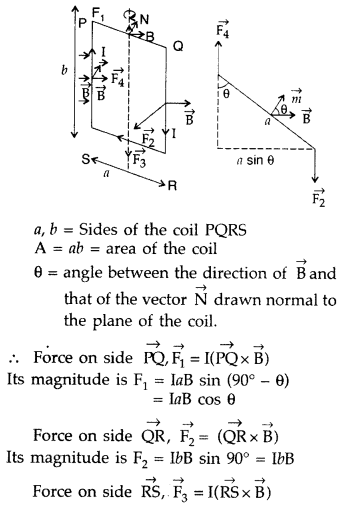

Its magnitude is, F3 = IaB sin(90° + 0)

Question 21.
(a) Explain, giving reasons, the basic difference in converting a galvanometer into
(i) a voltmeter and
(ii) an ammeter.
(b) Two long straight parallel conductors carrying steady currents I₁ and I₂ are separated by a distance’d’ Explain briefly, with the help of a suitable diagram, how the magnetic field due to one conductor acts on the other. Hence deduce the expression for the force acting between the two conductors. Mention the nature of this force.
Answer:
(a) (i) Voltmeter is connected in parallel with the circuit element across which the potential difference is intended to be measured.

A galvanometer can be converted into a voltmeter by connecting a higher resistance in series with it. The value of this resistance is so adjusted that only current I which produces full scale deflection in the galvanometer, passes through the galvanometer.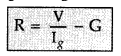

(ii) A galvanometer can be converted into an ammeter by connecting a low value
resistance in parallel with it.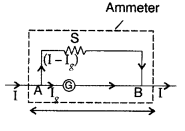


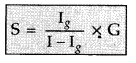
(b)
Consider two infinitely long parallel conductors carrying current I₁ and I₂ in the same direction.
Let d be the distance of separation between these two conductors.

Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10^-7 N on each metre of the other wire.
Then current flowing is 1A

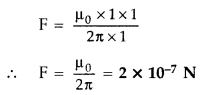
Question 22.
(a) Explain briefly with the help of a labelled diagram, the principle and working of a moving coil galvanometer.
(b) Define the term ‘current sensitivity’ of a galvanometer. How is it that increasing current sensitivity may not necessarily increase its voltage sensitivity? Explain. (Comptt. All India 2011)
Answer:
(a) Principle and working of a moving coil galvanometer:
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB

The spring S_p attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring

In equilibrium state,

Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.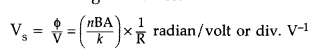

…where [R = Resistance of the coil

does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
(b) Current sensitivity:

(a)
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB

The spring S_p attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring

In equilibrium state,

Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.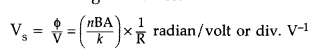

…where [R = Resistance of the coil

does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

(b) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

may not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

Question 23.
(a) State Biot-Savart law. Deduce the expression for the magnetic field due to a circular current carrying loop at a point lying on its axis.
(b) Two long parallel wires carry currents I₁ and I₂ flowing in the same direction. When a third current carrying wire is placed parallel and coplanar in between the two, find the condition when the third wire would experience no force due to these two wires. (Comptt. All India 2011)
Answer: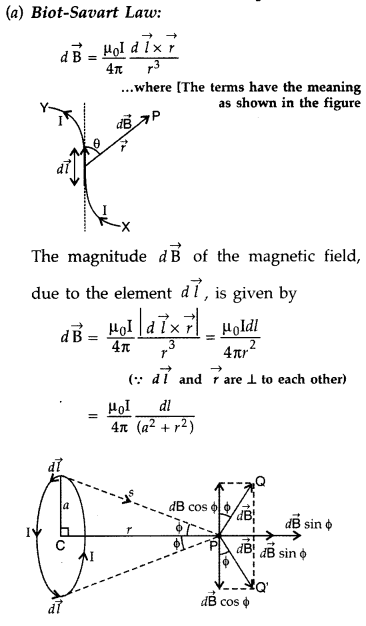


The components perpendicular to the axis of the loop will be equal and opposite to component along the axis of the loop and will cancel out. Their axial components will be in the same direction, i.e., along CP and get added up.
∴ Total magnetic field at point P in the direction CP is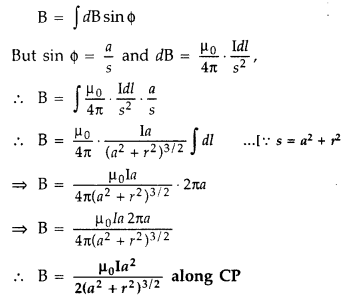

The direction of this field is along the axis, in the sense given by the right hand (thumb) rule.
(b) The force \(\overrightarrow{f_{1}}\) on the third wire due to wire 1 is directed opposite to the force \(\overrightarrow{f_{2}}\) on the third wire due to wire 2. Hence, the net force on the third wire would become 0.

Question 24.
(a) Derive the expression for the torque on a rectangular current carrying loop suspended in a uniform magnetic field.
(b) A proton and a deutron having equal momenta enter in a region of uniform magnetic field at right angle to the direction of the field. Depict their trajectories in the field. (Delhi 2013)
Answer:
(a) Torque on a rectangular current loop in a uniform magnetic field:
Let I = current through the coil
a, b – sides of the rectangular loop
A = ab = area of the loop
n = Number of turns in the loop
B = Magnetic field
θ = angle between magnetic field
\(\overrightarrow{\mathrm{B}}\) and area vector \(\overrightarrow{\mathrm{A}}\)

Force exerted on the arm DA inward
F₁ = I b B …[∵ F = ILB]
Force exerted on the arm BC outward
F₂ = I b B ∴ F₂ = F₁
Thus net force on the loop is zero
∴ Two equal and opposite forces form a couple which exerts a torque
∴ Magnitude of the torque on the loop is,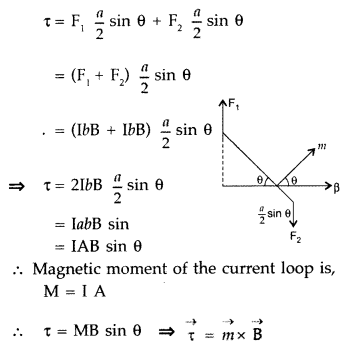

If loop has n turns then M = n I A
∴ τ = nIAB sin θ
When θ = 90° then \(\tau_{\max }=n I A B\)
When θ = 0° then τ = 0
(b) Since the momentum and the charge on both the proton and deutron are the same, the particle will follow a circular path with radius 1:1.

Question 25.
(a) Using Biot-Savart’s law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop.
(b) What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show that the magnetic field in the open space inside and exterior to the toroid is zero. (All India 2013)
Answer:
(a) Let P be the point on the axis of a circular loop or coil of radius a carrying current I. The distance of P from the centre of loop is x.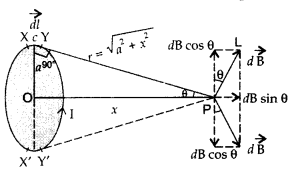

According to Biot-Savart’s Law, magnetic field due to a small element XY (dl) at point P is


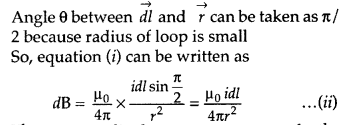
The perpendicular components of the magnetic field due to these elements being equal and opposite cancel each other. Hence the total contribution of perpendicular components, (i.e. dB cos θ) to the net magnetic field is zero.

On the other hand, dB sin θ component of magnetic field due to each element of the coil or loop is directed in the same direction.

Therefore, magnetic field at point P due to the whole coil or loop is equal to the sum of dB sin θ components of magnetic field due to each element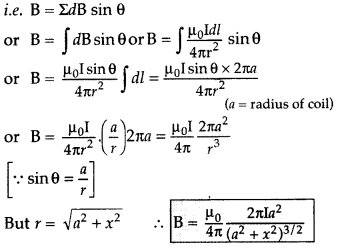

The right hand thumb rule can be used to find the direction of the field.
(b) A toroid is a solenoid bent to form a ring shape.
Let N number of turns per unit length of toroid and I be current flowing in it.

Consider a loop (region II) of radius r passes through the centre of the toroid.
Let (region II) \(\overrightarrow{\mathrm{B}}\) be magnetic field along the loop is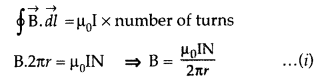

Let (region I) B₁ be magnetic field outside toroid in open space. Draw an amperian loop L₂ of radius r₂ through point Q.
Now applying ampere’s law :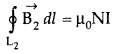

As I = 0, because the circular turn current coming out of plane of paper is cancelled exactly by current going into it, so net I = 0, equation (i) becomes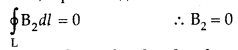

Question 26.
(a) Draw a schematic sketch of a cyclotron. Explain clearly the role of crossed electric and magnetic field in accelerating the charge. Hence derive the expression for the kinetic energy acquired by the particles.
(b) An α-particle and a proton are realeased from the centre of the cyclotron and made to accelerate.
(i) Can both be accelerated at the same cyclotron frequency? Give reason to justify your answer.
(ii) When they are accelerated in turn, which of the two will have higher velocity at the exit slit of the dees? (All India 2013)
Answer:
(a) Cyclotron :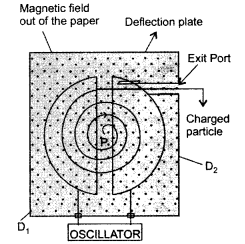

Role of crossed electric and magnetic field in cyclotron : The magnetic field makes the charged particle to cross the gap between the dees again and again by making it move along a circular path, while the oscillating electric field, applied across the dees, accelerates the charged particle again and again and hence increases its K.E.
Expression :
If the velocity v is perpendicular to the magnetic field B, the magnetic force is perpendicular to both v and B and acts like a centripetal force. It has a magnitude qvB. Equating the two expressions for centripetal force,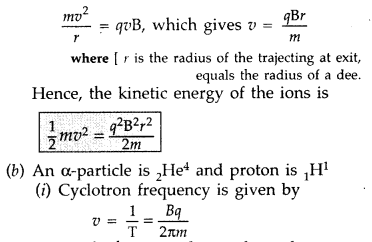

No, both cannot be accelerated to same frequency because frequency depends upon mass and charge.
(ii) Velocity is given by the formula v = \(\frac{B q r}{m}\)
Velocity is also inversely proportional to mass and directly proportional to charge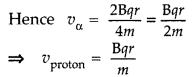

Velocity of proton is higher than that α-particle.

Question 27.
State Biot-Savart law, expressing it in the vector form. Use it to obtain the expression for the magnetic field at an axial point, distance ‘d’ from the centre of a circular coil of radius V carrying current T. Also find the ratio of the magnitudes of the magnetic field of this coil at the centre and at an axial point for which
d = a√3. (Comptt. Delhi 2013)
Answer:
(a) Biot-Savart law : It states that “the magnetic field dB due to a current element d l at any point P is:
(i) directly proportional to current dB ∝ I.
(ii) directly proportional to the length dl of the element \(d \vec{B}\) ∝ dl.
(iii) directly proportional to sin θ, where θ is the angle between d\(\overrightarrow{l}\) and \(\overrightarrow{r}\),
Therefore \(d \vec{B}\) ∝ sin θ
(iv) inversely proportional to the square of the distance r from the current element


Combining (i), (ii), (iii) and (iv), we get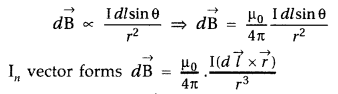

The direction of \(\overrightarrow{d \mathrm{B}}\) is perpendicular to the plane of the vector d \(\vec{l}\) and \(\vec{r}\) given by Right Handed Screw Rule.
(b) Consider a circular coil of radis r, carrying current I. It consists of a large number of small current elements of length dl. According to Biot-Savart law, magnetic field at the centre O due to current element dl is,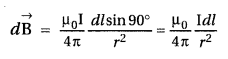

Magnetic field due to all such current elements will point into the plane of paper.
Hence total field at O is,


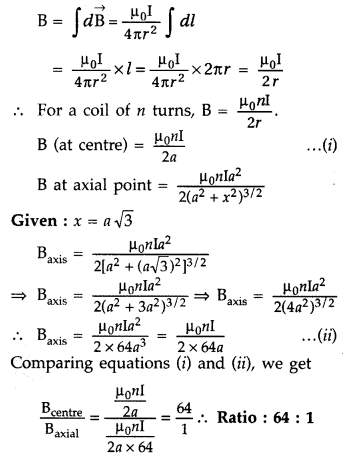
Question 28.
(a) Draw the magnetic field lines due to a current carrying loop.
(b) State using a suitable diagram, the working principle of a moving coil galvanometer. What is the function of a radial magnetic field and the soft iron core used in it?
(c) For converting a galvanometer into an ammeter, a shunt resistance of small value is used in parallel, whereas in the case of a voltmeter a resistance of large value is used in series. Explain why. (Comptt. Delhi 2011)
Answer:
(a) Magnetic field lines :

(b) Moving coil galvanometer. It is a device used for the detection and measurement of small electric current.
Principle. The working is based on the fact that a current carrying coil suspended in a magnetic field experiences a torque.
Construction. It consists of a coil having a large number of turns of insulated copper wire wound on a metallic frame. The coil is suspended by means of a phosphor-bronze strip and is surrounded by a horse-shoe magnet NS. A hair spring is attached to lower end of the coil. The other end of the spring is attached to the scale through a pointer.

Working. When current is passed, say along ABCD, the couple acts on it. Since the plane remains always parallel to the magnetic field in all positions of the coil (radial field), the force on the vertical arms always remains perpendicular to the place of the coil.

Let, I be the current flowing through coil,
B be magnetic field supposed to be uniform and always parallel to the coil, A be area of the coil
Deflecting torque acting on the coil is,
τ = nI BA sin 900

Due to deflecting torque, the coil rotates and suspension wire gets twisted. A restoring torque is set up in the suspension fibre. If <|) is angle through which the coil rotates and k is the restoring torque per unit angular twist, then restoring torque, τ = kϕ
In equilibrium,
Deflecting torque = Restoring torque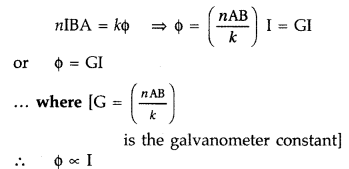

This provide a linear scale for the galvanometer.
Function of a radial magnetic field : Radial magnetic field being normal in all directions is formed to get maximum torque.
Function of Soft iron core, which not only makes the field radial but also increases the strength of the magnetic field.
(c) One uses a shunt resistance in parallel with the galvanometer, so that most of the current passes through the shunt. In the case of a voltmeter, a resistance of large value is used in series because it must draw a very small current, otherwise the voltage measurement will disturb the original set up by an amount which is very large.

Question 29.
(a) Deduce an expression for the frequency of revolution of a charged particle in a magnetic field and show that it is independent of velocity or energy of the particle.
(b) Draw a schematic sketch of a cyclotron. Explain, giving the essential details of its construction, how it is used to accelerate the charged particles. (All India 2011)
Answer:
(a) When a charged particle with charge q moves inside a magnetic field \(\overrightarrow{\mathrm{B}}\) with velocity v, it experiences a force, which is given by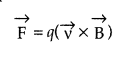

Here, \(\overrightarrow{\mathrm{v}}\) is perpendicular to \(\overrightarrow{\mathrm{B}}\), \(\overrightarrow{\mathrm{F}}\) is the force on the charged particle which acts as the centripetal force and makes it move along a circular path.

Let m be the mass of the charged particle and r be the radius of the circular path.
Time period of circular motion of the charged particle can be calculated as shown below:

Therefore, the frequency of the revolution of the charged particle is independent of the velocity or the energy of tire particle.
(b) Cyclotron.
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.

Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D₁ to be negative. It gets accelerated towards dee D₁. As it enters the dee D₁, it does not experience any electric field due to shielding effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.

At the instant the proton comes out of dee D₁. It finds dee D₁ positive and dee D₂ negative. It now gets accelerated towards dee D₂. It moves faster through dee D₂ describing a larger semicircle than before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.

Question 30.
(a) Draw a labelled diagram of a moving coil galvanometer. Describe briefly its principle and working.
(b) Answer the following :
(i) Why is it necessary to introduce a cylindrical soft iron core inside the coil of a galvanometer?
(ii) Increasing the current sensitivity of a galvanometer may not necessarily increase its voltage sensitivity. Explain, giving reason. (All India 2011)
Answer:
(a) Moving coil galvanometer.
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB

The spring S_p attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring

In equilibrium state,

Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.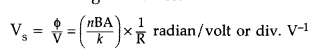

…where [R = Resistance of the coil

does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
(b) (i) Iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(ii) Current sensitivity and voltage sensitivity.

(a)
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB

The spring S_p attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring

In equilibrium state,

Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.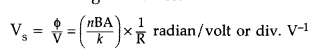

…where [R = Resistance of the coil

does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

(b) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

may not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

Question 31.
(a) State Ampere’s circuital law. Use this law to obtain the expression for the magnetic field inside an air cored toroid of average radius r, having ‘n’ turns per unit length and carrying a steady current I.
(b)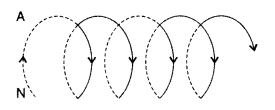
An observer to the left of a solenoid of N turns each of cross section area ‘A’ observes that a steady current I in it flows in the clockwise direction. Depict the magnetic field lines due to the solenoid specifying its polarity and show that it acts as a bar magnet of magnetic moment m = NIA. (Delhi 2011)
Answer:
(a) (i) Ampere’s Circuital Law. Line integral of magnetic field over a closed loop is equal to |i0 times the total current passing through the surface enclosed by the loop. Alternatively

(ii) Expression for magnetic field inside toroid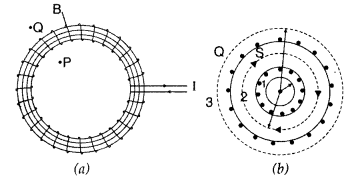

Let the current flowing through each turn of the toroid be I. The total number of turns equals n(2nr) where n is the number of turns per unit length. Applying Ampere’s circuital law, for the Amperian loop, for interior points.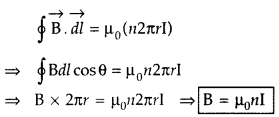

This is the expression for magnetic field inside air-cored toroid.
(b)
(i)Depiction of magnetic field for a solenoid.

(ii) The solenoid contains N loops, each carrying a current I. Therefore, each loop acts as a magnetic dipole. The magnetic moment for a current I, flowing in loop of area (vector) A is given by, m = IA. The magnetic moments of all loops are aligned along the same direction.
Hence, net magnetic moment equals NIA.

Question 32.
Explain, using a labelled diagram, the principle and working of a moving coil galvanometer.
(a) What is the function of
(i) uniform radial magnetic field,
(ii) soft iron core?
(b)Define the terms
(i) current sensitivity and
(ii) voltage sensitivity of a galvanometer. Why does increasing the current sensitivity not necessarily increase voltage sensitivity? (All India 2011)
Answer:
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB

The spring S_p attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring

In equilibrium state,

Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.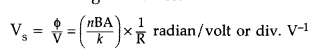

…where [R = Resistance of the coil

does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

Question 33.
(a) Write, using Biot-Savart law, the expression for the magnetic field \(\overrightarrow{\mathrm{B}}\) due to an element d\(\overrightarrow{\mathrm{l}}\) carrying current I at a distance r from it in a vector form.
Hence derive the expression for the magnetic field due to a current carrying loop of radius R at a point P distant x from its centre along the axis of the loop.
(b) Explain how Biot-Savart law enables one to express the Ampere’s circuital law in the integral form, viz.,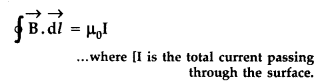
(All India 2011)
Answer:
According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.


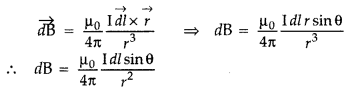
Magnetic field on the axis of circular current loop :

As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain

In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.

(b) Biot-Savart law can be expressed as Ampere’s Circuital law by considering the surface to be made up of a large number of loops. The sum of the tangential components of the magnetic field multiplied by the length of all such elements leads to integral. Ampere’s circuital law states that this’ integral is equal to p0 times the total current passing through that surface, i.e.,

Question 34.
(a) Use Biot-Savart law to derive the expression for the magnetic field due to a circular coil of radius R having N turns at a point on the axis at a distance V from its centre. Draw the magnetic field lines due to this coil.
(b) A current ‘I’ enters a uniform circular loop of radius ‘R’ at point M and flows out at N as shown in the figure.

Obtain the net magnetic field at the centre of the loop. (Comptt. Delhi 2011)
Answer:
(a) Biot-Savart Law to derive expression of magnetic field.
According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.


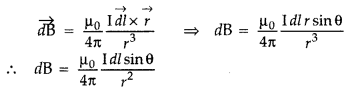
Magnetic field on the axis of circular current loop :

As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain

In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.
Magnetic field lines due to circular coil.

(a) Magnetic field lines :

(b) Moving coil galvanometer. It is a device used for the detection and measurement of small electric current.
Principle. The working is based on the fact that a current carrying coil suspended in a magnetic field experiences a torque.
Construction. It consists of a coil having a large number of turns of insulated copper wire wound on a metallic frame. The coil is suspended by means of a phosphor-bronze strip and is surrounded by a horse-shoe magnet NS. A hair spring is attached to lower end of the coil. The other end of the spring is attached to the scale through a pointer.

Working. When current is passed, say along ABCD, the couple acts on it. Since the plane remains always parallel to the magnetic field in all positions of the coil (radial field), the force on the vertical arms always remains perpendicular to the place of the coil.

Let, I be the current flowing through coil,
B be magnetic field supposed to be uniform and always parallel to the coil, A be area of the coil
Deflecting torque acting on the coil is,
τ = nI BA sin 900

Due to deflecting torque, the coil rotates and suspension wire gets twisted. A restoring torque is set up in the suspension fibre. If <|) is angle through which the coil rotates and k is the restoring torque per unit angular twist, then restoring torque, τ = kϕ
In equilibrium,
Deflecting torque = Restoring torque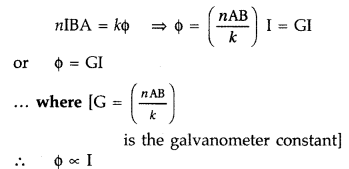

This provide a linear scale for the galvanometer.
Function of a radial magnetic field : Radial magnetic field being normal in all directions is formed to get maximum torque.
Function of Soft iron core, which not only makes the field radial but also increases the strength of the magnetic field.
(c) One uses a shunt resistance in parallel with the galvanometer, so that most of the current passes through the shunt. In the case of a voltmeter, a resistance of large value is used in series because it must draw a very small current, otherwise the voltage measurement will disturb the original set up by an amount which is very large.

(b) Let current I be divided at
point M into two parts I₁ and I₂; in bigger and smaller parts of the loop respectively. Magnetic field of current (clockwise) at point O :

Magnetic field of current I₂ (anticlockwise) at point O :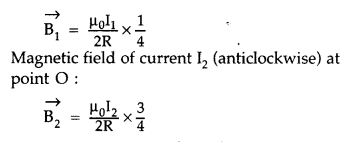

Net magnetic field, \(\overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{B}_{1}}+\overrightarrow{\mathrm{B}_{2}}\)
But I₁ = 3I₂ (AS resistance of bigger part is three times that of the smaller part of the loop)
Substituting I₁ = 3I₂ in equation (i), we get

∴ Magnetic field at the centre of loop is zero.

Question 35.
(a) Show how Biot-Savart law can be alternatively expressed in the form of Ampere’s circuital law. Use this law to obtain the expression for the magnetic field inside a solenoid of length ‘l’, cross-sectional area ‘A’ having ‘N’ closely wound turns and carrying a steady current ‘I’.
Draw the magnetic field lines of a finite solenoid carrying current I.
(b) A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.
Find the magnitude and direction of the magnetic field which should be set up in (Comptt. Delhi 2011)
Answer:
(a) (i) Bio-Savart law and Ampere’s Circuital law.
According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.


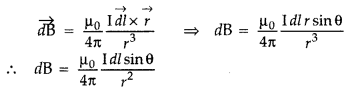
Magnetic field on the axis of circular current loop :

As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain

In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.

(b) Biot-Savart law can be expressed as Ampere’s Circuital law by considering the surface to be made up of a large number of loops. The sum of the tangential components of the magnetic field multiplied by the length of all such elements leads to integral. Ampere’s circuital law states that this’ integral is equal to p0 times the total current passing through that surface, i.e.,

(ii) Expression for magnetic field inside a solenoid. Let ‘n’ be the number of turns per unit length. Then total number of turns in the length ‘h’ is nh.
Hence, total enclosed current = nhl
Using Ampere’s circuital law,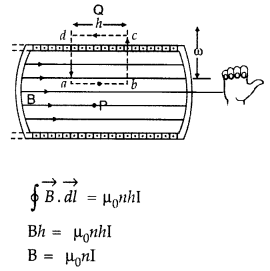

(iii) Magnetic field lines of a finite solenoid

(b) As per the figure given, magnetic field must be vertically inwards, to make tension zero.
Therefore, force on current carrying conductor and the weight of conductor are equal and opposite; and balance each other.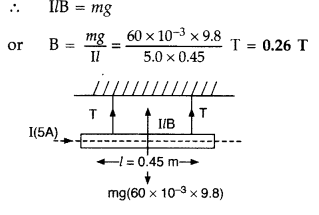

Direction : Perpendicular to the direction of

Question 36.
(a) State Ampere’s circuital law expressing it in the integral form.
(b) Two long coaxial insulated solenoids S₁ and S₂ of equal lengths are wound one over the other as shown in the figure. A steady current ‘l’ flows through the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current ‘l’ flows in the opposite direction so as to come out at end A. If n₁ and n₂ are the numbers of turns per unit length, find the magnitude and direction of the net magnetic field at a point
(i) inside on the axis and
(ii) outside the combined system. (CBSE Delhi 2014)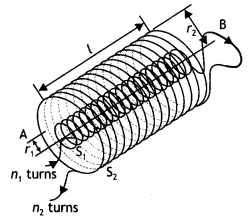

Answer:
(a) The line integral of B around any closed path equals µ_ol, where l is the total steady current passing through any surface bounded by the closed path.” Mathematically
\(\oint \vec{B} \cdot \overrightarrow{d L}=\mu_{0} I\)

(b) (i) The magnetic field due to a current-carrying solenoid:
B = µ_on l

where n = number of turns per unit length
l = current through the solenoid

Now, the magnetic field due to solenoid S₁ will be in the upward direction and the magnetic field due to S₂ will be in the downward direction (by right-hand screw rule).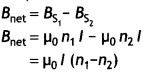

In the upward direction

(ii) The magnetic field is zero outside a solenoid.

Question 37.
Three long straight parallel wires are kept as shown in the Figure. The wire (3) carries a current l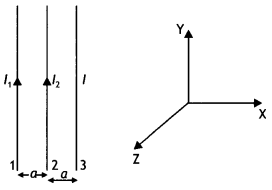

(i) The direction of flow of current l in wire (3) is such that the net force, on a wire (1), due to the other two wires, is zero.
(ii) By reversing the direction of l, the net force on the wire (2), due to the other two wires, becomes zero. What will be the direction of current l, in the two cases? Also obtain the relation between the magnitudes of currents l₁, l_2, and l. (CBSE Delhi 2016C)
Answer:
Case 1: The direction of flow of current in the wire (3) will be opposite to the direction of flow of current in the wire (1), i.e. downwards.
Also \(\frac{\mu_{0} l_{1} l}{2 \pi(2 a)}=\frac{\mu_{0} l_{1} l_{2}}{2 \pi a}\)
or
l = 2l₂

Case 2: The direction of flow of current in wire (3) will be same as the direction of flow of current in wire (1), i.e. upwards. For zero force on wire (2) we have
\(\frac{\mu_{0} l_{1} l_{2}}{2 \pi a}=\frac{\mu_{0} l l_{2}}{2 \pi a}\)
or
l = l₁
Therefore l = l₁ = 2 l₂

Question 38.
Show mathematically that the cyclotron frequency does not depend upon the speed of the particle.
Answer:
Due to the presence of the perpendicular magnetic field the particle moves in a circle of radius r given by
r = \(\frac{m v}{q B}\) ….(1)

The path of the particles in the dees is a semicircle and the time the particle spends in each dees is length of the semi circular path velocity
t = \(\frac{\text { length of the semi circular path }}{\text { velocity }}\)
= \(\frac{\pi r}{v}=\frac{\pi m}{B q}\) …(2)

using equation (1)
The above time is independent of the radius of the path and the velocity of the charged particle. Now the time period of the cyclotron is twice the time spent by the particle in each dee. Thus

T = 2t = \(\frac{2 \pi m}{B q}\) …(3)

Hence cyclotron frequency or the magnetic resonance frequency is given by
v = \(\frac{1}{T}=\frac{B q}{2 \pi m}\) …(4)

which is independent of the speed of the particle.

Question 39.
State the principle of a cyclotron. Show that the time period of revolution of particles in a cyclotron is independent of their speeds. Why is this property necessary for the operation of a cyclotron? (CBSE Al 2016)
Answer:
Principle of cyclotron: It is based on the principle that the positive ions can be accelerated to high energies with a comparatively smaller alternating potential difference by making them cross the electric field again and again, by making use of a strong magnetic field.

The necessary centripetal force required by charged particle to revolve in a circular path in magnetic field is provided by force due to magnetic field, i.e.
\(\frac{m v^{2}}{r}\) = Bqv
or
v = \(\frac{\text { Bqr }}{m}\)

So, the frequency of revolution is then given by
T = \(\frac{2 \pi r}{v}=2 \pi r \times \frac{m}{B q r}=\frac{2 \pi m}{B q}\)

It is clear from the expression that T is Independent of speed.

If this condition is not met the charged particle will very soon go out of step with the applied electricity and will not be accelerated.

Question 40.
(a) Write the expression for the magnetic force acting on a charged particle moving with velocity v in the presence of magnetic field B.
Answer:
\(\vec{F}\) = q\((\vec{v} \times \vec{B})\)

(b) A neutron, an electron and an alpha particle moving with equal velocities enter a uniform magnetic field going into the plane of the paper as shown. Trace their paths in the field and justify your answer. (CBSE Delhi 2016)

Answer:
The path area is shown.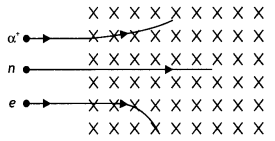

The radius of the circular path traveled by each particle is given by the expression
r = \(\frac{m v}{B q}\) since B and v is the same therefore

we have r ∝ \(\frac{m}{q}\). Since neutron does not have a charge therefore it passes straight without deflection. The ratio m/q for an alpha particle is greater for an alpha particle therefore its path will be less curved.

Also by Fleming’s left-hand rule the alpha particle and the electron will experience a force in the direction as shown.

Question 41.
A long solenoid of length ‘L’ having N turns carries a current l. Deduce the expression for the magnetic field in the interior of the solenoid. (CBSE AI 2011C)
Answer:
Consider a rectangular path abed of length L as shown in the figure below. Let us apply Ampere’s circuital law to this rectangular path so that we have



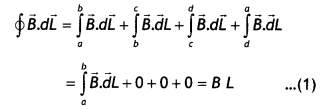
But by Ampere’s circuital law we have
\(\oint \vec{B} \cdot \vec{d} L\) = μ₀Nl = μ0(nL)l …(2)

From equations (1) and (2) we have
BL = μ₀nLl
or
B = μ₀ n l

But n = N/L, therefore we have
B = μ₀ \(\frac{N l}{L}\)

This gives the value of a magnetic field inside a solenoid.

Question 42.
Using Biot-Savart’s law, derive an expression for the magnetic field intensity at the center of a current-carrying circular coil.
Answer:
Consider a circular loop of radius r carrying a current l and having a center at O as shown in the figure below.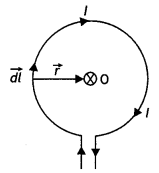

Consider a small current element dL on the loop. Then by Biot-Savart’s law the magnitude of the magnetic field at the center of the loop due to the current element we have
dB = \(\frac{\mu_{0}}{4 \pi} \frac{l d L \sin \theta}{r^{2}}\) …(1)

In this case, the angle between the current element dL and the radius vector is 90° therefore equation (1) can be written as
dB = \(\frac{\mu_{0}}{4 \pi} \frac{l d L}{r^{2}}\) ….(2)

The circular loop can be considered to be consisting of such small elements placed side by side, and then the magnetic intensities of these elements will be in the same direction. Thus, the net intensity of B at the center of the loop is given by

Question 43.
A charged particle q is moving in the presence of a magnetic field B which is inclined to an angle 300 with the direction of the motion of the particle. Draw the trajectory followed by the particle In the presence of the field and explain how the particle describes this path. (CBSE Delhi 2019)
Answer:
Two components of velocity vector V are responsible for the helical motion. Force on the charged particle due to the component normal to the magnetic field acts perpendicular to the velocity and the magnetic field and makes the particle follow a circular path. The component of velocity which is along the magnetic field does not cause any force on the particle, hence the particle continues to move in a straight line path due to this component so, the resultant path will be helical.

The path is as shown.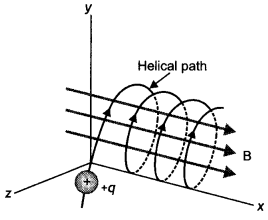

Question 44.
Two parallel coaxial circular costs of equal radius ‘R’ and an equal number of turns ‘N’, carry equal currents ‘I’ in the same direction and are separated by a distance ‘2R’. Find the magnitude and direction of the net magnetic field produced at the mid-point of the line joining their centers.
Answer:
The magnetic field at a distance R from a circular coil is given by the expression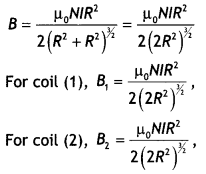

Both are directed in the same direction, therefore the resultant magnetic field at the center is
B = \(\frac{\mu_{0} N l R^{2}}{\left(2 R^{2}\right)^{1 / 2}}\)

Question 45.
(a) State Biot-Savart’s law. Using this law, derive the expression for the magnetic field due to a current-carrying circular loop of radius ‘R’, at a point which is at a distance ‘x’ from Its center along the axis of the loop.
Answer:
It states that for a small current element the small magnetic field is given by the expression Biot-Savart’s law for a small current element \(\overrightarrow{d B}=\frac{\mu_{0}}{4 \pi} \frac{I \overline{(d L} \times \hat{r})}{r^{2}}\).

(b) Two small identical circular loops, marked (1) and (2), carrying equal currents, are placed with the geometrical axes perpendicular to each other as shown in the figure. Find the magnitude and direction of the net magnetic field produced at point O.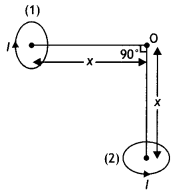

Answer:
The magnetic field at O due to the circular loop 1 is B₁ = \(\frac{\mu_{0} l R^{2}}{2\left(x^{2}+R^{2}\right)^{1 / 2}}\) directed towards left.

The magnetic field at O due to the circular loop is B₁ = \(\frac{\mu_{0} l R^{2}}{2\left(x^{2}+R^{2}\right)^{1 / 2}}\) directed upwards.

The net magnetic field is therefore
B = \(\sqrt{B_{1}^{2}+B_{2}^{2}}=\sqrt{2} B_{1}=\frac{\mu_{0} l R^{2}}{\sqrt{2}\left(x^{2}+R^{2}\right)^{3 / 2}}\)

The direction of the net magnetic field is 45° with the axis of the loop as shown in the figure below.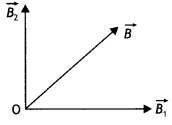

Question 46.
Derive an expression for the magnetic field along the axis of an air-cored solenoid, using Ampere’s circuital law. Sketch the magnetic field lines for a finite solenoid. Explain why the field at the exterior mid-point Is weak while at the interior it is uniform and strong.
Answer:
A solenoid is a coil of wire with a Length, which is Large as compared with its diameter.

Consider an ideaL soLenoid carrying current l and having n turns per unit length.
(a) Consider a rectangular path abed of length L as shown in the figure below. Let us apply Ampere’s circuital law to this rectangular path so that we have



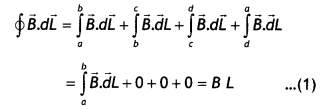
But by Ampere’s circuital law we have
\(\oint \vec{B} \cdot \vec{d} L\) = μ₀Nl = μ₀(nL)l …(2)

From equations (1) and (2) we have
BL = μ₀nLl
or
B = μ₀ n l

But n = N/L, therefore we have
B = μ₀ \(\frac{N l}{L}\)

This gives the value of a magnetic field inside a solenoid.

(b) The sketch Is as shown below.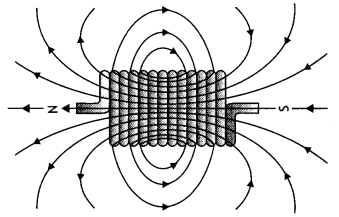

The magnetic field gets added inside the solenoid whereas it is not added outside the solenoid.

Question 47.
(a)Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis.
Answer:
Consider a rectangular path abed of length L as shown in the figure below. Let us apply Ampere’s circuital law to this rectangular path so that we have



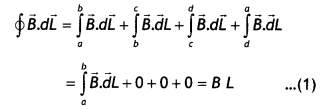
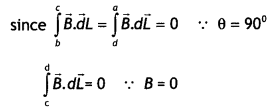
But by Ampere’s circuital law we have
\(\oint \vec{B} \cdot \vec{d} L\) = μ₀Nl = μ₀(nL)l …(2)

From equations (1) and (2) we have
BL = μ₀nLl
or
B = μ₀ n l

But n = N/L, therefore we have
B = μ₀ \(\frac{N l}{L}\)

This gives the value of a magnetic field inside a solenoid.

(b) In what respect is a toroid different from a solenoid? Draw and compare the pattern of the magnetic field lines in the two cases.
Answer:
(b) In a toroid magnetic field is uniform whereas in a solenoid it is different at the two ends and the center.
The magnetic field lines around the two are as shown.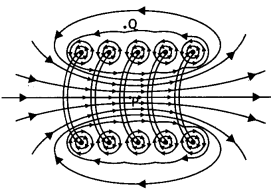


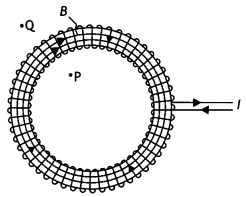
(c) How is the magnetic field inside a given solenoid made strong? (CBSE Al 2011)
Answer:
(i) By inserting a ferromagnetic substance inside the solenoid.
(ii) By increasing the amount of current through the solenoid.

Question 48.
(a) Explain, giving reasons, the basic difference in converting a galvanometer into
(i) a voltmeter
Answer:
A voltmeter is always connected in parallel with the section of the circuit whose potential difference has to be measured. Further, it must draw a small current, otherwise, the voltage measurement will disturb the original setup by an amount that is very large. Thus a large resistance is connected to the galvanometer in series so as to minimize this effect.

(ii) an ammeter
Answer:
An ammeter measures current and is to be connected in series in a circuit. A galvanometer has a large resistance, therefore a shunt is connected to it in order to decrease its resistance such that the current in the circuit is not altered.

(b) Two long straight parallel conductors carrying steady currents l₁ and l₂ are separated by a distanced’. Explain briefly, with the help of a suitable diagram, how the magnetic field due to one conductor acts on the other. Hence deduce the expression for the force acting between the two conductors. Mention the nature of this force. (CBSE At 2012)
Answer:

Consider two long, straight parallel wires separated by a distance ‘a’ and carrying currents l₁ and l₂ in the same direction as shown. We can easily determine the force on one wire due to the magnetic field set-up by the other wire. Wire 2, which carries a current l₂, sets up a magnetic field B₂ at the position of wire 1.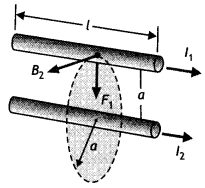

The direction of B₂ is perpendicular to the wire, as shown in figure. Now the magnetic force on length L of wire 1 is
\(\vec{F}_{1}=l_{1}\left(\vec{L} \times \vec{B}_{2}\right)\)

Since L is perpendicular to B₂, the magnitude of F, is given by F₁ = l₁ L B₂ …(1)
But the field due to wire 2 is given by the relation
B₂ = \(\frac{\mu_{0} l_{2}}{2 \pi a}\) ….(2)

Therefore, from equations 1 and 2 we have
F₁= l₁ L B₂ = l₁ L\(\left(\frac{\mu_{0} l_{2}}{2 \pi a}\right)=\frac{L \mu_{0} l_{1} l_{2}}{2 \pi a}\)

We can rewrite it in terms of force per unit length as
\(\frac{F_{1}}{L}=\frac{\mu_{0} l_{1} l_{2}}{2 \pi a}\) ….(3)

The direction of F₁ is downward, towards wire 2, since \(\vec{L} \times \vec{B}\) is downwards. If one considers the field set up at wire 2 due to wire 1, the force F₂ is found to be equal and opposite to F₁ which is in accordance with Newton’s third law of motion. When the currents are in opposite directions, the forces are reversed and the wires repel each other. Hence we find that the force per unit length of wire between two parallel current-carrying wires is given by
F = \(\frac{\mu_{0} l_{1} l_{2}}{2 \pi a}\)

Therefore, two conductors carrying current in the same direction attract each other whereas two conductors carrying current in the opposite directions repel each other.

The above expression can be used to define ampere, the SI unit of current.
Let l₁ = l₂ = 1 ampere, a = 1 m then F = 2 × 10^-7 Nm^-1

Thus we have
One ampere is that much current which when flowing through each of the two infinitely long straight conductors held 1 meter apart in space, produce a force of F = 2 × 10^-7 N per meter of their length.

Question 49.
(a) State the underlying principle of a moving coil galvanometer.
Answer:
A current-carrying coil placed in a magnetic field experiences a torque.

(b) Give two reasons to explain why a galvanometer cannot as such be used to measure the value of the current in a given circuit.
Answer:

1. A galvanometer is a very sensitive device; it gives a full-scale deflection for a current of the order of a few pA.
2. The resistance of the galvanometer is not very small, hence it will change the value of current in the circuit branch when connected in series in that branch.

(c) Define the terms:
(i) voltage sensitivity and
(ii) current sensitivity of a galvanometer. (CBSE Delhi 2019)
Answer:

• Voltage sensitivity: Voltage sensitivity is defined as the deflection per unit potential difference applied.
• Current sensitivity: It is defined as the deflection per unit current.

Question 50.
(a) State Biot-Savart law. Deduce the expression for the magnetic field due to a circular current carrying loop at a point lying on its axis.
Answer:
It states that for a small current element the small magnetic field is given by the expression Biot-Savart’s law for a small current element \(\overrightarrow{d B}=\frac{\mu_{0}}{4 \pi} \frac{I \overline{(d L} \times \hat{r})}{r^{2}}\).

(b) Two long parallel wires carry currents l₁ and l₁ flowing in the same direction. When a third current-carrying wire is placed parallel and coplanar in between the two, find the condition when the third wire would experience no force due to these two wires. (CBSE AI 2012C)
Answer:
Two current-carrying wires carrying current in the same direction attract and those carrying current in the opposite direction repel. The current in the third wire at the center should be opposite to the current in the two wires.

The conditions should be

• The center wire should carry current in the opposite direction to the two wires and
• The center wire should be closer to the wire carrying lesser current.

Question 51.
(a) Derive the expression for the torque on a rectangular current-carrying loop suspended in a uniform magnetic field.
Answer:
The figure below shows a rectangular loop of wire with length ‘a’ and breadth ‘b’. A line perpendicular to the plane of the loop (i.e. a normal to the plane) makes an angle Φ with the direction of the magnetic field B, and the loop carries a current / as shown. Let the forces acting on the various sides of the loop be \(\vec{F}_{1}\), \(\vec{F}_{2}\), \(\vec{F}_{3}\) and \(\vec{F}_{4}\) as shown.

It follows from the expression for the force experienced by a conductor in a magnetic field that force on arm AB is
\(\vec{F}_{1}=I(\overrightarrow{\mathrm{AB}} \times \vec{B})\) …(1)
(in the plane of the paper and is directed upwards as shown).

The force on arm CD is given by \(\vec{F}_{2}=l(\overrightarrow{\mathrm{CD}} \times \vec{B})\) …(2)
(in the plane of the paper and is directed downwards as shown.)

Since these two forces are equal and opposite and have the same line of action therefore they cancel out each other’s effect and their resultant effect on the coil is zero.

Now the force on arm BC is
\(\vec{F}_{3}=l(\overrightarrow{\mathrm{BC}} \times \vec{B})\) …(3)
(acts perpendicular to the plane of the paper and is directed outwards as shown) Finally the force on arm DA is
\(\vec{F}_{4}=I(\overrightarrow{\mathrm{DA}} \times \vec{B})\) …(4)
(acts perpendicular to the plane of the paper and is directed inwards as shown in figure).

Both forces F₃ and F4 make an angle of 90° with the direction of the magnetic field. Therefore, in magnitude, these forces are given by
F₃ = F₄ = l a B sin90° = l a B …(5)

The lines of action of both these forces are perpendicular to the plane of the paper. The two forces F₃ and F₄ lie along different lines and each give rise to a torque about the X-axis. The two torques produce a resultant torque in the + X direction. The arm of the couple (perpendicular distance between the lines of action of the two forces) from the figure below is given by
The arm of couple = b Sin Φ …(6)

Therefore, by the definition of torque we have
Torque = either force × arm of couple Using equations (5) and (6) we have
Torque = l B a × b Sin Φ
But a b = A, area of the coil, therefore τ = l B A Sin Φ

(b) A proton and a deuteron having equal momenta enter in a region of the uniform magnetic field at a right angle to the direction of the field. Depict their trajectories in the field. (CBSE Delhi 2013)
Answer:
The radius of the curved path which will be followed by the two particles is given by the expression r = \(\frac{m v}{B q}\)

As m_d > m_p it will follow the path of a bigger radius.

Question 52.
State Biot-Savart law, expressing it in the vector form. Use it to obtain the expression for the magnetic field at an axial point, distance ‘d’ from the center of a circular coil of radius ‘a’ carrying current ‘l’. Also, find the ratio of the magnitudes of the magnetic field of this coil at the center and at an axial point for which d = a \(\sqrt{3}\) (CBSE Delhi 2013C)
Answer:
(a) It states that the magnetic field due to a current element dl at a distance r from it is given by the expression

dB = \(\frac{\mu_{0}}{4 \pi} \frac{l d l \sin \theta}{r^{2}}\). In vector form it is written as
\(\overrightarrow{d B}=k_{m} \frac{l mid \overrightarrow{d L} \times \hat{r}}{r^{2}}\)

Consider a circular loop of wire of radius R located in the YZ plane and carrying a steady current / as shown in the figure below. Let us calculate the magnetic field at an axial point P a distance x from the center of the loop. From the figure it is clear that any element dL is perpendicular to r, furthermore, all the elements around the loop are at the same distance r from P, where r² = X² + R². Hence by Biot-Savart’s law, the magnetic field at point P due to the current element dL is given by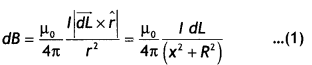


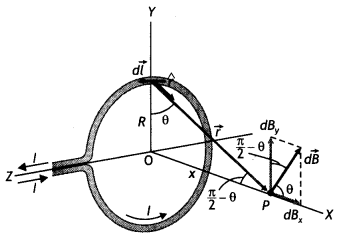
The direction of the magnetic field dB due to the eLement dL is perpendicular to the plane formed by r and dL as shown in the figure above. The vector dB can be resolved into components dB aLong the X-axis and dB which is perpendicular to the X-axis. When the components perpendicular to the X-axis are assumed over the whole loop, the result is zero. That is, by symmetry any element on one side of the loop will set up a perpendicular component that cancels the component setup by an element diametrically opposite it. Therefore, it is obvious that the resultant magnetic field at P will be along the X-axis. This result can be obtained by integrating the components dB_x = dB cos θ.
Therefore, we have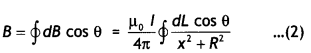

where the integral is to be taken over the entire loop since θ,x and R are constants for all elements of the loop and since
cos θ = \(\frac{R}{\sqrt{x^{2}+R^{2}}}\)

B = \(\frac{\mu_{0} l R}{4 \pi\left(x^{2}+R^{2}\right)^{3 / 2}} \oint d L=\frac{\mu_{0} l R^{2}}{2\left(x^{2}+R^{2}\right)^{1 / 2}}\)

To find the magnetic field at the centre of the loop setting x = O in equation the above equation we have B = \(\frac{\mu_{0} l}{2 R}\)

Now magnetic field at the centre of a circular coil is
\(B_{C}=\frac{\mu_{0} l}{2 a}\) …(1)

Also magnetic field on the axial line when
d = a\(\sqrt{3}\) is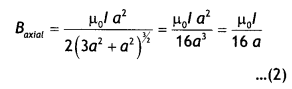

From (1) and (2) we have
\(\frac{B_{C}}{B_{\text {axial }}}=\frac{\mu_{0} l}{2 a} \times \frac{16 a}{\mu_{0} l}\) = 8

Question 53.
A straight wire carrying a current of 12 A is bent into a semi-circular arc of radius 2.0 cm as shown in figure (a) Consider the magnetic field B at the center of the arc
(a) What is the magnetic field due to the straight segments?
(b) In what way the contribution to B from the semicircle differs from that of a circular loop and in what way does it resemble?
(c) Would your answer be different if the wire were bent into a semi-circular arc of the same radius but in the opposite way as shown in figure (b)? (NCERT)

Answer:
(a) dl and r for each element of the straight segments are parallel. Therefore \(d \vec{L} \times \hat{r}\) =0. Straight segments do not contribute to the magnetic field at the center of the semicircular arc.

(b) For all segments of the semicircular arc \(d \vec{L} \times \hat{r}\) are all parallel to, each other (into the plane of the paper). All such contributions add up in magnitude. Hence the direction of B for a semicircular arc is given by the right-hand rule and magnitude is half that of a circular loop. Thus
B = \(\frac{1}{2} \frac{\mu_{0} l}{2 r}=\frac{4 \pi \times 10^{-7} \times 12}{4 \times 2 \times 10^{-2}}\) = 9 × 10^-4 T normal to the plane of the paper going into it.

(c) Same magnitude of B but opposite in direction to that in (b)

Question 54.
A long straight wire carrying a current of 25 A rests on a table as shown in the figure. Another wire PQ of length 1 m, mass 2.5 g carries the same current but in the opposite direction. The wire PQ is free to slide up and down. To what height will PQ rise? (NCERT Exemplar)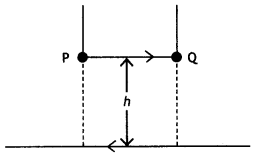

Answer:
Given l₁ = l₁ = 25 A, L = 1 m, m = 2.5 g = 2.5 × 10^-3 kg
The repulsive force between PQ and the wire on the table will balance the weight of wire PQ. Let this happen when PQ is at a height h above the wire, then
F = mg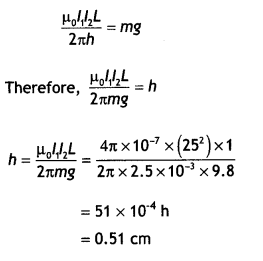

Question 55.
Two straight parallel conductors carry steady currents l₁ and l₂ separated by a distance d. if currents are flowing in the same direction, show how the magnetic field set-up in one produces an attractive force on the other. Obtain the expression for force. Hence define one ampere. (CBSE Delhi 2016)
Answer:
Consider two long, straight parallel wires separated by a distance ‘a’ and carrying currents l₁ and l₂ in the same direction as shown. We can easily determine the force on one wire due to the magnetic field set-up by the other wire. Wire 2, which carries a current l₂, sets up a magnetic field B₂ at the position of wire 1.

The direction of B₂ is perpendicular to the wire, as shown in figure. Now the magnetic force on length L of wire 1 is
\(\vec{F}_{1}=l_{1}\left(\vec{L} \times \vec{B}_{2}\right)\)

Since L is perpendicular to B₂, the magnitude of F, is given by F₁ = l₁ L B₂ …(1)
But the field due to wire 2 is given by the relation
B₂ = \(\frac{\mu_{0} l_{2}}{2 \pi a}\) ….(2)

Therefore, from equations 1 and 2 we have
F₁= l₁ L B₂ = l₁ L\(\left(\frac{\mu_{0} l_{2}}{2 \pi a}\right)=\frac{L \mu_{0} l_{1} l_{2}}{2 \pi a}\)

We can rewrite it in terms of force per unit length as
\(\frac{F_{1}}{L}=\frac{\mu_{0} l_{1} l_{2}}{2 \pi a}\) ….(3)

The direction of F₁ is downward, towards wire 2, since \(\vec{L} \times \vec{B}\) is downwards. If one considers the field set up at wire 2 due to wire 1, the force F₂ is found to be equal and opposite to F₁ which is in accordance with Newton’s third law of motion. When the currents are in opposite directions, the forces are reversed and the wires repel each other. Hence we find that the force per unit length of wire between two parallel current-carrying wires is given by
F = \(\frac{\mu_{0} l_{1} l_{2}}{2 \pi a}\)

Therefore, two conductors carrying current in the same direction attract each other whereas two conductors carrying current in the opposite directions repel each other.

The above expression can be used to define ampere, the SI unit of current.
Let l₁ = l₂ = 1 ampere, a = 1 m then F = 2 × 10^-7 Nm^-1

Thus we have
One ampere is that much current which when flowing through each of the two infinitely long straight conductors held 1 meter apart in space, produce a force of F = 2 × 10^-7 N per meter of their length.

Question 55 a.
(a) In a moving coil galvanometer, why is the magnetic field required to be radial?
Answer:
The radial field is always normal to the surface of the coil in all positions of the coil, i.e. θ = 0. The radial field ensures a linear relation between 0 and l in a moving coil galvanometer.

(b) A 100 turn closely wound circular coil of radius 10 cm carries a current of 3.2 A.
Calculate (i) the magnetic field at the centre of the coil, and
(ii) its magnetic moment. (CBSE2019C)
Answer:
Here N = 100, r = 10 cm = 0.1 m,
l = 3.2 A, B = ?, p = ?
(i) At the centre of the coil

(ii)Magnetic moment
p = NIA
= 100 × 3.2 × π × (0.1 )² ≃ 10 Am2

Question 56.
State Ampere’s circuital law. Use this law to find a magnetic field due to a straight infinite current-carrying wire. How are the magnetic field lines different from the electrostatic field lines? (CBSE Al 2016)
Answer:
Statement: “The line integral of B around any closed path equals μ₀ l, where l is the total steady current passing through any surface bounded by the closed path.”

Consider a long circular wire of radius ‘a’ carrying a steady current (dc) that is uniformly distributed along the cross-section of the wire as shown in the figure. Let us calculate the magnetic field in the regions r ≥ a and r < a. In region 1 let us choose a circular path of radius r centered at the wire. From symmetry, we find that B is perpendicular to dL at every point on the circular path.

Since total current linked with the circular path is l₀, therefore by Ampere’s law we have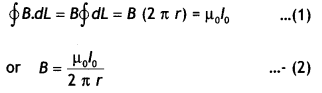

for r ≥ a
Magnetic field lines form closed loops while electrostatics field lines do not.

Question 57.
(a) State Biot-Savart law in vector form.
Answer:
It states that for a small current element the small magnetic field is given by the expression Biot-Savart’s law for a small current element \(\overrightarrow{d B}=\frac{\mu_{0}}{4 \pi} \frac{I \overline{(d L} \times \hat{r})}{r^{2}}\).

(b) Deduce the expression for the magnetic field at a point on the axis of a current-carrying circular loop of radius ‘R’, distant V from the center, hence write the magnetic field at the center of a loop. (CBSE AI 2015, Delhi 2018C)
Answer:
Consider a circular loop of wire of radius R located in the YZ plane and carrying a steady current / as shown in the figure below. Let us calculate the magnetic field at an axial point P a distance x from the center of the loop. From the figure it is clear that any element dL is perpendicular to r, furthermore, all the elements around the loop are at the same distance r from P, where r² = X² + R². Hence by Biot-Savart’s law, the magnetic field at point P due to the current element dL is given by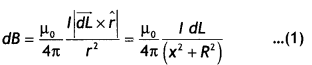


The direction of the magnetic field dB due to the element dL is perpendicular to the plane formed by r and dL as shown in the figure above. The vector dB can be resolved into components dB along the X-axis and dB which is perpendicular to the X-axis. When the components perpendicular to the X-axis are assumed over the whole loop, the result is zero. That is, by symmetry any element on one side of the loop will set up a perpendicular component that cancels the component setup by an element diametrically opposite it. Therefore, it is obvious that the resultant magnetic field at P will be along the X-axis. This result can be obtained by integrating the components dB_x = dB cos θ.
Therefore, we have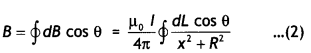

where the integral is to be taken over the entire loop since θ,x and R are constants for all elements of the loop and since
cos θ = \(\frac{R}{\sqrt{x^{2}+R^{2}}}\)

B = \(\frac{\mu_{0} l R}{4 \pi\left(x^{2}+R^{2}\right)^{3 / 2}} \oint d L=\frac{\mu_{0} l R^{2}}{2\left(x^{2}+R^{2}\right)^{1 / 2}}\)

To find the magnetic field at the centre of the loop setting x = O in equation the above equation we have B = \(\frac{\mu_{0} l}{2 R}\)

Question 58.
Derive an expression for the maximum force experienced by a straight conductor of length 1, carrying current I and kept in a uniform magnetic field, B.
Answer:
Consider a straight segment of a conducting wire; with length L and cross-section at area A, the current is from bottom to top as shown In the figure below. The wire is in a uniform magnetic field B perpendicular to the plane of the diagram and directed into the plane. Let us assume that the moving charges are positive.

The drift velocity is upward, perpendicular to B. The average force experienced by each charge is
\(\vec{f}=q\left(\vec{v}_{d} \times \vec{B}\right)\) …..(1)

Directed to the left as shown in the figure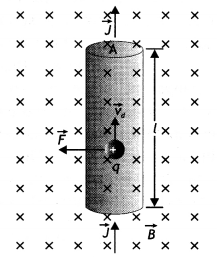

Since \(\vec{V}_{d}\) and \(\vec{B}\) are perpendicular, the magnitude of the force is given by
f = q v_d B …(2)

Let n be the number density of charges, i.e. number of charges per unit volume. A segment of the conductor with length L has volume V = A L and contains a number of charges N given by
N = n A L …(3)

Now the total force F on all the charges moving in this segment is
F = N f = (n A L) q v_d B = (n q v_d A) (L B)

But n q v_d A = l, therefore the above equation becomes
F = B l L …(4)

Question 59.
Derive an expression for the torque on a rectangular coil of area A, carrying a current l and placed in a magnetic field B, the angle between the direction of 8 and the vector perpendicular to the plane of the coil is θ. (CBSE Delhi 2019)
Answer:
The figure below shows a rectangular loop of wire with length ‘a’ and breadth ‘b’. A line perpendicular to the plane of the loop (i.e. a normal to the plane) makes an angle Φ with the direction of the magnetic field B, and the loop carries a current / as shown. Let the forces acting on the various sides of the loop be \(\vec{F}_{1}\), \(\vec{F}_{2}\), \(\vec{F}_{3}\) and \(\vec{F}_{4}\) as shown.

It follows from the expression for the force experienced by a conductor in a magnetic field that force on arm AB is
\(\vec{F}_{1}=I(\overrightarrow{\mathrm{AB}} \times \vec{B})\) …(1)
(in the plane of the paper and is directed upwards as shown).

The force on arm CD is given by \(\vec{F}_{2}=l(\overrightarrow{\mathrm{CD}} \times \vec{B})\) …(2)
(in the plane of the paper and is directed downwards as shown.)

Since these two forces are equal and opposite and have the same line of action therefore they cancel out each other’s effect and their resultant effect on the coil is zero.

Now the force on arm BC is
\(\vec{F}_{3}=l(\overrightarrow{\mathrm{BC}} \times \vec{B})\) …(3)
(acts perpendicular to the plane of the paper and is directed outwards as shown) Finally the force on arm DA is
\(\vec{F}_{4}=I(\overrightarrow{\mathrm{DA}} \times \vec{B})\) …(4)
(acts perpendicular to the plane of the paper and is directed inwards as shown in figure).

Both forces F₃ and F₄ make an angle of 90° with the direction of the magnetic field. Therefore, in magnitude, these forces are given by
F₃ = F₄ = l a B sin90° = l a B …(5)

The lines of action of both these forces are perpendicular to the plane of the paper. The two forces F₃ and F₄ lie along different lines and each give rise to a torque about the X-axis. The two torques produce a resultant torque in the + X direction. The arm of the couple (perpendicular distance between the lines of action of the two forces) from the figure below is given by
The arm of couple = b Sin Φ …(6)

Therefore, by the definition of torque we have
Torque = either force × arm of couple Using equations (5) and (6) we have
Torque = l B a × b Sin Φ
But a b = A, area of the coil, therefore τ = l B A Sin Φ

Question 60.
Draw a schematic sketch of a cyclotron. State its working principle and write its two uses. (CBSE 2019C)
Answer:
Cyclotron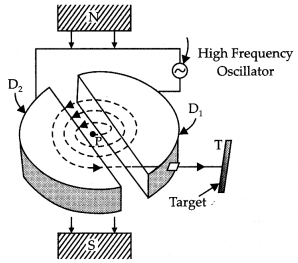

Working Principle: It is based on the principle that a positively charged particle can acquire very large energy with the small alternating potential difference if the particle is made to cross again and again the electric field produced by alternating potential difference applied and a strong perpendicular magnetic field is applied.

Uses:
(a) It is used to accelerate positively charged particles to very high energies.
(b) Cyclotrons are a source of high-energy beams for nuclear physics experiments.

Question 61.
(a) Draw a schematic sketch of a moving coil galvanometer and describe briefly its working.
Answer:
Principle: It is based on the principle that the positive ions can be accelerated to high energies with a comparatively smaller alternating potential difference by making them cross the electric field again and again, by making use of a strong magnetic field.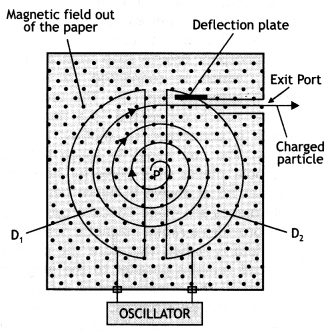

Construction: It consists of two D-shaped, hollow metal dees D₁ and D₂. The dees are placed with a small gap in between them. The dees are connected to a source of high frequency alternating potential difference. The dees are evacuated in order to minimize energy losses resulting from collisions between the ions and air molecules. The whole apparatus is placed between the poles of an electromagnet as shown in the figure below. The magnetic field is perpendicular to the plane of the dees.

Working: In a cyclotron, particles of mass m and charge q move inside an evacuated chamber in a uniform magnetic field B that is perpendicular to the plane of their paths. The alternating potential difference applied between the hollow electrodes D₁ and D₂ create an electric field in the gap between them which changes precisely twice in each revolution so that the particles get a push each time they cross the gap.

The pushes increase their speed and kinetic energy, boosting them into paths of larger radius. The electric field increases the speed and the magnetic field makes the particles move in circular paths. Due to the presence of the perpendicular magnetic field the particle moves in a circle of radius r given by
r = \(\frac{m v}{q B}\) …(1)

The path of the particles in the dees is a semicircle and the time the particle spends in each dee is semi-circular
τ = \(\frac{\text { length of the semi-circular path }}{\text { velocity }}=\frac{\pi r}{v}=\frac{\pi m}{B q}\) by using equation (1)

The above time is independent of the radius of the path and the velocity of the charged particle. Hence the charged particle spends the same time in each dee and encounters a dee of opposite polarity whenever it comes into the gap between the dees and thus is continuously accelerated.

(b) “Increasing the current sensitivity of a galvanometer does not necessarily increase the voltage sensitivity.” Justify’ this statement. (CBSE Delhi 2014C)
Answer:
Voltage and current sensitivities are related as VS = \(\frac{CS}{R}\) .

An increase in current sensitivity may lead to an increase in the resistance of the coil. Thus the factor CS/R may not be affected.

Question 62.
Explain with the help of a labeled diagram the underlying principle, construction, and working of a moving coil galvanometer.
Answer:
It is an instrument used to detect weak currents in a circuit.

Principle: It is based on the principle that, whenever a loop carrying current is placed in a magnetic field, it experiences a torque, which tends to rotate it.

Construction: It consists of a rectangular or circular coil made by winding a fine insulated copper wire on an aluminum frame. A thin phosphor bronze strip from a torsion head, which is connected to a terminal screw, suspends this coil. The lower end of the coil is connected to a fine spring which is connected to another terminal screw. The coil hangs in space between the pole pieces of a powerful horseshoe magnet NS as shown in the figure below. The pole pieces are made concave cylindrical.

This provides a radial magnetic field. Since the field is radial, therefore the plane of the coil remains parallel to the magnetic field in all the orientations of the coil. In between the pole pieces, within the coil, lies a soft iron cylindrical piece called ‘core’. The core does not touch the coil anywhere. The whole arrangement is enclosed in a non-magnetic box to protect it from air currents. Three leveling screws are provided at the base.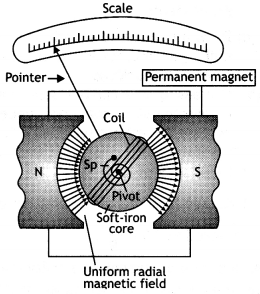

Question 63.
Explain with the help of a labeled diagram the underlying principle, construction, and working of a cyclotron. (CBSE Delhi 2019)
Answer:
Principle: It is based on the principle that the positive ions can be accelerated to high energies with a comparatively smaller alternating potential difference by making them cross the electric field again and again, by making use of a strong magnetic field.

Construction: It consists of two D-shaped, hollow metal dees D₁ and D₂. The dees are placed with a small gap in between them. The dees are connected to a source of high frequency alternating potential difference. The dees are evacuated in order to minimize energy losses resulting from collisions between the ions and air molecules. The whole apparatus is placed between the poles of an electromagnet as shown in the figure below. The magnetic field is perpendicular to the plane of the dees.

Working: In a cyclotron, particles of mass m and charge q move inside an evacuated chamber in a uniform magnetic field B that is perpendicular to the plane of their paths. The alternating potential difference applied between the hollow electrodes D₁ and D₂ create an electric field in the gap between them which changes precisely twice in each revolution so that the particles get a push each time they cross the gap. The pushes increase their speed and kinetic energy, boosting them into paths of larger radius. The electric field increases the speed and the magnetic field makes the particles move in circular paths. Due to the presence of the perpendicular magnetic field the particle moves in a circle of radius r given by
r = \(\frac{m v}{q B}\) …(1)

The path of the particles in the dees is a semicircle and the time the particle spends in each dee is semi-circular
τ = \(\frac{\text { length of the semi-circular path }}{\text { velocity }}=\frac{\pi r}{v}=\frac{\pi m}{B q}\) by using equation (1)

The above time is independent of the radius of the path and the velocity of the charged particle. Hence the charged particle spends the same time in each dee and encounters a dee of opposite polarity whenever it comes into the gap between the dees and thus is continuously accelerated.

Question 64.
The figure below shows a long straight wire of circular cross-section (radius a) carrying steady current l. The current is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a. Draw a graph showing the variation of a magnetic field for the above two cases.

Answer:
Consider a long circular wire of radius ‘a’ carrying a steady current (dc) that is uniformly distributed along the cross-section of the wire as shown in the figure. Let us calculate the magnetic field in the regions r ≥ a and r < a. In region 1 let us choose a circular path of radius r centered at the wire. From symmetry, we find that B is perpendicular to dL at every point on the circular path. Since total current linked with the circular path 1 is l0, therefore by Ampere’s law we have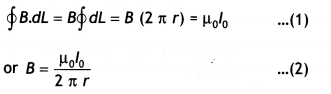

for r ≥ a

Now consider the interior of the wire, i.e. region 2 where r < a. In this, the current l enclosed by the path is less than l₀. Since the current is assumed to be uniform over the area of the wire,
Therefore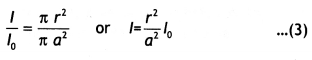

Now applying Ampere’s circuital rule to region 2 we have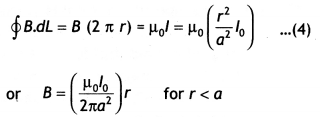

The magnetic field versus r for this system is as shown in the figure below.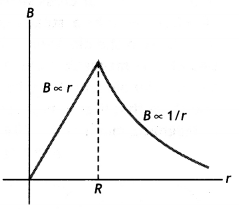

Question 64 a.
Draw the magnetic field lines due to a circular loop of area \(\vec{A}\) carrying current I. Show that it acts as a bar magnet of magnetic moment \(\vec{m}=I \vec{A}\). (CBSE Al 2015)
Answer:
The magnetic field lines are as shown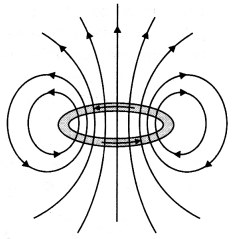

Magnetic field due to circular loop on its axis at far off points
B = \(\frac{\mu_{0}}{4 \pi} \frac{2 I A}{X^{3}}\)

Magnetic field due to a bar magnet at its axial point is
B = \(\frac{\mu_{0}}{4 \pi} \frac{2 m}{x^{3}}\)

Comparing the above two we have m = IA

Question 65.
(a) State Ampere’s circuital law. Use this law to obtain the expression for the magnetic field inside an air-cored toroid of average radius ‘r, having ‘n’ turns per unit length and carrying a steady current.
(b) An observer to the left of a solenoid of N turns each of cross-section area ‘A’ observes that a steady current I in it flows in the clockwise direction. Depict the magnetic field lines due to the solenoid specifying its polarity and show that it acts as a bar magnet of magnetic moment m = NIA. (CBSE Delhi 2015)

Answer:
(a) “The line integral of 8 around any closed path equal μ₀l, where l is the total steady current passing through any surface bounded by the closed path.” Consider a toroidal solenoid. Let N be the number of turns and l be the current passed through it. For a solenoid whose coils are closely spaced, the field inside the solenoid is tangent to the dotted circular path as shown in the figure and is the same at all points lying on the dotted line.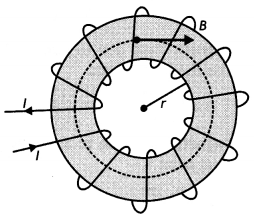

Therefore we have
\(\oint \vec{B} \cdot d \vec{L}\) = B ∮dL = B (2 π r) …(1)

By Ampere’s circuital law we have ∮\(\overrightarrow{\mathbf{B}} \cdot d \vec{L}\) = μ₀Nl …(2)

From equations 1 and 2 we have
B (2 π r) = μ₀NI
or
B = \(\frac{\mu_{0} N I}{2 \pi r}\) but
\(\frac{N}{2 \pi r}\) = n

i. e. number of turns per unit length Therefore we have B = μ₀ n I

This gives the field inside a toroidal solenoid.

(b) The magnetic field lines and the polarity of the solenoid is as shown.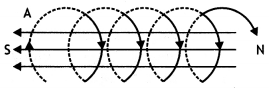

Magnetic field due to the coil on its axis at far off points
B = \(\frac{\mu_{0}}{4 \pi} \frac{2 N I A}{x^{3}}\)

Magnetic field due to a bar magnet at its axial point is
B = \(\frac{\mu_{0}}{4 \pi} \frac{2 m}{x^{3}}\)

Comparing the above two we have m = NIA

Question 66.
(a) Use Biot-Savart law to derive the expression for the magnetic field due to a circular coil of radius R having N turns at a point on the axis at a distance ‘x’ from its center.
Draw the magnetic field lines due to this coil.
(b) A current l enters a uniform loop of radius R at point M and flows out at point N as shown in the figure. Obtain the net magnetic field at the center of the loop. (CBSE Delhi 2015C)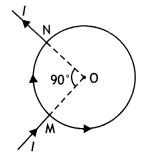

Answer:
(a) According to Biot-Savart law:
The magnitude of magnetic field d \(\vec{B}\) , is due to a current element d \(\vec{l}\), is proportional to current l and element length, dl.

inversely proportional to the square of the distance r.

Its direction is perpendicular to the plane containing d \(\vec{l}\) and \(\vec{r}\) .

In vector notation,
\(\overrightarrow{d B}=\frac{\mu_{0}}{4 \pi}, \frac{d \vec{l} \times \vec{r}}{r^{3}}\)

Using Biot-Savart law, obtain the expression for the magnetic field due to a circular coil of radius r, carrying a current I at a point on its axis distant x from the centre of the coil. (CBSE Delhi 2018C)
Answer: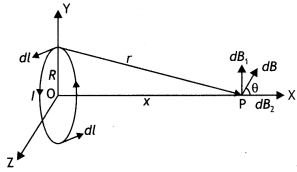

we have \(\overrightarrow{d B}=\frac{\mu_{0}}{4 \pi} I \frac{|d \vec{i} \times \vec{r}|}{r^{3}}\)
r² = x² + R²

∴ dB = \(\frac{\mu_{0} I}{4 \pi} \frac{d l}{\left(X^{2}+R^{2}\right)^{3 / 2}}\)

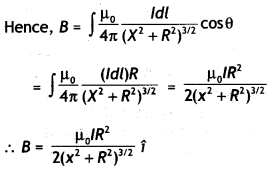
The magnetic fieLd Lines are as shown.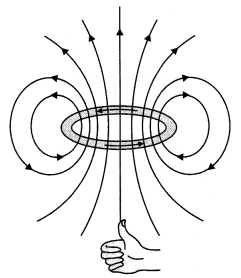

(b) At point O, the net magnetic field is the sum of fields due to two current segments carrying currents /1 and l2. If the potential difference between points A and B be V, then
V = I₁ R₁ = I₂R₂
where R, is the resistance of segment subtending an angle 90° at O and R₂ is the resistance of segment subtending an angle (360° – 90°) at O.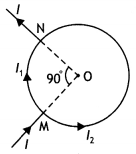

Now R₁ = \(\frac{\pi / 2}{2 \pi} R=\frac{R}{4}\)

Now field B₁, at O due to smaller segment is

directed inwards.

Now field B₂ at 0 due to larger segment is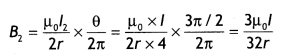

directed outwards

Hence net magnetic field in the center is
B₁ – B₂ = \(\frac{3 \mu_{0} I}{32 r}-\frac{3 \mu_{0} I}{32 r}\) = 0

(ii) The velocity of the particle inside a cyclotron is given by v = \(\frac{B q r}{m}\) , which again depends upon the q/m ratio. The q/m ratio of an a particle is less than that of a proton, therefore a proton will come out with higher velocity.

Question 67.
(a) Define the SI unit of current in terms of the force between two parallel current-carrying conductors.
(b) Two long straight parallel conductors carrying steady currents l_a and l_b along the same direction are separated by a distance d. How does one explain the force of attraction between them? If a third conductor carrying a current lc in the opposite direction is placed just in the middle of these conductors, find the resultant force acting on the third conductor. (CBSE Delhi 2018C)
Answer:
(a) The ampere is the value of that steady current which, when maintained in each of the two very long, straight, parallel conductors of negligible cross¬section, and placed one meter apart in vacuum, would produce on each of these conductors a force equal to 2 × 10^-7 newton per meter of length.
(b) The wire (ii) experiences a force due to the magnetic field caused by the current flowing in wire (i).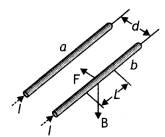

The magnetic field at any point on the wire (b) due to the current in the wire (a) is perpendicular to the plane of two wires and pointing inwards and hence force on it will be towards wire (a). Similarly, the force on the wire (a) will be towards wire (b). Hence two wires carrying currents in the same direction attract each other.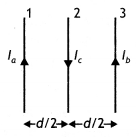

Force on wire (3) due to wire (1)
\(\frac{\mu_{0} l_{a} l_{c}}{2 \pi\left(\frac{d}{2}\right)}\) towards right

Force on wire 3 due to wire 2
\(\frac{\mu_{0} l_{b} l_{c}}{2 \pi\left(\frac{d}{2}\right)}\) towards Left

Net force on wire 3
\(\frac{\mu_{0} I_{c}}{\pi d}\left[I_{a}-I_{b}\right]\) towards right nd °

Also accept
\(\frac{\mu_{0} I_{c}}{\pi d}\left[I_{b}-I_{a}\right]\) towards left

Question 68.
(a) State Biot-Savart law and express it in the vector form.
Answer:
(a) According to Biot-Savart law:
The magnitude of magnetic field d \(\vec{B}\) , is due to a current element d \(\vec{l}\), is proportional to current l and element length, dl.

inversely proportional to the square of the distance r.

Its direction is perpendicular to the plane containing d \(\vec{l}\) and \(\vec{r}\) .

In vector notation,
\(\overrightarrow{d B}=\frac{\mu_{0}}{4 \pi}, \frac{d \vec{l} \times \vec{r}}{r^{3}}\)

(b) Using Biot-Savart law, obtain the expression for the magnetic field due to a circular coil of radius r, carrying a current I at a point on its axis distant x from the centre of the coil. (CBSE Delhi 2018C)
Answer:

we have \(\overrightarrow{d B}=\frac{\mu_{0}}{4 \pi} I \frac{|d \vec{i} \times \vec{r}|}{r^{3}}\)
r² = x² + R²

∴ dB = \(\frac{\mu_{0} I}{4 \pi} \frac{d l}{\left(X^{2}+R^{2}\right)^{3 / 2}}\)

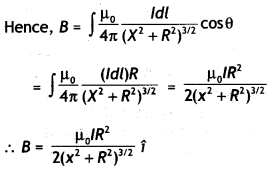
Question 69.
Derive an expression for the velocity y0 of a positive ion passing undeflected through a region where crossed uniform electric field E and magnetic field B are simultaneously present. Draw and justify the trajectory of identical positive ions whose velocity has a magnitude less than \(\left|v_{c}\right|\).
OR
A particle of mass m and charge q is in motion at speed Y parallel to a long straight conductor carrying current I as shown below.

Find the magnitude and direction of the electric field required so that the particle goes undefeated. (CBSE Sample Paper 2018-19)
Answer: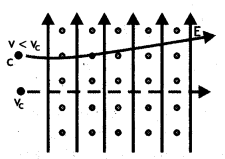

If the ion passes undeflected, therefore the magnetic and electric forces acting on the ion must be equal and opposite.
Therefore
qE = Bqv_c
v_c = \(\frac{E}{B}\)

The trajectory would be as shown. Justification: For positive ions with speed v < v_c. Force due to electric field wilt remains the same as It does not depend upon Vc.

But force due to the magnetic field will become Less than the initial value. This unbalances the two, electric and magnetic, forces hence, the ion will experience a net electric force. This will accelerate the ion along the direction of the electric field. Since initiaL velocity is perpendicular to E, the trajectory would be parabolic.
OR
For the charged particle to move undeflected

Electric force = magnetic force
qE = Bq v
or
E=Bv

Now magnetic field at a distance r from the long straight conductor is
B = \(\frac{\mu_{0} I}{2 \pi r}\)

This magnetic force Will act towards the wire.

Hence electric field is

E = \(\frac{\mu_{0} l v}{2 \pi r}\)

This electric field should act away from the wire.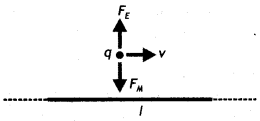

Numerical Problems:

Formulae for solving numerical problems

• Magnetic field due to a small current element dB = \(\frac{\mu_{0}}{4 \pi} \frac{l mid d L \sin \theta}{r^{2}}\)
• Magnetic field due to an infinitely long straight conductor B = \(\frac{\mu_{0}}{4 \pi} \frac{2l}{a}\)
• Magnetic field at the centre of a circular coil B = \(\frac{\mu_{0}}{4 \pi} \frac{2 \pi l}{r}\)
• Force on a charge moving in a magnetic field F = Bq v Sin θ
• The magnetic field inside a solenoid B = µ₀ n I
• Force on a current-carrying conductor placed in a magnetic field F = BIL Sin θ
• Force between two current carrying conductors \(\frac{F_{1}}{L}=\frac{\mu_{0} l_{1} l_{2}}{2 \pi a}\)
• Torque on a current loop τ = BI n A sin θ
• Current in a galvanometer l = \(\frac{C}{n B A}\) sin θ
• Shunt required S = \(\frac{l_{8} G}{l-I_{g}}\)
• Resistance required R = \(\frac{v}{l_{g}}\) – G
• Radius of a charged particle in a magnetic field r = \(\frac{m v}{B q}=\frac{\sqrt{2 m E}}{B q}\)

Question 1.
A proton and an alpha particle having the same kinetic energy are in turn allowed to pass through a uniform magnetic field perpendicular to their direction of motion. Compare the radii of the paths of the proton and the alpha particle.
Answer:
Given E_α = E_p, m_α = 4 mp, q_α = 2q_p, B is same for both. Now the radius of the path followed is given by the expression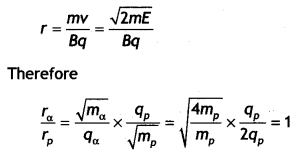

Question 2.
A circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is suspended vertically in a uniform horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of 60° with the normal to the coil. Calculate the magnitude of the counter-torque that must be applied to prevent the coil from turning.
Answer:
Given n = 30, r = 8.0 cm = 8 × 10^-2 m,
l = 6.0 A, B = 1.0 T, θ = 60°, τ = ?
Using the formula for torque
τ = BlnA

we have τ = Blnπr² sin θ
τ = 1 × 6 × 30 × 3.14 × (8 × 10^-2)² × sin 60°
= 3.1 N m

Question 3.
How can a moving coil galvanometer be converted into an ammeter? To increase the current sensitivity of a moving coil galvanometer by 50%, its resistance is increased so that the new resistance becomes twice its initial resistance. By what factor does its voltage sensitivity change?
Answer:
Voltage sensitivity
= \(\frac{\alpha}{V}=\frac{\alpha}{I R}=\frac{\text { current sensitivity }}{R}\)

When the current sensitivity increases by 50 % resistance becomes 2R.

New voltage sensitivity
= \(\frac{1+0.5}{2}\) = 0.75

Hence the voltage sensitivity decreases and becomes 75% of its original value.

Question 4.
A long straight conductor PQ carrying a current of 75 A is fixed horizontally. Another long conductor XY is kept parallel to PQ at a distance of 5 mm, in air. Conductor XY is free to move and carries a current l. Calculate the magnitude and direction of current l for which the magnetic repulsion just balances the weight of conductor XY (Mass per unit length for conductor XY is 10^-2 kg m^-1.)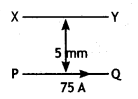

Answer:
Given l₁ = 75 A, r = 5 mm = 5 × 10^-3 m, l₂ = ? mass per unit length = 10^-2kg m^-1.

The force between the two wires should be repulsive and should balance the weight of the wire XY. Thus the current in wire XY will be opposite to that in wire PQ.

The force between the two current-carrying conductors is given by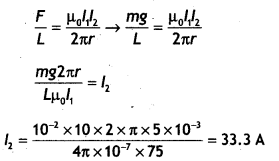

Question 5.
A galvanometer has a resistance of 30 Ω. It gives full-scale deflection with a current of 2 mA. Calculate the value of the resistance needed to convert it into an ammeter of range 0-0.3 A.
Answer:
Given G = 30 Ω, lg = 2 mA= 2 × 10^-3 A, S = ?, I = 0.3 A
Using the formula S = \(\frac{I_{g} G}{I-I_{g}}\)

we have
S = \(\frac{I_{g} G}{I-I_{g}}\) = \(\frac{30 \times 2 \times 10^{-3}}{0.3-2 \times 10^{-3}}\) = 0.20 Ω

Question 6.
An infinitely long straight current-carrying wire produces a magnetic field 8, at a point distant ‘a’ from it. What must be the radius of a circular loop, so that, for the same current through it, the magnetic field at (i) its center equals B/2 and (ii) an axial point, distant equal to the radius of the loop, equals B?
Answer:
The magnetic field at a distance ‘a’ from an infinitely long straight conductor is
B = \(\frac{\mu_{0} I}{2 \pi a}\)

(i) Given B_c = B/2. Let r be the radius of the circular coil for which the magnetic field is B/2.

Magnetic field at the centre of a circular coil is \(B=\frac{\mu_{0} I}{2 \pi a}\) Therefore
\(\frac{\mu_{0} l}{2 r}=\frac{1}{2} \times \frac{\mu_{0} l}{2 \pi a}\) or r = 2 π a

(ii) Magnetic field at the axial line of a loop is
B = \(\frac{\mu_{0} l R^{2}}{2\left(x^{2}+R^{2}\right)^{1 / 2}}\)

Here x = R radius of the loop.
Therefore \(\frac{\mu_{0} I}{2 \pi a}=\frac{\mu_{0} I R^{2}}{2\left(R^{2}+R^{2}\right)^{3 / 2}}\)

solving for R we have R = \(\frac{\pi a}{\sqrt{8}}\)

Question 7.
Calculate the value of resistance needed to convert a galvanometer of resistance 120 ft, which gives a full-scale deflection for a current of 5 mA, into a voltmeter of 0 – 50 V range.
Answer:
Given G = 120 Ω, l_g = 5 × 10^-3A, V= 50 V, R =?

Using the relation R = \(\frac{v}{l_{g}}\) – G we have
R = \(\frac{50}{5 \times 10^{-3}}\) -120 = 9880 Ω

Question 8.
Two infinitely long straight wires A₁ and A₂ carrying currents l₁ and l₂ flowing in the same directions are kept distance apart. Where should a third straight wire A₃ carrying current 1.5 l be placed between A₁ and A₂ so that it experiences no net force due to A₁ and A₂? Does the net force act on A3 depend on the current flowing through it? (CBSE Delhi 2019)
Answer:
The diagram is as shown.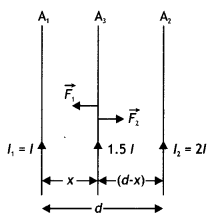


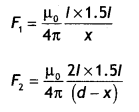
If no force is experienced by the conductor A₃, then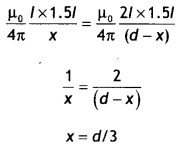

The net force on A₃ does not depend upon the current flowing through it.

Question 9.
An ammeter of resistance 0.80 Ω can measure current up to 1.0 A.
(a) What must be the value of shunt resistance to enable the ammeter to measure current up to 5.0 A?
Answer:
Given G = 0.80 Ω, /g = 1.0 A, l = 5.0 A, S = ?, R_A = ?
(a) Using the expression
S = \(\frac{I_{g} G}{I-I_{0}}=\frac{1 \times 0.8}{5-1}=\frac{0.8}{4}\) = 0.2 Ω

(b) What is the combined resistance of the ammeter and the shunt? (CBSE Delhi 2013)
Answer:
Now R_A = \(\frac{G S}{G+S}=\frac{0.8 \times 0.2}{0.8+0.2}\) = 0.016 Ω

Question 10.
A wire AB is carrying a steady current of 12 A and is lying on the table. Another wire CD carrying 5A is held directly above AB at a height of 1 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. (Take the value of g = 10 m s^-2) (CBSE AI 2013)
Answer:
Given l₁ = 12 A, r = 1 mm = 1 × 10^-3 m, l₂ = 5 A, mass per unit length = ?

The force between the two wires should be repulsive and should balance the weight of the wire CD. Thus the current in wire CD will be opposite to that in wire AB.

The force between the two current¬carrying conductors is given by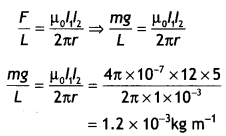

Question 11.
A square loop of side 20 cm carrying a current of I A is kept near an infinitely long straight wire carrying a current of 2 A in the same plane as shown in the figure.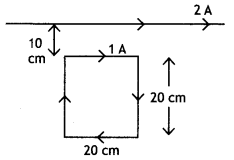

Calculate the magnitude and direction of the net force exerted on the loop due to the current carrying conductor. (CBSEAI 2015C)
Answer:
Here, PQ = 20 cm = 20 × 10^-2 m,
PS = 20 cm = 10 × 10^-2 m

Distance of PQ from AB,
r₁ = 10 cm = 10 × 10^-2 m

Distance of RS from AB,
r₂ = (10 + 20) = 30 cm = 30 × 10^-2 m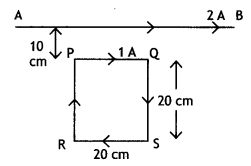

Current through long wire AB, l₁ = 2 A
Current through rectangular loop, l₂ = 1 A

Force on the arm PQ,

F₁ = \(\frac{\mu_{0} I_{1} I_{2}}{2 \pi a}\) × length PQ

F₂ = \(\frac{2 \times 10^{-7} \times 2 \times 1 \times 20 \times 10^{-2}}{10 \times 10^{-2}}\) = 8 × 10^-7 N
= 8 × 10^-7 N (towards AB)

Force on the arm RS,
F₁ = \(\frac{\mu_{0} I_{1} I_{2}}{2 \pi a}\) × length RS

F₂ = \(\frac{2 \times 10^{-7} \times 2 \times 1 \times 20 \times 10^{-2}}{30 \times 10^{-2}}\) =2.66 × 10^-7

= 2.66 × 10^-7 N (away from AB)

Effective force on the Loop,
F= F₁ – F₂
=8 × 10^-7 – 2.66 × 10^-7
= 5.34 × 10^-7 N (towards AB)

Question 12.
A square-shaped plane coil of area 100 cm2 of 200 turns carries a steady current of 5A. It is placed in a uniform magnetic field of 0.2 T acting perpendicular to the plane of the coil. Calculate the torque on the coil when its plane makes an angle. of 60° with the direction of the field. In which orientation will the coil be in stable equilibrium? (CBSE Al 2015C)
Answer:
Given A= 10-2 m², n = 200, l = 5 A, θ = 60°, B = 0.2 T, τ = ?
Using the expression τ = B I n A sin θ we have
τ = 0.2 × 5 × 200 × 10^-2 × sin 60° = 20 Nm
Stable equilibrium, when the magnetic field is in the direction of the coil.

Question 13.
A straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid-air by a uniform horizontal magnetic field B (figure). What is the magnitude of the magnetic field? (NCERT)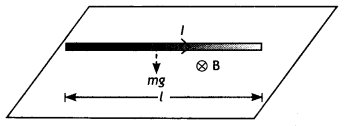

Answer:
For the wire to be suspended in mid-air, it must experience an upward force F of magnitude F = B I L to balance its weight W= mg
Therefore, BI L = mg
B = \(\frac{m g}{1 L}=\frac{0.2 \times 9.8}{2 \times 1.5}\) = 0.65 T

Question 14.
A cyclotron’s oscillator frequency is 10 MHz. What should be the operating magnetic field for accelerating proto is? If the radius of its dees is 60 cm what is the kinetic energy (in m MeV) of the proton beam produced by the accelerator (e =1.60 × 10^-19 C, mp = 1.67 × 10^-27 kg, 1 MeV = 1.6 × 10^-13 J) (NCERT)
Answer:
The oscillator frequency should be the same as the proton’s cyclotron frequency, i.e. 10 MHz = 107 Hz.
Therefore
B = \(\frac{2 \pi m v}{q}\)

= \(\frac{2 \times 3.14 \times 1.67 \times 10^{-27} \times 10^{7}}{1.6 \times 10^{-19}}\) = 0.66 T

Final velocity of protons is
V = r × 2πv = 0.6 × 6.3 × 10⁷ = 3.78 × 107 m s^-1.

E = 1/2mv² = 1.67 × 10^-27 × 14.3 × 10¹⁴ / (2 × 1.6 × 10^-13) = 7 MeV

Question 15.
A solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns. Does it carry a current of 5 A. What is the magnitude of the magnetic field inside the solenoid? (NCERT)
Answer:
Given n = 500/0.5 = 1000 turns per unit length. l = 5 A
The length L = 0.5 m and radius r = 0.01 m. Thus, L/a = 50,
Hence we have
B = μ_onl = 4π x 10^-7 × 1000 × 5 = 6.28 × 10^-3 T

Question 16.
A circular coil of wire consisting of 100 turns, each of a radius 8.0 cm, carries a current of 0.40 A. What is the magnitude of the magnetic field B at the center of the coil? (NCERT)
Answer:
Given n = 100, r = 8.0 cm = 8.0 × 10^-2 m,
l = 0.40 A,B = ?

Using the expression B = \(\frac{\mu_{0} n l}{2 r}\)
we have
B = \(\frac{\mu_{0} n l}{2 r}=\frac{4 \pi \times 10^{-7} \times 100 \times 0.40}{2 \times 8.0 \times 10^{-2}}\)

Question 17.
A horizontal overhead power line carries a current of 90 Ain the east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line? (NCERT)
Answer:
Given l = 90 A, r = 1.5 m, B = ?
Using the expression B = \(\frac{\mu_{0} l}{2 \pi r}\) we have

B = \(\frac{\mu_{0} l}{2 \pi r}=\frac{4 \pi \times 10^{-7} \times 90}{2 \times \pi \times 1.5}\) = 1.2 × 10^-5 T
The magnetic field will be towards the south.

Question 18.
A square coil of side 10 cm consists of 20 turns and carries a current of 12 A The coil is suspended vertically and the normal to the plane of the coil makes an angle of 30° with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil? (NCERT)
Answer:
Given L= 10 cm=0.1 m, A = (0.1)² = 0.01 m², n = 20 , l = 12 A, θ = 30°, B = 0.80T, τ = ?

Using the expression τ = B l n A sin θ we have
τ = 0.80 × 12 × 20 × 0.01 × sin 30° = 0.96 Nm

Question 19.
A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.
(i) What magnetic field should be set up normally to the conductor in order that the tension in the wires is zero?
(ii) What will be the total tension in the wires if the direction of the current is reversed keeping the magnetic field the same as before? (Ignore the mass of the wires.) g = 9.8 ms^-2 (NCERT)
Answer:
Given L = 0.45 m, m = 60 g, I = 5.0 A, B = ?
(i) The tension in the wires will be zero if the weight of the rod is balanced by the force on it due to the magnetic field.
Therefore we have
B I L = mg
B = \(\frac{m g}{I L}=\frac{0.06 \times 9.8}{5.0 \times 0.45}\) = 0.26 T

Thus a horizontal magnetic field of magnitude 0.26 T normal to the conductor should be applied in such a direction that Fleming’s left-hand rule gives a magnetic force in the upward direction.

(ii) The tension will become twice the weight of the wire i.e.,
T = B / L + mg = mg + mg = 2 mg
Or
T= 2 × 0.06 × 9.8 = 1.176 N

Question 20.
A galvanometer coil has a resistance of 12 ohms and the meter shows full-scale deflection for a current of 3 mA. How will you convert the meter into a voltmeter of range 0 to 18 V? (NCERT)(CBSE 2019C)
V= 18 V, R = ?
We will connect a resistance R = \(\left(\frac{V}{l_{g}}-G\right)\) in series with the galvanometer.

Therefore R = \(\frac{18}{3 \times 10^{-3}}\) – 12 = 5988 Ω

Question 21.
A galvanometer coil has a resistance of 15 ohms and the meter shows full-scale deflection for a current of 4 mA. How will you convert the meter into an ammeter of range 0 to 6A? (NCERT)
Answer:
Given G = 15 Ω, l_g = 4 mA = 4 × 10^-3 A, l = 6 A, S = ?

We will connect a resistance S = \(\frac{l_{s} G}{l-l_{s}}\) in parallel with the galvanometer.
Therefore S = \(\frac{4 \times 10^{-3} \times 15}{6-\left(4 \times 10^{-3}\right)}\) = 0.01 Ω
Or
S = 10 mΩ