Current Electricity

Class 12 Physics Chapter 3 Important Questions Current Electricity

Very Short Answer

Question 1.
A wire or resistivity ρ is stretched to double its length. What will be its new resistivity?
Answer:
The resistivity remains the same as it does not depend upon the length of the wire.

Question 2.
What is the effect of temperature on the relaxation time of electrons in a metal?
Answer:
The relaxation time of electrons decreases with the rise in temperature of the metal.

Question 3.
Which physical quantity does the voltage versus current graph for a metallic conductor depict? Give its SI unit.
Answer:
It represents resistance. It is measured in ohm.

Question 4.
Define drift velocity of electrons.
Answer:
The mean velocity acquired by electrons in a conductor when an external electric field is applied to it.

Question 5.
A resistance R is connected across a cell of emf ε and internal resistance r. A potentiometer now measures the potential difference between the terminals, of the cell as V., Write the expression for ‘r’ in terms of ε, V and R. (CBSE Delhi 2011)
Answer:
The required relation is r = \(\left(\frac{\varepsilon}{V}-1\right)\)R

Question 6.
How is the drift velocity in a conductor affected by the rise in temperature? (CBSE Delhi 2019)
Answer:
It decreases.

Question 7.
Two students A and B were asked to pick a resistor of 15 kΩ from a collection of carbon resistors. A picked a resistor with bands of colours brown, green, orange, while B chose a resistor with bands of black, green, red. Who picked the correct resistor? (CBSE AI 2013C)
Answer:
A

Question 8.
Define the term ‘Mobility’ of charge carriers in a conductor. Write its S.l. unit. (CBSE Delhi 2014, AI 2015)
Answer:
Mobility of charge carriers in a conductor is defined as the magnitude of their drift velocity per unit applied electric field. Its SI unit is m² V^-1 s^-1.

Question 9.
How does the mobility of electrons in a conductor change, if the potential difference applied across the conductor is doubled, keeping the length and temperature of the conductor constant? (CBSE Delhi 2019)
Answer:
No change.

Question 10.
Graph showing the variation of current versus voltage for a material GaAs is shown in the figure. Identify the region of
(i) negative resistance (ii) where Ohm’s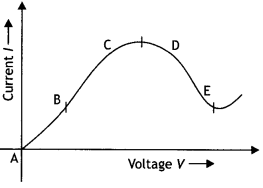

Answer:
(i) DE (ii) AB

Question 11.
Define mobility of a charge carrier. What is its relation with relaxation time? (CBSEAI 2016)
Answer:
It is defined as the drift velocity per unit electric field. The relation is μ = \(\frac{-e \tau}{m}\).

Question 12.
Nichrome and copper wires of the same length and same radius are connected in series. Current l is passed through them. Which wire gets heated up more? Justify your answer. (CBSEAI 2017)
Answer:
Nichrome, as it has more resistivity.

Question 13.
When a potential difference is applied across the ends of a conductor, how is the drift velocity of the electrons related to the relaxation time? (CBSE Delhi 2019)
Answer:
Drift velocity is directly proportional to the relaxation time.
V_d = \(\frac{e E}{m} \tau\)

Question 14.
Two bulbs are marked 60 W, 220 V and 100 W, 220 V. These are connected in parallel to 220 V mains. Which one out of the two will glow brighter?
Answer:
In parallel combination, the bulb having, more power glows more. Therefore the bulb marked 100 W, 220 V glows brighter.

Question 15.
A heater joined in parallel with a 60 W bulb is connected to the mains. If the 60 W bulb is replaced by a 100 W bulb, will the rate of heat produced by the heater be more, less or remain the same?
Answer:
The rate of heat produced in the heater will be the same as the two are connected in parallel.

Question 16.
Two conductors, one having resistance R and another 2R, are connected in turn across a dc source. If the rate of heat produced in the two conductors is Q₁ and Q₂ respectively, what is the value of Q₁/ Q₂?
Answer:
We know that Q = \(\frac{V^{2}}{R}\)t, therefore
\(\frac{Q_{1}}{Q_{2}}=\frac{R_{2}}{R_{1}}=\frac{2 R}{R}\) = 2

Question 17.
When electrons drift in metal from lower to higher potential, does it mean that all the free electrons of the metal are moving in the same direction? (CBSE Delhi 2012)
Answer:
No.

Question 18.
How does one explain the increase in resistivity of metal with an increase in temperature? (CBSE AI 2014C)
Answer:
With the increase in temperature, the average relaxation time decreases; this causes an increase in resistivity.

Question 19.
A carbon resistor is marked in red, yellow and orange bands. What is the approximate resistance of the resistor?
Answer:
24 × 10³  ohm ± 20%

Question 20.
If potential difference V applied across a conductor is increased to 2 V, how will the drift velocity of the electrons change?
Answer:
The drift velocity is given by the expression V_d = \(\frac{e V}{m L}\)τ Therefore if the potential is doubled, drift velocity is also doubled.

Question 21.
What is the largest voltage you can safely put across a resistor marked 98 ohm – 0.5 W?
Answer:
Using the expression
V = \(\sqrt{P R}=\sqrt{0.5 \times 98}\) = 7 V

Question 22.
Two wires A and B are of the same metal, have the same area of cross-section and have their lengths in the ratio 2:1. What will be the ratio of currents flowing through them respectively, when the same potential difference is applied across the length of each of them?
Answer:
\(\frac{I_{\mathrm{A}}}{I_{\mathrm{B}}}=\frac{R_{\mathrm{B}}}{R_{\mathrm{A}}}=\frac{l_{\mathrm{A}}}{l_{\mathrm{B}}}=\frac{2}{1}\)

Question 23.
How does the heat produce in a resistor depend on its resistance when
(i) a constant current is passed through it
Answer:
For l = constant, heat produced H ∝ R

(ii) a constant potential difference is applied across its ends?
Answer:
For constant potential difference V, the heat produced, H ∝ \(\frac{1}{R}\)

Question 24.
Two wires of equal length, one of copper and the other of manganin have the same resistance. Which wire is thicker? (CBSE AI 2012)
Answer:
Manganin.

Question 25.
Two identical cells, each of emf E, having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance? (CBSE AI 2013)
Answer:
The current is l = E/R

Question 26.
Define temperature coefficient of resistivity. (CBSE Sample Paper 2018-2019)
Answer:
It is defined as the fractional change in resistivity per unit change in temperature.

Question 27.
A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation of P.D. across R, versus R. (NCERT Exemplar)
Answer:
The graph is as shown.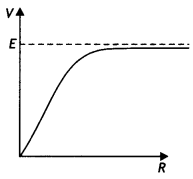

Question 28.
The plot of the variation of potential difference across a combination of three identical cells in series, versus current is as shown in the figure. What is the emf of each cell? (Delhi 2008)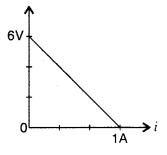

Answer:
Total emf of three cells in series = P.D corresponding to zero current = 6V
∴ The emf of each cell = \(\frac{6}{3}\) = 2V

Question 29.
A wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a A diameter 2AB? (Delhi 2008)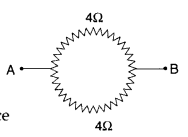

Answer:
The effective resistance between A and BO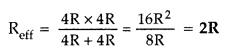

Question 30.
Two conducting wires X and Y of same diameter across a battery. If the number density of electro in X is twice that in Y, find the ratio of drift velocity of electrons in the two wires. (All India 2008)
Answer: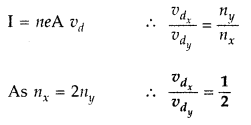

Question 31.
A resistance R is connected across a cell of emf ε and internal resestance r. A potentiometer now measures the potential difference between the terminals of the cell as V. write the expression for ‘r’ in terms of ε, V and R. (Delhi 2011)
Answer: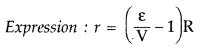

Question 32.
When electrons drift in a metal from lower to higher potential, does it mean that all the free electrons of the metal are moving in the same direction? (Delhi 2012)
Answer: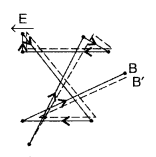

No, only the drift velocities of the electrons are superposed over their random (haphazard) thermal velocities. The solid line shows the random path followed by a free electron in the absence of an external field.

The electron proceeds from A to B, making six collisions on its path. The dotted curve shows how the random motion of the same electron gets modified when an electric field is applied.

Question 33.
Show on a graph the variation of resistivity with temperature for a typical semiconductor . (Delhi 2012)
Answer: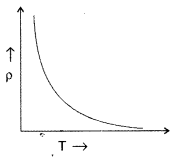

Resistivity of a semi conductor decreases rapidly with temperature.

Question 34.
Two wires of equal length, one of copper and the other of manganin have the same resistance. Which wire is thicker? (All India 2012)
Answer:

For both wires R and l are same and ρ copper < p manganin.
∴ A copper < A manganin
i.e. Manganin wire is thicker than copper wire.

Question 35.
A 10 v battery of negligible internal resistance is connected across a 200 V battery and a resistance of 38Ω as shown in the figure. Find the value of the current in circuit. (Delhi 2013)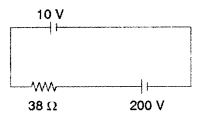

Answer:
Applying Kirchhof s rule, we get 200 -10 = 190 V

Question 36.
A 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39 Ω as shown in the figure. Find the value of the current (Delhi 2013)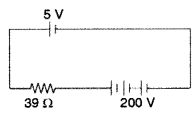

Answer:

Question 37.
The emf of a cell is always greater than its terminal voltage. Why? Give reason. (Delhi 2013)
Answer:
Emf is the p.d. when no current is drawn. When current is drawn, there will be potential drop across the internal resistance of the cell. So, terminal voltage will be less than the emf.

Question 37 a.
A cell of emf ‘E’ and internal resistance ‘r’ draws a current ‘I’. Write the relation between terminal voltage ‘V’ in terms of E, I and r. (Delhi 2013)
Answer:
V = E – I

Question 38.
Two identical cells, each of emf E, having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance ?
Answer:

[When cells are connected in parallel, emf remains unchanged]

Question 39.
Why is the terminal voltage of a cell less than its emf? (Comptt. All India 2013)
Answer:
Terminal voltage of a cell is less than emf because some curent, however small, may be is drawn to measure terminal voltage due to internal resistance of the cell.

Question 40.
Two students A and B were asked to pick a resistor of 15 kΩ from a collection of carbon resis-tors. A picked a resistor with bands of colours : brown, green, orange while B chose a resistor with bands of black, green, red. Who picked the correct resistor? (Comptt. All India 2013)
Answer:
Student ‘A’ picked up the correct resistor of 15 kΩ.

Question 40 a.
Define the term ‘Mobility’ of charge carriers in a conductor. Write its S.I. unit. (Delhi 2014)
Answer:
Mobility of charge carriers is defined as the magnitude of the drift velocity per unit electric field E.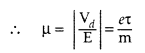

Question 41.
Show variation of resistivity of copper as a function of temperature in a graph. (Delhi 2014)
Answer: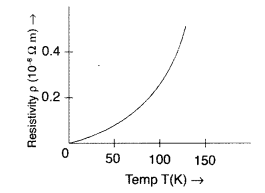

Question 42.
Define the term ‘electrical conductivity’ of a metallic wire. Write its S.I. unit. (Delhi 2014)
Answer:
Conductivity. The reciprocal of the resistivity of the material of a conductor is called its conductivity ‘σ’

The SI unit of conductivity is Ohm^-1 metre^-1 (Ω^-1im^-1’).

Question 43.
Define the term ‘drift velocity’ of charge carriers in a conductor and write its relationship with the current flowing through it. (Delhi 2014)
Answer:
Drift velocity. It is the velocity with which a free electron in the conductor gets drifted under the influence of the applied external electric field

Question 44.
How does the random motion of free electrons in a conductor get affected when a potential difference is applied across its ends? (Comptt. Delhi 2014)
Answer:
Random motion of free electrons gets directed towards the point at a higher potential.

Question 45.
State the underlying principle of a potentiometer. (Comptt. Delhi 2014)
Answer:
When a constant current flows through a wire of uniform cross-section and of uniform composition, the potential difference across any length of wire is directly proportional to its length, i.e.,
V_l\(\infty\) l

Question 46.
Write the expression for the drift velocity of charge carriers in a conductor of length T across which a potential difference ‘V’ is applied. (Comptt. All India 2014)
Answer: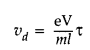

Question 47.
How does one explain increase in resistivity of a metal with increase of temperature? (Comptt. All India 2014)
Answer:
With increase in temperature, the relaxation time (average time between successive collisions) decreases and hence resistivity increases. Also,

resistivity increases, as x decreases with increase in temperature.

Question 48.
Graph showing the variation of current versus voltage for a material GaAs is shown in the figure. Identify the region of
(i) negative resistance
(ii) where Ohm’s law is obeyes (Delhi 2014)
versus for a GaAs is in the Identify the region of
Answer:
DE : Negative resistance region.
AB : Where Ohm’s law is obeyed.

Question 49.
I – V graph for a metallic wire at two different temperatures, T₁ and T₂ is as shown in the figure. Which of the two temperatures is lower and why? (All India 2015)
Answer:
The temperature T₁ is lower. Larger the slope of V-I graph, smaller the resistance. As the resistance of a metal increases with the increase of temperature, resistance at temperature T₁ is lower.

Question 50.
The plot of the variation of potential difference A across a combination of three identical cells in series, versus current is shown along the question. What is the emf and internal resistance of each cell? (All India 2016)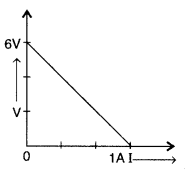

Answer: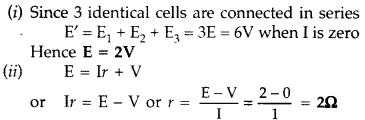

(From the graph, current is 1A corresponding to V = 0)

Question 51.
Why is a potentiometer preferred over a voltmeter for determining the emf of a cell? (Comptt. Delhi 2016)
Answer:
Potentiometer does not draw any (net) current from the cell; while Voltmeter draws some current from cell, when connected across it, hence it measures terminal voltage. It is why a potentiometer is preferred over a voltmeter to measure emf.

Question 52.
Nichrome and copper wires of same length and same radius are connected in series. Current I is passed through them. Which wire gets heated up more? Justify your answer. (Outside Delhi 2017)
Answer:
Nichrome :
Nichrome wire gets heated up more because of higher resistivity of nichrome.
Resistivity_NI > Resistivity_Cu

Question 53.
Define the conductivity of a conductor. Write its SI unit. (Comptt. Outside Delhi 2017)
Answer:
Conductivity is defined as the reciprocal of resistivity, i.e., σ = \(\frac{1}{\rho}\)
Its SI unit is S(Siemen)

Short Answer Type

Question 1.
Two metallic wires of the same material have the same length but cross-sectional area is in the ratio 1 : 2. They are connected
(i) in series and
(ii) in parallel. Compare the drift velocities of electrons in the two wires in both the cases (i) and (ii). (All India 2008)
Answer: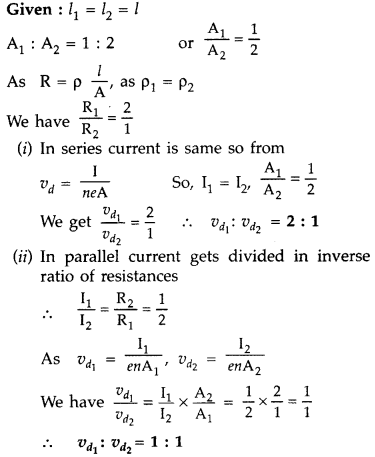

Question 2.
Derive an expression for the resistivity of a good conductor, in terms of the relaxation time of electrons. (All India 2008)
Answer:
Drift speed gained by an electron under the effect of electric field \(\overrightarrow{\mathrm{E}}\) in a conductor is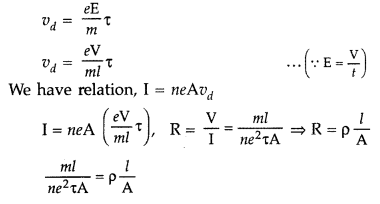

\(\rho=\frac{m}{n e^{2} \tau}\) between resistivity and relaxation time of electrons.

Question 3.
Using the mathematical expression for the conductivity of a material, explain how it varies with temperature for
(i) semiconductors,
(ii) good conductors. (All India 2008)
Answer:
Conductivity σ = \(\frac{n e^{2} \tau}{m}\)
(i) Semiconductors: With increase in temperature, conductivity of semiconductor increases. It is due to increase in V. It dominates the effect caused by decrease in ‘x’.
(ii) Good conductors : With increase in temperature, conductivity of good conductors decreases. It is due to decrease in the value of relaxation time. The effect of increased value of V is negligible.

Question 4.
A cell of emf ‘E’ and internal resistance V is connected across a variable resistor ‘R’. Plot a graph showing the variation of terminal potential ‘V’ with resistance R.
Predict from the graph the condition under which ‘V’ becomes equal to ‘E’. (Delhi 2009)
Answer:
(i) V = ε – Ir gives the terminal voltage and can be plotted as shown in Figure 1.
(ii) The graph between V and R, is shown in Figure 2.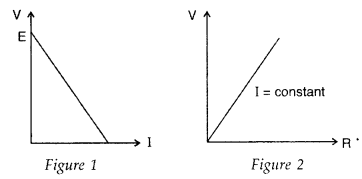

V becomes E when no current is down.

Question 5.
Derive an expression for drift velocity of free electrons in a conductor in terms of relaxation time. (Delhi 2009)
Answer:
In the absence of electric field the electrons motion is random and the net velocity is zero. In the presence of electric field, they tend to flow opposite to that of the electric field in the conduction. If an electric field ‘E’ is applied across a length l of the conductor, the electrons will experience an acceleration, a = \(\frac{e \mathrm{E}}{m}\).
If the average time for the acceleration is x, the velocity required is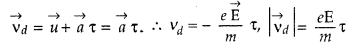

Question 6.
Calculate the current drawn from the battery in the given network. (All India 2009)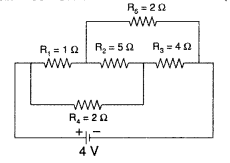

Answer: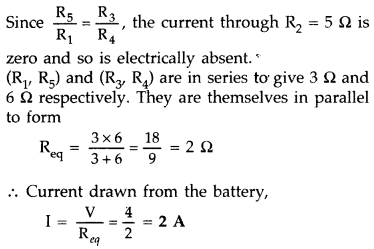

Question 7.
Define current sensitivity and voltage sensitivity of a galvanometer. Increasing the current sensitivity may not necessarily increase the voltage sensitivity of a galvanometer. Justify. (All India 2009)
Answer:
Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.

Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.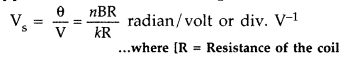

Since V_s = \(\frac{\mathrm{I}_{\mathrm{s}}}{\mathrm{R}}\), increase in current sensitivity may
not necessarily increase the voltage sensitivity. It may be affected by the resistance used.

Question 8.
A wire of 15 Ω resistance is gradually stretched to double its original length. It is then cut into two equal parts. These parts are then connected in parallel across a 3.0 volt battery. Find the current drawn from the battery. (All India 2009)
Answer:
R = 15 Ω
On stretching to double its original length, the resistance becomes R₁ = 60 Ω, as on stretching volume is constant and R\(\alpha\) l².
The two cut parts will have a resistance of 30 Ω each as they are connected in parallel, the

Question 9.
A wire of 20 Ω resistance is gradually stretched to double its original length. It is then cut into two equal parts. These parts are then connected in parallel across a 4.0 volt battery. Find the current drawn from the battery. (All India 2009)
Answer:
On stretching, the resistance of the wire will get to four times, i.e., 80 Ω as volume is constant and
R \(\alpha\) l².
So the two equal parts will have a resistance of 40 Ω each.
When connected in parallel, the equivalent resistance will be 20 Ω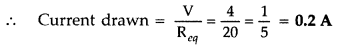

Question 10.
In the given circuit, assuming point A to be at zero potential, use Kirchhoff’s rules to determine the potential A at point B. (All India 2011)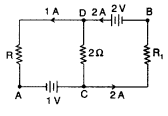

Answer:
Applying Kirchhoff’s law by moving along ACDE,
we get,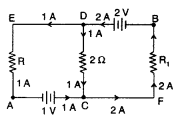

Question 11.
In the meter bridge experiment, balance point was observed at J with AJ = l.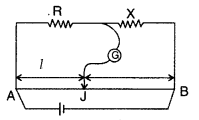

(i) The values of R and X were doubled and then interchanged. What would be the new position of balance point?
(ii) If the galvanometer and battery are interchanged at the balance position, how will the balance point get affected? (All India 2011)
Answer:
(i) Balance point will change from l to (100 – l),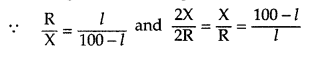

(ii) From the principle of Wheatstone bridge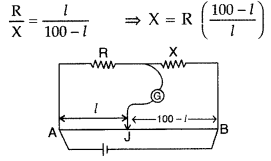

Hence, the galvanometer and cell are interchanged, the condition for a balance bridge is still satisfied. Therefore, the galvanometer will not show any deflection.

Question 12.
A cell of emf E and internal resistance r is connected to two external resistances R₁ and R₂ and a perfect ammeter. The current in the circuit is measured in four different situations:
(i) without any external resistance in the circuit
(ii) with resistance R₂ only
(iii) with R₁ and R₂ in series combination
(iv) with R₁ and R₂ in parallel combination
The currents measured in the four cases are 0.42A, 1.05A, 1.4A and 4.2A, but not necessarily in that order. Identify the currents corresponding to the four cases mentioned above.
Answer:

Question 13.
A battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, find
(i) the resistance of the resistor;
(ii) the terminal voltage of the battery. (Comptt. Delhi 2012)
Answer: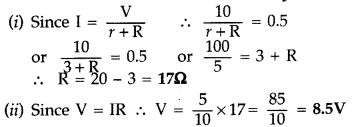

Question 14.
A battery of emf 6 V and internal resistance 2Ω is connected to a resistor. If the current in the circuit is 0.25 A, find
(i) the resistance of the resistors;
(ii) the terminal voltage of the battery. (Comptt. Delhi)
Answer: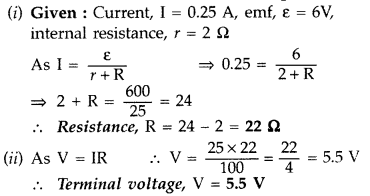

Question 15.
The network PQRS, shown in the circuit diagram, has the batteries of 4 V and 5 V and negligible internal resistance. A milliammeter of 20 Ω resistance is connected between P and R. Calculate the reading in the milliammeter. (Comptt. All India 2012)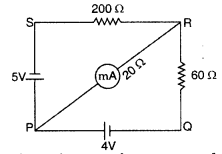

Answer:
Applying loop rule to loop PQRP
-4 = 60(I – I₁) – 20 I₁ = 0
or – 4 = 60I – 60I₁ – 20I₁
or 20I₁ -15 I = 1 …[+ by 4 …(i)]
Applying loop Yule to loop PRSP, we get
-5 + 200 I + 20 I₁ = 0
4I₁ + 40 I = 1 …[+ by 5 …(ii)]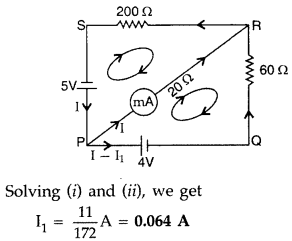

∴ Reading of milliammeter = 0.064 A

Question 16.
The network PQRS, shown m the circuit diagram, has the batteries of 5 V and 10 V and negligible internal resistance. A milliammeter of 50Ω resistance is connected between P and R. Calculate the reading in the milliammeter. (Comptt. All India 2012)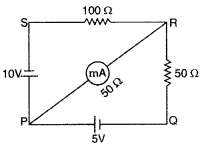

Answer:
Applying loop rule to loop PSRP
-10 + 100 I + 50 I₁ = 0
or 100 I + 50 I₁ = 10
or 10 I + 5 I₁ = 1 …[+ by 10 …(i)
Applying loop rule to loop PRQP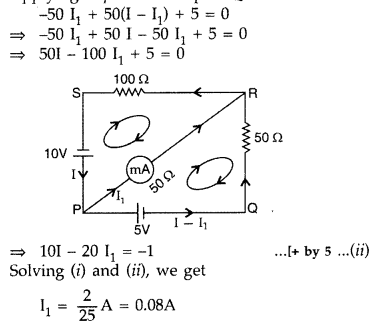

Reading in milliammeter = 0.08A

Question 17.
State the principle of a potentiometer. Describe briefly, with the help of a circuit diagram, how this device is used to compare the emf’s of two cells. (Comptt. All India 2012)
Answer:
Potentiometer : A potentiometer is a device used to measure potential difference.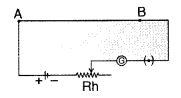

Principle : The basic principle of a potentiometer is that when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length.

…where [K is called potential gradient
Close the key K₁. A constant current flows through the potentiometer wire. With key K₂ kept open, move the jockey along AB till it balances the emf e of the cell. Let l, be the balancing length of the wire. If K is the potential gradient, then emf of the cell will be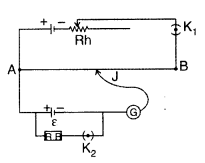


With the help of resistance box R.B, introduce a resistance R and close key K₂. Find the balance point for the terminal potential difference V of the cell. If l₂ is the balancing length, then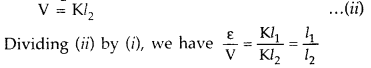

Let r be the internal resistance of the cell ε = I (R + r) and V = IR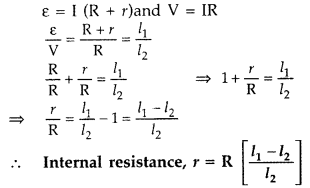

Question 18.
An ammeter of resitance 1 Ω can measure current upto 1.0 A
(i) What must be the value of the shunt resistance to enable the ammeter to measure upto 5.0 (A)?
(ii) What is the combined resistance of the ammeter and the shunt? (Delhi 2013)
Answer: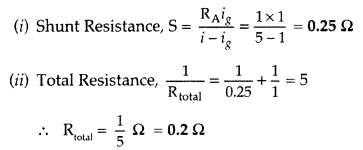

Question 19.
Explain the term ‘drift velocity’ of electrons in a conductor. Hence obtain the expression for the current through a conductor in terms of ‘drift velocity’
Answer:
Definition : Drift velocity is defined as the velocity with which fress electrons in a conductor get drifted in a direction opposite to the direction of the applied field. Its unit is m^-1s and dimensions [LT^-1]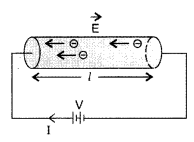

Expression : The magnitude of electric field set up across the conductor is given by
E = \(\frac{\mathrm{V}}{l}\)
Let n be the number of free electrons per unit volume of the conductor.
Then, total number of free electrons in the conductor
= n × Volume of the conductor
Hence, Q = (nAl)e
Time taken by the charge to cross the conductor length l is given by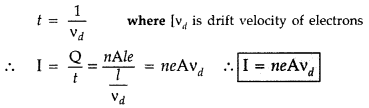

Question 20.
Write the expression for the current in a conductor of cross-sectional area A in terms of drift velocity. (Comptt. All India 2013)
Answer:
Drift velocity. Drift velocity is defined as the velocity of the free electrons with which they get drifted towards the positive terminal under the influence of the external electric field. The drift velocity of electron is of the order of 10^-5 m/sec. Expression for current in terms of drift velocity is :

Expression : Consider a conductor of length l and of uniform cross-section area A .
∴ Volume of the conductor = Al
If n is the number of the conductors, then total number of free electrons in the conductor = Aln
If e is the charge on ” each electron, then
total charge on all A the free electrons in the conductor, q = Alne
The electric field set up across the conductor of potential difference V is given by,


Due to this field, the free electrons present in the conductor will begin to move with a drift velocity v_d towards the positive terminal of the battery
∴ Time taken by free electrons to cross the conductor,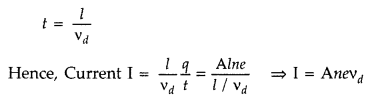

SinceA, n and e are constants,

Therefore, the current flowing through a conductor is directly proportional to the drift velocity.

Question 21.
Describe briefly, with the help of a circuit diagram, how a potentiometer is used to determine the internal resistance of a cell.
(All India 2013)
Answer:
The apparatus is set up as per circuit diagram drawn here.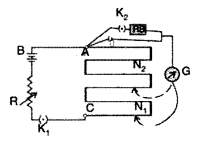

The cell (emf ε), whose internal resistance (r) is to be determined, is connected across a resistance box through a key K₂, as shown in the figure. With key K₂ is open, balance is obtained at length l₁ (AN₁), then

When key K₂ is closed, the cell sends a current (I) through the resistance box (R). If V is the terminal potential difference of the cell and balance is obtained at length l₂ (AN₂)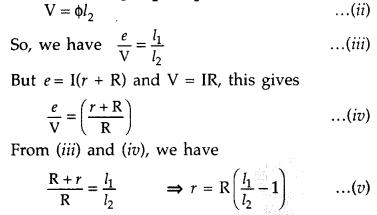

Using equation (v) we can find internal resistance of the cell.

Question 22.
Write a relation between current and drift veloc¬ity of electrons in a conductor. Use this relation to explain how the resistance of a conductor changes with the rise in temperature. (Comptt. Delhi 2013)
Answer:
Relation between current and drift velocity :

On increasing temperature, the resistance of the conductor increases due to increase in frequent collisions of electrons with each other, resulting into decrease in the drift velocity.

Question 23.
Use Kirchhoff’s rules to determine the value of the current I₁ flowing in the circuit shown in the figure. (Comptt. Delhi 2013)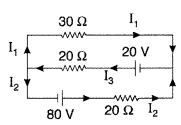

Answer:
Using Kirchoff’s first law at junction E, we get
I₃ = I₃ + I₂
In loop ABCDA, using Kirchoff’s second law, we get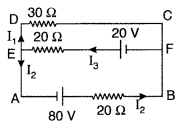

80 – 20 I₂ + 30 I₁ = 0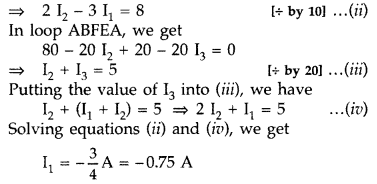

So (-) sign of current indicates that the direction of current is opposite to that as shown in the circuit diagram.

Question 24.
Draw a graph showing variation of resistivity with temperature for nichrome. Which property of nichrome is used to make standard resistance coils? (Comptt. All India 2013)
Answer:
Temperature coefficient of resistivity (α) is very small for nichrome.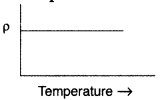

Question 25.
A battery of emf E and internal resistance r when connected across an external resistance of 12 ft, produces a current of 0.5 A. When connected across a resistance of 25 ft, it produces a current of 0.25 A. Determine
(i) the emf and
(ii) the internal resistance of the cell. (Comptt. All India 2013)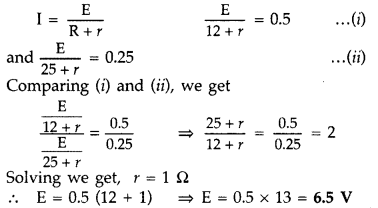

Question 26.
Define mobility of a charge carrier. Write the relation expressing mobility in terms of relaxation time. Give its SI unit. (Comptt. All India 2013)
Answer:
Mobility. Mobility of electron p is defined as the magnitude of the drift velocity per unit electric field E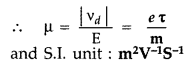

Question 27.
A uniform wire of resistance 12 Ω is cut into three pieces so that the ratio of the resistances R₁ : R₂ : R₃ = 1 : 2 : 3 and the three pieces are connected to form a triangle across which a cell of emf 8V and internal resistance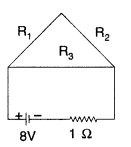

1 Ω is connected as shown. Calculate the current through each part of the circuit. (Comptt. All India 2013)
Answer: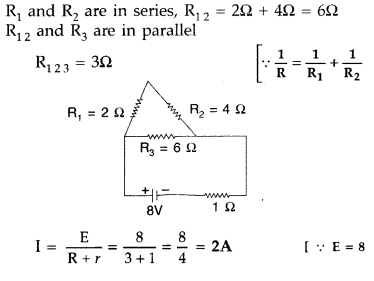

Question 28.
State Kirchhoff’s rules. Explain briefly how these rules are justified. (Delhi 2014)
Answer:
Kirchhoff’s rules.

1. Kirchhoff’s junction rule : At any junction, the sum of the currents entering the junction is equal to the sum of currents leaving the junction.
2. Kirchhoff’s loop rule : The algebraic sum of changes in potential in any closed loop involving resistors and cells is zero.

These two laws are justified on the basis of law of conservation of charge and the law of conservation of energy respectively.

Question 29.
A cell of emf ‘E’ and internal resistance V is connected across a variable resistor ‘R’. Plot a graph showing variation of terminal voltage ‘V’ of the cell versus the current ‘I’. Using the plot, show how the emf of the cell and its internal resistance can be determined. (All India 2014)
Answer: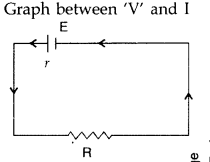

Intercept of Y-axis will give the value of ‘E’; while the slope of the line will give the value of internal resistance.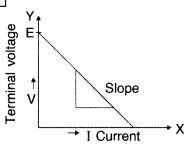

Question 30.
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 1.0 × 10 ^-7 m² carrying a current of 1.5 A. Assume the density of conduction electrons to be 9 × 10²⁸ m^-3. (All India 2014)
Answer: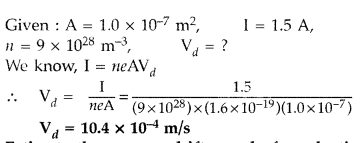

Question 31.
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2.5 × 10^-7 m² carrying a current of 1.8 A. Assume the density of conduction electrons to be 9 × 10²⁸ m^-3. (All India 2014)
Answer: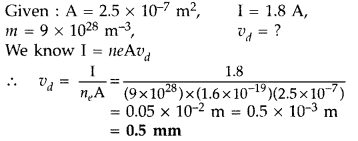

Question 32.
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2.5 × 10^-7 m² carrying a current of 2.7 A. Assume the density of conduction electrons to be 9 × 10²⁸ m^-3. (All India 2014)
Answer:
0.75 × 10^-3 ms^-1

Question 33.
Draw a plot showing the variation of resistivity of a
(i) conductor and
(ii) semiconductor, with the increase in temperature.
How does one explain this behaviour in terms of number density of charge carriers and the relaxation time? (Comptt. Delhi 2014)
Answer:
(i) For conductor :
(ii) For semiconductor :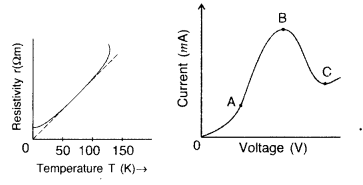

(iii) Behaviour :

In conductors, average relaxation time decreases with increase in temperature, resulting in an increase in resistivity.
In semiconductors, the increase in number density (with increase in temperature) is more than the decrease in relaxation time; the net result is, therefore, a decrease in resistivity.

Question 34.
Distinguish between emf (ε) and terminal voltage (V) of a cell having internal resistance r. Draw a plot showing the variation of terminal voltage (V) vs the current (I) drawn from the cell. Using this plot, how does one determine the internal resistance of the cell?
– (Comptt All India 2014)
Answer:
emf is the potential difference between two terminals of the cell, when no current is drawn from the cell I while
• terminal voltage is the potential difference between two terminals when current passes through it.
• negative slope of the graph gives internal resistance.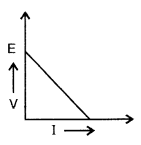

Question 35.
Use Kirchhoff’s rules to obtain conditions for the balance condition in a Wheatstone bridge. (Delhi 2015)
Answer:
Conditions for the balance condition in a Wheatstone bridge :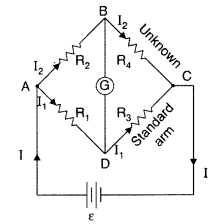

Applying Kirchhoff’s loop rule to closed loop ADBA,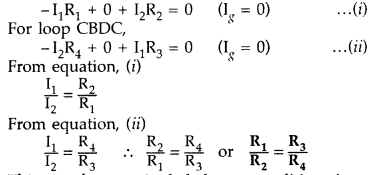

This is the required balance condition in a Wheatstone bridge arrangement.

Question 36.
Use Kirchhoff’s rules to determine the potential difference between the points A and D when no current flows in the arm BE of the electric network shown in the figure.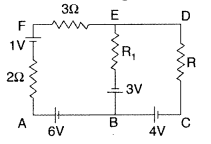

Answer:
Let us consider the loop ABED.
Using Kirchhoff’s second law, we have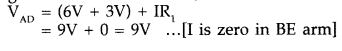

Question 37.
Calculate the current drawn from the battery by the network of resistors shown in the figure. (Comptt. All India 2015)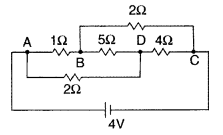

Answer:
Given : Circuit diagram can be rearranged as shown below :
It forms a wheatstone’s bridge

It is the condition of null point when no current flows through BD arm, i.e. 5 Ω.
Resistances P = (1 Ω) and R = (2 Ω) are in series;
Similarly, Resistances Q = (2 Ω) and S in series,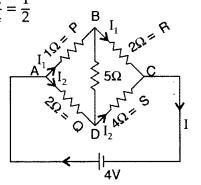

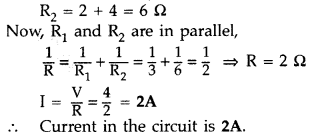
Question 38.
Using the concept of drift velocity of charge carriers in a conductor, deduce the relationship between current density and resistivity of the conductor. (Comptt. Delhi 2015)
Answer:
The drift velocity is given by,

Question 39.
Two cells of emfs 1.5 V and 2.0 V having internal resistance 0.2 Ω and 0.3 Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.(Delhi 2016)
Answer:
Given : E₁ = 1.5 V, E₂ = 2.0 V,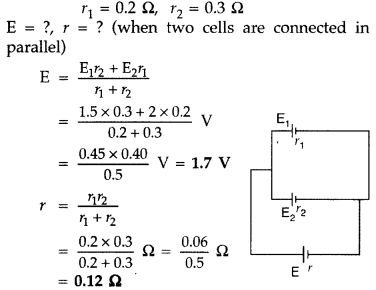

Question 40.
A battery of emf 12V and internal resistance 2 Ω is connected to a 4 Ω resistor as shown in the figure.
(a) Show that a voltmeter when placed across the cell and across the resistor, in turn, gives the
(b) To record the voltage and the current in the circuit, why is voltmeter placed in parallel and ammeter in series in the circuit? (All India)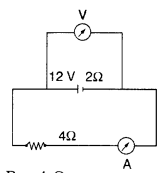

Answer: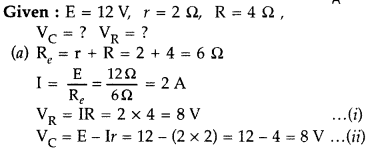

We find from the equations (i) and (ii), the voltmeter gives the same reading, i.e. 8 V.
(b) An ammeter is connected in series because same current is flowing in the circuit, while voltmeter is connected in parallel to measure potential difference across two points in the circuit.

Question 41.
The figure shows a plot of terminal voltage ‘V’ versus the current ‘i’ of a given cell. Calculate from the graph
(a) emf of the cell and
(b) internal resistance of the cell. (Comptt. Outside Delhi 2017)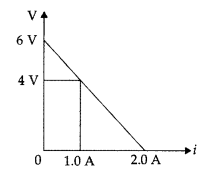

Answer: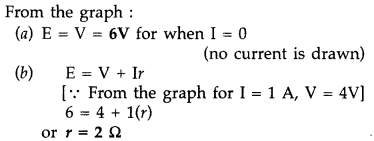

Question 42.
A cell of emf 4 V and internal resistance 1 Ω is connected to a d.c. source of 10 V through a resistor of 5 Ω. Calculate the terminal voltage across the cell during charging.
Answer: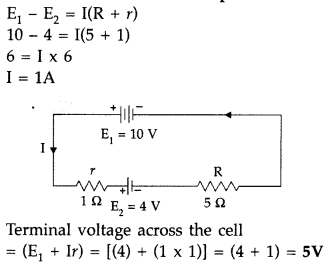

Question 43.
Why is a potentiometer preferred over a voltmeter for determining the emf of a cell? (CBSE Delhi 2016C)
Answer:
The potentiometer is based on the null method or it does not draw any (net) current from the cell and measures emf However, the voltmeter draws some current from the cell when connected across it, hence measures terminal voltage.

Question 44.
The figure shows the V – l graph for a parallel and series combination of two resistors A and B. Which line represents the parallel combination?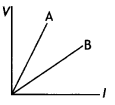

Answer:
For the same potential, the current is less in series combination than parallel combination. Therefore from the graph, it is apparent that the same potential current is less in A. Therefore B represents the parallel combination.
As, R = \(\frac{V}{l}\)

The slope of B > Slope of A

Question 45.
V – l graph for a given metallic wire at two temperatures is shown. Which of these is at a higher temperature?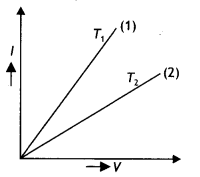

Answer:
At higher temperature resistance of a metallic wire is more or its conductance is low. Hence, graph (2) is at a higher temperature, i.e. T₂ > T₁.

Question 46.
In an experiment on a metre bridge, if the balancing length AC is ‘x’, what would be its value, when the radius of the metre bridge wire AB is doubled? Justify your answer. (CBSE AI 2011C)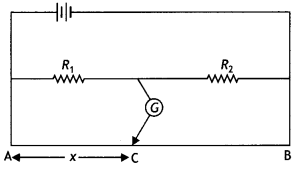

Answer:
In a metre bridge, at the balance point we have
\(\frac{R_{1}}{R_{2}}=\frac{x}{100-x}\)

As R1 and R2 remain the same, x will also remain the same. It does not depend upon the diameter of the wire.

Question 47.
The emf of a cell is always greater than its terminal voltage. Why? Give reason. (CBSE Delhi 2013)
Answer:
When current passes through a cell, there is a drop in potential across it due to its internal resistance. This is called the lost volt. Thus terminal voltage is less than the emf of the cell.

Question 48.
Draw a graph showing the variation of resistivity with temperature for nichrome. Which property of nichrome is used to make standard resistance coils? (CBSEAI 2013C)
Answer:
The graph is as shown.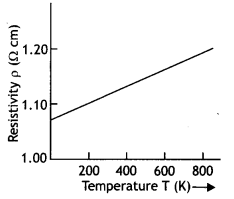

The property has a low-temperature coefficient of resistance.

Question 49.
Define the term ‘mobility’ for a charge carrier and state its SI unit.
Name the mobile charge carriers in
(i) an electrolyte,
(ii) a semiconductor and
(iii) an ionised gas. (CBSE Al 2015)
Answer:
Mobility is defined as the ratio of the drift velocity of the charge to the applied electric field.
(i) Anions and cations.
(ii) Electrons and holes
(iii) Free electrons.

Question 50.
Define the term current density of a metallic conductor. Deduce the relation connecting current density (J) and the conductivity (a) of the conductor, when an electric field E is applied to it. (CBSE AI 2015)
Answer:
Current density is defined as the current flowing per unit area of the conductor.

Mathematically current density is given by the expression J = \(\frac{l}{A}\)

But l = V/R and R = \(\frac{ρl}{A}\) = \(\frac{L}{σA}\). Substituting in the above relation, we have

J = \(\frac{l}{A}\) = \(\frac{V}{AL}\) × σA= \(\frac{V}{L}\) × σ = Eσ

Question 51.
(a) Define the terms ‘drift velocity’ and ‘relaxation time’ giving their physical significance.
Answer:
Drift Velocity: It is the average velocity of the free electrons with which they get drifted towards the positive terminal under the influence of the external field.

Significance: The net current flowing through any cross-section is controlled by drift velocity and there is no transport of charges in a direction perpendicular to the applied field. Relaxation Time (T): The average time between successive collisions of electrons or ions in a conductor is called the relaxation time.

Significance: It determines the drift velocity acquired by the electrons under the given applied electric force and also determines the electrical conductivity of a conductor at different temperatures.

(b) A conductor of length L is connected across a dc source of emf E. If the conductor is replaced by another of the same material and area of cross-section but of length 5L, by what factor will the drift velocity change? (CBSE2019C)
Answer:
In the first case:
V_d= \(\frac{e V}{m L}\)τ

In the second case: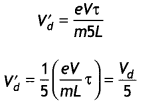

Thus we find that the drift velocity becomes \(\frac{1}{5}\) of its original value.

Question 52.
A cell of emf ‘E’ and internal resistance ‘r’ is connected across a variable resistor. ‘R’. Plot a graph showing the variation of terminal voltage ‘ V’ of the cell versus the current ‘l’. Using the plot, show how the emf of the cell and its internal resistance can be determined. (CBSE AI 2014)
Answer:
The graph is as shown.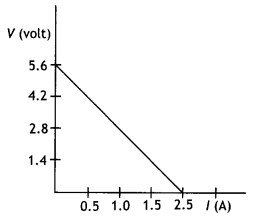

For l = 0,V= E
The internal resistance can be found by using the expression
V = E – l_r

For V = 0
E = l_r
r = E/l

Question 53.
Two electric bulbs P and Q have their resistances in the ratio of 1: 2. They are connected in series across a battery. Find the ratio of the power dissipation in these bulbs. (CBSE AI, Delhi 2018)
Answer:
Given \(\frac{R_{\mathrm{p}}}{R_{\mathrm{Q}}}\) = \(\frac{1}{2}\)

Power dissipated \(\frac{P_{\mathrm{p}}}{P_{\mathrm{Q}}}=\frac{I^{2} R_{\mathrm{p}}}{I^{2} R_{\mathrm{Q}}}=\frac{1}{2}\)

Question 53 a.
A 10 V cell of negligible Internal resistance Is connected In parallel across a battery of emf 200 V and Internal resIstance 38 š as shown in the figure. Find the value of current in the circuit. (CBSE AI, Delhi 2018)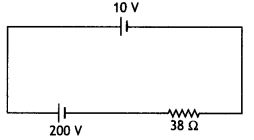

Answer:
Given ε₁ = 10 V, r₁ = 0, ε₂ = 200 V, r₂ = 38 Ω
The two cells send current in the opposite direction; therefore, net emf of the combination
E = 200 – 10 = 190V

Hence current in the circuit
l = \(\frac{E}{R}=\frac{190}{38}\) = 5 A

Question 54.
In a potentiometer arrangement for determining the emf of a cell, the balance point of the cell In an open circuit is 350 cm. When the resistance of 9 Ω Is used In the external circuit of the cell, the balance point shifts to 300 cm. Determine the internal resistance of the cell. (CBSE AI, Delhi 2018)
Answer:
Given L₁ = 350 cm, L₂ – 300 cm, R = 9 Ω, r = ? Using the expression
r = \(\left(\frac{L_{1}-L_{2}}{L_{2}}\right) R=\left(\frac{350-300}{300}\right)\) × 9 = 1.5 Ω

Question 55.
TWo bulbs are rated (P₁ V) and (P₂, V). If they are connected (i) in series and (ii) in parallel across a supply V, find the power dissipated in the two combinations in terms of P₁ and P₂. (CBSE Delhi 2019)
Answer:
Resistances of the two bulbs R₁ = \(\frac{V^{2}}{P_{1}}\) and R₂ = \(\frac{V^{2}}{P_{2}}\)

(i) Net resistance in series
R_s = R₁ + R₂ = \(\frac{V^{2}}{P_{1}}+\frac{V^{2}}{P_{2}}=V^{2}\left(\frac{P_{1}+P_{2}}{P_{1} P_{2}}\right)\)

(ii) Net resistance in parallel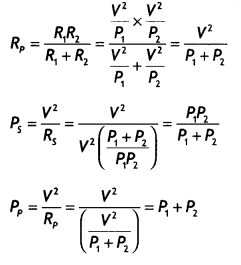

Question 56.
What is the advantage of using thick metallic strips to join wires in a potentiometer? (NCERT Exemplar)
Answer:
The metal strips have low resistance and need not be counted in the potentiometer Length l of the null point. One measures only their lengths along with the straight segments (of lengths 1 metre each). This is easily done with the help of centimetre rulings or metre ruler and leads to accurate measurements.

Question 57.
AB is a potentiometer wire (figure). If the value of R is increased, in which direction will the balance point J shift? (NCERT Exemplar)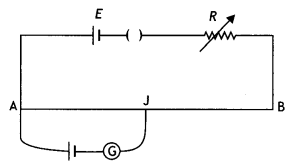

Answer:
If R is increased, the current through the wire will decrease. This will decrease the potential gradient across the potentiometer wire (k = V/L = l_pR_p/L). Hence more length of the wire will be required to balance the same cell. Therefore J will shift towards B.

Question 58.
While doing an experiment with a potentiometer (figure) it was found that the deflection is one-sided and
(i) the deflection decreased while moving from one end A of the wire to the end B;
(ii) the deflection increased while the jockey was moved towards the end B.
(iii) Which terminal + or -ve of the cell E1 is connected at X in case (i) and how is E1 related to E?
(iv) Which terminal of the cell E1 is connected at X in case (ii)? (NCERT Exemplar)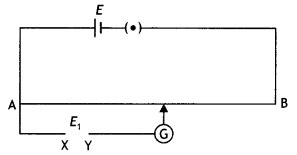

Answer:
(i) Positive terminal of E₁ is connected at Xand E₁ > E.
(ii) Negative terminal of E₁ is connected at X.

Question 59.
The circuit in the figure shows two cells connected in opposition to each other. Cell E₁ is of emf 6 V and internal resistance 2 Ω; the cell E₂ is of emf 4 V and internal resistance 8 Ω. Find the potential difference between the points A and B. (NCERT Exemplar)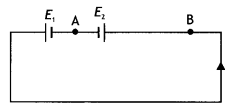

Answer:
The cells are connected in the opposite direction, therefore net emf in the circuit is
E = E₁ – E₂ = 6 – 4 = 2 V

Hence current in the circuit is
l = \(\frac{E}{R+r}\) = \(\frac{2}{10}\) = 0.2 A

P.D. across E₁ = 6 – 0.2 × 2 = 5.6 V
P.D. across E₂ = VAB = 4 + 0.2 × 8 = 5.6 V
Point B is at a higher potential than A

Question 60.
Prove that the current density of a metallic conductor is directly proportional to the drift speed of electrons. (Delhi 2008)
Or
Derive an expression for the current density of a conductor in terms of the drift speed of electrons. (All India 2008)
Answer:
Suppose a potential difference V is applied across a conductor of length l and of uniform cross-section A. The electric field E set up inside the conductor is given by
E = \(\frac{V}{l}\)
Under the influence of field \(\overrightarrow{\mathrm{E}}\), the free electrons begin to drift in the opposite direction \(\overrightarrow{\mathrm{E}}\) with an average drift velocity v_d.
Let the number of electrons per unit volume or electron density = n
Charge on an electron = e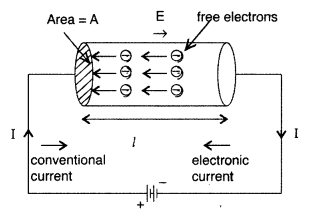

No. of electrons in length l of the conductor = n x volume of the conductor = n × Al
Total charge contained in length l of the conductor is
q = enAl … (i)
All the electrons which enter the conductor at the right end will pass through the conductor at the left end in time,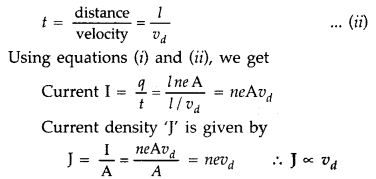

Hence the current density of a metallic conductor is directly proportional to the drift speed of electrons.

Question 61.
A number of identical cells n, each of emf e, internal resistance r connected in series are charged by a d.c. source of emf elr using a resistor R.
(i) Draw the circuit arrangement.
(ii) Deduce the expressions for
(a) the charging current and
(b) the potential difference across the combination of the cells. (Delhi 2008)
Answer: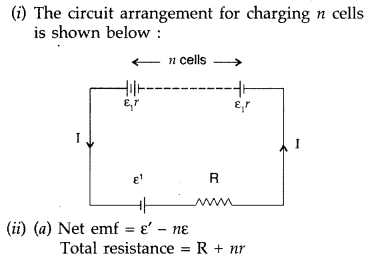

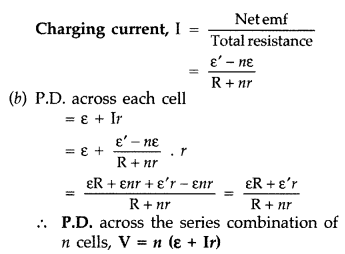
Question 62.
A potentiometer wire of length 1 m is connected to a driver cell of emf 3 V as shown in the figure. When a cell of 1.5 V emf is used in the secondary circuit, the balance point is found to be 60 cm. On replacing this cell and using a cell of unknown emf, the balance point shifts to 80 cm.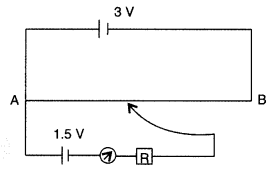

(i) Calculate unknown emf of the cell.
(ii) Explain with reason, whether the circuit works, if the driver cell is replaced with a cell of emf 1 V.
(iii) Does the high resistance R, used in the secondary circuit affect the balance point? Justify your answer. (Delhi 2008)
Answer:

(ii) The circuit will not work. If emf of auxiliary battery is greater than the emf of the driver cell of the potentiometer, there will be no balance point on the wire AB. The maximum potential drop across the wire will be of 1 V and will not be able to balance 1.5 V emf.
(iii) No, the balance point is not affected by the high resistance R because no current flows through the cell at the balance point.

Question 63.
Define resistivity of a conductor. Plot a graph showing the variation of resistivity with temperature for a metallic conductor. How does one explain such a behaviour, using the mathematical expression of the resistivity of a material. (Delhi 2008)
Answer:
(i) Resistivity of conductor : It is the resistance of a conductor of unit length and unit area of cross-section.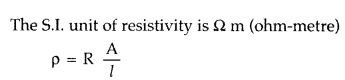

(ii) Variation of resistivity with temperature :
The resistivity of a material is given by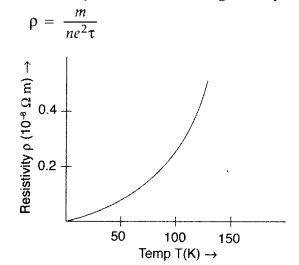

On increasing temperature, average speed of drifting electrons increases. As a result collisions are more frequent. Average relaxation time τ decreases, hence ‘ρ’ increases.

Question 64.
(i) Calculate the equivalent resistance of the given electrical network between points A and B.

(ii) Also calculate the current through CD and ACB, if a 10 V d.c. source is connected between A and B, and the value of R is assumed as 2 Ω. (All India 2008)
Answer:
(i) Equivalent circuit of the given problem is shown in the given diagram. The simplified circuit is equivalent to a balanced wheatstone bridge.
Hence there will be no current in arm CD,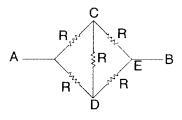

(ii) Being a balanced wheatstone bridge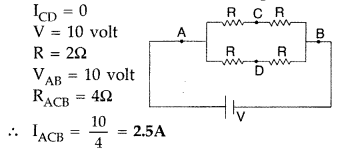

Question 65.
The figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10 Ω is connected in series with X, the null point shifts by 10 cm.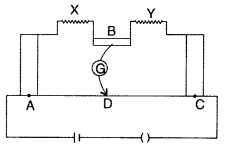

Find the position of the null point when the 10 Ω resistance is instead connected in series with resistance ‘Y’. Determine the values of the resistances X and Y. (Delhi 2008)
Answer: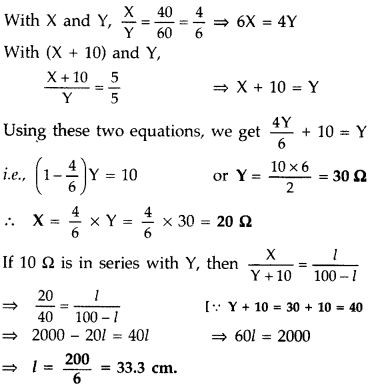

Question 66.
(i) State the principle of working of a meter bridge. x
(ii) In a meter bridge balance point is found at a distance l₁ with resistances R and S as shown in the figure.
When an unknown resistance X is connected in parallel with the resistance S, the balance point shifts to a distance l₂. Find the expression for X in terms of l₁ l₂ and S. (All India 2009)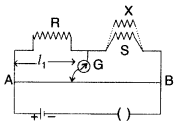

Answer:
(i) Meter bridge : Meter bridge is an arrangement of four resistances used for measuring one unknown resistance in terms of other three known resistances.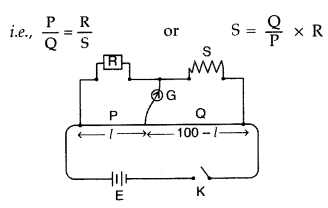

At the balance condition, no current flows through the galvanometer arm. By using the balance condition of meter bridge, the value of unknown resistance can be determined, knowing the other three resistances.
(ii) With R and S alone, we have

With S and X in parallel and R on the left gap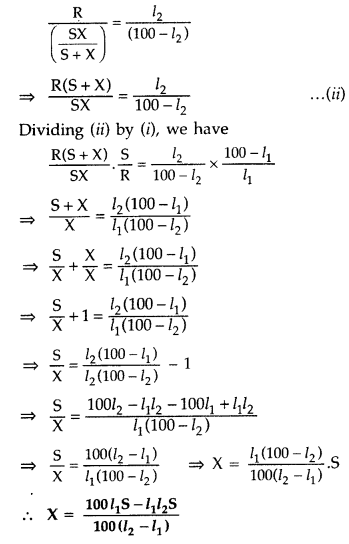

Question 67.
Write the principle of working of a potentiometer. Describe briefly, with the help of a circuit diagram, how a potentiometer is used to determine the internal resistance of a given cell. (Delhi 2009)
Answer:
Potentiometer : A potentiometer is a device used to measure potential difference.

Principle : The basic principle of a potentiometer is that when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length.

…where [K is called potential gradient
Close the key K₁. A constant current flows through the potentiometer wire. With key K₂ kept open, move the jockey along AB till it balances the emf e of the cell. Let l, be the balancing length of the wire. If K is the potential gradient, then emf of the cell will be


With the help of resistance box R.B, introduce a resistance R and close key K₂. Find the balance point for the terminal potential difference V of the cell. If l₂ is the balancing length, then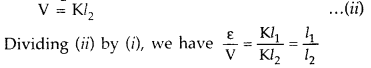

Let r be the internal resistance of the cell ε = I (R + r) and V = IR

Question 68.
In a meter bridge, the null point is found at a distance of 40 cm from A. If a resistance of 12 Ω is connected in parallel with S, the null point occurs at 50.0 cm from A. Determine the values of R and S ?
Answer: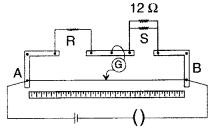

Answer:
Since the wire is of uniform cross-section, the resistances of the two segments of the wire AD and DB are in the ratio of the lengths of AD and DB.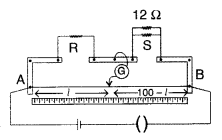

Using the null point condition of wheatstone bridge,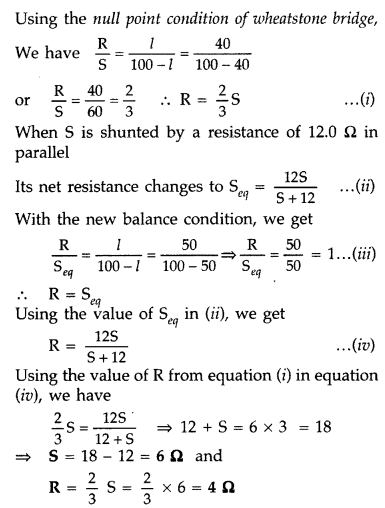

Question 69.
In a meter bridge, the null point is found at a distance of 60.0 cm from A.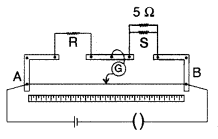

If now a resistance of 5 Q is connected in series with S, the null point occurs at 50 cm. Determine the values of R and S. (Delhi 2010)
Answer:
Using the null point condition of wheatstone bridge, we have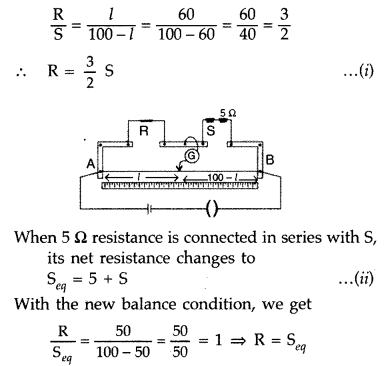

Question 70.
In a meter bridge, the null point is found at a distance of l₁ cm from A. If now a resistance of X is connected in parallel with S, the null point occurs at l₂. Obtain a formula for X in terms of l₁ l₂ and S. (Delhi 2010)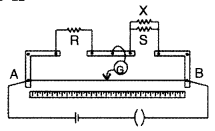

Answer:
(i) Meter bridge : Meter bridge is an arrangement of four resistances used for measuring one unknown resistance in terms of other three known resistances.

At the balance condition, no current flows through the galvanometer arm. By using the balance condition of meter bridge, the value of unknown resistance can be determined, knowing the other three resistances.
(ii) With R and S alone, we have

With S and X in parallel and R on the left gap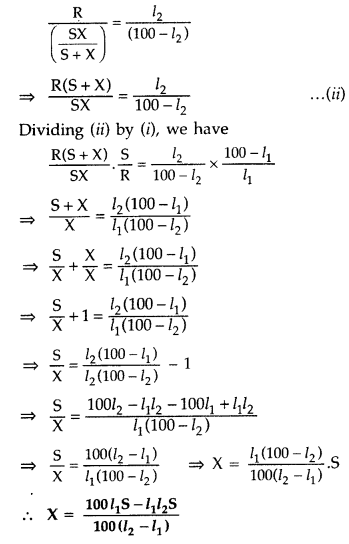

Question 71.
Write any two factors on which internal resistance of a cell depends. The reading on a high resistance voltmeter, when a cell is connected across it, is 2.2 V. When the terminals of the cell are also connected to a resistance of 5 Ω as shown in the circuit, the voltmeter reading drops to 1.8 V. Find the internal resistance of the cell. (All India 2010)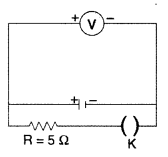

Answer:
(a) Internal resistance of a cell depends upon :
(i) nature of electrolyte of the cell
(ii) separation between the electrodes.
(b) Given: emf of cell, e = 2.2 V, R = 5 Ω, V = 1.8 V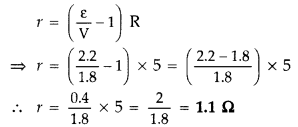

Question 72.
Write any two factors on which internal resistance of a cell depends. The reading on a high resistance voltmeter, when a cell is connected across it, is 2.0 V.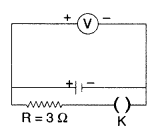

When the terminals of the cell are also connected to a resistance of 3Ω as shown in the circuit, the voltmeter reading drops to 1.5 V. Find the internal resistance of the cell. (All India 2010)
Answer:
Factors affecting internal resistance of a cell :

(a) Internal resistance of a cell depends upon :
(i) nature of electrolyte of the cell
(ii) separation between the electrodes.
(b) Given: emf of cell, e = 2.2 V, R = 5 Ω, V = 1.8 V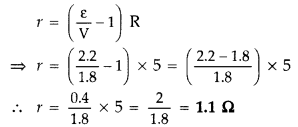

Let r be the internal resistance of the cell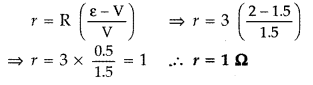

Question 73.
State Kirchhoff’s rules. Use these rules to write the expressions for the current I₁ I₂ and I₃ in the circuit diagram shown. (All India 2010)

Answer:
(i) Kirchhoff’s junction rule : At any junction, the sum of the currents entering the junction is equal to the sum of currents leaving the junction.
(ii) Kirchhoff’s loop rule : The algebraic sum of changes in potential-in any closed loop involving resistors and cells is zero.
(b) According to Kirchhoff’s junction rule,

Question 74.
State Kirchhoff’s rules. Apply Kirchhoff’s rales to the loops ACBPA and ACBQA to write the expressions for the currents I₁, I₂ and I₃ in the network. (All India 2010)

Answer:
Kirchhoff’s rules :
(i) Kirchhoff’s junction rule : At any junction, the sum of the currents entering the junction is equal to the sum of currents leaving the junction.
(ii) Kirchhoff’s loop rule : The algebraic sum of changes in potential-in any closed loop involving resistors and cells is zero.
(b) According to Kirchhoff’s junction rule,

Numerical : Applying Kirchhoff’s rule in loop ACBPA, we have

In loop ACBQA, by Kirchhoff’s rule, we have
12I₃ + 1I₂ = 10 …(ii)
Subtracting (i) from (ii), we have

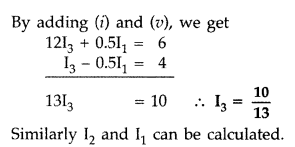
Question 75.
Define the terms
(i) drift velocity,
(ii) relaxation time.
A conductor of length L is connected to a dc source of emf e. If this conductor is replaced by another conductor of same material and same area of cross-section but of length 3L, how will the drift velocity change? (Delhi 2010)
Answer:
(i) Drift velocity : It may be defined as the average velocity gained by the free electrons of a conductor in the opposite direction of the externally applied field.
(ii) Relaxation time : The average time that elapses between two successive collisions of an electron is called relaxation time.

When length is tripled (3L), drift velocity becomes one-third of the original.
For details :
(i) Drift velocity. Drift velocity is defined as the velocity of the free electrons with which they get drifted towards the positive terminal under the influence of the external electric field. The drift velocity of electron is of the order of 10~5 m/ sec.
Derivation. Let ‘m’ be the mass of an electron and ‘e’ be the charge on it. When an external electric field ‘E is applied, the acceleration
acquired by an electron is given by

Let v₁ v₂, v₃ … v_n be final velocities of electrons then average velocity of the electrons is given by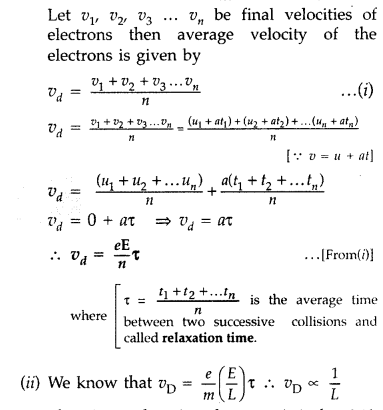

Therefore, when length is tripled, the drift velocity becomes one-third.

Question 76.
In the circuit shown, R₁ = 4Ω, R₂ = R₃ = 15 Ω, R₄ = 30Ω and E = 10V. Calculate the equivalent resistance of the circuit and the current in each resistor. (Delhi 2010)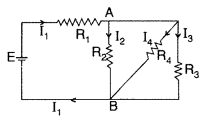

Answer:

Question 77.
In the circuit shown, R1 = 4Ω, R2 = R3 = 5Ω, R4 = 10Ω and E = 6V. Work out the equivalent resistance of the circuit and the current in each resistor. (Delhi 2010)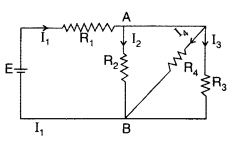

Answer:

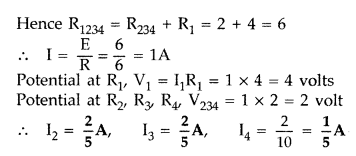
Question 78.
In the figure a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null points for the two primary cells of emfs ε₁ and ε₂ connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A.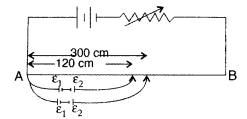

Find (i) ε₁/ε₂
(ii) position of null point for the cell ε₁
How is the sensitivity of a potentiometer increased ?
Answer: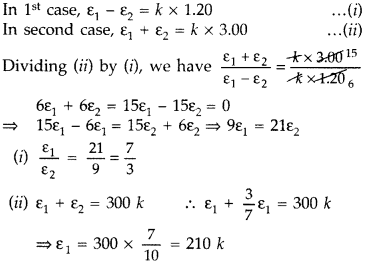

∴ Balancing length for cell ε₁ = 210 cm
The sensitivity of a potentiometer can be increased by reducing the potential gradient.

Question 79.
Using Kirchoff’s rules determine the value of unknown resistance R into circuit so that no current flows through 4ω resistance. Also find the potential difference between A and D. (Delhi 2012)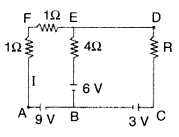

Answer: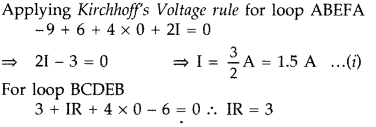

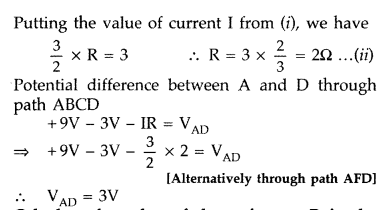
Question 80.
Calculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would be the potential difference between points B and E? (All India 2012)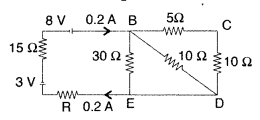

Answer:

Question 81.
Calculate the value of the resistance R in the circuit shown in the figure so that the current is 0.2 A. What would be the potential difference between points A and B?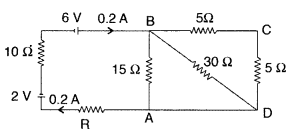

Answer: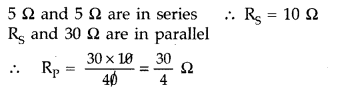

Question 82.
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material. (All India 2012)
Answer:
Relaxation time : The average time that elapses between two successive collisions of an electron is called relaxation time.

Suppose a potential difference V is applied across a conductor of length T and of uniform cross-section A, then
Electric field E set up inside the conductor is given by

Under the influence of field \(\overrightarrow{\mathrm{E}}\), the free electrons begin to drift in the opposite direction \(\overrightarrow{\mathrm{E}}\) with an average drift velocity v_d.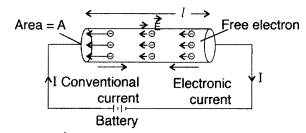

Let the number of electrons per unit volume or electron density = n
Charge on an electron = e
Number of electrons in length l of the conductor = n × volume of the conductor = nAl
Total charge contained in length l of the conductor, q = enAl
According to the electrons which enter the conductor at the right end will pass through the conductor at the left end in time,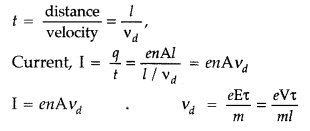

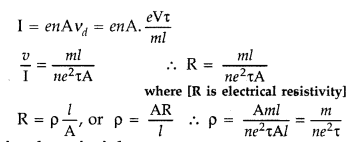
Question 83.
Write the principle on which the working of a meter bridge is based. In an experiment on meter bridge, a student obtains the balance point at the point J such that AJ = 40 cm as shown in the figure. The values of ‘R’ and ‘X’ are both doubled and then interchanged. Find the new position of the balance point. If the galvanometer and battery are also interchanged, how will the position of balance point be affected? (Comptt. All India 2012)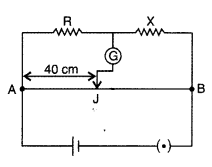

Answer:
The principle on which the working of a meter bridge is based, is Wheatstone bridge.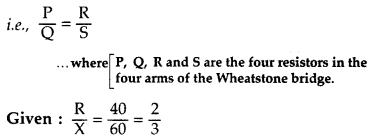

When R and X are doubled and interchanged Let the new balancing length be l.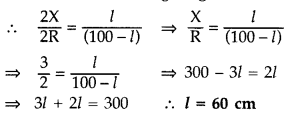

If the galvanometer and battery are also inter¬changed then there will be no effect on the posi¬tion of the balance point.

Question 84.
Write the principle on which the working of a meter bridge is based. In an experiment on meter bridge, a student obtains the balance point at the point J such that AJ = 60 cm as shown in the figure. The values of ‘R’ and ‘X’ are both doubled and then interchanged. Find the new position of the balance point. If the galvanometer and battery are also interchanged, how will the position of balance point be affected? (Comptt. All India 2012)
Answer:
The principle on which the working of a meter bridge is based, is Wheatstone bridge.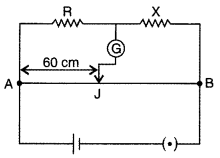

If the galvanometer and battery are interchanged, then there will be no effect on the position of balancing point.

Question 85.
Define the current sensitivity of galvanometer. Write its S.I. unit.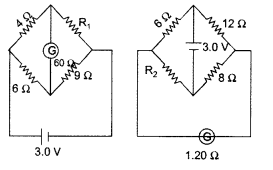

Figure shows two circuits each having a galvanometer and a battery of 3 V.
When the galvanometers in each arrangment do not show any deflection, obtain the ratio R₁/R₂.
(All India 2012)
Answer:
Current sensitivity of a galvanometer : Current sensitivity of a moving coil galvanometer is defined as deflection produced in the galvanometer per unit current passed through it. Its SI unit is rad A^-1
(i) For circuit on the left side—
If G has zero deflection, then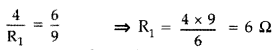

(ii) For circuit on the right side—
If galvanometer and battery are inter-changed, there is no change in the circuit as such.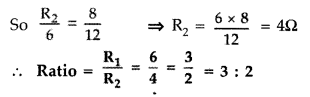

Question 86.
State the underlying principle of a potentiometer. Write two factors on which the sensitivity of a potentiometer depends.
In the potentiometer circuit shown in the figure, the balance point is at X. State, giving reason, how the balance point is shifted when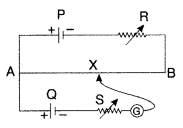

(i) resistance R is increased?
(ii) resistance S is increased, keeping R constant? (Comptt. Delhi 2012)
Answer:
Potentiometer : A potentiometer is a device used to measure potential difference.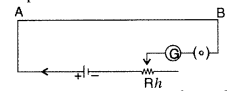

Principle. When a current flows through a wire of uniform thickness, the potential difference be¬tween its two points is directly proportional to the length of the wire between these two points.

… when [K is called construction potential gradient]
Two factors :
(a) Potential gradient
(b) Length of potentiometer wire.
(i) When R is increased, the balance point will shift towards B.
(ii) If resistance S increased keeping ‘R’ constant, the balance points will not change.

Question 87.
A potentiometer wire of length 1 m has a resistance of 10 Ω. It is connected to a 6 V battery in series with a resistance of 5 Ω. Determine the emf of the primary cell which gives a balance point at 40 cm. (Delhi 2012)
Answer:
Length (l) = 1 m
Resistance of potentiometer wire = 10Ω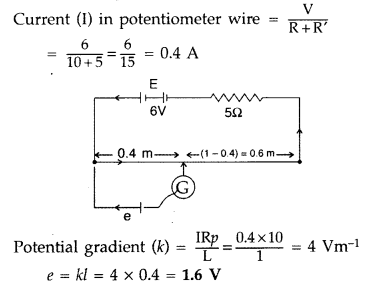

Question 88.
A potentiometer wire of length 1.0 m has a resistance of 15 Ω. It is connected to a 5 V battery in series with a resistance of 5 Ω. Determine the emf of the primary cell which gives a balance point at 60 cm. (Delhi 2012)
Answer:

Length (l) = 1 m
Resistance of potentiometer wire = 10Ω

Question 89.
A potentiometer wire of length 1 m has a resistance of 5 Ω. It is connected to a 8 V battery in series with a resistance of 15 Ω. Determine the emf of the primary cell which gives a balance point at 60 cm. (Delhi 2012)
Answer:

Length (l) = 1 m
Resistance of potentiometer wire = 10Ω

Question 90.
Answer the following :
(a) Why are the connections between the resistors in a meter bridge made of thick copper strips?
(b) Why is it generally preferred to obtain the balance point in the middle of the meter bridge wire?
(c) Which material is used for the meter bridge wire and why? (All India 2012)
Answer:
(a) The connections between the resistors in a meter bridge are made of thick copper strip, so as to have the minimum possible resistances.
(b) It is generally preferred to obtain the balance point in the middle of the meter bridge, so as to minimise the error of balance.
(c) The material used for meter bridge is an alloy ‘constantant’ or ‘manganin’ because of
(i) hight resistivity and
(ii) low temperature coefficient of resistivity.

Question 91.
A resistance of R Ω draws current from a potentiometer shown in the figure.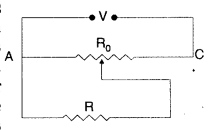

The potentiometer has a total resistance R₀ Ω. A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.
Answer: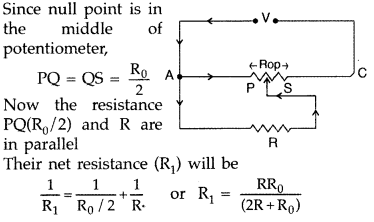

Question 92.
In the electric network shown in the figure, use Kirchhoffs rules to calculate the power consumed by the resistance R = 4 Ω. (Comptt. Delhi 2012)
Answer:
-12 + 2I₁ + 4(I₁ + I₂) = 0
-12 + 2I₁ + 4 I₁ + 4I₂ = 0
6I₁ + 4I₂ = 12 ⇒ 3I₁ + 2I₂ = 6 … (i)
For loop ADFEA
-4(I₁ + I₂) + 6 = 0
-4I₁ – 4I₂ = -6 ⇒ 2I₁ + 2I₂ = 3 … (ii)
Solving (i) and (ii), we get
I₁ = 3A and I₂ = -1.5A
∴ Power consumed in 4Ω resistance (R) = I²R
= (I₁ + I₂)² × R
= (3 – 1.5)² × 4 W
= 9 watt

Question 93.
In the electric network shown in the figure use Kirchhoffs rules to calculate the power consumed by the resistance R = 8 Ω. (Comptt. Delhi 2012)
Answer:
In loop BCDA,
I₁ × 4 + (I₁ + I₂) × 8 = 12
4I₁ + 8I₁ + 8I₂ = 12
12I₁ + 8I₂ = 12
∴ 3I₁ + 2I₂ = 3 … (Dividing by 4) … (i)
In loop ADFE,
(I₁+ I₂) × 8 = 8 => 8I₁, + 8I₂ = 8
∴ I₁ + I₂ = 1 …(Dividing by 8)
Solving equations (i) and (ii), we get
I₁ = 1A and I₂ = 0A
∴ Power consumed in 80 resistance (R) = I²R
= (I₁ + I₂)² × R
= (1 + 0)² × 8 = 8 watt

Question 94.
(a) State the underlying principle of a potentiometer. Why is it necessary to
(i) use a long wire,
(ii) have uniform area of cross-section of the wire and
(iii) use a driving cell whose emf is taken to be greater than the emfs of the primary cells?
(b) In a potentiometer experiment, if the area of the cross-section of the wire increases uniformly from one end to the other, draw a graph showing how potential gradient would vary as the length of the wire increases from one end.(Comptt. All India 2012)
Answer:
(a) Principle of potentiometer: A potentiometer is a device used to measure potential difference.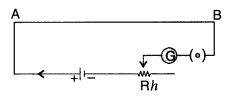

Principle. When a current flows through a wire of uniform thickness, the potential difference between its two points is directly proportional to the length of the wire between these two points.

… when [K is called construction potential gradient]
Reasons :
(i) We use a long wire to have a lower value of potential gradient (i.e. a lower ‘least count’ or greater sensitivity of the potentiometer).
(ii) The area of cross section has to be uniform to get a ‘uniform wire’ as per the principle of the potentiometer to ensure a constant value of resistance per unit length of the wire.
(iii) The emf of the driving cell has to be greater than the emf of the primary cells as otherwise no balance point would be obtained.
(b) Potential gradient K = \(\frac{\mathrm{V}}{\mathrm{L}}\)
Therefore the required graph is as shown here.

Question 95.
A cell of emf ‘E’ and internal resistance V is connected across a variable load resistor R. Draw the plots of the terminal voltage V versus
(i) R and
(ii) the current I.
It is found that when R = 4 Ω, the current is 1 A and when R is increased to 9 Ω, the current reduces to 0.5 A. Find the values of the emf E and internal resistance r. (Delhi 2012)
Answer: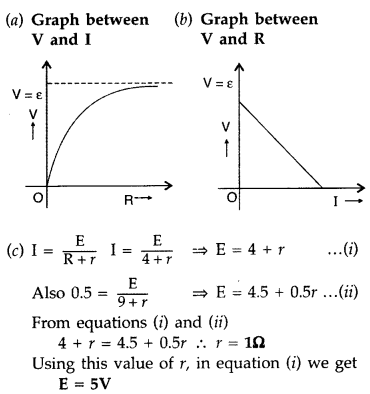

Question 96.
State the principle of working of a galvanometer.
A galvanometer of resistance G is converted into a voltmeter to measure upto V volts by connecting a resistance Rx in series with the coil. If a resistance R₂ is connected in series with it, then it can measure upto V/2 volts. Find the resistance, in terms of R₁ and R₂, required to be connected to convert it into a voltmeter that can read upto 2V. Also find the resistance G of the galvanometer in terms of R₁ and R₂. (Delhi 2012)
Answer:
(a) Working principle of galvanometer :
A current carrying coil experiences a torque when placed in a magnetic field which tends to rotate the coil and produces an angular defletion.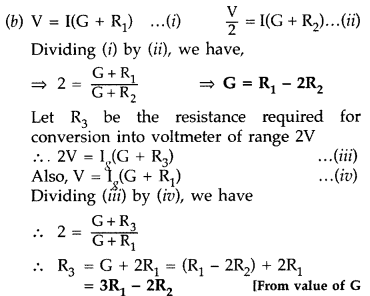

Question 97.
Find the relation between drift velocity and relaxation time of charge carriers in a conductor. A conductor of length L is connected to a d,c. source of emf ‘E’. If the length of the conductor is tripled by stretching it, keeping ‘E’ constant, explain how its drift velocity would be affected. (All India 2012)
Answer:
(i) Drift velocity. Drift velocity is defined as the velocity of the free electrons with which they get drifted towards the positive terminal under the influence of the external electric field. The drift velocity of electron is of the order of 10^-5 m/ sec.
Derivation. Let ‘m’ be the mass of an electron and ‘e’ be the charge on it. When an external electric field ‘E is applied, the acceleration
acquired by an electron is given by

Let v₁ v₂, v₃ … v_n be final velocities of electrons then average velocity of the electrons is given by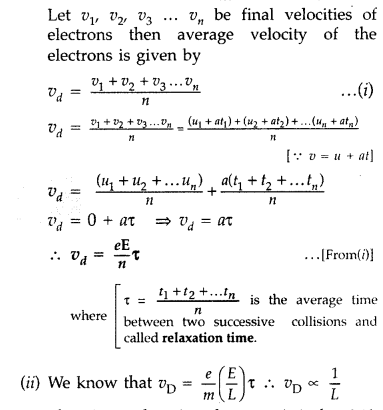

Therefore, when length is tripled, the drift velocity becomes one-third.

Question 98.
In the two electric circuits shown in the figure, determine the reading of ideal ammeter (A) and the ideal voltmeter (V). (Comptt. Delhi 2012)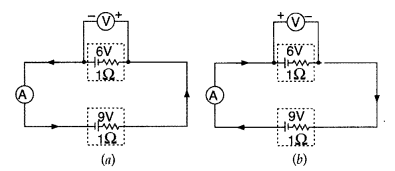

Answer:
(i) In circuit (a)
Total emf = 15 V, Total Resistance = 2Ω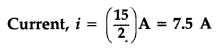

Potential difference between the terminals of 6 V battery
V = E – iR = [6 – (7.5 × 1) = -1.5 V
(ii) In circuit (b)
Effective emf = (9 – 6)V = 3V,
Total Resitance = 2Ω

Potential Difference across 6 V cell,
V = E – (- I)R = V + IR
(∵ Current is in opposite direction to 6 V cell)
= 6 + 1.5 × 1 = 7.5 V

Question 99.
In the circuit shown in the figure, find the current through each resistor. (Comptt. Delhi 2012)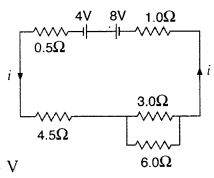

Answer:
Total emf of the circuit
=8V – 4V = 4V
Since two resistors 30 and 60 are connected in parallel, their combined resistance is

Since all resistors are in series,
R = 0.5 + 4.5 + 2 + 1 = 8Ω

0.5Ω A current will flow in 3 resistors, i.e., 0.5Ω, 4.5Ω and 1Ω.
Current through resistors 30 and 60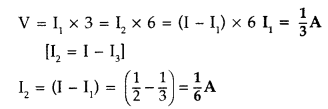

Question 100.
(a) Deduce the relation between current I flowing through a conductor and drift velocity \(\overrightarrow{\mathbf{v}}_{d}\) of the electrons.
(b) Figure shows a plot of current ‘I’ flowing through the cross-section 5 of a wire versus the time ‘t’. Use the plot to find the charge flowing in 10s through the wire.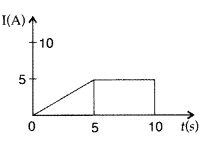
(Comptt. All India 2012)
Answer:
(a) Relation between electric current and drift velocity : Consider a uniform metallic wire XY of length l and cross-sectional area A. A potential difference V is applied across the ends X and Y of the wire. This causes an electric field at each point of the wire of strength :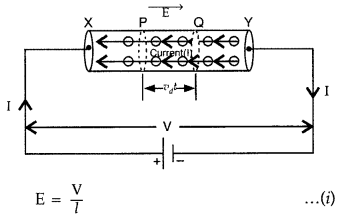

Due to this electric field, the electrons gain a drift velocity V_d opposite to direction of electric field. If q be the charge passing through the cross-section of wire in t seconds, then, current in wire, I = \(\frac{q}{t}\)

The distance transversed by each electron in time (t) = drift velocity × time = V_dt

If we consider two planes P and Q at a distance V_dt in a conductor, then the total charge flowing in time t will be equal to the total charge on the electrons present within the cylinder PQ.

The volume of this cylinder = cross sectional area × length = A V_dt

If n is the number of free electrons in the wire per unit volume, then the number of free electrons in the cylinder = n(A V_dt)
If charge on each electron is -e (e = 1.6 × 10^-19 C), then the total charge flowing through a cross-section of the wire,

This is the relation between electric current and drift velocity. Negative sign shows that the direction of current is opposite to the drift velocity.
(b) Charge = Current × time
(i) For 0 to 5 seconds, the current

Hence, q₁ = (2.5) × (5) = 12.5 C
(ii) For 5 sec to 10 sec, the current = 5A
Hence, q₂ = 5 × (10 – 5) = 5 × 5 = 25 C
q = q₁ + q₂ = 12.5 + 25 = 37.5 C

Question 101.
Draw a circuit diagram of a potentiometer. State its working principle. Derive the necessary formula to describe how it is used to compare the emfs of the two cells. (Comptt. All India)
Answer:
(a) Principle : The basic principle of a potentiometer is that “when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length.
\(v \propto l\)

Comparison of emf’s of two cells: First of all the ends of potentiometer are connected to a battery Bx,
key K and rheostat Rh such that the positive terminal of battery B, is connected to end A of the wire. This completes the primary circuit.

Now the positive terminals of the cells C₁ and C₂ whose emfs are to be compared are connected to A and the negative terminals to the jockey J through a two-way key and a galvanometer (fig). This is the secondary circuit.

Method:
(i) By closing key K, a potential difference is established and rheostat is so adjusted that when jockey J’is made to touch at ends A and B of wire, the deflection in galvano¬meter is on both sides. Suppose in this position the potential gradient is k.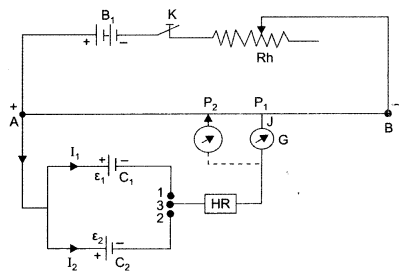

(ii) Now plug is inserted between the terminals 1 and 3. so that cell C₁ is included in the secondary circuit and jockey J is slided on the wire at P₁ (say) to obtain the null point. The distance of P₁ from A is measured. Suppose this length is l₁, i.e. AP₁ = l₁

(iii) Now plug is taken off between the terminals 1 and 3 and inserted in between the terminals 2 and 3 to bring cell C₂ in the circuit. Jockey is slided on wire and null deflection position P₂ is noted. Suppose distance of P₂ from A is l₂ i.e. AP₂ = Z₂ The emf of cell C₂, e₂ = kl₂ … (ii)

Thus emf’s of cells may be compared. Out of these cells if one is standard cell, then the emf of other cell may be calculated.
(b) Causes for one sided deflection :
(i) Potential difference between the ends of the potentiometer wire is less than the emf of the cell in the secondary circuit.
(ii) The positive side of the driving cell is connected to the negative terminal of the cell in the secondary circuit.

Question 102.
With the help of the circuit diagram, explain the working principle of meter bridge. How is it used to determine the unknown resistance of a given wire? Write the necessary precautions to minimize the error in the result. (Comptt. All India 2012)
Answer:
Metre Bridge is special case of Wheatstone Bridge
It is a device based on Wheatstone bridge to determine the unknown resistance of a wire. Principle : Meter bridge is based on the principle of wheatstone bridge, i.e. when bridge is balanced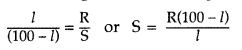

Circuit : To find the unknown resistance S, the circuit is completed as shown in figure. The unknown resistance wire of resistance S is connected across the gap between points C and D and a resistance box (R) is connected across the gap between the points A and D. A cell, a rheostat and a key (K) is connected between the point A and C by means of connecting screws. In the experiment when the sliding jockey touches the wire AC at any point, then the wire is divided into two parts. These two parts AB and BC act as the resistances P and Q of the Wheatstone bridge. In this way the resistances of arms AB, BC, AD and DC form the resistances P, Q, R and S of Wheatstone bridge. Thus the circuit of meter bridge is the same as that of Wheatstone bridge.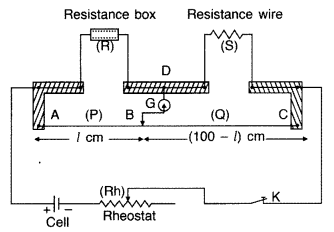

Method : To determine the unknown resistance first of all key K is closed and a resistance R is taken in the resistance box in such a way that on pressing jockey B at end points A and C, the deflection in galvanometer is on both the sides. Now jockey is slided on wire at such a position that on pressing the jockey on the wire at that point, there is no deflection in the galvanometer G. In this position the points B and D are at the same potential, therefore the bridge is balanced. The point B is called the null point. The length of both parts AB and BC of the wire are read on the scale. The condition of balance of Wheatstone bridge is,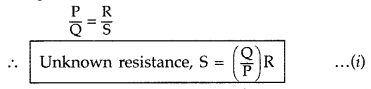

If r is the resistance per cm length of wire AC and l cm is the length of wire AB, then length of wire BC will be (100 – l) cm
∴ P = resistance of wire AB = lr
Q = resistance of wire BC = (100 – l)r
Substituting these values in equation (i), we get

As the resistance (R) of wire (AB) is known, the resistance S may be calculated.

A number of observations are taken for different resistances taken in resistance box and S is calculated each time and the mean value of S is found.

Precautions:
(i) In this experiment the resistance of the copper strips and connecting screws have not been taken into account. These resistances are called end-resistances. Therefore very small resistances cannot be found accurately by metre bridge. The resistance S should not be very small.
(ii) The current should not flow in the metre bridge wire for a long time, otherwise the wire will become hot and its resistance will be changed.

Question 103.
(i) Derive an expression for drift velocity of free electrons.
(ii) How does drift velocity of electrons in a metallic conductor vary with increase in temperature? Explain. (All India)
Answer:
(i) Expression for drift velocity : When a potential difference is applied across a conductor, an electric field is produced and free electrons are acted upon by an electric force (= -Ee). Due to this, electrons accelerate and keep colliding with each other and acquire a constant (average) velocity v_d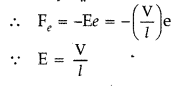


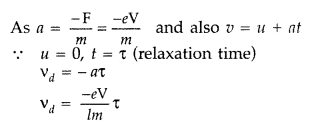
(ii) The drift velocity of electrons decreases with temperature, because the time of relaxation decreases.

Question 104.
The reading of the (ideal) ammeter, in the circuit shown here, equals :
(i) I when key K₁ is closed but key K₂ is open.
(ii) \(\frac{\mathbf{I}}{2}\) when both keys K₁ and K₂ are closed.
Find the expression for the resistance of X in terms of the resistances of R and S. (Comptt. Delhi 2012)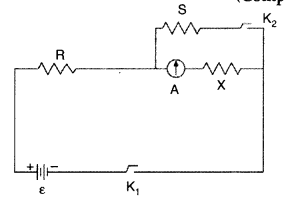

Answer:
Finding the expression for the resistance X
(i) Current I when K2 is open and Kj is closed E

Question 105.
The temperature coefficient of resistivity, for two materials A and B, are 0.0031/°C and 0.0068/ °C, respectively.
Two resistors, R₁ and R₂ made from materials A and B, respectively, have resistances of 200Ω and 100Ω at 0°C. Show on a diagram, the ‘colour code’, of a carbon resistor, that would have a resistance equal to the series combination of R₁ and R₂, at a temperature of 100°C.
(Neglect the ring corresponding to the tolerance of the carbon resistor) (comptt. Delhi 2012)
Answer:

Question 106.
A student connects a cell, of emf E₂ and internal resistance r₂ with a cell of emf E₁ and internal resistance r₁, such that their combination has a net internal combination resistance R.
Draw a diagram of the ‘set-up’ and obtain an expression for the current flowing through the resistance R. (Comptt. Outside Delhi 2016)
Answer:
Since the net internal resistance of two cells is less than r₁
it means that the two cells must have been
connected in parallel
The diagram of the setup is as shown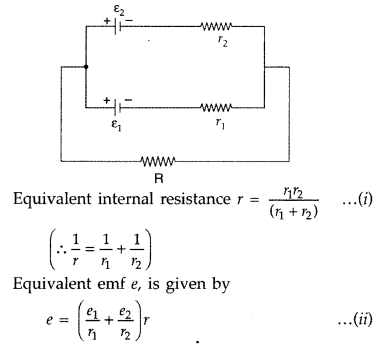

Question 107.
A resistance of R draws current from a potentiometer. The potentiometer wire, AB, has a total resistance of R0. A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of potentiometer wire. (Delhi 2016)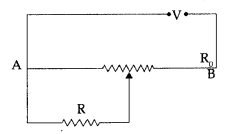

Answer:
Given : Total resistance of potentiometer wire AB = R₀
Voltage applied = V,
Given resistance = R Resistance between points A and C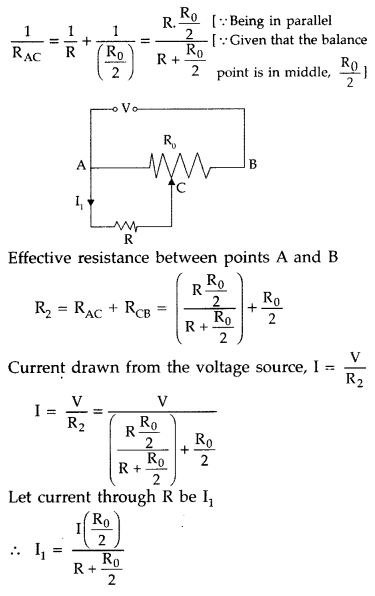

Question 108.
(a) The potential difference applied across a given resistor is altered so that the heat produced per second increases by a factor of 9. By what factor does the applied potential difference change?
(b) In the figure shown, an ammeter A and a resistor of 40 are connected to the terminals of the source. The emf of the source is 12 V having an internal resistance of 2 O. Calculate the voltmeter and ammeter readings. (Outside Delhi 2017)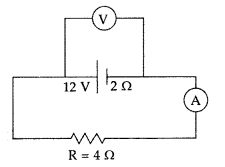

Answer:
(a) Heat produced in a resistor ‘R’ when applied, potential difference V, is :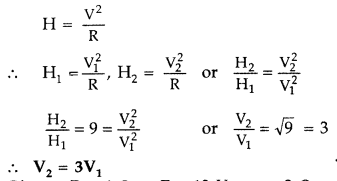

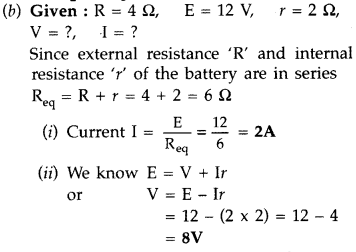
Question 109.
(a) write the principle of working of a metre bridge.
(b) In a metre bridge, the balance point is found at a distance l₁ with resistances R and S as shown in the figure.
An unknown resistance X is now connected in parallel to the resistance S and the balance point is found at a distance l₂. Obtain a formula for X in terms of l₁, l₂ and S. (Outside Delhi 2017)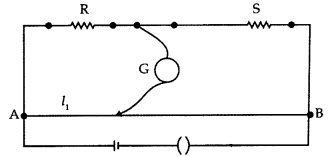

An unknown resistance X is now connected in parallel to the resistance S and the balance point is found at a distance l₂. Obtain a formula for X in terms of l₁ l₂ and S. (Outside Delhi) R
Answer:
Metre Bridge is special case of Wheatstone Bridge
It is a device based on Wheatstone bridge to determine the unknown resistance of a wire.
Principle : Meter bridge is based on the principle of wheatstone bridge, i.e. when bridge is balanced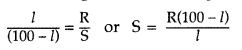

Circuit : To find the unknown resistance S, the circuit is completed as shown in figure. The unknown resistance wire of resistance S is connected across the gap between points C and D and a resistance box (R) is connected across the gap between the points A and D. A cell, a rheostat and a key (K) is connected between the point A and C by means of connecting screws. In the experiment when the sliding jockey touches the wire AC at any point, then the wire is divided into two parts. These two parts AB and BC act as the resistances P and Q of the Wheatstone bridge. In this way the resistances of arms AB, BC, AD and DC form the resistances P, Q, R and S of Wheatstone bridge. Thus the circuit of meter bridge is the same as that of Wheatstone bridge.

Method : To determine the unknown resistance first of all key K is closed and a resistance R is taken in the resistance box in such a way that on pressing jockey B at end points A and C, the deflection in galvanometer is on both the sides. Now jockey is slided on wire at such a position that on pressing the jockey on the wire at that point, there is no deflection in the galvanometer G. In this position the points B and D are at the same potential, therefore the bridge is balanced. The point B is called the null point. The length of both parts AB and BC of the wire are read on the scale. The condition of balance of Wheatstone bridge is,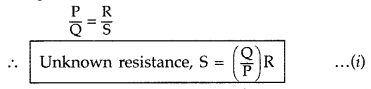

If r is the resistance per cm length of wire AC and l cm is the length of wire AB, then length of wire BC will be (100 – l) cm
∴ P = resistance of wire AB = lr
Q = resistance of wire BC = (100 – l)r
Substituting these values in equation (i), we get

As the resistance (R) of wire (AB) is known, the resistance S may be calculated.

A number of observations are taken for different resistances taken in resistance box and S is calculated each time and the mean value of S is found.

Precautions:
(i) In this experiment the resistance of the copper strips and connecting screws have not been taken into account. These resistances are called end-resistances. Therefore very small resistances cannot be found accurately by metre bridge. The resistance S should not be very small.
(ii) The current should not flow in the metre bridge wire for a long time, otherwise the wire will become hot and its resistance will be changed.

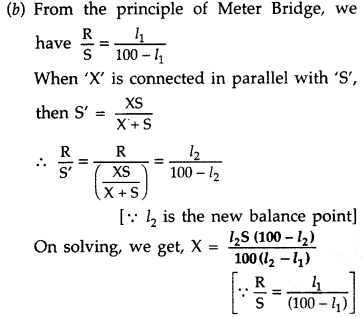
Question 110.
Derive the expression for the current density of a conductor in terms of the conductivity and applied electric field. Explain, with reason how the mobility of electrons in a conductor changes when the potential difference applied is doubled, keeping the temperature of the conductor constant. (Comptt. Delhi 2017)
Answer:
(i) Derivation of expression for current density—
Using Ohm’s law,

Potential difference (V), across the ends of a conductor of length ‘l’ where field ‘E’ is applied, is given by


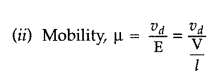
So, as potential is doubled, drift velocity also gets doubled, therefore, there will be no change in mobility.

Question 111.
Define the term current sensitivity of a galvanotmer. In the circuits shown in the figures, the galvanometer shows no deflection in each case. Find the ratio of R₁ and R₂. (Comptt. All India 2017)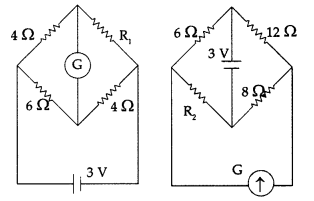

Answer: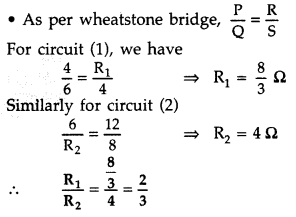

Long Answer Type

Question 1.
(a) Derive the relation between current density ‘\(\overrightarrow{\mathbf{J}}\)‘ and potential difference ‘V’ across a current carrying conductor of length area of cross-section ‘A’ and the number density of free electrons.
(b) Estimate the average drift speed of conduc¬tion electrons in a copper wire of cross-sectional area 1.0 × 10^-7 m² carrying a current of 1.5 A. [Assume that the number density of conduction electrons is 9 × 10²⁸ m^-3] (Comptt. Delhi 2012)
(a)
Suppose a potential difference V is applied across a conductor of length l and of uniform cross-section A. The electric field E set up inside the conductor is given by
E = \(\frac{V}{l}\)
Under the influence of field \(\overrightarrow{\mathrm{E}}\), the free electrons begin to drift in the opposite direction \(\overrightarrow{\mathrm{E}}\) with an average drift velocity v_d.
Let the number of electrons per unit volume or electron density = n
Charge on an electron = e

No. of electrons in length l of the conductor = n x volume of the conductor = n × Al
Total charge contained in length l of the conductor is
q = enAl … (i)
All the electrons which enter the conductor at the right end will pass through the conductor at the left end in time,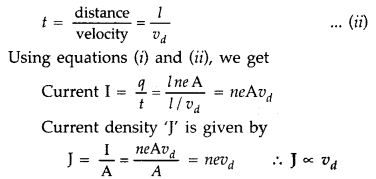

Hence the current density of a metallic conductor is directly proportional to the drift speed of electrons.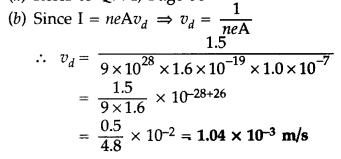

Question 2.
Use Kirchhoff’s rules to obtain the balance condition in a Wheatstone bridge.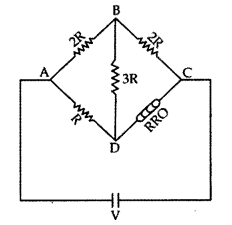

Calculate the value of R in the balance condition of the Wheatstone bridge, if the carbon resistor connected across the arm CD has the colour sequence red, red and orange, as is shown in the figure.
If now the resistances of the arms BC and CD are interchanged, to obtain the balance condition, another carbon resistor is connected in place of R. What would now be the sequence of colour bands of the carbon resistor? (Comptt. Delhi 2012)
Answer:
(a) Derivation of balance condition from Kirchhoff’s laws :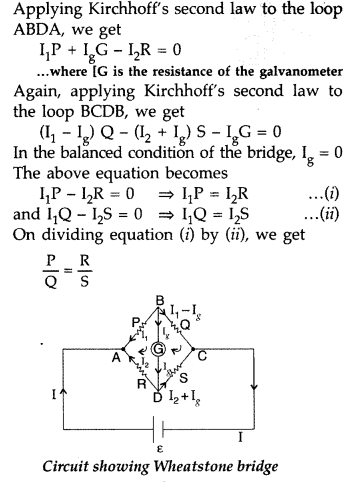

Thus this equation relating to the four resistors is called the balance condition for the galvanometer to give zero or null deflection.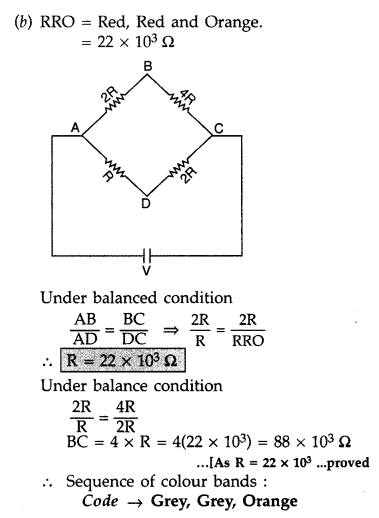

Question 3.
(a) State the working principle of a potentiometer. With the help of the circuit diagram, explain how a potentiometer is used to compare the emf’s of two primary cells. Obtain the required expression used for comparing the emfs.
(b) Write two possible causes for one sided deflection in a potentiometer experiment. (Delhi 2012)
Answer:
(a) Principle : The basic principle of a potentiometer is that “when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length.
\(v \propto l\)

Comparison of emf’s of two cells: First of all the ends of potentiometer are connected to a battery Bx,
key K and rheostat Rh such that the positive terminal of battery B, is connected to end A of the wire. This completes the primary circuit.

Now the positive terminals of the cells C₁ and C₂ whose emfs are to be compared are connected to A and the negative terminals to the jockey J through a two-way key and a galvanometer (fig). This is the secondary circuit.

Method:
(i) By closing key K, a potential difference is established and rheostat is so adjusted that when jockey J’is made to touch at ends A and B of wire, the deflection in galvano¬meter is on both sides. Suppose in this position the potential gradient is k.

(ii) Now plug is inserted between the terminals 1 and 3. so that cell C₁ is included in the secondary circuit and jockey J is slided on the wire at P₁ (say) to obtain the null point. The distance of P₁ from A is measured. Suppose this length is l₁, i.e. AP₁ = l₁

(iii) Now plug is taken off between the terminals 1 and 3 and inserted in between the terminals 2 and 3 to bring cell C₂ in the circuit. Jockey is slided on wire and null deflection position P₂ is noted. Suppose distance of P₂ from A is l₂ i.e. AP₂ = Z₂ The emf of cell C₂, e₂ = kl₂ … (ii)

Thus emf’s of cells may be compared. Out of these cells if one is standard cell, then the emf of other cell may be calculated.
(b) Causes for one sided deflection :
(i) Potential difference between the ends of the potentiometer wire is less than the emf of the cell in the secondary circuit.
(ii) The positive side of the driving cell is connected to the negative terminal of the cell in the secondary circuit.

Question 4.
(a) State Kirchhoff’s rules for an electric network. Using Kirchhoff’s rules, obtain the . balance condition in terms of the resistances
of four arms of Wheatstone bridge.
(b) In the meterbridge experimental set up, shown in the figure, the null point ‘D’ is obtained at a distance of 40 cm from end A of the meterbridge wire. If a resistance of 10 Ω is connected in series with R₁, null point is obtained at AD = 60 cm. Calculate the values of R₁ and R₂ (Delhi 2012)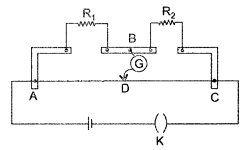

Answer:
(a) Kirchhoff’s Rules:
(i) Junction rule. At any junction of circuit elements, the algebraic sum of currents entering the junction must be equal to the sum of currents leaving it. i.e. ΣI = 1
(ii) Loop rule. The algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero.

Balance condition of wheatstone bridge :
(a) Derivation of balance condition from Kirchhoff’s laws :

Thus this equation relating to the four resistors is called the balance condition for the galvanometer to give zero or null deflection.

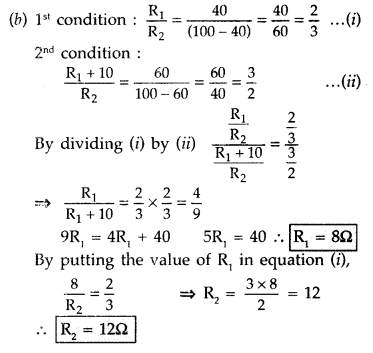
Question 5.
(i) Define the term drift velocity.
(ii) On the basis of electron drift, derive an expression for resistivity of a conductor in terms of number density of free electrons and relaxation time. On what factors does resistivity of a conductor depend?
(iii) Why alloys like constantan and manganin are used for making standard resistors? (Delhi 2017)
Answer:
(i) Drift velocity may be defined as the average velocity gained by the free electrons of a conductor in the opposite direction of the externally applied field.
(ii)
Relaxation time : The average time that elapses between two successive collisions of an electron is called relaxation time.

Suppose a potential difference V is applied across a conductor of length T and of uniform cross-section A, then
Electric field E set up inside the conductor is given by

Under the influence of field \(\overrightarrow{\mathrm{E}}\), the free electrons begin to drift in the opposite direction \(\overrightarrow{\mathrm{E}}\) with an average drift velocity v_d.

Let the number of electrons per unit volume or electron density = n
Charge on an electron = e
Number of electrons in length l of the conductor = n × volume of the conductor = nAl
Total charge contained in length l of the conductor, q = enAl
According to the electrons which enter the conductor at the right end will pass through the conductor at the left end in time,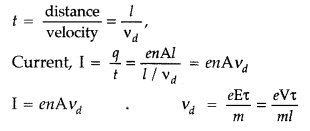


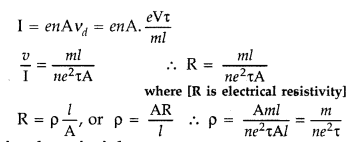
(iii) Because constantan and manganin show very weak dependence of resistivity on temperature. .

Question 6.
State the principle potentiometer.
(i) State the principle of working of a potentiometer
(ii) In the given potentiometer circuit AB is a uniform wire of length 1 m and resistance 10Ω. Calculate the potential gradient along the wire and balance length AO (= l). (Delhi 2017)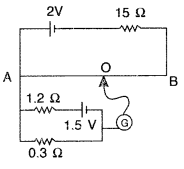

Answer:
(i)

(a) Principle : The basic principle of a potentiometer is that “when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length.
\(v \propto l\)

Comparison of emf’s of two cells: First of all the ends of potentiometer are connected to a battery Bx,
key K and rheostat Rh such that the positive terminal of battery B, is connected to end A of the wire. This completes the primary circuit.

Now the positive terminals of the cells C₁ and C₂ whose emfs are to be compared are connected to A and the negative terminals to the jockey J through a two-way key and a galvanometer (fig). This is the secondary circuit.

Method:
(i) By closing key K, a potential difference is established and rheostat is so adjusted that when jockey J’is made to touch at ends A and B of wire, the deflection in galvano¬meter is on both sides. Suppose in this position the potential gradient is k.

(ii) Now plug is inserted between the terminals 1 and 3. so that cell C₁ is included in the secondary circuit and jockey J is slided on the wire at P₁ (say) to obtain the null point. The distance of P₁ from A is measured. Suppose this length is l₁, i.e. AP₁ = l₁

(iii) Now plug is taken off between the terminals 1 and 3 and inserted in between the terminals 2 and 3 to bring cell C₂ in the circuit. Jockey is slided on wire and null deflection position P₂ is noted. Suppose distance of P₂ from A is l₂ i.e. AP₂ = Z₂ The emf of cell C₂, e₂ = kl₂ … (ii)

Thus emf’s of cells may be compared. Out of these cells if one is standard cell, then the emf of other cell may be calculated.
(b) Causes for one sided deflection :
(i) Potential difference between the ends of the potentiometer wire is less than the emf of the cell in the secondary circuit.
(ii) The positive side of the driving cell is connected to the negative terminal of the cell in the secondary circuit.

Question 7.
(a) Obtain the condition under which the current flowing, in the ‘current detecting device’, used in the circuit shown in the figure, becomes zero.
(b) Describe briefly the device, based on the above condition. Draw a circuit diagram for this device and discuss, in brief, how it is used for finding an unknown resistance. (Comptt All India 2016)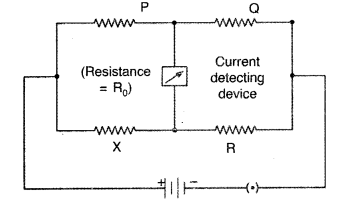

Answer:
(a) The given circuit can be redrawn as :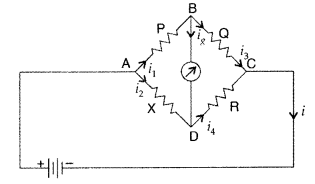

It is, therefore, a wheatstone bridge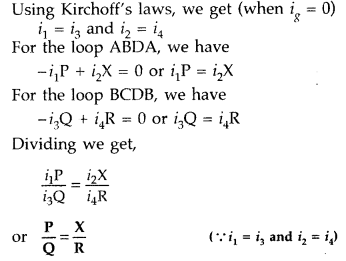

(b) A simple device, based on the above condition is ‘Meter Bridge’.
Working of Meter Bridge :

Metre Bridge is special case of Wheatstone Bridge
It is a device based on Wheatstone bridge to determine the unknown resistance of a wire. Principle : Meter bridge is based on the principle of wheatstone bridge, i.e. when bridge is balanced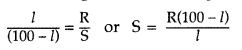

Circuit : To find the unknown resistance S, the circuit is completed as shown in figure. The unknown resistance wire of resistance S is connected across the gap between points C and D and a resistance box (R) is connected across the gap between the points A and D. A cell, a rheostat and a key (K) is connected between the point A and C by means of connecting screws. In the experiment when the sliding jockey touches the wire AC at any point, then the wire is divided into two parts. These two parts AB and BC act as the resistances P and Q of the Wheatstone bridge. In this way the resistances of arms AB, BC, AD and DC form the resistances P, Q, R and S of Wheatstone bridge. Thus the circuit of meter bridge is the same as that of Wheatstone bridge.

Method : To determine the unknown resistance first of all key K is closed and a resistance R is taken in the resistance box in such a way that on pressing jockey B at end points A and C, the deflection in galvanometer is on both the sides. Now jockey is slided on wire at such a position that on pressing the jockey on the wire at that point, there is no deflection in the galvanometer G. In this position the points B and D are at the same potential, therefore the bridge is balanced. The point B is called the null point. The length of both parts AB and BC of the wire are read on the scale. The condition of balance of Wheatstone bridge is,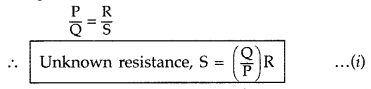

If r is the resistance per cm length of wire AC and l cm is the length of wire AB, then length of wire BC will be (100 – l) cm
∴ P = resistance of wire AB = lr
Q = resistance of wire BC = (100 – l)r
Substituting these values in equation (i), we get

As the resistance (R) of wire (AB) is known, the resistance S may be calculated.

A number of observations are taken for different resistances taken in resistance box and S is calculated each time and the mean value of S is found.

Precautions:
(i) In this experiment the resistance of the copper strips and connecting screws have not been taken into account. These resistances are called end-resistances. Therefore very small resistances cannot be found accurately by metre bridge. The resistance S should not be very small.
(ii) The current should not flow in the metre bridge wire for a long time, otherwise the wire will become hot and its resistance will be changed.

Question 8.
(a) Why do the ‘free electrons’, in a metal wire, ‘flowing by themselves’, not cause any current flow in the wire?
Define ‘drift velocity’ and obtain an expression for the current flowing in a wire, in terms of the ‘drift velocity’ of the free electrons.
(b) Use the above expression to show that the ‘resistivity’, of the material of a wire, is’ inversely proportional to the ‘relaxation time’ for the ‘free electrons’ in the metal. (Comptt. Outside Delhi 2016)
Answer:
(a) (i) The free electrons, in a metal, (flowing by themselves), have a random distribution of their velocities. Hence the net charge crossing any cross section in a unit time is zero.
(ii) The drift velocity equals the average (time dependent) velocity acquired by free electrons, under the action of an applied (external) electric field.
(iii) Expression for current in terms of drift velocity :
Definition : Drift velocity is defined as the velocity with which fress electrons in a conductor get drifted in a direction opposite to the direction of the applied field. Its unit is m^-1s and dimensions [LT^-1]

Expression : The magnitude of electric field set up across the conductor is given by
E = \(\frac{\mathrm{V}}{l}\)
Let n be the number of free electrons per unit volume of the conductor.
Then, total number of free electrons in the conductor
= n × Volume of the conductor
Hence, Q = (nAl)e
Time taken by the charge to cross the conductor length l is given by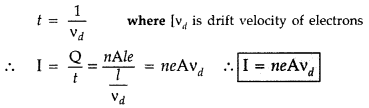

(b) We know from above

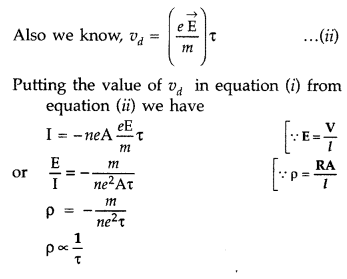
Question 9.
(i) Derive an expression for drift velocity of electrons in a conductor. Hence deduce Ohm’s law.
(ii) A wire whose cross-sectional area is increasing linearly from its one end to the other, is connected across a battery of V volts. Which of the following quantities remain constant in the wire?
(a) drift speed
(b) current density
(c) electric current (d) electric field Justify your answer. (Delhi 2016)
Answer:
(i)
(a) Relation between electric current and drift velocity : Consider a uniform metallic wire XY of length l and cross-sectional area A. A potential difference V is applied across the ends X and Y of the wire. This causes an electric field at each point of the wire of strength :

Due to this electric field, the electrons gain a drift velocity V_d opposite to direction of electric field. If q be the charge passing through the cross-section of wire in t seconds, then, current in wire, I = \(\frac{q}{t}\)

The distance transversed by each electron in time (t) = drift velocity × time = V_dt

If we consider two planes P and Q at a distance V_dt in a conductor, then the total charge flowing in time t will be equal to the total charge on the electrons present within the cylinder PQ.

The volume of this cylinder = cross sectional area × length = A V_dt

If n is the number of free electrons in the wire per unit volume, then the number of free electrons in the cylinder = n(A V_dt)
If charge on each electron is -e (e = 1.6 × 10^-19 C), then the total charge flowing through a cross-section of the wire,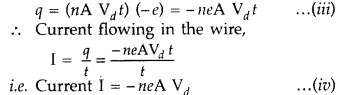

This is the relation between electric current and drift velocity. Negative sign shows that the direction of current is opposite to the drift velocity.
(b) Charge = Current × time
(i) For 0 to 5 seconds, the current

Hence, q₁ = (2.5) × (5) = 12.5 C
(ii) For 5 sec to 10 sec, the current = 5A
Hence, q₂ = 5 × (10 – 5) = 5 × 5 = 25 C
q = q₁ + q₂ = 12.5 + 25 = 37.5 C

(ii) (c) Electric current will remain constant in the wire.
Reason : All other quantities depend on the cross sectional area of the wire and hence will not remain constant.

Question 10.
(a) State the two Kirchhoff’s laws. Explain briefly how these rules are justified.
(b) The current is drawn from a cell of emf E and internal resistance r connected to the network of resistors each of resistance r as shown in the figure. Obtain the expression for
(i) the current drawn from the cell and
(ii) the power consumed in the network. (Delhi 2016)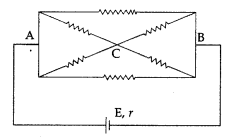

Answer:
(a) Junction Rule : At any Junction, the sum of currents, entering the junction, is equal to the sum of currents leaving the junction.
Loop Rule : The Algebraic sum of changes in potential, around any closed loop involving resistors and cells, in the loop is zero.

Justification : The first law is in accordance with the law of conservation of charge. The second law is in accordance with the law of conservation of energy.
(b) Given : EMF = E, internal resistance = r, resistance of each resistor = r
The equivalent circuit diagram is shown below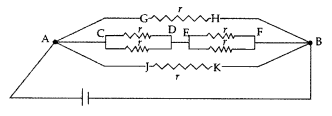

(i) The two resistances of V each between points C and D are in parallel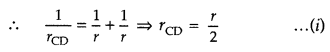

Similarly two resistances between points E and F are in parallel,

Now these resistances r_CD and r_EF are in series,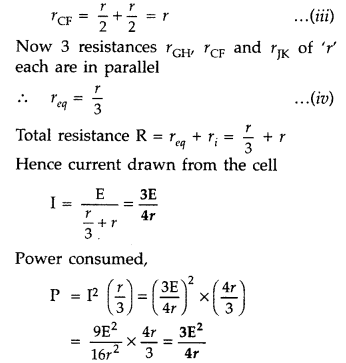

Question 11.
(a) Draw a circuit diagram of a meter bridge used to determine the unknown resistance R of a given wire. Hence derive the expression for R in terms of the known resistance S.
(b) What does the term ‘end error’ in a metre bridge circuit mean and how is it corrected? How will the balancing point be affected, if the positions of the battery and galvanometer are interchanged in a metre bridge experiment? Give reason for your answer. (Comptt. Delhi 2016)
Answer:
(a)

Metre Bridge is special case of Wheatstone Bridge
It is a device based on Wheatstone bridge to determine the unknown resistance of a wire. Principle : Meter bridge is based on the principle of wheatstone bridge, i.e. when bridge is balanced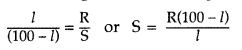

Circuit : To find the unknown resistance S, the circuit is completed as shown in figure. The unknown resistance wire of resistance S is connected across the gap between points C and D and a resistance box (R) is connected across the gap between the points A and D. A cell, a rheostat and a key (K) is connected between the point A and C by means of connecting screws. In the experiment when the sliding jockey touches the wire AC at any point, then the wire is divided into two parts. These two parts AB and BC act as the resistances P and Q of the Wheatstone bridge. In this way the resistances of arms AB, BC, AD and DC form the resistances P, Q, R and S of Wheatstone bridge. Thus the circuit of meter bridge is the same as that of Wheatstone bridge.

Method : To determine the unknown resistance first of all key K is closed and a resistance R is taken in the resistance box in such a way that on pressing jockey B at end points A and C, the deflection in galvanometer is on both the sides. Now jockey is slided on wire at such a position that on pressing the jockey on the wire at that point, there is no deflection in the galvanometer G. In this position the points B and D are at the same potential, therefore the bridge is balanced. The point B is called the null point. The length of both parts AB and BC of the wire are read on the scale. The condition of balance of Wheatstone bridge is,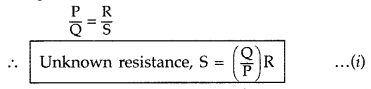

If r is the resistance per cm length of wire AC and l cm is the length of wire AB, then length of wire BC will be (100 – l) cm
∴ P = resistance of wire AB = lr
Q = resistance of wire BC = (100 – l)r
Substituting these values in equation (i), we get

As the resistance (R) of wire (AB) is known, the resistance S may be calculated.

A number of observations are taken for different resistances taken in resistance box and S is calculated each time and the mean value of S is found.

(b) The error which arises on account of resistance of copper strips and the connecting wire at both ends of the meter bridge is called end error.
It is minimized by adjusting the balance point near the middle point of the bridge.
• The balancing point will not be affected, as the bridge remains balanced.

Question 12.
(a) State the working principle of a potentiometer with help of a circuit diagram, explain how the internal resistance of a cell is determined.
(b) How are the following affected in the potentiometer circuit when
(i) the internal resistance of the driver cell increases and
(ii) the series resistor connected to the driver cell is reduced? Justify your answer. (Comptt. Delhi 2016)
Answer:
(a) Potentiometer principle : When a constant current flows through a wire of uniform cross sectional area, the potential difference, across any length, is directly proportional to the length.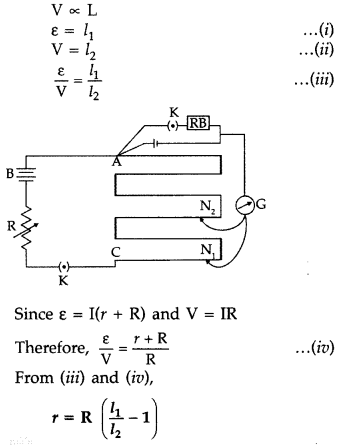

(b) As per CBSE guidelines this question is incomplete hence NOT attempted.

Question 13.
Explain the term ‘drift velocity’ of electrons in a conductor. Hence obtain the expression for the current through a conductor in terms of ‘drift velocity’. (CBSE AI 2013, 2013C)
Answer:
Drift velocity (V_d) is defined as the average velocity with which the free electrons get drifted inside a conductor under the effect of the electric field, opposite to the direction of the field.

Let n be the electrons per unit volume in the conductor. Here n is called the number density of electrons. Assume that all electrons move with the same drift velocity V_d. In a time interval dt, each electron moves a distance vdt. Now the volume of the cylinder covered by the electrons in time dt is
V = A v_ddt …(1)

and the number of electrons in this volume is
N = nV = nA v_ddt …(2)

If e is the charge on the electron, then charge flowing through the conductor in small time dt is
dQ = e(nA v_ddt) …(3)

Hence the current through the conductor is
l = \(\frac{dQ}{dt}\) = nAev_d

Question 14.
Draw a plot showing the variation of resistivity of an (i) conductor and (ii) semiconductor, with the increase in temperature.
How does one explain this behaviour in terms of the number density of charge carriers and the relaxation time? (CBSE Delhi 2014C)
Answer:
The plots are as shown.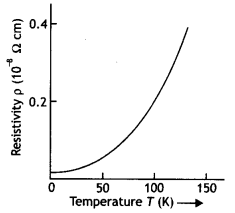


With a rise in temperature the average relaxation time for a conductor decreases and resistivity increases, while for a semiconductor the number density of charge carriers increases, hence the resistivity decreases.

Question 15.
State the two Kirchhoff’s rules used in electric networks. How are these rules justified? (CBSE Delhi 2015)
Answer:
The two rules are

Kirchhoff’s junction rule: The algebraic sum of currents meeting at a junction is zero.
Kirchhoff’s loop rule: The algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero.

The two rules are justified as they are based on the law of conservation of charge and law of conservation of energy respectively.

Question 16.
(a) Deduce the relation between current l flowing through a conductor and drift velocity \(\vec{v}_{\mathrm{d}}\) of the electrons.
(b) Figure shows a plot of current ‘l’ flowing through the cross-section of a wire versus the time ‘t’. Use the plot to find the charge flowing in 10 s through the wire. (CBSE AI 2015C, 2016C)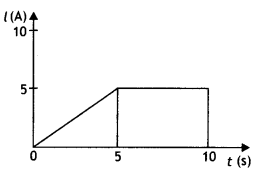

Answer:
Suppose there are n electrons per unit volume, where n is called the number density of electrons. Assume that all electrons move with the same drift velocity V_d. In a time interval dt, each electron moves a distance v_ddt. Now the volume of the cylinder covered by the electrons in time dt is
V = A v_ddt ….(1)

and the number of electrons in this volume is
N = nV=nA v_ddt …(2)

If e is the charge on the electron, then charge flowing through the conductor in small time dt is
dQ= e(nA v_ddt) …(3)

Hence the current through the conductor is
l = \(\frac{dQ}{dt}\) = vdenA

The area under the l – t curve gives the value of the charge
Q = 1/2 × 5 × 5 + (10 – 5) × 5 = 12.5 + 25
= 37.5 C

Question 17.
Answer the following:
(a) Why are the connections between the resistors in a metre bridge made of thick copper strips?
Answer:
The metal strips have low resistance;
hence their resistance does not come into play while calculating the unknown resistance.

(b) Why is it generally preferred to obtain the balance point in the middle of the metre bridge wire?
Answer:
It is done to reduce the index correction.

(c) Which material is used for the metre bridge wire and why? (CBSE Al 2014)
Answer:
Alloys are used due to their high resistivity.

Question 18.
(a) State the underlying principle of a potentiometer. Why is it necessary to (i) use a long wire, (ii) have a uniform area of cross-section of the wire and (iii) use a driving cell whose emf is taken to be greater than the EMFs of the primary cells?
Answer:
Principle: It is based on the principle that if a wire of uniform area of cross-section carries a constant current, the potential drop across any portion of the wire is directly proportional to the length of that portion of the wire.

The diagram is as shown.
First, the key K is inserted. This brings the cell of emf E₁ in the circuit. The jockey is moved on the wire to obtain a balance point, i.e. a point on the wire where the galvanometer gives zero deflection. Let the balancing length be L₁. Therefore by the potentiometer principle, we have
E₁ ∝ L₁ …(1)

Now, the key K₂ is inserted. This brings the cell of emf E₂ into the circuit. The jockey is again moved on the wire to obtain the balance point. Let the balancing length be L₂. Then by potentiometer principle, we have
E₂ ∝ L₂ …(2)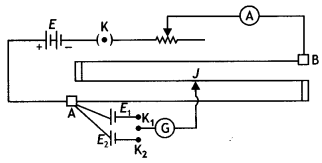

Dividing equations (1) by (2) we have
\(\frac{E_{1}}{E_{2}}=\frac{L_{1}}{L_{2}}\) …. (3)

Knowing the values of L₁ and L₂, the EMFs can be compared.

1. The least count of the potentiometer is given by k = V/l, where l is the length of the potentiometer wire. The larger the value of l, the smaller is the least count. Hence a long wire is used so that there is more accuracy.
2. If the area of cross-section is not uniform, the value of the potential ‘ gradient will not be the same along
   the length of the wire.
3. The balance point will be obtained on the wire.

(b) In a potentiometer experiment, if the area of the cross-section of the wire increases uniformly from one end to the other, draw a graph showing how potential gradient would vary as the length of the wire increases from one end. (CBSE AI 2014C)
Answer:
k = \(\frac{V}{l}\) = \(\frac{lR}{l}\)

⇒ k ∝ \(\frac{1}{l}\)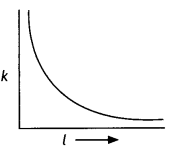

Question 19.
Plot a graph showing the variation of current density (j) versus the electric field (E) for two conductors of different materials. What information from this plot regarding the properties of the conducting material, can be obtained which can be used to select suitable materials for use in making (i) standard resistance and (ii) connecting wires in electric circuits?
Electron drift speed is estimated to be of the order of mm s^-1. Yet large current of the order of few amperes can be set up in the wire. Explain briefly. (CBSEAI 2015)
Answer:
We know that J = σE
Therefore the graph between J and E will be a straight line passing through the origin.

This is as shown.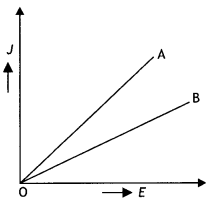

The slope of the graph = conductivity (σ)

Hence materiaL with Less slope (smaller conductivity) is used for making standard resistors and materiaL with greater slope (higher conductivity) for making connecting wires.

A large current can be set up in the wire because the electron number density is enormous, 10²⁹ m^-3.

Question 20.
The reading of the (ideal) ammeter, In the circuit shown here, equals: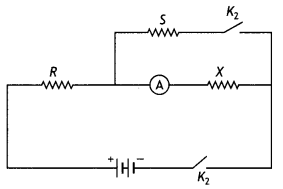

(i) l when key K₁ is closed but key K₂ is open.
Answer:
(i) Current l when K₂ is open
l = \(\frac{ε}{R+X}\)

(ii) l/2 when both keys K₁ and K₂ are closed.
Find the expression for the resistance of X In terms of the resistances of R and S. (CBSE Delhi 2016C)
Answer:
Let current be l when both K₁ and K₂ are closed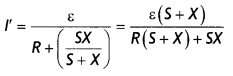

Current through X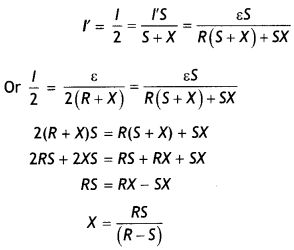

Question 21.
Define the current sensitivity of a galvanometer. Write Its S.I. unit. The figure shows two circuits each having a galvanometer and a battery of 3 V. When the galvanometers in each arrangement do not show any deflection, obtain the ratio R₁/R₂. (CBSE AI 2013)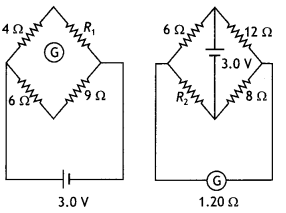

Answer:
The current sensitivity of a galvanometer is defined as the deflection produced in the galvanometer per unit current passing through It. It is measured in div per ampere. In both cases the Wheatstone bridge is in the balanced state. Therefore we have
\(\frac{4}{R_{1}}=\frac{6}{9}\) Or R₁ = 6 ohm

\(\frac{6}{12}=\frac{R_{2}}{8}\) Or R2 = 4 ohm

Therefore \(\frac{R_{1}}{R_{2}}=\frac{6}{4}=\frac{3}{2}\)

Question 22.
The following circuit shows the use of a potentiometer to measure the internal resistance of a cell, (i) When the key K is open, how does the balance point change, if the current from the driver cell decreases? (ii) When the key K is closed, how does the balance point change if R is increased, keeping the current from the driver cell constant?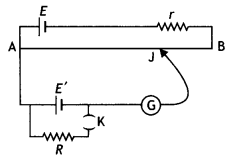

Answer:
(i) When the key K is open, a decrease in the current from the driver cell decreases the potential drop across the potentiometer wire. Therefore to balance the same emf again, more length of the wire will be required. Thus the balance point will shift towards point B.
(ii) When key K is closed and R is increased, it increases the terminal potential difference of the cell. Thus to balance the new terminal potential difference, more length of the wire will be required. Thus the balance point will shift towards point B.

Question 23.
(a) State, with the help of a circuit diagram, the working principle of a metre bridge. Obtain the expression used for determining the unknown resistance.
Answer:
(a) The experiment is based on the Wheatstone bridge principle.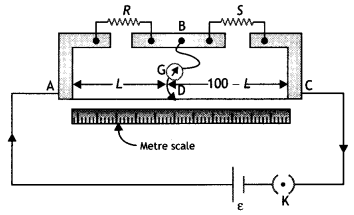

The connections are made as shown in the figure. A resistance R is introduced from the resistance box and the key K is closed. The jockey is moved on the wire to the point where there is no deflection in the galvanometer. In such case points, B and D are at the same potential. Point B is called the “null” point.

Let in this position AB = L cm and BC = (100 – L) cm. Therefore resistance of AB, i.e.
P ∝ L
and resistance of BC, i.e. Q ∝ (100 – L)

hence
\(\frac{P}{Q}=\frac{L}{100-L}\) …..(1)

In the balanced state by the Wheatstone bridge Principle we have
\(\frac{P}{Q}=\frac{R}{X}\) … (2)

Substituting equation (1) in equation (2) we have
\(\frac{R}{x}=\frac{L}{100-L}\) ….(3)

rewriting equation (3) we have
X = \(\left(\frac{100-L}{L}\right)\)R

(b) What happens if the galvanometer and cell are interchanged at the balance point of the bridge?
Answer:
There is no change in the position of the balance point if the galvanometer and the cell are interchanged.

(c) Why is it considered important to obtain the balance point near the mid-point of the wire? (CBSE Delhi 2011C)
Answer:
It is important to get the balance point near the mid-point of the wire because then the resistances in the four arms of the bridge are of the same order. The sensitivity of the bridge is maximum and the resistance is determined most accurately.

Question 24.
(a) Which material is used for potentiometer wire and why?
Answer:
The potentiometer wire is usually of constantan or manganin.
The material of the wire should have

• high specific resistance and
• low-temperature coefficient of resistance.

(b) How can the sensitivity of a potentiometer be increased? (CBSE Delhi 2011C)
Answer:
For greater sensitivity of the measurement, the fall of potential per cm should be less. The smaller the value of K, the greater will be the balancing length and the greater will be the accuracy of the measurement. For this, a wire of longer length should be taken or the current in the wire should be less.

Question 25.
Write two possible causes for one-sided deflection in a potentiometer experiment. (CBSE Delhi 2013)
Answer:

1. The Emf of the auxiliary battery may be less than the emf of the test cell.
2. The positive terminal of the test cell and the auxiliary cell may not be connected to the same point.

Question 26.
(a) Derive a relation between the internal resistance, emf and terminal potential difference of a cell from which current l is drawn. Draw V vs l graph for a cell and explain its significance.
Answer:
Consider the circuit shown.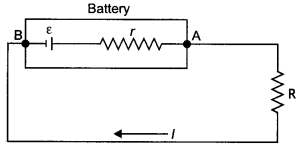

By Kirchhoff’s rules we have
E – lR – rl = 0
E – V – lr = 0
E = V + lr

The V-l graph is as shown.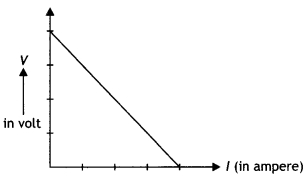

Significance of Graph: To find emf and internal resistance of the cell.

(b) A voltmeter of resistance 998 0 is connected across a cell of emf 2 V and internal resistance 2Q. Find the potential difference across the voltmeter and also across the terminals of the cell. Estimate the percentage error in the reading of the voltmeter.
Answer:
The diagram is as shown.

V= E – lr
998 × l = 2 – 2l
1000 l = 2
l = 0.002 A

Therefore,
V= 0.002 × 998= 1.996 V

Percentage error
\(\frac{2-1.996}{2}\) × 100 = \(\frac{0.004}{2}\) = 0.2%

Question 27.
Two cells of the same emf E but internal resistance r₁ and r₂ are connected in series to an external resistor R (figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero? (NCERT Exemplar)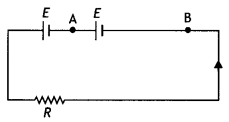

Answer:
Since the cells are connected in series,
total emf is
E_T = E + E = 2E

Now current in the circuit Is
l = \(\frac{2 E}{R+r_{1}+r_{2}}\)

For terminal potential difference across the first cell to be zero we have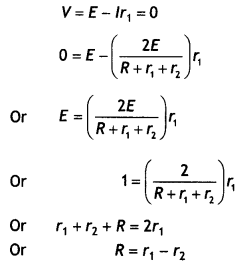

Question 28.
Two cells of EMFs ε₁ and ε₂ and Internal resistances r1 and r2 respectively are connected in parallel. Obtain expressions for the equivalent
(i) resistance and
(ii) emf of the combination (CBSE Delhi 2018C, 2019C)
Answer: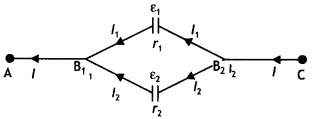

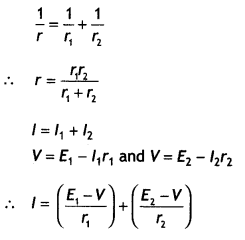
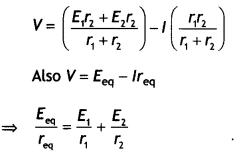
Question 29.
Using Kirchhoff’s rules, calculate the potential difference between B and D In the circuit diagram as shown in the figure. (CBSE Delhi 2018C)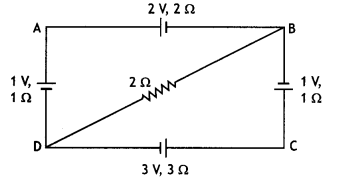

Answer:
Using Kirchhoff’s voLtage ruLe, we have:
For Loop DABD
l₁ × 1 + (1) + (-2) + 2l₁ + 2(l₁ + l₂) = 0
Or 5l₁ + 2l₂ = 1 …. (i)

For Loop DCBD
l₂ × 3 + (3) + (-1) + l₂ + 2(l₁ + l₂) = 0
Or 2l₁ + 6 l₂ = -2 …. (ii)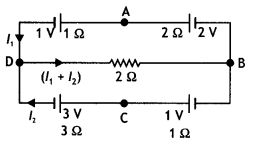

Solving (i) and (ii), we get
l₁ = \(\frac{5}{13}\)A

l₂ = \(\frac{-6}{13}\)A

∴ Current through DB = l₁ + l₂ = \(\frac{-1}{13}\)A
∴ P.D. between B and D = 0.154 V

Question 30.
Define the term resistivity of a conductor. Give its SI unit. Show that the resistance R of a conductor Is given by \(\frac{m L}{n e^{2} A \tau}\)where the symbols have their usual meaning.
Answer:
The resistivity of a conductor is the resistance of the conductor of unit length and unit cross-sectional area.

Let V_d be the drift velocity of the electrons, then its relation with the electric field is
V_d = \(-\frac{e E}{m}\)τ …..(1)

Let V be the potential difference applied across the two ends of a conductor of length L and area of cross-section A, then
E = \(\frac{-V}{L}\) …..(2)

Substituting equation (1) in (2) we have
V_d = \(\frac{\mathrm{eV}}{\mathrm{mL}}\)τ ….(3)

Also l = neAV_d ….(4)
Substituting equation (3) in equation (4),
we have

l = neA\(\left[\frac{e V}{m L} \tau\right]=\left[\frac{n e^{2} A \tau}{m L}\right]\)V ….(5)

Comparing with Ohm’s “Law”, i.e
l = \(\frac{V}{R}\) …. (6)

we have
R = \(\left[\frac{m L}{n e^{2} A \tau}\right]\) ….(7)

Question 31.
The given figure shows a network of resistances R₁, R₂, R₃ and R₄.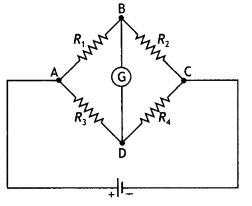

Using Kirchhoff’s laws, establish the balance condition for the network. (CBSEAI 2015)
Answer:
Consider the diagram as shown below.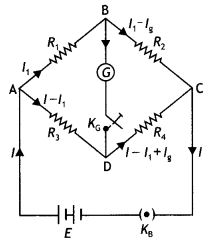

Now applying Kirchhoff’s Loop rule to the closed Loop ABDA, we have
– l₁R₁ – l_gG + (l – l₁) R₃ = 0 ….(1)

Again applying Kirchhoff’s Loop rule to closed-loop BCDB, we have
– (l₁ – l_g)R₂ + (l – l₁ + l_g)R₄ + l_gG = 0 …(2)

The values of R₁, R₂, R₃ and R₄ are so adjusted that the galvanometer gives zero deflection. This means that both B and D will be at the same potential and hence no current will flow through the galvanometer,

i.e. l_g = 0. In this situation, the Wheatstone bridge is said to be balanced. Putting l_g = 0 in equations (1) and (2) we have
– l₁R₁ + (l – l₁) R₃ = 0
and
-l₁R₂ + (l – l₁)R₄ = 0 …(4)

Rewriting the above two equations we have
– l₁R₁ = (l – l₁) R₃ ….(5)
and
– l₁R₂ + (l – l₁)R₄ ….(6)

Dividing the above equations we have
\(\frac{R_{1}}{R_{2}}=\frac{R_{3}}{R_{4}}\) … (7)

The above expression gives the condition for the balance of a Wheatstone bridge.

Question 32.
Draw a circuit diagram of a potentiometer. State its working principle. Derive the necessary formula to describe how it is used to compare the EMFs of the two cells. (CBSE AI 2015C)
Answer:
PRINCIPLE: It is based on the principle that if a wire of uniform area of cross-section carries a constant current, the potential drop across any portion of the wire is directly proportional to the length of that portion of the wire.

The diagram is as shown.
First, the key K is inserted. This brings the cell of emf E₁ into the circuit. The jockey is moved on the wire to obtain a balance point, i.e. a point on the wire where the galvanometer gives zero deflection. Let the balancing length be L₁. Therefore by the potentiometer principle, we have
E₁ ∝ L₁ …(1)

Now, the key K₂ is inserted. This brings the cell of emf E₂ into the circuit. The jockey is again moved on the wire to obtain the balance point. Let the balancing length be L₂. Then by potentiometer principle, we have
E₂ ∝ L₂ …(2)

Dividing equations (1) by (2) we have
\(\frac{E_{1}}{E_{2}}=\frac{L_{1}}{L_{2}}\) …. (3)

Knowing the values of L₁ and L₂, the EMFs can be compared.

Question 33.
(i) Define the term ‘conductivity’ of a metallic wire. Write its SI unit.
Answer:
The property of a material that allows a flow of electrons between two points of the material when a potential difference is applied between these two points is called the conductivity of a wire. SI unit of conductivity: siemens per metre.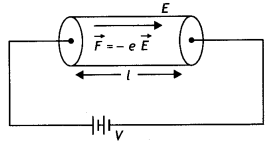

(ii) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E. (CBSE At 2018, Delhi 2018)
Answer:
Drift velocity of electrons in a conductor is given as
V_d = eEτ/m …(1)

Small distance covered in time
Δt = V_dΔt

Amount of charge passing through the area A in time Δt, q = lΔt
Δt = neAV_dΔt
or l = neAV_d …(2)
where
n → Number of free electrons per unit volume or number density

Now from equations (1) and (2), we get
l = ne₂AτE/m …(3)

Since resistivity of a conductor is given as
ρ = m/ne₂τ

Now, we know that the conductivity of a conductor is mathematically defined as the reciprocal of resistivity of the conductor. Thus,
σ = \(\frac{1}{ρ}\) …(4)

where σ = conductivity of the conductor. Thus, from equations (3) and (4), we get
σ = ne₂τ/m ….(5)

Now, from equations (3) and (5), we have
lA = σE …(6)
and current density is given as
J = lA
Thus, J = σE

Question 34.
(a) You are required to select a carbon resistor of resistance of 56 kΩ ± 10% from a shopkeeper. What would be the sequence of colour bands required to code the desired resistor?
Answer:
Number 5 corresponds to green, No. 6 corresponds to blue, 10³ corresponds to orange and 10% corresponds to silver.
∴ The sequence of Colours is
Green, blue, orange, silver

(b) Write two characteristic properties of the material of a metre bridge wire.
Answer:
Metre bridge wire must have

• High resistivity
• Low-temperature coefficient of resistivity

(c) What precautions do you take to minimise the error in finding the unknown resistance of the given wire? (CBSE2019C)
Answer:
To minimise the error in determining the resistance of a wire, the

• The wire should be of uniform thickness
• The balance point should be near the midpoint of the wire

Question 35.
The diagram below shows a potentiometer set-up. On touching the jockey near the end X of the potentiometer wire, the galvanometer pointer deflects to left. On touching the jockey near to end Y of the potentiometer, the galvanometer pointer again deflects to left but now by a larger amount. Identify the fault in the circuit and explain, using appropriate equations or otherwise, how it leads to such a one¬sided deflection. (CBSE Sample Paper 2018-19)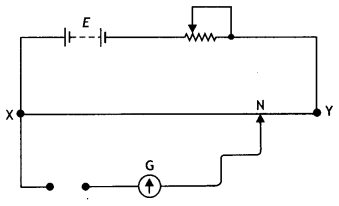

Or
The following circuit was set up in a metre bridge experiment to determine the value X of unknown resistance.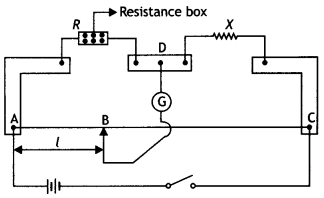

(i) Write the formula to be used for finding X from the observations. 39.5 cm from end A, when the resistor Y is 12.5 Ω. Determine the resistance of X. Why are the connections between resistors in a Wheatstone or metre bridge made of thick copper strips?
(ii) If the resistance R is increased, what will happen to balance length?
Answer:
The positive of E₁ is not connected to terminal X.
In Loop XGNX,
E₁ – V_G + E = 0
V_G = E₁ + E_XN
V_G = E₁ + kl

So, V_G (or deflection) Will be maximum when l is maximum, i.e. when Jockey Is touched near the end Y. Also, VG (or deflection) Will, be minimum when l is minimum, i.e. when a jockey is touched near end X.
Or
(i) X = (100 – l) R/l
(ii) The balancing Length wilt increase.

Question 36.
(i) In a metre bridge as shown, the balance point is found to be at 39.5 cm from the end A, when the resistor Y is 12.5. Determine the resistance of X. Why are the connections between resistors In a Wheatstone or metre bridge made of thick copper strips?
(ii) Determine the balance point of the bridge above if X and Y are interchanged.
(iii) What happens if the galvanometer and cell are interchanged at the balance point of the bridge? Would the galvanometer show any current? (NCERT)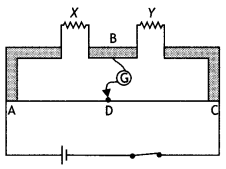

Answer:
(i) Given L₁ = 39.5 cm and L₂ =100 – 39.5 = 60.5 cm, Y=12.5Q, X=?
Using the Wheatstone bridge principle we have
\(\frac{39.5}{60.5}=\frac{X}{12.5}\) or X = 8.2 Ω

The connections between resistors in a Wheatstone or metre bridge are made of thick copper strips to minimise the resistance of the connection which are not accounted for in the bridge formula.

(ii) If X and Y are interchanged, then
\(\frac{L}{(100-L)}=\frac{12.5}{8.2}\); solving for L we have
L = 60.4 cm from point A.

(iii) When the galvanometer and cell are interchanged, the condition for the balance of the bridge remains satisfied. Hence galvanometer will not show any current.

Question 37.
The figure below shows a potentiometer with a cell of 2.0 V and internal resistance of 0. 40 Ω maintaining a potential drop across the resistor wire AB. A standard cell that maintains a constant emf of 1.02 V (for very moderate currents up to a few mA) gives a balance point at 67.3 cm length of the wire. To ensure very low currents drawn from the standard cell, very high resistance of 600 kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf e and the balance point found similarly, turns out to be at 82.3 cm length of the wire.
1. What is the value of e?
2. What purpose does the high resistance of 600 kΩ have?
3. Is the balance point affected by this high resistance?
4. Is the balance point affected by internal resistance?
5. Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V?
6. Would the circuit work well for determining an extremely small emf, say of the order of a few mV (such as the typical emf of a thermo-couple)? If not, how will you modify the circuit?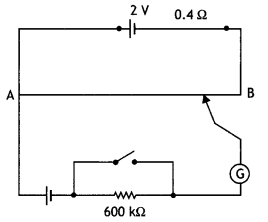

Answer:
1. Given ε₁ = 1.02 V, L₁ = 67.3 cm, L₂ = 82.3 cm, ε₂ = ?
By potentiometer principle we have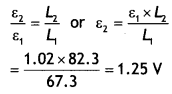

2. This resistance reduces the current through the galvanometer when the movable contact (a jockey) is far away from the balance point. This, in turn, protects the galvanometer from the damage likely to be caused by the high current.
3. There is no effect of this resistance on the balance point.
4. There is no effect.
5. In case, the driving emf is smaller than the emf to be measured, the balance point cannot be found on the potentiometer wire.
6. In such a case, the balance point will be very close to the end giving a very large error in the measurement of e. If resistance is placed in series with the wire AB such that the potential drop across AB is only slightly larger than the emf to be measured, the balance point will be found on a larger length. This will make the error very small.

Numerical Problems:

Formulae for solving numerical problems.

• The mobility of electrons is given by μ = \(\frac{V_{d}}{E}=\frac{e \tau}{m}\)
• By Ohm’s law, l = \(\frac{V}{R}\) and J = σE
• The current density is J = \(\frac{l}{A}\) = nevd
• Theresistanceofawireis R = ρ\(\frac{L}{A}\) = \(\left[\frac{m L}{n e^{2} A \tau}\right]\)
• The resistivity of a wire is ρ = \(\frac{m}{n e^{2} \tau}\)
• The resistance of a wire at t°C is R = R₀ (1 + αt)
• In parallel combination \(\frac{1}{R_{p}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}\)
• In series combination R_s = R₁ + R₂ + R₃ + ……..
• Ratio of resistances in series and parallel \(\frac{R_{\mathrm{s}}}{R_{\mathrm{p}}}\) = n²
• The Wheatstone bridge principle is \(\frac{P}{Q}=\frac{R}{S}\)
• V = E – lr, where V is the terminal potential difference, E is emf and r is the internal resistance of the cell.
• The internal resistance of a cell is r = \(\frac{(E-V) R}{V}=\frac{\left(L_{1}-L_{2}\right) R}{L_{2}}\)

Question 1.
A cell of emf ‘E’ and internal resistance ‘r’ is connected across a variable load resistor R. Draw the plots of the terminal voltage V versus (i) R and (ii) the current l.
It is found that when R = 4 Ω the current is 1 A and when R is increased to 9 Ω, the current reduces to 0.5 A. Find the values of the emf E and internal resistance r. (CBSE Delhi 2015)
Answer:
The plots are as shown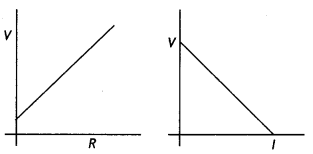

Here l₁ = 1.0 A, R₁ =4 ohm, l₂ = 0.5 A, R₂ =9 ohm
Using the equation l = \(\frac{E}{(R+r)}\) Or E = l(R + r)

we have
1.0 × (4 + r) = 0.5 × (9 + r)

Solving the above equation for r we have r = 1 ohm
Also E = 0.5 (9 + 1) = 5 V

Question 2.
A wire of resistance R, length l and area of cross-section A is cut into two parts, having their lengths in the ratio 1:2. The shorter wire is now stretched till its length becomes equal to that of the longer wire. If they are now connected in parallel, find the net resistance of the combination. (CBSE Al 2019)
Answer:
Since the wires are cut in the ratio of 1:2 therefore,
Resistance of the shorter wire R₁ = \(\frac{R}{3}\) and

Resistance of the longer wire R₂ = \(\frac{2R}{3}\)

Since the shorter wire is stretched to make it equal to the longer wire therefore, it is stretched by n = 2 times its length. Hence New resistance of the shorter wire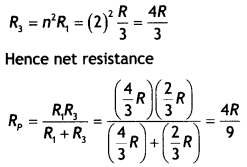

Question 3.
In the figure, a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null points for the two primary cells of EMFs ε₁ and ε₂ connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i) ε₁/ε₂ and (ii) position of null point for the cell ε₁. How is the sensitivity of a potentiometer increased? (CBSE Delhi 2012)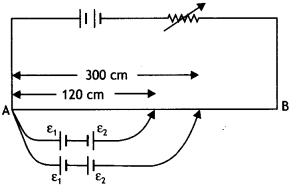

Answer:
From the diagram we have
\(\frac{\varepsilon_{1}-\varepsilon_{2}}{\varepsilon_{1}+\varepsilon_{2}}=\frac{120}{300}=\frac{2}{5}\)
Or
5ε₁ – 5ε₂ = 2ε₁ + 2ε₂

Solving we have
\(\frac{\varepsilon_{1}}{\varepsilon_{2}}=\frac{7}{3}\) ….(1)

Also let L be the balancing length for cell of emf ε1, then
\(\frac{\varepsilon_{1}}{\varepsilon_{1}+\varepsilon_{2}}=\frac{L}{300}\)

Using equation (1) we have
\(\frac{\varepsilon_{1}}{\varepsilon_{1}+\frac{3}{7} \varepsilon_{1}}=\frac{L}{300}\)

Solving for L we have L = 210 cm
The sensitivity of a potentiometer can be increased by increasing the length of the potentiometer wire.

Question 4.
The network PQRS, shown in the circuit diagram, has batteries of 4 V and 5 V and negligible internal resistance. A milli- ammeter of 20 Ω resistance is connected between P and R. Calculate the reading in the milliammeter. (CBSE AI 2012C)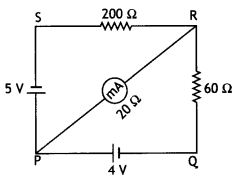

Answer:
Using Kirchhoff’s junction rule to distribute current we have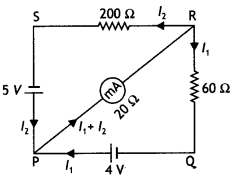

Consider the loop SRPS, by Kirchhoff’s loop rule we have
200 l₂ + 20 (l₁ + l₂ ) – 5 = 0 …(1)
Or
220 l₂ + 20 l₁ = 5 …(2)

Consider the loop PRQP, by Kirchhoff’s loop rule we have
– 60 l₁ + 4 – 20 (l₁ + l₂) = 0 …(3)
80 l₁ + 20 l₂ =4 …(4)

Multiplying equation (2) by (4) we have
880 l₂ + 80 l₁ = 20 …(5)

Subtracting equation (4) from equation (5)
we have
860 l₂ = 16 or l₂ = 4/215 A

Substituting in equation (4) we have
l₁ = \(\frac{39}{860}\)A

Therefore reading of the milliammeter is
l₁+ l₂ = \(\frac{4}{215}+\frac{39}{860}\) = 0.063 A = 63 mA

Question 5.
A set of ‘n’ identical resistors, each of resistance ‘R’ when connected in series have an effective resistance ‘X’. When they are connected in parallel, their effective resistance becomes ‘Y’. Find out the product of X and Y. (CBSEAI2019) Answer:
In series
R_s = R₁ + R₂ + R₃ + ……
R_s = X = R + R + R + …. upto n
X=nR

In Parallel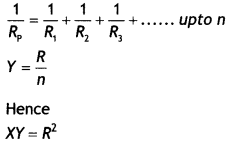

Question 6.
In the following circuit, a metre bridge is shown in its balanced state. The metre bridge wire has a resistance of 1 ohm per centimetre. Calculate the value of the unknown resistance X and the current drawn from the battery of negligible internal resistance.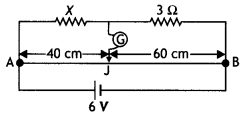

Answer:
Using the Wheatstone bridge principle we have
\(\frac{40}{60}=\frac{X}{3}\)
or X = 2 Ω

Now total resistance of the combination is
R = \(\frac{5 \times 100}{5+100}=\frac{500}{105}\) = 4.76 Ω

Current drawn is
l = V/R = 6/4.76 = 1.26 A

Question 7.
Calculate the electrical conductivity of the material of a conductor of length 3 m, area of cross-section 0.02 mm² having a resistance of 2 ohms.
Answer:
Given L = 3 m,
A = 0.02 mm2 = 0.02 × 10-6 m2
R = 2 ohm.

Using the equation
R = \(\frac{ρL}{A}\)
Or
ρ = \(\frac{RA}{L}\)

σ = \(\frac{L}{AR}\) = \(\frac{3}{0.02 \times 10^{-6} \times 2}\) = 7.5 × 107 Sm-1

Question 8.
A potential difference of 2 volts is applied between points A and B has shown in the network drawn in the figure. Calculate (i) equivalent resistance of the network across the points A and B and (ii) the magnitudes of currents in the arms AFCEB and AFDEB.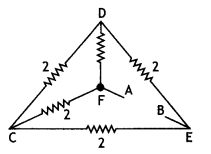

Answer:
The circuit can be redrawn as shown below.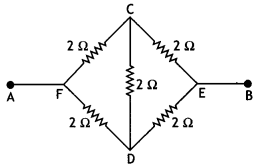

As seen the circuit is a balanced Wheatstone bridge; therefore the resistance in the arm CD is superfluous.
(i) Resistance of arm FCE = 2 + 2 = 4 Ω
Resistance of arm FDE = 2 + 2 = 4 Ω
Hence net resistance of the circuit between A and B is
R = \(\frac{4 \times 4}{4+4}=\frac{16}{8}\) = 2 Ω

(ii) current in the arm AFCEB
l = V/R = 2/4 = 0.5 A

Current in the arm AFDEB
l = V/R = 2/4 = 0.5 A

Question 9.
A cell of emf E and internal resistance ‘r’ gives a current of 0.8 A with an external resistor of 24 ohms and a current of 0.5 A with an external resistor of 40 ohms.
Calculate
(i) emf E and
(ii) internal resistance ‘r’ of the cell.
Answer:
Given l₁ = 0.8 A, R₁ = 24 ohm l₂ = 0.5 A, R₂ = 40 ohm
Using the equation
E = l(R + r) we have
0.8 × (24 + r) = 0.5 × (40 + r)

Solving for r we have r = 2.67 ohm
Also E = 0.5( 40 + 2.67) = 21.3 V

Question 10.
In the circuit diagram of the metre bridge given below, the balance point is found to be at 40 cm from A. The resistance of X is unknown and Y is 10 ohms.
(i) Calculate the value of X;
(ii) if the positions of X and Y are interchanged in the bridge, find the position of the new balance point from A; and
(iii) if the galvanometer and the cell are interchanged at the balance point, would the galvanometer show any current.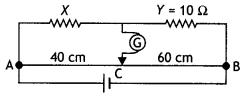

Answer:
(i) Using the Wheatstone bridge principle we have
\(\frac{40}{60}=\frac{X}{10}\)
Or
X = 6.67 Ω

(ii) If X and Y are interchanged then
\(\frac{L}{(100-L)}=\frac{10}{6.67}\) solving for L we have
L = 59.9cm

(iii) The ga(vanometer will not show any current.

Question 11.
The length of a potentiometer wire is 600 cm and it carries a current of 40 mA. For a cell of emf 2.0 V and internal resistance 10 ohms, the null point is found to be at 500 cm. If a voltmeter is connected across the cell, the balancing length is decreased by 10 cm. Find (i) the resistance of the whole wire, (ii) reading of the voltmeter and (iii) resistance of the voltmeter.
Answer:
Here total length of potentiometer wire L = 600 cm, current flowing
l = 40 mA = 0.04 A,
Emf of cell E = 2 V,

Internal resistance of cell r = 10 Ω, balancing length for cell l = 500 cm
(i) Since ε = kl
k = \(\frac{\varepsilon}{l}=\frac{2}{500}\) , V = kl

∴ V = \(\frac{2}{500}\) × 600 = 2.4 V

Therefore resistance of the potentiometer wire =\(\frac{V}{l}=\frac{2.4}{0.04}\) = 60 Ω.

(ii) With voltmeter connected across the cell, balancing Length
L’ = l – 10 = 500 – 10 = 490cm

Therefore, potential difference, i.e. reading of voltmeter,
= \(\frac{L^{\prime}}{L} \times V=\frac{490}{600}\) × 2.4 = 1.96 V

(iii) Let resistance of the voltmeter be R,
R = \(\frac{V}{l}=\frac{1.96}{0.04}\) = 49 Ω
R = 49 ohm

Question 12.
Find the value of the unknown resistance X in the following circuit, if no current flows through the section AO. Also, calculate the current drawn by the circuit from the battery of emf 6 V and negligible internal resistance.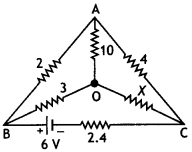

Answer:
If no current flows through the section AO, the given circuit is an example of a balanced Wheatstone bridge. The circuit can be redrawn as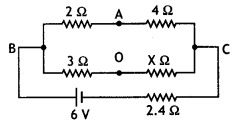

Then \(\frac{2}{4}=\frac{3}{X}\)
Or
X = \(\frac{3 \times 4}{2}\) = 6 Ω

Now 2 Ω and 4 Ω are in series and 3 Ω and 6 Ω are also in series; so the circuit becomes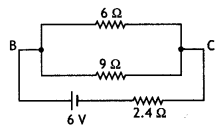

Hence total resistance of the circuit
R = 2.4 + \(\left(\frac{9 \times 6}{15}\right)\) = 6 Ω

Hence current drawn from the battery
l = V/R = 6/6 = 1 A

Question 13.
In the given circuit, calculate the value of current in a 4.5-ohm resistor and indicate its direction. Also, calculate the potential difference across each cell.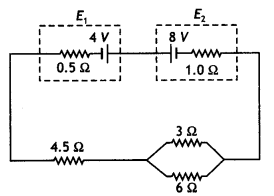

Answer:
The effective resistance of 3 ohms and 6-ohm resistors in parallel is
R = \(\frac{3 \times 6}{3+6}\) =2Q

Hence the resistance of the entire circuit
R = 2 + 4.5 + 0.5 + 1 = 8 ohm

Effective emf of the circuit E = 8 – 4 = 4 V.

Therefore current through the circuit and hence through the 4.5-ohm resistor is
l = E/R = 4/8 = 0.5 A.

The direction of the current is from cell E₂ towards cell E₁.

The potential difference across 8 V battery
V = E – lr = 8 – 0.5 × 1 = 7.5 V

The potential difference across 4 V battery
V = E + lr = 4 + o.5 × 0.5 = 4.25 V

Question 14.
Potentiometer wire PQ of 1-metre length is connected to a standard cell E₁. Another cell, E₂ of emf 1.02 V, is connected as shown In the circuit diagram with a resistance ‘r’ and a switch, S. with the switch open, the null position is obtained at a distance of 51 cm from P.
Calculate (i) the potential gradient of the potentiometer wire and
(ii) the emf of the cell E₁.
(iii) When switch S is closed, will the null point move towards P or towards Q? Give a reason for your answer.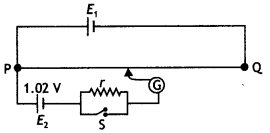

Answer:
Here E₂ = 1.02V and with switch open L = 51 cm

(i) Potential gradient k = E/L
= 1.02 /51 = 0.02 V cm^-1

(ii) As total length of potentiometer wire L = 1 m = 100 cm
Therefore E₁ = kL = 0.02 × 100 = 2 V

(iii) When switch S is closed, the null point will remain unaffected because cell E₂ is even now in an open circuit and no current is being drawn from it.

Question 15.
Three identical resistors when connected in series to a dc source dissipate a power of X watt. If these resistors are connected in parallel to the same dc source, what will be the power dissipation in this case?
Answer:
Given P_s = X, R_s = 3R, R_p = R/3

Power in series Ps = \(\frac{V^{2}}{R_{s}}\) or X = \(\frac{V^{2}}{3 R}\) or 3X = \(\frac{V^{2}}{R}\)

When resistors are connected In parallel, we have
P_p = \(\frac{V^{2}}{R_{p}}=\frac{V^{2}}{R / 3}=\frac{3 V^{2}}{R}\) = 3 × 3X = 9X

Question 16.
A heater coil is rated 100W, 200V. It is cut into two Identical parts. Both parts are connected In parallel, to the same source of 200 V. Calculate the energy liberated per second in the new combination.
Answer:
The resistance of the coil
R = \(\frac{V^{2}}{P}=\frac{(200)^{2}}{100}\) = 400 Ω

When the coil is cut into two equal halves, the resistance of each half becomes 200 ohms.

When these two parts are connected in parallel, the resultant resistance is
R_p = \(\frac{200 \times 200}{200+200}\) = 100 Ω

Now energy Liberated
H = \(\frac{V^{2}}{R_{\mathrm{p}}}=\frac{(200)^{2}}{100}\) = 400 Ω

Question 17.
AB is a 1 m long uniform wire of 10 Ω resistance. The other data are as shown in the circuit diagram given in the figure below. Calculate (i) potential gradient along with AB and (ii) length AO of the wire, when the galvanometer shows no deflection.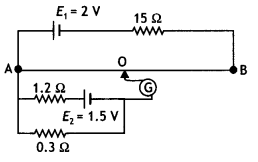

Answer:
Emf of battery E₁ = 2 V.
Resistance of potentiometer R = 10 Ω,
Resistance joined in series R₁ = 15 Ω and
Length of potentiometer wire L = 1 m = 100 cm
(i) Potential gradient
k = \(\frac{E_{1} R}{\left(R+R_{1}\right) L}=\frac{2 \times 10}{(10+15) \times 100}\) = 0.008 Vcm^-1

(ii) Current through 0.3 Ω resistance due
to cell E₁, l = \(\frac{1.5}{1.2+0.3}\) = 1 A

Potential difference across 0.3 Ω resistance = l × 0.3 = l × 0.3 = 0.3 V

∴ Length AO = \(\frac{\text { Potential difference }}{\text { Potential gradient }}\) = 37.5 cm

Question 18.
In a potentiometer, a standard cell of emf 5V and of negligible resistance maintains a steady current through the potentiometer wire of length 5 m. Two primary cells of EMFs E₁ and E₂ are joined in series with (a) the same polarity and (b) opposite polarity. The combination Is connected through a galvanometer and a jockey to the potentiometer. The balancing lengths In the two cases are found to be 350 cm and 50 cm, respectively.
(i) Draw the necessary circuit diagram.
(ii) Find the value of the EMFs of the two cells.
Answer:
(i) The circuit diagram is as shown below.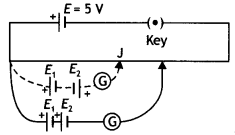

(ii) With cells E₁ and E₂ joined in series with the same polarity, the resultant emf
E = E₁ + E₂ and

Balancing Length L = 350 cm.
With celLs joined in series with opposite polarity, the resuLtant emf
E’ = E₁ – E₂ and

Balancing Length L = 50 cm.

Moreover, the potentiaL gradient

k = \(\frac{V}{L}=\frac{5 \mathrm{~V}}{5 \mathrm{~m}}=\frac{5 \mathrm{~V}}{500 \mathrm{~cm}}\) = 0.01 Vcm^-1

Therefore
E₁ + E₂ = kL = 0.01 × 350 = 3.5 V and
E₁ – E₂ = kL = 0.01 × 50 = 0.5 V

Solving for the two EMFs we get E₁ = 2V and E₂ = 1.5 V

Question 19.
Using Kirchhoff’s rules, calculate the current through the 40 Q and 200 resistors in the following circuit: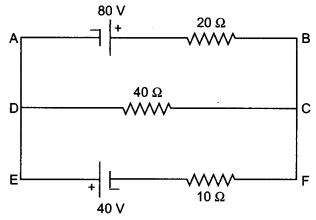

Or
What is the end error in a metre bridge? How is it overcome? The resistances in the two arms of the metre bridge are R = 5 Ω and S respectively. When the resistance S is shunted with equal resistance, the new balance length found to be 1.5 L₁, where L₁ is the initial balancing length. Calculate the value of S. (CBSE Delhi 2019)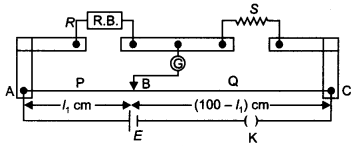

Answer:
The distribution of current is as shown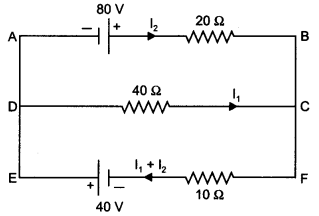

In loop ABCDA
+ 80 – 20 l₂ + 40 l₁ = 0
4 = l₂ – 2 l₁

In loop DCFED
– 40 l₁ – 10(l₁ + l₂) + 40 = 0
-50 l₁ – 10 l₂ + 40 = 0
5 l₁ + l₂ = 4

Solving these two equations
l₁ = 0 A and
l₂ = 4 A
Or
The end error, in a meter bridge, is the error arising due to
(i) Ends of the wire not coinciding with the 0 cm/100 cm mark on the meter scale.
(ii) Presence of contact resistance at the joints of the meter bridge wire with the metallic strips.

It can be reduced/overcome by finding balance length with two interchanged positions of R and S and taking the average value of ‘S’ from these two readings.

For a metre bridge, we have
\(\frac{R}{S}=\frac{L}{100-L}\)

For the two given conditions, we have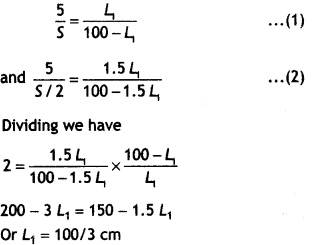

Putting this value in equation (1) we have S = 10 Ω.

Question 20.
A 10 m long wire of uniform cross-section and 20-ohm resistance is used in a potentiometer. The wire is connected in series with a battery of 5 V along with an external resistance of 480 ohms. If an unknown emf E is balanced at 6.0 m length of the wire, calculate:
(i) the potential gradient of the potentiometer wire
(ii) the value of unknown emf E.
Answer:
Total resistance of the circuit
R = 20 + 480 = 500 ohm

Therefore current through the potentiometer
l = \(\frac{V}{R}=\frac{5}{500}\) = 0.01 A

Now potential drop across the potentiometer wire of 20 ohm = 20 × 0.01 = 0.2 V

(i) Potential gradient
\(\frac{V}{L}=\frac{0.2}{10}\) = 0.02 Vm^-1

(ii) Unknown emf = balancing length × potential gradient = 6 × 0.02 = 0.12 V

Question 21.
In a potentiometer arrangement, a cell of emf 1.20 volt gives a balance point at 30 cm length of the wire. This cell is now replaced by another cell of unknown emf. If the ratio of the EMFs of the two cells is 1.5, calculate the difference in the balancing length of the potentiometer wire in the two cases.
Answer:
Given E₁ = 1.20 V, L₁ = 30 cm, E₂ = ?,
E₁/E₂ = 1.5, L₁ – L₂ = ?

Now \(\frac{E_{1}}{E_{2}}=\frac{L_{1}}{L_{2}}\) or 1.5 = \(\frac{30}{L_{2}}\) or L₂ = 20 cm

Therefore L₁ – L₂ = 30 – 20 = 10 cm

Question 22.
A uniform wire of resistance 12 Ω is cut into three pieces so that the ratio of the resistances R₁: R₂: R₃ = 1: 2: 3 and the three pieces are connected to form a triangle across which a cell of emf 8 V and internal resistance 1 Ω is connected as shown. Calculate the current through each part of the circuit. (CBSE A! 2013C)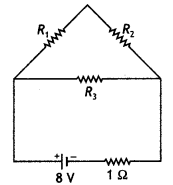

Answer:
Value of the three resistances are
R₁ = \(\frac{1}{6}\) × 12 = 2 Ω,
R₂ = \(\frac{2}{6}\) × 12 = 4 Ω
and R₃ = \(\frac{3}{6}\) × 12 = 6 Ω

Now R1 and R2 are connected in series, therefore we have
R = R₁ + R₂ = 2 + 4 = 6 Ω

Now R and R3 are connected in parallel, therefore net resistance
R_p = \(\frac{R R_{3}}{R+R_{3}}=\frac{6 \times 6}{6+6}\) = 3 Ω

Now Rp and the internal resistance of the cell are connected in series, therefore net resistance of the circuit is
R_N = R_p + 1 = 3 + 1 = 4 Ω

Hence current in the circuit is
l = V/R_N = 8/4 = 2 A

This is equally divided amongst R₁, R₂ and R₃. Therefore current through all the three resistors is 1 A.

Question 23.
A battery of emf E and internal resistance r when connected across an external resistance of 12 ohms produces a current of 0.5 A. When connected across a resistance of 25 ohms it produces a current of 0.25 A. Determine the (i) emf and (ii) internal resistance of the cell. (CBSEAI2013C)
Answer:
Here l₁ = 0.5 A, R₁ =12 ohm, l₂ = 0.25 A, R2₂ = 25 ohm

Using the equation l = \(\frac{E}{(R+r)}\) or E = l(R + r)

we have
0. 5 × (12 + 1) = 0.25 × (25 + r)

Solving the above equation for r we have
r = 1 ohm

Also E = 0.5 (12 + 1) = 6.5 V

Question 24.
The resistance of the platinum wire of a platinum resistance thermometer at the ice point is 5 Ω and at steam, the point is 5.23 Ω. When the thermometer is inserted into a hot bath, the resistance of the platinum wire is 5.795 Ω. Calculate the temperature of the bath. (NCERT)
Answer:
R_o = 5 Ω, R₁₀₀ = 5.23 Ω, R_t = 5.795 Ω

Question 25.
A battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1 Ω. Determine the equivalent resistance of the network and the current along each edge of the cube. (NCERT)

Answer:
The distribution of current is as shown.

Next take a closed-loop, say, ABCC’EA and apply Kirchhoff’s second rule:
lR – (1/2)lR – lR + E = 0
where R is the resistance of each edge and E is the emf of the battery.
Thus E = 5lR/2

Now if R_eq is the equivalent resistance, then
R = E/31 = 5lR/6l = 5/6 R

Now current in the circuit is 3l × 5/6 R = 10 or l = 4 A.

Hence the other currents can also be found.

Question 26.
Determine the current in each branch of the network shown. (NCERT)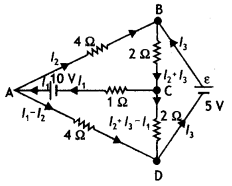

Answer:
Each branch of the network is assigned an unknown current to be determined by the application of Kirchhoff’s rules. To reduce the number of unknowns at the outset, the first rule of Kirchhoff is used at every junction to assign the unknown current in each branch. We then have three unknowns l₁, l₂ and l₃ which can be found by applying the second rule of Kirchhoff to three different closed loops.

Kirchhoff’s second rule for the closed loop ADCA gives,
10 – 4(l₁ – l₂) + 2(l₂ + l3 – l₁) – l₁ = 0 …(1)
that is, 7 l₁ – 6l₂ – 2l₃ = 10

For the closed loop ABCA, we get
10 – 4l₂ – 2 (l₂ + l₃) – l₁ = 0 …(2)

That is, l₁ + 6l₂ + 2l₃ = 10

For the closed loop BCDEB, we get
5 – 2(l₂ + l₃) – 2(l₂ + l₃– l₁) = 0 ….(3)

That is 2 l₁ – 4l₂ – 4l₃ = – 5

Equations (1), (2) and (3) are three simultaneous equations in three unknowns. These can be solved by the usual method to give
l₁ = 2.5 A, l₂ = 5/8 A, l₃ = 15/8 A

The currents in the various branches of the network are
AB = 5/8 A, CA = 5/2 A, DEB = 15/8 A, AD = 15/8 A, CD = 0 A, BC = 5/2 A

Question 27.
In a metre bridge, the null point is found at a distance of 33.7 cm from A. If now resistance of 12 Ω is connected in parallel with 5, the null point occurs at 51.9 cm. Determine the values of R and S. (NCERT)
Answer:
From the first balance point we get
\(\frac{R}{S}=\frac{33.7}{66.3}\)

After S is connected in parallel with a resistance of 12 Ω, the resistance across the gap changes from S to S_eq where and hence the new balance condition now gives
\(\frac{R}{S_{e q}}=\frac{51.9}{48.1}=\frac{R(S+12)}{12 S}\)

Substituting for R/S we have
\(\frac{51.9}{48.1}=\frac{(5+12)}{12} \times \frac{33.7}{66.3}\)
which gives S = 13.5 Ω and R = 6.86 Ω

Question 28.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell? (NCERT)
Answer:
Given ε₁ = 1.25 V, L₁ = 35.0 cm and L₂ = 63.0 cm, ε₂ = ?
ε₂ = \(\frac{L_{2} \times \varepsilon_{1}}{L_{1}}=\frac{1.25 \times 63.0}{35.0}\) = 2.25 V

Question 29.
The figure below shows a potentiometer circuit for the comparison of two resistances. The balance point with a standard resistor R = 10.0 Ω is found to be 58.3 cm, while that with the unknown resistance X is 68.5 cm. Determine the value of X. What might you do if you failed to find a balance point with the given cell of emf ε? (NCERT)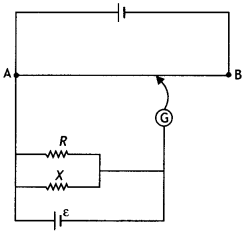

Answer:
Given R= 10.0 Ω, L₁ = 58.3 cm, L₂ = 68.5 cm, X = 1

Let k be the potential gradient along the wire AB, then
\(\frac{X}{R}=\frac{k L_{2}}{k L_{1}}\)
or
X = \(\frac{R \times L_{2}}{L_{1}}=\frac{10 \times 68.5}{58.3}\)
or
X= 11.75 Ω

If we fail to find a balance point with the given cell of emf e, it means the potential drop across R or X is greater than the potential drop across the potentiometer wire AB. Therefore to obtain the balance point on the wire, reduce the current in the circuit by putting a resistor in series with the circuit.

Question 30.
The figure below shows a 2.0 V potentiometer used for the determination of the internal resistance of a 1.5 V cell. The balance point of the cell in the open circuit is 76.3 cm. When a resistor of 9.5 Q is used in the external circuit of the cell, the balance point shifts to 64.8 cm length of the potentiometer wire. Determine the internal resistance of the cell. (NCERT)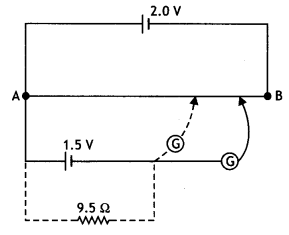

Answer:
Given 4 = 76.3 cm, ε = 1.5 V, R = 9.5 Ω, L₂ = 64.8 cm
Internal resistance of a cell is given by the expression
r = \(\frac{\left(L_{1}-L_{2}\right) R}{L_{2}}\)
or
r = \(\frac{(76.3-64.8) \times 9.5}{64.8}\)
= 1.7 Ω