Atoms

Class 12 Physics Chapter 12 Important Extra Questions Atoms

Short Answer Type

Question 1.
Name the spectral series which lies in the visible region.
Answer:
Balmer series.

Question 2.
What is the maximum number of spectral lines emitted by a hydrogen atom when it is in the third excited state? (CBSE AI 2013C)
Answer:
Six.

Question 3.
When is H_α line of the Balmer series in the emission spectrum of hydrogen atom obtained? (CBSE Delhi 2013C)
Answer:
It is obtained when an electron jumps from n =3 to n = 2 level.

Question 4.
A mass of lead is embedded in a block of wood. Radiations from a radioactive source incident on the side of the block produce a shadow on a fluorescent screen placed beyond the block. The shadow of the wood is faint but the shadow of lead is dark. Give a reason for this difference.
Answer:
The shadow of the wood is faint because only the a-radiations are stopped by the wood (since a-radiations are least penetrating). The shadow of lead is dark because p and y-radiations are also stopped by lead.

Question 5.
What was the source of alpha particles in Rutherford’s alpha scattering experiment?
Answer:
The source was ²¹⁴₈₃Bi.

Question 6.
Define ionisation energy. What is its value for a hydrogen atom? (All India 2010)
Answer:
Ionisation energy : The energy required to knock out an electron from an atom is called ionisation energy of the atom.
For hydrogen atom it is 13.6 eV.

Question 7.
Write the expression for Bohr’s radius in hydrogen atom. (Delhi 2010)
Answer:
Bohr’s radius in hydrogen atom,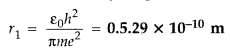

Question 8.
What is the ratio of radii of the orbits corresponding to first excited state and ground state in a hydrogen atom? (Delhi 2010)
Answer:

Question 9.
The radius of innermost electron orbit of a hydrogen atom is 5.3 × 10^-11 m. What is the radius of orbit in the second excited state? (Delhi 2011)
Answer: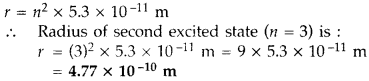

Question 10.
Find the ratio of energies of photons produced due to transition of an electron of hydrogen atom from its
(i) second permitted energy level to the first level, and
(ii) the highest permitted energy level to the first permitted level. (All India 2010)
Answer: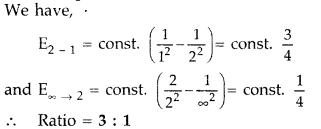

Question 11.
The ground state energy of hydrogen atom is -13.6 eV. What are the kinetic and potential energies of electron in this state? (All India)
Answer:
Kinetic energy, K_e = + T.E. = 13.6 eV
Potential energy, P_e = 2 T.E. = 2 (-13.6) = – 27.2 eV

Question 12.
Why is the classical (Rutherford) model for an atom—of electron orbitting around the nucleus—not able to explain the atomic structure? (All India 2012)
Answer:
As the revolving electron loses energy continuously, it must spiral inwards and eventually fall into the nucleus. So it was not able to explain the atomic structure.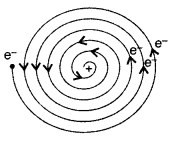

Question 13.
When is Ha line of the Balmer series in the emission spectrum of hydrogen atom obtained? (Comptt. Delhi 2012)
Answer:
Balmer series is obtained when an electron jumps to the second orbit (n₁ = 2) from any orbit n₂ = n > 2 .

Question 14.
What is the maximum number of spectral lines emitted by a hydrogen atom when it is in the third excited state? (Comptt. All India 2012)
Answer:
For third excited state, n₂ = 4, and n₁ = 3, 2, 1 Hence there are 3 spectral lines.

Question 15.
If the radius of the ground level of a hydrogen atom is 5.3 nm, what is the radius of the first excited state?
Answer:
It is 4 × 5.3 = 21.2 nm ( ∵ r = n²r_o)

Question 16.
Calculate the ratio of energies of photons produced due to the transition of electron of a hydrogen atom from its
(a) Second permitted energy level to the first level, and
Answer:
energy of photon E₁ = – 3.4 – (-13.6) = 10.2 eV

(b) Highest permitted energy level to the second permitted level.
Answer:
energy of photon E₂ = 0 – (-3.4) = 3.4 eV
Ratio \(\frac{E_{1}}{E_{2}}=\frac{10.2}{3.4}\) = 3

Question 17.
The mass of an H-atom is less than the sum of the masses of a proton and electron. Why is this? (NCERT Exemplar) Answer:
Einstein’s mass-energy equivalence gives E = mc². Thus the mass of an H-atom is m_p + m_e – B/c² where B ≈ 13.6 eV

Short Answer Type

Question 1.
(i) In hydrogen atom, an electron undergoes transition from 2nd excited state to the first excited state and then to the ground state. Identify the spectral series to which these transitions belong.
(ii) Find out the ratio of the wavelengths of the emitted radiations in the two cases. (Comptt. All India 2012)
Answer:

Question 2.
(i) In hydrogen atom, an electron undergoes transition from third excited state to the second excited state and then to the first excited state. Identify the spectral series to which these transitions belong.
(ii) Find out the ratio of the wavelengths of the emitted radiations in the two cases. (Comptt. All India 2012)
Answer:

Question 3.
In hydrogen atom, an electron undergoes transition from 3rd excited state to the first excited state and then to the ground state. Identify the spectral series to which these transitions belong.
(ii) Find out the ratio of the wavelengths of the emitted radiations in the two cases. (Comptt. All India 2012) Answer:
(i) These transitions belong to :
1. Balmer series,
2. Lyman series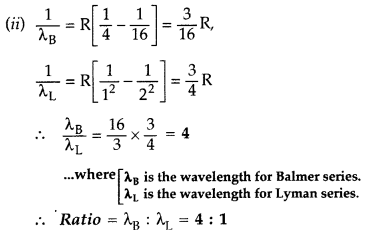

Question 4.
Using Rutherford model of the atom, derive the expression for the total energy of the electron in hydrogen atom. What is the significance of total negative energy possessed by the electron? (All India 2012)
Answer:
Expression for total energy of electron in H-atom using Rutherford model : As per Rutherford model of atom, centripetal force (F_c) required to keep electron revolving in orbit is provided by the electrostatic force (Fe) of attraction between the revolving electron and nucleus.

The negative sign indicates that the revolving electron is bound to the positive nucleus.

Question 5.
Using Bohr’s postulates of the atomic model, derive the expression for radius of nth electron orbit. Hence obtain the expression for Bohr’s radius. (All India 2012)
Answer:
Basic postulates of Bohr’s atomic model:
(i) Every atom consists of a central core called nucleus in which entire positive charge and mass of the atom are concentrated. A suitable number of electrons revolve around the nucleus in circular orbit. The centripetal force required for revolution is provided by the electrostatic force of attraction between the electron and the nucleus.
(ii) Electron can resolve only in certain discrete non-radiating orbits, called stationary orbit. Total angular momentum of the revolving electron in an integral multiple of h/2π.
… where [h is plank constant]

(iii) The radiation of energy occurs only when an electron jumps from one permitted orbit to another. The difference in the total energy of electron in the two permitted orbit is absorbed when the electron jumps from inner to the outer orbit and emitted when electron jumps from outer to inner orbit.

Radii of Bohr’s stationary orbits. According to Bohr’s postulates, angular momentum of electron for any permitted orbit is,

Also, according to Bohr’s postulates, the centripetal force is equal to electrostatic force between the electron and nucleus.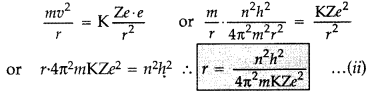

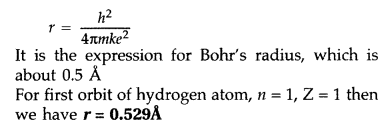
Question 6.
Show that the radius of the orbit in hydrogen atom varies as n², where n is the principal quantum number of the atom. (Delhi 2012)
Answer:
When an electron moves around hydrogen nucleus, the electrostatic force between electron and hydrogen nucleus provides necessary centrepetal force.

Also we know from Bohr’s postulate,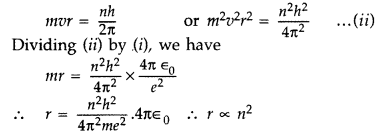

Question 7.
When an electron in hydrogen atom jumps from the third excited state to the ground state, how would the de Broglie wavelength associated with the electron change? Justify your answer. (All India 2012)
Answer: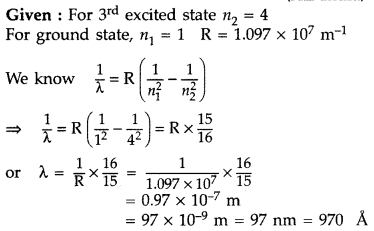

It lies in the ultra-violet region.

Question 8.
Calculate the shortest wavelength in the Balmer series of hydrogen atom. In which region (infra-red, visible, ultraviolet) of hydrogen spectrum does this wavelength lie? (All India 2012)
Answer:
In Balmer series, an electron jumps from higher orbits to the second stationary orbit (n_f = 2). Thus for this series :

Question 9.
The figure shows energy level diagram of hydogen atom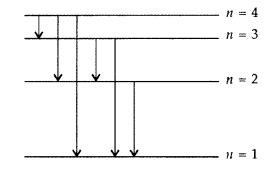

(a) Find out the transition which results in the emission of a photon of wavelength 496 nm.
(b) Which transition corresponds to the emission of radiation of maximum wavelength? Justify your answer. (Comptt. All India 2012)
Answer:
(a) Transition emitting wavelength λ = 496 nm The given wavelength lies in visible region (Balmer series) when,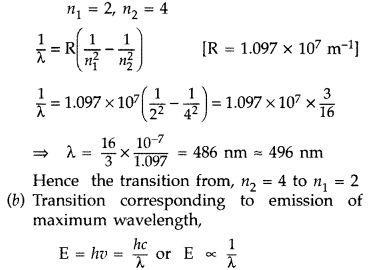

which means that the maximum wavelength emmission will be there when the energy level difference is minimum. From the given energy level diagram, it corresponds to :

Question 10.
In Rutherford scattering experiment, draw the trajectory traced by a-particles in the coulomb field of target nucleus and explain how this led to estimate the size of the nucleus. (Comptt. All India 2012)
Answer:
Note: The Rutherford scattering experiment is also known as the Geiger Marsden experiment.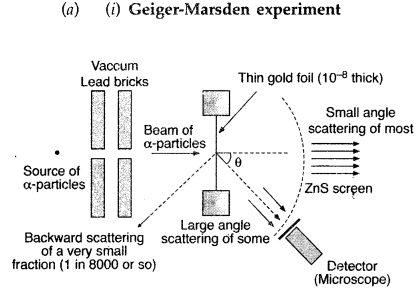

(ii) For most of the α-particles, impact parameter is large, hence they suffer very small repulsion due to nucleus and go right through the foil.
(iii) Trajectory of α-particles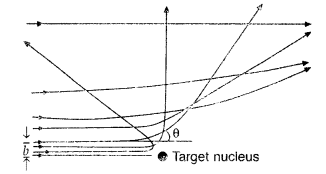

It gives an estimate of the size of nucleus, that it relatively very very small as compared to the size of atom.

Question 11.
Define ionization energy.
How would the ionization energy change when electron in hydrogen atom is replaced by a particle of mass 200 times that of the electron but having the same charge? (All India 2016)
Answer:
Definition of ionization energy : “The minimum energy, required to free the electron from the ground state of the hydrogen atom, is known as Ionization Energy.”
The ionization energy is given by :

∴Ionization Energy will become 200 times,
∵ the mass of given particle is 200 times.

Question 12.
Calculate the shortest wavelength of the spectral lines emitted in Balmer series.
[Given Rydberg constant, R = 10⁷ m^-1] (All India 2016)
Answer: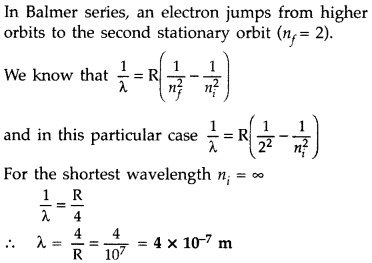

Question 13.
The electron, in a hydrogen atom, is in its second excited state.
Calculate the wavelength of the lines in the Lyman series, that can be emitted through the permissible transitions of this electron.
(Given the value of Rydberg constant, R = 1.1 × 107 m^-1) (Comptt. Delhi 2016)
Answer: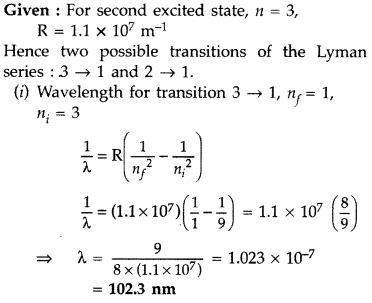

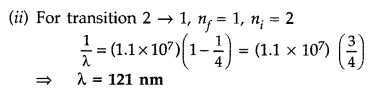
Question 14.
An α-particle moving with initial kinetic energy K towards a nucleus of atomic number z approaches a distance ‘d’ at which it reverses its direction. Obtain the expression for the distance of closest approach ‘d’ in terms of the kinetic energy of α-particle K. (Comptt. All India 2016)
Answer:

Question 15.
Find the ratio between the wavelengths of the ‘most energetic’ spectral lines in the Balmer and Paschen series of the hydrogen spectrum. (Comptt. All India 2016)
Answer: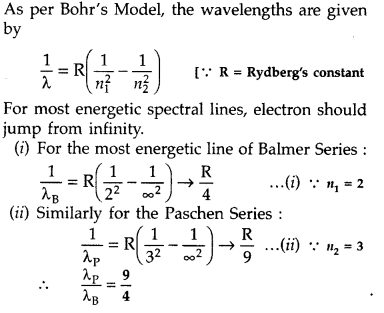

Question 16.
Define the distance of closest approach. An a-particle of kinetic energy ‘K’ is bombarded on a thin gold foil. The distance of the closest approach is V. What will be the distance of closest approach for an a-particle of double the kinetic energy? (Delhi 2016)
Answer:
The distance of closest approach is defined as “the distance of charged particle from the centre of the nucleus, at which the whole of the initial kinetic energy of the (far off) charged particle gets converted into the electric potential energy of the system”.
Distance of closest approach (r_c) is given by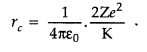

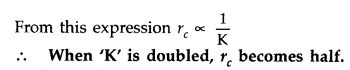
Question 17.
Write two important limitations of Rutherford nuclear model of the atom. (Delhi 2016)
Answer:
Important limitations of Rutherford Model :

1. According to Rutherford model, electron orbiting around the nucleus, continuously radiates energy due to the acceleration; hence the atom will not remain stable.
2. As electron spirals inwards; its angular velocity and frequency change continuously; therefore it. will emit a continuous spectrum.

Question 18.
Find out the wavelength of the electron orbiting in the ground state of hydrogen atom. (Delhi 2016)
Answer: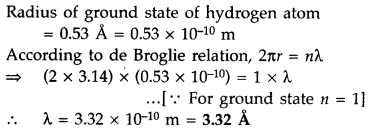

Question 19.
Find the wavelength of the electron orbiting in the first excited state in hydrogen atom. (Delhi 2016)
Answer: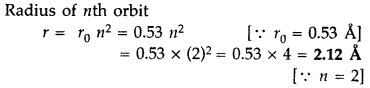

Question 20.
A 12.5 eV electron beam is used to excite a gaseous hydrogen atom at room temperature. Determine the wavelengths and the corresponding series of the lines emitted. (All India 2016)
Answer:

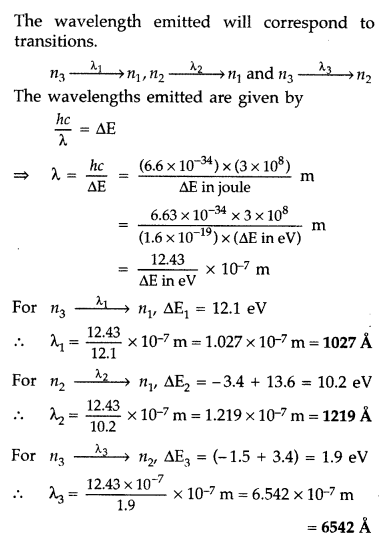
Question 21.
The short wavelength limit for the Lyman series of the hydrogen spectrum is 913.4 A Calculate the short wavelength limit for Balmer series of the hydrogen spectrum. (All India 2016)
Answer: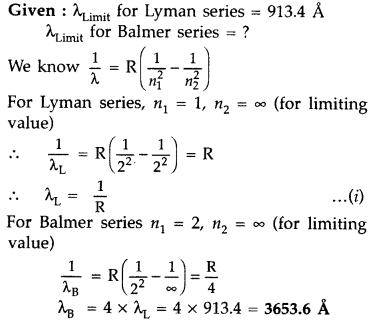

Question 22.
The ground state energy of hydrogen atom is -13.6 eV. If an electron makes a transition from an energy level -1.51 eV to -3.4 eV, calculate the wavelength of the spectral line emitted and name the series of hydrogen spectrum to which it belongs. (All India 2016)
Answer:

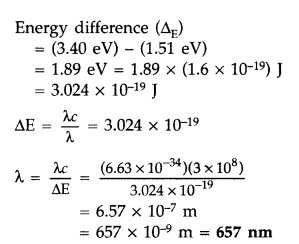
Question 23.
Calculate the shortest wavelength of light emitted in the Paschen series of hydrogen spectrum. Which part of the electromagnetic spectrum, does it belong to ? (Given : Rydberg constant, R = 1.1 × 10⁷ m^-1) (Comptt. Delhi 2016)
Answer: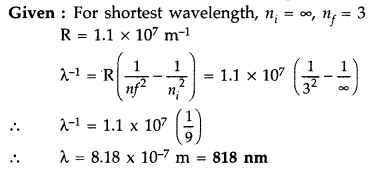

It belongs to the Infrared part of the spectrum.

Question 24.
Calculate the shortest wavelength of photons emitted in the Bracket series of hydrogen spectrum. Which part of the e.m. spectrum, does it belong? [Given Rydberg constant, R = 1.1 × 10⁷ m^-1] (Comptt. Delhi 2016)
Answer:
In bracket series, n_f = 4

Question 25.
Calculate the longest wavelength of the photons emitted in the Balmer series of hydrogen spectrum. Which part of the e.m. spectrum, does it belong to?
[Given Rydberg constant, R = 1.1 × 107 m^-1]. (Comptt. Delhi 2016)
Answer:
Balmer series is produced when an electron jumps from higher orbits to second stationary orbit (n_f = 2).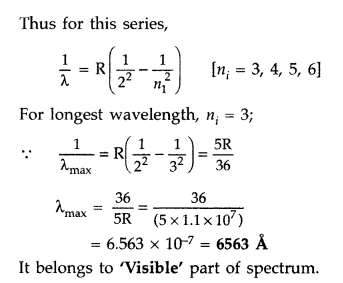

Question 26.
Define electron-volt and atomic mass unit. Calculate the energy in joule equivalent to the mass of one proton.
Answer:
Electron volt: It is defined as the energy gained by an electron when accelerated through a potential difference of 1 volt. Atomic mass unit: It is defined as one-twelfth of the mass of one atom of carbon 12.

The mass of a proton is 1.67 × 10^-27 kg. Therefore, energy equivalent of this mass is E = mc² = 1.67 × 10^-27 × (3 × 10⁸)² = 1.5 × 10^-10 J

Question 27.
State Bohr’s quantization condition of angular momentum. Calculate the shortest wavelength of the Bracket series and state to which part of the electromagnetic spectrum does it belong. (CBSE Delhi 2019)
Or
Calculate the orbital period of the electron in the first excited state of the hydrogen atom.
Answer:
Bohr’s Quantisation condition: Only those orbits are permitted in which the angular momentum of the electron is an integral multiple of h/2π.

For Brackett Series,
The shortest wavelength is for the transition of electrons from n_i = ∞ to n_f = 4

Using the equation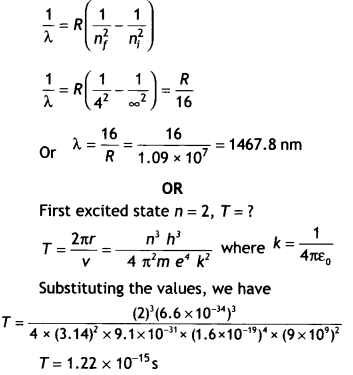

Question 28.
Write two important limitations of the Rutherford nuclear model of the atom. (CBSE AI2018, Delhi 2018)
Answer:

1. Rutherford’s model fails to explain the line spectra of the atom.
2. Rutherford’s model cannot explain the stability of the nucleus.

Question 29.
Find out the wavelength of the electron orbiting in the ground state of the hydrogen atom. (CBSEAI 2018, Delhi 2018)
Answer:
The wavelength of an electron in the ground state of hydrogen atom is given by
E = \(\frac{hc}{λ}\)
or
λ = \(\frac{hc}{E}\)

For ground state
E = – 13.6 eV = 13.6 × 1.6 × 10^-19 J

Hence wavelength of electron in the first orbit
λ = \(\frac{h c}{E}=\frac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{13.6 \times 1.6 \times 10^{-19}}\) = 0.9 × 10-7 J

Question 30.
(a) State Bohr’s postulate to define stable orbits in a hydrogen atom. How does de Broglie’s hypothesis explain the stability of these orbits?
Answer:
Bohr’s postulate for stable orbits states the electron in an atom revolves around the nucleus only in those orbits for which its angular momentum is an integral multiple of h/2π (h = Planck’s constant), (n = 1, 2, 3 …)

As per de Broglie’s hypothesis λ = h/p = h/mv
For a stable orbit, we must have a circumference of the orbit = nλ (n = 1, 2, 3,…)
∴ 2πr = nλ
or
mvr = nh/2π

Thus de-Broglie showed that the formation . of stationary patterns for integral “n” gives rise to the stability of the atom.
This is nothing but Bohr’s postulate.

(b) A hydrogen atom initially in the ground state absorbs a photon which excites it to the n = 4 level. Estimate the frequency of the photon.
Answer:
Energy in the n = 4 level n₁ = 1 and n₂ = 4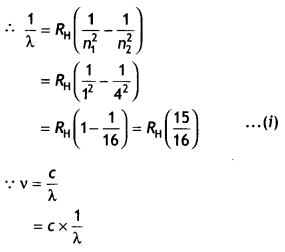


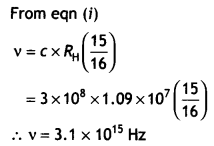
Question 31.
An alpha particle moving with initial kinetic energy K towards a nucleus of atomic number Z approaches a distance ‘d’ at which it reverses its direction. Obtain an expression for the distance of closest approach ‘d’ in terms of the kinetic energy of the alpha particle, K. (CBSEAI2016C)
Answer:
At the distance of the closest approach, the kinetic energy of the alpha particle is converted into the electrostatic potential energy of the alpha particle-nucleus system. Therefore, at the distance of the closest approach

we have
Kinetic energy = Potential energy
Therefore,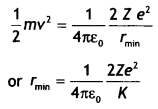

where K is the kinetic energy.

Question 32.
The figure shows the energy level diagram of the hydrogen atom.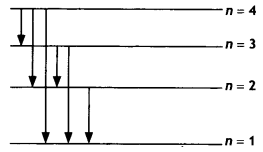

(a) Find out the transition which results in the emission of a photon of wavelength 496 nm.
Answer:
The wavelength of photon emitted is given by \(\frac{1}{λ}\) = R_H\(\left(\frac{1}{n_{\mathrm{f}}^{2}}-\frac{1}{n_{\mathrm{i}}^{2}}\right)\)

None of these transitions correspond to a wavelength of 496 nm. The closest is 4 to 2 of 489 nm

(b) Which transition corresponds to the emission of radiation of maximum wavelength? Justify your answer. (CBSE AI 2015 C)
Answer:
Transition 4 to 3 as the frequency of this radiation is maximum.

Question 33.
A nucleus makes a transition from one permitted energy level to another level of lower energy. Name the region of the electromagnetic spectrum to which the emitted photon belongs. What is the order of its energy in electron-volts? Write four characteristics of nuclear forces.
Answer:
(a) Emitted photon belongs to gamma-rays part of the electromagnetic spectrum.
(b) the energy is of the order of MeV.
(c) Four characteristics of nuclear forces are:

1. Nuclear forces are independent of charges.
2. Nuclear forces are short-range forces.
3. Nuclear forces are the strongest forces in nature, in their own small range of few fermis.
4. Nuclear forces are saturated forces.

Question 34.
The energy level diagram of an element is given. Identify, by doing necessary calculations, which transition corresponds to the emission of a spectral line of wavelength 102.7 nm. (Delhi 2008)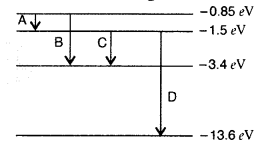

Answer: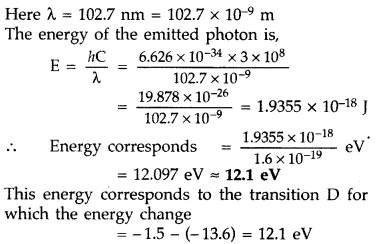

Question 35.
The ground state energy of hydrogen atom is -13.6 eV.
(i) What is the kinetic energy of an electron in the 2^nd excited state?
(ii) If the electron jumps to the ground state from the 2^nd excited state, calculate the wavelength of the spectral line emitted. (All India 2008)
Answer: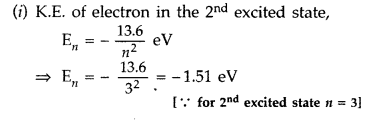

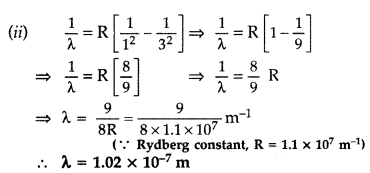
Question 36.
The ground state energy of hydrogen atom is -13.6 eV.
(i) What is the potential energy of an electron in the 3^rd excited state?
(ii) If the electron jumps to the ground state from the 3^rd excited state, calculate the wavelength of the photon emitted. (All India 2008)
Answer:

Question 37.
(a) The energy levels of an atom are as shown here. Which of them will result in the transition of a photon of wavelength 275 nm?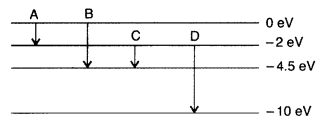

(b) Which transition corresponds to emission of radiation of maximum wavelength? (Delhi 2008)
Answer:

Question 38.
The energy levels of a hypothetical atom are shown below. Which of the shown transitions will result in the emission of a photon of wavelength 275 nm? Which of these transitions correspond to emission of radiation of
(i) maximum and
(ii) minimum wavelength ?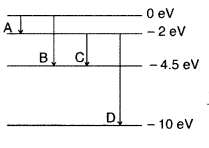

(Delhi 2011)
Answer: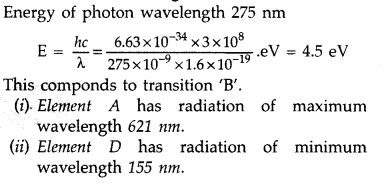

Question 39.
(a) Using Bohr’s second postulate of quantization of orbital angular momentum show that the circumference of the electron in the n,h orbital state in hydrogen atom is n times the de-Broglie wavelength associated with it.
(b) The electron in hydrogen atom is initially in the third excited state. What is the maximum number of spectral lines which can be emitted when it finally moves to the ground state? (Delhi 2012)
Answer:
(a) According to the de-Broglie hypothesis, this electron is also associated with wave character.
Hence a circular orbit can be taken to be a stationary energy state only if it contains an integral number of de- Broglie wavelengths i.e. we must have
2πr = nλ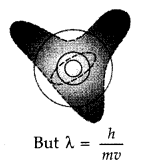

According to Bohr’s-second postulate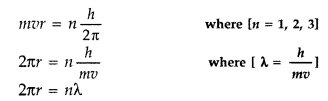

Hence the circumference of the electron in the n^th orbital state in hydrogen atom is n times the de-Broglie wavelength associated with it.

(b) For third excited state n = 4
For ground state n = 1
Hence, possible transitions are :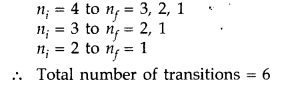

Question 40.
In a Geiger-Marsden experiment, calculate the distance of closest approach to the nucleus of Z = 80, when an α-particle of 8 MeV energy impinges on it before it comes momentarily to rest and reverses its direction.
How will the distance of closest approach be affected when the kinetic energy of the α-particle is doubled? (All India 2012)
Answer: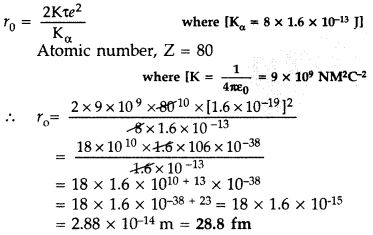

When kinetic energy of a-particle is doubled, then distance of closest approach becomes half

Question 41.
The ground state energy of hydrogen atom is -13.6 eV. If an electron makes a transition from an energy level -0.85 eV to -3.4 eV, calculate the wavelength of the spectral line emitted. To which series of hydrogen spectrum does this wavelength belong? (All India 2012)
Answer: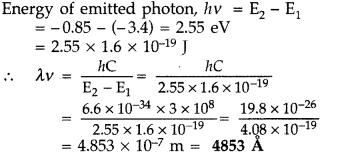

(ii) This wavelength belongs to Balmer series of hydrogen spectrum.

Question 42.
Using Bohr’s postulates, obtain the expression for the total energy of the electron in the stationary states of the hydrogen atom. Hence draw the energy level diagram showing how the line spectra corresponding to Balmer series occur due to transition between energy levels. (Delhi 2012)
Answer: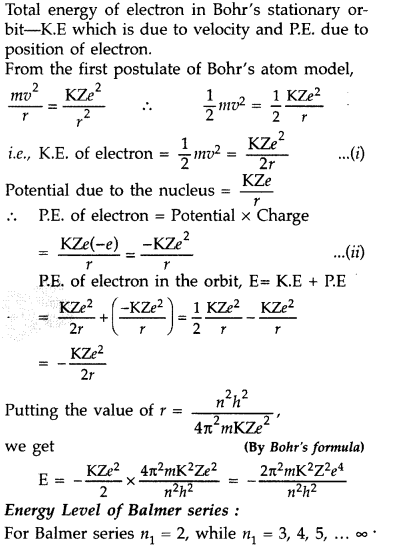

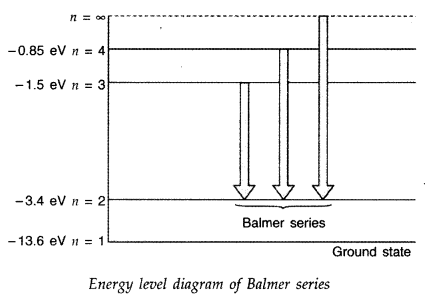
Question 43.
Using Bohr’s postulates, obtain the expressions for
(i) kinetic energy and
(ii) potential energy of the electron in stationary state of hydrogen atom. Draw the energy level diagram showing how the transitions between energy levels result in the appearance of Lyman Series. (Delhi 2012)
Answer:

Question 44.
In the ground state of hydrogen atom, its Bohr radius is given as 5.3 × 10^-11 m. The atom is excited such that the radius becomes 21.2 × 10^-11 m. Find
(i) the value of the principal quantum number and
(ii) the total energy of the atom in this excited state. (Comptt. Delhi 2012)
Answer: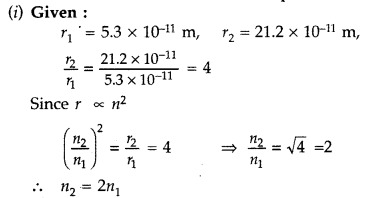

Therefore, Value of principal quantum number in this excited state is 2.
(ii) Energy of electron in ground state = -13.6 eV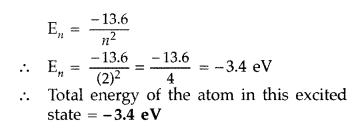

Question 45.
A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. Upto which energy level the hydrogen atoms would be excited? Calculate the wavelengths of the first member of Lyman and first member of Balmer series. (Delhi 2014)
Answer:

Hydrogen atom will be excited upto third energy level, because energy of electron is less than that of 4^th energy level.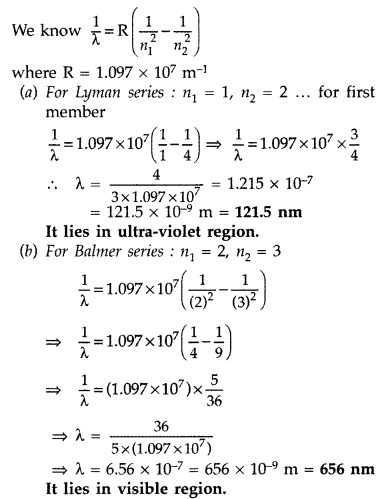

Question 46.
A 12.9 eV beam of electrons is used to bombard gaseous hydrogen at room temperature. Upto which energy level the hydrogen atoms would be excited?
Calculate the wavelength of the first member of Paschen series and first member of Balmer series. (Delhi 2014)
Answer:
1st part: Similar to Q. 46, Page 280
Wavelength of the first member of Paschen series: n₁ = 3, n₂ = 4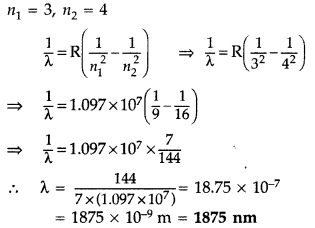

It lies in infra-red region.

Question 47.
A 12.3 eV electron beam is used to bombard gaseous hydrogen at room temperature. Upto which energy level the hydrogen atoms would be excited?
Calculate the wavelengths of the second member of Lyman series and second member of Balmer series. (Delhi 2014)
Answer:
1st part: Similar to Q. 46, Page 280
(i) Wavelength of second member of Lyman series : n₁ = 1, n₂ = 3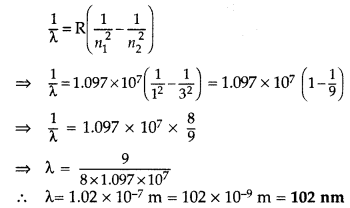

∴ It lies in ultra violet region.
(ii) Wavelength of second member of Balmer series (n₁ = 2, n₂ = 4)
It lies in visible region.

Question 48.
(a) The radius of the innermost electron orbit of a hydrogen atom is 5.3 × 10^-11 m. Calculate its radius in n = 3 orbit.
(b) The total energy of an electron in the first excited state of the hydrogen atom is -3.4 eV. Find out its
(i) kinetic energy and
(ii) potential energy in this state. (Comptt. Delhi 2014)
Answer: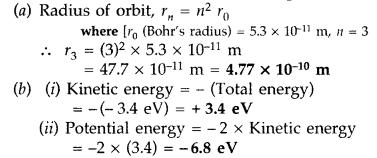

Question 49.
(a) The radius of the innermost electron orbit of a hydrogen atom is 5.3 × 10¹¹ m. Calculate its radius in n = 2 orbit.
(b) The total energy of an electron in the second excited state of the hydrogen atom is -1.51 eV. Find out its
(i) kinetic energy and
(ii) potential energy in this state. (Comptt. Delhi 2014)
Answer: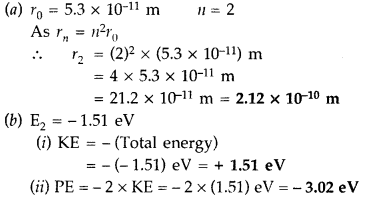

Question 50.
(a) The orbital radius of the electron in the first excited state of hydrogen atom is 21.2 × 10^-11 m. Find out its radius in the second excited state.
(b) The total energy of the electron in the ground state is -13.6 eV. Find out
(i) its. kinetic energy and
(ii) potential energy in the first excited state. (Comptt. Delhi 2014)
Answer: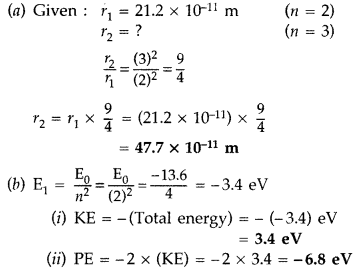

Question 51.
The value of a ground state energy of hydrogen atom is -13.6 eV.
(i) Find the energy required to move an electron from the ground state to the first excited state of the atom.
(ii) Determine
(a) the kinetic energy and
(b) orbital radius in the first excited state of the atom. (Given the value of Bohr radius = 0.53 Å) (Comptt. All India 2014)
Answer: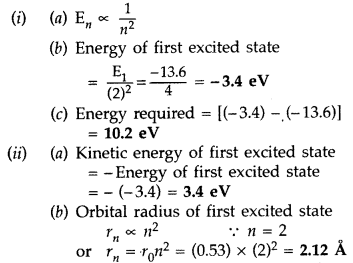

Question 52.
The value of ground state energy of hydogen atom is -13.6 eV and Bohr radius is 0.53Å. Calculate
(i) the energy required to move an electron from the ground state to the second excited state.
(ii) (a) the kinetic energy and
(b) the orbital radius in the second excited state of the atom. (Comptt. All India 2014)
Answer: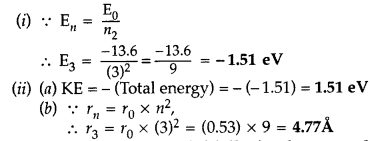

Question 53.
(i) A hydrogen atom initially in the ground state absorbs a photon which excites it to the n- 4 level. Determine the wavelength of the photon.
(ii) The radius of innermost electron orbit of a hydrogen atom is 5.3 × 10^-11m. Determine its radius in n = 4 orbit.(Comptt. All India 2014)
Answer: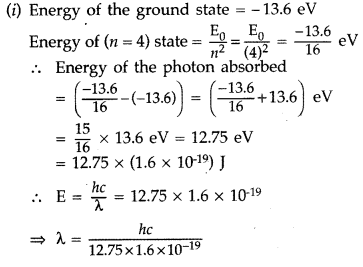

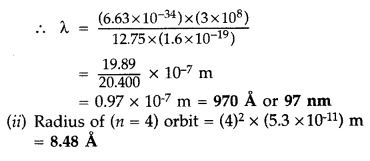
Question 54.
In the study of Geiger-Marsdon experiment on scattering of a particles by a thin foil of gold, draw the trajectory of a-particles in the coulomb field of target nucleus. Explain briefly how one gets the information on the size of the nucleus from this study.
From the relation, R = R₀ \(\mathbf{A}^{1 / 3}\), where R₀, is constant and A is the mass number of the nucleus, show that nuclear matter density is independent of A. (Delhi 2015)
Answer:
(i) Trajectory of α-particles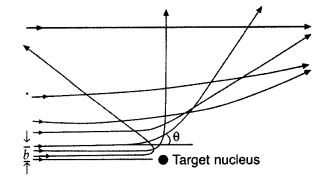

(ii) Size of nucleus : Only a small fraction of the incident a-particles rebound. This shows that the mass of the atom is concentrated in a small volume in the form of nucleus and gives an idea of the size of nucleus.

Question 55.
(i) State Bohr’s quantization condition for defining stationary orbits. How does de-Broglie hypothesis explain the stationary orbits?
(ii) Find the relation between the three wave-lengths λ₁, λ₂ and λ₃ from the energy level diagram shown below: (Delhi 2016)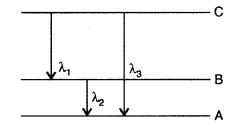

Answer:

Question 56.
Using Bohr’s postulates, derive the expression for the total energy of the electron revolving in n^th orbit of hydrogen atom. Find the wavelength of H line, given value of Ryderg constant, R = 1.1 × 10⁷m^-1.
Answer:
For total energy of the electron orbiting in n^th orbit :
Total energy of electron in Bohr’s stationary orbit K.E. which is due to velocity and P.E. due to position of electron
From the first postulate of Bohr’s atom modal

Long Answer Type

Question 1.
Explain Rutherford’s experiment on the scattering of alpha particles and state the significance of the results.
Answer:
The schematic arrangement in the Geiger Marsden experiment is shown in the figure.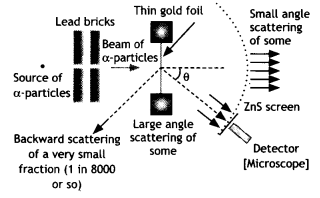

Alpha-particles emitted by a Bismuth (²¹⁴₈₃Bi) radioactive source were collimated into a narrow beam by their passage through lead bricks. The beam was allowed to fall on a thin foil of gold of thickness 2.1 × 10^-7 m. The scattered alpha-particles were observed through a rotatable detector consisting of a zinc sulfide screen and a microscope. The scattered alpha-particles on striking the screen produced bright light flashes or scintillations. These scintillations could be viewed through the microscope and counted at different angles from the direction of the incident beam.

Significance: The experiment established the existence of a nucleus that contained the entire positive charge and about 99.95% of the mass.

Question 2.
Using Bohr’s postulates, obtain the expression for the total energy of the electron in the stationary states of the hydrogen atom. Hence draw the energy level diagram showing how the line spectra corresponding to the Balmer series occur due to the transition between energy levels. (CBSE Delhi 2013)
Answer:
The electron revolving around the nucleus has two types of energy:

Kinetic energy due to its motion.
Potential energy due to it lying in the electric field of the nucleus.

Thus the total energy of the electron is given by
E = K. E. + P. E. …(1)

An electron of mass m moving around the nucleus with an orbital velocity v has kinetic energy given by
K.E. = \(\frac{1}{2}\)mv² = \(\frac{1}{2} \frac{k e^{2}}{r}\) …(2)

Now the potential energy of the electron at a distance r from the nucleus is given by
PE = potential due to the nucleus at a distance r × charge on the electron = V × – e …(3)

Now the potential at a distance r from the nucleus having a charge e is given by
V = k \(\frac{e}{r}\) …..(4)

Substituting in equation (3) we have
P.E. = V × – e = -k\(\frac{e^{2}}{r}\) …(5)

Substituting equations (2) and (3) in equation 1 we have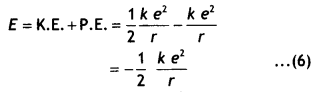

But the radius of the nth orbit is given by
r_n = \(\frac{n^{2} h^{2}}{4 \pi^{2} m e^{2} k}\)

Substituting in equation (6) we have
E = – \(\frac{2 \pi^{2} m e^{4} \mathrm{k}^{2}}{n^{2} \mathrm{~h}^{2}}\) …(7)

This gives the expression for the energy possessed by the electron in the nth orbit of the hydrogen atom.

Question 3.
Hydrogen atoms are excited with an electron beam of energy of 12.5 eV. Find
(a) The highest energy level up to which the hydrogen atoms will be excited.
Answer:
The maximum energy that the excited hydrogen atom can have is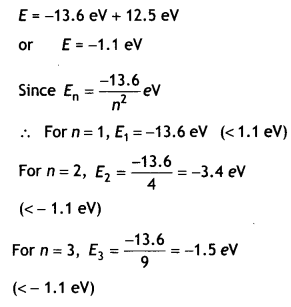

For n=4, E4 = \(\frac{-13.6}{16}\) = – 0.85eV
(> – 1.1 eV)

∴ The eLectron can only be excited up to n = 3 states.

(b) The longest wavelengths in the (i) Lyman series, (ii) Balmer series of the spectrum of these hydrogen atoms. (CBSE 2019C)
Answer:
From energy tevet of hydrogen atom,
we have
\(\frac{1}{λ}\) = R\(\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right]\)

Longest wavelength of Lyman senes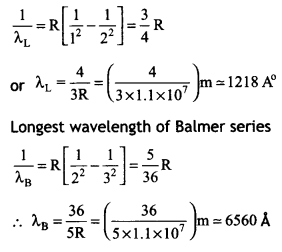

Question 4.
Using Bohr’s postulates of the atomic model derive the expression for the radius of the 11^th electron orbit. Hence obtain the expression for Bohr’s radius. (CBSE AI 2014)
Answer:
Let us consider a mechanical model of the hydrogen atom as shown in the figure that incorporates this quantization assumption.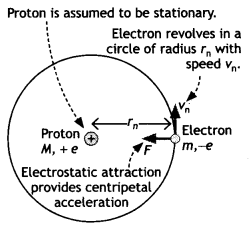

This atom consists of a single electron with mass m and charge – e revolving around a single proton of charge + e. The proton is nearly 2000 times as massive as the electron, so we can assume that the proton does not move. As the electron revolves around the nucleus the electrostatic force of attraction between the electron and the proton provides the necessary centripetal force. Therefore, we have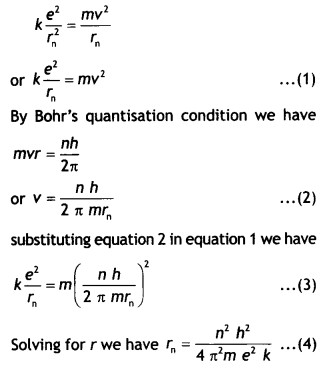

This gives the radius of the nth orbit of the hydrogen atom.
If n = 1 we have r = a_o which is called Bohr’s radius.
a_o = \(\frac{h^{2}}{4 \pi^{2} m e^{2} k}\)

Question 5.
Draw a schematic arrangement of the Geiger-Marsden experiment. How did the scattering of α-particles by a thin foil of gold provide an important way to determine an upper limit on the size of the nucleus? Explain briefly.
(All India 2009)
Answer: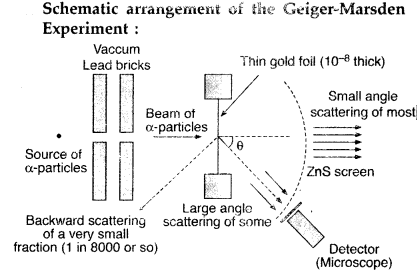

(i) Beam of α-particles get deviated at various angles with different probabilities.
(ii) α-particles with least impact parameter suffers larger scattering – rebounding on head on collision.
(iii) For larger impact parameter, the particle remains almost undeviated.

Explanation:
The fact that the number of incident particles rebounding back is only a small of fraction, means that numer of α-particles headon collision is small. This implies that the entire positive charge of the atom is concentrated in a small volume. This confirms that the nucleus of the atom has an apper size limit.

Question 6.
(a) Using Bohr’s theory of hydrogen atom, derive the expression for the total energy of the electron in the stationary states of the atom.
(b) If electron in the atom is replaced by a particle (muon) having the same charge but mass about 200 times as that of the electron to form a muonic atom, how would
(i) the radius and
(ii) the ground state energy of this be affected?
(c) Calculate the wavelength of the first spectral line in the corresponding Lyman series of this atom. (Comptt. Delhi 2012)
Answer:
(a) Total energy of electron in Bohr’s stationary orbit—K.E which is due to velocity and P.E. due to position of electron.
From the first postulate of Bohr’s atom model,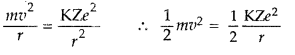

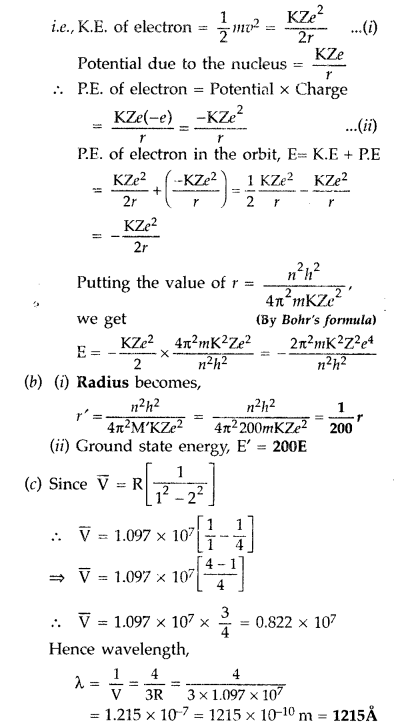
Question 7.
Using Bohr’s postulates, derive the expression for the frequency of radiation emitted when electron in hydrogen atom undergoes transition from higher energy state (quantum number n_i) to the lower state (n_f).
When electron in hydrogen atom jumps from energy state n_i = 4 to n_f = 3, 2, 1, identify the spectral series to which the emission lines belong. (All India 2013)
Answer:
When a hydrogen atom receives energy by process such as electron collisions of heat, the atom may acquire sufficient energy to raise the electron to higher energy states from n = 1 to n = 2, it is said to be in an excited state. When an electron falls back from excited state to lower energy state by emitting, there is a photon of particular energy and of particular frequency.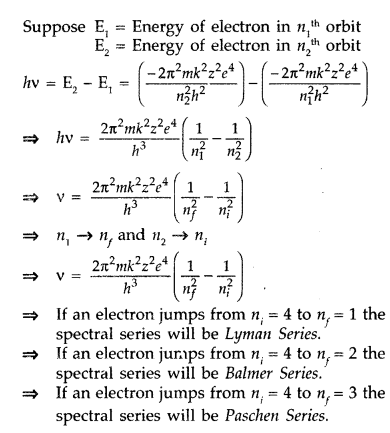

Question 8.
(a) Draw a schematic arrangement of Geiger- Marsden experiment showing the scattering of a-particles by a thin foil of gold. Why is it that most of the a-particles go right through the foil and only a small fraction gets scattered at large angles?
Draw the trajectory of the a-particle in the coulomb field of a nucleus. What is the significance of impact parameter and what information can be obtained regarding the size of the nucleus?
(b) Estimate the distance of closest approach to the nucleus (Z = 80) if a 7.7 MeV a-particle before it comes momentarily to rest and reverses its direction. (Comptt. Delhi 2015)
Answer:

(ii) For most of the α-particles, impact parameter is large, hence they suffer very small repulsion due to nucleus and go right through the foil.
(iii) Trajectory of α-particles

It gives an estimate of the size of nucleus, that it relatively very very small as compared to the size of atom.

(b) K.E. of the a-particle = Potential energy possessed by beam at distance of closest approach.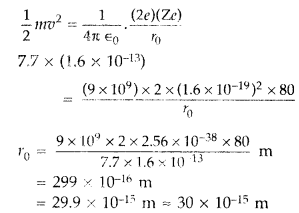

Question 9.
(a) Write two important limitations of Rutherford model which could not explain the observed features of atomic spectra. How were these explained in Bohr’s model. of hydrogen atom?
Use the Rydberg formula to calculate the wavelength of the H_α line.
(Take R = 1.1 × 10⁷ m^-1).
(b) Using Bohr’s postulates, obtain the expression for the radius of the n^th orbit in hydrogen atom. (Comptt. Delhi 2015)
Answer:
(a) Limitations of Rutherford Model :
(i) Electrons moving in a circular orbit around the nucleus would get, accelerated, therefore it would spiral into the nucleus, as it looses its energy.
(ii) It must emit a continuous spectrum.

Explanation according to Bohr’s model of hydrogen atom :

(i) Electron in an atom can revolve in certain stable orbits without the emission of radiant energy.
(ii) Energy is released/absorbed only, when an electron jumps from one stable orbit to another stable orbit. This results in a discrete spectrum.

Wavelength of H_α line :
H_α line is formed when an electron jumps from n_f = 3 to n_i = 2 orbit. It is the Balmer series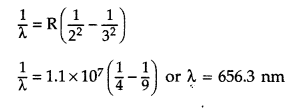

(b) Radius of n^th orbit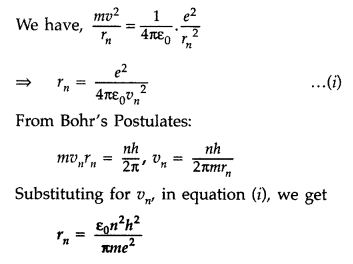

Question 10.
State Bohr’s postulate of the hydrogen atom successfully explains the emission lines in the spectrum of the hydrogen atoms.
Use the Rydberg formula to determine the wavelength of Ha line. [Given Rydberg constant R = 1.03 × 10⁷ m^-1] (CBSE AI 2015)
Answer:
It states that an electron might make a transition from one of its specified non¬radiating orbits to another of lower energy. When it does so, a photon is emitted having energy equal to the energy difference between the initial and final states. The frequency of the emitted photon is then given by

hv = E_i – E_f where E_i and E_f are the energies of the initial and final states
Using the formula \(\frac{1}{λ}\) = R_H\(\left(\frac{1}{n_{f}^{2}}-\frac{1}{n_{i}^{2}}\right)\) we have for Ha Line n_i = 3 and n_f = 2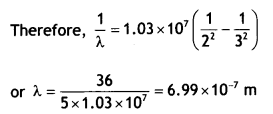

Question 11.
Using Bohr’s postulates derive the expression for the frequency of radiation emitted when an electron In a hydrogen atom undergoes a transition from a higher energy state (quantum number n-) to the towering state (n,). When an electron in a hydrogen atom jumps from the energy state n_i =4 to n = 3, 2, 1, identify the spectral series to which the emission lines belong. (CBSE Delhi 201 1C)
Answer:
According to Bohr’s frequency condition, if an electron jumps from an energy Level E to E₁, then the frequency of the emitted radiation is given by
hv = E – E₁ …(1)

Let ni and nf be the corresponding orbits then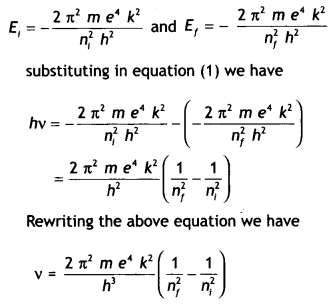

This gives the frequency of the emitted radiation.
When n_i =4 and n_f = 3, Paschen series
When n_i = 4 and n_f = 2, Balmer series
When n_i = 4 and n_f = 1, Lyman senes

Question 12.
Calculate the ratio of the frequencies of the radiation emitted due to the transition of the electron In a hydrogen atom from Its (i) second permitted energy level to the first level and (ii) highest permitted energy level to the second permitted level. (CBSE Delhi 2018C)
Answer:
We have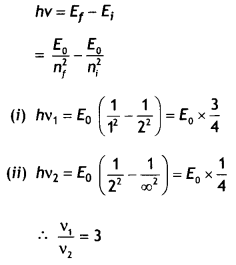

Question 13.
Monochromatic radiation of wavelength 975 A excites the hydrogen atom from its ground state to a higher state. How many different spectral lines are possible In the resulting spectrum? Which transition corresponds to the longest wavelength amongst them? (CBSE Sample Paper 201819)
Answer:
The energy corresponding to the given wavelength: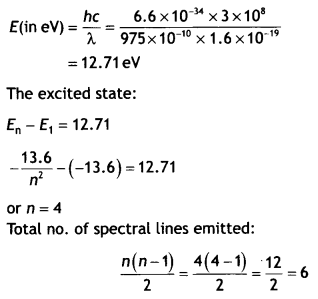

The longest wavelength Will correspond to the transition n = 4 to n = 3

Question 14.
(a) Using postulates of Bohr’s theory of hydrogen atom, show that
(i) the radii of orbits increases as n², and
Answer:
Let us consider a mechanical. model of the hydrogen atom as shown in the figure.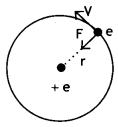

This atom consists of a single electron with mass m and charge – e revolving around a single proton of charge + e. As the electron revolves around the nucleus the electrostatic force of attraction between the electron and the proton provides the necessary centripetal force. Therefore we have,

Substituting equation 3 in equation 2 we have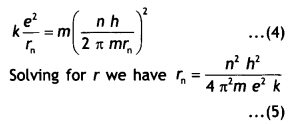

This gives the radius of the n^th orbit of the hydrogen atom which shows that E ∝ \(\frac{1}{n^{2}}\)

(ii) the total energy of the electron increases as 1/n², where n is the principal quantum number of the atom.
Answer:
the total energy possessed by an electron in the nth orbit of the hydrogen atom is given by
E = T + U …(1)
i.e. the sum of its kinetic and electrostatic potential energies.

An electron of mass m moving around the nucleus with an orbital velocity v has kinetic energy given by
K.E. = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\frac{k e^{2}}{r}\) ….(2)

Now the potential energy of the electron at a distance r from the nucleus is given by
PE = potential due to the nucleus at a distance r × charge on the electron
= V × – e …(3)

Now the potential at a distance r from the nucleus having a charge e is given by
V = k\(\frac{e}{r}\) ….(4)

Substituting in equation 2 we have
P.E. = V × – e = – k \(\frac{e^{2}}{r}\) …(5)

Substituting equations 2 and 5 in equation 1 we have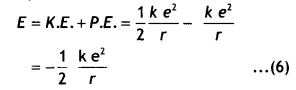

But the radius of the nth orbit is given by r_n = \(\frac{n^{2} h^{2}}{4 \pi^{2} m e^{2} k}\)

Substituting in equation 6 we have
E = – \(\frac{2 \pi^{2} m e^{4} k^{2}}{n^{2} h^{2}}\) …(7)

This gives the expression for the energy possessed by the eLectron in the nth orbit of the hydrogen atom which shows that E ∝ \(\frac{1}{n^{2}}\)

(b) Calculate the wavelength of H2 line In Balmer series of hydrogen atom, given Rydberg constant R = 1.097 × 10⁷ m^-1. (CBSE AI 2011C)
Answer:
For H₂ Line in Balmer series n₁ = 2 and n₂ = 3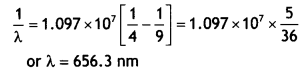

Question 15.
State Bohr’s quantization condition for defining stationary orbits. How does de Brogue hypothesis explain the stationary orbits?
Find the relation between the three wavelengths λ1 λ2 and λ3 from the energy level diagram shown below. (CBSE Delhi 2016)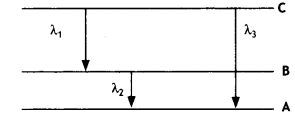

Answer:
It states that only those orbits are permitted in which the angular momentum of the electron about the nucleus is an integral multiple of \(\frac{h}{2π}\), where his Planck’s constant.

According to de Broglie, an electron of mass m moving with speed v would have a wavelength λ given by
λ = h/mv.

Now according to Bohr’s postulate,
mvr_n = \(\frac{n h}{2 \pi}\)
or
2πr_n = \(\frac{nh}{mv}\)

But h / mv = A is the de BrogUe wavelength of the electron, therefore, the above equation becomes 2πr_n = nλ where 2πr_n is the circumference of the permitted orbit. If the wavelength of a wave does not close upon itself, destructive interference takes place as the wave travels around the loop and quickly dies out. Thus only waves that persist are those for which the circumference of the circular orbit contains a whole number of wavelengths.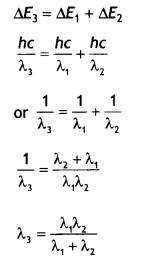

Numerical Problem :

Formulae for solving numerical problems

• Distance of closest approach r_o = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{2 z E^{2}}{E_{k}}\)
• Radius of the nth orbit of hydrogen atom rn = \(\frac{n^{2} h^{2}}{4 \pi^{2} m e^{2} k}\)
• Velocity of eLectron in the ntt orbit v = \(v=\frac{c}{137 n}\)
• Wavelength of radiation emitted when electron jumps form ni to nf \(\frac{1}{\lambda}=R_{\mathrm{H}}\left(\frac{1}{n_{\mathrm{f}}^{2}}-\frac{1}{n_{\mathrm{i}}^{2}}\right)\)
• Energy of electron in the nth orbit of hydrogen atom
  E = – \(\frac{2 \pi^{2} m e^{4} k^{2}}{n^{2} h^{2}}\)
  or
  E = – \(\frac{13.6}{n^{2}}\) eV

Question 1.
A hydrogen atom in its excited state emits radiations of wavelengths 1218 Å and 974.3 Å when it finally comes to the ground state. Identify the energy levels from where transitions occur. Given Rydberg constant R = 1.1 × 10⁷ m^-1. Also, specify the spectral series to which these lines belong. (CBSE AI 2019)
Answer:
We know that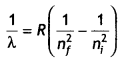


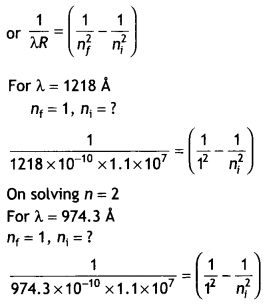
On solving n = 4
Lyman series.

Question 2.
Obtain the first Bohr’s radius and the ground state energy of a muonic hydrogen atom, i.e. an atom where the electron is replaced by a negatively charged muon (μ^–) of mass about 207 me that orbits around a proton. (Given for hydrogen atom, the radius of first orbit and ground state energy are 0.53 × 10^-10m and – 13.6 eV respectively) (CBSE AI 2019)
Answer:
In Bohr’s model of hydrogen atom the radius of n^th orbit is given by
r_n = \(\frac{n^{2} h^{2}}{4 \pi^{2} e^{2} m_{e} k}\)

As n = 1
Therefore, we have 1

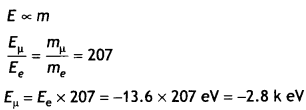
Question 3.
The electron in a given Bohr orbit has a total energy of – 1.5 eV. Calculate Its
(a) kinetic energy.
(b) potential energy.
(C) the wavelength of radiation emitted, when this electron makes a transition to the ground state.
(Given Energy in the ground state = – 13.6 eV and Rydberg’s constant = 1.09 × 1o⁷ m^-1) (CBSE Delhi 2011C)
Answer:
Total energy of the electron In a Bohr’s orbit is – 1.5 eV

We know that kinetic energy of the electron in any orbt is half of the potential energy in magnitude and potential energy is negative
(a) Total energy = kinetic energy + potential energy
– 1.5 = E_k – 2E_k
1.5 = E_k

(b) E_p = – 2 × 1.5 = – 3 eV

(c) Energy released when the transition of this electron takes place from this orbit to the ground state
= – 1.5 – (- 13.6)
= 12.1 eV
= 12.1 × 1.6 × 10¹⁹ = 1.936 × 10^-18 J

Let be the wavelength of the Light emitted then,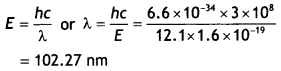

Question 4.
In a Geiger—Marsden experiment, calculate the distance of closest approach to the nucleus of Z = 80, when an a-particle of 8 MeV energy Impinges on it before It comes momentarily to rest and reverses its direction. How will the distance of the closest approach be affected when the kinetic energy of the a-particle is doubled? (CBSEAI 2012)
Answer:
Given Z = 80, E = 8 MeV = 8 × 10⁶ × 1.6 × 10¹⁹ J, r_o =?
Using the expression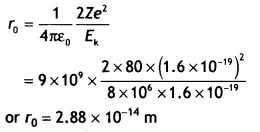

When the kinetic energy of a-particle has doubled the distance of the closest approach becomes half its previous value, i.e. 1.44 × 10¹⁴ m

Question 5.
The ground state energy of the hydrogen atom is – 13.6 eV. If an electron makes a transition from an energy level – 0.85 eV to – 3.4 eV, calculate the wavelength of the spectral line emitted. To which series of hydrogen spectrum does this wavelength belong? (CBSE AI 2012)
Answer:
Energy released = – 0.85 – (- 3.4) = 2.55 eV = 2.55 × 1.6 × 10^-19 J
Using E = hc/λ we have
λ = \(\frac{h c}{E}=\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{2.55 \times 1.6 \times 10^{-19}}\) = 4.87 × 10^-7 m

It belongs to the Balmer series.

Question 6.
A hydrogen atom in the third excited state de-excites to the first excited state. Obtain the expressions for the frequency of radiation emitted in this process.
Also, determine the ratio of the wavelengths of the emitted radiations when the atom de-excites from the third excited state to the second excited state and from the third excited state to the first excited state. (CBSEAI2019)
Answer:
We know that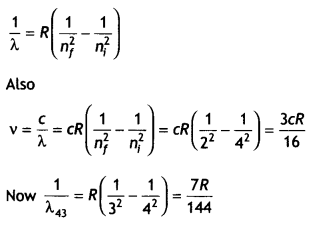


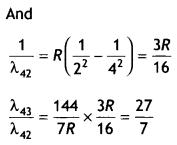
Question 7.
Obtain the expression for the ratio of the de Broglie wavelengths associated with the electron orbiting in the second and third excited states of the hydrogen atom. (CBSE Delhi 2019)
Answer:
We know that
2πr = nλ ….(i)
For the second excited state (n = 3)
r = 0.529(n)² A = 0.529(3)²

Putting in (i) we get 2π(0.529)(3)² = 3 λ₂

For third excited state n = 4
r = 0.529 (4)²
Putting in (i) we get 2π (0.529)(4)² = 4 λ₃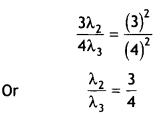

Question 8.
(a) The radius of the innermost electron orbit of a hydrogen atom is 5.3 × 10^-10 m. Calculate its radius in n = 3 orbit.
(b) The total energy of an electron in the first excited state of the hydrogen atom is 3.4 eV. Find out its (i) kinetic energy and (ii) potential energy in this state. (CBSE Delhi 2014C)
Answer:
(a) The radius is given by
r_n = \(\frac{n^{2} h^{2}}{4 \pi^{2} m e^{2} k}\) = n²ao

where n is the number of orbit, hence r3 = 5.3 × 10^-10 × 32 = 4.77 × 10^-9 m

(b) Total kinetic energy = + 3.4 eV
Total potential energy = – 6.8 eV

Question 9.
Given the ground state energy E0 = – 13.6 eV and Bohr radius a0 = 0.53 Å. Find out how the de Broglie wavelength associated with the electron orbiting in the ground state would change when it jumps into the first excited state.
Answer:
The de-Broglie wavelength is given by 2πrn = nλ.
In ground state, n = 1 and r_o = 0.53 Å, therefore, λ_o = 2 × 3.14 × 0.53 = 3.33 Å

In first excited state, n = 2 and r₁ = 4 × 0.53 Å = 2.12 Å, therefore,
r₁ = (2 × 3.14 × 2.12)/2 = 6.66Å

Therefore, λ₁ – λ_o = 6.66 – 3.33 = 3.33 Å.
In other words, the de-Broglie wavelength becomes double.

Question 10.
When is the H_α line in the emission spectrum of hydrogen atom obtained? Calculate the frequency of the photon emitted during this transition. (CBSE AI 2016)
Answer:
Hα is obtained when n_i = 3 and n_f = 2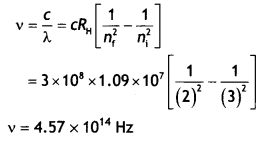

Question 11.
A 12.5 eV beam is used to excite a gaseous hydrogen atom at room temperature. Determine the wavelength and the corresponding series of lines emitted. (CBSE AI 2017)
Answer:
Given the energy of electron beam E = 12.5 eV
This will make the energy of the electrons 12.5 – 13.6 = – 1.1 eV.
Thus, the electrons of hydrogen will be raised to the third orbit.
Lines emitted will be n_i = 3, n_f = 2 Balmer series.

The wavelength is given by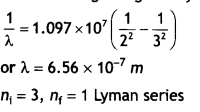

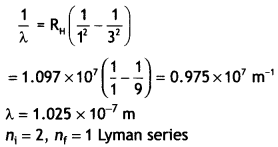
For first member n_i = 2, therefore, the wavelength of the first member of the Lyman series.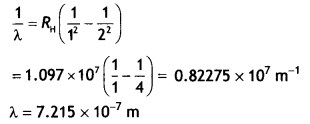

Question 12.
Calculate the longest wavelength of the photons emitted in the Balmer series of the hydrogen spectrum. Which part of the e.m. spectrum does it belong to? [Given Rydberg constant, R = 1.1 × 10⁷ m^-1 J] (CBSE Delhi 2017C)
Answer:
The longest wavelength is obtained when the electron jumps from n_i = 3 to n_f = 2 in the Balmer series. Therefore we have,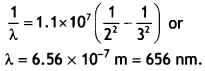

It lies in the visible region.

Question 13.
10 kg satellite circles earth once every 2 h in an orbit having a radius of 8000 km. ‘ Assuming that Bohr’s angular momentum postulate applies to satellites just as it does to an electron in the hydrogen atom, find the quantum number of the orbit of the satellite. (NCERT Exemplar)
Answer:
From Bohr’s postulate, we have mv_n r_n = nh/2π
Here m = 10 kg and r_n = 8 × 10⁶ m

We have the time period T of the circling satellite as 2 h.
That is T = 7200 s
Thus the velocity v_n = 2πr_n/T

The quantum number of the orbit of the satellite
N = (2πr)² × m/(T × h).

Substituting the values,
n = (2π × 8 × 106 )² × 10/(7200 × 6.64 × 10^-34)
= 5.3 × 1045

Note that the quantum number for the satellite motion is extremely large. In fact, for such large quantum numbers, the results of quantization conditions tend to those of classical physics.

Question 14.
Consider two different hydrogen atoms. The electron in each atom is in an excited state. Is it possible for the electrons to have different energies but the same orbital angular momentum according to the Bohr model?
Answer:
No, because according to the Bohr model, E = – 13.6 /n² eV and electrons having different energies belong to different levels having different values of n.

So, their angular momenta will be different, as nh/2π = mvr

Question 15.
Using the Bohr model, calculate the electric current created by the electron when the H-atom is in the ground state. (NCEFU Exemplar)
Answer:
Let v be the velocity of the electron in the ground state. Let a0 be the Bohr radius.
Now time is taken to complete one revolution

Question 16.
What is the minimum energy that must be given to an H atom in the ground state so that it can emit a H_y line in the Balmer series? If the angular momentum of the system is conserved, what would be the angular momentum of such H_y photon? (NCERJ Exemplar)
Answer:
The H_y in Balmer series corresponds to transition n = 5 to n = 2. So, the electron in ground state n = 1 must first be put in state n = 5.

Hence energy required for the same.
Energy required = E₁ – E₅ = 13.6 – 0.54 = 13.06 eV.

If angular momentum is conserved, angular momentum of photon = change in angular momentum of electron = L₅ – L₂ = 5h – 2h = 3h = 3 × 1.06 × 10^-34 = 3.18 × 10^-34 kg m² s^-1