Chapter 1 The Solid State

Here’s a detailed and long-format set of HOTS questions and answers for CBSE Class 12 Chemistry Chapter 1: The Solid State. Each answer is explained in depth, incorporating theoretical concepts, analytical thinking, and numerical applications.

---

1. Explain the various types of crystal systems and their characteristics. Derive the relationship between the unit cell parameters for cubic and tetragonal systems.

Answer:
Crystals are classified into seven crystal systems based on their unit cell dimensions and interaxial angles. These systems include:

1. Cubic:

   • Axial lengths: $a = b = c$
   • Axial angles: $\alpha = \beta = \gamma = 90^\circ$

2. Tetragonal:

   • Axial lengths: $a = b \neq c$
   • Axial angles: $\alpha = \beta = \gamma = 90^\circ$

3. Orthorhombic:

   • Axial lengths: $a \neq b \neq c$
   • Axial angles: $\alpha = \beta = \gamma = 90^\circ$

4. Hexagonal:

   • Axial lengths: $a = b \neq c$
   • Axial angles: $\alpha = \beta = 90^\circ, \gamma = 120^\circ$

5. Monoclinic:

   • Axial lengths: $a \neq b \neq c$
   • Axial angles: $\alpha = \gamma = 90^\circ, \beta \neq 90^\circ$

6. Triclinic:

   • Axial lengths: $a \neq b \neq c$
   • Axial angles: $\alpha \neq \beta \neq \gamma \neq 90^\circ$

7. Rhombohedral:

   • Axial lengths: $a = b = c$
   • Axial angles: $\alpha = \beta = \gamma \neq 90^\circ$

Relationship for Cubic System:

In the cubic system, the edge length $a$ is directly related to the atomic radius $r$ . For different arrangements:

• Simple Cubic (SC): $a = 2r$ .
• Body-Centered Cubic (BCC): $a = \frac{4r}{\sqrt{3}}$ .
• Face-Centered Cubic (FCC): $a = 2\sqrt{2}r$ .

Relationship for Tetragonal System:

In tetragonal systems, the volume of the unit cell is $V = a^2c$ , where $a$ is the edge length of the square base, and $c$ is the height.

• Example: In a tetragonal crystal with $a = 4 \, \text{Å}$ and $c = 6 \, \text{Å}$ , $V = 4^2 \times 6 = 96 \, \text{Å}^3$ .

---

2. Discuss the concept of voids in crystal structures. How are tetrahedral and octahedral voids formed, and why are they significant in ionic solids?

Answer:
Voids are empty spaces between atoms in a close-packed structure. In an ideal close packing, atoms occupy about $74\%$ of the space, leaving $26\%$ voids. Voids are categorized as:

1. Tetrahedral Voids:
   Formed when a triangular base of atoms in one layer is capped by one atom from the adjacent layer.

   • Radius ratio ($r/R$ ) for fitting: $0.225 - 0.414$ .

2. Octahedral Voids:
   Formed by two interpenetrating triangular planes, one inverted relative to the other.

   • Radius ratio ($r/R$ ) for fitting: $0.414 - 0.732$ .

Significance:

• Ionic solids: Smaller cations occupy tetrahedral voids, and larger cations occupy octahedral voids.
• Example: In NaCl, Cl$^-$ ions form FCC lattice, and Na$^+$ ions occupy octahedral voids.

Numerical Example:

Calculate the number of octahedral voids in FCC lattice of NaCl.

• In FCC, there are $4$ atoms per unit cell.
• Number of octahedral voids = $1$ per atom = $4$ .
  Thus, $4$ Na$^+$ ions occupy octahedral voids.

---

3. Derive the expression for the density of a unit cell and calculate the density of iron given that it crystallizes in a BCC lattice with an edge length of $286 \, \text{pm}$ and atomic mass of $56 \, \text{g/mol}$ .

Answer:
The density $(\rho)$ of a unit cell is given by:

$$\rho = \frac{Z \cdot M}{a^3 \cdot N_A}$$

Where:

• $Z$ = Number of atoms per unit cell.
• $M$ = Molar mass of the element.
• $a$ = Edge length of the unit cell in cm.
• $N_A$ = Avogadro's number ($6.022 \times 10^{23} \, \text{mol}^{-1}$ ).

For BCC lattice: $Z = 2$ .

Substituting values:

$$a = 286 \, \text{pm} = 286 \times 10^{-10} \, \text{cm}$$ $$\rho = \frac{2 \cdot 56}{(286 \times 10^{-10})^3 \cdot 6.022 \times 10^{23}}$$

Calculation yields:

$$\rho \approx 7.86 \, \text{g/cm}^3$$

---

4. What are Schottky and Frenkel defects? Derive the expression for the number of Schottky defects in a solid at a given temperature.

Answer:
Schottky Defect:
Occurs when equal numbers of cations and anions are missing from the lattice.

• Results in a decrease in density.
• Common in ionic solids with high coordination numbers (e.g., NaCl).

Frenkel Defect:
Occurs when a smaller ion (usually a cation) is displaced from its lattice site to an interstitial site.

• Does not affect density.
• Common in solids with low coordination numbers (e.g., ZnS).

Expression for Schottky Defects:

Let $n_s$ be the number of Schottky defects.

$$\Delta G = \Delta H - T \Delta S$$

At equilibrium, $n_s = N \exp{\left(\frac{-\Delta H}{2RT}\right)}$ ,
where:

• $N$ = Total number of lattice sites.
• $\Delta H$ = Enthalpy for defect formation.
• $T$ = Temperature in Kelvin.
• $R$ = Gas constant.

---

5. Explain band theory of solids. Why do conductors, insulators, and semiconductors have different electrical properties? Provide examples.

Answer:
Band Theory:

• In solids, atomic orbitals overlap to form energy bands.
• Two important bands:
  1. Valence Band: Occupied by valence electrons.
  2. Conduction Band: Higher energy band where electrons move freely.

Key Differences:

1. Conductors (e.g., Cu, Ag):

   • Valence and conduction bands overlap.
   • Electrons flow freely, enabling high conductivity.

2. Insulators (e.g., Diamond):

   • Large energy gap ($> 3 \, \text{eV}$ ) between bands.
   • Electrons cannot move, resulting in no conductivity.

3. Semiconductors (e.g., Si, Ge):

   • Small energy gap ($0.1 - 2 \, \text{eV}$ ).
   • Conductivity increases with temperature or doping.

Doping with phosphorus creates an n-type semiconductor, while doping with boron creates a p-type semiconductor.

6. Explain how X-ray diffraction is used to determine the structure of a crystal. Derive Bragg’s equation.

Answer:
X-ray diffraction helps in determining the arrangement of atoms in a crystal by analyzing the pattern of X-rays scattered by the crystal.

Principle:
When X-rays strike the crystal planes, they are scattered. Constructive interference occurs when the path difference between rays reflected from successive planes is an integral multiple of the wavelength ($\lambda$ ).

Derivation of Bragg’s Equation:
Consider parallel planes in a crystal separated by distance $d$ :

• Path difference = $2d\sin\theta$ , where $\theta$ is the angle of incidence.
• For constructive interference:

$$2d\sin\theta = n\lambda \quad \text{(Bragg’s equation)}$$

where $n$ is the order of reflection.

Application:

• Bragg’s equation is used to calculate interplanar spacing $d$ and analyze crystal structures.

Numerical Example:

If a beam of X-rays of wavelength $1.54 \, \text{Å}$ is diffracted at an angle $20^\circ$ , calculate the interplanar spacing.

$$2d\sin\theta = n\lambda \quad \text{(for } n = 1\text{)}$$ $$d = \frac{\lambda}{2\sin\theta} = \frac{1.54}{2 \times \sin(20^\circ)} \approx 2.25 \, \text{Å}.$$

---

7. What is anisotropy? How does it arise in crystalline solids? Give examples of its importance in real-world applications.

Answer:
Anisotropy refers to the directional dependence of properties in a crystalline solid. Properties like electrical conductivity, refractive index, and thermal expansion vary with direction due to the ordered arrangement of atoms.

Cause:

• Crystals have different atomic densities along different directions, causing varying interactions with external fields or forces.

Examples:

1. Electrical Conductivity: Graphite is more conductive along its planes than perpendicular to them.
2. Optics: Calcite shows double refraction due to its anisotropic nature.

Applications:

• Technology: Liquid crystal displays (LCDs) rely on anisotropic optical properties.
• Industry: Diamond cutting depends on its anisotropic hardness.

---

8. A compound forms a hexagonal close-packed (hcp) lattice. Calculate the number of atoms in a unit cell and the packing efficiency of the structure.

Answer:
In an hcp lattice:

• Unit Cell Composition:

  • Contribution from 12 corner atoms: $\frac{1}{6} \times 12 = 2$ .
  • Contribution from 2 atoms on each face: $2$ .
  • Total = $4$ atoms per unit cell.

• Packing Efficiency:
  Volume occupied by atoms in the unit cell:

$$\text{Volume occupied} = 4 \times \frac{4}{3} \pi r^3 = \frac{16}{3} \pi r^3.$$

Volume of the unit cell:

$$\text{Volume of cell} = 6 \times \frac{\sqrt{2}}{3} a^3 \quad (\text{where } a = 2r).$$

Efficiency:

$$\text{Packing efficiency} = \frac{\text{Volume occupied}}{\text{Volume of cell}} \times 100 \approx 74\%.$$

---

9. Explain the differences between metallic, ionic, and covalent solids with examples. Why do covalent solids like diamond have high melting points?

Answer:

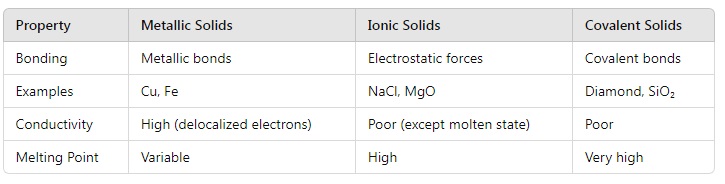
Explanation for Diamond:

• Diamond has a 3D network of strong covalent bonds. Breaking these bonds requires a lot of energy, leading to its exceptionally high melting point.

---

10. Differentiate between primitive and non-primitive unit cells. Discuss their significance in crystallography.

Answer:
Primitive Unit Cell:

• Atoms are present only at the corners.
• Simplest form of a unit cell.
• Example: Simple cubic lattice.

Non-Primitive Unit Cell:

• Atoms are present at corners and other positions (face, body, edge).
• Complex but accurately represents crystal symmetry.
• Examples: FCC, BCC.

Significance:

Non-primitive unit cells are crucial for understanding high packing efficiency and stability in crystals like NaCl (FCC).

---

11. Sodium crystallizes in a BCC lattice with an edge length of $429 \, \text{pm}$ . Calculate its atomic radius and density.

Answer:
Atomic Radius for BCC:

$$a = \frac{4r}{\sqrt{3}} \implies r = \frac{\sqrt{3} \cdot a}{4}.$$

Substitute $a = 429 \, \text{pm}$ :

$$r = \frac{\sqrt{3} \cdot 429}{4} \approx 186 \, \text{pm}.$$

Density Calculation:

$$\rho = \frac{Z \cdot M}{a^3 \cdot N_A}.$$

For BCC: $Z = 2$ .
Substitute $M = 23 \, \text{g/mol}, a = 429 \times 10^{-10} \, \text{cm}, N_A = 6.022 \times 10^{23}$ :

$$\rho = \frac{2 \cdot 23}{(429 \times 10^{-10})^3 \cdot 6.022 \times 10^{23}} \approx 0.97 \, \text{g/cm}^3.$$

---

12. Explain the relationship between ionic radius and coordination number in ionic solids. Why does CsCl have a higher coordination number than NaCl?

Answer:
Relationship:

• Larger cations can accommodate more anions around them, increasing the coordination number.
• Radius ratio ($r_c/r_a$ ) determines stability.

CsCl vs. NaCl:

• CsCl: Radius ratio is $0.93$ , allowing 8:8 coordination.
• NaCl: Radius ratio is $0.52$ , leading to 6:6 coordination.

---

13. Calculate the number of atoms per unit cell in an FCC lattice. Derive the packing efficiency.

Answer:
Number of Atoms:

• $8$ corner atoms: $8 \times \frac{1}{8} = 1$ .
• $6$ face atoms: $6 \times \frac{1}{2} = 3$ .
• Total: $4$ atoms.

Packing Efficiency:

$$\text{Volume occupied} = 4 \times \frac{4}{3} \pi r^3, \quad \text{Volume of cube} = a^3 = (2\sqrt{2}r)^3.$$ $$\text{Efficiency} = \frac{\text{Volume occupied}}{\text{Volume of cube}} \times 100 \approx 74\%.$$

 

14. Discuss the defects in solids with examples. Why do defects play an important role in materials science?

Answer:
Defects in solids are irregularities in the ideal arrangement of constituent particles. These are categorized as:

(a) Point Defects:

• Vacancy Defect: Atoms missing from lattice points. Example: Alkali halides.
• Interstitial Defect: Extra atoms occupy interstitial positions. Example: Steel (C atoms in Fe).
• Substitutional Defect: Foreign atoms replace host atoms. Example: Brass (Zn replacing Cu).

(b) Line Defects:

• Irregularities along rows of atoms, such as dislocations.

Importance of Defects:

1. Conductivity: Intrinsic defects increase carrier concentration in semiconductors.
2. Strength: Line defects strengthen alloys (e.g., steel).
3. Catalysis: Defect sites increase catalytic activity.

---

15. Calculate the density of a crystal given its edge length and molecular mass. Example: NaCl has $a = 564 \, \text{pm}$ , $M = 58.5 \, \text{g/mol}$ , FCC structure.

Answer:
Formula for density:

$$\rho = \frac{Z \cdot M}{a^3 \cdot N_A}.$$

Substitute values:

• $Z = 4$ (FCC), $a = 564 \times 10^{-10} \, \text{cm}$ , $M = 58.5 \, \text{g/mol}$ , $N_A = 6.022 \times 10^{23}$ :

$$\rho = \frac{4 \cdot 58.5}{(564 \times 10^{-10})^3 \cdot 6.022 \times 10^{23}} \approx 2.165 \, \text{g/cm}^3.$$

---

16. Why does Frenkel defect occur in ionic solids? Give examples. How does it differ from Schottky defect?

Answer:
Frenkel Defect:

• Occurs when smaller ions (usually cations) leave their lattice positions and occupy interstitial sites.
• Common in solids with a large size difference between cations and anions, e.g., AgCl, ZnS.

Schottky Defect:

• Equal numbers of cations and anions are missing, reducing the density. Example: NaCl, KCl.

Key Differences:

---

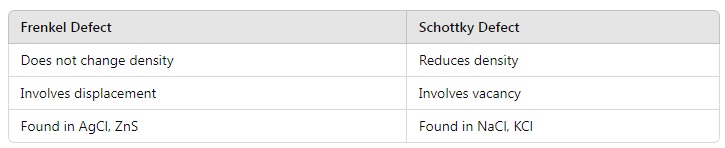
17. Explain the significance of radius ratio rules in determining the structure of ionic solids. Use the example of ZnS and NaCl.

Answer:
The radius ratio ($r_c/r_a$ ) determines the coordination number (CN) and hence the structure of ionic solids.

Range of Ratios:

• $0.414 - 0.732:$ Octahedral geometry, CN = 6 (e.g., NaCl).
• $0.225 - 0.414:$ Tetrahedral geometry, CN = 4 (e.g., ZnS).

Examples:

1. ZnS: Radius ratio $\approx 0.40$ , resulting in tetrahedral voids.
2. NaCl: Radius ratio $\approx 0.52$ , leading to octahedral voids.

---

18. What is the importance of doping in semiconductors? How does n-type and p-type conductivity arise?

Answer:
Doping: Adding impurities to intrinsic semiconductors enhances conductivity.

n-Type Semiconductor:

• Dopant: Pentavalent atoms (e.g., P, As) provide extra electrons, increasing conductivity.
• Majority carriers: Electrons.

p-Type Semiconductor:

• Dopant: Trivalent atoms (e.g., B, Al) create holes, which act as positive charge carriers.
• Majority carriers: Holes.

Applications:
Used in diodes, transistors, and solar cells.

---

19. Why does glass not exhibit a sharp melting point? How does it differ from crystalline solids?

Answer:
Glass is an amorphous solid, meaning its particles are randomly arranged.

Properties of Amorphous Solids:

• Lack a definite melting point; they soften over a range of temperatures.
• Isotropic properties (uniform in all directions).

Difference from Crystalline Solids:

1. Order: Crystalline solids have long-range order; amorphous solids have short-range order.
2. Melting Point: Crystalline solids melt sharply, while amorphous solids soften gradually.

---

20. The conductivity of a metal decreases with an increase in temperature, whereas that of semiconductors increases. Explain.

Answer:

• Metals: As temperature increases, lattice vibrations increase, scattering electrons and reducing conductivity.
• Semiconductors: Higher temperatures provide energy to valence electrons to cross the band gap, increasing charge carriers and conductivity.

---

21. Discuss the relationship between lattice defects and electrical conductivity in ionic solids. Provide examples.

Answer:
Defects increase charge carriers:

• Schottky Defects: Increase ion mobility, enhancing conductivity. Example: NaCl at high temperatures.
• Frenkel Defects: Introduce interstitial ions, aiding conduction in AgCl.

---

22. Explain why graphite is soft and conducts electricity, but diamond is hard and an insulator.

Answer:

• Graphite:
  • Soft due to weak van der Waals forces between layers.
  • Conducts electricity due to delocalized $\pi$ -electrons.
• Diamond:
  • Hard because of a 3D covalent bond network.
  • Insulator as no free electrons are present.

---

23. Derive the expression for the volume of a unit cell in terms of the lattice parameter $a$ for a cubic system.

Answer:
For cubic lattices:

• Simple Cubic: $V = a^3$ .
• Body-Centered Cubic: Atoms touch along body diagonal ($\sqrt{3}a = 4r$ ):

$$V = a^3, \quad r = \frac{\sqrt{3}a}{4}.$$

• Face-Centered Cubic: Atoms touch along face diagonal ($\sqrt{2}a = 4r$ ):

$$V = a^3, \quad r = \frac{\sqrt{2}a}{4}.$$

24. Calculate the void space in a simple cubic unit cell.

Answer:

1. Volume of Atoms:

   • $1$1 atom in the unit cell occupies volume: $$\text{Volume} = \frac{4}{3} \pi r^3.$$

2. Volume of Cube:

   • Edge length $a = 2r$ , so volume: $$a^3 = (2r)^3 = 8r^3.$$

3. Packing Efficiency:

   $$\text{Efficiency} = \frac{\frac{4}{3} \pi r^3}{8r^3} \times 100 \approx 52.4\%.$$

4. Void Space:

   $$100 - 52.4 = 47.6\%.$$

25. A solid AB has a rock salt structure. If the edge length of the unit cell is $400 \, \text{pm}$ and the density is $2.16 \, \text{g/cm}^3$ , calculate the formula mass of AB.

Answer:
Using the formula:

$$\rho = \frac{Z \cdot M}{a^3 \cdot N_A},$$

where $Z = 4$ (for FCC), $a = 400 \times 10^{-8} \, \text{cm}$ , and $N_A = 6.022 \times 10^{23} \, \text{mol}^{-1}$ .

Substitute values:

$$2.16 = \frac{4 \cdot M}{(400 \times 10^{-8})^3 \cdot 6.022 \times 10^{23}}.$$

Simplify to get $M = 58.5 \, \text{g/mol}$ , indicating the formula mass corresponds to NaCl.