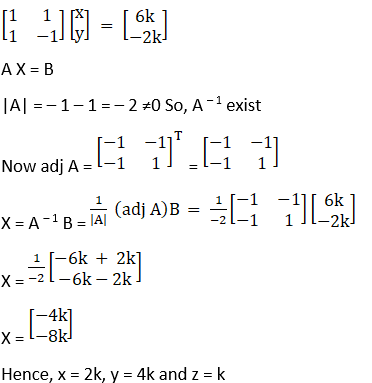Chapter 8 SOLUTIONS OF SIMULTANEOUS

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 8 – Solution of Simultaneous Linear Equations

Exercise 8.1 Page No: 8.14

1. Solve the following system of equations by matrix method:

(i) 5x + 7y + 2 = 0

4x + 6y + 3 = 0

(ii) 5x + 2y = 3

3x + 2y = 5

(iii) 3x + 4y – 5 = 0

x – y + 3 = 0

(iv) 3x + y = 19

3x – y = 23

(v) 3x + 7y = 4

x + 2y = -1

(vi) 3x + y = 7

5x + 3y = 12

Solution:

(i) Given 5x + 7y + 2 = 0 and 4x + 6y + 3 = 0

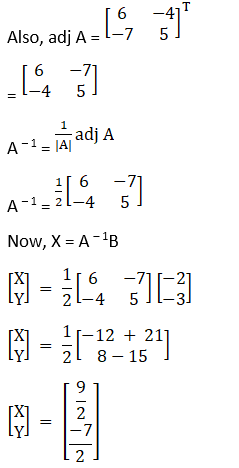
Hence, x = 9/2 and y = -7/2

(ii) Given 5x + 2y = 3

3x + 2y = 5

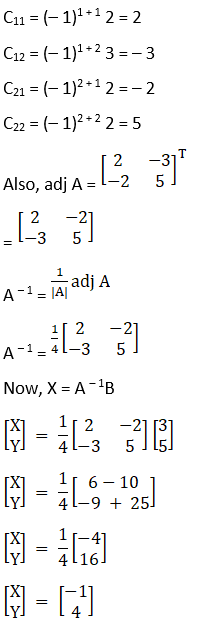
Hence, x = -1 and y = 4

(iii) Given 3x + 4y – 5 = 0

x – y + 3 = 0

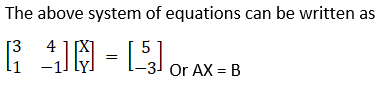
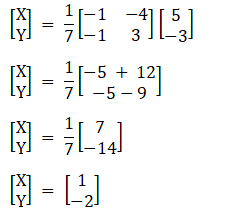
Hence, X = 1 Y = – 2

(iv) Given 3x + y = 19

3x – y = 23

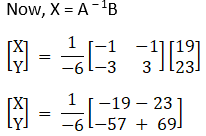
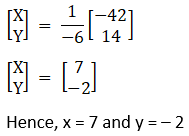
(v) Given 3x + 7y = 4

x + 2y = -1

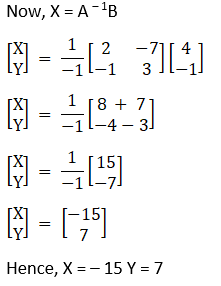
(vi) Given 3x + y = 7

5x + 3y = 12

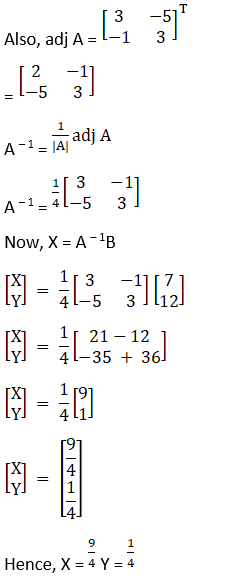
2. Solve the following system of equations by matrix method:

(i) x + y –z = 3
2x + 3y + z = 10
3x – y – 7z = 1

(ii) x + y + z = 3

2x – y + z = -1

2x + y – 3z = -9

(iii) 6x – 12y + 25z = 4

4x + 15y – 20z = 3

2x + 18y + 15z = 10

(iv) 3x + 4y + 7z = 14

2x – y + 3z = 4

x + 2y – 3z = 0

(v) (2/x) – (3/y) + (3/z) = 10

(1/x) + (1/y) + (1/z) = 10

(3/x) – (1/y) + (2/z) = 13

(vi) 5x + 3y + z = 16

2x + y + 3z = 19

x + 2y + 4z = 25

(vii) 3x + 4y + 2z = 8

2y – 3z = 3

x – 2y + 6z = -2

(viii) 2x + y + z = 2

x + 3y – z = 5

3x + y – 2z = 6

(ix) 2x + 6y = 2

3x – z = -8

2x – y + z = -3

(x) 2y – z = 1

x – y + z = 2

2x – y = 0

(xi) 8x + 4y + 3z = 18

2x + y + z = 5

x + 2y + z = 5

(xii) x + y + z = 6

x + 2z = 7

3x + y + z = 12

(xiii) (2/x) + (3/y) + (10/z) = 4,

(4/x) – (6/y) + (5/z) = 1,

(6/x) + (9/y) – (20/z) = 2, x, y, z ≠ 0

(xiv) x – y + 2z = 7

3x + 4y – 5z = -5

2x – y + 3z = 12

Solution:

(i) Given x + y –z = 3

2x + 3y + z = 10

3x – y – 7z = 1

= (– 20) – 1(– 17) – 1(11)

= – 20 + 17 + 11 = 8

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} – 21 + 1 = – 20

C₂₁ = (– 1)^{2 + 1} – 7 – 1 = 8

C₃₁ = (– 1)^{3 + 1} 1 + 3 = 4

C₁₂ = (– 1)^{1 + 2} – 14 – 3 = 17

C₂₂ = (– 1)^{2 + 1} – 7 + 3 = – 4

C₃₂ = (– 1)^{3 + 1} 1 + 2 = – 3

C₁₃ = (– 1)^{1 + 2} – 2 – 9 = – 11

C₂₃ = (– 1)^{2 + 1} – 1 – 3 = 4

C₃₃ = (– 1)^{3 + 1} 3 – 2 = 1

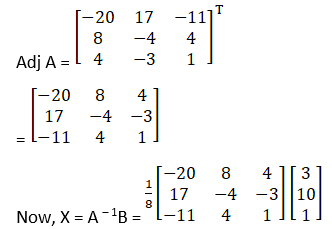
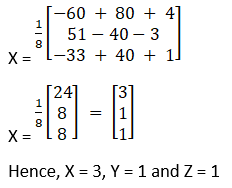
(ii) Given x + y + z = 3

2x – y + z = -1

2x + y – 3z = -9

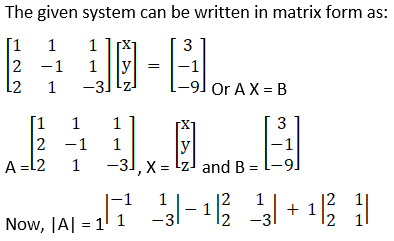
= (3 – 1) – 1(– 6 – 2) + 1(2 + 2)

= 2 + 8 + 4

= 14

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 3 – 1 = 2

C₂₁ = (– 1)^{2 + 1} – 3 – 1 = 4

C₃₁ = (– 1)^{3 + 1} 1 + 1 = 2

C₁₂ = (– 1)^{1 + 2} – 6 – 2 = 8

C₂₂ = (– 1)^{2 + 1} – 3 – 2 = – 5

C₃₂ = (– 1)^{3 + 1} 1 – 2 = 1

C₁₃ = (– 1)^{1 + 2} 2 + 2 = 4

C₂₃ = (– 1)^{2 + 1} 1 – 2 = 1

C₃₃ = (– 1)^{3 + 1} – 1 – 2 = – 3

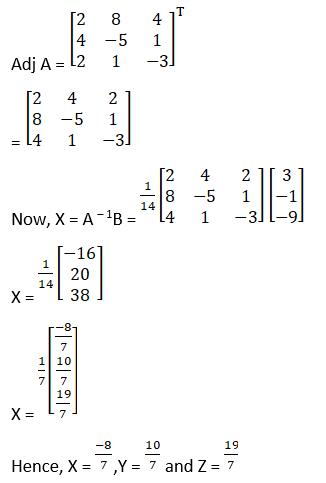
(iii) Given 6x – 12y + 25z = 4

4x + 15y – 20z = 3

2x + 18y + 15z = 10

= 6(225 + 360) + 12(60 + 40) + 25(72 – 30)

= 3510 + 1200 + 1050

= 5760

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} (225 + 360) = 585

C₂₁ = (– 1)^{2 + 1} (– 180 – 450) = 630

C₃₁ = (– 1)^{3 + 1} (240 – 375) = – 135

C₁₂ = (– 1)^{1 + 2} (60 + 40) = – 100

C₂₂ = (– 1)^{2 + 1} (90 – 50) = 40

C₃₂ = (– 1)^{3 + 1} (– 120 – 100) = 220

C₁₃ = (– 1)^{1 + 2} (72 – 30) = 42

C₂₃ = (– 1)^{2 + 1}(108 + 24) = – 132

C₃₃ = (– 1)^{3 + 1} (90 + 48) = 138

(iv) Given 3x + 4y + 7z = 14

2x – y + 3z = 4

x + 2y – 3z = 0

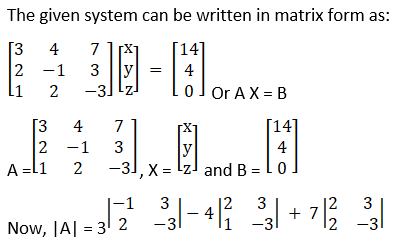
= 3(3 – 6) – 4(– 6 – 3) + 7(4 + 1)

= – 9 + 36 + 35

= 62

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 3 – 6 = – 3

C₂₁ = (– 1)^{2 + 1} – 12 – 14 = 26

C₃₁ = (– 1)^{3 + 1}12 + 7 = 19

C₁₂ = (– 1)^{1 + 2} – 6 – 3 = 9

C₂₂ = (– 1)^{2 + 1} – 3 – 7 = – 10

C₃₂ = (– 1)^{3 + 1} 9 – 14 = 5

C₁₃ = (– 1)^{1 + 2} 4 + 1 = 5

C₂₃ = (– 1)^{2 + 1} 6 – 4 = – 2

C₃₃ = (– 1)^{3 + 1} – 3 – 8 = – 11

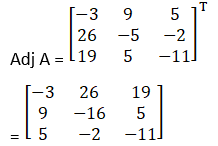
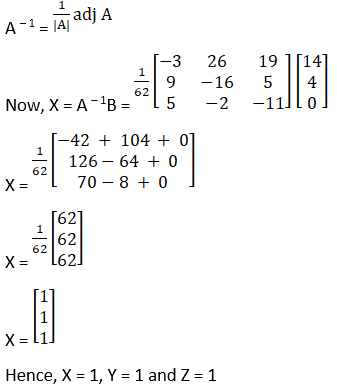
(v) Given (2/x) – (3/y) + (3/z) = 10

(1/x) + (1/y) + (1/z) = 10

(3/x) – (1/y) + (2/z) = 13

= 5(4 – 6) – 3(8 – 3) + 1(4 – 2)

= – 10 – 15 + 3

= – 22

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} (4 – 6) = – 2

C₂₁ = (– 1)^{2 + 1}(12 – 2) = – 10

C₃₁ = (– 1)^{3 + 1}(9 – 1) = 8

C₁₂ = (– 1)^{1 + 2} (8 – 3) = – 5

C₂₂ = (– 1)^{2 + 1} 20 – 1 = 19

C₃₂ = (– 1)^{3 + 1} 15 – 2 = – 13

C₁₃ = (– 1)^{1 + 2} (4 – 2) = 2

C₂₃ = (– 1)^{2 + 1} 10 – 3 = – 7

C₃₃ = (– 1)^{3 + 1} 5 – 6 = – 1

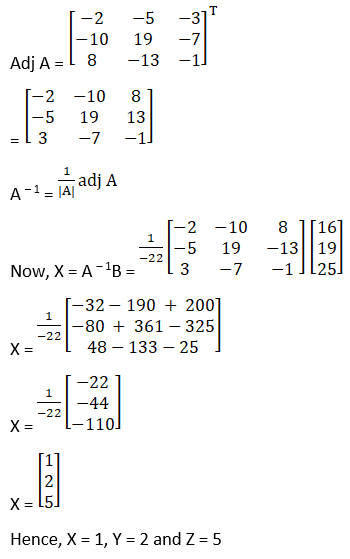
(vi) Given 5x + 3y + z = 16

2x + y + 3z = 19

x + 2y + 4z = 25

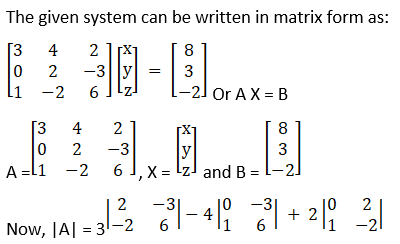
= 3(12 – 6) – 4(0 + 3) + 2(0 – 2)

= 18 – 12 – 4

= 2

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} (12 – 6) = 6

C₂₁ = (– 1)^{2 + 1}(24 + 4) = – 28

C₃₁ = (– 1)^{3 + 1}(– 12 – 4) = – 16

C₁₂ = (– 1)^{1 + 2} (0 + 3) = – 3

C₂₂ = (– 1)^{2 + 1} 18 – 2 = 16

C₃₂ = (– 1)^{3 + 1} – 9 – 0 = 9

C₁₃ = (– 1)^{1 + 2} (0 – 2) = – 2

C₂₃ = (– 1)^{2 + 1} (– 6 – 4) = 10

C₃₃ = (– 1)^{3 + 1} 6 – 0 = 6

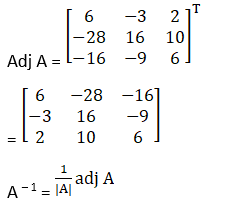
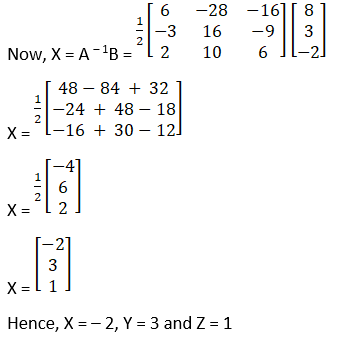
(vii) Given 3x + 4y + 2z = 8

2y – 3z = 3

x – 2y + 6z = -2

= 2(– 6 + 1) – 1(– 2 + 3) + 1(1 – 9)

= – 10 – 1 – 8

= – 19

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} – 6 + 1 = – 5

C₂₁ = (– 1)^{2 + 1}(24 + 4) = – 28

C₃₁ = (– 1)^{3 + 1} – 1 – 3 = – 4

C₁₂ = (– 1)^{1 + 2} – 2 + 3 = – 1

C₂₂ = (– 1)^{2 + 1} – 4 – 3 = – 7

C₃₂ = (– 1)^{3 + 1} – 2 – 1 = 3

C₁₃ = (– 1)^{1 + 2}1 – 9 = – 8

C₂₃ = (– 1)^{2 + 1}2 – 3 = – 1

C₃₃ = (– 1)^{3 + 1} 6 – 1 = 5

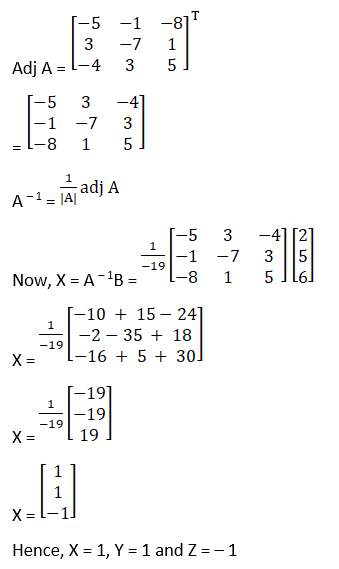
(viii) Given 2x + y + z = 2

x + 3y – z = 5

3x + y – 2z = 6

= 2(– 6 + 1) – 1(– 2 + 3) + 1(1 – 9)

= – 10 – 1 – 8

= – 19

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} – 6 + 1 = – 5

C₂₁ = (– 1)^{2 + 1}(24 + 4) = – 28

C₃₁ = (– 1)^{3 + 1} – 1 – 3 = – 4

C₁₂ = (– 1)^{1 + 2} – 2 + 3 = – 1

C₂₂ = (– 1)^{2 + 1} – 4 – 3 = – 7

C₃₂ = (– 1)^{3 + 1} – 2 – 1 = 3

C₁₃ = (– 1)^{1 + 2}1 – 9 = – 8

C₂₃ = (– 1)^{2 + 1}2 – 3 = – 1

C₃₃ = (– 1)^{3 + 1} 6 – 1 = 5

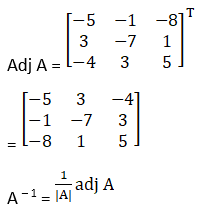
(ix) Given 2x + 6y = 2

3x – z = -8

2x – y + z = -3

= 2(0 – 1) – 6(3 + 2)

= – 2 – 30

= – 32

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 0 – 1 = – 1

C₂₁ = (– 1)^{2 + 1}6 + 0 = – 6

C₃₁ = (– 1)^{3 + 1} – 6 = – 6

C₁₂ = (– 1)^{1 + 2} 3 + 2 = 5

C₂₂ = (– 1)^{2 + 1} 2 – 0 = 2

C₃₂ = (– 1)^{3 + 1} – 2 – 0 = 2

C₁₃ = (– 1)^{1 + 2} – 3 – 0 = – 3

C₂₃ = (– 1)^{2 + 1} – 2 – 12 = 14

C₃₃ = (– 1)^{3 + 1} 0 – 18 = – 18

(x) Given 2y – z = 1

x – y + z = 2

2x – y = 0

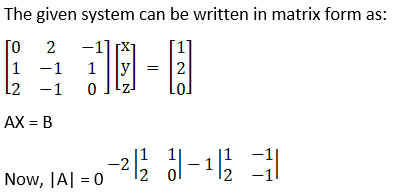
= 0 + 4 – 1

= 3

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 1 – 0 = 1

C₂₁ = (– 1)^{2 + 1}1 – 2 = 1

C₃₁ = (– 1)^{3 + 1}0 + 1 = 1

C₁₂ = (– 1)^{1 + 2} – 2 – 0 = 2

C₂₂ = (– 1)^{2 + 1} – 1 – 0 = – 1

C₃₂ = (– 1)^{3 + 1} 0 – 2 = 2

C₁₃ = (– 1)^{1 + 2} 4 – 0 = 4

C₂₃ = (– 1)^{2 + 1} 2 – 0 = – 2

C₃₃ = (– 1)^{3 + 1} – 1 + 2 = 1

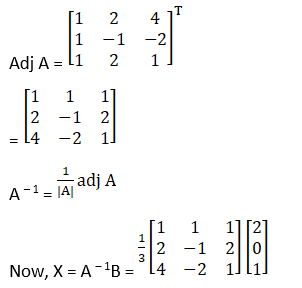
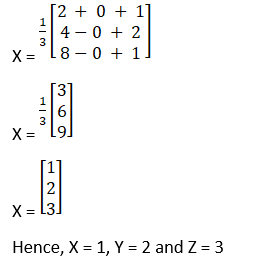
(xi) Given 8x + 4y + 3z = 18

2x + y + z = 5

x + 2y + z = 5

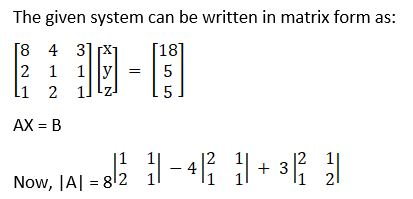
= 8(– 1) – 4(1) + 3(3)

= – 8 – 4 + 9

= – 3

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 1 – 2 = – 1

C₂₁ = (– 1)^{2 + 1} 4 – 6 = 2

C₃₁ = (– 1)^{3 + 1} 4 – 3 = 1

C₁₂ = (– 1)^{1 + 2} 2 – 1 = – 1

C₂₂ = (– 1)^{2 + 1} 8 – 3 = 5

C₃₂ = (– 1)^{3 + 1} 8 – 6 = – 2

C₁₃ = (– 1)^{1 + 2} 4 – 1 = 3

C₂₃ = (– 1)^{2 + 1} 16 – 4 = – 12

C₃₃ = (– 1)^{3 + 1} 8 – 8 = 0

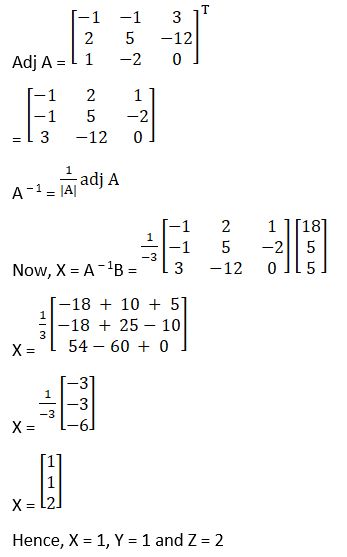
(xii) Given x + y + z = 6

x + 2z = 7

3x + y + z = 12

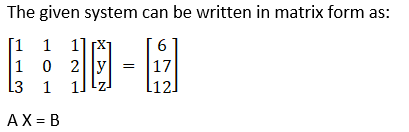
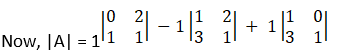
= 1(– 2) – 1(1 – 6) + 1(1)

= – 2 + 5 + 1

= 4

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 0 – 2 = – 2

C₂₁ = (– 1)^{2 + 1} 1 – 1 = 0

C₃₁ = (– 1)^{3 + 1} 2 – 0 = 2

C₁₂ = (– 1)^{1 + 2} 1 – 6 = 5

C₂₂ = (– 1)^{2 + 1} 1 – 3 = – 2

C₃₂ = (– 1)^{3 + 1} 2 – 1 = – 1

C₁₃ = (– 1)^{1 + 2} 1 – 0 = 1

C₂₃ = (– 1)^{2 + 1} 1 – 3 = 2

C₃₃ = (– 1)^{3 + 1} 0 – 1 = – 1

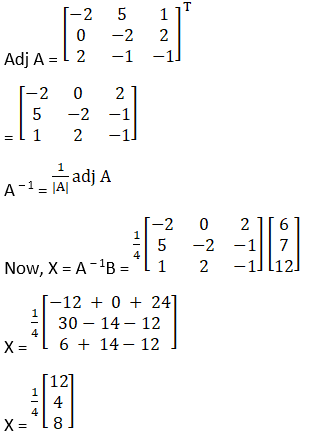
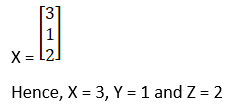
(xiii) Given (2/x) + (3/y) + (10/z) = 4,

(4/x) – (6/y) + (5/z) = 1,

(6/x) + (9/y) – (20/z) = 2, x, y, z ≠ 0

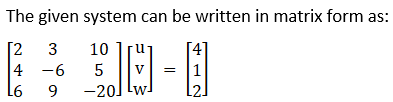
AX = B

Now,

|A| = 2(75) – 3(– 110) + 10(72)

= 150 + 330 + 720

= 1200

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 120 – 45 = 75

C₂₁ = (– 1)^{2 + 1} – 60 – 90 = 150

C₃₁ = (– 1)^{3 + 1} 15 + 60 = 75

C₁₂ = (– 1)^{1 + 2} – 80 – 30 = 110

C₂₂ = (– 1)^{2 + 1} – 40 – 60 = – 100

C₃₂ = (– 1)^{3 + 1} 10 – 40 = 30

C₁₃ = (– 1)^{1 + 2} 36 + 36 = 72

C₂₃ = (– 1)^{2 + 1} 18 – 18 = 0

C₃₃ = (– 1)^{3 + 1} – 12 – 12 = – 24

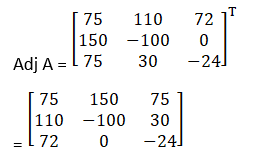
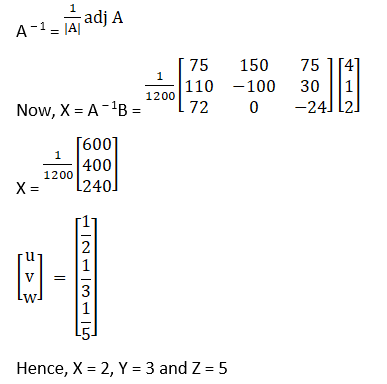
(xiv) Given x – y + 2z = 7

3x + 4y – 5z = -5

2x – y + 3z = 12

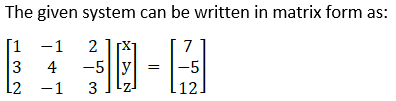
A X = B

Now,

|A| = 1(12 – 5) + 1(9 + 10) + 2(– 3 – 8)

= 7 + 19 – 22

= 4

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 12 – 5 = 7

C₂₁ = (– 1)^{2 + 1} – 3 + 2 = 1

C₃₁ = (– 1)^{3 + 1} 5 – 8 = – 3

C₁₂ = (– 1)^{1 + 2} 9 + 10 = – 19

C₂₂ = (– 1)^{2 + 1} 3 – 4 = – 1

C₃₂ = (– 1)^{3 + 1} – 5 – 6 = 11

C₁₃ = (– 1)^{1 + 2} – 3 – 8 = – 11

C₂₃ = (– 1)^{2 + 1} – 1 + 2 = – 1

C₃₃ = (– 1)^{3 + 1} 4 + 3 = 7

3. Show that each one of the following systems of linear equations is consistent and also find their solutions:

(i) 6x + 4y = 2

9x + 6y = 3

(ii) 2x + 3y = 5

6x + 9y = 15

(iii) 5x + 3y + 7z = 4

3x + 26y + 2z = 9

7x + 2y + 10z = 5

(v) x + y + z = 6

x + 2y + 3z = 14

x + 4y + 7z = 30

(vi) 2x + 2y – 2z = 1

4x + 4y – z = 2

6x + 6y + 2z = 3

Solution:

(i) Given 6x + 4y = 2

9x + 6y = 3

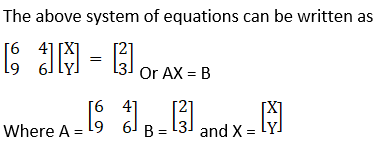
|A| = 36 – 36 = 0

So, A is singular, Now X will be consistence if (Adj A) x B = 0

C₁₁ = (– 1)^{1 + 1} 6 = 6

C₁₂ = (– 1)^{1 + 2} 9 = – 9

C₂₁ = (– 1)^{2 + 1} 4 = – 4

C₂₂ = (– 1)^{2 + 2} 6 = 6

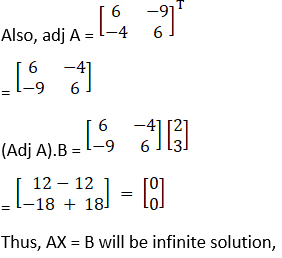
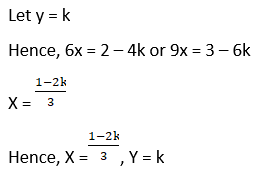
(ii) Given 2x + 3y = 5

6x + 9y = 15

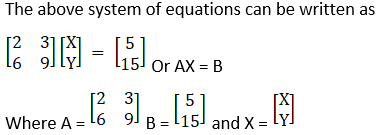
|A| = 18 – 18 = 0

So, A is singular,

Now X will be consistence if (Adj A) x B = 0

C₁₁ = (– 1)^{1 + 1} 9 = 9

C₁₂ = (– 1)^{1 + 2} 6 = – 6

C₂₁ = (– 1)^{2 + 1} 3 = – 3

C₂₂ = (– 1)^{2 + 2} 2 = 2

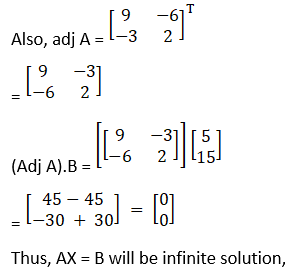
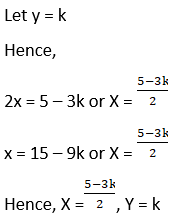
(iii) Given 5x + 3y + 7z = 4

3x + 26y + 2z = 9

7x + 2y + 10z = 5

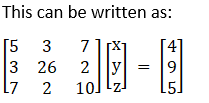
|A| = 5(260 – 4) – 3(30 – 14) + 7(6 – 182)

= 5(256) – 3(16) + 7(176)

|A| = 0

So, A is singular. Thus, the given system is either inconsistent or it is consistent with infinitely many solution according to as:

(Adj A) x B≠0 or (Adj A) x B = 0

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 260 – 4 = 256

C₂₁ = (– 1)^{2 + 1} 30 – 14 = – 16

C₃₁ = (– 1)^{3 + 1} 6 – 182 = – 176

C₁₂ = (– 1)^{1 + 2} 30 – 14 = – 16

C₂₂ = (– 1)^{2 + 1} 50 – 49 = 1

C₃₂ = (– 1)^{3 + 1} 10 – 21 = 11

C₁₃ = (– 1)^{1 + 2} 6 – 182 = – 176

C₂₃ = (– 1)^{2 + 1} 10 – 21 = 11

C₃₃ = (– 1)^{3 + 1} 130 – 9 = 121

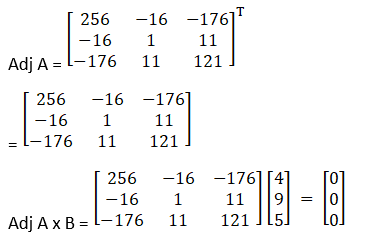
Now, AX = B has infinite many solution

Let z = k

Then, 5x + 3y = 4 – 7k

3x + 26y = 9 – 2k

This can be written as

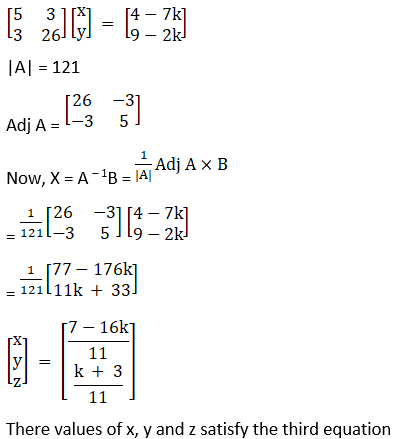
(v) Given x + y + z = 6

x + 2y + 3z = 14

x + 4y + 7z = 30

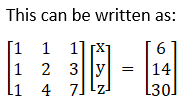
|A| = 1(2) – 1(4) + 1(2)

= 2 – 4 + 2

|A| = 0

So, A is singular. Thus, the given system is either inconsistent or it is consistent with infinitely many solution according to as:

(Adj A) x B≠0 or (Adj A) x B = 0

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 14 – 12 = 2

C₂₁ = (– 1)^{2 + 1} 7 – 4 = – 3

C₃₁ = (– 1)^{3 + 1} 3 – 2 = 1

C₁₂ = (– 1)^{1 + 2} 7 – 3 = – 4

C₂₂ = (– 1)^{2 + 1} 7 – 1 = 6

C₃₂ = (– 1)^{3 + 1} 3 – 1 = 2

C₁₃ = (– 1)^{1 + 2} 4 – 2 = 2

C₂₃ = (– 1)^{2 + 1} 4 – 1 = – 3

C₃₃ = (– 1)^{3 + 1} 2 – 1 = 1

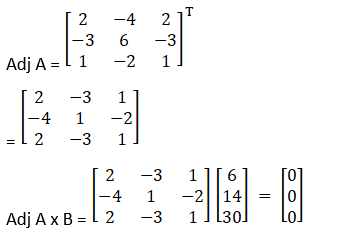
Now, AX = B has infinite many solution

Let z = k

Then, x + y = 6 – k

x + 2y = 14 – 3k

This can be written as:

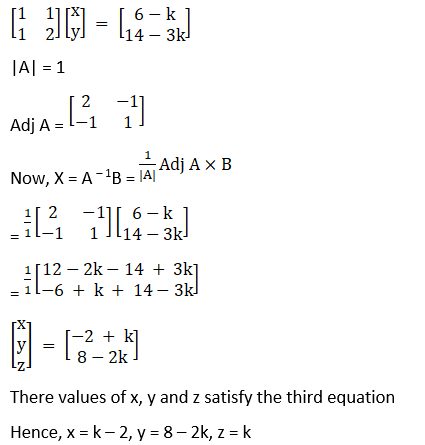
(vi) Given x + y + z = 6

x + 2y + 3z = 14

x + 4y + 7z = 30

This can be written as

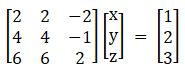
|A| = 2(14) – 2(14) – 2(0)

|A| = 0

So, A is singular. Thus, the given system is either inconsistent or it is consistent

with infinitely many solution according to as:

(Adj A) x B≠0 or (Adj A) x B = 0

Cofactors of A are:

C₁₁ = (– 1)^{1 + 1}8 + 6 = 14

C₂₁ = (– 1)^{2 + 1} 4 + 12 = – 16

C₃₁ = (– 1)^{3 + 1} – 2 + 8 = 6

C₁₂ = (– 1)^{1 + 2} 8 + 6 = – 14

C₂₂ = (– 1)^{2 + 1} 4 + 12 = 16

C₃₂ = (– 1)^{3 + 1} – 2 + 8 = – 6

C₁₃ = (– 1)^{1 + 2} 24 – 24 = 0

C₂₃ = (– 1)^{2 + 1} 12 – 12 = 0

C₃₃ = (– 1)^{3 + 1} 8 – 8 = 0

4. Show that each one of the following systems of linear equations is consistent:

(i) 2x + 5y = 7

6x + 15y = 13

(ii) 2x + 3y = 5

6x + 9y = 10

(iii) 4x – 2y = 3

6x – 3y = 5

(iv) 4x – 5y – 2z = 2

5x – 4y + 2z = -2

2x + 2y + 8z = -1

(v) 3x – y – 2z = 2

2y – z = -1

3x – 5y = 3

(vi) x + y – 2z = 5

x – 2y + z = -2

-2x + y + z = 4

Solution:

(i) Given 2x + 5y = 7

6x + 15y = 13

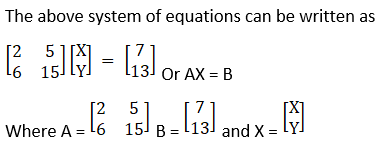
|A| = 30 – 30 = 0

So, A is singular,

Now X will be consistence if (Adj A) x B = 0

C₁₁ = (– 1)^{1 + 1} 15 = 15

C₁₂ = (– 1)^{1 + 2} 6 = – 6

C₂₁ = (– 1)^{2 + 1} 5 = – 5

C₂₂ = (– 1)^{2 + 2} 2 = 2

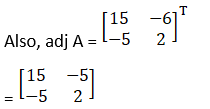
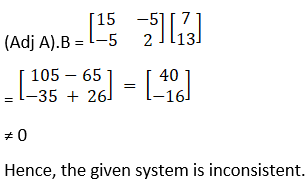
(ii) Given 2x + 3y = 5

6x + 9y = 10

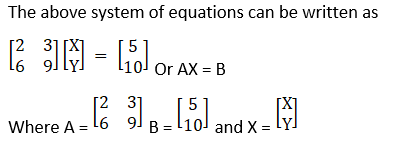
|A| = 18 – 18 = 0

So, A is singular,

Now X will be consistence if (Adj A) x B = 0

C₁₁ = (– 1)^{1 + 1} 9 = 9

C₁₂ = (– 1)^{1 + 2} 6 = – 6

C₂₁ = (– 1)^{2 + 1} 3 = – 3

C₂₂ = (– 1)^{2 + 2} 2 = 2

(iii) Given 4x – 2y = 3

6x – 3y = 5

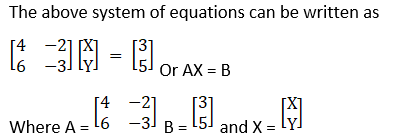
|A| = – 12 + 12 = 0

So, A is singular,

Now X will be consistence if (Adj A) x B = 0

C₁₁ = (– 1)^{1 + 1} – 3 = – 3

C₁₂ = (– 1)^{1 + 2} 6 = – 6

C₂₁ = (– 1)^{2 + 1} – 2 = 2

C₂₂ = (– 1)^{2 + 2} 4 = 4

(iv) Given 4x – 5y – 2z = 2

5x – 4y + 2z = -2

2x + 2y + 8z = -1

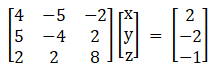
|A| = 4(– 36) + 5(36) – 2(18)

|A| = 0

Cofactors of A are:

C₁₁ = (– 1)^{1 + 1} – 32 – 4 = – 36

C₂₁ = (– 1)^{2 + 1} – 40 + 4 = – 36

C₃₁ = (– 1)^{3 + 1} – 10 – 8 = – 18

C₁₂ = (– 1)^{1 + 2} 40 – 4 = – 36

C₂₂ = (– 1)^{2 + 1} 32 + 4 = 36

C₃₂ = (– 1)^{3 + 1} 8 + 10 = – 18

C₁₃ = (– 1)^{1 + 2} 10 + 8 = 18

C₂₃ = (– 1)^{2 + 1} 8 + 10 = – 18

C₃₃ = (– 1)^{3 + 1} – 16 + 25 = 9

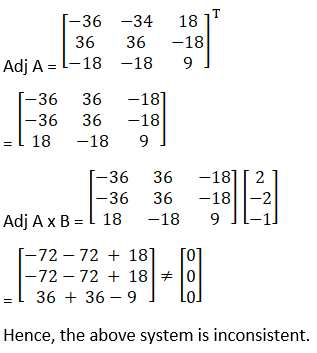
(v) Given 3x – y – 2z = 2

2y – z = -1

3x – 5y = 3

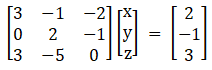
|A| = 3(– 5) + 1(3) – 2(– 6)

|A| = 0

Cofactors of A are

C₁₁ = (– 1)^{1 + 1} 0 – 5 = – 5

C₂₁ = (– 1)^{2 + 1} 0 – 10 = 10

C₃₁ = (– 1)^{3 + 1} 1 + 4 = 5

C₁₂ = (– 1)^{1 + 2} 0 + 3 = – 3

C₂₂ = (– 1)^{2 + 1} 0 + 6 = 6

C₃₂ = (– 1)^{3 + 1} – 3 – 0 = 3

C₁₃ = (– 1)^{1 + 2} 0 – 6 = – 6

C₂₃ = (– 1)^{2 + 1} – 15 + 3 = 12

C₃₃ = (– 1)^{3 + 1} 6 – 0 = 6

(vi) Given x + y – 2z = 5

x – 2y + z = -2

-2x + y + z = 4

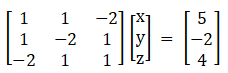
|A| = 1(– 3) – 1(3) – 2(– 3) = – 3 – 3 + 6

|A| = 0

Cofactors of A are:

C₁₁ = (– 1)^{1 + 1} – 2 – 1 = – 3

C₂₁ = (– 1)^{2 + 1} 1 + 2 = – 3

C₃₁ = (– 1)^{3 + 1} 1 – 4 = – 3

C₁₂ = (– 1)^{1 + 2} 1 + 2 = – 3

C₂₂ = (– 1)^{2 + 1} 1 – 4 = – 3

C₃₂ = (– 1)^{3 + 1} 1 + 2 = – 3

C₁₃ = (– 1)^{1 + 2} 1 – 4 = – 3

C₂₃ = (– 1)^{2 + 1} 1 + 2 = – 3

C₃₃ = (– 1)^{3 + 1} – 2 – 1 = – 3

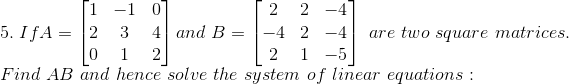
x – y = 3, 2x + 3y + 4z = 17, y + 2z = 7

Solution:

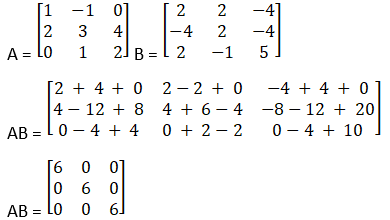
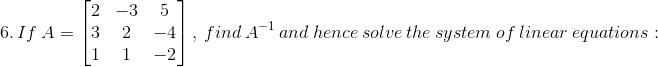
2x – 3y + 5z = 11, 3x + 2y – 4z = -5, x + y – 2z = -3.

Solution:

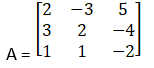
|A| = 2(0) + 3(– 2) + 5(1)

= – 1

Now, the cofactors of A

C₁₁ = (– 1)^{1 + 1} – 4 + 4 = 0

C₂₁ = (– 1)^{2 + 1} 6 – 5 = – 1

C₃₁ = (– 1)^{3 + 1} 12 – 10 = 2

C₁₂ = (– 1)^{1 + 2} – 6 + 4 = 2

C₂₂ = (– 1)^{2 + 1} – 4 – 5 = – 9

C₃₂ = (– 1)^{3 + 1} – 8 – 15 = 23

C₁₃ = (– 1)^{1 + 2} 3 – 2 = 1

C₂₃ = (– 1)^{2 + 1} 2 + 3 = – 5

C₃₃ = (– 1)^{3 + 1} 4 + 9 = 13

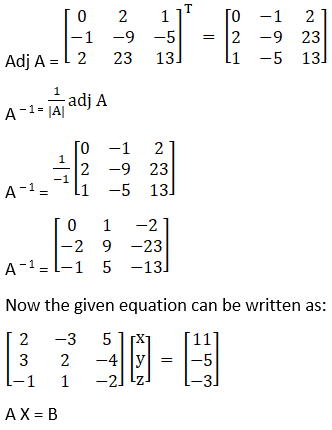
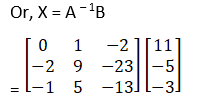
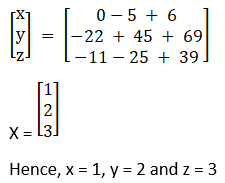
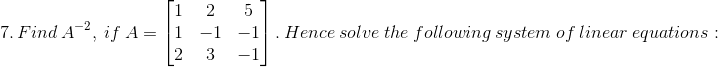
x + 2y + 5z = 10, x – y – z = -2, 2x + 3y – z = -11.

Solution:

Given

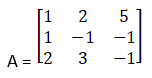
|A| = 1(1 + 3) + 2(– 1 + 2) + 5(3 + 2)

= 4 + 2 + 25

= 27

Now, the cofactors of A

C₁₁ = (– 1)^{1 + 1} 1 + 3 = 4

C₂₁ = (– 1)^{2 + 1} – 2 – 15 = 17

C₃₁ = (– 1)^{3 + 1} – 2 + 5 = 3

C₁₂ = (– 1)^{1 + 2} – 1 + 2 = – 1

C₂₂ = (– 1)^{2 + 1} – 1 – 10 = – 11

C₃₂ = (– 1)^{3 + 1} – 1 – 5 = 6

C₁₃ = (– 1)^{1 + 2} 3 + 2 = 5

C₂₃ = (– 1)^{2 + 1} 3 – 4 = 1

C₃₃ = (– 1)^{3 + 1} – 1 – 2 = – 3

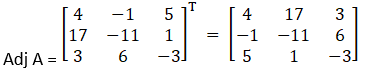
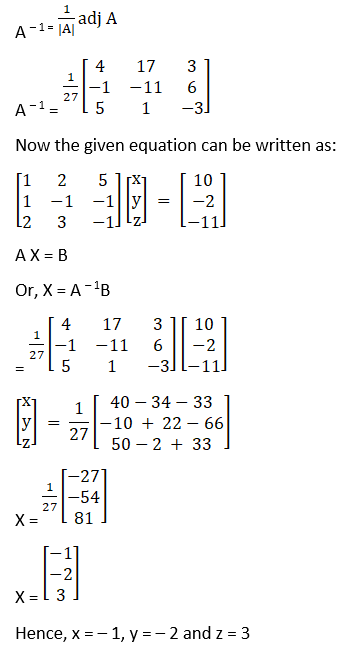
Solution:

Given

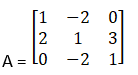
|A| = 1(1 + 6) + 2(2 – 0) + 0

= 7 + 4

= 11

Now, the cofactors of A

C₁₁ = (– 1)^{1 + 1} 1 + 6 = 7

C₂₁ = (– 1)^{2 + 1} – 2 – 0 = 2

C₃₁ = (– 1)^{3 + 1} – 6 – 0 = – 6

C₁₂ = (– 1)^{1 + 2} 2 – 0 = – 2

C₂₂ = (– 1)^{2 + 1} 1 – 0 = 1

C₃₂ = (– 1)^{3 + 1} 3 – 0 = – 3

C₁₃ = (– 1)^{1 + 2} – 4 – 0 = – 4

C₂₃ = (– 1)^{2 + 1} – 2 – 0 = 2

C₃₃ = (– 1)^{3 + 1} 1 + 4 = 5

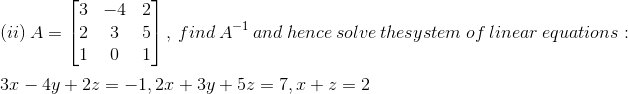
Solution:

Given

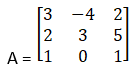
|A| = 3(3 – 0) + 4(2 – 5) + 2(0 – 3)

= 9 – 12 – 6

= – 9

Now, the cofactors of A

C₁₁ = (– 1)^{1 + 1} 3 – 0 = 3

C₂₁ = (– 1)^{2 + 1} – 4 – 0 = 4

C₃₁ = (– 1)^{3 + 1} – 20 – 6 = – 26

C₁₂ = (– 1)^{1 + 2} 2 – 5 = 3

C₂₂ = (– 1)^{2 + 1} 3 – 2 = 1

C₃₂ = (– 1)^{3 + 1} 15 – 4 = – 11

C₁₃ = (– 1)^{1 + 2} 0 – 3 = – 3

C₂₃ = (– 1)^{2 + 1} 0 + 4 = – 4

C₃₃ = (– 1)^{3 + 1} 9 + 8 = 17

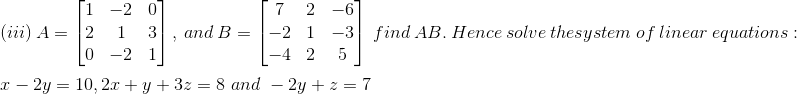
Solution:

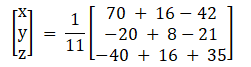
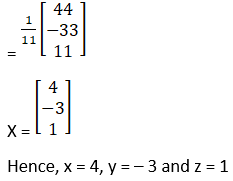
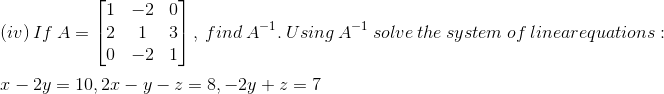
Solution:

Given

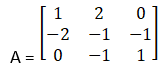
|A| = 1(– 1 – 1) – 2(– 2 – 0) + 0

= – 2 + 4

= 2

Now, the cofactors of A

C₁₁ = (– 1)^{1 + 1} – 1 – 1 = – 2

C₂₁ = (– 1)^{2 + 1} 2 – 0 = 2

C₃₁ = (– 1)^{3 + 1} – 2 – 0 = – 2

C₁₂ = (– 1)^{1 + 2} 2 – 0 = – 2

C₂₂ = (– 1)^{2 + 1} 1 – 0 = 1

C₃₂ = (– 1)^{3 + 1} – 1 – 0 = 1

C₁₃ = (– 1)^{1 + 2} – 2 – 0 = – 2

C₂₃ = (– 1)^{2 + 1} – 1 – 0 = 1

C₃₃ = (– 1)^{3 + 1} – 1 + 4 = 3

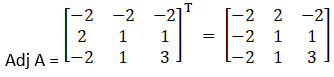
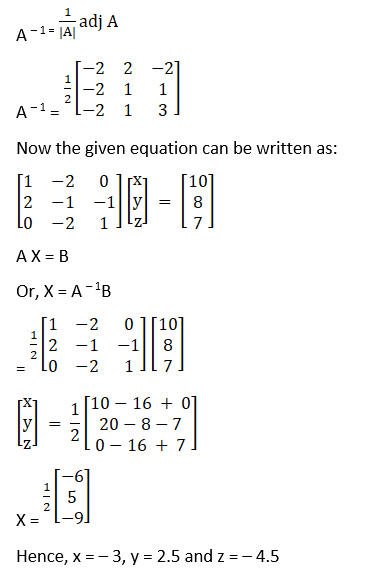
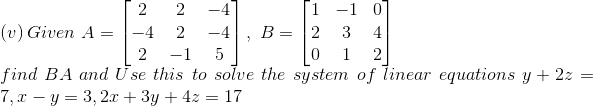
Solution:

Given

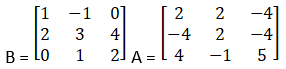
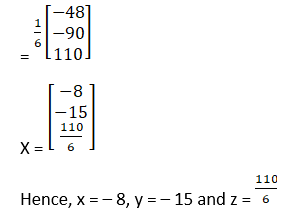
9. The sum of three numbers is 2. If twice the second number is added to the sum of first and third, the sum is 1. By adding second and third number to five times the first number, we get 6. Find the three numbers by using matrices.

Solution:

Let the numbers are x, y, z

x + y + z = 2
…… (i)

Also, 2y + (x + z) + 1

x + 2y + z = 1 …… (ii)

Again,

x + z + 5(x) = 6

5x + y + z = 6 …… (iii)

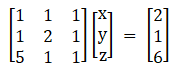
A X = B

|A| = 1(1) – 1(– 4) + 1(– 9)

= 1 + 4 – 9

= – 4

Hence, the unique solution given by x = A ^{– 1}B

C_{11 =} (– 1)^{1 + 1} (2 – 1) = 1

C₁₂ = (– 1)^{1 + 2} (1 – 5) = 4

C₁₃ = (– 1)^{1 + 3} (1 – 10) = – 9

C₂₁ = (– 1)^{2 + 1} (1 – 1) = 0

C₂₂ = (– 1)^{2 + 2} (1 – 5) = – 4

C₂₃ = (– 1)^{2 + 3} (1 – 5) = 4

C₃₁ = (– 1)^{3 + 1} (1 – 2) = – 1

C₃₂ = (– 1)^{3 + 2} (1 – 1) = 0

C₃₃ = (– 1)^{3 + 3} (2 – 1) = 1

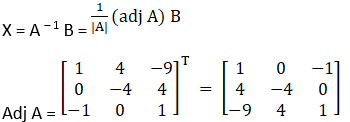
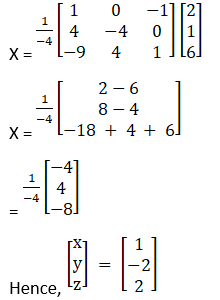
10. An amount of ₹10,000 is put into three investments at the rate of 10, 12 and 15% per annum. The combined incomes are ₹1310 and the combined income of first and second investment is ₹ 190 short of the income from the third. Find the investment in each using matrix method.

Solution:

Let the numbers are x, y, and z

x + y + z = 10,000 …… (i)

Also,

0.1x + 0.12y + 0.15z = 1310 …… (ii)

Again,

0.1x + 0.12y – 0.15z = – 190 …… (iii)

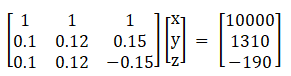
A X = B

|A| = 1(– 0.036) – 1(– 0.03) + 1(0)

= – 0.006

Hence, the unique solution given by x = A ^{– 1}B

C_{11 =} – 0.036

C₁₂ = 0.27

C₁₃ = 0

C₂₁ = 0.27

C₂₂ = – 0.25

C₂₃ = – 0.02

C₃₁ = 0.03

C₃₂ = – 0.05

C₃₃ = 0.02

Exercise 8.2 Page No: 8.20

Solve the following systems of homogeneous linear equations by matrix method:

1. 2x – y + z = 0

3x + 2y – z = 0

x + 4y + 3z = 0

Solution:

Given

2x – y + z = 0

3x + 2y – z = 0

X + 4y + 3z = 0

The system can be written as

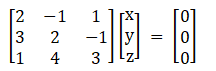
A X = 0

Now, |A| = 2(6 + 4) + 1(9 + 1) + 1(12 – 2)

|A| = 2(10) + 10 + 10

|A| = 40 ≠ 0

Since, |A|≠ 0, hence x = y = z = 0 is the only solution of this homogeneous equation.

2. 2x – y + 2z = 0
5x + 3y – z = 0
X + 5y – 5z = 0

Solution:

Given 2x – y + 2z = 0

5x + 3y – z = 0

X + 5y – 5z = 0

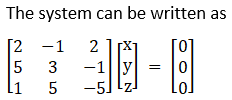
A X = 0

Now, |A| = 2(– 15 + 5) + 1(– 25 + 1) + 2(25 – 3)

|A| = – 20 – 24 + 44

|A| = 0

Hence, the system has infinite solutions

Let z = k

2x – y = – 2k

5x + 3y = k

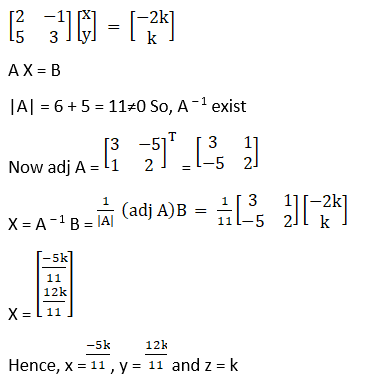
3. 3x – y + 2z = 0
4x + 3y + 3z = 0
5x + 7y + 4z = 0

Solution:

Given 3x – y + 2z = 0

4x + 3y + 3z = 0

5x + 7y + 4z = 0

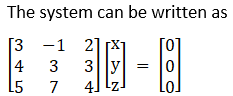
A X = 0

Now, |A| = 3(12 – 21) + 1(16 – 15) + 2(28 – 15)

|A| = – 27 + 1 + 26

|A| = 0

Hence, the system has infinite solutions

Let z = k

3x – y = – 2k

4x + 3y = – 3k

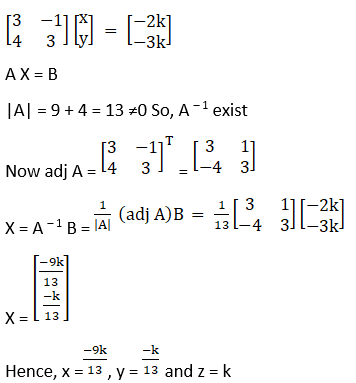
4. x + y – 6z = 0
x – y + 2z = 0
– 3x + y + 2z = 0

Solution:

Given x + y – 6z = 0

x – y + 2z = 0

– 3x + y + 2z = 0

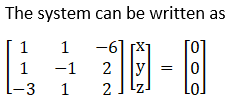
A X = 0

Now, |A| = 1(– 2 – 2) – 1(2 + 6) – 6(1 – 3)

|A| = – 4 – 8 + 12

|A| = 0

Hence, the system has infinite solutions

Let z = k

x + y = 6k

x – y = – 2k