Chapter 7 ADJOINT AND INVERSE OF A MATRIX

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 7 – Adjoint and Inverse of a Matrix

Exercise 7.1 Page No: 7.22

1. Find the adjoint of each of the following matrices:

Verify that (adj A) A = |A| I = A (adj A) for the above matrices.

Solution:

(i) Let

A =

Cofactors of A are

C₁₁ = 4

C₁₂ = – 2

C₂₁ = – 5

C₂₂ = – 3

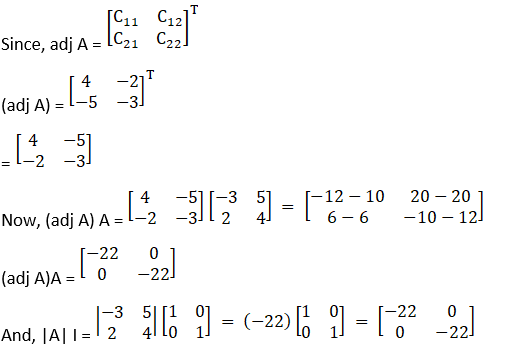
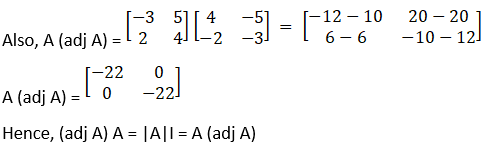
(ii) Let

A =

Therefore cofactors of A are

C₁₁ = d

C₁₂ = – c

C₂₁ = – b

C₂₂ = a

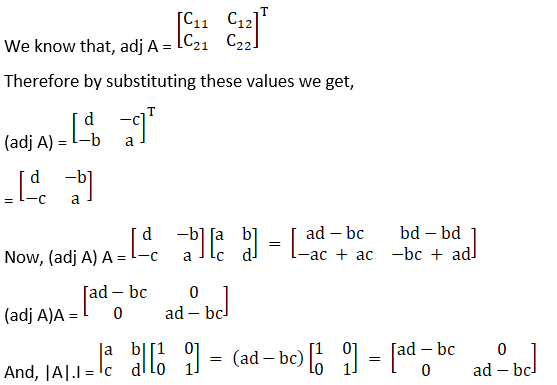
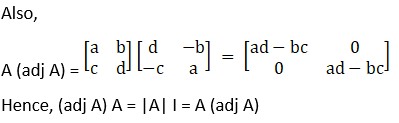
(iii) Let

A =

Therefore cofactors of A are

C₁₁ = cos α

C₁₂ = – sin α

C₂₁ = – sin α

C₂₂ = cos α

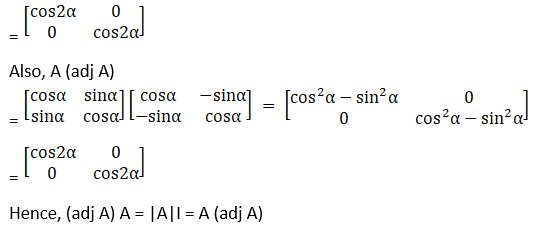
(iv) Let

A =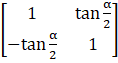

Therefore cofactors of A are

C₁₁ = 1

C₁₂ = tan α/2

C₂₁ = – tan α/2

C₂₂ = 1

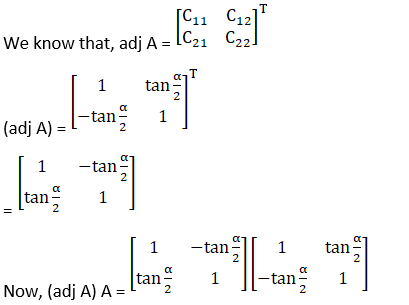
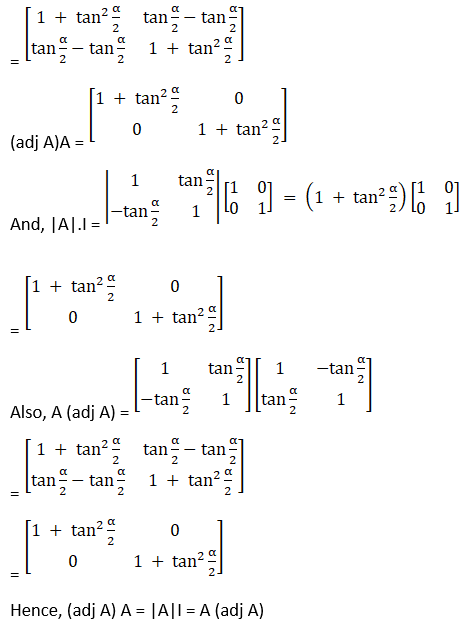
2. Compute the adjoint of each of the following matrices.

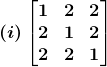
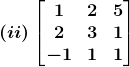
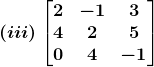
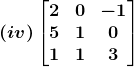
Solution:

(i) Let

A =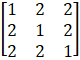

Therefore cofactors of A are

C₁₁ = – 3

C₂₁ = 2

C₃₁ = 2

C₁₂ = 2

C₂₂ = – 3

C₂₃ = 2

C₁₃ = 2

C₂₃ = 2

C₃₃ = – 3

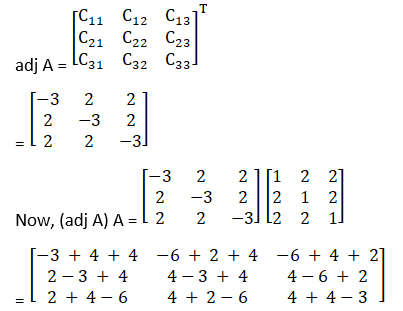
(ii) Let

A =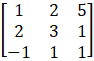

Cofactors of A

C₁₁ = 2

C₂₁ = 3

C₃₁ = – 13

C₁₂ = – 3

C₂₂ = 6

C₃₂ = 9

C₁₃ = 5

C₂₃ = – 3

C₃₃ = – 1

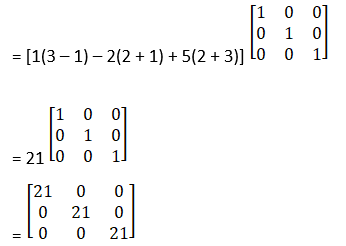
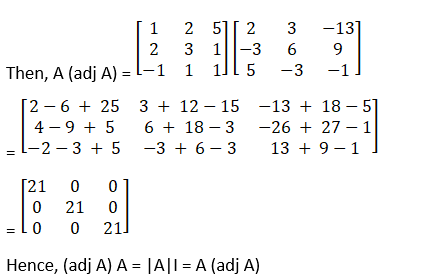
(iii) Let

A =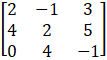

Therefore cofactors of A

C₁₁ = – 22

C₂₁ = 11

C₃₁ = – 11

C₁₂ = 4

C₂₂ = – 2

C₃₂ = 2

C₁₃ = 16

C₂₃ = – 8

C₃₃ = 8

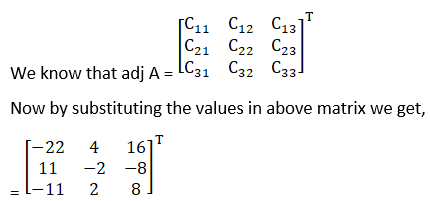
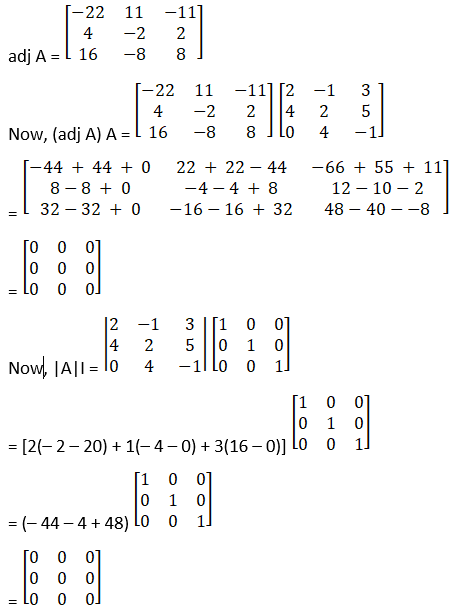
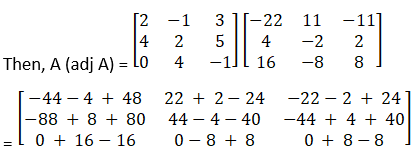
(iv) Let

A =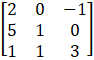

Therefore cofactors of A

C₁₁ = 3

C₂₁ = – 1

C₃₁ = 1

C₁₂ = – 15

C₂₂ = 7

C₃₂ = – 5

C₁₃ = 4

C₂₃ = – 2

C₃₃ = 2

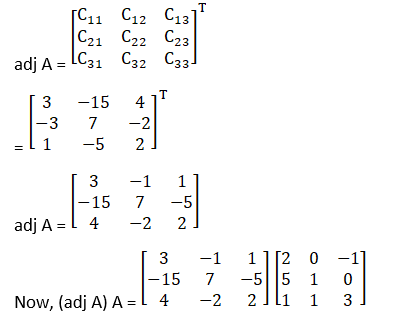
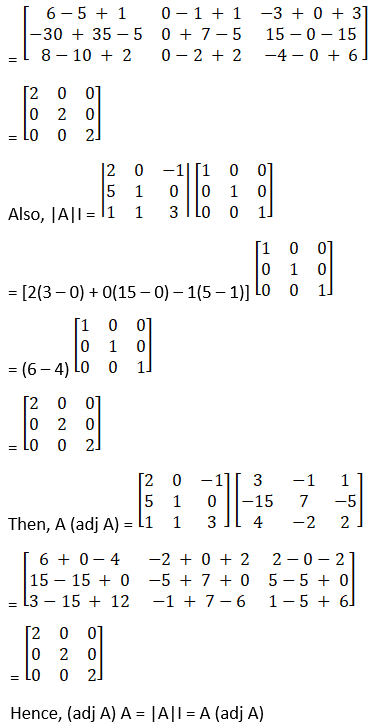
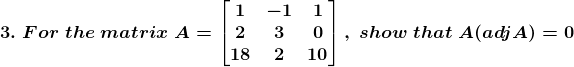
Solution:

Given

A =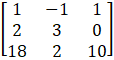

Therefore cofactors of A

C₁₁ = 30

C₂₁ = 12

C₃₁ = – 3

C₁₂ = – 20

C₂₂ = – 8

C₃₂ = 2

C₁₃ = – 50

C₂₃ = – 20

C₃₃ = 5

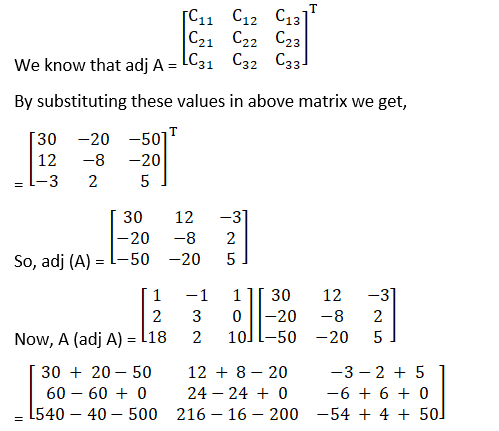
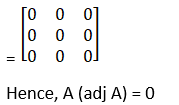
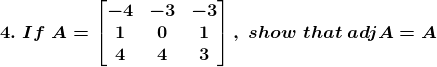
Solution:

Given

A =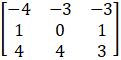

Cofactors of A

C₁₁ = – 4

C₂₁ = – 3

C₃₁ = – 3

C₁₂ = 1

C₂₂ = 0

C₃₂ = 1

C₁₃ = 4

C₂₃ = 4

C₃₃ = 3

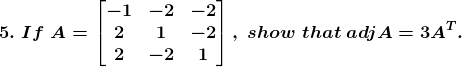
Solution:

Given

A =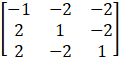

Cofactors of A are

C₁₁ = – 3

C₂₁ = 6

C₃₁ = 6

C₁₂ = – 6

C₂₂ = 3

C₃₂ = – 6

C₁₃ = – 6

C₂₃ = – 6

C₃₃ = 3

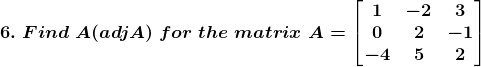
Solution:

Given

A =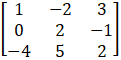

Cofactors of A are

C₁₁ = 9

C₂₁ = 19

C₃₁ = – 4

C₁₂ = 4

C₂₂ = 14

C₃₂ = 1

C₁₃ = 8

C₂₃ = 3

C₃₃ = 2

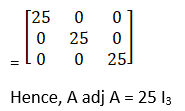
7. Find the inverse of each of the following matrices:

Solution:

(i) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

Now, |A| = cos θ (cos θ) + sin θ (sin θ)

= 1

Hence, A ^{– 1} exists.

Cofactors of A are

C₁₁ = cos θ

C₁₂ = sin θ

C₂₁ = – sin θ

C₂₂ = cos θ

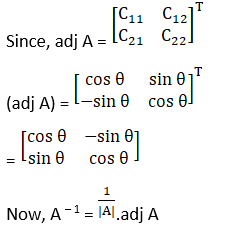
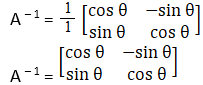
(ii) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

Now, |A| = – 1 ≠ 0

Hence, A ^{– 1} exists.

Cofactors of A are

C₁₁ = 0

C₁₂ = – 1

C₂₁ = – 1

C₂₂ = 0

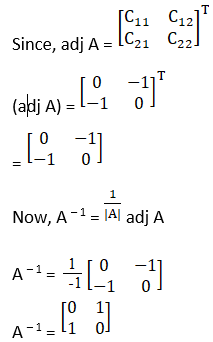
(iii) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

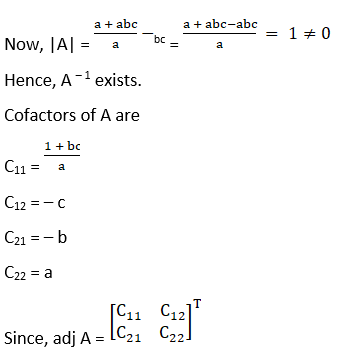
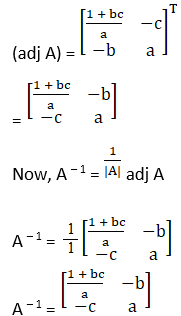
(iv) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

Now, |A| = 2 + 15 = 17 ≠ 0

Hence, A ^{– 1} exists.

Cofactors of A are

C₁₁ = 1

C₁₂ = 3

C₂₁ = – 5

C₂₂ = 2

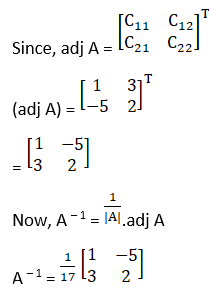
8. Find the inverse of each of the following matrices.

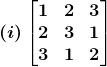
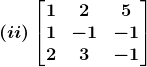
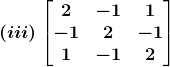
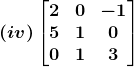
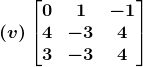
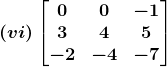
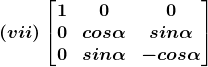
Solution:

(i) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

|A| =

= 1(6 – 1) – 2(4 – 3) + 3(2 – 9)

= 5 – 2 – 21

= – 18≠ 0

Hence, A ^{– 1} exists

Cofactors of A are

C₁₁ = 5

C₂₁ = – 1

C₃₁ = – 7

C₁₂ = – 1

C₂₂ = – 7

C₃₂ = 5

C₁₃ = – 7

C₂₃ = 5

C₃₃ = – 1

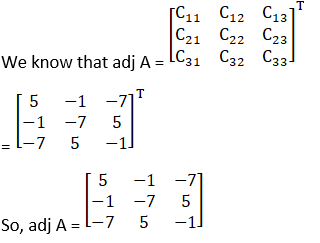
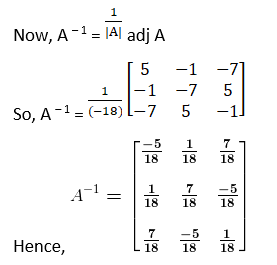
(ii) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

|A| =

= 1 (1 + 3) – 2 (– 1 + 2) + 5 (3 + 2)

= 4 – 2 + 25

= 27≠ 0

Hence, A ^{– 1} exists

Cofactors of A are

C₁₁ = 4

C₂₁ = 17

C₃₁ = 3

C₁₂ = – 1

C₂₂ = – 11

C₃₂ = 6

C₁₃ = 5

C₂₃ = 1

C₃₃ = – 3

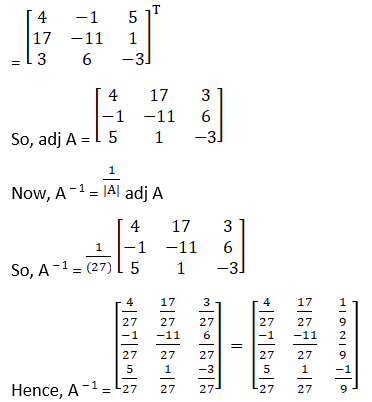
(iii) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

|A| =

= 2(4 – 1) + 1(– 2 + 1) + 1(1 – 2)

= 6 – 2

= – 4≠ 0

Hence, A ^{– 1} exists

Cofactors of A are

C₁₁ = 3

C₂₁ = 1

C₃₁ = – 1

C₁₂ = + 1

C₂₂ = 3

C₃₂ = 1

C₁₃ = – 1

C₂₃ = 1

C₃₃ = 3

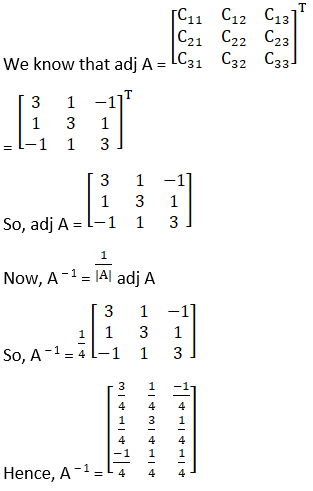
(iv) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

|A| =

= 2(3 – 0) – 0 – 1(5)

= 6 – 5

= 1≠ 0

Hence, A ^{– 1} exists

Cofactors of A are

C₁₁ = 3

C₂₁ = – 1

C₃₁ = 1

C₁₂ = – 15

C₂₂ = 6

C₃₂ = – 5

C₁₃ = 5

C₂₃ = – 2

C₃₃ = 2

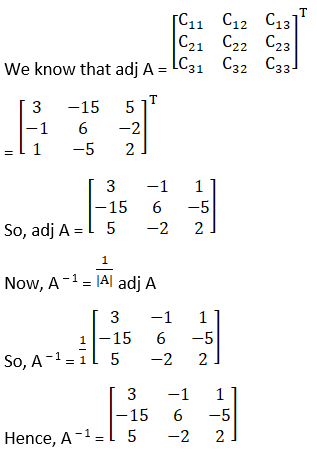
(v) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

|A| =

= 0 – 1 (16 – 12) – 1 (– 12 + 9)

= – 4 + 3

= – 1≠ 0

Hence, A ^{– 1} exists

Cofactors of A are

C₁₁ = 0

C₂₁ = – 1

C₃₁ = 1

C₁₂ = – 4

C₂₂ = 3

C₃₂ = – 4

C₁₃ = – 3

C₂₃ = 3

C₃₃ = – 4

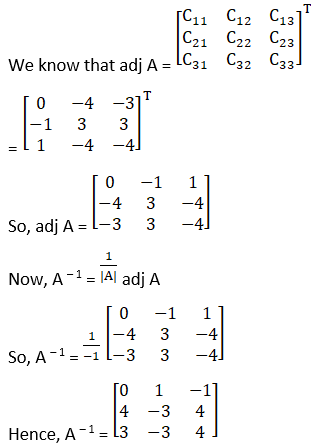
(vi) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

|A| =

= 0 – 0 – 1(– 12 + 8)

= 4≠ 0

Hence, A ^{– 1} exists

Cofactors of A are

C₁₁ = – 8

C₂₁ = 4

C₃₁ = 4

C₁₂ = 11

C₂₂ = – 2

C₃₂ = – 3

C₁₃ = – 4

C₂₃ = 0

C₃₃ = 0

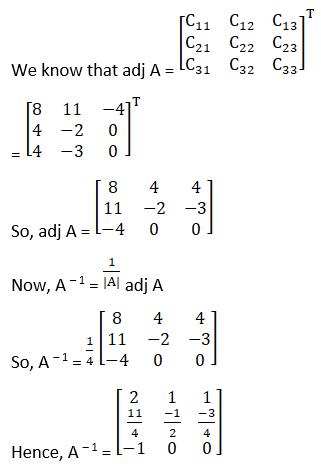
(vii) The criteria of existence of inverse matrix is the determinant of a given matrix should not equal to zero.

|A| =
 – 0 + 0

= – (cos² α – sin² α)

= – 1≠ 0

Hence, A ^{– 1} exists

Cofactors of A are

C₁₁ = – 1

C₂₁ = 0

C₃₁ = 0

C₁₂ = 0

C₂₂ = – cos α

C₃₂ = – sin α

C₁₃ = 0

C₂₃ = – sin α

C₃₃ = cos α

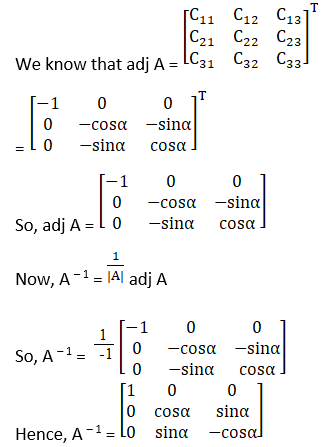
9. Find the inverse of each of the following matrices and verify that A^-1A = I₃.

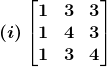
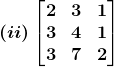
Solution:

(i) We have

|A| =

= 1(16 – 9) – 3(4 – 3) + 3(3 – 4)

= 7 – 3 – 3

= 1≠ 0

Hence, A ^{– 1} exists

Cofactors of A are

C₁₁ = 7

C₂₁ = – 3

C₃₁ = – 3

C₁₂ = – 1

C₂₂ = 1

C₃₂ = 0

C₁₃ = – 1

C₂₃ = 0

C₃₃ = 1

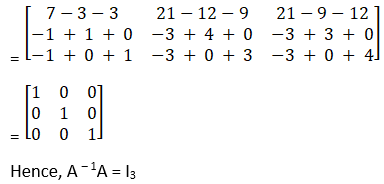
(ii) We have

|A| =

= 2(8 – 7) – 3(6 – 3) + 1(21 – 12)

= 2 – 9 + 9

= 2≠ 0

Hence, A ^{– 1} exists

Cofactors of A are

C₁₁ = 1

C₂₁ = 1

C₃₁ = – 1

C₁₂ = – 3

C₂₂ = 1

C₃₂ = 1

C₁₃ = 9

C₂₃ = – 5

C₃₃ = – 1

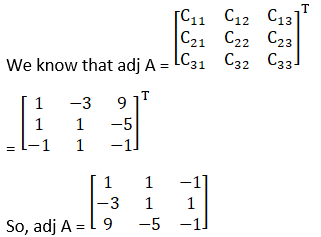
10. For the following pair of matrices verify that (AB)^-1 = B^-1A^-1.

Solution:

(i) Given

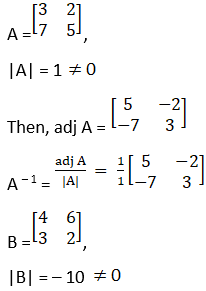
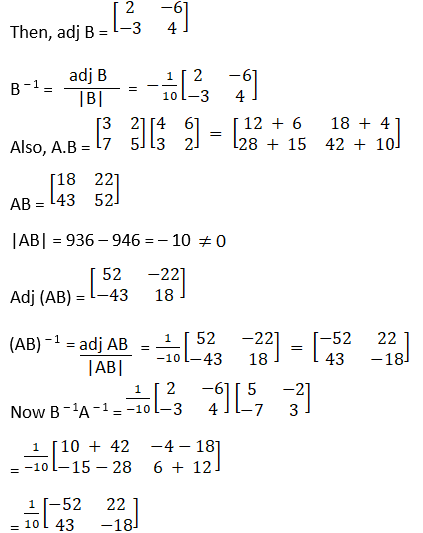
Hence, (AB)^-1 = B^-1A^-1

(ii) Given

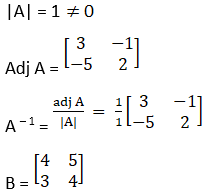
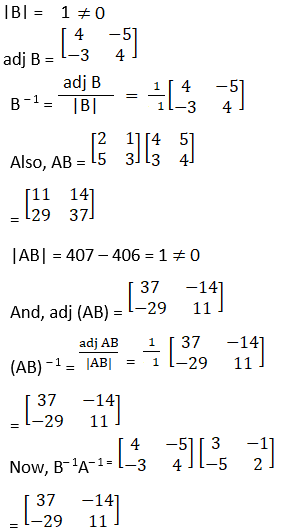
Hence, (AB)^-1 = B^-1A^-1

Solution:

Given

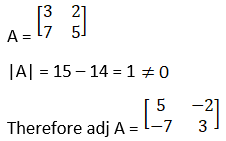
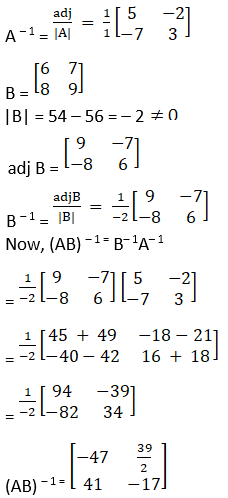
Solution:

Given

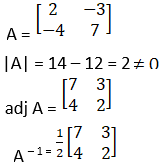
Solution:

Given

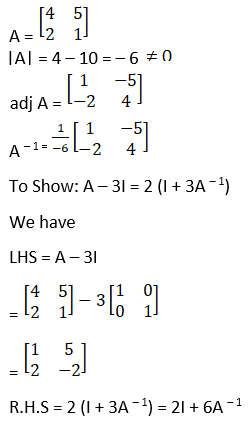
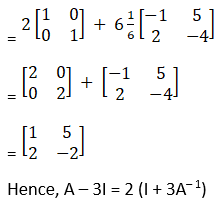
Solution:

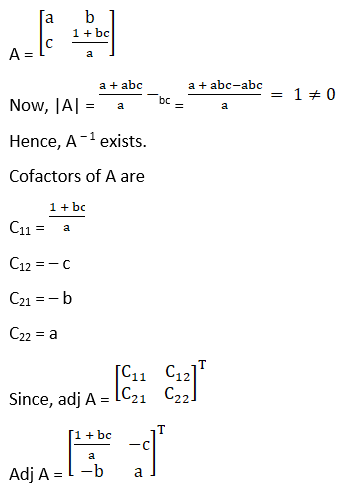
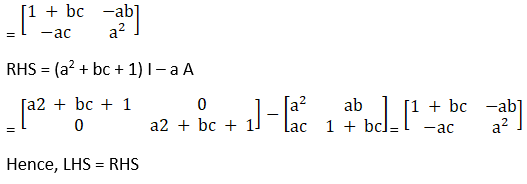
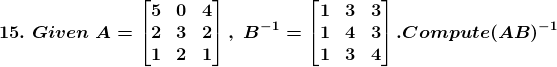
Solution:

Given

A =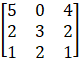
 and B ^{– 1} =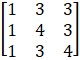

Here, (AB) ^{– 1 =} B ^{– 1} A ^{– 1}

|A| = – 5 + 4 = – 1

Cofactors of A are

C₁₁ = – 1

C₂₁ = 8

C₃₁ = – 12

C₁₂ = 0

C₂₂ = 1

C₃₂ = – 2

C₁₃ = 1

C₂₃ = – 10

C₃₃ = 15

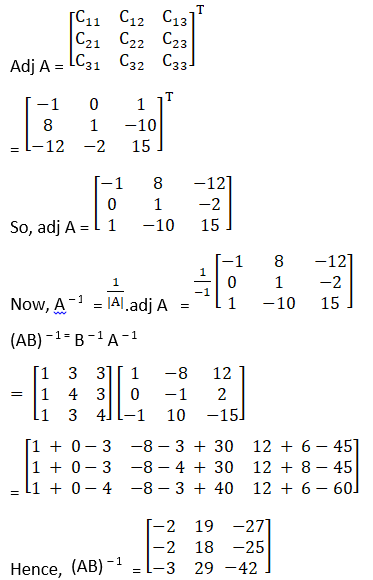
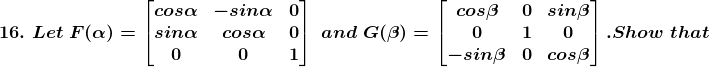
(i) [F (α)]^-1 = F (-α)

(ii) [G (β)]^-1 = G (-β)

(iii) [F (α) G (β)]^-1 = G (-β) F (-α)

Solution:

(i) Given

F (α) =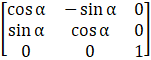

|F (α)| = cos² α + sin² α = 1≠ 0

Cofactors of A are

C₁₁ = cos α

C₂₁ = sin α

C₃₁ = 0

C₁₂ = – sin α

C₂₂ = cos α

C₃₂ = 0

C₁₃ = 0

C₂₃ = 0

C₃₃ = 1

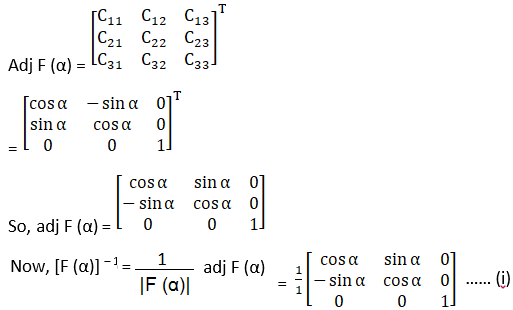
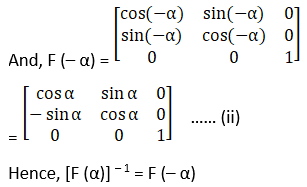
(ii) We have

|G (β)| = cos² β + sin² β = 1

Cofactors of A are

C₁₁ = cos β

C₂₁ = 0

C₃₁ = -sin β

C₁₂ = 0

C₂₂ = 1

C₃₂ = 0

C₁₃ = sin β

C₂₃ = 0

C₃₃ = cos β

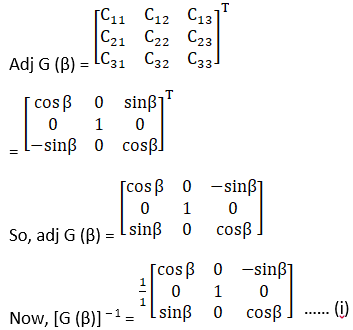
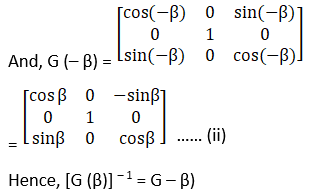
(iii) Now we have to show that

[F (α) G (β)] ^{– 1} = G (– β) F (– α)

We have already know that

[G (β)] ^{– 1} = G (– β) [F (α)] ^{– 1} = F (– α)

And LHS = [F (α) G (β)] ^{– 1}

= [G (β)] ^{– 1} [F (α)] ^{– 1}

= G (– β) F (– α)

Hence = RHS

Solution:

Consider,

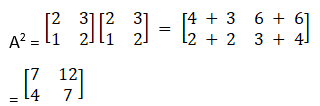
Solution:

Given

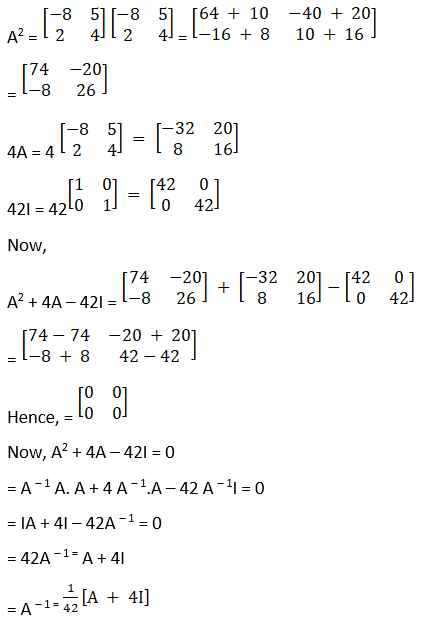
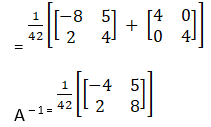
Solution:

Given

---

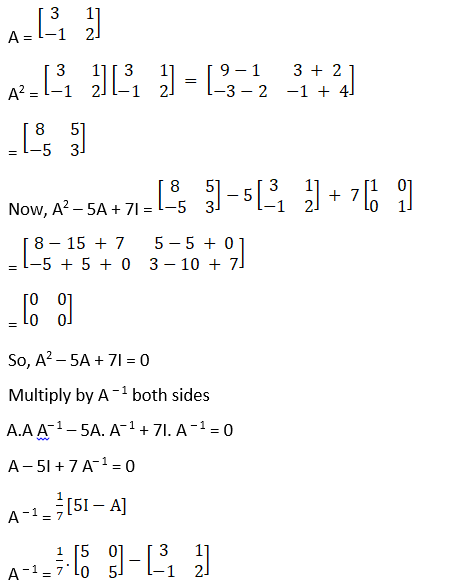
Exercise 7.2 Page No: 7.34

Find the inverse of the following matrices by using elementary row transformations:

Solution:

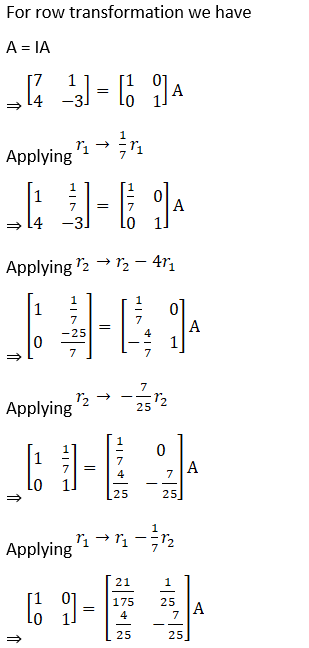
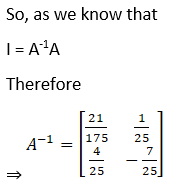
Solution:

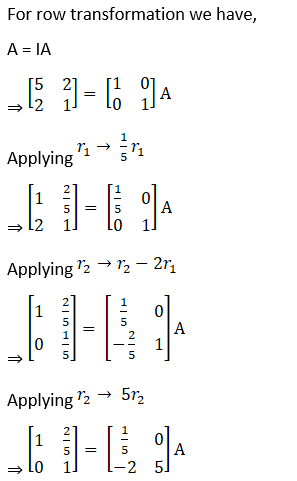
Solution:

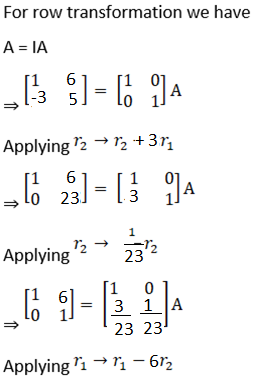
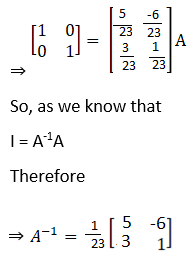
Solution:

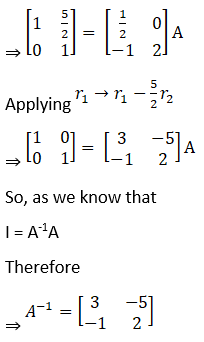
Solution:

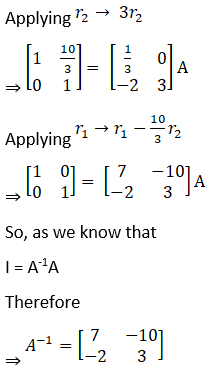
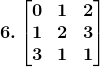
Solution:

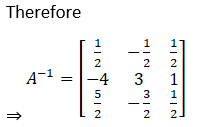
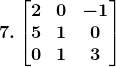
Solution:

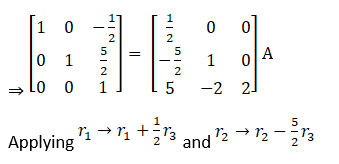
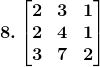
Solution: