Chapter 6 DETERMINANTS
Class 12th Maths R D Sharma Solution
Access answers to Maths RD Sharma Solutions For Class 12 Chapter 6 – Determinants
Exercise 6.1 Page No: 6.10
1. Write the minors and cofactors of each element of the first column of the following matrices and hence evaluate the determinant in each case:
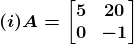
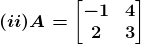
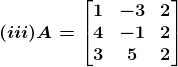
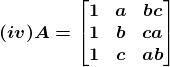
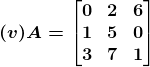
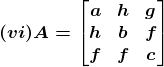
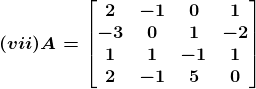
Solution:
(i) Let Mij and Cij represents the minor and co–factor of an element, where i and j represent the row and column.The minor of the matrix can be obtained for a particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.
Also, Cij = (–1)i+j × Mij
Given,
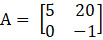
From the given matrix we have,
M11 = –1
M21 = 20
C11 = (–1)1+1 × M11
= 1 × –1
= –1
C21 = (–1)2+1 × M21
= 20 × –1
= –20
Now expanding along the first column we get
|A| = a11 × C11 + a21× C21
= 5× (–1) + 0 × (–20)
= –5
(ii) Let Mij and Cij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of matrix can be obtained for particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.
Also, Cij = (–1)i+j × Mij
Given
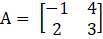
From the above matrix we have
M11 = 3
M21 = 4
C11 = (–1)1+1 × M11
= 1 × 3
= 3
C21 = (–1)2+1 × 4
= –1 × 4
= –4
Now expanding along the first column we get
|A| = a11 × C11 + a21× C21
= –1× 3 + 2 × (–4)
= –11
(iii) Let Mij and Cij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of the matrix can be obtained for a particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.
Also, Cij = (–1)i+j × Mij
Given,
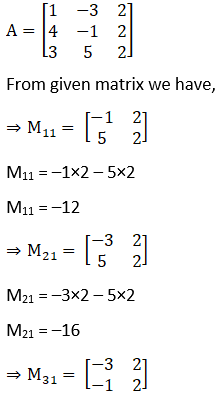
M31 = –3 × 2 – (–1) × 2
M31 = –4
C11 = (–1)1+1 × M11
= 1 × –12
= –12
C21 = (–1)2+1 × M21
= –1 × –16
= 16
C31 = (–1)3+1 × M31
= 1 × –4
= –4
Now expanding along the first column we get
|A| = a11 × C11 + a21× C21+ a31× C31
= 1× (–12) + 4 × 16 + 3× (–4)
= –12 + 64 –12
= 40
(iv) Let Mij and Cij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of the matrix can be obtained for a particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.
Also, Cij = (–1)i+j × Mij
Given,
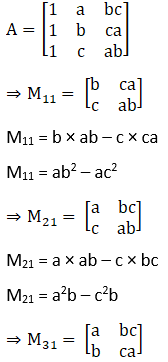
M31 = a × c a – b × bc
M31 = a2c – b2c
C11 = (–1)1+1 × M11
= 1 × (ab2 – ac2)
= ab2 – ac2
C21 = (–1)2+1 × M21
= –1 × (a2b – c2b)
= c2b – a2b
C31 = (–1)3+1 × M31
= 1 × (a2c – b2c)
= a2c – b2c
Now expanding along the first column we get
|A| = a11 × C11 + a21× C21+ a31× C31
= 1× (ab2 – ac2) + 1 × (c2b – a2b) + 1× (a2c – b2c)
= ab2 – ac2 + c2b – a2b + a2c – b2c
(v) Let Mij and Cij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of matrix can be obtained for particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.
Also, Cij = (–1)i+j × Mij
Given,
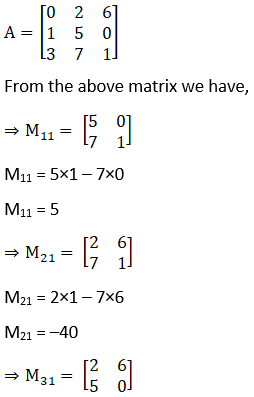
M31 = 2×0 – 5×6
M31 = –30
C11 = (–1)1+1 × M11
= 1 × 5
= 5
C21 = (–1)2+1 × M21
= –1 × –40
= 40
C31 = (–1)3+1 × M31
= 1 × –30
= –30
Now expanding along the first column we get
|A| = a11 × C11 + a21× C21+ a31× C31
= 0× 5 + 1 × 40 + 3× (–30)
= 0 + 40 – 90
= 50
(vi) Let Mij and Cij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of matrix can be obtained for particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.
Also, Cij = (–1)i+j × Mij
Given,
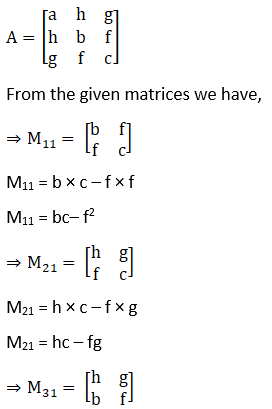
M31 = h × f – b × g
M31 = hf – bg
C11 = (–1)1+1 × M11
= 1 × (bc– f2)
= bc– f2
C21 = (–1)2+1 × M21
= –1 × (hc – fg)
= fg – hc
C31 = (–1)3+1 × M31
= 1 × (hf – bg)
= hf – bg
Now expanding along the first column we get
|A| = a11 × C11 + a21× C21+ a31× C31
= a× (bc– f2) + h× (fg – hc) + g× (hf – bg)
= abc– af2 + hgf – h2c +ghf – bg2
(vii) Let Mij and Cij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of matrix can be obtained for particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.
Also, Cij = (–1)i+j × Mij
Given,
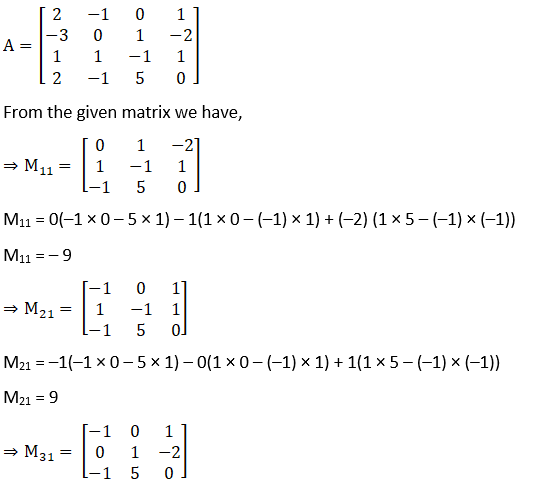
M31 = –1(1 × 0 – 5 × (–2)) – 0(0 × 0 – (–1) × (–2)) + 1(0 × 5 – (–1) × 1)
M31 = –9
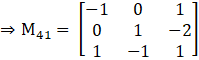
M41 = –1(1×1 – (–1) × (–2)) – 0(0 × 1 – 1 × (–2)) + 1(0 × (–1) – 1 × 1)
M41 = 0
C11 = (–1)1+1 × M11
= 1 × (–9)
= –9
C21 = (–1)2+1 × M21
= –1 × 9
= –9
C31 = (–1)3+1 × M31
= 1 × –9
= –9
C41 = (–1)4+1 × M41
= –1 × 0
= 0
Now expanding along the first column we get
|A| = a11 × C11 + a21× C21+ a31× C31 + a41× C41
= 2 × (–9) + (–3) × –9 + 1 × (–9) + 2 × 0
= – 18 + 27 –9
= 0
2. Evaluate the following determinants:
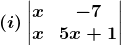
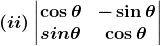
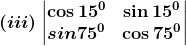
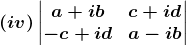
Solution:
(i) Given
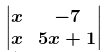
⇒ |A| = x (5x + 1) – (–7) x
|A| = 5x2 + 8x
(ii) Given
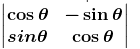
⇒ |A| = cos θ × cos θ – (–sin θ) x sin θ
|A| = cos2θ + sin2θ
We know that cos2θ + sin2θ = 1
|A| = 1
(iii) Given
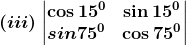
⇒ |A| = cos15° × cos75° + sin15° x sin75°
We know that cos (A – B) = cos A cos B + Sin A sin B
By substituting this we get, |A| = cos (75 – 15)°
|A| = cos60°
|A| = 0.5
(iv) Given
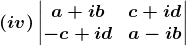
⇒ |A| = (a + ib) (a – ib) – (c + id) (–c + id)
= (a + ib) (a – ib) + (c + id) (c – id)
= a2 – i2 b2 + c2 – i2 d2
We know that i2 = -1
= a2 – (–1) b2 + c2 – (–1) d2
= a2 + b2 + c2 + d2
3. Evaluate:
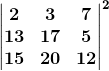
Solution:
Since |AB|= |A||B|
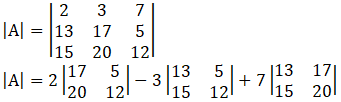
= 2(17 × 12 – 5 × 20) – 3(13 × 12 – 5 × 15) + 7(13 × 20 – 15 × 17)
= 2 (204 – 100) – 3 (156 – 75) + 7 (260 – 255)
= 2×104 – 3×81 + 7×5
= 208 – 243 +35
= 0
Now |A|2 = |A|×|A|
|A|2= 0
4. Show that
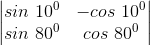
Solution:
Given
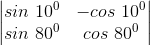
Let the given determinant as A
Using sin (A+B) = sin A × cos B + cos A × sin B
⇒ |A| = sin 10° × cos 80° + cos 10° x sin 80°
|A| = sin (10 + 80)°
|A| = sin90°
|A| = 1
Hence Proved
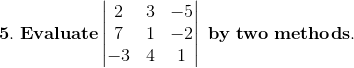
Solution:
Given,
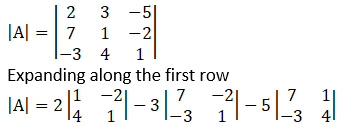
= 2(1 × 1 – 4 × (–2)) – 3(7 × 1 – (–2) × (–3)) – 5(7 × 4 – 1 × (–3))
= 2(1 + 8) – 3(7 – 6) – 5(28 + 3)
= 2 × 9 – 3 × 1 – 5 × 31
= 18 – 3 – 155
= –140
Now by expanding along the second column
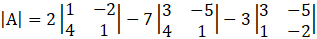
= 2(1 × 1 – 4 × (–2)) – 7(3 × 1 – 4 × (–5)) – 3(3 × (–2) – 1 × (–5))
= 2 (1 + 8) – 7 (3 + 20) – 3 (–6 + 5)
= 2 × 9 – 7 × 23 – 3 × (–1)
= 18 – 161 +3
= –140
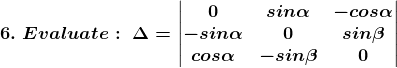
Solution:
Given
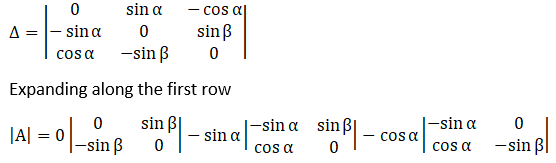
⇒ |A| = 0 (0 – sinβ (–sinβ)) –sinα (–sinα × 0 – sinβ cosα) – cosα ((–sinα) (–sinβ) – 0 × cosα)
|A| = 0 + sinα sinβ cosα – cosα sinα sinβ
|A| = 0
Exercise 6.2 Page No: 6.57
1. Evaluate the following determinant:
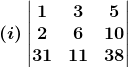

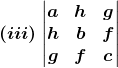
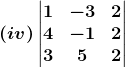
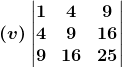
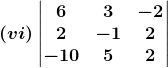
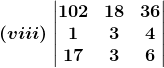
Solution:
(i) Given
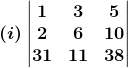
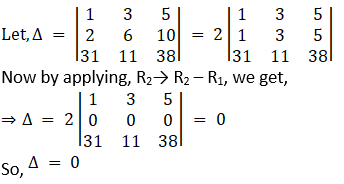
(ii) Given

= 1[(109) (12) – (119) (11)]
= 1308 – 1309
= – 1
So, Δ = – 1
(iii) Given,
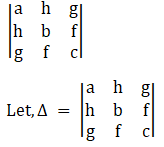
= a (bc – f2) – h (hc – fg) + g (hf – bg)
= abc – af2 – ch2 + fgh + fgh – bg2
= abc + 2fgh – af2 – bg2 – ch2
So, Δ = abc + 2fgh – af2 – bg2 – ch2
(iv) Given

= 2[1(24 – 4)] = 40
So, Δ = 40
(v) Given
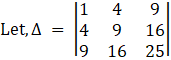

= 1[(– 7) (– 36) – (– 20) (– 13)]
= 252 – 260
= – 8
So, Δ = – 8
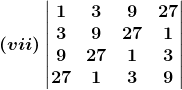
(vi) Given,
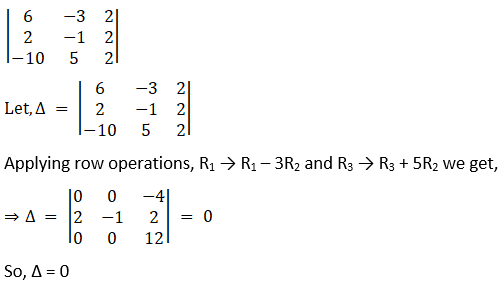
(vii) Given

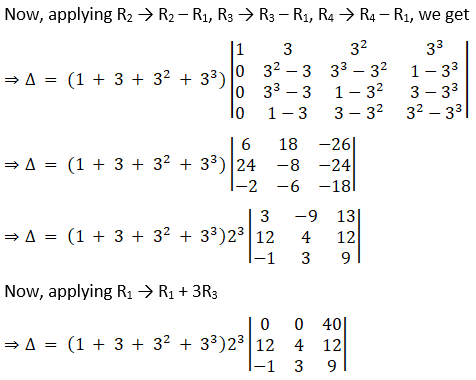
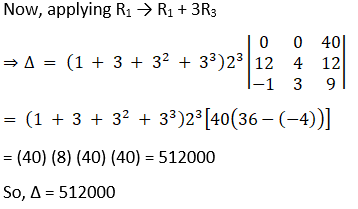
(viii) Given,
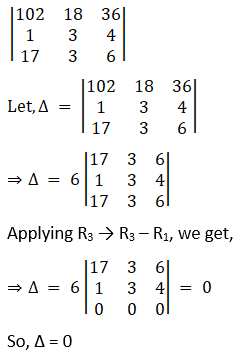
2. Without expanding, show that the value of each of the following determinants is zero:
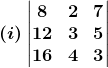
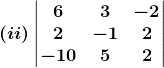
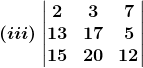
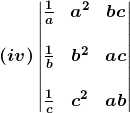
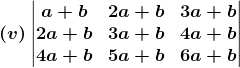
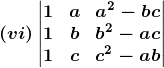
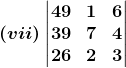
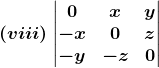
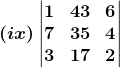
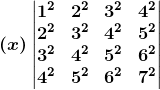
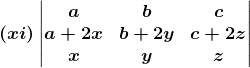
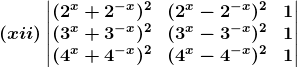
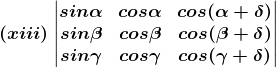
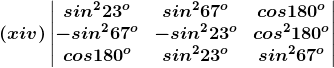
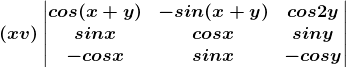
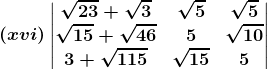
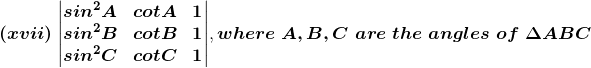
Solution:
(i) Given,

(ii) Given,
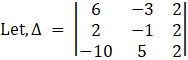
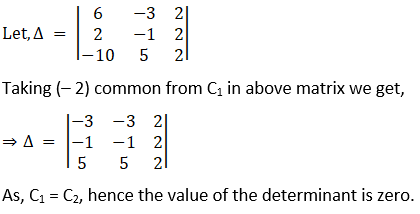
(iii) Given,

(iv) Given,

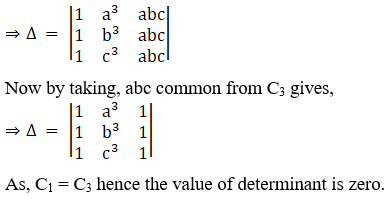
(v) Given,

(vi) Given,
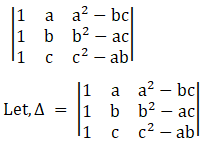
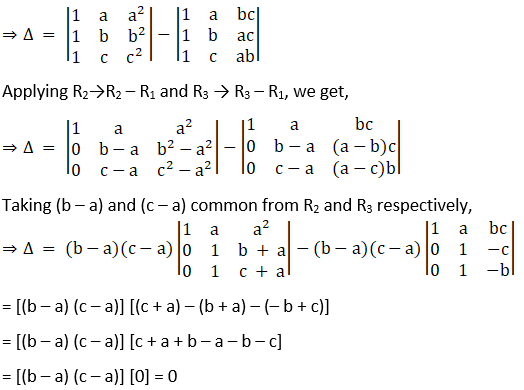
(vii) Given,

(viii) Given,

(ix) Given,

As, C1 = C2, hence determinant is zero
(x) Given,

(xi) Given,
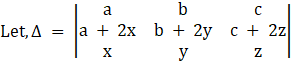
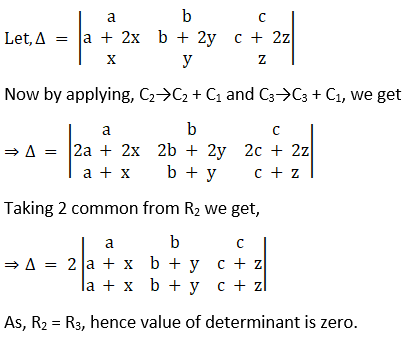
(xii) Given,

(xiii) Given,

(xiv) Given,
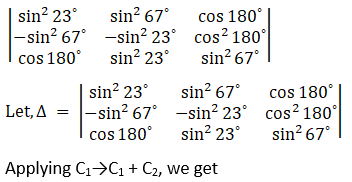
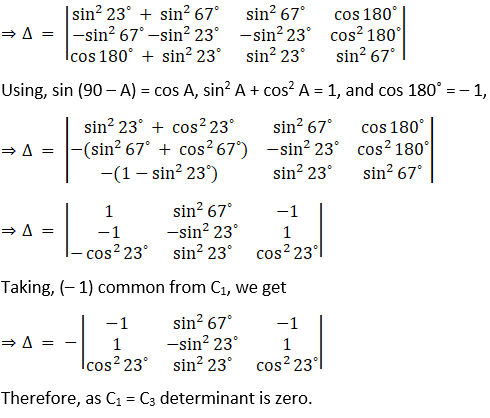
(xv) Given,
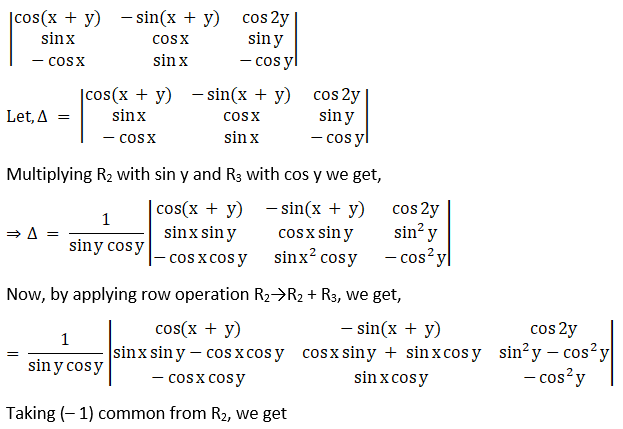
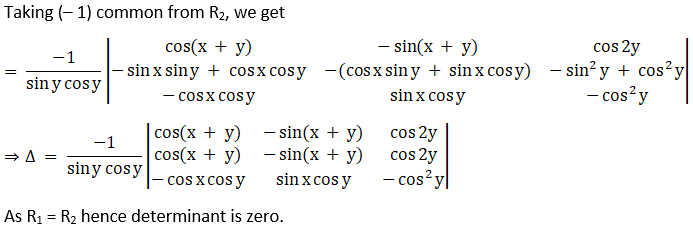
(xvi) Given,


(xvii) Given,
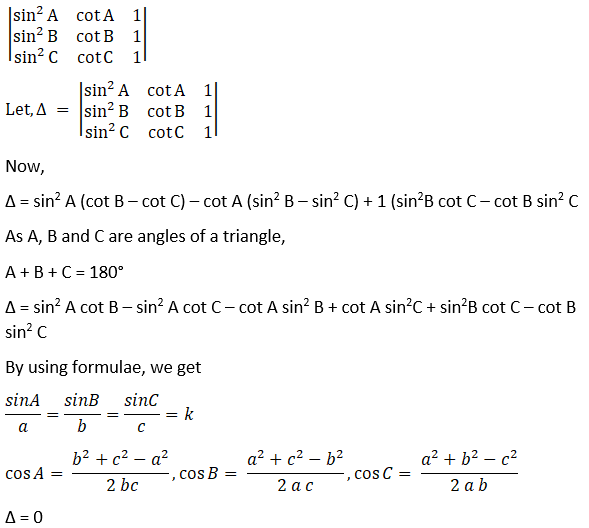
Hence proved.
Evaluate the following (3 – 9):
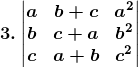
Solution:
Given,

= (a + b + c) (b – a) (c – a) (b – c)
So, Δ = (a + b + c) (b – a) (c – a) (b – c)
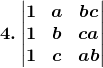
Solution:
Given,

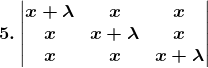
Solution:
Given,
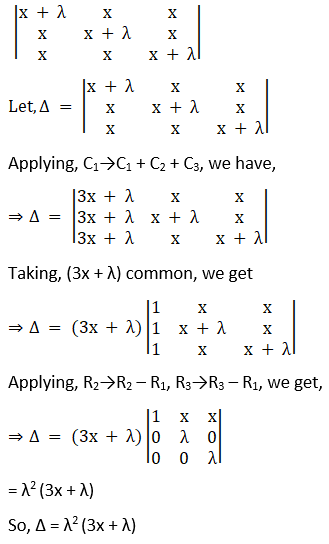
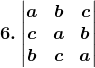
Solution:
Given,


Solution:
Given,

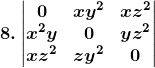
Solution:
Given,
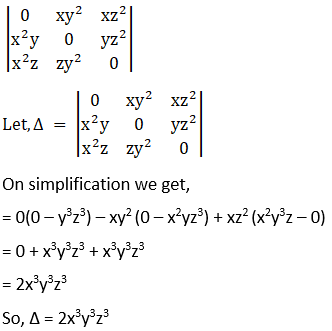
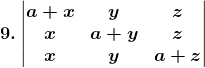
Solution:
Given,

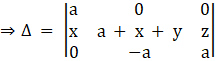
= a [a (a + x + y) + az] + 0 + 0
= a2 (a + x + y + z)
So, Δ = a2 (a + x + y + z)
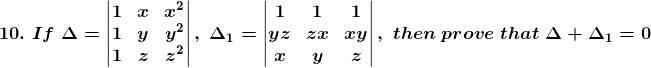
Solution:

Prove the following identities (11 – 45):
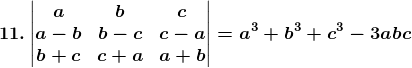
Solution:
Given,
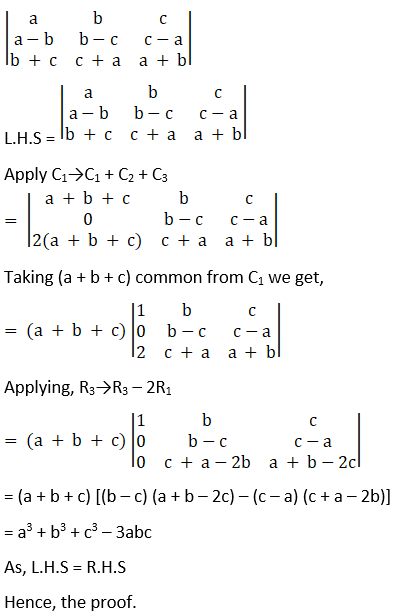
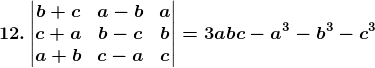
Solution:
Consider,

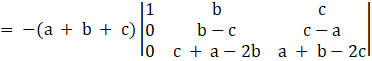
= – (a + b + c) [(b – c) (a + b – 2c) – (c – a) (c + a – 2b)]
= 3abc – a3 – b3 – c3
Therefore, L.H.S = R.H.S,
Hence the proof.
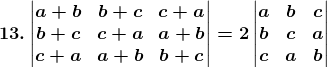
Solution:
Given,


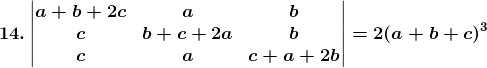
Solution:
Consider,
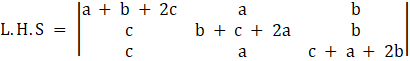 ,
,

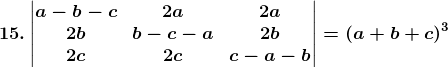
Solution:
Consider,
L.H.S =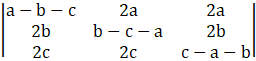
Now by applying, R1→R1 + R2 + R3, we get,
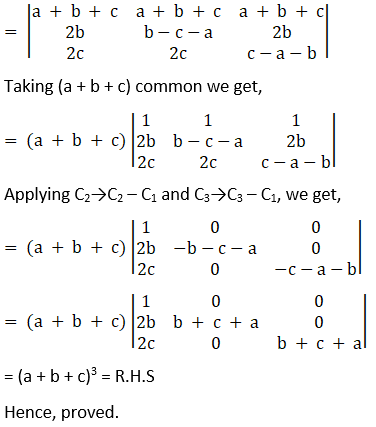
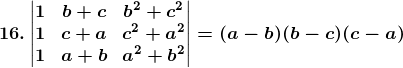
Solution:
Consider,
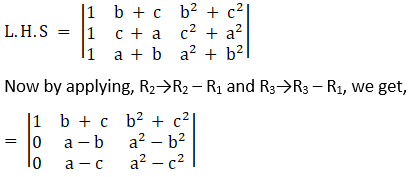
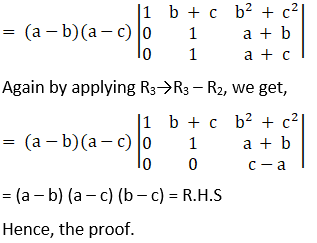
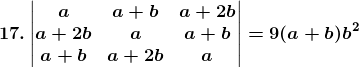
Solution:
Consider,
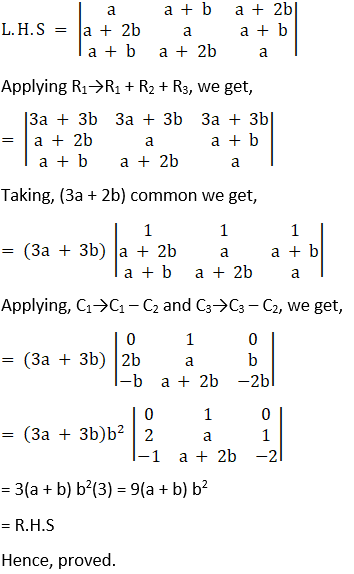
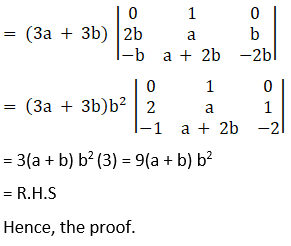
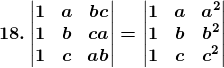
Solution:
Consider,
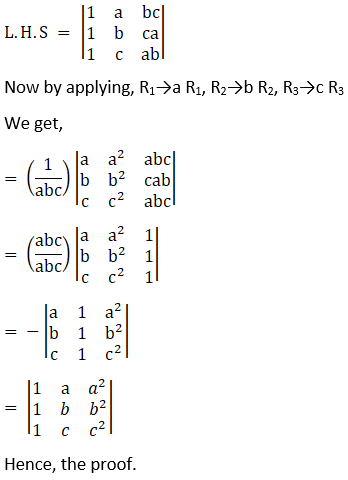
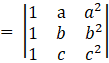
Hence, the proof.
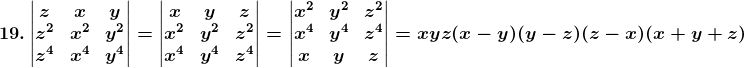
Solution:
Given,

= – xyz(x – y) (z – y) [z2 + y2 + zy – x2 – y2 – xy]
= – xyz(x – y) (z – y) [(z – x) (z + x0 + y (z – x)]
= – xyz(x – y) (z – y) (z – x) (x + y + z)
= R.H.S
Hence, the proof.
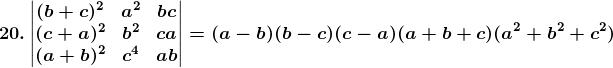
Solution:
Consider,

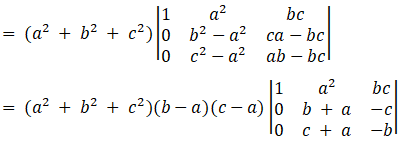
= (a2 + b2 + c2) (b – a) (c – a) [(b + a) (– b) – (– c) (c + a)]
= (a2 + b2 + c2) (a – b) (c – a) (b – c) (a + b + c)
= R.H.S
Hence, the proof.
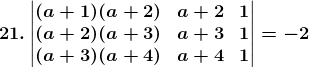
Solution:
Consider,

= [(2a + 4) (1) – (1) (2a + 6)]
= – 2
= R.H.S
Hence, the proof.
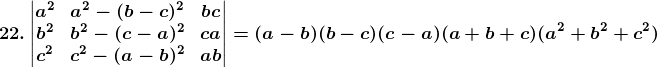
Solution:
Consider,
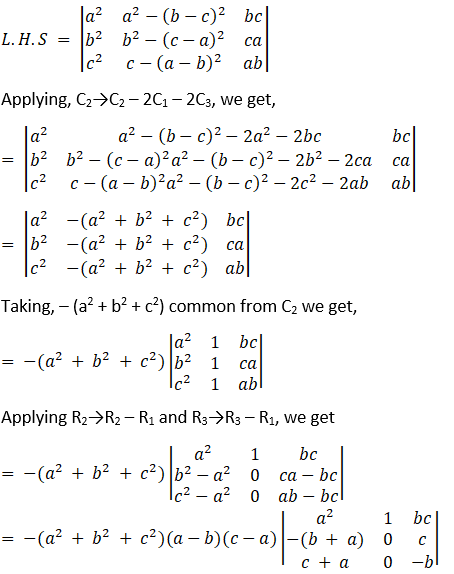
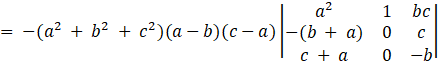
= – (a2 + b2 + c2) (a – b) (c – a) [(– (b + a)) (– b) – (c) (c + a)]
= (a – b) (b – c) (c – a) (a + b + c) (a2 + b2 + c2)
= R.H.S
Hence, the proof.
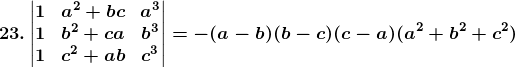
Solution:
Consider,
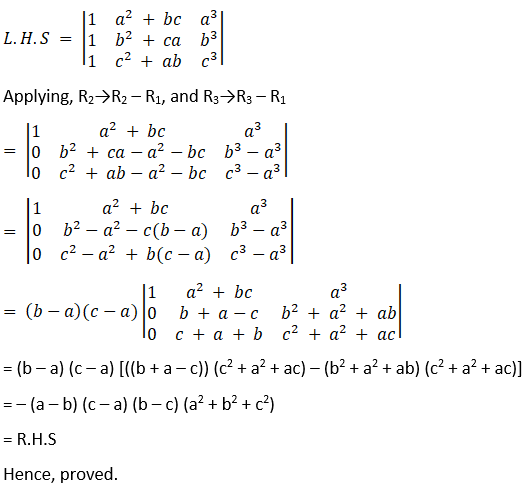
= R.H.S
Hence, the proof.
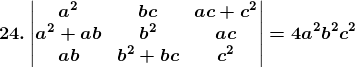
Solution:
Consider,


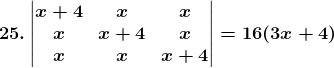
Solution:
Consider,
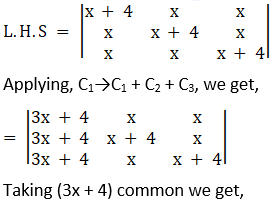
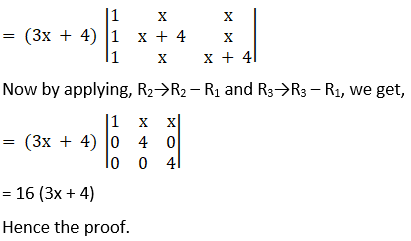
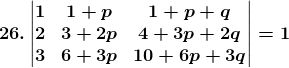
Solution:

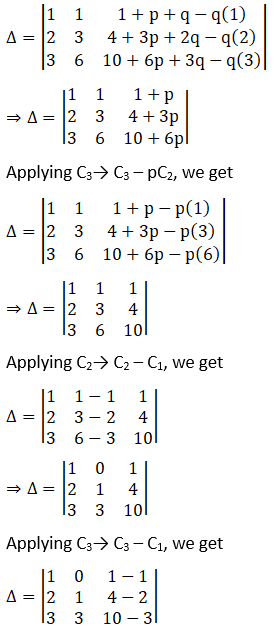
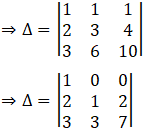
Expanding the determinant along R1, we have
Δ = 1[(1) (7) – (3) (2)] – 0 + 0
∴ Δ = 7 – 6 = 1
Thus,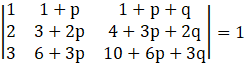
Hence the proof.
Exercise 6.3 Page No: 6.71
1. Find the area of the triangle with vertices at the points:
(i) (3, 8), (-4, 2) and (5, -1)
(ii) (2, 7), (1, 1) and (10, 8)
(iii) (-1, -8), (-2, -3) and (3, 2)
(iv) (0, 0), (6, 0) and (4, 3)
Solution:
(i) Given (3, 8), (-4, 2) and (5, -1) are the vertices of the triangle.
We know that, if vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by:

(ii) Given (2, 7), (1, 1) and (10, 8) are the vertices of the triangle.
We know that if vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by:

(iii) Given (-1, -8), (-2, -3) and (3, 2) are the vertices of the triangle.
We know that if vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by:
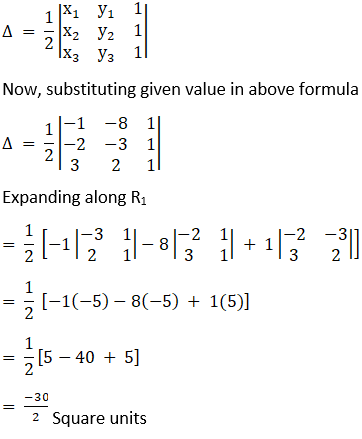
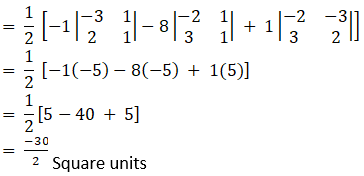
As we know area cannot be negative. Therefore, 15 square unit is the area
Thus area of triangle is 15 square units
(iv) Given (-1, -8), (-2, -3) and (3, 2) are the vertices of the triangle.
We know that if vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by:

2. Using the determinants show that the following points are collinear:
(i) (5, 5), (-5, 1) and (10, 7)
(ii) (1, -1), (2, 1) and (10, 8)
(iii) (3, -2), (8, 8) and (5, 2)
(iv) (2, 3), (-1, -2) and (5, 8)
Solution:
(i) Given (5, 5), (-5, 1) and (10, 7)
We have the condition that three points to be collinear, the area of the triangle formed by these points will be zero. Now, we know that, vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by
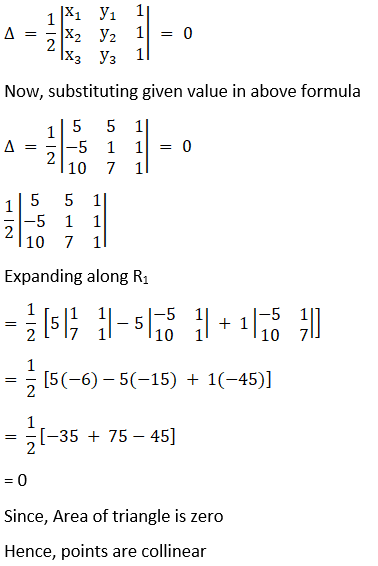
(ii) Given (1, -1), (2, 1) and (10, 8)
We have the condition that three points to be collinear, the area of the triangle formed by these points will be zero. Now, we know that, vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by,

(iii) Given (3, -2), (8, 8) and (5, 2)
We have the condition that three points to be collinear, the area of the triangle formed by these points will be zero. Now, we know that, vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by,
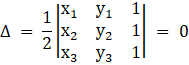
Now, by substituting given value in above formula
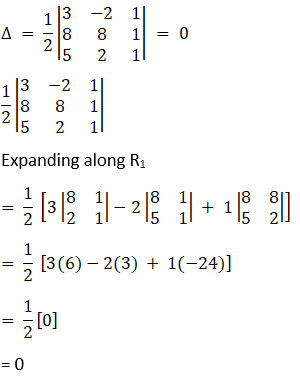
Since, Area of triangle is zero
Hence, points are collinear.
(iv) Given (2, 3), (-1, -2) and (5, 8)
We have the condition that three points to be collinear, the area of the triangle formed by these points will be zero. Now, we know that, vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by,

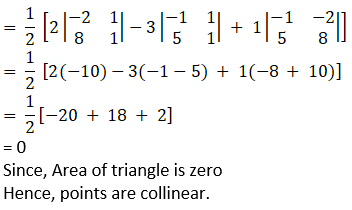
3. If the points (a, 0), (0, b) and (1, 1) are collinear, prove that a + b = ab
Solution:
Given (a, 0), (0, b) and (1, 1) are collinear
We have the condition that three points to be collinear, the area of the triangle formed by these points will be zero. Now, we know that, vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by,
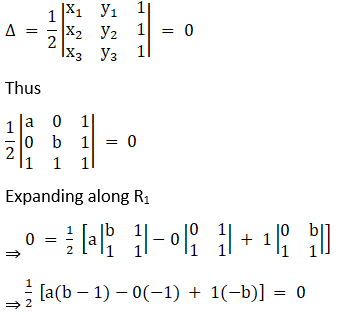
⇒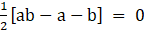
⇒ a + b = ab
Hence Proved
4. Using the determinants prove that the points (a, b), (a’, b’) and (a – a’, b – b) are collinear if a b’ = a’ b.
Solution:
Given (a, b), (a’, b’) and (a – a’, b – b) are collinear
We have the condition that three points to be collinear, the area of the triangle formed by these points will be zero. Now, we know that, vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by,
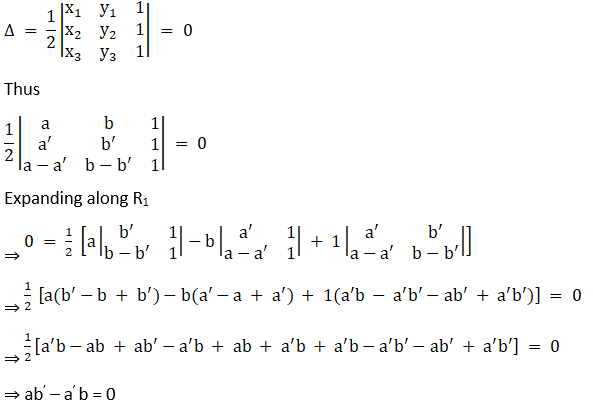
⇒ a b’ = a’ b
Hence, the proof.
5. Find the value of λ so that the points (1, -5), (-4, 5) and (λ, 7) are collinear.
Solution:
Given (1, -5), (-4, 5) and (λ, 7) are collinear
We have the condition that three points to be collinear, the area of the triangle formed by these points will be zero. Now, we know that, vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by,
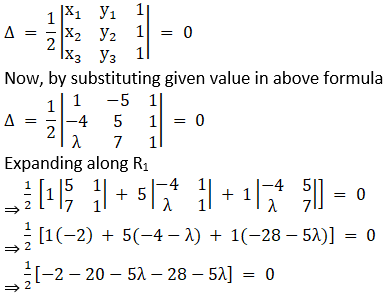
⇒ – 50 – 10λ = 0
⇒ λ = – 5
6. Find the value of x if the area of ∆ is 35 square cms with vertices (x, 4), (2, -6) and (5, 4).
Solution:
Given (x, 4), (2, -6) and (5, 4) are the vertices of a triangle.
We have the condition that three points to be collinear, the area of the triangle formed by these points will be zero. Now, we know that, vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by,

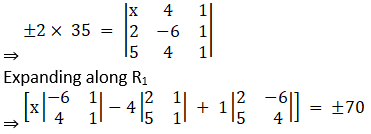
⇒ [x (– 10) – 4(– 3) + 1(8 – 30)] = ± 70
⇒ [– 10x + 12 + 38] = ± 70
⇒ ±70 = – 10x + 50
Taking positive sign, we get
⇒ + 70 = – 10x + 50
⇒ 10x = – 20
⇒ x = – 2
Taking –negative sign, we get
⇒ – 70 = – 10x + 50
⇒ 10x = 120
⇒ x = 12
Thus x = – 2, 12
Exercise 6.4 Page No: 6.84
Solve the following system of linear equations by Cramer’s rule:
1. x – 2y = 4
-3x + 5y = -7
Solution:
Given x – 2y = 4
-3x + 5y = -7
Let there be a system of n simultaneous linear equations and with n unknown given by

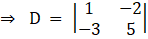
Solving determinant, expanding along 1st row
⇒ D = 5(1) – (– 3) (– 2)
⇒ D = 5 – 6
⇒ D = – 1
Again,
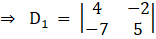
Solving determinant, expanding along 1st row
⇒ D1 = 5(4) – (– 7) (– 2)
⇒ D1 = 20 – 14
⇒ D1 = 6
And
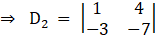
Solving determinant, expanding along 1st row
⇒ D2 = 1(– 7) – (– 3) (4)
⇒ D2 = – 7 + 12
⇒ D2 = 5
Thus by Cramer’s Rule, we have
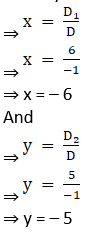
2. 2x – y = 1
7x – 2y = -7
Solution:
Given 2x – y = 1 and
7x – 2y = -7
Let there be a system of n simultaneous linear equations and with n unknown given by

Solving determinant, expanding along 1st row
⇒ D1 = 1(– 2) – (– 7) (– 1)
⇒ D1 = – 2 – 7
⇒ D1 = – 9
And
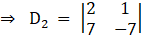
Solving determinant, expanding along 1st row
⇒ D2 = 2(– 7) – (7) (1)
⇒ D2 = – 14 – 7
⇒ D2 = – 21
Thus by Cramer’s Rule, we have
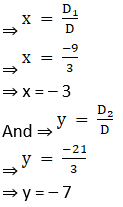
3. 2x – y = 17
3x + 5y = 6
Solution:
Given 2x – y = 17 and
3x + 5y = 6
Let there be a system of n simultaneous linear equations and with n unknown given by


Solving determinant, expanding along 1st row
⇒ D1 = 17(5) – (6) (– 1)
⇒ D1 = 85 + 6
⇒ D1 = 91
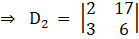
Solving determinant, expanding along 1st row
⇒ D2 = 2(6) – (17) (3)
⇒ D2 = 12 – 51
⇒ D2 = – 39
Thus by Cramer’s Rule, we have
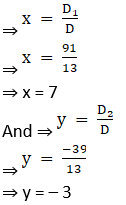
4. 3x + y = 19
3x – y = 23
Solution:
Let there be a system of n simultaneous linear equations and with n unknown given by

Solving determinant, expanding along 1st row
⇒ D = 3(– 1) – (3) (1)
⇒ D = – 3 – 3
⇒ D = – 6
Again,
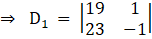
Solving determinant, expanding along 1st row
⇒ D1 = 19(– 1) – (23) (1)
⇒ D1 = – 19 – 23
⇒ D1 = – 42
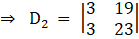
Solving determinant, expanding along 1st row
⇒ D2 = 3(23) – (19) (3)
⇒ D2 = 69 – 57
⇒ D2 = 12
Thus by Cramer’s Rule, we have
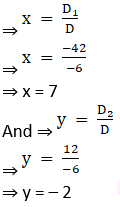
5. 2x – y = -2
3x + 4y = 3
Solution:
Given 2x – y = -2 and
3x + 4y = 3
Let there be a system of n simultaneous linear equations and with n unknown given by
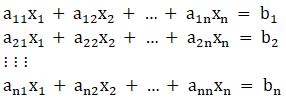

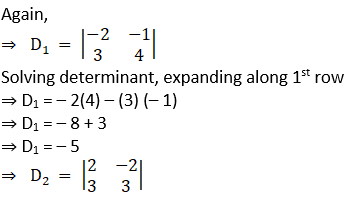
Solving determinant, expanding along 1st row
⇒ D2 = 3(2) – (– 2) (3)
⇒ D2 = 6 + 6
⇒ D2 = 12
Thus by Cramer’s Rule, we have
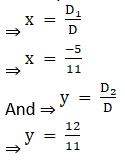
6. 3x + ay = 4
2x + ay = 2, a ≠ 0
Solution:
Given 3x + ay = 4 and
2x + ay = 2, a ≠ 0
Let there be a system of n simultaneous linear equations and with n unknown given by

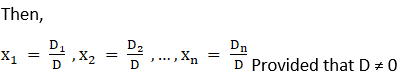
3x + ay = 4
2x + ay = 2, a≠0
So by comparing with the theorem, let’s find D, D1 and D2
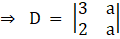
Solving determinant, expanding along 1st row
⇒ D = 3(a) – (2) (a)
⇒ D = 3a – 2a
⇒ D = a
Again,
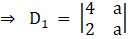
Solving determinant, expanding along 1st row
⇒ D1 = 4(a) – (2) (a)
⇒ D = 4a – 2a
⇒ D = 2a
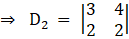
Solving determinant, expanding along 1st row
⇒ D2 = 3(2) – (2) (4)
⇒ D = 6 – 8
⇒ D = – 2
Thus by Cramer’s Rule, we have
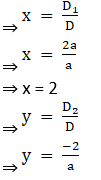
7. 2x + 3y = 10
x + 6y = 4
Solution:
Let there be a system of n simultaneous linear equations and with n unknown given by

Solving determinant, expanding along 1st row
⇒ D = 2 (6) – (3) (1)
⇒ D = 12 – 3
⇒ D = 9
Again,
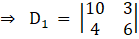
Solving determinant, expanding along 1st row
⇒ D1 = 10 (6) – (3) (4)
⇒ D = 60 – 12
⇒ D = 48
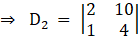
Solving determinant, expanding along 1st row
⇒ D2 = 2 (4) – (10) (1)
⇒ D2 = 8 – 10
⇒ D2 = – 2
Thus by Cramer’s Rule, we have
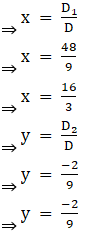
8. 5x + 7y = -2
4x + 6y = -3
Solution:
Let there be a system of n simultaneous linear equations and with n unknown given by
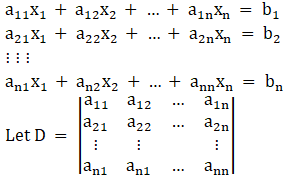

Now, here we have
5x + 7y = – 2
4x + 6y = – 3
So by comparing with the theorem, let’s find D, D1 and D2
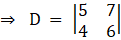
Solving determinant, expanding along 1st row
⇒ D = 5(6) – (7) (4)
⇒ D = 30 – 28
⇒ D = 2
Again,
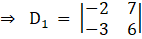
Solving determinant, expanding along 1st row
⇒ D1 = – 2(6) – (7) (– 3)
⇒ D1 = – 12 + 21
⇒ D1 = 9
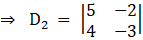
Solving determinant, expanding along 1st row
⇒ D2 = – 3(5) – (– 2) (4)
⇒ D2 = – 15 + 8
⇒ D2 = – 7
Thus by Cramer’s Rule, we have
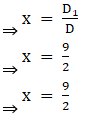
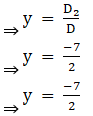
9. 9x + 5y = 10
3y – 2x = 8
Solution:
Let there be a system of n simultaneous linear equations and with n unknown given by

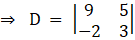
Solving determinant, expanding along 1st row
⇒ D = 3(9) – (5) (– 2)
⇒ D = 27 + 10
⇒ D = 37
Again,
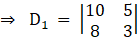
Solving determinant, expanding along 1st row
⇒ D1 = 10(3) – (8) (5)
⇒ D1 = 30 – 40
⇒ D1 = – 10
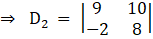
Solving determinant, expanding along 1st row
⇒ D2 = 9(8) – (10) (– 2)
⇒ D2 = 72 + 20
⇒ D2 = 92
Thus by Cramer’s Rule, we have
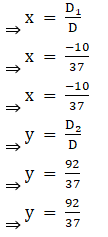
10. x + 2y = 1
3x + y = 4
Solution:
Let there be a system of n simultaneous linear equations and with n unknown given by

Solving determinant, expanding along 1st row
⇒ D = 1(1) – (3) (2)
⇒ D = 1 – 6
⇒ D = – 5
Again,
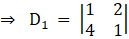
Solving determinant, expanding along 1st row
⇒ D1 = 1(1) – (2) (4)
⇒ D1 = 1 – 8
⇒ D1 = – 7
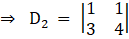
Solving determinant, expanding along 1st row
⇒ D2 = 1(4) – (1) (3)
⇒ D2 = 4 – 3
⇒ D2 = 1
Thus by Cramer’s Rule, we have
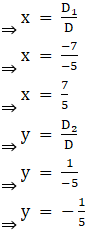
Solve the following system of linear equations by Cramer’s rule:
11. 3x + y + z = 2
2x – 4y + 3z = -1
4x + y – 3z = -11
Solution:
Let there be a system of n simultaneous linear equations and with n unknown given by

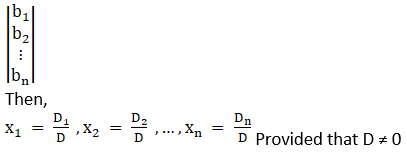
Now, here we have
3x + y + z = 2
2x – 4y + 3z = – 1
4x + y – 3z = – 11
So by comparing with the theorem, let’s find D, D1, D2 and D3
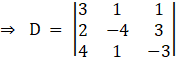
Solving determinant, expanding along 1st row
⇒ D = 3[(– 4) (– 3) – (3) (1)] – 1[(2) (– 3) – 12] + 1[2 – 4(– 4)]
⇒ D = 3[12 – 3] – [– 6 – 12] + [2 + 16]
⇒ D = 27 + 18 + 18
⇒ D = 63
Again,
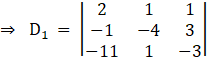
Solving determinant, expanding along 1st row
⇒ D1 = 2[( – 4)( – 3) – (3)(1)] – 1[( – 1)( – 3) – ( – 11)(3)] + 1[( – 1) – ( – 4)( – 11)]
⇒ D1 = 2[12 – 3] – 1[3 + 33] + 1[– 1 – 44]
⇒ D1 = 2[9] – 36 – 45
⇒ D1 = 18 – 36 – 45
⇒ D1 = – 63
Again
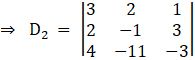
Solving determinant, expanding along 1st row
⇒ D2 = 3[3 + 33] – 2[– 6 – 12] + 1[– 22 + 4]
⇒ D2 = 3[36] – 2(– 18) – 18
⇒ D2 = 126
⇒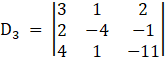
Solving determinant, expanding along 1st row
⇒ D3 = 3[44 + 1] – 1[– 22 + 4] + 2[2 + 16]
⇒ D3 = 3[45] – 1(– 18) + 2(18)
⇒ D3 = 135 + 18 + 36
⇒ D3 = 189
Thus by Cramer’s Rule, we have
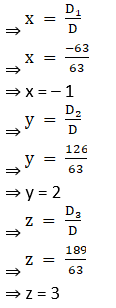
12. x – 4y – z = 11
2x – 5y + 2z = 39
-3x + 2y + z = 1
Solution:
Given,
x – 4y – z = 11
2x – 5y + 2z = 39
-3x + 2y + z = 1
Let there be a system of n simultaneous linear equations and with n unknown given by

Now, here we have
x – 4y – z = 11
2x – 5y + 2z = 39
– 3x + 2y + z = 1
So by comparing with theorem, now we have to find D, D1 and D2
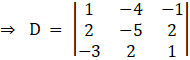
Solving determinant, expanding along 1st row
⇒ D = 1[(– 5) (1) – (2) (2)] + 4[(2) (1) + 6] – 1[4 + 5(– 3)]
⇒ D = 1[– 5 – 4] + 4[8] – [– 11]
⇒ D = – 9 + 32 + 11
⇒ D = 34
Again,
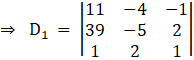
Solving determinant, expanding along 1st row
⇒ D1 = 11[(– 5) (1) – (2) (2)] + 4[(39) (1) – (2) (1)] – 1[2 (39) – (– 5) (1)]
⇒ D1 = 11[– 5 – 4] + 4[39 – 2] – 1[78 + 5]
⇒ D1 = 11[– 9] + 4(37) – 83
⇒ D1 = – 99 – 148 – 45
⇒ D1 = – 34
Again
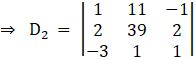
Solving determinant, expanding along 1st row
⇒ D2 = 1[39 – 2] – 11[2 + 6] – 1[2 + 117]
⇒ D2 = 1[37] – 11(8) – 119
⇒ D2 = – 170
And,
⇒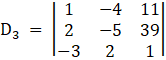
Solving determinant, expanding along 1st row
⇒ D3 = 1[– 5 – (39) (2)] – (– 4) [2 – (39) (– 3)] + 11[4 – (– 5)(– 3)]
⇒ D3 = 1 [– 5 – 78] + 4 (2 + 117) + 11 (4 – 15)
⇒ D3 = – 83 + 4(119) + 11(– 11)
⇒ D3 = 272
Thus by Cramer’s Rule, we have
13. 6x + y – 3z = 5
x + 3y – 2z = 5
2x + y + 4z = 8
Solution:
Given
6x + y – 3z = 5
x + 3y – 2z = 5
2x + y + 4z = 8
Let there be a system of n simultaneous linear equations and with n unknown given by

Now, here we have
6x + y – 3z = 5
x + 3y – 2z = 5
2x + y + 4z = 8
So by comparing with theorem, now we have to find D , D1 and D2
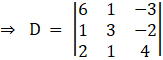
Solving determinant, expanding along 1st Row
⇒ D = 6[(4) (3) – (1) (– 2)] – 1[(4) (1) + 4] – 3[1 – 3(2)]
⇒ D = 6[12 + 2] – [8] – 3[– 5]
⇒ D = 84 – 8 + 15
⇒ D = 91
Again, Solve D1 formed by replacing 1st column by B matrices
Here
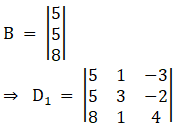
Solving determinant, expanding along 1st Row
⇒ D1 = 5[(4) (3) – (– 2) (1)] – 1[(5) (4) – (– 2) (8)] – 3[(5) – (3) (8)]
⇒ D1 = 5[12 + 2] – 1[20 + 16] – 3[5 – 24]
⇒ D1 = 5[14] – 36 – 3(– 19)
⇒ D1 = 70 – 36 + 57
⇒ D1 = 91
Again, Solve D2 formed by replacing 1st column by B matrices
Here
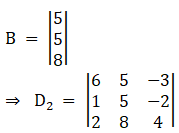
Solving determinant
⇒ D2 = 6[20 + 16] – 5[4 – 2(– 2)] + (– 3)[8 – 10]
⇒ D2 = 6[36] – 5(8) + (– 3) (– 2)
⇒ D2 = 182
And, Solve D3 formed by replacing 1st column by B matrices
Here
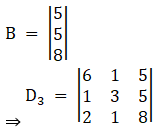
Solving determinant, expanding along 1st Row
⇒ D3 = 6[24 – 5] – 1[8 – 10] + 5[1 – 6]
⇒ D3 = 6[19] – 1(– 2) + 5(– 5)
⇒ D3 = 114 + 2 – 25
⇒ D3 = 91
Thus by Cramer’s Rule, we have
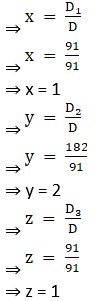
14. x + y = 5
y + z = 3
x + z = 4
Solution:
Given x + y = 5
y + z = 3
x + z = 4
Let there be a system of n simultaneous linear equations and with n unknown given by
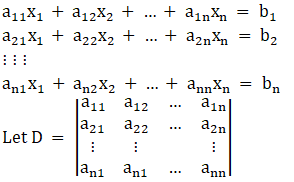
Let Dj be the determinant obtained from D after replacing the jth column by
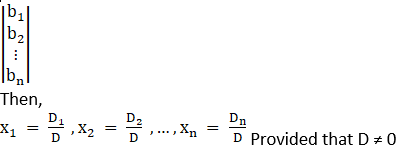
Now, here we have
x + y = 5
y + z = 3
x + z = 4
So by comparing with theorem, now we have to find D, D1 and D2
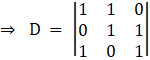
Solving determinant, expanding along 1st Row
⇒ D = 1[1] – 1[– 1] + 0[– 1]
⇒ D = 1 + 1 + 0
⇒ D = 2
Again, Solve D1 formed by replacing 1st column by B matrices
Here
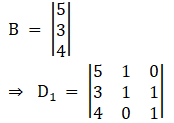
Solving determinant, expanding along 1st Row
⇒ D1 = 5[1] – 1[(3) (1) – (4) (1)] + 0[0 – (4) (1)]
⇒ D1 = 5 – 1[3 – 4] + 0[– 4]
⇒ D1 = 5 – 1[– 1] + 0
⇒ D1 = 5 + 1 + 0
⇒ D1 = 6
Again, Solve D2 formed by replacing 1st column by B matrices
Here
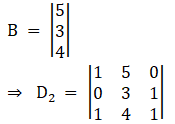
Solving determinant
⇒ D2 = 1[3 – 4] – 5[– 1] + 0[0 – 3]
⇒ D2 = 1[– 1] + 5 + 0
⇒ D2 = 4
And, Solve D3 formed by replacing 1st column by B matrices
Here
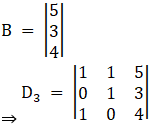
Solving determinant, expanding along 1st Row
⇒ D3 = 1[4 – 0] – 1[0 – 3] + 5[0 – 1]
⇒ D3 = 1[4] – 1(– 3) + 5(– 1)
⇒ D3 = 4 + 3 – 5
⇒ D3 = 2
Thus by Cramer’s Rule, we have
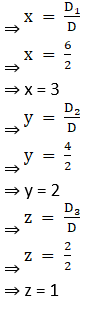
15. 2y – 3z = 0
x + 3y = -4
3x + 4y = 3
Solution:
Given
2y – 3z = 0
x + 3y = -4
3x + 4y = 3
Let there be a system of n simultaneous linear equations and with n unknown given by

Now, here we have
2y – 3z = 0
x + 3y = – 4
3x + 4y = 3
So by comparing with theorem, now we have to find D, D1 and D2
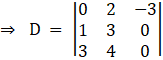
Solving determinant, expanding along 1st Row
⇒ D = 0[0] – 2[(0) (1) – 0] – 3[1 (4) – 3 (3)]
⇒ D = 0 – 0 – 3[4 – 9]
⇒ D = 0 – 0 + 15
⇒ D = 15
Again, Solve D1 formed by replacing 1st column by B matrices
Here
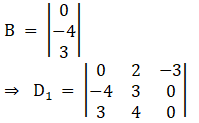
Solving determinant, expanding along 1st Row
⇒ D1 = 0[0] – 2[(0) (– 4) – 0] – 3[4 (– 4) – 3(3)]
⇒ D1 = 0 – 0 – 3[– 16 – 9]
⇒ D1 = 0 – 0 – 3(– 25)
⇒ D1 = 0 – 0 + 75
⇒ D1 = 75
Again, Solve D2 formed by replacing 2nd column by B matrices
Here
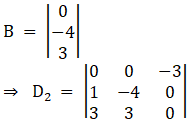
Solving determinant
⇒ D2 = 0[0] – 0[(0) (1) – 0] – 3[1 (3) – 3(– 4)]
⇒ D2 = 0 – 0 + (– 3) (3 + 12)
⇒ D2 = – 45
And, Solve D3 formed by replacing 3rd column by B matrices
Here
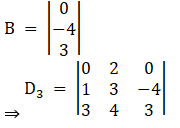
Solving determinant, expanding along 1st Row
⇒ D3 = 0[9 – (– 4) 4] – 2[(3) (1) – (– 4) (3)] + 0[1 (4) – 3 (3)]
⇒ D3 = 0[25] – 2(3 + 12) + 0(4 – 9)
⇒ D3 = 0 – 30 + 0
⇒ D3 = – 30
Thus by Cramer’s Rule, we have
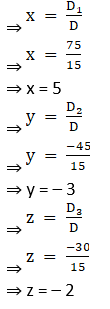
16. 5x – 7y + z = 11
6x – 8y – z = 15
3x + 2y – 6z = 7
Solution:
Given
5x – 7y + z = 11
6x – 8y – z = 15
3x + 2y – 6z = 7
Let there be a system of n simultaneous linear equations and with n unknown given by

Now, here we have
5x – 7y + z = 11
6x – 8y – z = 15
3x + 2y – 6z = 7
So by comparing with theorem, now we have to find D, D1 and D2
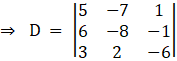
Solving determinant, expanding along 1st Row
⇒ D = 5[(– 8) (– 6) – (– 1) (2)] – 7[(– 6) (6) – 3(– 1)] + 1[2(6) – 3(– 8)]
⇒ D = 5[48 + 2] – 7[– 36 + 3] + 1[12 + 24]
⇒ D = 250 – 231 + 36
⇒ D = 55
Again, Solve D1 formed by replacing 1st column by B matrices
Here
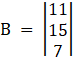
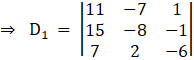
Solving determinant, expanding along 1st Row
⇒ D1 = 11[(– 8) (– 6) – (2) (– 1)] – (– 7) [(15) (– 6) – (– 1) (7)] + 1[(15)2 – (7) (– 8)]
⇒ D1 = 11[48 + 2] + 7[– 90 + 7] + 1[30 + 56]
⇒ D1 = 11[50] + 7[– 83] + 86
⇒ D1 = 550 – 581 + 86
⇒ D1 = 55
Again, Solve D2 formed by replacing 2nd column by B matrices
Here
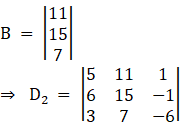
Solving determinant, expanding along 1st Row
⇒ D2 = 5[(15) (– 6) – (7) (– 1)] – 11 [(6) (– 6) – (– 1) (3)] + 1[(6)7 – (15) (3)]
⇒ D2 = 5[– 90 + 7] – 11[– 36 + 3] + 1[42 – 45]
⇒ D2 = 5[– 83] – 11(– 33) – 3
⇒ D2 = – 415 + 363 – 3
⇒ D2 = – 55
And, Solve D3 formed by replacing 3rd column by B matrices
Here
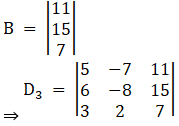
Solving determinant, expanding along 1st Row
⇒ D3 = 5[(– 8) (7) – (15) (2)] – (– 7) [(6) (7) – (15) (3)] + 11[(6)2 – (– 8) (3)]
⇒ D3 = 5[– 56 – 30] – (– 7) [42 – 45] + 11[12 + 24]
⇒ D3 = 5[– 86] + 7[– 3] + 11[36]
⇒ D3 = – 430 – 21 + 396
⇒ D3 = – 55
Thus by Cramer’s Rule, we have
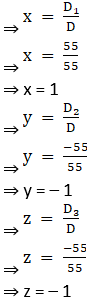
Exercise 6.5 Page No: 6.89
Solve each of the following system of homogeneous linear equations:
1. x + y – 2z = 0
2x + y – 3z =0
5x + 4y – 9z = 0
Solution:
Given x + y – 2z = 0
2x + y – 3z =0
5x + 4y – 9z = 0
Any system of equation can be written in matrix form as AX = B
Now finding the Determinant of these set of equations,
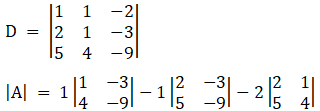
= 1(1 × (– 9) – 4 × (– 3)) – 1(2 × (– 9) – 5 × (– 3)) – 2(4 × 2 – 5 × 1)
= 1(– 9 + 12) – 1(– 18 + 15) – 2(8 – 5)
= 1 × 3 –1 × (– 3) – 2 × 3
= 3 + 3 – 6
= 0
Since D = 0, so the system of equation has infinite solution.
Now let z = k
⇒ x + y = 2k
And 2x + y = 3k
Now using the Cramer’s rule
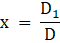
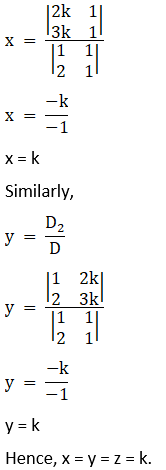
2. 2x + 3y + 4z = 0
x + y + z = 0
2x + 5y – 2z = 0
Solution:
Given
2x + 3y + 4z = 0
x + y + z = 0
2x + 5y – 2z = 0
Any system of equation can be written in matrix form as AX = B
Now finding the Determinant of these set of equations,
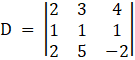
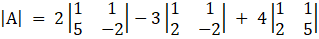
= 2(1 × (– 2) – 1 × 5) – 3(1 × (– 2) – 2 × 1) + 4(1 × 5 – 2 × 1)
= 2(– 2 – 5) – 3(– 2 – 2) + 4(5 – 2)
= 1 × (– 7) – 3 × (– 4) + 4 × 3
= – 7 + 12 + 12
= 17
Since D ≠ 0, so the system of equation has infinite solution.
Therefore, the system of equation has only solution as x = y = z = 0.