Chapter 4 INVERSE TRIGONOMETRIC FUNCTION

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 4 – Inverse Trigonometric Functions

Exercise 4.1 Page No: 4.6

1. Find the principal value of the following:

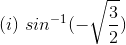
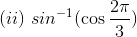
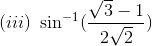
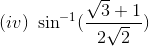
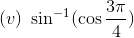
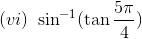
Solution:

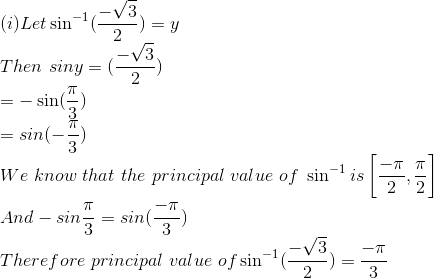
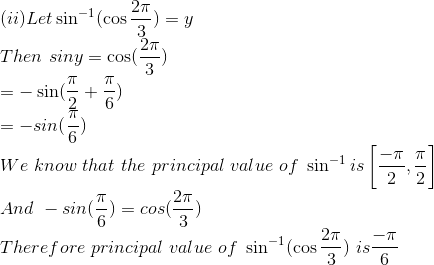
(iii) Given functions can be written as

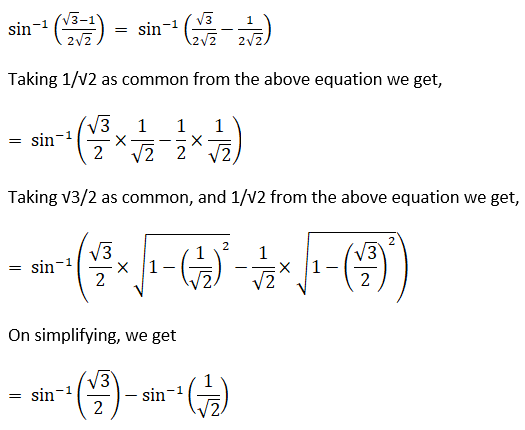
(iv) The given question can be written as

(v) Let

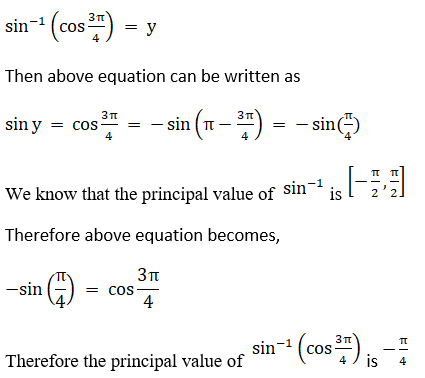
(vi) Let

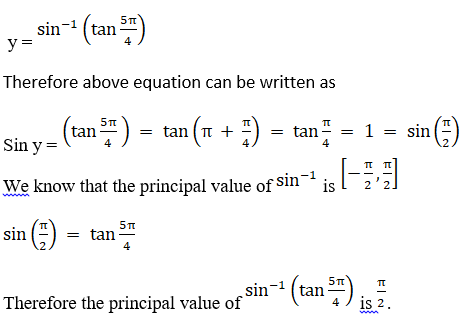
2.

(i)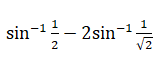

(ii)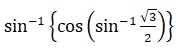

Solution:

(i) The given question can be written as,

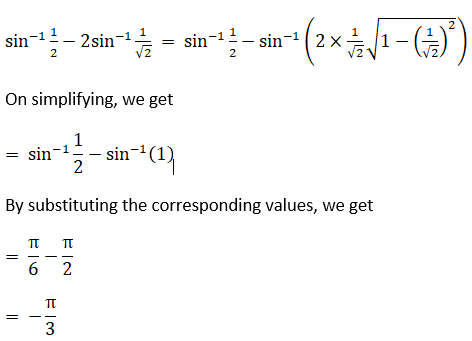
(ii) Given question can be written as

---

---

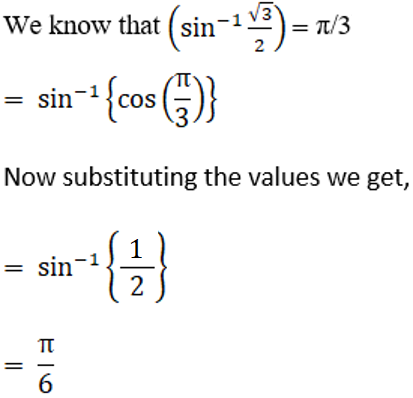
Exercise 4.2 Page No: 4.10

1. Find the domain of definition of f(x) = cos ^-1 (x² – 4)

Solution:

Given f(x) = cos ^-1 (x² – 4)

We know that domain of cos^-1 (x² – 4) lies in the interval [-1, 1]

Therefore, we can write as

-1 ≤ x² – 4 ≤ 1

4 – 1 ≤ x² ≤ 1 + 4

3 ≤ x² ≤ 5

±√ 3 ≤ x ≤ ±√5

– √5 ≤ x ≤ – √3 and √3 ≤ x ≤ √5

Therefore domain of cos^-1 (x² – 4) is [- √5, – √3] ∪ [√3, √5]

2. Find the domain of f(x) = cos^-1 2x + sin^-1 x.

Solution:

Given that f(x) = cos^-1 2x + sin^-1 x.

Now we have to find the domain of f(x),

We know that domain of cos^-1 x lies in the interval [-1, 1]

Also know that domain of sin^-1 x lies in the interval [-1, 1]

Therefore, the domain of cos^-1 (2x) lies in the interval [-1, 1]

Hence we can write as,

-1 ≤ 2x ≤ 1

– ½ ≤ x ≤ ½

Hence, domain of cos^-1(2x) + sin^-1 x lies in the interval [- ½, ½]

---

Exercise 4.3 Page No: 4.14

1. Find the principal value of each of the following:

(i) tan^-1 (1/√3)

(ii) tan^-1 (-1/√3)

(iii) tan^-1 (cos (π/2))

(iv) tan^-1 (2 cos (2π/3))

Solution:

(i) Given tan^-1 (1/√3)

We know that for any x ∈ R, tan^-1 represents an angle in (-π/2, π/2) whose tangent is x.

So, tan^-1 (1/√3) = an angle in (-π/2, π/2) whose tangent is (1/√3)

But we know that the value is equal to π/6

Therefore tan^-1 (1/√3) = π/6

Hence the principal value of tan^-1 (1/√3) = π/6

(ii) Given tan^-1 (-1/√3)

We know that for any x ∈ R, tan^-1 represents an angle in (-π/2, π/2) whose tangent is x.

So, tan^-1 (-1/√3) = an angle in (-π/2, π/2) whose tangent is (1/√3)

But we know that the value is equal to -π/6

Therefore tan^-1 (-1/√3) = -π/6

Hence the principal value of tan^-1 (-1/√3) = – π/6

(iii) Given that tan^-1 (cos (π/2))

But we know that cos (π/2) = 0

We know that for any x ∈ R, tan^-1 represents an angle in (-π/2, π/2) whose tangent is x.

Therefore tan^-1 (0) = 0

Hence the principal value of tan^-1 (cos (π/2) is 0.

(iv) Given that tan^-1 (2 cos (2π/3))

But we know that cos π/3 = 1/2

So, cos (2π/3) = -1/2

Therefore tan^-1 (2 cos (2π/3)) = tan^-1 (2 × – ½)

= tan^-1(-1)

= – π/4

Hence, the principal value of tan^-1 (2 cos (2π/3)) is – π/4

---

Exercise 4.4 Page No: 4.18

1. Find the principal value of each of the following:

(i) sec^-1 (-√2)

(ii) sec^-1 (2)

(iii) sec^-1 (2 sin (3π/4))

(iv) sec^-1 (2 tan (3π/4))

Solution:

(i) Given sec^-1 (-√2)

Now let y = sec^-1 (-√2)

Sec y = -√2

We know that sec π/4 = √2

Therefore, -sec (π/4) = -√2

= sec (π – π/4)

= sec (3π/4)

Thus the range of principal value of sec^-1 is [0, π] – {π/2}

And sec (3π/4) = – √2

Hence the principal value of sec^-1 (-√2) is 3π/4

(ii) Given sec^-1 (2)

Let y = sec^-1 (2)

Sec y = 2

= Sec π/3

Therefore the range of principal value of sec^-1 is [0, π] – {π/2} and sec π/3 = 2

Thus the principal value of sec^-1 (2) is π/3

(iii) Given sec^-1 (2 sin (3π/4))

But we know that sin (3π/4) = 1/√2

Therefore 2 sin (3π/4) = 2 × 1/√2

2 sin (3π/4) = √2

Therefore by substituting above values in sec^-1 (2 sin (3π/4)), we get

Sec^-1 (√2)

Let Sec^-1 (√2) = y

Sec y = √2

Sec (π/4) = √2

Therefore range of principal value of sec^-1 is [0, π] – {π/2} and sec (π/4) = √2

Thus the principal value of sec^-1 (2 sin (3π/4)) is π/4.

(iv) Given sec^-1 (2 tan (3π/4))

But we know that tan (3π/4) = -1

Therefore, 2 tan (3π/4) = 2 × -1

2 tan (3π/4) = -2

By substituting these values in sec^-1 (2 tan (3π/4)), we get

Sec^-1 (-2)

Now let y = Sec^-1 (-2)

Sec y = – 2

– sec (π/3) = -2

= sec (π – π/3)

= sec (2π/3)

Therefore the range of principal value of sec^-1 is [0, π] – {π/2} and sec (2π/3) = -2

Thus, the principal value of sec^-1 (2 tan (3π/4)) is (2π/3).

---

Exercise 4.5 Page No: 4.21

1. Find the principal values of each of the following:

(i) cosec^-1 (-√2)

(ii) cosec^-1 (-2)

(iii) cosec^-1 (2/√3)

(iv) cosec^-1 (2 cos (2π/3))

Solution:

(i) Given cosec^-1 (-√2)

Let y = cosec^-1 (-√2)

Cosec y = -√2

– Cosec y = √2

– Cosec (π/4) = √2

– Cosec (π/4) = cosec (-π/4) [since –cosec θ = cosec (-θ)]

The range of principal value of cosec^-1 [-π/2, π/2] – {0} and cosec (-π/4) = – √2

Cosec (-π/4) = – √2

Therefore the principal value of cosec^-1 (-√2) is – π/4

(ii) Given cosec^-1 (-2)

Let y = cosec^-1 (-2)

Cosec y = -2

– Cosec y = 2

– Cosec (π/6) = 2

– Cosec (π/6) = cosec (-π/6) [since –cosec θ = cosec (-θ)]

The range of principal value of cosec^-1 [-π/2, π/2] – {0} and cosec (-π/6) = – 2

Cosec (-π/6) = – 2

Therefore the principal value of cosec^-1 (-2) is – π/6

(iii) Given cosec^-1 (2/√3)

Let y = cosec^-1 (2/√3)

Cosec y = (2/√3)

Cosec (π/3) = (2/√3)

Therefore range of principal value of cosec^-1 is [-π/2, π/2] – {0} and cosec (π/3) = (2/√3)

Thus, the principal value of cosec^-1 (2/√3) is π/3

(iv) Given cosec^-1 (2 cos (2π/3))

But we know that cos (2π/3) = – ½

Therefore 2 cos (2π/3) = 2 × – ½

2 cos (2π/3) = -1

By substituting these values in cosec^-1 (2 cos (2π/3)) we get,

Cosec^-1 (-1)

Let y = cosec^-1 (-1)

– Cosec y = 1

– Cosec (π/2) = cosec (-π/2) [since –cosec θ = cosec (-θ)]

The range of principal value of cosec^-1 [-π/2, π/2] – {0} and cosec (-π/2) = – 1

Cosec (-π/2) = – 1

Therefore the principal value of cosec^-1 (2 cos (2π/3)) is – π/2

---

Exercise 4.6 Page No: 4.24

1. Find the principal values of each of the following:

(i) cot^-1(-√3)

(ii) Cot^-1(√3)

(iii) cot^-1(-1/√3)

(iv) cot^-1(tan 3π/4)

Solution:

(i) Given cot^-1(-√3)

Let y = cot^-1(-√3)

– Cot (π/6) = √3

= Cot (π – π/6)

= cot (5π/6)

The range of principal value of cot^-1 is (0, π) and cot (5 π/6) = – √3

Thus, the principal value of cot^-1 (- √3) is 5π/6

(ii) Given Cot^-1(√3)

Let y = cot^-1(√3)

Cot (π/6) = √3

The range of principal value of cot^-1 is (0, π) and

Thus, the principal value of cot^-1 (√3) is π/6

(iii) Given cot^-1(-1/√3)

Let y = cot^-1(-1/√3)

Cot y = (-1/√3)

– Cot (π/3) = 1/√3

= Cot (π – π/3)

= cot (2π/3)

The range of principal value of cot^-1(0, π) and cot (2π/3) = – 1/√3

Therefore the principal value of cot^-1(-1/√3) is 2π/3

(iv) Given cot^-1(tan 3π/4)

But we know that tan 3π/4 = -1

By substituting this value in cot^-1(tan 3π/4) we get

Cot^-1(-1)

Now, let y = cot^-1(-1)

Cot y = (-1)

– Cot (π/4) = 1

= Cot (π – π/4)

= cot (3π/4)

The range of principal value of cot^-1(0, π) and cot (3π/4) = – 1

Therefore the principal value of cot^-1(tan 3π/4) is 3π/4

---

Exercise 4.7 Page No: 4.42

1. Evaluate each of the following:

(i) sin^-1(sin π/6)

(ii) sin^-1(sin 7π/6)

(iii) sin^-1(sin 5π/6)

(iv) sin^-1(sin 13π/7)

(v) sin^-1(sin 17π/8)

(vi) sin^-1{(sin – 17π/8)}

(vii) sin^-1(sin 3)

(viii) sin^-1(sin 4)

(ix) sin^-1(sin 12)

(x) sin^-1(sin 2)

Solution:

(i) Given sin^-1(sin π/6)

We know that the value of sin π/6 is ½

By substituting this value in sin^-1(sin π/6)

We get, sin^-1 (1/2)

Now let y = sin^-1 (1/2)

Sin (π/6) = ½

The range of principal value of sin^-1(-π/2, π/2) and sin (π/6) = ½

Therefore sin^-1(sin π/6) = π/6

(ii) Given sin^-1(sin 7π/6)

But we know that sin 7π/6 = – ½

By substituting this in sin^-1(sin 7π/6) we get,

Sin^-1 (-1/2)

Now let y = sin^-1 (-1/2)

– Sin y = ½

– Sin (π/6) = ½

– Sin (π/6) = sin (- π/6)

The range of principal value of sin^-1(-π/2, π/2) and sin (- π/6) = – ½

Therefore sin^-1(sin 7π/6) = – π/6

(iii) Given sin^-1(sin 5π/6)

We know that the value of sin 5π/6 is ½

By substituting this value in sin^-1(sin 5π/6)

We get, sin^-1 (1/2)

Now let y = sin^-1 (1/2)

Sin (π/6) = ½

The range of principal value of sin^-1(-π/2, π/2) and sin (π/6) = ½

Therefore sin^-1(sin 5π/6) = π/6

(iv) Given sin^-1(sin 13π/7)

Given question can be written as sin (2π – π/7)

Sin (2π – π/7) can be written as sin (-π/7) [since sin (2π – θ) = sin (-θ)]

By substituting these values in sin^-1(sin 13π/7) we get sin^-1(sin – π/7)

As sin^-1(sin x) = x with x ∈ [-π/2, π/2]

Therefore sin^-1(sin 13π/7) = – π/7

(v) Given sin^-1(sin 17π/8)

Given question can be written as sin (2π + π/8)

Sin (2π + π/8) can be written as sin (π/8)

By substituting these values in sin^-1(sin 17π/8) we get sin^-1(sin π/8)

As sin^-1(sin x) = x with x ∈ [-π/2, π/2]

Therefore sin^-1(sin 17π/8) = π/8

(vi) Given sin^-1{(sin – 17π/8)}

But we know that – sin θ = sin (-θ)

Therefore (sin -17π/8) = – sin 17π/8

– Sin 17π/8 = – sin (2π + π/8) [since sin (2π – θ) = -sin (θ)]

It can also be written as – sin (π/8)

– Sin (π/8) = sin (-π/8) [since – sin θ = sin (-θ)]

By substituting these values in sin^-1{(sin – 17π/8)} we get,

Sin^-1(sin – π/8)

As sin^-1(sin x) = x with x ∈ [-π/2, π/2]

Therefore sin^-1(sin -π/8) = – π/8

(vii) Given sin^-1(sin 3)

We know that sin^-1(sin x) = x with x ∈ [-π/2, π/2] which is approximately equal to [-1.57, 1.57]

But here x = 3, which does not lie on the above range,

Therefore we know that sin (π – x) = sin (x)

Hence sin (π – 3) = sin (3) also π – 3 ∈ [-π/2, π/2]

Sin^-1(sin 3) = π – 3

(viii) Given sin^-1(sin 4)

We know that sin^-1(sin x) = x with x ∈ [-π/2, π/2] which is approximately equal to [-1.57, 1.57]

But here x = 4, which does not lie on the above range,

Therefore we know that sin (π – x) = sin (x)

Hence sin (π – 4) = sin (4) also π – 4 ∈ [-π/2, π/2]

Sin^-1(sin 4) = π – 4

(ix) Given sin^-1(sin 12)

We know that sin^-1(sin x) = x with x ∈ [-π/2, π/2] which is approximately equal to [-1.57, 1.57]

But here x = 12, which does not lie on the above range,

Therefore we know that sin (2nπ – x) = sin (-x)

Hence sin (2nπ – 12) = sin (-12)

Here n = 2 also 12 – 4π ∈ [-π/2, π/2]

Sin^-1(sin 12) = 12 – 4π

(x) Given sin^-1(sin 2)

We know that sin^-1(sin x) = x with x ∈ [-π/2, π/2] which is approximately equal to [-1.57, 1.57]

But here x = 2, which does not lie on the above range,

Therefore we know that sin (π – x) = sin (x)

Hence sin (π – 2) = sin (2) also π – 2 ∈ [-π/2, π/2]

Sin^-1(sin 2) = π – 2

2. Evaluate each of the following:

(i) cos^-1{cos (-π/4)}

(ii) cos^-1(cos 5π/4)

(iii) cos^-1(cos 4π/3)

(iv) cos^-1(cos 13π/6)

(v) cos^-1(cos 3)

(vi) cos^-1(cos 4)

(vii) cos^-1(cos 5)

(viii) cos^-1(cos 12)

Solution:

(i) Given cos^-1{cos (-π/4)}

We know that cos (-π/4) = cos (π/4) [since cos (-θ) = cos θ

Also know that cos (π/4) = 1/√2

By substituting these values in cos^-1{cos (-π/4)} we get,

Cos^-1(1/√2)

Now let y = cos^-1(1/√2)

Therefore cos y = 1/√2

Hence range of principal value of cos^-1 is [0, π] and cos (π/4) = 1/√2

Therefore cos^-1{cos (-π/4)} = π/4

(ii) Given cos^-1(cos 5π/4)

But we know that cos (5π/4) = -1/√2

By substituting these values in cos^-1{cos (5π/4)} we get,

Cos^-1(-1/√2)

Now let y = cos^-1(-1/√2)

Therefore cos y = – 1/√2

– Cos (π/4) = 1/√2

Cos (π – π/4) = – 1/√2

Cos (3 π/4) = – 1/√2

Hence range of principal value of cos^-1 is [0, π] and cos (3π/4) = -1/√2

Therefore cos^-1{cos (5π/4)} = 3π/4

(iii) Given cos^-1(cos 4π/3)

But we know that cos (4π/3) = -1/2

By substituting these values in cos^-1{cos (4π/3)} we get,

Cos^-1(-1/2)

Now let y = cos^-1(-1/2)

Therefore cos y = – 1/2

– Cos (π/3) = 1/2

Cos (π – π/3) = – 1/2

Cos (2π/3) = – 1/2

Hence range of principal value of cos^-1 is [0, π] and cos (2π/3) = -1/2

Therefore cos^-1{cos (4π/3)} = 2π/3

(iv) Given cos^-1(cos 13π/6)

But we know that cos (13π/6) = √3/2

By substituting these values in cos^-1{cos (13π/6)} we get,

Cos^-1(√3/2)

Now let y = cos^-1(√3/2)

Therefore cos y = √3/2

Cos (π/6) = √3/2

Hence range of principal value of cos^-1 is [0, π] and cos (π/6) = √3/2

Therefore cos^-1{cos (13π/6)} = π/6

(v) Given cos^-1(cos 3)

We know that cos^-1(cos θ) = θ if 0 ≤ θ ≤ π

Therefore by applying this in given question we get,

Cos^-1(cos 3) = 3, 3 ∈ [0, π]

(vi) Given cos^-1(cos 4)

We have cos^–1(cos x) = x if x ϵ [0, π] ≈ [0, 3.14]

And here x = 4 which does not lie in the above range.

We know that cos (2π – x) = cos(x)

Thus, cos (2π – 4) = cos (4) so 2π–4 belongs in [0, π]

Hence cos^–1(cos 4) = 2π – 4

(vii) Given cos^-1(cos 5)

We have cos^–1(cos x) = x if x ϵ [0, π] ≈ [0, 3.14]

And here x = 5 which does not lie in the above range.

We know that cos (2π – x) = cos(x)

Thus, cos (2π – 5) = cos (5) so 2π–5 belongs in [0, π]

Hence cos^–1(cos 5) = 2π – 5

(viii) Given cos^-1(cos 12)

Cos^–1(cos x) = x if x ϵ [0, π] ≈ [0, 3.14]

And here x = 12 which does not lie in the above range.

We know cos (2nπ – x) = cos (x)

Cos (2nπ – 12) = cos (12)

Here n = 2.

Also 4π – 12 belongs in [0, π]

∴ cos^–1(cos 12) = 4π – 12

3. Evaluate each of the following:

(i) tan^-1(tan π/3)

(ii) tan^-1(tan 6π/7)

(iii) tan^-1(tan 7π/6)

(iv) tan^-1(tan 9π/4)

(v) tan^-1(tan 1)

(vi) tan^-1(tan 2)

(vii) tan^-1(tan 4)

(viii) tan^-1(tan 12)

Solution:

(i) Given tan^-1(tan π/3)

As tan^-1(tan x) = x if x ϵ [-π/2, π/2]

By applying this condition in the given question we get,

Tan^-1(tan π/3) = π/3

(ii) Given tan^-1(tan 6π/7)

We know that tan 6π/7 can be written as (π – π/7)

Tan (π – π/7) = – tan π/7

We know that tan^-1(tan x) = x if x ϵ [-π/2, π/2]

Tan^-1(tan 6π/7) = – π/7

(iii) Given tan^-1(tan 7π/6)

We know that tan 7π/6 = 1/√3

By substituting this value in tan^-1(tan 7π/6) we get,

Tan^-1 (1/√3)

Now let tan^-1 (1/√3) = y

Tan y = 1/√3

Tan (π/6) = 1/√3

The range of the principal value of tan^-1 is (-π/2, π/2) and tan (π/6) = 1/√3

Therefore tan^-1(tan 7π/6) = π/6

(iv) Given tan^-1(tan 9π/4)

We know that tan 9π/4 = 1

By substituting this value in tan^-1(tan 9π/4) we get,

Tan^-1 (1)

Now let tan^-1 (1) = y

Tan y = 1

Tan (π/4) = 1

The range of the principal value of tan^-1 is (-π/2, π/2) and tan (π/4) = 1

Therefore tan^-1(tan 9π/4) = π/4

(v) Given tan^-1(tan 1)

But we have tan^-1(tan x) = x if x ϵ [-π/2, π/2]

By substituting this condition in given question

Tan^-1(tan 1) = 1

(vi) Given tan^-1(tan 2)

As tan^-1(tan x) = x if x ϵ [-π/2, π/2]

But here x = 2 which does not belongs to above range

We also have tan (π – θ) = –tan (θ)

Therefore tan (θ – π) = tan (θ)

Tan (2 – π) = tan (2)

Now 2 – π is in the given range

Hence tan^–1 (tan 2) = 2 – π

(vii) Given tan^-1(tan 4)

As tan^-1(tan x) = x if x ϵ [-π/2, π/2]

But here x = 4 which does not belongs to above range

We also have tan (π – θ) = –tan (θ)

Therefore tan (θ – π) = tan (θ)

Tan (4 – π) = tan (4)

Now 4 – π is in the given range

Hence tan^–1 (tan 2) = 4 – π

(viii) Given tan^-1(tan 12)

As tan^-1(tan x) = x if x ϵ [-π/2, π/2]

But here x = 12 which does not belongs to above range

We know that tan (2nπ – θ) = –tan (θ)

Tan (θ – 2nπ) = tan (θ)

Here n = 2

Tan (12 – 4π) = tan (12)

Now 12 – 4π is in the given range

∴ tan^–1 (tan 12) = 12 – 4π.

---

Exercise 4.8 Page No: 4.54

1. Evaluate each of the following:

(i) sin (sin^-1 7/25)

(ii) Sin (cos^-1 5/13)

(iii) Sin (tan^-1 24/7)

(iv) Sin (sec^-1 17/8)

(v) Cosec (cos^-1 8/17)

(vi) Sec (sin^-1 12/13)

(vii) Tan (cos^-1 8/17)

(viii) cot (cos^-1 3/5)

(ix) Cos (tan^-1 24/7)

Solution:

(i) Given sin (sin^-1 7/25)

Now let y = sin^-1 7/25

Sin y = 7/25 where y ∈ [0, π/2]

Substituting these values in sin (sin^-1 7/25) we get

Sin (sin^-1 7/25) = 7/25

(ii) Given Sin (cos^-1 5/13)

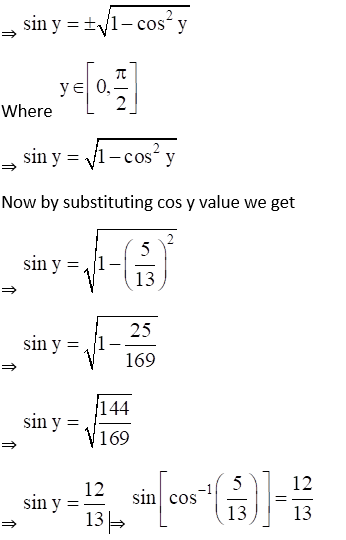
(iii) Given Sin (tan^-1 24/7)

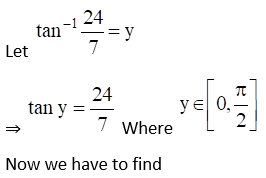
(iv) Given Sin (sec^-1 17/8)

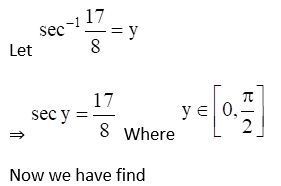
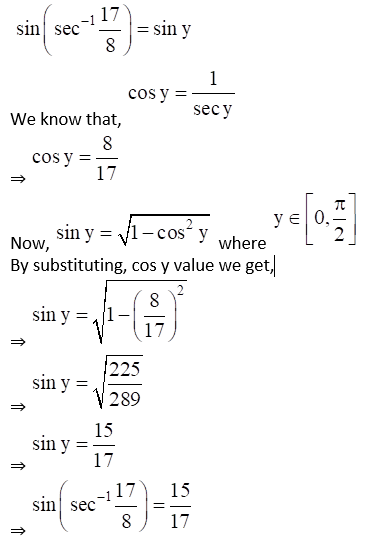
(v) Given Cosec (cos^-1 8/17)

Let cos^-1(8/17) = y

cos y = 8/17 where y ∈ [0, π/2]

Now, we have to find

Cosec (cos^-1 8/17) = cosec y

We know that,

sin² θ + cos² θ = 1

sin² θ = √ (1 – cos² θ)

So,

sin y = √ (1 – cos² y)

= √ (1 – (8/17)²)

= √ (1 – 64/289)

= √ (289 – 64/289)

= √ (225/289)

= 15/17

Hence,

Cosec y = 1/sin y = 1/ (15/17) = 17/15

Therefore,

Cosec (cos^-1 8/17) = 17/15

(vi) Given Sec (sin^-1 12/13)

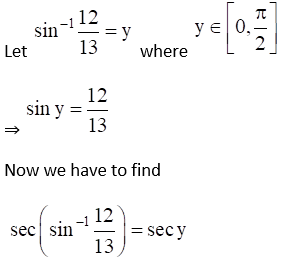
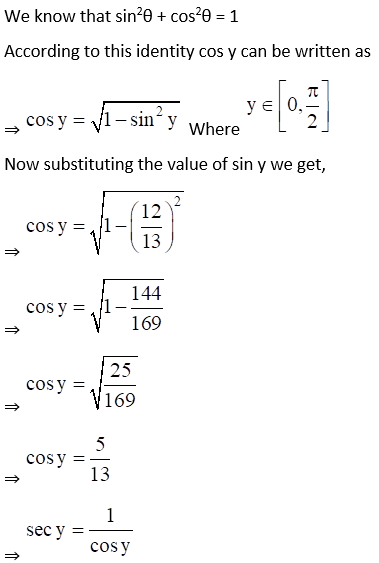
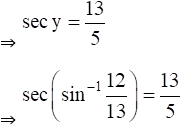
(vii) Given Tan (cos^-1 8/17)

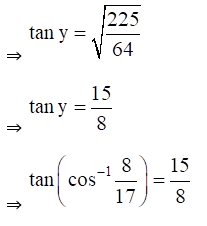
(viii) Given cot (cos^-1 3/5)

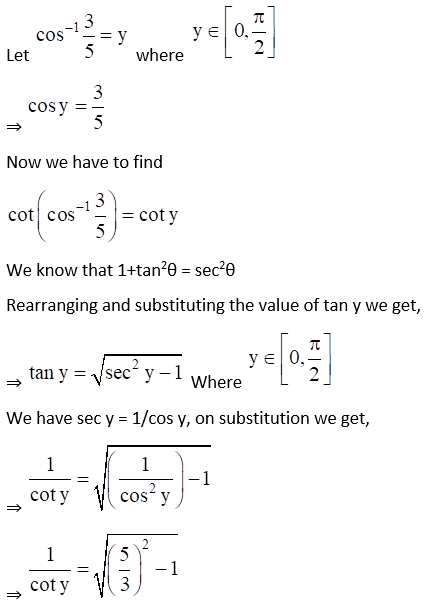
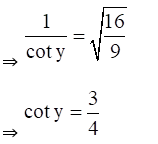
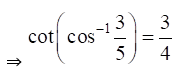
(ix) Given Cos (tan^-1 24/7)

.

---

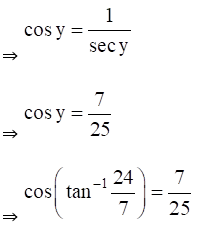
Exercise 4.9 Page No: 4.58

1. Evaluate:

(i) Cos {sin^-1 (-7/25)}

(ii) Sec {cot^-1 (-5/12)}

(iii) Cot {sec^-1 (-13/5)}

Solution:

(i) Given Cos {sin^-1 (-7/25)}

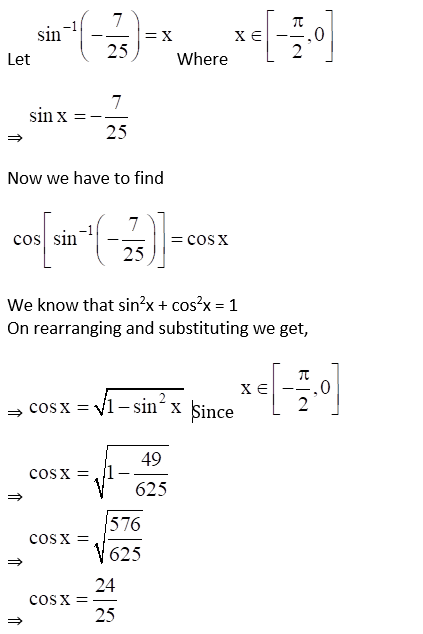
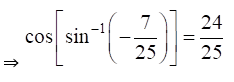
(ii) Given Sec {cot^-1 (-5/12)}

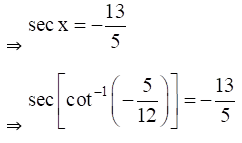
(iii) Given Cot {sec^-1 (-13/5)}

---

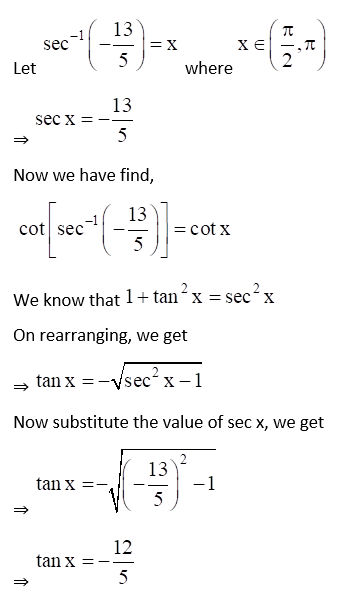
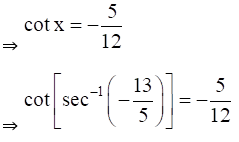
Exercise 4.10 Page No: 4.66

1. Evaluate:

(i) Cot (sin^-1 (3/4) + sec^-1 (4/3))

(ii) Sin (tan^-1 x + tan^-1 1/x) for x < 0

(iii) Sin (tan^-1 x + tan^-1 1/x) for x > 0

(iv) Cot (tan^-1 a + cot^-1 a)

(v) Cos (sec^-1 x + cosec^-1 x), |x| ≥ 1

Solution:

(i) Given Cot (sin^-1 (3/4) + sec^-1 (4/3))

(ii) Given Sin (tan^-1 x + tan^-1 1/x) for x < 0

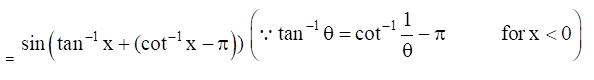
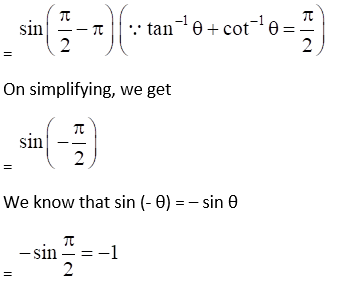
(iii) Given Sin (tan^-1 x + tan^-1 1/x) for x > 0

(iv) Given Cot (tan^-1 a + cot^-1 a)

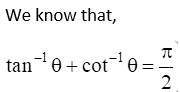
(v) Given Cos (sec^-1 x + cosec^-1 x), |x| ≥ 1

= 0

2. If cos^-1 x + cos^-1 y = π/4, find the value of sin^-1 x + sin^-1 y.

Solution:

Given cos^-1 x + cos^-1 y = π/4

3. If sin^-1 x + sin^-1 y = π/3 and cos^-1 x – cos^-1 y = π/6, find the values of x and y.

Solution:

Given sin^-1 x + sin^-1 y = π/3 ……. Equation (i)

And cos^-1 x – cos^-1 y = π/6 ……… Equation (ii)

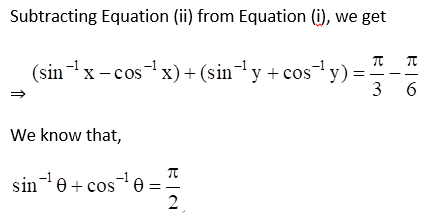
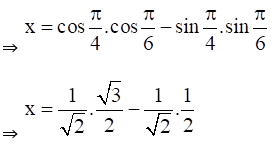
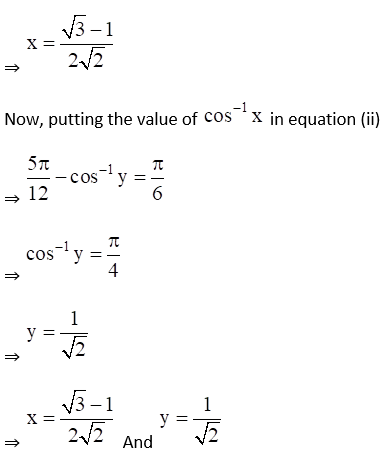
4. If cot (cos^-1 3/5 + sin^-1 x) = 0, find the value of x.

Solution:

Given cot (cos^-1 3/5 + sin^-1 x) = 0

On rearranging, we get,

(cos^-1 3/5 + sin^-1 x) = cot^-1 (0)

(Cos^-1 3/5 + sin^-1 x) = π/2

We know that cos^-1 x + sin^-1 x = π/2

Then sin^-1 x = π/2 – cos^-1 x

Substituting the above in (cos^-1 3/5 + sin^-1 x) = π/2 we get,

(Cos^-1 3/5 + π/2 – cos^-1 x) = π/2

Now on rearranging, we get,

(Cos^-1 3/5 – cos^-1 x) = π/2 – π/2

(Cos^-1 3/5 – cos^-1 x) = 0

Therefore Cos^-1 3/5 = cos^-1 x

On comparing the above equation, we get,

x = 3/5

5. If (sin^-1 x)² + (cos^-1 x)² = 17 π²/36, find x.

Solution:

Given (sin^-1 x)² + (cos^-1 x)² = 17 π²/36

We know that cos^-1 x + sin^-1 x = π/2

Then cos^-1 x = π/2 – sin^-1 x

Substituting this in (sin^-1 x)² + (cos^-1 x)² = 17 π²/36 we get

(sin^-1 x)² + (π/2 – sin^-1 x)² = 17 π²/36

Let y = sin^-1 x

y² + ((π/2) – y)² = 17 π²/36

y² + π²/4 – y² – 2y ((π/2) – y) = 17 π²/36

π²/4 – πy + 2 y² = 17 π²/36

On rearranging and simplifying, we get

2y² – πy + 2/9 π² = 0

18y² – 9 πy + 2 π² = 0

18y² – 12 πy + 3 πy + 2 π² = 0

6y (3y – 2π) + π (3y – 2π) = 0

Now, (3y – 2π) = 0 and (6y + π) = 0

Therefore y = 2π/3 and y = – π/6

Now substituting y = – π/6 in y = sin^-1 x we get

sin^-1 x = – π/6

x = sin (- π/6)

x = -1/2

Now substituting y = -2π/3 in y = sin^-1 x we get

x = sin (2π/3)

x = √3/2

Now substituting x = √3/2 in (sin^-1 x)² + (cos^-1 x)² = 17 π²/36 we get,

= π/3 + π/6

= π/2 which is not equal to 17 π²/36

So we have to neglect this root.

Now substituting x = -1/2 in (sin^-1 x)² + (cos^-1 x)² = 17 π²/36 we get,

= π²/36 + 4 π²/9

= 17 π²/36

Hence x = -1/2.

---

Exercise 4.11 Page No: 4.82

1. Prove the following results:

(i) Tan^-1 (1/7) + tan^-1 (1/13) = tan^-1 (2/9)

(ii) Sin^-1 (12/13) + cos^-1 (4/5) + tan^-1 (63/16) = π

(iii) tan^-1 (1/4) + tan^-1 (2/9) = Sin^-1 (1/ √5)

Solution:

(i) Given Tan^-1 (1/7) + tan^-1 (1/13) = tan^-1 (2/9)

Hence, proved.

(ii) Given Sin^-1 (12/13) + cos^-1 (4/5) + tan^-1 (63/16) = π

Consider LHS

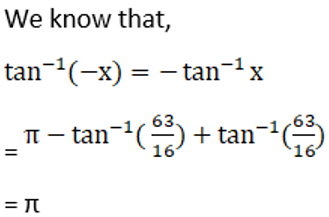
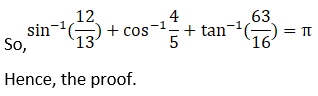
Hence, proved.

(iii) Given tan^-1 (1/4) + tan^-1 (2/9) = Sin^-1 (1/ √5)

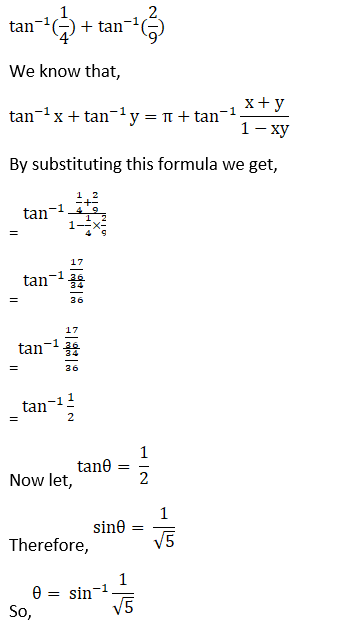
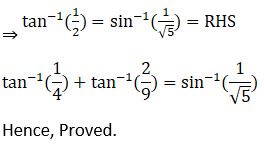
2. Find the value of tan^-1 (x/y) – tan^-1 {(x-y)/(x + y)}

Solution:

Given tan^-1 (x/y) – tan^-1 {(x-y)/(x + y)}

---

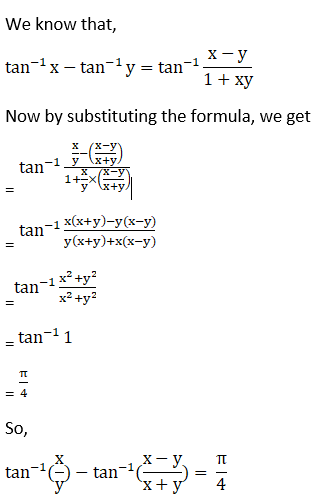
Exercise 4.12 Page No: 4.89

1. Evaluate: Cos (sin ^-1 3/5 + sin^-1 5/13)

Solution:

Given Cos (sin ^-1 3/5 + sin^-1 5/13)

We know that,

---

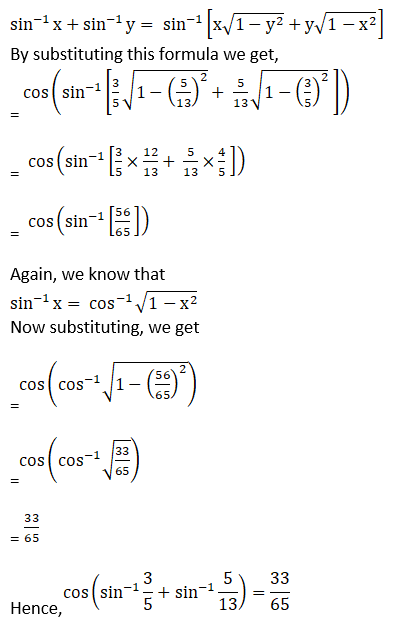
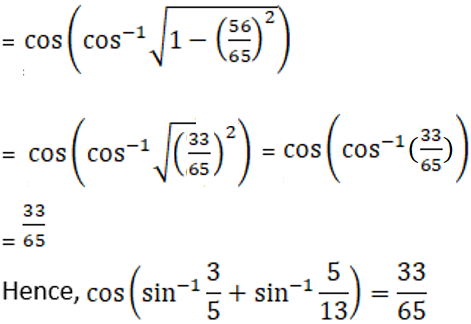
Exercise 4.13 Page No: 4.92

1. If cos^-1 (x/2) + cos^-1 (y/3) = α, then prove that 9x² – 12xy cos α + 4y² = 36 sin² α

Solution:

Given cos^-1 (x/2) + cos^-1 (y/3) = α

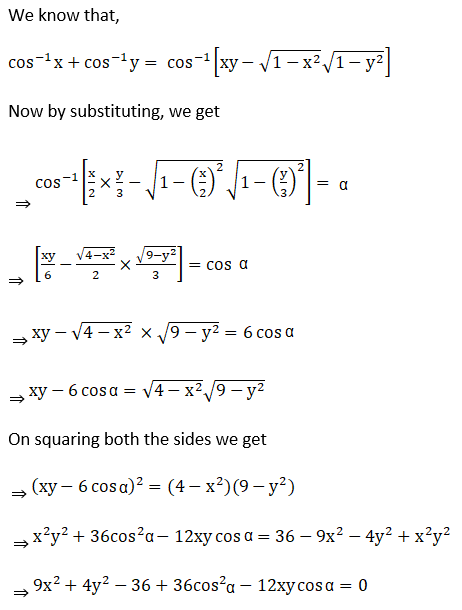
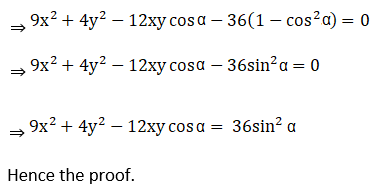
Hence, proved.

2. Solve the equation: cos^-1 (a/x) – cos^-1 (b/x) = cos^-1 (1/b) – cos^-1 (1/a)

Solution:

Given cos^-1 (a/x) – cos^-1 (b/x) = cos^-1 (1/b) – cos^-1 (1/a)

---

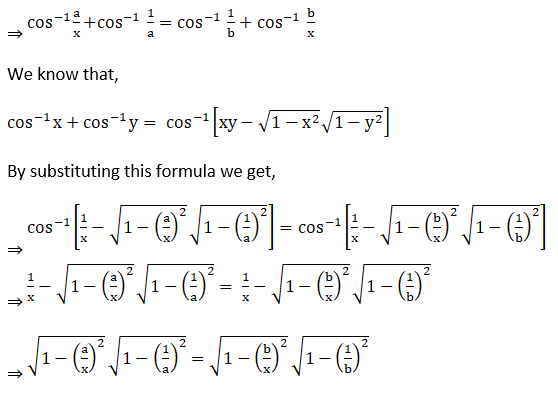
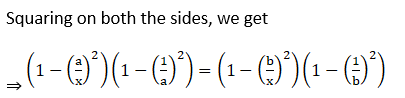
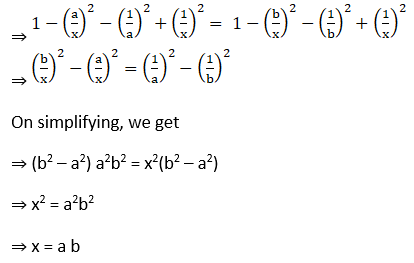
Exercise 4.14 Page No: 4.115

1. Evaluate the following:

(i) tan {2 tan^-1 (1/5) – π/4}

(ii) Tan {1/2 sin^-1 (3/4)}

(iii) Sin {1/2 cos^-1 (4/5)}

(iv) Sin (2 tan ^-1 2/3) + cos (tan^-1 √3)

Solution:

(i) Given tan {2 tan^-1 (1/5) – π/4}

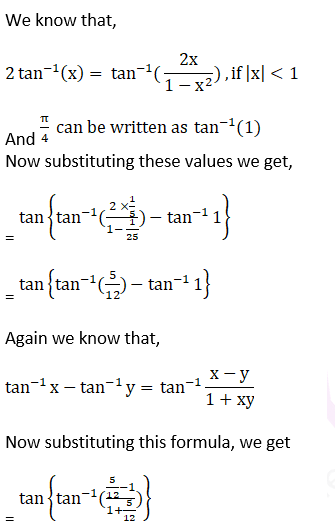
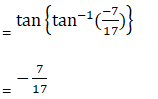
(ii) Given tan {1/2 sin^-1 (3/4)}

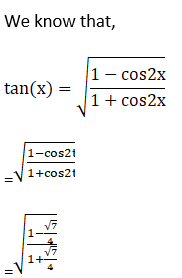
(iii) Given sin {1/2 cos^-1 (4/5)}

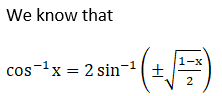
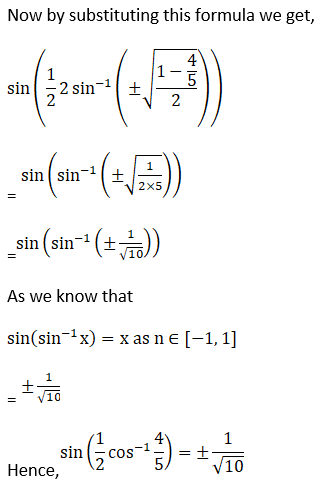
(iv) Given Sin (2 tan ^-1 2/3) + cos (tan^-1 √3)

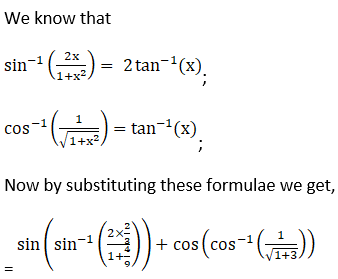
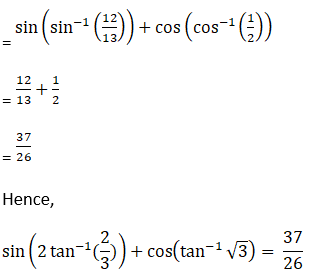
2. Prove the following results:

(i) 2 sin^-1 (3/5) = tan^-1 (24/7)

(ii) tan^-1 ¼ + tan^-1 (2/9) = ½ cos^-1 (3/5) = ½ sin^-1 (4/5)

(iii) tan^-1 (2/3) = ½ tan^-1 (12/5)

(iv) tan^-1 (1/7) + 2 tan^-1 (1/3) = π/4

(v) sin^-1 (4/5) + 2 tan^-1 (1/3) = π/2

(vi) 2 sin^-1 (3/5) – tan^-1 (17/31) = π/4

(vii) 2 tan^-1 (1/5) + tan^-1 (1/8) = tan^-1 (4/7)

(viii) 2 tan^-1 (3/4) – tan^-1 (17/31) = π/4

(ix) 2 tan^-1 (1/2) + tan^-1 (1/7) = tan^-1 (31/17)

(x) 4 tan^-1(1/5) – tan^-1(1/239) = π/4

Solution:

(i) Given 2 sin^-1 (3/5) = tan^-1 (24/7)

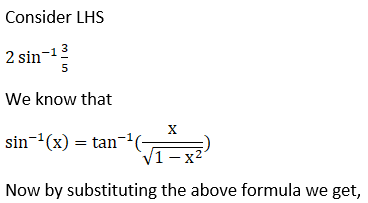
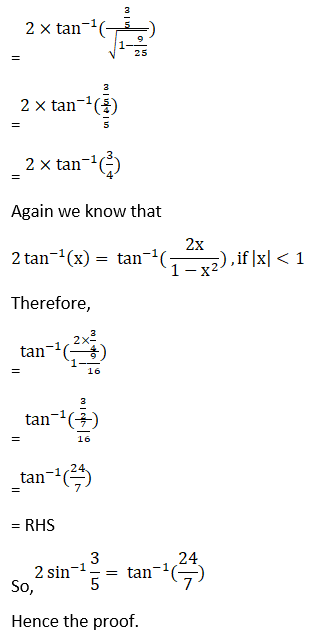
Hence, proved.

(ii) Given tan^-1 ¼ + tan^-1 (2/9) = ½ cos^-1 (3/5) = ½ sin^-1 (4/5)

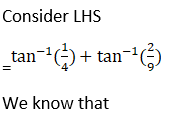
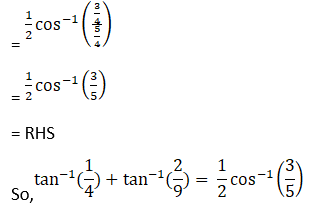
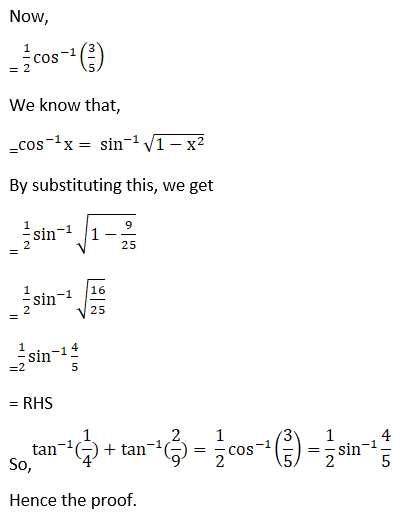
Hence, proved.

(iii) Given tan^-1 (2/3) = ½ tan^-1 (12/5)

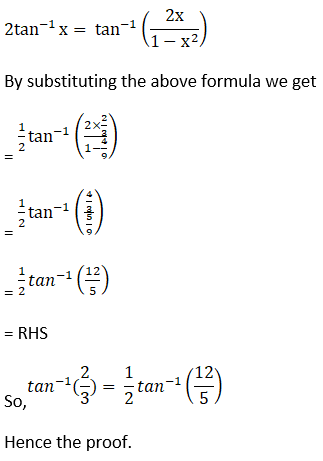
Hence, proved.

(iv) Given tan^-1 (1/7) + 2 tan^-1 (1/3) = π/4

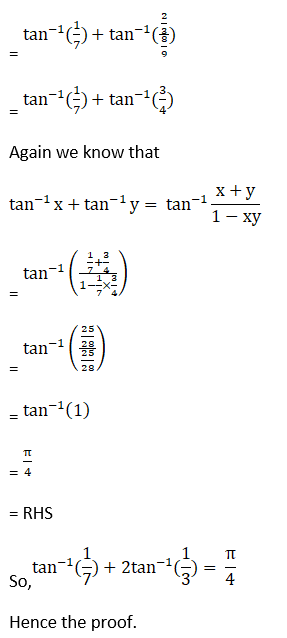
Hence, proved.

(v) Given sin^-1 (4/5) + 2 tan^-1 (1/3) = π/2

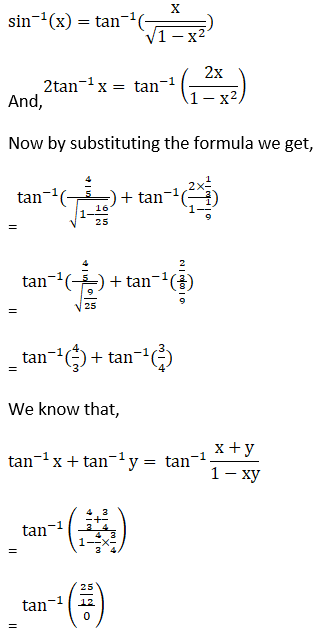
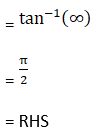
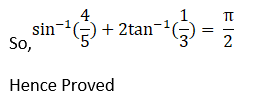
(vi) Given 2 sin^-1 (3/5) – tan^-1 (17/31) = π/4

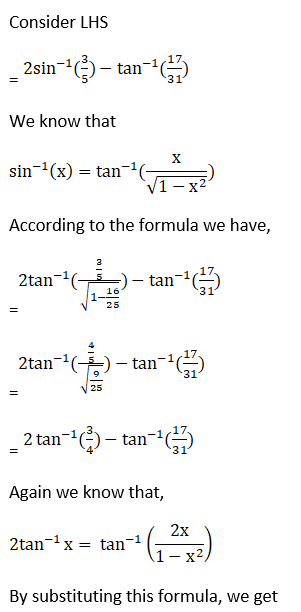
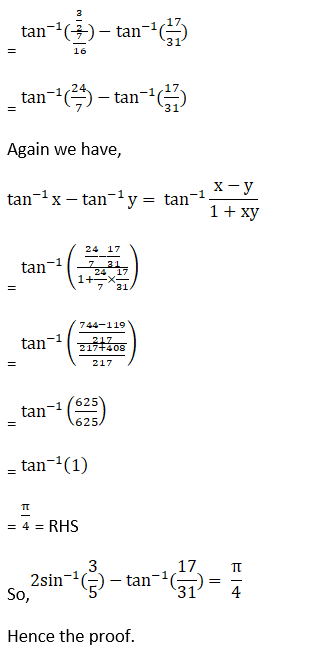
(vii) Given 2 tan^-1 (1/5) + tan^-1 (1/8) = tan^-1 (4/7)

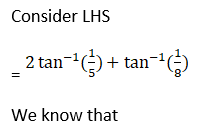
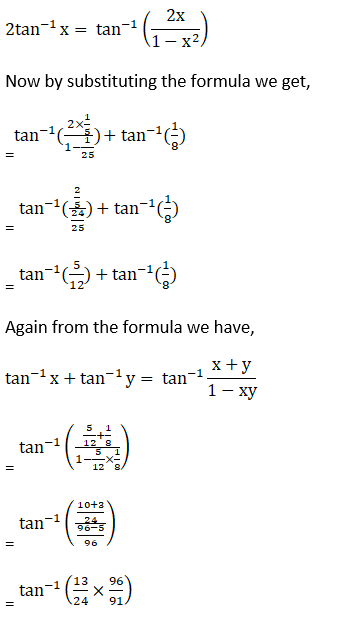
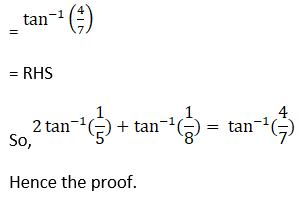
Hence, proved.

(viii) Given 2 tan^-1 (3/4) – tan^-1 (17/31) = π/4

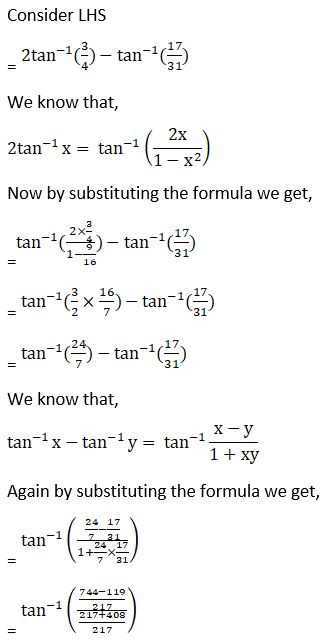
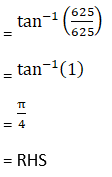
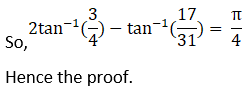
Hence, proved.

(ix) Given 2 tan^-1 (1/2) + tan^-1 (1/7) = tan^-1 (31/17)

Hence, proved.

(x) Given 4 tan^-1(1/5) – tan^-1(1/239) = π/4

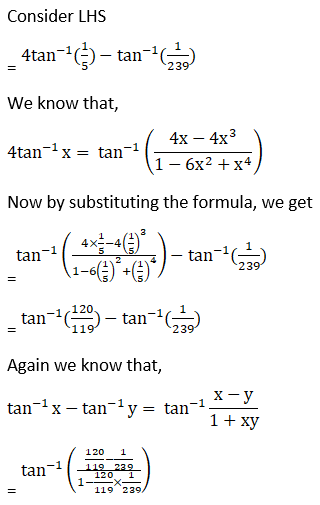
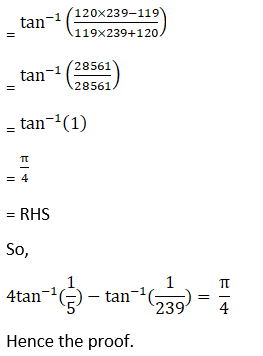
Hence, proved.

3. If sin^-1 (2a/1 + a²) – cos^-1(1 – b²/1 + b²) = tan^-1(2x/1 – x²), then prove that x = (a – b)/ (1 + a b)

Solution:

Given sin^-1 (2a/1 + a²) – cos^-1(1 – b²/1 + b²) = tan^-1(2x/1 – x²)

Hence, proved.

4. Prove that:

(i) tan^-1{(1 – x²)/ 2x)} + cot^-1{(1 – x²)/ 2x)} = π/2

(ii) sin {tan^-1 (1 – x²)/ 2x) + cos^-1 (1 – x²)/ (1 + x²)} = 1

Solution:

(i) Given tan^-1{(1 – x²)/ 2x)} + cot^-1{(1 – x²)/ 2x)} = π/2

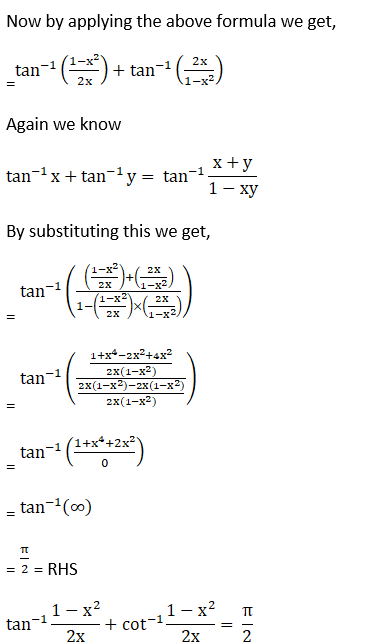
Hence, proved.

(ii) Given sin {tan^-1 (1 – x²)/ 2x) + cos^-1 (1 – x²)/ (1 + x²)}

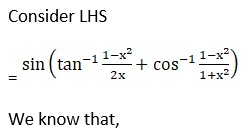
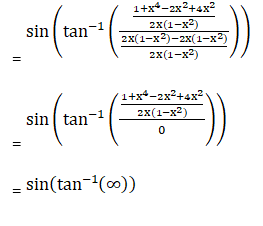
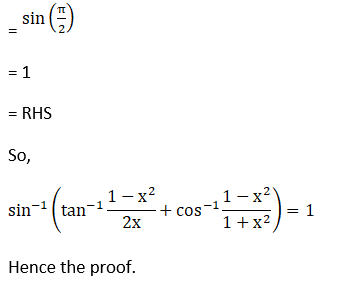
Hence, proved.

5. If sin^-1 (2a/ 1+ a²) + sin^-1 (2b/ 1+ b²) = 2 tan^-1 x, prove that x = (a + b/ 1 – a b)

Solution:

Given sin^-1 (2a/ 1+ a²) + sin^-1 (2b/ 1+ b²) = 2 tan^-1 x

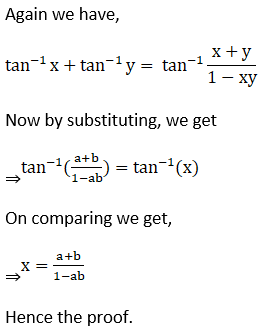
Hence, proved.