Chapter 31 PROBABILITY
Class 12th Maths R D Sharma Solution
Access RD Sharma Solutions for Class 12 Maths Chapter 31 Exercise 1
Exercise 31.1
1. Solution:
Here,
The sample space S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Let,
A = Number on the card drawn is even
So, A = {2, 4, 6, 8, 10}
n (A) = 5
And,
B = Number on the card is greater than 3
So, B = {4, 5, 6, 7, 8, 9, 10}
n (B) = 7
Now,
A ⋂ B = {4, 6, 8, 10}
n (A ⋂ B) = 4
Thus, the required probability is given by
P(A/B) = n (A ⋂ B)/ n (B)
= 4/7
2. Solution:
Let b and g represent the boy and the girl child respectively. If a family has two children, the sample space will be
S = {(b, b), (b, g), (g, b), (g, g)}
n (S) = 4
Let A be the event that both children are girls.
A = {(g, g)}
n (A) = 1
(i) Let B the event that the youngest child is a girl
B = {(b, g), (g, g)}
n (B) = 2
So,
A ⋂ B = {(g, g)}
n (A ⋂ B) = 1
P (A ⋂ B) = n (A ⋂ B)/ n (S)
= ¼
Now, the conditional probability that both are girls, given that the youngest child is a girl, is given by
P (A/B) = P (A ⋂ B)/ P(B)
= ¼ / ½
= ½
Therefore, the required probability is ½.
(ii) Let C the event that at least one child is a girl
C = {(b, g), (g, b), (g, g)}
n (B) = 3
So,
A ⋂ C = {(g, g)}
n (A ⋂ C) = 1
P (A ⋂ C) = n (A ⋂ C)/ n (S)
= ¼
Now, the conditional probability that both are girls, given that the youngest child is a girl, is given by
P (A/C) = P (A ⋂ C)/ P(C)
= ¼ / ¾
= 1/3
Therefore, the required probability is 1/3.
3. Solution:
Let A be the event of having two different numbers on the dice.
So,
A = {(1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
n (A) = 30
And,
Let B be the event getting a sum of 4 on the dice
B = {(1, 3), (2, 2), (3, 1)}
n (B) = 3
Now,
A ⋂ B = {(1, 3), (3, 1)}
n (A ⋂ B) = 2
Hence, the required conditional probability is given by
P(B/A) = n (A ⋂ B)/ n (A)
= 2/30
= 1/15
4. Solution:
Let A be the event of a head appearing on the first two tosses
A = {HHT, HHH}
n (A) = 2
And, B be the event of getting a head on the third toss
B = {HHH, HTH, THH, TTH}
n (B) = 4
Now,
A ⋂ B = {HHH}
n (A ⋂ B) = 1
Hence, the required conditional probability is given by
P (B/A) = n (A ⋂ B)/ n (A)
= ½
5. Solution:
Let A be the event of 4 appearing on the third toss, if a die is thrown three times
A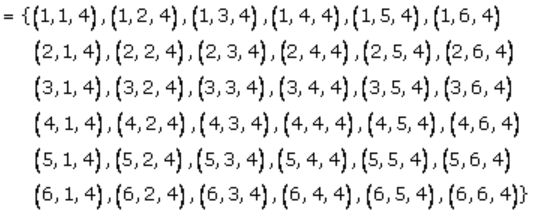
n (A) = 36
And, let B be the event of 6 and 5 appearing respectively on first two tosses, if the die is tossed three times
B = {(6, 5, 1), (6, 5, 2), (6, 5, 3), (6, 5, 4), (6, 5, 5), (6, 5, 6)}
n (B) = 6
Now,
A ⋂ B = {(6, 5, 4)}
n (A ⋂ B) = 1
Hence, the required probability is given by
P(A/B) = n (A ⋂ B)/ n (B)
= 1/6
6. Solution:
Given,
P(B) = 0.5, P(A ⋂ B) = 0.32
We know that,
P(A/B) = P(A ⋂ B)/ P(B)
= 0.32/ 0.5
= 32/50
= 16/25
Therefore, P(A/B) = 16/25
7. Solution:
Given,
P(A) = 0.4, P(B) = 0.3 and P(B/A) = 0.5
We know that,
P(B/A) = P(A ⋂ B)/ P(A)
0.5 = P(A ⋂ B)/ 0.4
P(A ⋂ B) = 0.5 x 0.4
= 0.2
Now,
P(A/B) = P(A ⋂ B)/ P(B)
= 0.2/ 0.3
Thus,
P(A/B) = 2/3
8. Solution:
Given,
P(A) = 1/3, P (B) = 1/5 and P(A ⋂ B) = 11/30
We know that,
P(A ⋂ B) = P(A) + P(B) – P(A ⋂ B)
11/30 = 1/3 + 1/5 – P(A ⋂ B)
P(A ⋂ B) = 1/3 + 1/5 – 11/30
= (10 + 6 – 11)/ 30
= 5/30
= 1/6
Now,
P(A/B) = P(A ⋂ B)/ P(B)
= (1/6)/ (1/5)
= 5/6
And,
P(B/A) = P(A ⋂ B)/ P(A)
= (1/6)/ (1/3)
= 3/6
= ½
Thus, P(A/B) = 5/6 and P(B/A) = ½.
Access RD Sharma Solutions for Class 12 Maths Chapter 31 Exercise 2
Exercise 31.2
1. Solution:
Let A be the event of getting king in the first card and B be the event of getting king in as the second card too.
n (S) = 52
Now,
Probability of getting two kings (Without replacement) is given by
= P(A). P(B/A)
= (4/52) x (3/51) [Since, there are 4 only kings out of 52 cards]
= (1/13) x (1/17)
= 1/221
Hence, the required probability is 1/221.
2. Solution:
Let the various events be defined as,
A = first card is an ace
B = second card is an ace
C = third card is an ace
D = fourth card is an ace
Now,
P(all four draw are ace, without replacement) = P(A). P(B/A). P(C/ A ⋂ B). P(D/ A ⋂ B ⋂ C)
= 4/52 x 3/51 x 2/50 x 1/49
= 1/270725
Hence, the required probability is 1/270725.
3. Solution:
Here,
Bag contains 5 red and 7 white balls
Let the event A and B be defined as
A = first ball is white
B = second ball is white
Now,
P(two white balls are drawn without replacement) = P(A). P(B/A)
= 7/12 x 6/11
= 7/22
Therefore, the required probability is 7/22.
4. Solution:
It’s given that,
Tickets are numbered from 1 to 25
So, the total number of tickets are 25
Now,
Number of tickets with even numbers on it is 12
i.e. {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24}
Let,
A = event of getting an even number in the first ticket
B = event of getting an even number in the second ticket
So,
P(both tickets will show even number, without replacement) = P(A). P(B/A)
= 12/25 x 11/24
= 11/50
Hence, the required probability is 11/50.
5. Solution:
We know that, a deck of has 52 cards
Let, various events be defined as
A = the first card is a spade
B = the second card is a spade
C = the third card is a spade
Now,
P(each of the three cards drawn without replacement is a spade) is given by
= P(A). P(B/A). P(C/ A ⋂ B)
= 13/52 x 12/51 x 11/50
= 11/850
Therefore, the required probability is 11/850.
6.
(i) Solution:
We know that, in a deck of cards there are 4 kings.
And, two cards are drawn without replacement
Let,
A be the event of getting a king as the first card
B be the event of getting another king as the second card
Now,
P(both drawn cards are king) = P(A). P(B/A)
= 4/52 x 3/51
= 1/221
Hence, the required probability is 1/221.
(ii) Solution:
We know that, there are 4 kings and 4 aces in a pack of 52 cards.
Two cards are drawn without replacement
Let,
A = event of getting a king as the first card
B = event of getting an ace as the second card
Now,
P(the first card is a king and second card is an ace) = P(A). P(B/A)
= 4/52 x 4/51
= 4/663
Therefore, the required probability is 4/663.
(iii) Solution:
We know that, in a pack of cards there are 13 hearts and 26 red cards
And, all heart cards are red
Let,
A = event of getting a heart as the first card
B = event of getting a red card as the second card
Now,
P(first card is a heart and second card is a red card) is given by
= P(A). P(B/A)
= 13/52 x 25/51
= 25/204
Hence, the required probability is 25/204.
7. Solution:
Here,
Total number of tickets are 20 and are numbered from 1, 2, 3, …, 20
So,
The number of tickets with even numbers are 10 i.e. {2, 4, 6, 8, ….. , 20}
The number of tickets with odd numbers are 10 i.e. {1, 3, 5, 7, …., 19}
Also, it is mentioned that two cards are drawn
Let,
A = event of getting an even numbered ticket
B = event of getting an odd numbered ticket
Now,
P(First ticket has an even number and the second one has an odd number) is given by
= P(A). P(A/B)
= 10/20 x 10/19
= 5/19
Hence, the required probability is 5/19.
8. Solution:
Given, that an urn contains 3 white, 4 red and 5 black balls.
So, total number of balls = 12
Two balls are drawn without replacement
Let,
A = event of getting a black ball as the first
B = event of getting another black ball as the second
Now,
P(At least one ball is black) = P(A ⋃ B)
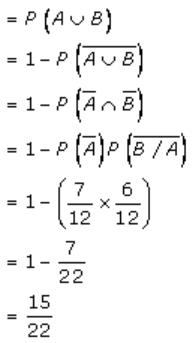
Hence, the required probability is 15/22.
Access RD Sharma Solutions for Class 12 Maths Chapter 31 Exercise 3
Exercise 31.3
1. Solution:
Given,
P(A) = 7/13, P(B) = 9/13 and P(A ⋂ B) = 4/13
We know that,
P(A/B) = P(A ⋂ B)/ P(B)
= (4/13)/ (9/13)
= 4/9
2. Solution:
Given,
P(A) = 0.6, P(B) = 0.3 and P(A ⋂ B) = 0.2
We know that,
P(A/B) = P(A ⋂ B)/ P(B)
= 0.2/ 0.3
= 2/3
And,
P(B/A) = P(A ⋂ B)/ P(A)
= 0.2/ 0.6
= 1/3
Therefore, P(A/B) = 2/3 and P(B/A) = 1/3.
3. Solution:
Given,
P(A ⋂ B) = 0.32 and P(B) = 0.5
We know that,
P(A/B) = P(A ⋂ B)/ P(B)
= 0.32/ 0.5
= 16/25
= 0.64
Therefore, P(A/B) = 0.64
4. Solution:
Given,
P(A) = 0.4, P(B) = 0.8 and P(B/A) = 0.6
We know that,
P(B/A) = P(A ⋂ B)/ P(A)
0.6 = P(A ⋂ B)/ 0.4
P(A ⋂ B) = 0.6 x 0.4
= 0.24
Now,
P(A/B) = P(A ⋂ B)/ P(B)
= 0.24/ 0.8
= 0.3
And,
P(A ⋃ B) = P(A) + P(B) – P(A ⋂ B)
= 0.4 + 0.8 – 0.24
= 0.96
Therefore, P(A/B) = 0.3 and P(A ⋃ B) = 0.96
5.
(i) Solution:
Given,
P(A) = 1/3, P(B) = ¼ and P(A ⋃ B) = 5/12
We know that,
P(A ⋃ B) = P(A) + P(B) – P(A ⋂ B)
5/12 = 1/3 + ¼ – P(A ⋂ B)
P(A ⋂ B) = 1/3 + ¼ – 5/12
= (4 + 3 – 5)/ 12
= 2/12
= 1/6
Now,
P(A/B) = P(A ⋂ B)/ P(B)
= (1/6)/ (1/4)
= 4/6
= 2/3
And,
P(B/A) = P(A ⋂ B)/P(A)
= (1/6) / (1/3)
= 3/6
= ½
Therefore, P(A/B) = 2/3 and P(B/A) = ½.
(ii) Solution:
Given,
P(A) = 6/11, P(B) = 5/11 and P(A ⋃ B) = 7/11
We know that,
P(A ⋃ B) = P(A) + P(B) – P(A ⋂ B)
So,
P(A ⋂ B) = P(A) + P(B) – P(A ⋃ B)
P(A ⋂ B) = 6/11 + 5/11 – 7/11
= 4/11
Now,
P(A/B) = P(A ⋂ B)/ P(B)
= (4/11)/ (5/11)
= 4/5
And,
P(B/A) = P(A ⋂ B)/P(A)
= (4/11) / (6/11)
= 4/6
= 2/3
Therefore, P(A/B) = 4/5 and P(B/A) = 2/3.
Access RD Sharma Solutions for Class 12 Maths Chapter 31 Exercise 4
Exercise 31.4
1.
(i) Solution:
Here,
A coin is tossed thrice
So, sample space = {HHH, HHT, HTH, HTT, TTT, TTH, THT, THH}
n (S) = 8
Let,
A = event for getting a head in the first throw
A = {HHH, HHT, HTH, HTT}
n(A) = 4
And,
B = event of getting a tail in the last throw
B = {HHT, HTT, TTT, THT}
n(B) = 4
Now,
A ⋂ B = {HHT, HTT}
n(A ⋂ B) = 2
So,
P(A) = n (A)/ n (S) = 4/8 = ½
P(B) = n (B)/ n (S) = 4/8 = ½
P(A ⋂ B) = n (A ⋂ B)/ n (S) = 2/8 = ¼
P(A). P(B) = ½ x ½ = ¼
Thus,
P(A). P(B) = P(A ⋂ B)
Therefore, A and B are independent events.
(ii) Solution:
Here,
A coin is tossed thrice
So, sample space = {HHH, HHT, HTH, HTT, TTT, TTH, THT, THH}
n (S) = 8
Let,
A = event for getting an odd number of heads
A = {HTT, THT, TTH, HHH}
n(A) = 4
And,
B = event of getting an odd number of tails
B = {HHT, HTH, TTT, THH}
n(B) = 4
Now,
A ⋂ B = { } = Ø
n(A ⋂ B) = 0
So,
P(A) = n (A)/ n (S) = 4/8 = ½
P(B) = n (B)/ n (S) = 4/8 = ½
P(A ⋂ B) = n (A ⋂ B)/ n (S) = 0/8 = 0
P(A). P(B) = ½ x ½ = ¼
Thus,
P(A). P(B) ≠ P(A ⋂ B)
Therefore, A and B are not independent events.
(iii) Solution:
Here,
A coin is tossed thrice
So, sample space = {HHH, HHT, HTH, HTT, TTT, TTH, THT, THH}
n (S) = 8
Let,
A = event for getting two heads
A = {HHT, THH, HTH}
n(A) = 3
And,
B = event of getting a head in the last throw
B = {HHH, HTH, TTH, THH}
n(B) = 4
Now,
A ⋂ B = {THH, HTH}
n(A ⋂ B) = 2
So,
P(A) = n (A)/ n (S) = 3/8
P(B) = n (B)/ n (S) = 4/8 = ½
P(A ⋂ B) = n (A ⋂ B)/ n (S) = 2/8 = ¼
P(A). P(B) = 3/8 x ½ = 3/16
Thus,
P(A). P(B) ≠ P(A ⋂ B)
Therefore, A and B are not independent events.
2. Solution:
When a pair of dice are thrown, we get 36 outcomes
So, the sample space (s) has 36 elements
Let,
A = Event of occurrence of number 4 on the first die
= {(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)}
n (A) = 6
And,
B = Event of occurrence of 5 on the second die
= {(1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5)}
n (B) = 6
Now,
A ⋂ B = {(4, 5)}
n (A ⋂ B) = 1
P(A) = n (A)/ n (S) = 6/36 = 1/6
P(B) = n (B)/ n (S) = 6/36 = 1/6
P(A ⋂ B) = 1/36
P(A). P(B) = 1/6 x 1/6 = 1/36
Thus,
P(A). P(B) = P(A ⋂ B)
Therefore, A and B are independent events.
3.
(i) Solution:
A card is drawn from a pack of 52 cards.
And, it contains 4 kings, 4 Queens and 4 Jacks
Now, if
A = event of drawing a king or a queen
P(A) = (4 + 4)/ 52
= 8/52
= 2/13
B = event of drawing a queen or a jack
P(B) = (4 + 4)/ 52
= 8/52
= 2/13
A ⋂ B = Event of drawing a queen
P(A ⋂ B) = 4/52
= 1/13
Now,
P(A). P(B) = 2/13 x 2/13
= 4/169
Thus,
P(A). P(B) ≠ P(A ⋂ B)
Therefore, A and B are not independent events.
(ii) Solution:
A card is drawn from a pack of 52 cards.
And, it contains 26 black cards and 4 kings, of which 2 kings are black
Now, if
A = event of drawing a black card
P(A) = (4 + 4)/ 52
= 26/52
= ½
B = event of drawing a king
P(B) = 4/ 52
= 1/13
A ⋂ B = Event of drawing a black king
P(A ⋂ B) = 2/52
= 1/26
Now,
P(A). P(B) = 1/2 x 1/13
= 1/26
Thus,
P(A). P(B) = P(A ⋂ B)
Therefore, A and B are independent events.
(iii) Solution:
A card is drawn from a pack of 52 cards.
And, it contains 13 spades and 4 aces, of which one card is an ace of spade
Now, if
A = event of drawing a spade
P(A) = 13/52
= 1/4
B = event of drawing an ace
P(B) = 4/ 52
= 1/13
A ⋂ B = Event of drawing an ace of spade
P(A ⋂ B) = 1/52
Now,
P(A). P(B) = 1/4 x 1/13
= 1/52
Thus,
P(A). P(B) = P(A ⋂ B)
Therefore, A and B are independent events.
Access RD Sharma Solutions for Class 12 Maths Chapter 31 Exercise 5
Exercise 31.5
1. Solution:
Let the given 2 bags be considered as Bag 1 and Bag 2
Bag 1 contains 6 black and 3 white balls
Bag 2 contains 5 black and 4 white balls
Now,
One ball is drawn from each bag
P(one black from bag 1) = 6/9
P(B1) = 2/3
P(one black from bag 2) = 5/9
P(B2) = 5/9
P(one white from bag 1) = 3/9
P(W1) = 1/3
And,
P(one white from bag 2) = 4/9
P(W2) = 4/9
So,
P(two balls of same colour) = P[(W1 ⋂ W2) ⋃ (B1 ⋂ B2)]
= P(W1 ⋂ W2) + P(B1 ⋂ B2)
= P(W1). P(W2) + P(B1). P(B2)
= (1/3 x 4/9) + (2/3 x 5/9)
= 4/27 + 10/27
= 14/27
Thus, the required probability is 14/27.
2. Solution:
Let the given two bags be considered as Bag 1 and Bag 2
Bag 1 contains 3 red and 5 black balls
Bag 2 contains 6 red and 4 black balls
Now,
One ball is drawn from each bag
P(one red from bag 1) = 3/8
P(R1) = 3/8
P(one red from bag 2) = 6/10
P(R2) = 3/5
P(one black from bag 1) = 5/8
P(B1) = 5/8
And,
P(one black from bag 2) = 4/10
P(W2) = 2/5
So,
When one ball is drawn from each bag
P(one ball is red and the other is black)
= P[(R1 ⋂ B2) ⋃ (B1 ⋂ R2)]
= P(R1 ⋂ B2) + P(B1 ⋂ R2)
= P(R1). P(B2) + P(B1). P(R2)
= (3/8 x 2/5) + (5/8 x 3/5)
= 6/40 + 15/40
= 21/40
Thus, the required probability is 21/40.
3.
Solution:
Given,
A box contains 10 black and 8 red balls. Total number of balls is 18.
So, P(B) = 10/18 and P(R) = 8/18
Two balls are drawn with replacement
(i)
P(both the balls are red) = P(R1 ⋂ R2)
= P(R1). P(R2)
= (8/18) x (8/18)
= 16/81
Thus, the required probability is 16/81.
(ii)
P(first ball is black and second is red) = P(B ⋂ R)
= P(B). P(R)
= (10/18) x (8/18)
= 20/81
Thus, the required probability is 20/81.
(iii)
P(one of them is red and the other is black) is given by
= P[(B ⋂ R) ⋃ (R ⋂ B)]
= P(B ⋂ R) + P(R ⋂ B)
= P(B). P(R) + P(R). P(B)
= (10/18 x 8/18) + (8/18 x 10/18)
= (20 + 20)/ 81
= 40/81
Thus, the required probability is 40/81.
4. Solution:
Here, two cards are drawn without replacement
In a pack of cards there are total of 4 aces
Let,
A = Event of getting an ace
Now,
P(exactly one ace out of 2 cards) is given by
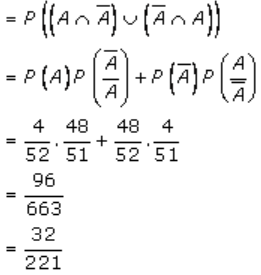
Therefore, the required probability is 32/221.
5. Solution:
Given,
A speaks truth in 75% cases
B speaks truth in 80% cases
So,

Therefore, the required probability is 35%.
6. Solution:
Given,
Probability of selection of Kamal (K) = P(K) = 1/3
Probability of selection of Monika (M) = P(M) = 1/5
(i)
P(Both of them are selected) is given by
= P(K ⋂ M)
= P(K). P(M)
= 1/3 x 1/5
= 1/15
Thus, the required probability is 1/15.
(ii)
P(none of them will be selected) is given by
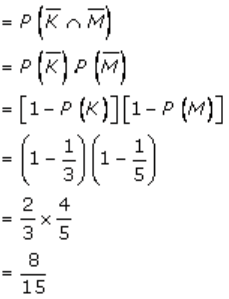
Thus, the required probability is 8/15.
(iii)
P(At least one of them is selected) = 1 – P(none of them will be selected)
= 1 – 8/15 [From the answer of (ii)]
= 7/15
Thus, the required probability is 7/15.
(iv)
P(only one of them will be selected) is given by
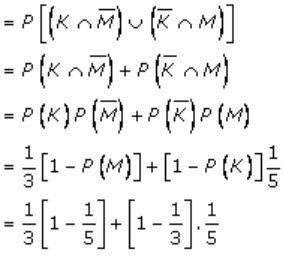
= (1/3 x 4/5) + (2/3 x 1/5)
= 4/15 + 2/15
= 6/15
= 2/5
Thus, the required probability is 2/5.
7. Solution:
Given,
A bag containing 3 white, 4 red and 5 black balls
And, two balls are drawn without replacement
So,
P(one ball is white and the other is black)
= P[(W ⋂ B) ⋃ (B ⋂ W)]
= P(W ⋂ B) + P(B ⋂ W)
= P(W).P(B/W) + P(B). P(W/B)
= (3/12 x 5/11) + (5/12 x 3/11)
= 15/132 + 15/132
= 30/132
= 5/22
Thus, the required probability is 5/22.
Access RD Sharma Solutions for Class 12 Maths Chapter 31 Exercise 6
Exercise 31.6
1. Solution:
Given,
Bag A contains 5 white and 6 black balls
Bag B contains 4 white and 3 black balls
Now, there are two ways of transferring a ball from bag A to bag B
Way – 1
By transferring one white ball from bag A to bag B, then drawing one black ball from bag B.
Way – 2
By transferring one black ball from bag A to bag B, then drawing one black ball from bag B.
Let E1, E2 and A be events as below:
E1 – One white ball drawn from bag A
E2 – One black ball drawn from bag A
A – One black ball drawn from bag B
So, we have
P(E1) = 5/11
P(E2) = 6/11
Now,
P(A/E1) = 3/8 [Since, E1 has increased one white ball in bag B]
P(A/E2) = 4/8 [Since, E2 has increased one black ball in bag B]
By the law of total probability, we get
P(A) = P(E1). P(A/E1) + P(E2). P(A/E2)
= (5/11 x 3/8) + (6/11 x 4/8)
= 15/88 + 24/88
= 39/88
Hence, the required probability is 39/88.
2. Solution:
Given,
Purse (I) contains 2 silver and 4 copper coins
Purse (II) contains 4 silver and 3 copper coins
Now, one coin is drawn from one of the two purse and it is silver
Let E1, E2 and A be events as below:
E1 – selecting purse I
E2 – selecting purse II
A – drawing a silver coin
So, we have
P(E1) = 1/2
P(E2) = 1/2 [As there are only 2 purses]
Now,
P(A/E1) = P(drawing a silver from purse I)
= 2/6
= 1/3
P(A/E2) = P(drawing a silver coin from purse II)
= 4/7
By the law of total probability, we get
P(A) = P(E1). P(A/E1) + P(E2). P(A/E2)
= (1/2 x 1/3) + (1/2 x 4/7)
= 1/6 + 4/14
= (7 + 12)/42
= 19/42
Hence, the required probability is 19/42.
3. Solution:
Given,
Bag I contains 4 yellow and 5 red balls
Bag II contains 6 yellow and 3 red balls
Now, there are two ways of transferring a ball from bag I to bag II
Way – 1
By transferring one yellow ball from bag I to bag II, then one yellow ball is drawn from bag II.
Way – 2
By transferring one red ball from bag I to bag II, then one yellow ball is drawn from bag II.
Let E1, E2 and A be events as below:
E1 – One yellow ball drawn from bag I
E2 – One red ball drawn from bag I
A – One yellow ball drawn from bag II
So, we have
P(E1) = 4/9
P(E2) = 5/9
Now,
P(A/E1) = 7/10 [Since, E1 has increased one yellow ball in bag II]
P(A/E2) = 6/10 [Since, E2 has increased one red ball in bag II]
By the law of total probability, we get
P(A) = P(E1). P(A/E1) + P(E2). P(A/E2)
= (4/9 x 7/10) + (5/9 x 6/10)
= (28 + 30)/90
= 58/90
= 29/45
Hence, the required probability is 29/45.
4. Solution:
Given,
Bag I contains 3 white and 2 black balls
Bag II contains 2 white and 4 black balls
One bag is chosen at random, then one ball is drawn and it is white
Let E1, E2 and A be events as below:
E1 – Choosing bag I
E2 – Choosing bag II
A – Drawing one white ball
So, we have
P(E1) = 1/2
P(E2) = 1/2 [Since, there are only 2 bags]
Now,
P(A/E1) = P(drawing a white ball from Bag I)
= 3/5
P(A/E2) = P(drawing a white ball from Bag II)
= 2/6
By the law of total probability, we get
P(A) = P(E1). P(A/E1) + P(E2). P(A/E2)
= (½ x 3/5) + (½ x 2/6)
= 3/10 + 2/12
= (18 + 10)/60
= 28/60
= 7/15
Hence, the required probability is 7/15.
5. Solution:
Given,
Bag I contains 1 white, 2 black and 3 red balls
Bag II contains 2 white, 1 black and 1 red balls
Bag III contains 4 white, 5 black and 3 red balls
One bag is chosen at random, then one red ball and one white ball is drawn
Let E1, E2, E3 and A be events as below:
E1 – Choosing bag I
E2 – Choosing bag II
E3 – Choosing bag III
A – Drawing one red and one white ball
So, we have
P(E1) = 1/3
P(E2) = 1/3
P(E3) = 1/3 [Since, there are only 3 bags]
Now,
P(A/E1) = P(drawing one red and one white ball from Bag I)
= (1C1 x 3C1)/ 6C2
= (1 x 3)/ (30/2)
= 1/5
P(A/E2) = P(drawing one red and one white ball from Bag II)
= (2C1 x 1C1)/ 4C2
= (2 x 1)/ (12/2)
= 1/3
P(A/E3) = P(drawing one red and one white ball from Bag III)
= (4C1 x 3C1)/ 12C2
= (4 x 3)/ (132/2)
=2/11
By the law of total probability, we get
P(A) = P(E1). P(A/E1) + P(E2). P(A/E2) + P(E3). P(A/E3)
= (1/3 x 1/5) + (1/3 x 1/3) + (1/3 x 2/11)
= 1/15 + 1/9 + 2/33
= (33 + 55 + 30)/495
= 118/495
Hence, the required probability is 118/495.
Access RD Sharma Solutions for Class 12 Maths Chapter 31 Exercise 7
Exercise 31.7
1. Solution:
Given,
Urn I contains 1 white, 2 black and 3 red balls.
Urn II contains 2 white, 1 black and 1 red balls.
Urn III contains 4 white, 5 black and 4 red balls.
Let E1, E2, E3 and A be the events as defined:
E1 = Selecting urn I
E2 = Selecting urn II
E3 = Selecting urn III
A = Drawing 1 white ball and 1 red ball
Now.
P(E1) = P(E2) = P(E3) = 1/3 [As there are only 3 urns]
And,
P(A/E1) = P(Drawing 1 red ball and 1 white ball from urn I)
= (1C1 x 3C1)/ 6C2
= (1 x 3)/ (6 x 5/2)
= 1/5
P(A/E2) = P(Drawing 1 red ball and 1 white ball from urn II)
= (2C1 x 1C1)/ 4C2
= (2 x 1)/ (4 x 3/2)
= 1/3
P(A/E3) = P(Drawing 1 red ball and 1 white ball from urn III)
= (4C1 x 3C1)/ 12C2
= (4 x 3)/ (12 x 11)/2
= 2/11
We have to find,
P(both balls came from urn I) = P(E1/A)
P(both balls came from urn II) = P(E2/A)
P(both balls came from urn III) = P(E3/A)
So, by Baye’s theorem, we get
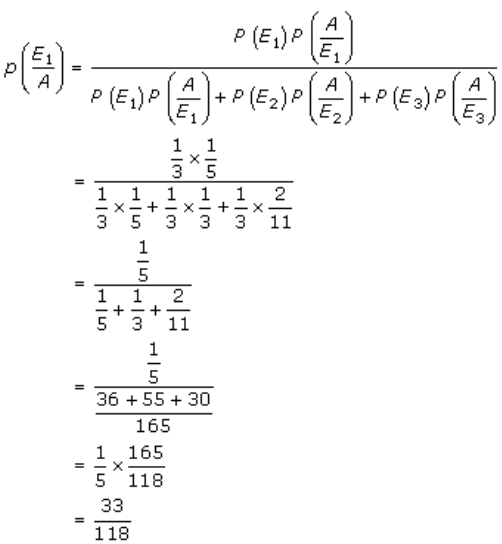
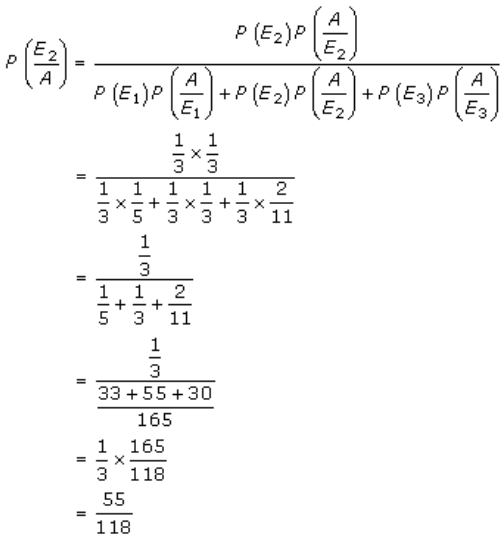
And,
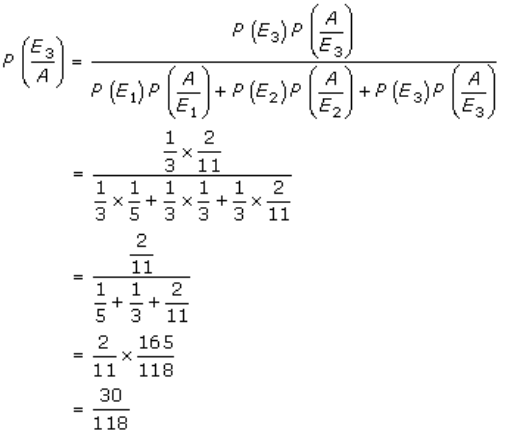
Therefore, the required probabilities are 33/118, 55/118 and 30/118.
2. Solution:
Given,
Bag A contains 2 white and 3 red balls.
Bag B contains 4 white and 5 red balls.
Let E1, E2 and A be events as given below.
E1 – Choosing bag A
E2 – Choosing bag B
A – Drawing one red ball
So, we have
P(E1) = P(E2) = 1/2 [Since, there are only 2 bags]
Now,
P(A/E1) = P(drawing a red ball from Bag A)
= 3/5
P(A/E2) = P(drawing a red ball from Bag B)
= 5/9
So, by Baye’s theorem, we get
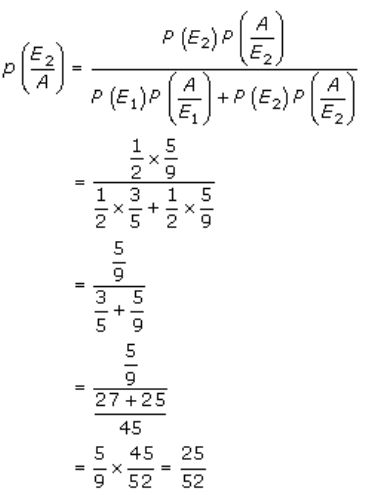
Hence, the required probability is 25/52.
3. Solution:
Given,
Urn I contains 2 white and 3 black balls.
Urn II contains 3 white and 2 black balls.
Urn III contains 4 white and 1 black balls.
Let E1, E2, E3 and A be the events as defined:
E1 = Selecting urn I
E2 = Selecting urn II
E3 = Selecting urn III
A = Drawing 1 white ball
Now.
P(E1) = P(E2) = P(E3) = 1/3 [As there are only 3 urns]
And,
P(A/E1) = P(Drawing one white ball from urn I)
= 2/5
P(A/E2) = P(Drawing one white ball from urn II)
= 3/5
P(A/E3) = P(Drawing one white ball from urn III)
= 4/5
According to the question, we need to find
P(Drawn one white ball is from urn 1) = P(E1/A)
So, By Baye’s theorem, we get
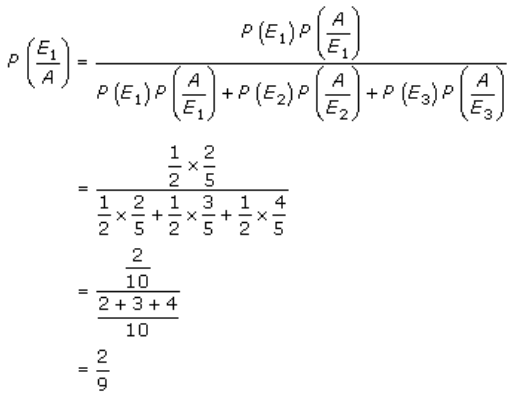
Therefore, the required probability is 2/9.
4. Solution:
Given,
Urn I contains 7 white and 3 black balls.
Urn II contains 4 white and 6 black balls.
Urn III contains 2 white and 8 black balls.
Let E1, E2, E3 and A be the events as defined:
E1 = Selecting urn I
E2 = Selecting urn II
E3 = Selecting urn III
A = Drawing 2 white balls without replacement
Also given,
P(E1) = 0.20
P(E2) = 0.60
P(E3) = 0.20
Now,
P(A/E1) = P(Drawing two white balls from urn I)
= 7C2/10C2
= (7×6)/2 ÷ (10×9)/2
= 7/15
P(A/E2) = P(Drawing two white balls from urn II)
= 4C2/10C2
= (4×3)/2 ÷ (10×9)/2
= 12/90
= 2/15
P(A/E3) = P(Drawing two white balls from urn III)
= 2C2/10C2
= 1 ÷ (10×9)/2
= 1/45
According to the question, we need to find
P(Drawn two white balls are from urn III) = P(E3/A)
So, By Baye’s theorem, we get
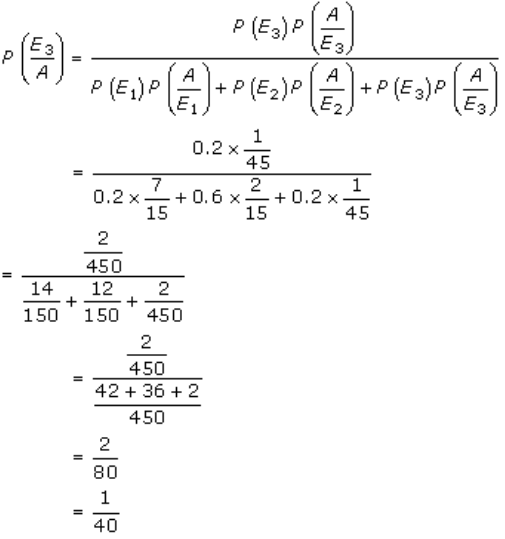
Thus, the required probability is 1/40.
5. Solution:
Let’s consider the following events,
E1 – Getting 1 or 2 in a throw of die.
E2 – Getting 3, 4, 5 or 6 in a throw of die.
A – Getting exactly one tail
So clearly, we have
P(E1) = 2/6 = 1/3
P(E2) = 4/6 = 2/3
P(A/E1) = 3/8
P(A/E2) = ½
Now, the required probability is given by

6. Solution:
Let’s consider the following events:
E1 – The first group wins
E2 – The second group wins
A – New product is introduced
It’s given that,
P(E1) = 0.6
P(E2) = 0.4
P(A/E1) = 0.7
P(A/E2) = 0.3
So, the required probability P(E2/A) is given by
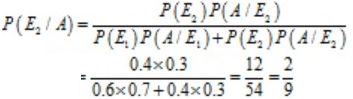
Hence,
P(E2/A) = 2/9