Chapter 30 LINEAR PROGRAMMING

Access RD Sharma Solutions for Class 12 Maths Chapter 30 Exercise 1

EXERCISE 30.1

Q1.

Solution:

Let us consider the data in the tabular form:

Gadget	Foundry	Machine-shop	Profit
A	10	5	Rs 30
B	6	4	Rs 20
Firm’s capacity per week	1000	600

Now, let x and y be the required weekly production of gadgets A and B.

Given:

Profit on each gadget A is = Rs 30

So, profit on x gadget of type A = 30x

Profit on each gadget B is = Rs 20

So, profit on x gadget of type B = 20y

Let total profit be ‘Z’

So, Z = 30x + 20y

Case I:

Given:

Production of one gadget A requires 10hours per week for foundry.

Production of one gadget B requires 6hours per week for foundry.

So, x units of gadget A requires 10x hours per week and

y unit of gadget B requires 6y hours per week.

Maximum capacity of foundry per week is 1000 hours, so => 10x + 6y ≤ 1000

Case II:

Given:

Production of one gadget A requires 5hours per week of machine-shop.

Production of one unit of gadget B requires 4hours per week of machine-shop.

So, x units of gadget A requires 5x hours per week and

y unit of gadget B requires 4y hours per week.

Maximum capacity of machine-shop per week is 600 hours, so => 5x + 4y ≤ 600

Hence, the required mathematical formulation of linear programming is:

Maximize Z = 30x + 20y

Subject to

10x + 6y ≤ 1000

5x + 4y ≤ 600

Where, x, y ≥ 0

Q2.

Solution:

Let us consider the data in the tabular form:

Product	Machine hours	Labour hours	Profit
A	1	1	Rs 60
B	–	1	Rs 80
Total capacity Minimum supply of product B is 200 units.	400 for A	500

Now, let x and y be the required production of products A and B.

Given:

Profit on one unit of product A is = Rs 60

So, profit on x unit of product A = 60x

Profit on one unit of product B is = Rs 80

So, profit on x unit of product B = 80y

Let total profit be ‘Z’

So, Z = 60x + 80y

First constraint:

Given, Minimum supply of product B is 200

So, y ≥ 200

Second constraint:

Given:

Production of one unit of product A requires 1hour per week of machine hours.

So, x units of product A requires 1x hour per week and

Total machine hours available for product A is 400hours,

So, x ≤ 400

Third constraint:

Given:

Production of one unit of product A requires 1hour per week of labour hours.

Production of one unit of product B requires 1hour per week of labour hours.

So, x units of product A requires 1x hour per week and

y units of product B requires 1x hour per week.

Total labour hours available is 500hours,

So, x + y ≤ 500

Hence, the required mathematical formulation of linear programming is:

Minimize Z = 60x + 80y

Subject to

x ≤ 400

x + y ≤ 500

Where, x, y ≥ 0

Q3.

Solution:

Let us consider the data in the tabular form:

Product	Machine (M1)	Machine (M2)	Profit
A	4	2	3
B	3	2	2
C	5	4	4
Capacity maximum	2000	2500

Now, let x, y and z units be the required production of products A,B and C.

Given:

Profit on one unit of product A is = Rs 3

So, profit on x unit of product A = 3x

Profit on one unit of product B is = Rs 20

So, profit on x unit of product B = 2y

Profit on one unit of product C is = Rs 4

So, profit on x unit of product C = 4z

Let total profit be ‘U’

So, U = 3x + 2y + 4z

First Constraint:

Given:

One unit of product A requires 4minutes on machine, M₁

One unit of product B requires 3minutes on machine, M₁

One unit of product C requires 5minutes on machine, M₁

So,

x unit of product A requires 4x minutes on machine, M₁

y unit of product B requires 3y minutes on machine, M₁

z unit of product C requires 5z minutes on machine, M₁

Total minutes on M₁ = 2000 minutes

i.e., 4x + 3y + 5z ≤ 2000

Second constraint:

Given:

One unit of product A requires 2minutes on machine, M₂

One unit of product B requires 2minutes on machine, M₂

One unit of product C requires 4minutes on machine, M₂

So,

x unit of product A requires 2x minutes on machine, M₂

y unit of product B requires 2y minutes on machine, M₂

z unit of product C requires 4z minutes on machine, M₂

Total minutes on M₂ = 2500 minutes

i.e., 2x + 2y + 4z ≤ 2500

Other constraints:

Given:

Firm must manufacture 100A’s, 200B’s and 50C’s but not more than 150A’s.

100 ≤ x ≤ 150

y ≥ 200

z ≥ 50

Hence, the required mathematical formulation of linear programming is:

Maximize U = 3x + 2y + 4z

Subject to

4x + 3y + 5z ≤ 2000

2x + 2y + 4z ≤ 2500

100 ≤ x ≤ 150

y ≥ 200

z ≥ 50

Where, x, y, z ≥ 0

Q4.

Solution:

Let us consider the data in the tabular form:

Product	M1	M2	Profit
A	1	2	2
B	1	1	3
Capacity	6 hours 40minutes = 400minutes	10 hours = 600 minutes

Now, let x and y be the required production of products A and B.

Given:

Profit on one unit of product A is = Rs 2

So, profit on x unit of product A = 2x

Profit on one unit of product B is = Rs 3

So, profit on x unit of product B = 3y

Let total profit be ‘Z’

So, Z = 2x + 3y

First Constraint:

Given:

One unit of product A requires 1minutes on machine, M₁

One unit of product B requires 1minutes on machine, M₁

So,

x unit of product A requires 1x minutes on machine, M₁

y unit of product B requires 1y minutes on machine, M₁

Total minutes on M₁ = 2000 minutes

i.e., x + y ≤ 400

Second constraint:

Given:

One unit of product A requires 2minutes on machine, M₂

One unit of product B requires 1minutes on machine, M₂

So,

x unit of product A requires 2x minutes on machine, M₂

y unit of product B requires 1y minutes on machine, M₂

Total minutes on M₂ = 2500 minutes

i.e., 2x + y ≤ 600

Hence, the required mathematical formulation of linear programming is:

Maximize Z = 2x + 3y

Subject to x + y ≤ 400

2x + y ≤ 600

Where, x, y ≥ 0

Q5.

Solution:

Let us consider the data in the tabular form:

Plant	A	B	C	Cost
I	50	100	100	2500
II	60	60	200	3500
Monthly demand	2500	3000	7000

Now, let x and y be the required days of plant I and II to minimize cost.

Given:

Plant I costs per day = Rs 2500

So, cost to run plant x requires per month = Rs 2500x

Plant II costs per day = Rs 3500

So, cost to run plant y requires per month = Rs 3500y

Let total cost per month be ‘Z’

So, Z = 2500x + 3500y

First Constraint:

Given:

Production of type A from plant I requires = 50

Production of type A from plant II requires = 60

So,

x unit of production of type A from plant I requires = 50x

y unit of production of type A from plant II requires = 60y

Total demand of type A per month = 2500

i.e., 50x + 60y ≥ 2500

Second Constraint:

Given:

Production of type B from plant I requires = 100

Production of type B from plant II requires = 60

So,

x unit of production of type B from plant I requires = 100x

y unit of production of type B from plant II requires = 60y

Total demand of type B per month = 3000

i.e., 100x + 60y ≥ 3000

Third Constraint:

Given:

Production of type C from plant I requires = 100

Production of type C from plant II requires = 200

So,

x unit of production of type C from plant I requires = 100x

y unit of production of type C from plant II requires = 200y

Total demand of type C per month = 7000

i.e., 100x + 200y ≥ 7000

Hence, the required mathematical formulation of linear programming is:

Minimize Z = 2500x + 3500y

Subject to

50x + 60y ≥ 2500

100x + 60y ≥ 3000

100x + 200y ≥ 7000

Access RD Sharma Solutions for Class 12 Maths Chapter 30 Exercise 2

EXERCISE 30.2

Q1.

Solution:

Firstly, let us convert the given inequations into equations, we get

3x + 5y = 15,

5x + 2y = 10,

x = 0,

y = 0

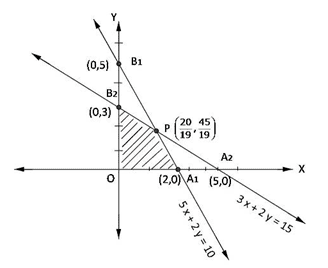
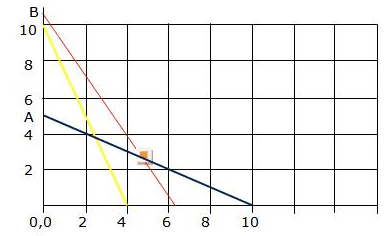
Region represented by 3x + 5y ≤ 15:

The line meets the coordinate axes at A₂(5,0) and B₂(0,3). By joining these points we obtain the line 3x + 5y = 15.

So, (0,0) satisfies the inequation 3x + 5y ≤ 15. Hence, the region containing the origin represents the solution set of the inequation 3x + 5y ≤ 15.

Region represented by 5x + 2y ≤ 10:

The line meets the coordinate axes at A₁(2,0) and B₁(0,5). By joining these points we obtain the line 5x + 2y = 10.

So, (0,0) satisfies the inequation 5x + 2y ≤ 10. Hence, the region containing the origin represents the solution set of the inequation 5x + 2y ≤ 10.

Region represented by x ≥ 0, y ≥ 0:

Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, y ≥ 0.

The coordinates of the corner points of shaded region are O(0,0), A(2,0), P(20/19, 45/19), B₂(0,3)

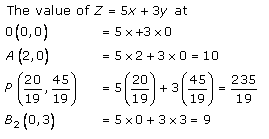
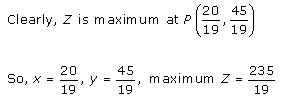
Q2.

Solution:

Firstly let us convert the given Inequations into equations, we get

2x + 3y = 13,

3x + y = 5,

x = 0,

y = 0

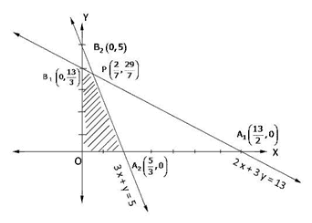
Region represented by 2x + 3y ≤ 13:

The line meets the coordinate axes at A₁(13/2,0) and B₁(0,13/3). By joining these points we obtain the line 2x + 3y = 13.

So, (0,0) satisfies the inequation 2x + 3y ≤ 13. Hence, the region containing the origin represents the solution set of the inequation 2x + 3y ≤ 13.

Region represented by 3x + y ≤ 5:

The line meets the coordinate axes at A₂(5/3,0) and B₂(0,5). By joining these points we obtain the line 3x + y = 5.

So, (0,0) satisfies the inequation 3x + y ≤ 5. Hence, the region containing the origin represents the solution set of the inequation 3x + y ≤ 5.

Region represented by x ≥ 0, y ≥ 0:

Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, y ≥ 0.

The coordinates of the corner points of shaded region are O(0,0), A(5/3,0), P(2/7, 29/7), B₂(0,13/3)

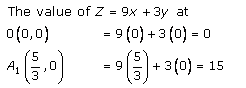
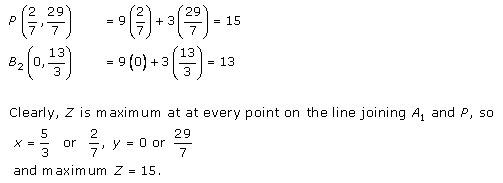
Q3.

Solution:

Firstly let us convert the given Inequations into equations, we get

4x + y = 20,

2x + 3y = 30,

x = 0,

y = 0

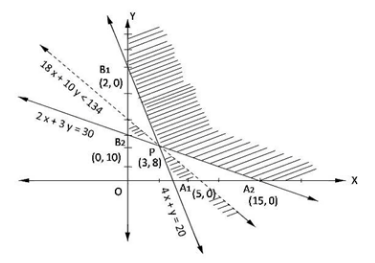
Region represented by 4x + y ≥ 20:

The line meets the coordinate axes at A₁(5,0) and B₁(0,20). By joining these points we obtain the line 4x + y = 20.

So, (0,0) satisfies the inequation 4x + y ≥ 20. Hence, the region containing the origin represents the solution set of the inequation 4x + y ≥ 20.

Region represented by 2x + 3y ≥ 30:

The line meets the coordinate axes at A₂(15,0) and B₂(0,10). By joining these points we obtain the line 2x + 3y = 30.

So, (0,0) satisfies the inequation 2x + 3y ≥ 30. Hence, the region containing the origin represents the solution set of the inequation 2x + 3y ≥ 30.

Region represented by x ≥ 0, y ≥ 0:

Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, y ≥ 0.

The coordinates of the corner points of shaded region are A₂(15,0), P(3,8), B₁(0,20)

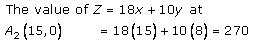
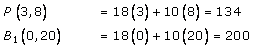
It is clear that, x = 3 and y = 8 is optimal. Hence, Minimum value of Z is 134 at points (3,8).

Q4.

Solution:

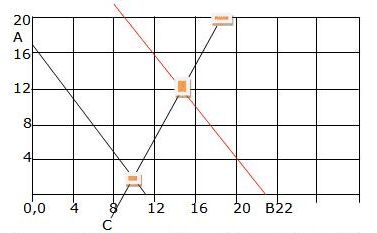
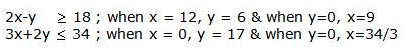
Let us plot these points, we get lines AB and CD.

We know that the feasible area is the unbounded area D-E-12

Corner point	Value of Z = 50x + 30y
10, 2	560
11.3, 17	1076.66

The maximum value of Z = 50x + 30y which occurs at x = 34/3, y = 17

Since we have an unbounded region as the feasible area plot 50x + 30y > 1076.66

The region D-F-B has common points with region D-E-12 the problem has no optimal maximum value.

Q5.

Solution:

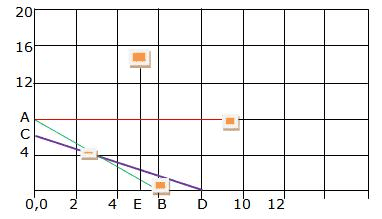
3x + 4y ≤ 24; when x = 0, y = 6 and when y = 0, x = 8, line AB.

8x + 6y ≤ 48; when x = 0, y = 8 and when y = 0, x = 6, line CD.

Let us plot these points, x ≤ 5 we get line EF and y ≤ 6 we get line AG.

We know that the feasible area is the unbounded area O, O-C-H-G-E

Corner point	Value of Z = 4x + 3y
0,0	0
0,6	18
3.4, 3.4	24
5, 1	23
5, 0	20

 

Access RD Sharma Solutions for Class 12 Maths Chapter 30 Exercise 3

EXERCISE 30.3

Q1.

Solution:

Let us consider x and y be number of 25gms of food packets, F₁ and F₂

Minimum cost of diet Z = 0.20x + 0.15y

Therefore the constraints are:

0.25x + 0.1y ≥ 1; when x = 0, y = 10 and y = 0, x = 4 10-4

0.75x + 1.5y ≥ 7.5; when x = 0, y = 5 and y = 0, x = 10 A-10

1.6x + 0.8y ≥ 10; when x = 0, y = 25/2 and y = 0, x = 25/4

The feasible region is the open region B-E-10

The minimum cost of the diet can be checked by finding the value of Z at corner points B, E and 10.

Corner points	Value of Z = 20x + 15y
0, 12.5	187.5
10, 0	200
5, 2.5	137.5

Since the feasible region is an open region so we plot 20x + 15y < 137.5, to check whether the resulting open half plane has any point common with the feasible region.

Since it has common points Z = 20x + 15y

Hence there is no optimal minimum value subject to the given constraints.

Q2.

Solution:

Let us consider the required quantity of food A and B be x and y units.

Given:

Costs of one unit of food A and B are Rs 4 and Rs 3 per unit.

So, cost of x unit of food A and y unit of food B = 4x and 3y.

Let Z be minimum total cost,

So, Z = 4x + 3y

First Constraint:

One unit of food A and B contain = 200 and 100 units of vitamins

So, x units of food A and y units of food B contain = 200x and 100y units of vitamins

Minimum requirement of vitamin = 4000 units

So,

200x + 100y ≥ 4000

2x + y ≥ 40

Second constraint:

One unit of food A and B contain = 1 and 2 units of minerals

So, x units of food A and y units of food B contain = x and 2y units of minerals

Minimum requirement of minerals = 50 units

So,

x + 2y ≥ 50

Third constraint:

One unit of food A and B contain = 40 calories each

So, x units of food A and y units of food B contain = 40x and 40y units of calories

Minimum requirement of calories = 1400 units

So,

40x + 40y ≥ 1400

2x + 2y ≥ 70

x + y ≥ 35

Hence, the required mathematical formulation of linear programming is:

Minimize Z = 4x + 3y

Subject to constraints

2x + y ≥ 40

x + 2y ≥ 50

x + y ≥ 35

Where, x, y ≥ 0

Now, region 2x + y ≥ 40:

The line 2x + y = 40 meets axes at A₁(20, 0), B₁(0, 40) region not containing origin represents 2x + y ≥ 40 as (0, 0) does not satisfy 2x + y ≥ 40.

Region x + 2y ≥ 50:

The line x + 2y = 50 meets axes at A₂(50, 0), B₂(0, 25) region not containing origin represents x + 2y ≥ 50 as (0, 0) does not satisfy x + 2y ≥ 50.

Region x + y ≥ 35:

The line x + y = 35 meets axes at A₃(35, 0), B₃(0, 35) region not containing origin represents x + y ≥ 35 as (0, 0) does not satisfy x + y ≥ 35.

Region x, y ≥ 0: it represents first quadrant in xy-plane.

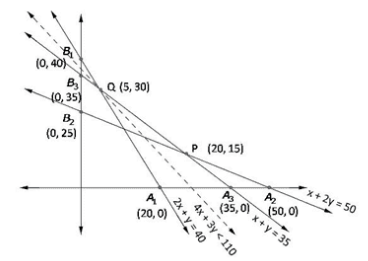
Unbounded shaded region A₂ P Q B₁ represents feasible region with corner points A₂(50, 0), P(20,15), Q(5, 30), B₁(0, 40)

The value of Z = 4x + 3y at

A₂(50, 0) = 4(50) + 3(0) = 2000

P(20, 15) = 4(20) + 3(15) = 125

Q(5, 30) = 4(5) + 3(30) = 110

B₁(0, 40) = 4(0) + 3(40) = 110

Hence, smallest value of Z = 110

Open half plane 4x + 3y < 110 has no point in common with feasible region

So, smallest value is the minimum value.

Quantity of food A = x = 5 units

Quantity of food B = y = 30 units

Minimum cost = Rs 110

Q3.

Solution:

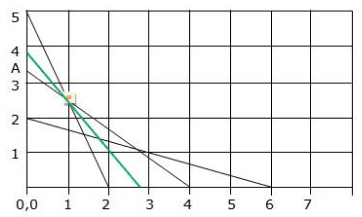
Let us consider x and y be units of food, F I and F II

The objective function is to minimize the function Z = 0.6x + y

Where,

10x + 4y ≥ 20; requirement of calcium, line 5-2

5x + 6y ≥ 20; requirement of protein, line A-4

2x + 6y ≥ 12; requirement of calories, line 2-6

The feasible region is the open unbounded region 5-F-E-6

The function 20x + 15y < 57.5 needs to be plotted to check if there are any common points. The green line shows that there are no common points.

So,

Corner points	Value of Z = 0.6x + y
0, 5	5
F(1, 2.5)	3.1
E(2.67, 1.11)	2.71
6, 0	3.6

The minimum cost occurs when Food I is 1 unit and Food II is 2.5 units.

Since it is an unbounded region plotting Z < 3.1 gives the green line which has no common points.

So, (1, 2.5) is aid to be a minimum point.

Q4.

Solution:

Let us consider the required quantity of food A and B be x and y units.

Given:

Costs of one unit of food A and B are 10paise per unit.

So, cost of x unit of food A and y unit of food B = 10x and 10y.

Let Z be minimum total cost,

So, Z = 10x + 10y

First Constraint:

One unit of food A and B contain = 0.12mg and 0.10mg of Thiamin

So, x units of food A and y units of food B contain = 0.12x and 0.10y mg of Thiamin

Minimum requirement of Thiamin = 0.5mg

So,

0.12x + 0.10y ≥ 0.5

12x + 10y ≥ 50

6x + 5y ≥ 25

Second constraint:

One unit of food A and B contain = 100 and 150 calories

So, x units of food A and y units of food B contain = 100x and 150y units of calories

Minimum requirement of calories = 600 units

So,

100x + 150y ≥ 600

2x + 3y ≥ 12

Hence, the required mathematical formulation of linear programming is:

Minimize Z = 10x + 10y

Subject to constraints

6x + 5y ≥ 25

2x + 3y ≥ 12

Where, x, y ≥ 0

Now, region 6x + 5y ≥ 25:

The line 6x + 5y = 25 meets axes at A₁(25/6, 0), B₁(0, 5) region not containing origin represents 6x + 5y ≥ 25 as (0, 0) does not satisfy 6x + 5y ≥ 25.

Region 2x + 3y ≥ 12:

The line 2x + 3y = 12 meets axes at A₂(6, 0), B₂(0, 4) region not containing origin represents 2x + 3y ≥ 12 as (0, 0) does not satisfy 2x + 3y ≥ 12.

Region x, y ≥ 0: it represents first quadrant in xy-plane.

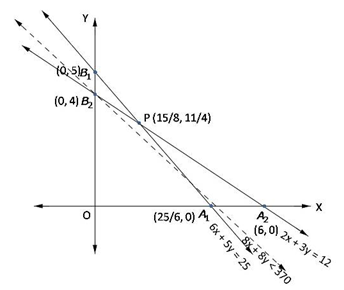
Unbounded shaded region A₂ P B₁ represents feasible region with corner points A₂(6, 0), P(15/8,11/4), B₁(0, 5)

The value of Z = 10x + 10y at

A₂(6, 0) = 10(6) + 10(0) = 60

P(15/8, 11/4) = 10(15/8) + 10(11/4) = 370/8 = 46 ¼

B₁(0, 5) = 10(0) + 10(5) = 50

Hence, smallest value of Z = 46 ¼

Open half plane 10x + 10y < 370/8 has no point in common with feasible region

So, smallest value is the minimum value.

Required quantity of food A = x = 15/8 units

Required quantity of food B = y = 11/4 units

Minimum cost = Rs 46. 25

Q5.

Solution:

Let us consider the required quantity of food A and B be x and y kg.

Given:

Costs of one kg of food A and B are Rs 5 and Rs 8 kg.

So, cost of x kg of food A and y kg of food B = 5x and 8y.

Let Z be minimum total cost,

So, Z = 5x + 8y

First Constraint:

One kg of food A and B contain = 1 and 2 units of vitamin A

So, x kg of food A and y kg of food B contain = x and 2y kg of vitamin A

Minimum requirement of vitamin A = 6 units

So,

x + 2y ≥ 6

Second constraint:

One kg of food A and B contain = 1 unit of Vitamin B each

So, x kg of food A and y kg of food B contain = x and y units of vitamin B

Minimum requirement of vitamin B = 7 units

So,

x + y ≥ 7

Third constraint:

One kg of food A and B contain = 1 and 3 units of vitamin C

So, x kg of food A and y kg of food B contain = x and 3y units of vitamin C

Minimum requirement of vitamin C = 11 units

So,

x + 3y ≥ 11

Fourth constraint:

One kg of food A and B contain = 2 and 1 units of vitamin D

So, x kg of food A and y kg of food B contain = 2x and y units of vitamin D

Minimum requirement of vitamin D = 9 units

So,

2x + y ≥ 9

Hence, the required mathematical formulation of linear programming is:

Minimize Z = 5x + 8y

Subject to constraints

x + 2y ≥ 6

x + y ≥ 7

x + 3y ≥ 11

2x + y ≥ 9

Where, x, y ≥ 0

Now, region x + 2y ≥ 6:

The line x + 2y = 6 meets axes at A₁(6, 0), B₁(0, 3) region not containing origin represents x + 2y ≥ 6 as (0, 0) does not satisfy x + 2y ≥ 6.

Region x + y ≥ 7:

The line x + y = 7 meets axes at A₂(7, 0), B₂(0, 7) region not containing origin represents x + y ≥ 7 as (0, 0) does not satisfy x + y ≥ 7.

Region x + 3y ≥ 11:

The line x + 3y ≥ 11 meets axes at A₃(11, 0), B₃(0, 11/3) region not containing origin represents x + 3y ≥ 11 as (0, 0) does not satisfy x + 3y ≥ 11.

Region 2x + y ≥ 9:

The line 2x + y = 9 meets axes at A₄(9/2, 0), B₄(0, 9) region not containing origin represents 2x + y ≥ 9 as (0, 0) does not satisfy 2x + y ≥ 9.

Region x, y ≥ 0: it represents first quadrant in xy-plane.

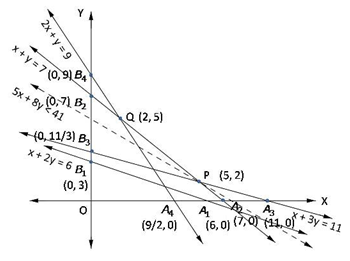
Unbounded shaded region A₂ P Q B₄ represents feasible region with corner points A₃(11, 0), P(5, 2), Q(2, 5), B₄(0, 9)

The value of Z = 5x + 8y at

A₃(11, 0) = 5(11) + 8(0) = 55

P(5, 2) = 5(5) + 8(2) = 41

Q(2, 5) = 5(2) + 8(5) = 50

B₄(0, 9) = 5(0) + 8(9) = 72

Hence, smallest value of Z = 41

Open half plane 5x + 8y < 41 has no point in common with feasible region

So, smallest value is the minimum value.

Last cost of mixture = Rs 41

Access RD Sharma Solutions for Class 12 Maths Chapter 30 Exercise 4

EXERCISE 30.4

Q1.

Solution:

Let us consider a young man drive x km at a speed of 25km/hr and y km at a speed of 40km/hr.

Let Z be the total distance travelled by young man.

So, Z = x + y

First constraint:

When speed is 25km/hr, the young man spends = Rs 2 per km

When speed is 40km/hr, the young man spends = Rs 5 per km

So,

Expenses on x km and y km = Rs 2x and Rs 5y

But young man has only Rs 100

So, 2x + 5y ≤ 100

Second constraint:

Time taken to travel x km = Distance/speed

= x/25 hr

Time taken to travel y km = Distance/speed

= y/40 hr

It is given that, 1hr to travel,

So, x/25 + y/40 ≤ 1

40x + 25y ≤ 1000

8x + 5y ≤ 200

Hence, the required mathematical formulation of linear programming is:

Minimize Z = x + y

Subject to constraints

2x + 5y ≤ 100

8x + 5y ≤ 200

Where, x, y ≥ 0

Now, region 2x + 5y ≤ 100:

The line 2x + 5y = 100 meets axes at A₁(50, 0), B₁(0, 20) region containing origin represents 2x + 5y ≤ 100 as (0, 0) satisfies 2x + 5y ≤ 100.

Region 8x + 5y ≤ 200:

The line 8x + 5y = 200 meets axes at A₂(25, 0), B₂(0, 40) region containing origin represents 8x + 5y ≤ 200 as (0, 0) satisfies 8x + 5y ≤ 200.

Region x, y ≥ 0: it represents first quadrant in xy-plane.

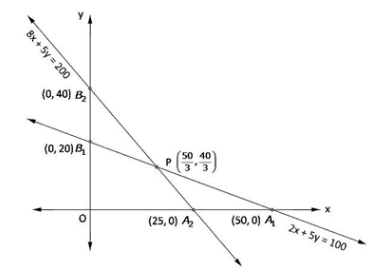
Shaded region O A₂ P B₁ represents feasible region.

Point P(50/3, 40/3) is obtained by solving 8x + 5y = 200, 2x + y = 100

The value of Z = x + y at

O(0, 0) = 0 + 0 = 0

A₂(25, 0) = 25 + 0 = 25

P(50/3, 40/3) = 50/3 + 40/3 = 30

B₁(0, 20) = 0 + 20 = 20

Hence, maximum value of Z = 30 at x = 50/3, y = 40/3

Distance travelled at speed of 25km/hr = 50/3 km

And at speed of 40 km/hr = 40/3 km

So maximum distance = 30 km

Q2.

Solution:

Let us consider the required quantity of items be A and B.

Given:

Profits on one item A and B = Rs 6 and Rs 4

So, profits on x items of type A and y items on type B = 6x and 4y

Let the total profit be Z,

Z = 6x + 4y

First constraint:

Machine I works 1 hour and 2hours on item A and B

So, x no. of item A and y no. of item B = x hour and 2y hours on machine I

Machine I works at most = 12 hours

x + 2y ≥ 12

Second constraint:

Machine II works 2 hours and 1hour on item A and B

So, x no. of item A and y no. of item B = 2x hours and y hours on machine II

Machine II works maximum of = 12 hours

2x + y ≥ 12

Third constraint:

Machine III works 1 hour and 5/4hour on item A and B

So, x no. of item A and y no. of item B = x hours and 5/4y hours on machine III

Machine III works at least = 5 hours

x + 5/4y ≥ 5

4x + 5y ≥ 20

Hence, the required mathematical formulation of linear programming is:

Minimize Z = 6x + 4y

Subject to constraints

x + 2y ≥ 12

2x + y ≥ 12

4x + 5y ≥ 20

Where, x, y ≥ 0

Now, region x + 2y ≥ 12:

The line x + 2y = 12 meets axes at A₁(12, 0), B₁(0, 6) region containing origin represents x + 2y ≥ 12 as (0, 0) satisfies x + 2y ≥ 12.

Region 2x + y ≥ 12:

The line 2x + y = 12 meets axes at A₁(6, 0), B₁(0, 12) region containing origin represents 2x + y ≥ 12 as (0, 0) satisfies 2x + y ≥ 12.

Region 4x + 5y ≥ 20:

The line 4x + 5y = 20 meets axes at A₃(5, 0), B₃(0, 4) region not containing origin represents 4x + 5y ≥ 20 as (0, 0) does not satisfy 4x + 5y ≥ 20.

Region x, y ≥ 0: it represents first quadrant in xy-plane.

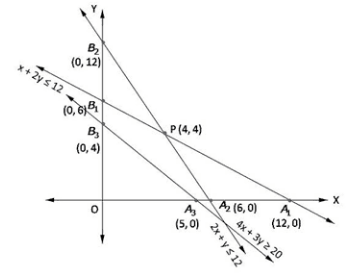
Shaded region A₂ A₃ P B₃ B₁ represents feasible region.

The value of Z = 6x + 4y at

A₂(6, 0) = 6(6) + 4(0) = 36

A₃(5, 0) = 6(5) + 4(0) = 30

B₃(0, 4) = 6(0) + 4(4) = 16

B₂(0, 6) = 6(0) + 4(6) = 24

P(4,4) = 6(4) + 4(4) = 40

Hence, maximum value of Z = 40 at x = 4, y = 4

Required number of product A =4, product B = 4

So maximum profit = Rs 40

Q3.

Solution:

Let us consider tailor A and B work for x and y days.

Given:

Tailor A and B earn = Rs 15 and Rs 20

So, tailor A and B earn is x and y days = Rs 15x and 20y

Let the total maximum profit be Z which gives minimum labour cost,

Z = 15x + 20y

First constraint:

Tailor A and B stitches = 6 and 10 shirts in a day

So, tailor A and B can stitch = 6x and 10y shirts in a day

But, tries to produce atleast = 60 shirts

So, 6x + 10y ≥ 60

3x + 5y ≥ 30

Second constraint:

Tailor A and B stitches = 4 pants each in a day

So, tailor A and B can stitch = 4x and 4y pants in a day

But, tries to produce atleast = 32 pants

So, 4x + 4y ≥ 32

x + y ≥ 8

Hence, the required mathematical formulation of linear programming is:

Minimize Z = 15x + 20y

Subject to constraints

3x + 5y ≥ 30

x + y ≥ 8

Where, x, y ≥ 0

Now, region 3x + 5y ≥ 30:

The line 3x + 5y = 30 meets axes at A₁(10, 0), B₁(0, 6) region not containing origin represents 3x + 5y ≥ 30 as (0, 0) does not satisfy 3x + 5y ≥ 30.

Region x + y ≥ 8:

The line x + y = 8 meets axes at A₂(8, 0), B₂(0, 8) region not containing origin represents x + y ≥ 8 as (0, 0) does not satisfy x + y ≥ 8.

Region x, y ≥ 0: it represents first quadrant in xy-plane.

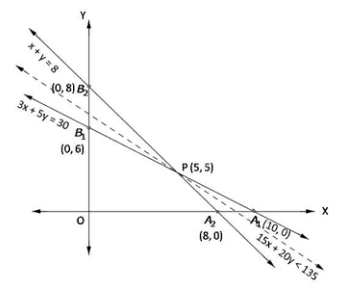
Unbounded shaded region A₁ P B₂ represents feasible region with corner points A₁(10, 0), P(5, 3), B₂(0, 8)

The value of Z = 15x + 20y at

A₁(10, 0) = 15(10) + 20(0) = 150

P(5, 3) = 15(5) + 20(3) = 135

B₂(0, 8) = 15(0) + 20(8) = 160

Hence, smallest value of Z = 135

Open half plane 15x + 20y < 135 has no point in common with feasible region

So, smallest value is the minimum value.

Z = 135, at x = 5, y = 3

Therefore, tailor A should work for 5 days and B should work for 3 days.

Q4.

Solution:

Let us consider the factory manufactures x screws of type A and y screws of type B per day.

So, x ≥ 0 and y ≥ 0

	Screw A	Screw B	Availability
Automatic Machine (min)	4	6	4 x 60 = 120
Hand operated Machine (min)	6	3	4 x 60 = 120

The profit on package of screws A and screws B is Rs 7 and Rs 10.

So the constraints are:

4x + 6y ≤ 240

6x + 3y ≤ 240

Total profit, Z = 7x + 10y

Hence, the required mathematical formulation of linear programming is:

Minimize Z = 7x + 10y

Subject to constraints

4x + 6y ≤ 240

6x + 3y ≤ 240

Where, x, y ≥ 0

The feasible region obtained by the constraints is:

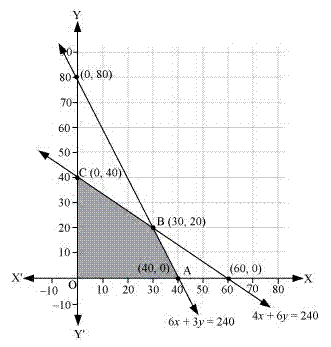
The corner points are A(40, 0), B(30, 20) and C(0, 40)

So the value of Z at these corner points is:

Corner point	Z = 7x + 10y
A(40, 0)	280
B(30, 20)	410	maximum
C(0, 40)	400

Hence, the maximum value of Z = 410 at B(30, 20).

So, the factory should produce 30 packages of screws A and 20 packages of screws B to get the maximum profit of Rs 410.

Q5.

Solution:

Let us consider the required number of belt A and belt B be x and y.

Given:

Profits on belt A and B = Rs 2 and Rs 1.50 per belt

So, profits on x belts of type A and y belts on type B = 2x and 1.5y

Let the total profit be Z,

Z = 2x + 1.5y

First constraint:

Each belt of type A requires twice as much as belt B.

Each belt of type B requires = 1 hour to make, so A requires = 2 hours

So for x and y belts of type A and B requires = 2x and y hours to make

Total time available is equal to production of 1000 belts B = 1000 hours

2x + y ≤ 1000

Second constraint:

It is given that, supply of leather for = 800 belts per day for both A and B

So, x + y ≤ 800

Third constraint:

It is given that, buckles available for A = 400 and

Buckles available for B = 700

So, x ≤ 400

y ≤ 700

Hence, the required mathematical formulation of linear programming is:

Maximize Z = 2x + 1.5y

Subject to constraints

2x + y ≤ 1000

x + y ≤ 800

x ≤ 400

y ≤ 700

Where, x, y ≥ 0

Now, region 2x + y ≤ 1000:

The line 2x + y = 1000 meets axes at A₁(500, 0), B₁(0, 1000) region containing origin represents 2x + y ≤ 1000 as (0, 0) satisfies 2x + y ≤ 1000.

Region x + y ≤ 800:

The line x + y = 800 meets axes at A₂(800, 0), B₂(0, 800) region containing origin represents x + y ≤ 800 as (0, 0) satisfies x + y ≤ 800.

Region x ≤ 400:

The line x ≤ 400 is parallel to y-axis and meets x-axis at A₃(400, 0) region containing origin represents x ≤ 400 as (0, 0) satisfies x ≤ 400.

Region y ≤ 400:

The line y ≤ 700 is parallel to x-axis and meets y-axis at B₃(0, 700) region containing origin represents y ≤ 700 as (0, 0) satisfies y ≤ 700.

Region x, y ≥ 0: it represents first quadrant in xy-plane.

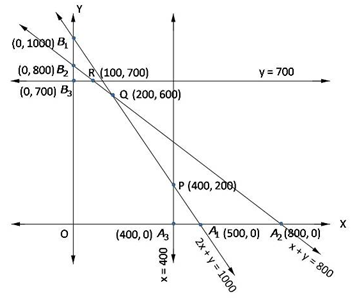
Shaded region O A₃ P Q R B₃ represents feasible region.

Point P is obtained by intersection of x + y = 800, 2x + y = 1000,

R is not point of intersection of y = 700, x + y = 800.

The value of Z = 2x + 1.5y at

O(0, 0) = 2(0) + 1.5(0) = 0

A₃(400, 0) = 2(400) + 1.5(0) = 800

P(400, 200) = 2(400) + 1.5(200) = 1100

Q(200, 600) = 2(200) + 1.5(600) = 1300

R(100, 700) = 2(100) + 1.5(700) = 1250

B₃(0, 700) = 2(0) + 1.5(700) = 1050

Hence, maximum value of Z = 1300 at x = 200, y = 600

Required no. of belt A = 200,

Required no. of belt B = 600,

So maximum profit = Rs 1300

Access RD Sharma Solutions for Class 12 Maths Chapter 30 Exercise 5

EXERCISE 30.5

Q1.

Solution:

Let us consider godown A supply x and y quintals of grain to the shops D and E.

Then, (100 – x – y) will be supplied to shop F.

The requirement at shop D is 60 quintals since, x quintals are transported from godown A.

Therefore, the remaining (60 − x) quintals will be transported from godown B.

Similarly, (50 − y) quintals and 40 − (100 − x − y) i.e. (x + y − 60) quintals will be transported from godown B to shop E and F respectively.

Here is the diagrammatic representation of the given problem:

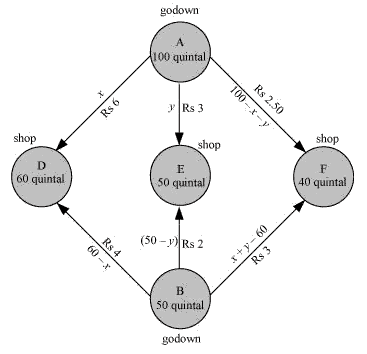
x ≥ 0 , y ≥ 0 and 100 – x – y ≥ 0

⇒ x ≥ 0 , y ≥ 0 , and x + y ≤ 100

60 – x ≥ 0 , 50 – y ≥ 0 , and x + y – 60 ≥ 0

⇒ x ≤ 60 , y ≤ 50 , and x + y ≥ 60

Total transportation cost Z is given by,

Z = 6x + 3y + 2.5(100 – x – y) + 4(60 – x) + 2(50 – y) + 3( x + y – 60)

= 6x + 3y + 250 – 2.5x – 2.5y + 240 – 4x + 100 – 2y + 3x + 3y – 180

= 2.5x + 1.5y + 410

Hence, the required mathematical formulation of linear programming is:

Minimize Z = 2.5x + 1.5y + 410

subject to the constraints,

x + y ≤ 100

x ≤ 60

y ≤ 50

x + y ≥ 60

x, y ≥ 0

The feasible region obtained by the system of constraints is:

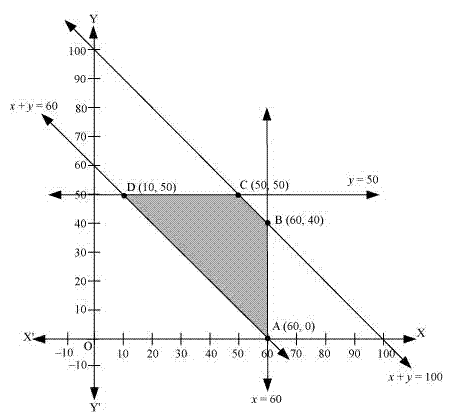
The corner points are A(60, 0), B(60, 40), C(50, 50), and D(10, 50).

The values of Z at these corner points are as follows.

Corner point	Z = 2.5x + 1.5y + 410
A (60, 0)	560
B (60, 40)	620
C (50, 50)	610
D (10, 50)	510 -> minimum

Hence, the minimum value of Z is 510 at D (10, 50).

Thus, the amount of grain transported from A to D, E, and F is 10 quintals, 50 quintals, and 40 quintals respectively.

From B to D, E, and F is 50 quintals, 0 quintals, and 0 quintals respectively.

The minimum cost is Rs 510.

Q2.

Solution:

The diagrammatic representation of the given problem:

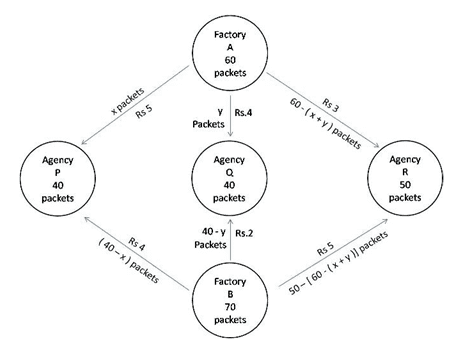
Let x and y packets be transported from factory A to the agencies P and Q respectively.

Then, [60 − (x + y)] packets be transported to the agency R.

First constraint:

x, y ≥ 0 and

Second constraint:

60 − (x + y) ≥ 0

(x + y) ≤ 60

The requirement at agency P is 40 packets. Since, x packets are transported from factory A,

Therefore, the remaining (40 − x) packets are transported from factory B.

Similarly, (40 − y) packets are transported by B to Q and 50− [60 − (x + y)] i.e. (x + y − 10) packets will be transported from factory B to agency R respectively.

Number of packets cannot be negative.

Therefore,

Third constraint:

40 – x ≥ 0

=> x ≤ 40

Fourth constraint:

40 – y ≥ 0

=> y ≤ 40

Fifth constraint:

x + y – 10 ≥ 0

=> x + y ≥ 10

So, costs of transportation of each packet from factory A to agency P, Q, R are Rs 5, 4, 3.

Costs of transportation of each packet from factory B to agency P, Q, R are Rs 4, 2, 5.

Let total cost of transportation be Z.

Z = 5x + 4y + 3[60 – x + y] + 4(40 – x) + 2(40 – y) + 5(x + y – 10]

= 3x + 4y + 10

Hence, the required mathematical formulation of linear programming is:

Minimize Z = 3x + 4y + 370

subject to constraints,

x + y ≤ 60

x ≤ 40

y ≤ 40

x + y ≥ 10

where, x, y ≥ 0

Let us convert inequations into equations as follows:

x + y = 60, x = 40, y = 40, x + y = 10, x = 0 and y = 0

Region represented by x + y ≤ 60:

The line x + y = 60 meets the coordinate axes at A₁(60, 0) and B₁(0, 60) respectively. Region containing origin represents x + y ≤ 60 as (0, 0) satisfies x + y ≤ 60.

Region represented by x ≤ 40:

The line x = 40 is parallel to y-axis, meets x-axis at A₂(40, 0). Region containing origin represents x ≤ 40 as (0, 0) satisfies x ≤ 40.

Region represented by y ≤ 40:

The line y = 40 is parallel to x-axis, meets y-axis at B₂(0, 40). Region containing origin represents y ≤ 40 as (0, 0) satisfies y ≤ 40.

Region represented by x + y ≥ 10:

The line x + y = 10 meets the coordinate axes at A₂(10, 0) and B₃(0, 10) respectively. Region not containing origin represents x + y ≥ 10 as (0, 0) does not satisfy x + y ≥ 10.

Shaded region A₃ A₂ P Q B₂ B₃ represents feasible region.

Point P(40, 20) is obtained by solving x = 40 and x + y = 60

Point Q(20, 40) is obtained by solving y = 40 and x + y = 60

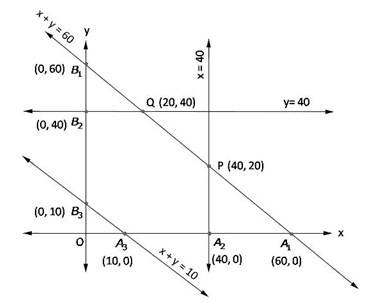
The value of Z = 3x + 4y + 370 at

A₃(10, 0) = 3(10) + 4(0) + 370 = 400

A₂(40, 0) = 3(40) + 4(0) + 370 = 490

P(40, 20) = 3(40) + 4(20) + 370 = 570

Q(20, 40) = 3(20) + 4(40) + 370 = 590

B₂(0, 40) = 3(0) + 4(40) + 370 = 530

B₃(0, 10) = 3(0) + 4(10) + 370 = 410

Hence, minimum value of Z = 400 at x = 10, y = 0

So, from A -> P = 10 packets

From A -> Q = 0 packets

From A -> R = 50 packets

From B -> P = 30 packets

From B -> Q = 40 packets

From B -> R = 0 packets

Therefore, minimum cost = Rs 400