Chapter 3 BINARY OPERATIONS
Class 12th Maths R D Sharma Solution
Access RD Sharma Solutions for Class 12 Maths Chapter 3 – Binary Operations
Exercise 3.1 Page No: 3.4
1. Determine whether the following operation define a binary operation on the given set or not:
(i) ‘*’ on N defined by a * b = ab for all a, b ∈ N.
(ii) ‘O’ on Z defined by a O b = ab for all a, b ∈ Z.
(iii) ‘*’ on N defined by a * b = a + b – 2 for all a, b ∈ N
(iv) ‘×6‘ on S = {1, 2, 3, 4, 5} defined by a ×6 b = Remainder when a b is divided by 6.
(v) ‘+6’ on S = {0, 1, 2, 3, 4, 5} defined by a +6 b
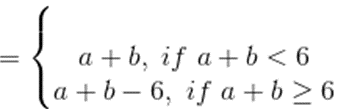
(vi) ‘⊙’ on N defined by a ⊙ b= ab + ba for all a, b ∈ N
(vii) ‘*’ on Q defined by a * b = (a – 1)/ (b + 1) for all a, b ∈ Q
Solution:
(i) Given ‘*’ on N defined by a * b = ab for all a, b ∈ N.
Let a, b ∈ N. Then,
ab ∈ N [∵ ab≠0 and a, b is positive integer]
⇒ a * b ∈ N
Therefore,
a * b ∈ N, ∀ a, b ∈ N
Thus, * is a binary operation on N.
(ii) Given ‘O’ on Z defined by a O b = ab for all a, b ∈ Z.
Both a = 3 and b = -1 belong to Z.
⇒ a * b = 3-1
= 1/3 ∉ Z
Thus, * is not a binary operation on Z.
(iii) Given ‘*’ on N defined by a * b = a + b – 2 for all a, b ∈ N
If a = 1 and b = 1,
a * b = a + b – 2
= 1 + 1 – 2
= 0 ∉ N
Thus, there exist a = 1 and b = 1 such that a * b ∉ N
So, * is not a binary operation on N.
(iv) Given ‘×6‘ on S = {1, 2, 3, 4, 5} defined by a ×6 b = Remainder when a b is divided by 6.
Consider the composition table,
| X6 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 4 | 0 | 2 | 4 |
| 3 | 3 | 0 | 3 | 0 | 3 |
| 4 | 4 | 2 | 0 | 4 | 2 |
| 5 | 5 | 4 | 3 | 2 | 1 |
Here all the elements of the table are not in S.
⇒ For a = 2 and b = 3,
a ×6 b = 2 ×6 3 = remainder when 6 divided by 6 = 0 ≠ S
Thus, ×6 is not a binary operation on S.
(v) Given ‘+6’ on S = {0, 1, 2, 3, 4, 5} defined by a +6 b
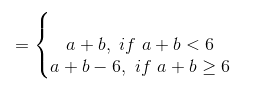
Consider the composition table,
| +6 | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 2 | 3 | 4 | 5 | 0 | 1 |
| 3 | 3 | 4 | 5 | 0 | 1 | 2 |
| 4 | 4 | 5 | 0 | 1 | 2 | 3 |
| 5 | 5 | 0 | 1 | 2 | 3 | 4 |
Here all the elements of the table are not in S.
⇒ For a = 2 and b = 3,
a ×6 b = 2 ×6 3 = remainder when 6 divided by 6 = 0 ≠ Thus, ×6 is not a binary operation on S.
(vi) Given ‘⊙’ on N defined by a ⊙ b= ab + ba for all a, b ∈ N
Let a, b ∈ N. Then,
ab, ba ∈ N
⇒ ab + ba ∈ N [∵Addition is binary operation on N]
⇒ a ⊙ b ∈ N
Thus, ⊙ is a binary operation on N.
(vii) Given ‘*’ on Q defined by a * b = (a – 1)/ (b + 1) for all a, b ∈ Q
If a = 2 and b = -1 in Q,
a * b = (a – 1)/ (b + 1)
= (2 – 1)/ (- 1 + 1)
= 1/0 [which is not defined]
For a = 2 and b = -1
a * b does not belongs to Q
So, * is not a binary operation in Q.
2. Determine whether or not the definition of * given below gives a
binary operation. In the event that * is not a binary operation give
justification of this.
(i) On Z+, defined *
by a * b = a – b
(ii) On Z+, define * by a*b = ab
(iii) On R, define * by a*b = ab2
(iv) On Z+ define * by a * b = |a − b|
(v) On Z+ define * by a * b = a
(vi) On R, define * by a * b = a + 4b2
Here, Z+ denotes the set of all non-negative integers.
Solution:
(i) Given On Z+, defined * by a * b = a – b
If a = 1 and b = 2 in Z+, then
a * b = a – b
= 1 – 2
= -1 ∉ Z+ [because Z+ is the set of non-negative integers]
For a = 1 and b = 2,
a * b ∉ Z+
Thus, * is not a binary operation on Z+.
(ii) Given Z+, define * by a*b = a b
Let a, b ∈ Z+
⇒ a, b ∈ Z+
⇒ a * b ∈ Z+
Thus, * is a binary operation on R.
(iii) Given on R, define by a*b = ab2
Let a, b ∈ R
⇒ a, b2 ∈ R
⇒ ab2 ∈ R
⇒ a * b ∈ R
Thus, * is a binary operation on R.
(iv) Given on Z+ define * by a * b = |a − b|
Let a, b ∈ Z+
⇒ | a – b | ∈ Z+
⇒ a * b ∈ Z+
Therefore,
a * b ∈ Z+, ∀ a, b ∈ Z+
Thus, * is a binary operation on Z+.
(v) Given on Z+ define * by a * b = a
Let a, b ∈ Z+
⇒ a ∈ Z+
⇒ a * b ∈ Z+
Therefore, a * b ∈ Z+ ∀ a, b ∈ Z+
Thus, * is a binary operation on Z+.
(vi) Given On R, define * by a * b = a + 4b2
Let a, b ∈ R
⇒ a, 4b2 ∈ R
⇒ a + 4b2 ∈ R
⇒ a * b ∈ R
Therefore, a *b ∈ R, ∀ a, b ∈ R
Thus, * is a binary operation on R.
3. Let * be a binary operation on the set I of integers, defined by a * b = 2a + b − 3. Find the value of 3 * 4.
Solution:
Given a * b = 2a + b – 3
3 * 4 = 2 (3) + 4 – 3
= 6 + 4 – 3
= 7
4. Is * defined on the set {1, 2, 3, 4, 5} by a * b = LCM of a and b a binary operation? Justify your answer.
Solution:
| LCM | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 2 | 6 | 4 | 10 |
| 3 | 3 | 5 | 3 | 12 | 15 |
| 4 | 4 | 4 | 12 | 4 | 20 |
| 5 | 5 | 10 | 15 | 20 | 5 |
In the given composition table, all the elements are not in the set {1, 2, 3, 4, 5}.
If we consider a = 2 and b = 3, a * b = LCM of a and b = 6 ∉ {1, 2, 3, 4, 5}.
Thus, * is not a binary operation on {1, 2, 3, 4, 5}.
5. Let S = {a, b, c}. Find the total number of binary operations on S.
Solution:
Number of binary operations on a set with n elements is
Here, S = {a, b, c}
Number of elements in S = 3
Number of binary operations on a set with 3 elements is
Exercise 3.2 Page No: 3.12
1. Let ‘*’ be a binary operation on N defined by
a * b = l.c.m. (a, b) for
all a, b ∈ N
(i) Find 2 * 4, 3 * 5, 1 * 6.
(ii) Check the commutativity and associativity of ‘*’ on N.
Solution:
(i) Given a * b = 1.c.m. (a, b)
2 * 4 = l.c.m. (2, 4)
= 4
3 * 5 = l.c.m. (3, 5)
= 15
1 * 6 = l.c.m. (1, 6)
= 6
(ii) We have to prove commutativity of *
Let a, b ∈ N
a * b = l.c.m (a, b)
= l.c.m (b, a)
= b * a
Therefore
a * b = b * a ∀ a, b ∈ N
Thus * is commutative on N.
Now we have to prove associativity of *
Let a, b, c ∈ N
a * (b * c ) = a * l.c.m. (b, c)
= l.c.m. (a, (b, c))
= l.c.m (a, b, c)
(a * b) * c = l.c.m. (a, b) * c
= l.c.m. ((a, b), c)
= l.c.m. (a, b, c)
Therefore
(a * (b * c) = (a * b) * c, ∀ a, b , c ∈ N
Thus, * is associative on N.
2. Determine which of the following binary operation is associative and which is commutative:
(i) * on N defined by a * b = 1 for all a, b ∈ N
(ii) * on Q defined by a * b = (a + b)/2 for all a, b ∈ Q
Solution:
(i) We have to prove commutativity of *
Let a, b ∈ N
a * b = 1
b * a = 1
Therefore,
a * b = b * a, for all a, b ∈ N
Thus * is commutative on N.
Now we have to prove associativity of *
Let a, b, c ∈ N
Then a * (b * c) = a * (1)
= 1
(a * b) *c = (1) * c
= 1
Therefore a * (b * c) = (a * b) *c for all a, b, c ∈ N
Thus, * is associative on N.
(ii) First we have to prove commutativity of *
Let a, b ∈ N
a * b = (a + b)/2
= (b + a)/2
= b * a
Therefore, a * b = b * a, ∀ a, b ∈ N
Thus * is commutative on N.
Now we have to prove associativity of *
Let a, b, c ∈ N
a * (b * c) = a * (b + c)/2
= [a + (b + c)]/2
= (2a + b + c)/4
Now, (a * b) * c = (a + b)/2 * c
= [(a + b)/2 + c] /2
= (a + b + 2c)/4
Thus, a * (b * c) ≠ (a * b) * c
If a = 1, b= 2, c = 3
1 * (2 * 3) = 1 * (2 + 3)/2
= 1 * (5/2)
= [1 + (5/2)]/2
= 7/4
(1 * 2) * 3 = (1 + 2)/2 * 3
= 3/2 * 3
= [(3/2) + 3]/2
= 4/9
Therefore, there exist a = 1, b = 2, c = 3 ∈ N such that a * (b * c) ≠ (a * b) * c
Thus, * is not associative on N.
3. Let A be any set containing more than one element. Let ‘*’ be a binary operation on A defined by a * b = b for all a, b ∈ A Is ‘*’ commutative or associative on A?
Solution:
Let a, b ∈ A
Then, a * b = b
b * a = a
Therefore a * b ≠ b * a
Thus, * is not commutative on A
Now we have to check associativity:
Let a, b, c ∈ A
a * (b * c) = a * c
= c
Therefore
a * (b * c) = (a * b) * c, ∀ a, b, c ∈ A
Thus, * is associative on A
4. Check the commutativity and associativity of each of the following binary operations:
(i) ‘*’ on Z defined by a * b = a + b + a b for all a, b ∈ Z
(ii) ‘*’ on N defined by a * b = 2ab for all a, b ∈ N
(iii) ‘*’ on Q defined by a * b = a – b for all a, b ∈ Q
(iv) ‘⊙’ on Q defined by a ⊙ b = a2 + b2 for all a, b ∈ Q
(v) ‘o’ on Q defined by a o b = (ab/2) for all a, b ∈ Q
(vi) ‘*’ on Q defined by a * b = ab2 for all a, b ∈ Q
(vii) ‘*’ on Q defined by a * b = a + a b for all a, b ∈ Q
(viii) ‘*’ on R defined by a * b = a + b -7 for all a, b ∈ R
(ix) ‘*’ on Q defined by a * b = (a – b)2 for all a, b ∈ Q
(x) ‘*’ on Q defined by a * b = a b + 1 for all a, b ∈ Q
(xi) ‘*’ on N defined by a * b = ab for all a, b ∈ N
(xii) ‘*’ on Z defined by a * b = a – b for all a, b ∈ Z
(xiii) ‘*’ on Q defined by a * b = (ab/4) for all a, b ∈ Q
(xiv) ‘*’ on Z defined by a * b = a + b – ab for all a, b ∈ Z
(xv) ‘*’ on Q defined by a * b = gcd (a, b) for all a, b ∈ Q
Solution:
(i) First we have to check commutativity of *
Let a, b ∈ Z
Then a * b = a + b + ab
= b + a + ba
= b * a
Therefore,
a * b = b * a, ∀ a, b ∈ Z
Now we have to prove associativity of *
Let a, b, c ∈ Z, Then,
a * (b * c) = a * (b + c + b c)
= a + (b + c + b c) + a (b + c + b c)
= a + b + c + b c + a b + a c + a b c
(a * b) * c = (a + b + a b) * c
= a + b + a b + c + (a + b + a b) c
= a + b + a b + c + a c + b c + a b c
Therefore,
a * (b * c) = (a * b) * c, ∀ a, b, c ∈ Z
Thus, * is associative on Z.
(ii) First we have to check commutativity of *
Let a, b ∈ N
a * b = 2ab
= 2ba
= b * a
Therefore, a * b = b * a, ∀ a, b ∈ N
Thus, * is commutative on N
Now we have to check associativity of *
Let a, b, c ∈ N
Then, a * (b * c) = a * (2bc)
=
(a * b) * c = (2ab) * c
=
Therefore, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on N
(iii) First we have to check commutativity of *
Let a, b ∈ Q, then
a * b = a – b
b * a = b – a
Therefore, a * b ≠ b * a
Thus, * is not commutative on Q
Now we have to check associativity of *
Let a, b, c ∈ Q, then
a * (b * c) = a * (b – c)
= a – (b – c)
= a – b + c
(a * b) * c = (a – b) * c
= a – b – c
Therefore,
a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Q
(iv) First we have to check commutativity of ⊙
Let a, b ∈ Q, then
a ⊙ b = a2 + b2
= b2 + a2
= b ⊙ a
Therefore, a ⊙ b = b ⊙ a, ∀ a, b ∈ Q
Thus, ⊙ on Q
Now we have to check associativity of ⊙
Let a, b, c ∈ Q, then
a ⊙ (b ⊙ c) = a ⊙ (b2 + c2)
= a2 + (b2 + c2)2
= a2 + b4 + c4 + 2b2c2
(a ⊙ b) ⊙ c = (a2 + b2) ⊙ c
= (a2 + b2)2 + c2
= a4 + b4 + 2a2b2 + c2
Therefore,
(a ⊙ b) ⊙ c ≠ a ⊙ (b ⊙ c)
Thus, ⊙ is not associative on Q.
(v) First we have to check commutativity of o
Let a, b ∈ Q, then
a o b = (ab/2)
= (b a/2)
= b o a
Therefore, a o b = b o a, ∀ a, b ∈ Q
Thus, o is commutative on Q
Now we have to check associativity of o
Let a, b, c ∈ Q, then
a o (b o c) = a o (b c/2)
= [a (b c/2)]/2
= [a (b c/2)]/2
= (a b c)/4
(a o b) o c = (ab/2) o c
= [(ab/2) c] /2
= (a b c)/4
Therefore a o (b o c) = (a o b) o c, ∀ a, b, c ∈ Q
Thus, o is associative on Q.
(vi) First we have to check commutativity of *
Let a, b ∈ Q, then
a * b = ab2
b * a = ba2
Therefore,
a * b ≠ b * a
Thus, * is not commutative on Q
Now we have to check associativity of *
Let a, b, c ∈ Q, then
a * (b * c) = a * (bc2)
= a (bc2)2
= ab2 c4
(a * b) * c = (ab2) * c
= ab2c2
Therefore a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Q.
(vii) First we have to check commutativity of *
Let a, b ∈ Q, then
a * b = a + ab
b * a = b + ba
= b + ab
Therefore, a * b ≠ b * a
Thus, * is not commutative on Q.
Now we have to prove associativity on Q.
Let a, b, c ∈ Q, then
a * (b * c) = a * (b + b c)
= a + a (b + b c)
= a + ab + a b c
(a * b) * c = (a + a b) * c
= (a + a b) + (a + a b) c
= a + a b + a c + a b c
Therefore a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Q.
(viii) First we have to check commutativity of *
Let a, b ∈ R, then
a * b = a + b – 7
= b + a – 7
= b * a
Therefore,
a * b = b * a, for all a, b ∈ R
Thus, * is commutative on R
Now we have to prove associativity of * on R.
Let a, b, c ∈ R, then
a * (b * c) = a * (b + c – 7)
= a + b + c -7 -7
= a + b + c – 14
(a * b) * c = (a + b – 7) * c
= a + b – 7 + c – 7
= a + b + c – 14
Therefore,
a * (b * c ) = (a * b) * c, for all a, b, c ∈ R
Thus, * is associative on R.
(ix) First we have to check commutativity of *
Let a, b ∈ Q, then
a * b = (a – b)2
= (b – a)2
= b * a
Therefore,
a * b = b * a, for all a, b ∈ Q
Thus, * is commutative on Q
Now we have to prove associativity of * on Q
Let a, b, c ∈ Q, then
a * (b * c) = a * (b – c)2
= a * (b2 + c2 – 2 b c)
= (a – b2 – c2 + 2bc)2
(a * b) * c = (a – b)2 * c
= (a2 + b2 – 2ab) * c
= (a2 + b2 – 2ab – c)2
Therefore, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Q.
(x) First we have to check commutativity of *
Let a, b ∈ Q, then
a * b = ab + 1
= ba + 1
= b * a
Therefore
a * b = b * a, for all a, b ∈ Q
Thus, * is commutative on Q
Now we have to prove associativity of * on Q
Let a, b, c ∈ Q, then
a * (b * c) = a * (bc + 1)
= a (b c + 1) + 1
= a b c + a + 1
(a * b) * c = (ab + 1) * c
= (ab + 1) c + 1
= a b c + c + 1
Therefore, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Q.
(xi) First we have to check commutativity of *
Let a, b ∈ N, then
a * b = ab
b * a = ba
Therefore, a * b ≠ b * a
Thus, * is not commutative on N.
Now we have to check associativity of *
a * (b * c) = a * (bc)
=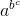
(a * b) * c = (ab) * c
= (ab)c
= abc
Therefore, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on N
(xii) First we have to check commutativity of *
Let a, b ∈ Z, then
a * b = a – b
b * a = b – a
Therefore,
a * b ≠ b * a
Thus, * is not commutative on Z.
Now we have to check associativity of *
Let a, b, c ∈ Z, then
a * (b * c) = a * (b – c)
= a – (b – c)
= a – (b + c)
(a * b) * c = (a – b) – c
= a – b – c
Therefore, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Z
(xiii) First we have to check commutativity of *
Let a, b ∈ Q, then
a * b = (ab/4)
= (ba/4)
= b * a
Therefore, a * b = b * a, for all a, b ∈ Q
Thus, * is commutative on Q
Now we have to check associativity of *
Let a, b, c ∈ Q, then
a * (b * c) = a * (b c/4)
= [a (b c/4)]/4
= (a b c/16)
(a * b) * c = (ab/4) * c
= [(ab/4) c]/4
= a b c/16
Therefore,
a * (b * c) = (a * b) * c for all a, b, c ∈ Q
Thus, * is associative on Q.
(xiv) First we have to check commutativity of *
Let a, b ∈ Z, then
a * b = a + b – ab
= b + a – ba
= b * a
Therefore, a * b = b * a, for all a, b ∈ Z
Thus, * is commutative on Z.
Now we have to check associativity of *
Let a, b, c ∈ Z
a * (b * c) = a * (b + c – b c)
= a + b + c- b c – ab – ac + a b c
(a * b) * c = (a + b – a b) c
= a + b – ab + c – (a + b – ab) c
= a + b + c – ab – ac – bc + a b c
Therefore,
a * (b * c) = (a * b) * c, for all a, b, c ∈ Z
Thus, * is associative on Z.
(xv) First we have to check commutativity of *
Let a, b ∈ N, then
a * b = gcd (a, b)
= gcd (b, a)
= b * a
Therefore, a * b = b * a, for all a, b ∈ N
Thus, * is commutative on N.
Now we have to check associativity of *
Let a, b, c ∈ N
a * (b * c) = a * [gcd (a, b)]
= gcd (a, b, c)
(a * b) * c = [gcd (a, b)] * c
= gcd (a, b, c)
Therefore,
a * (b * c) = (a * b) * c, for all a, b, c ∈ N
Thus, * is associative on N.
5. If the binary operation o is defined by a0b = a + b – ab on the set Q – {-1} of all rational numbers other than 1, show that o is commutative on Q – [1].
Solution:
Let a, b ∈ Q – {-1}.
Then aob = a + b – ab
= b+ a – ba
= boa
Therefore,
aob = boa for all a, b ∈ Q – {-1}
Thus, o is commutative on Q – {-1}
6. Show that the binary operation * on Z defined by a * b = 3a + 7b is not commutative?
Solution:
Let a, b ∈ Z
a * b = 3a + 7b
b * a = 3b + 7a
Thus, a * b ≠ b * a
Let a = 1 and b = 2
1 * 2 = 3 × 1 + 7 × 2
= 3 + 14
= 17
2 * 1 = 3 × 2 + 7 × 1
= 6 + 7
= 13
Therefore, there exist a = 1, b = 2 ∈ Z such that a * b ≠ b * a
Thus, * is not commutative on Z.
7. On the set Z of integers a binary operation * is defined by a 8 b = ab + 1 for all a, b ∈ Z. Prove that * is not associative on Z.
Solution:
Let a, b, c ∈ Z
a * (b * c) = a * (bc + 1)
= a (bc + 1) + 1
= a b c + a + 1
(a * b) * c = (ab+ 1) * c
= (ab + 1) c + 1
= a b c + c + 1
Thus, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Z.
Exercise 3.3 Page No: 3.15
1. Find the identity element in the set I+ of all positive integers defined by a * b = a + b for all a, b ∈ I+.
Solution:
Let e be the identity element in I+ with respect to * such that
a * e = a = e * a, ∀ a ∈ I+
a * e = a and e * a = a, ∀ a ∈ I+
a + e = a and e + a = a, ∀ a ∈ I+
e = 0, ∀ a ∈ I+
Thus, 0 is the identity element in I+ with respect to *.
2. Find the identity element in the set of all rational numbers except – 1 with respect to * defined by a * b = a + b + ab
Solution:
Let e be the identity element in I+ with respect to * such that
a * e = a = e * a, ∀ a ∈ Q – {-1}
a * e = a and e * a = a, ∀ a ∈ Q – {-1}
a + e + ae = a and e + a + ea = a, ∀ a ∈ Q – {-1}
e + ae = 0 and e + ea = 0, ∀ a ∈ Q – {-1}
e (1 + a) = 0 and e (1 + a) = 0, ∀ a ∈ Q – {-1}
e = 0, ∀ a ∈ Q – {-1} [because a not equal to -1]
Thus, 0 is the identity element in Q – {-1} with respect to *.
Exercise 3.4 Page No: 3.25
1. Let * be a binary operation on Z defined by a * b = a + b – 4 for all a, b ∈ Z.
(i) Show that * is both commutative and associative.
(ii) Find the identity element in Z
(iii) Find the invertible element in Z.
Solution:
(i) First we have to prove commutativity of *
Let a, b ∈ Z. then,
a * b = a + b – 4
= b + a – 4
= b * a
Therefore,
a * b = b * a, ∀ a, b ∈ Z
Thus, * is commutative on Z.
Now we have to prove associativity of Z.
Let a, b, c ∈ Z. then,
a * (b * c) = a * (b + c – 4)
= a + b + c -4 – 4
= a + b + c – 8
(a * b) * c = (a + b – 4) * c
= a + b – 4 + c – 4
= a + b + c – 8
Therefore,
a * (b * c) = (a * b) * c, for all a, b, c ∈ Z
Thus, * is associative on Z.
(ii) Let e be the identity element in Z with respect to * such that
a * e = a = e * a ∀ a ∈ Z
a * e = a and e * a = a, ∀ a ∈ Z
a + e – 4 = a and e + a – 4 = a, ∀ a ∈ Z
e = 4, ∀ a ∈ Z
Thus, 4 is the identity element in Z with respect to *.
(iii) Let a ∈ Z and b ∈ Z be the inverse of a. Then,
a * b = e = b * a
a * b = e and b * a = e
a + b – 4 = 4 and b + a – 4 = 4
b = 8 – a ∈ Z
Thus, 8 – a is the inverse of a ∈ Z
2. Let * be a binary operation on Q0 (set of non-zero rational numbers) defined by a * b = (3ab/5) for all a, b ∈ Q0. Show that * is commutative as well as associative. Also, find its identity element, if it exists.
Solution:
First we have to prove commutativity of *
Let a, b ∈ Q0
a * b = (3ab/5)
= (3ba/5)
= b * a
Therefore, a * b = b * a, for all a, b ∈ Q0
Now we have to prove associativity of *
Let a, b, c ∈ Q0
a * (b * c) = a * (3bc/5)
= [a (3 bc/5)] /5
= 3 abc/25
(a * b) * c = (3 ab/5) * c
= [(3 ab/5) c]/ 5
= 3 abc /25
Therefore a * (b * c) = (a * b) * c, for all a, b, c ∈ Q0
Thus * is associative on Q0
Now we have to find the identity element
Let e be the identity element in Z with respect to * such that
a * e = a = e * a ∀ a ∈ Q0
a * e = a and e * a = a, ∀ a ∈ Q0
3ae/5 = a and 3ea/5 = a, ∀ a ∈ Q0
e = 5/3 ∀ a ∈ Q0 [because a is not equal to 0]
Thus, 5/3 is the identity element in Q0 with respect to *.
3. Let * be a binary operation on Q – {-1} defined by a * b = a + b + ab for all a, b ∈ Q – {-1}. Then,
(i) Show that * is both commutative and associative on Q – {-1}
(ii) Find the identity element in Q – {-1}
(iii) Show that every element of Q – {-1} is invertible. Also, find inverse of an arbitrary element.
Solution:
(i) First we have to check commutativity of *
Let a, b ∈ Q – {-1}
Then a * b = a + b + ab
= b + a + ba
= b * a
Therefore,
a * b = b * a, ∀ a, b ∈ Q – {-1}
Now we have to prove associativity of *
Let a, b, c ∈ Q – {-1}, Then,
a * (b * c) = a * (b + c + b c)
= a + (b + c + b c) + a (b + c + b c)
= a + b + c + b c + a b + a c + a b c
(a * b) * c = (a + b + a b) * c
= a + b + a b + c + (a + b + a b) c
= a + b + a b + c + a c + b c + a b c
Therefore,
a * (b * c) = (a * b) * c, ∀ a, b, c ∈ Q – {-1}
Thus, * is associative on Q – {-1}.
(ii) Let e be the identity element in I+ with respect to * such that
a * e = a = e * a, ∀ a ∈ Q – {-1}
a * e = a and e * a = a, ∀ a ∈ Q – {-1}
a + e + ae = a and e + a + ea = a, ∀ a ∈ Q – {-1}
e + ae = 0 and e + ea = 0, ∀ a ∈ Q – {-1}
e (1 + a) = 0 and e (1 + a) = 0, ∀ a ∈ Q – {-1}
e = 0, ∀ a ∈ Q – {-1} [because a not equal to -1]
Thus, 0 is the identity element in Q – {-1} with respect to *.
(iii) Let a ∈ Q – {-1} and b ∈ Q – {-1} be the inverse of a. Then,
a * b = e = b * a
a * b = e and b * a = e
a + b + ab = 0 and b + a + ba = 0
b (1 + a) = – a Q – {-1}
b = -a/1 + a Q – {-1} [because a not equal to -1]
Thus, -a/1 + a is the inverse of a ∈ Q – {-1}
4. Let A = R0 × R, where R0 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: (a, b) O (c, d) = (ac, bc + d) for all (a, b), (c, d) ∈ R0 × R.
(i) Show that ‘O’ is commutative and associative on A
(ii) Find the identity element in A
(iii) Find the invertible element in A.
Solution:
(i) Let X = (a, b) and Y = (c, d) ∈ A, ∀ a, c ∈ R0 and b, d ∈ R
Then, X O Y = (ac, bc + d)
And Y O X = (ca, da + b)
Therefore,
X O Y = Y O X, ∀ X, Y ∈ A
Thus, O is not commutative on A.
Now we have to check associativity of O
Let X = (a, b), Y = (c, d) and Z = (e, f), ∀ a, c, e ∈ R0 and b, d, f ∈ R
X O (Y O Z) = (a, b) O (ce, de + f)
= (ace, bce + de + f)
(X O Y) O Z = (ac, bc + d) O (e, f)
= (ace, (bc + d) e + f)
= (ace, bce + de + f)
Therefore, X O (Y O Z) = (X O Y) O Z, ∀ X, Y, Z ∈ A
(ii) Let E = (x, y) be the identity element in A with respect to O, ∀ x ∈ R0 and y ∈ R
Such that,
X O E = X = E O X, ∀ X ∈ A
X O E = X and EOX = X
(ax, bx +y) = (a, b) and (xa, ya + b) = (a, b)
Considering (ax, bx + y) = (a, b)
ax = a
x = 1
And bx + y = b
y = 0 [since x = 1]
Considering (xa, ya + b) = (a, b)
xa = a
x = 1
And ya + b = b
y = 0 [since x = 1]
Therefore (1, 0) is the identity element in A with respect to O.
(iii) Let F = (m, n) be the inverse in A ∀ m ∈ R0 and n ∈ R
X O F = E and F O X = E
(am, bm + n) = (1, 0) and (ma, na + b) = (1, 0)
Considering (am, bm + n) = (1, 0)
am = 1
m = 1/a
And bm + n = 0
n = -b/a [since m = 1/a]
Considering (ma, na + b) = (1, 0)
ma = 1
m = 1/a
And na + b = 0
n = -b/a
Therefore the inverse of (a, b) ∈ A with respect to O is (1/a, -b/a)
Exercise 3.5 Page No: 3.33
1. Construct the composition table for ×4 on set S = {0, 1, 2, 3}.
Solution:
Given that ×4 on set S = {0, 1, 2, 3}
Here,
1 ×4 1 = remainder obtained by dividing 1 × 1 by 4
= 1
0 ×4 1 = remainder obtained by dividing 0 × 1 by 4
= 0
2 ×4 3 = remainder obtained by dividing 2 × 3 by 4
= 2
3 ×4 3 = remainder obtained by dividing 3 × 3 by 4
= 1
So, the composition table is as follows:
| ×4 | 0 | 1 | 2 | 3 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 |
| 2 | 0 | 2 | 0 | 2 |
| 3 | 0 | 3 | 2 | 1 |
2. Construct the composition table for +5 on set S = {0, 1, 2, 3, 4}
Solution:
1 +5 1 = remainder obtained by dividing 1 + 1 by 5
= 2
3 +5 1 = remainder obtained by dividing 3 + 1 by 5
= 2
4 +5 1 = remainder obtained by dividing 4 + 1 by 5
= 3
So, the composition table is as follows:
| +5 | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
3. Construct the composition table for ×6 on set S = {0, 1, 2, 3, 4, 5}.
Solution:
Here,
1 ×6 1 = remainder obtained by dividing 1 × 1 by 6
= 1
3 ×6 4 = remainder obtained by dividing 3 × 4 by 6
= 0
4 ×6 5 = remainder obtained by dividing 4 × 5 by 6
= 2
So, the composition table is as follows:
| ×6 | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 2 | 4 | 0 | 2 | 4 |
| 3 | 0 | 3 | 0 | 3 | 0 | 3 |
| 4 | 0 | 4 | 2 | 0 | 4 | 2 |
| 5 | 0 | 5 | 4 | 3 | 2 | 1 |
4. Construct the composition table for ×5 on set Z5 = {0, 1, 2, 3, 4}
Solution:
Here,
1 ×5 1 = remainder obtained by dividing 1 × 1 by 5
= 1
3 ×5 4 = remainder obtained by dividing 3 × 4 by 5
= 2
4 ×5 4 = remainder obtained by dividing 4 × 4 by 5
= 1
So, the composition table is as follows:
| ×5 | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
5. For the binary operation ×10 set S = {1, 3, 7, 9}, find the inverse of 3.
Solution:
Here,
1 ×10 1 = remainder obtained by dividing 1 × 1 by 10
= 1
3 ×10 7 = remainder obtained by dividing 3 × 7 by 10
= 1
7 ×10 9 = remainder obtained by dividing 7 × 9 by 10
= 3
So, the composition table is as follows:
| ×10 | 1 | 3 | 7 | 9 |
| 1 | 1 | 3 | 7 | 9 |
| 3 | 3 | 9 | 1 | 7 |
| 7 | 7 | 1 | 9 | 3 |
| 9 | 9 | 7 | 3 | 1 |
From the table we can observe that elements of first row as same as the top-most row.
So, 1 ∈ S is the identity element with respect to ×10
Now we have to find inverse of 3
3 ×10 7 = 1
So the inverse of 3 is 7.