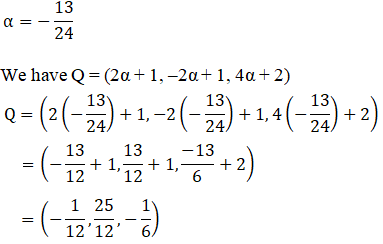Chapter 29 THE PLANE

Access RD Sharma Solutions For Class 12 Maths Chapter 29 Exercise 1

EXERCISE 29.1

Q1. i.

Solution:

Given:

The three points are:

(2, 1, 0), (3, -2, -2) and (3, 1, 7)

By using the formula, the equation of the plane passing through the three points is given as:

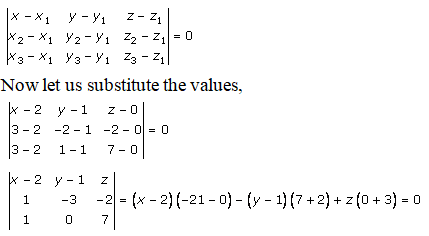
= -21x + 42 – 9y + 9 + 3z = 0

= -21x – 9y + 3z + 51 = 0

Let us divide by -3, and we get

Hence, the equation of the plane is 7x + 3y – z – 17 = 0.

ii.

Solution:

Given:

The three points are:

(-5, 0, -6), (-3, 10, -9) and (-2, 6, -6)

By using the formula, the equation of the plane passing through the three points is given as:

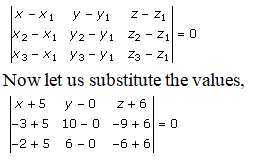
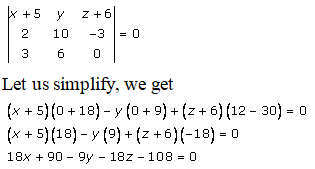
Divide by 9, and we get

Hence, the equation of the plane is 2x – y – 2z – 2 = 0.

iii.

Solution:

Given:

The three points are:

(1, 1, 1), (1, -1, 2) and (-2, -2, -2)

By using the formula, the equation of the plane passing through the three points is given as:

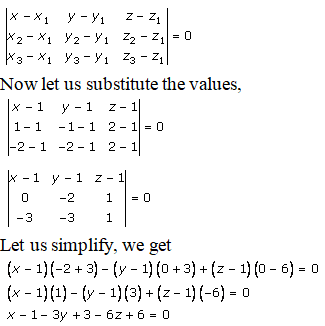
x – 3y – 6z + 8 = 0

Hence, the equation of the plane is x – 3y – 6z + 8 = 0.

iv.

Solution:

Given:

The three points are:

(2, 3, 4), (-3, 5, 1) and (4, -1, 2)

By using the formula, the equation of a plane passing through the three points is given as:

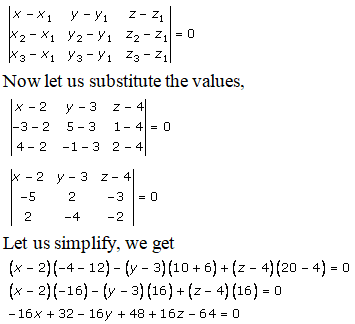
-16x – 16y + 16z + 16 = 0

Divide by -16, we get

Hence, the equation of the plane is x + y – z – 1 = 0.

v.

Solution:

Given:

The three points are:

(0, -1, 0), (3, 3, 0) and (1, 1, 1)

By using the formula, the equation of a plane passing through the three points is given as:

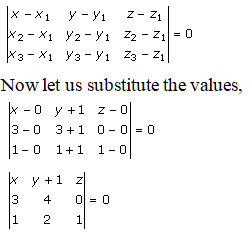
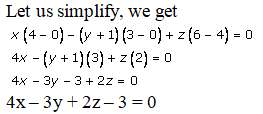
Hence, the equation of the plane is 4x – 3y + 2z – 3 = 0.

Q2.

Solution:

We have to prove that points (0, -1, -1), (4, 5, 1), (3, 9, 4) and (-4, 4, 4) are coplanar.

Now let us find the equation of the plane passing through the three points, i.e.:

(0, -1, -1), (4, 5, 1), (3, 9, 4)

By using the formula, the equation of the plane passing through the three points is given as:

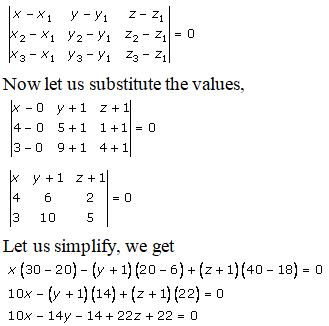
10x – 14y + 22z + 8 = 0

Divide by 2, and we get

5x – 7y + 11z + 4 = 0 ……. (1)

By using the fourth point (-4, 4, 4),

Substitute the values as x = -4, y =4, z = 4 in equation (1), we get

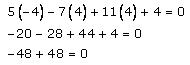
0 = 0

LHS = RHS

Since the fourth point satisfies the equation of the plane passing through the three points. So, all the points are coplanar.

Hence, the equation of the common plane is 5x – 7y + 11z + 4 = 0.

Q3.i

Solution:

Given:

Four points are:

(0, -1, 0), (2, 1, -1), (1, 1, 1) and (3, 3, 0)

Now let us find the equation of the plane passing through the three points, i.e.:

(0, -1, 0), (2, 1, -1), (1, 1, 1)

By using the formula, the equation of the plane passing through the three points is given as:

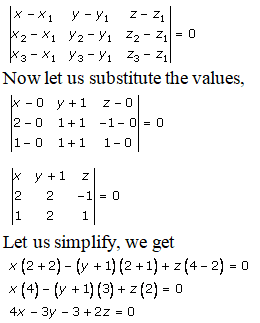
4x – 3y – 3 + 2z = 0

4x – 3y + 2z – 3 = 0 ……. (1)

By using the fourth point (3, 3, 0),

Substitute the values as x = 3, y =3, z = 0 in equation (1), we get

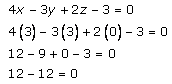
0 = 0

LHS = RHS

Since the fourth point satisfies the equation of plane passing through three points. So, all the points are coplanar.

Hence, the equation of the common plane is 4x – 3y + 2z – 3 = 0.

ii.

Solution:

Given:

Four points are:

(0, 4, 3), (-1, -5, -3), (-2, -2, 1) and (1, 1, -1)

Now let us find the equation of the plane passing through the three points, i.e.:

(0, 4, 3), (-1, -5, -3), (-2, -2, 1)

By using the formula, the equation of the plane passing through the three points is given as:

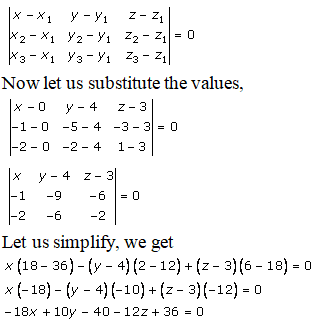
-18x + 10y – 12z – 4 = 0 ………. (1)

By using the fourth point (1, 1, -1),

Substitute the values as x = 1, y =1, z = -1 in equation (1), we get

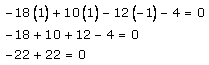
0 = 0

LHS = RHS

Since the fourth point satisfies the equation of the plane passing through the three points. So, all the points are coplanar.

Hence, the equation of the common plane is -18x + 10y – 12z – 4 = 0.

Access RD Sharma Solutions For Class 12 Maths Chapter 29 Exercise 2

Q1.

Solution:

Given:

Intercepts on the coordinate axes are 2, -3 and 4.

We know that,

The equation of a plane whose intercepts on the coordinate axes are a, b, c is given by,

6x – 4y + 3z = 12

Hence, the equation of the plane is 6x – 4y + 3z = 12.

Q2.i

Solution:

Let us reduce the given equation 4x + 3y – 6z – 12 = 0 in intercept form:

4x + 3y – 6z – 12 = 0

4x + 3y – 6z = 12

Divide by 12, and we get

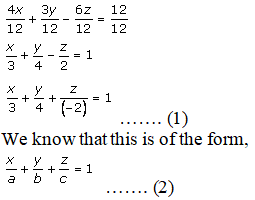
Now, compare equations 1 and 2, and we get

a = 3, b = 4, c = -2

Therefore intercepts on the coordinate axes are 3, 4, and -2.

ii.

Solution:

Let us reduce the given equation 2x + 3y – z = 6 in intercept form:

Divide the given equation by 6, and we get

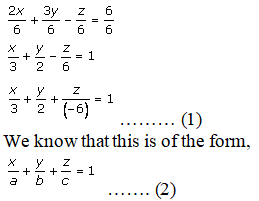
Now, compare equations 1 and 2, and we get

a = 3, b = 2, c = -6

Therefore intercepts on the coordinate axes are 3, 2, -6.

iii.

Solution:

Given:

The equation of plane is 2x – y + z = 5

Divide the given equation by 5, and we get

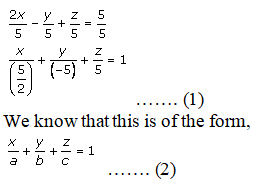
Now, compare equations 1 and 2, and we get

a = 5/2, b = -5, c = 5

Therefore intercepts on the coordinate axes are 5/2, -5, 5.

Q3.

Solution:

Given:

The plane meets axes in A, B and C.

Let A = (a, 0, 0), B = (0, b, 0) and C = (0, 0, c)

Given that the centroid of the triangle = (α, β, γ)

By using the formula,

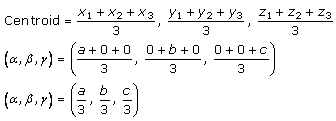
So,

a/3 = α

=> a = 3α …… (i)

b/3 = β

=> b = 3β ……. (2)

c/3 = γ

=> c = 3γ ……. (3)

If a, b, c is intercepted by plane on coordinate axes,

Then the equation of the plane is given by:

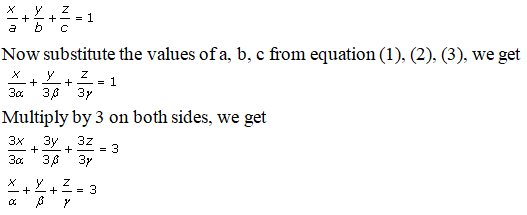
Hence, the equation of the plane is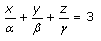
.

Q4.

Solution:

Given:

The intercepts on the coordinate axes are equal.

We know that the equation of the plane whose intercepts on the coordinate axes is given as:

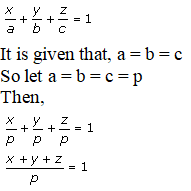
x + y + z = p …… (1)

It is also given that the plane is passing through the point (2, 4, 6)

By using equation (1),

x + y + z = p

2 + 4 + 6 = p

p = 12

Now, substitute the value of p back in equation (1), and we get

x + y + z = 12

Hence, the required equation of the plane is x + y + z = 12.

Q5.

Solution:

Given:

The plane meets the coordinate axes at A, B and C, with the centroid of triangle ABC being at (1, -2, 3).

We know that the equation of the plane whose intercepts on the coordinate axes is given as:

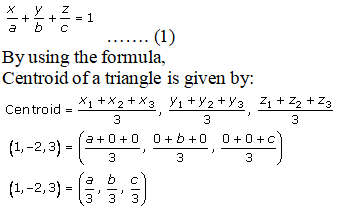
Now let us compare LHS and RHS,

a/3 = 1

=> a = 3

b/3 = -2

=> b = -6

c/3 = 3

=> c = 9

Now, substitute the values of a, b, c in equation (1), and we get

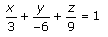
6x – 3y + 2z = 18

Hence, the required equation of the plane is 6x – 3y + 2z = 18.

Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 3

EXERCISE 29.3

Q1.

Solution:

Q2. i

Solution:

Given:

The vector equation of the plane is

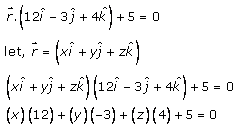
12x – 3y + 4z + 5 = 0

Hence, the Cartesian form of the equation of the plane is 12x – 3y + 4z + 5 = 0.

ii.

Solution:

Given:

The equation of the plane is:

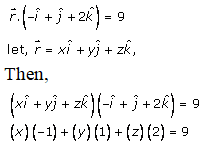
-x + y + 2z = 9

Hence, the Cartesian form of the equation of the plane is -x + y + 2z = 9.

Q3.

Solution:

Given:

For xy-plane,

This plane passes through the origin and is perpendicular to the z-axis.

So,

For xz-plane,

It passes through the origin and is perpendicular to the y-axis,

So,

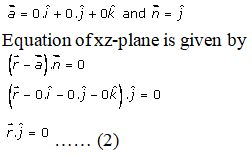
For yz-plane,

It passes through the origin and is perpendicular to the x-axis,

So,

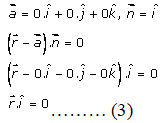
Hence, the equation of xy, yz and xz-plane is given by

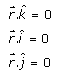
Q4.i.

Solution:

Given:

The equation of the plane is:

2x – y + 2z = 8

By putting the values, we get

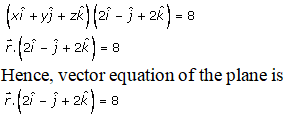
ii.

Solution:

Given:

The Cartesian equation of the plane is:

x + y – z = 5

By putting the values, we get

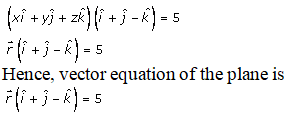
iii.

Solution:

Given:

The Cartesian equation of the plane is:

x + y = 3

By putting the values, we get

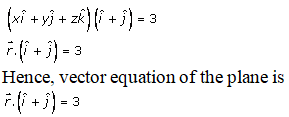
Q5.

Solution:

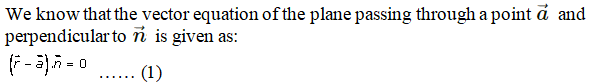
The given plane passes through the point (1, -1, 1) and normal to the line joining A(1, 2, 5) and B(-1, 3, 1).

So,

Now, multiply by (-1) on both sides

So,

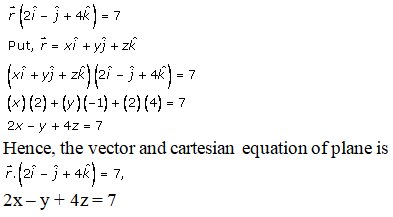
Access RD Sharma Solutions For Class 12 Maths Chapter 29 Exercise 4

EXERCISE 29.4

Q1.

Solution:

Q2.

Solution:

We know that,

The vector equation of a plane in normal form is given as

Q3.

Solution:

Given:

The equation of the plane is,

Hence, the distance of the plane from origin = 2 units

Direction cosine of normal to plane = 2/7, -3/7, 6/7

Q4.

Solution:

Given:

The equation of the plane is,

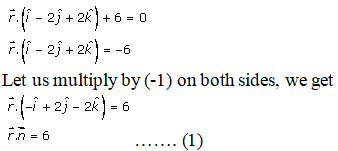
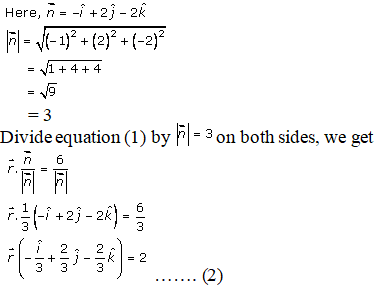
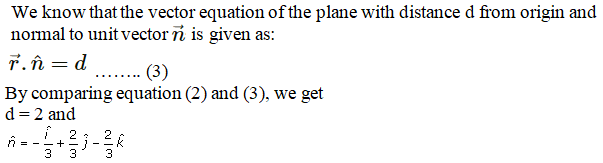
Hence, the distance of the plane from origin = 2 units

Direction cosine of normal to plane = -1/3, 2/3, -2/3

Q5.

Solution:

Given:

The equation of plane is,

2x – 3y + 6z + 14 = 0

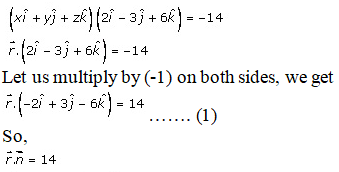
Hence, the distance of the plane from origin = 2 units

Direction cosine of normal to plane = -2/7, 3/7, -6/7

Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 5

EXERCISE 29.5

Q1.

Solution:

Given:

The plane passes through points,

(1, 1, 1), (1, -1, 1) and (-7, -3, -5)

So by using these points, we know that the equation of the plane that passes through these points,

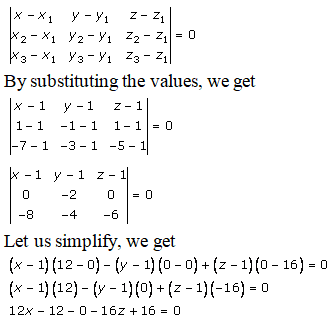
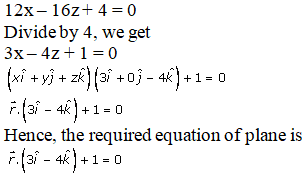
Q2.

Solution:

Let us consider three points P, Q and R.

So P(2, 5, -3), Q(-2, -3, 5) and R(5, 3, -3) are the points on the plane having position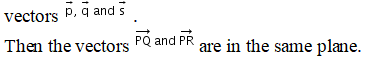

Q3.

Solution:

Let us consider three points A, B and C.

So A(a, 0, 0), B(0, b, 0) and C(0, 0, c) are the points on the plane having position vectors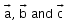
.

Then vectors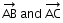
are in the same plane.

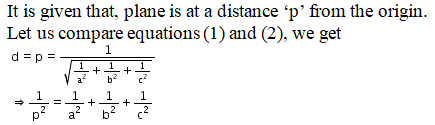
Q4.

Solution:

Let us consider three points P, Q and R.

So P(1, 1, -1), Q(6, 4, -5) and R(-4, -2, 3) are the points on the plane having position vectors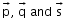
.

Then the vectors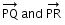
are in the same plane.

Q5.

Solution:

Let us consider three points A, B and C.

So now let A, B, C be the points with position vector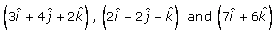
.

Then,

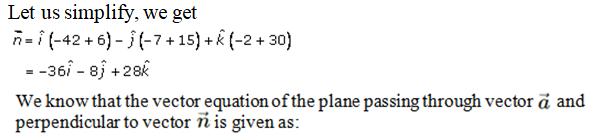
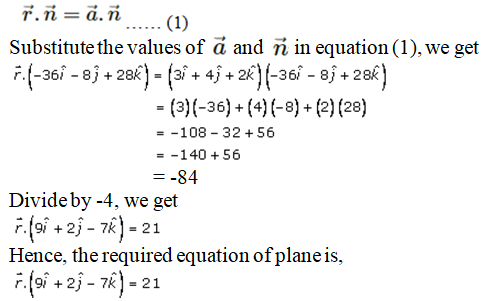
Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 6

EXERCISE 29.6

Q1. i.

Solution:

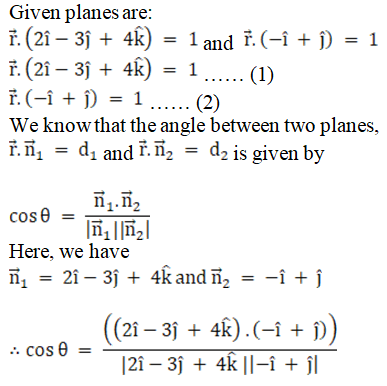
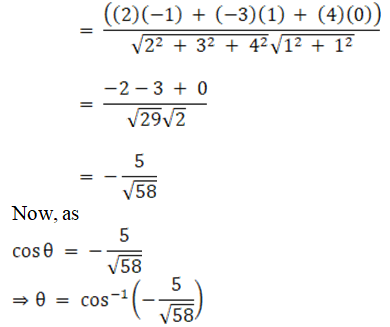
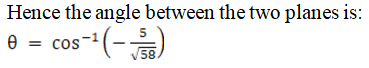
ii.

Solution:

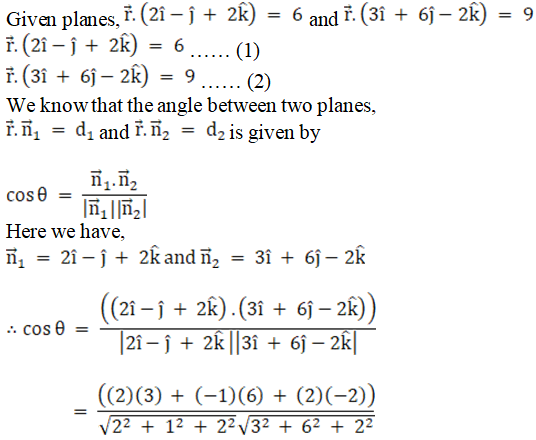
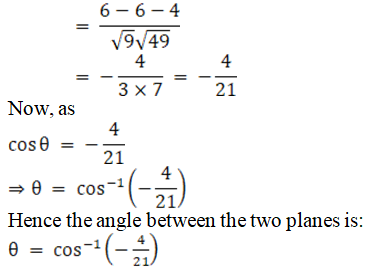
iii.

Solution:

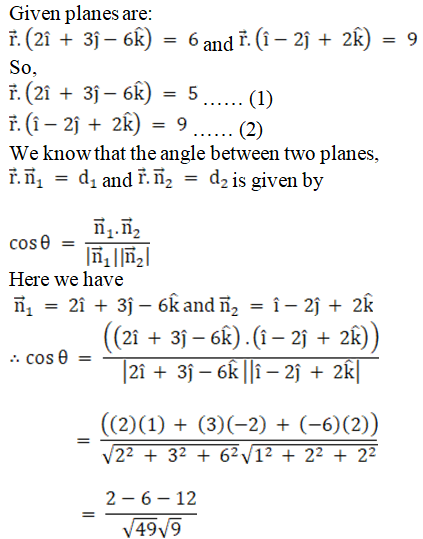
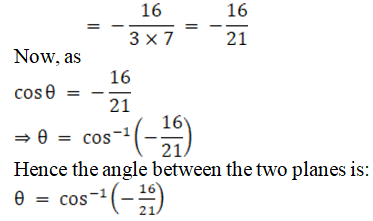
Q2. i

Solution:

Given planes are:

2x – y + z = 4 and x + y + 2z = 3

We know that angle between two planes,

a₁x + b₁y + c₁z + d₁ = 0 and

a₂x + b₂y + c₂z + d₂ = 0 is given as

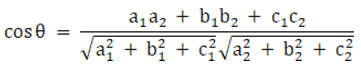
So here we have,

a₁ = 2, b₁ = – 1, c₁ = 1

a₂ = 1, b₂ = 1, c₂ = 2

Now let us substitute the values in the above expression, we get

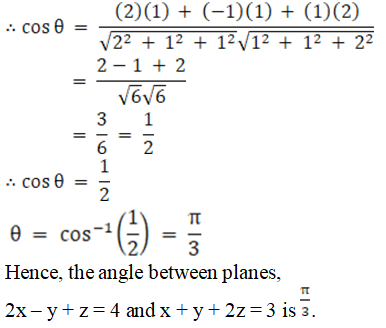
ii.

Solution:

Given planes are:

x + y – 2z = 3 and 2x – 2y + z = 5

We know that angle between two planes,

a₁x + b₁y + c₁z + d₁ = 0

a₂x + b₂y + c₂z + d₂ = 0 is given as

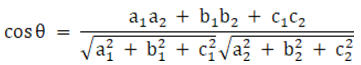
So here we have,

a₁ = 1, b₁ = 1, c₁ = – 2

a₂ = 2, b₂ = – 2, c₂ = 1

Now let us substitute the values in the above expression, we get

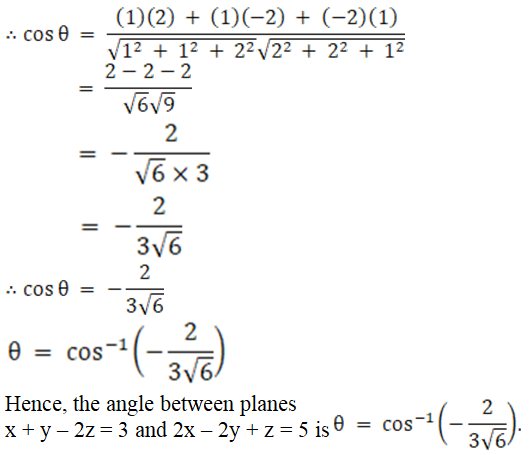
iii.

Solution:

Given planes are:

x – y + z = 5 and x + 2y + z = 9

We know that angle between two planes,

a₁x + b₁y + c₁z + d₁ = 0

a₂x + b₂y + c₂z + d₂ = 0 is given as

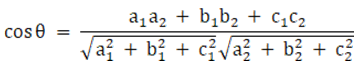
So here we have,

a₁ = 1, b₁ = – 1, c₁ = 1

a₂ = 1, b₂ = 2, c₂ = 1

Now let us substitute the values in the above expression, we get

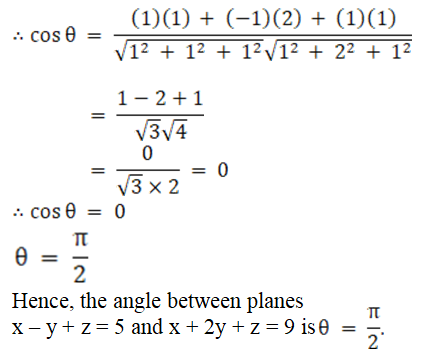
iv.

Solution:

Given planes are:

2x – 3y + 4z = 1 and – x + y = 4

We know that angle between two planes,

a₁x + b₁y + c₁z + d₁ = 0

a₂x + b₂y + c₂z + d₂ = 0 is given as

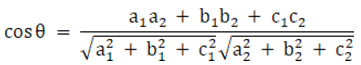
So here we have,

a₁ = 2, b₁ = – 3, c₁ = 4

a₂ = – 1, b₂ = 1, c₂ = 0

Now let us substitute the values in the above expression, we get

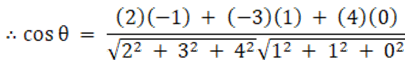
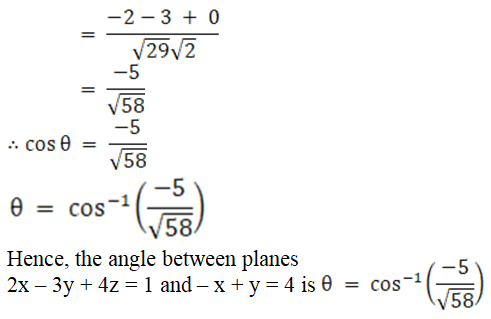
v.

Solution:

Given planes are:

2x + y – 2z = 5 and 3x – 6y – 2z = 7

We know that angle between two planes,

a₁x + b₁y + c₁z + d₁ = 0

a₂x + b₂y + c₂z + d₂ = 0 is given as

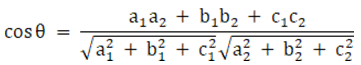
So here we have,

a₁ = 2, b₁ = 1, c₁ = – 2

a₂ = 3, b₂ = – 6, c₂ = – 2

Now let us substitute the values in the above expression, we get

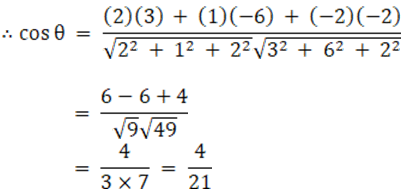
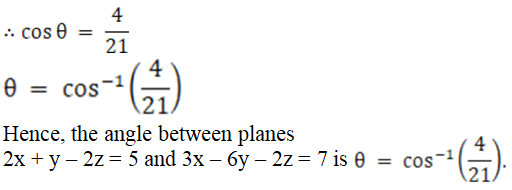
Q3.i.

Solution:

ii.

Solution:

Given planes,

x – 2y + 4z = 10 and

18x + 17y + 4z = 49

We know that planes

a₁x + b₁y + c₁z + d₁ = 0 and

a₂x + b₂y + c₂z + d₂ = 0 are at right angles if,

a₁a₂ + b₁b₂ + c₁c₂ = 0 …… (1)

Now we have,

a₁ = 1, b₁ = – 2, c₁ = 4 and

a₂ = 18, b₂ = 17, c₂ = 4

Using equation (1), we have,

a₁a₂ + b₁b₂ + c₁c₂ = (1) (18) + (– 2) (17) + (4) (4)

= 18 – 34 + 16 = 0

Hence, the planes are at a right angle to each other.

Q4.i.

Solution:

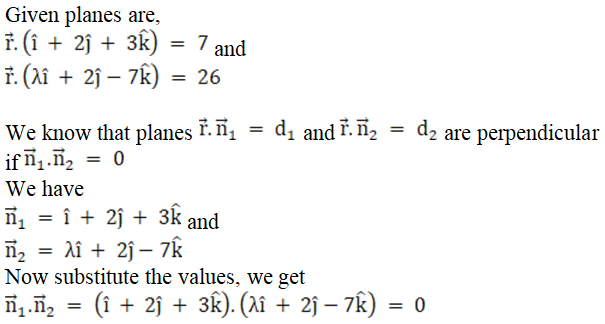
So, (λ + 4 – 21) = 0

λ = 21 – 4

= 17

Hence, for λ = 17, the given planes are perpendicular.

ii.

Solution:

Given planes are,

2x – 4y + 3z = 5 and

x + 2y + λz = 5

We know that planes

a₁x + b₁y + c₁z + d₁ = 0 and

a₂x + b₂y + c₂z + d₂ = 0 are at right angles if,

a₁a₂ + b₁b₂ + c₁c₂ = 0 …… (1)

We have,

a₁ = 2, b₁ = – 4, c₁ = 3 and

a₂ = 1, b₂ = 2, c₂ = λ

Let us substitute the values in equation (1), we get

a₁a₂ + b₁b₂ + c₁c₂ => (2) (1) + (– 4) (2) + (3) (λ) = 0

=> 2 – 8 + 3λ = 0

6 = 3λ

2 = λ

Hence, for λ = 2, the given planes are perpendicular.

iii.

Solution:

Given planes are,

3x – 6y – 2z = 7 and

2x + y – λz = 5

We know that planes

a₁x + b₁y + c₁z + d₁ = 0 and

a₂x + b₂y + c₂z + d₂ = 0 are at right angles if,

a₁a₂ + b₁b₂ + c₁c₂ = 0 …… (1)

We have,

a₁ = 3, b₁ = – 6, c₁ = – 2 and

a₂ = 2, b₂ = 1, c₂ = – λ

Let us substitute the values in equation (1), we get

a₁a₂ + b₁b₂ + c₁c₂ = (3) (2) + (– 6) (1) + (– 2) (– λ) = 0

=> 6 – 6 + 2λ = 0

0 = – 2λ

0 = λ

Hence, for λ = 0, the given planes are perpendicular to each other.

Q5.

Solution:

We know that the solution of a plane passing through (x₁, y₁, z₁) is given as:

a(x – x₁) + b(y – y₁) + c(z – z₁) = 0

The required plane passes through (– 1, – 1, 2),

So the equation of the plane is

a(x + 1) + b(y + 1) + c(z – 2) = 0

⇒ ax + by + cz = 2c – a – b …… (1)

Now, the required plane is also perpendicular to the planes,

3x + 2y – 3z = 1 and

5x – 4y + z = 5

We know that planes

a₁x + b₁y + c₁z + d₁ = 0 and

a₂x + b₂y + c₂z + d₂ = 0 are at right angles if,

a₁a₂ + b₁b₂ + c₁c₂ = 0 …… (2)

Using equation (2), we have,

3a + 2b – 3c = 0 …… (3)

5a – 4b + c = 0 …… (4)

Now let us solve equations (3) and (4), and we get,

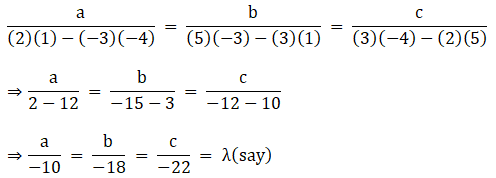
So,

a = – 10λ, b = – 18λ, c = – 22λ

Now substitute the values of a, b, c in equation (1), and we get,

(– 10λ)x + (– 18λ)y + (– 22λ)z = 2(– 22)λ – (– 10λ) – (– 18λ)

– 10λx – 18λy – 22λz = – 44λ + 10λ + 18λ

– 10λx – 18λy – 22λz = – 16λ

Divide both sides by (– 2λ), we get

5x + 9y + 11z = 8

Hence, the required equation of the plane is 5x + 9y + 11z = 8.

Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 7

EXERCISE 29.7

Q1.i.

Solution:

ii.

Solution:

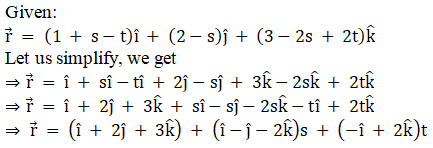
iii.

Solution:

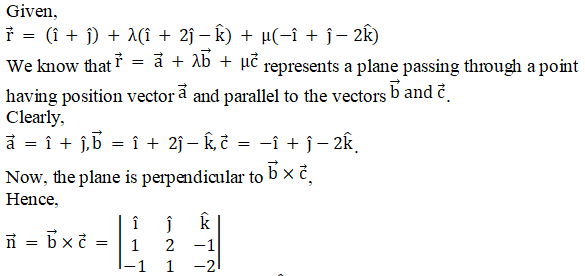
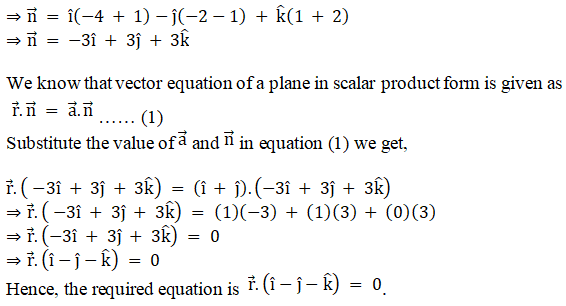
iv.

Solution:

Q2.i.

Solution:

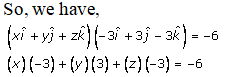
-3x + 3y – 3z = -6

Divide by -3, we get

x – y + z = 2

Hence, the required equation is x – y + z = 2.

ii.

Solution:

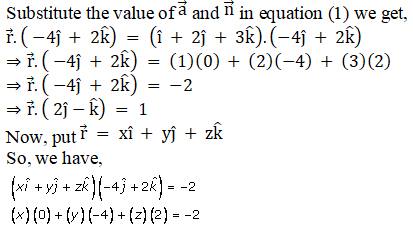
-4y + 2z = -2

Divide by -2, and we get

2y – z = 1

Hence, the required equation of the plane is 2y – z = 1.

Q3.i.

Solution:

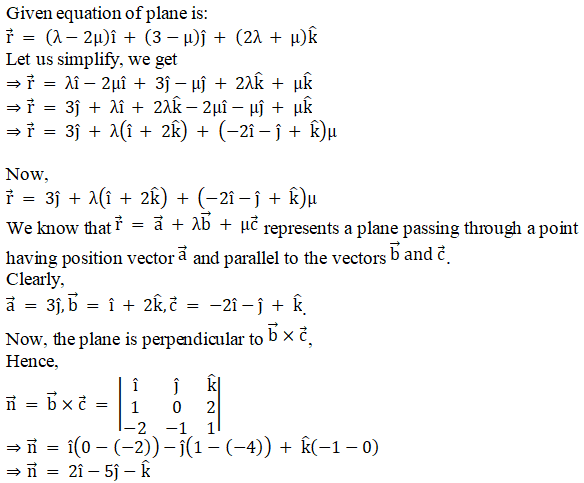
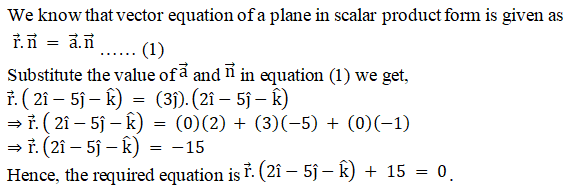
ii.

Solution:

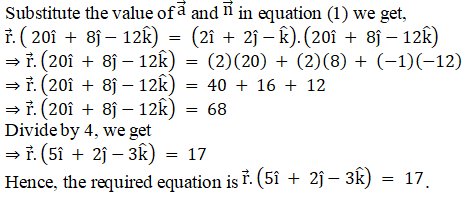
Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 8

EXERCISE 29.8

Q1.

Solution:

Given:

Equation of plane is 2x – 3y + z = 0 …… (1)

We know that equation of a plane is parallel to the given plane (1) is given as

2x – 3y + z + k = 0 …… (2)

Given that, plane (2) is passing through point (1, – 1, 2). So it must satisfy plane (2),

2(1) – 3(– 1) + (2) + k = 0

2 + 3 + 2 + k = 0

7 + k = 0

k = – 7

Now, substitute the value of k in equation (2), we get

2x – 3y + z – 7 = 0

Hence, the equation of the required plane is, 2x – 3y + z = 7.

Q2.

Solution:

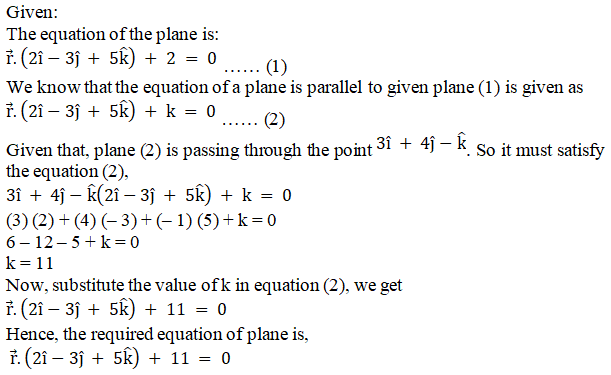
Q3.

Solution:

We know that the equation of a plane passing through the line of intersection of two planes

a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is given by

(a₁x + b₁y + c₁z + d₁) + k(a₂x + b₂y + c₂z + d₂) = 0

Given that the equation of the plane is,

2x – 7y + 4z – 3 = 0 and

3x – 5y + 4z + 11 = 0

So the equation of the plane passing through the line of intersection of given two planes is

(2x – 7y + 4z – 3) + k(3x – 5y + 4z + 11) = 0

2x – 7y + 4z – 3 + 3kx – 5ky + 4kz + 11k = 0

x(2 + 3k) + y( – 7 – 5k) + z(4 + 4k) – 3 + 11k = 0 ……(1)

It is given that plane (1) is passing through the point (–2, 1, 3). So it must satisfy the equation (1),

(– 2) (2 + 3k) + (1) (– 7 – 5k) + (3) (4 + 4k) – 3 + 11k = 0

– 2 + 12k = 0

12k = 2

k = 2/12

= 1/6

Now substitute the value of k in equation (1), we get

x(2 + 3k) + y(– 7 – 5k) + z(4 + 4k) – 3 + 11k = 0

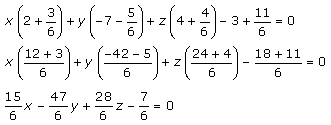
Multiply by 6, we get

15x – 47y + 28z – 7 = 0

Hence, the required equation of the plane is 15x – 47y + 28z – 7 = 0.

Q4.

Solution:

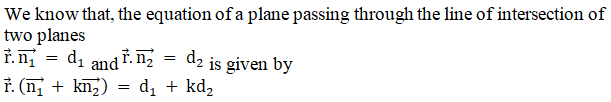
Q5.

Solution:

We know that the equation of a plane passing through the line of intersection of two planes

a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is given by

(a₁x + b₁y + c₁z + d₁) + k(a₂x + b₂y + c₂z + d₂) = 0

So the equation of the plane passing through the line of intersection of given two planes

2x – y = 0 and 3z – y = 0 is

(2x – y) + k(3z – y) = 0

2x – y + 3kz – ky = 0

x(2) + y( – 1 – k) + z(3k) = 0 …… (1)

We know that two planes are perpendicular if

a₁a₂ + b₁b₂ + c₁c₂ = 0 …… (2)

It is given that plane (1) is perpendicular to plane

4x + 5y – 3z = 8 …… (3)

By using equations (1) and (3) in equation (2), we get

(2) (4) + (–1 – k) (5) + (3k) (–3) = 0

8 – 5 – 5k – 9k = 0

3 – 14k = 0

–14k = –3

k = 3/14

Now, substitute the value of k in equation (1), and we get

x(2) + y( – 1 – k) + z(3k) = 0

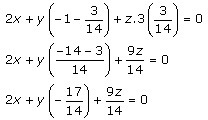
Multiply by 14, and we get

28x – 17y + 9z = 0

Hence, the required equation of the plane is 28x – 17y + 9z = 0.

Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 9

EXERCISE 29.9

Q1.

Solution:

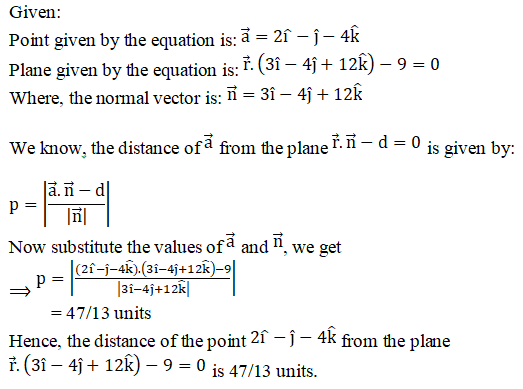
Q2.

Solution:

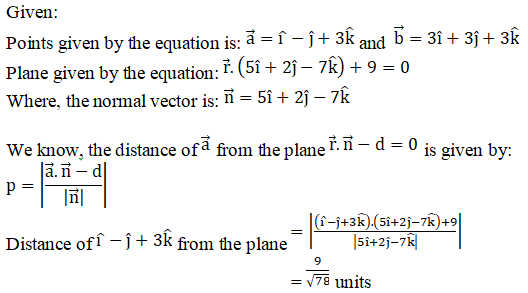
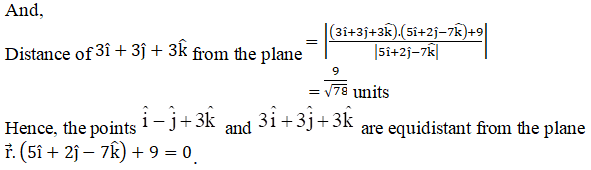
Q3.

Solution:

Given:

Point: A(2, 3, –5)

Plane: π = x + 2y – 2z – 9 = 0

We know, the distance of point (x₁, y₁, z₁) from the plane π: ax + by + cz + d = 0 is given by:

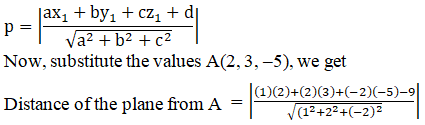
= 3 units

Hence, the distance of the point (2, 3, –5) from the plane is 3 units.

Q4.

Solution:

Given:

The equation of the plane is:

x + 2y – 2z + 8 = 0

Since the planes are parallel to x + 2y – 2z + 8 = 0, they must be of the form:

x + 2y – 2z + θ = 0

We know, the distance of point (x₁, y₁, z₁) from the plane π: ax + by + cz + d = 0 is given by:

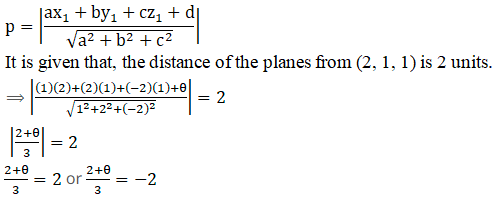
θ = 4 or –8

Now, substitute the values in x + 2y – 2z + θ = 0, we get

x + 2y – 2z + 4 = 0

x + 2y – 2z – 8 = 0

Hence, the required planes are:

x + 2y – 2z + 4 = 0 and x + 2y – 2z – 8 = 0.

Q5.

Solution:

Given:

Points: A(1, 1, 1) and B(–3, 0, 1)

Plane: π = 3x + 4y – 12z + 13 = 0

We know, the distance of point (x₁, y₁, z₁) from the plane π: ax + by + cz + d = 0 is given by:

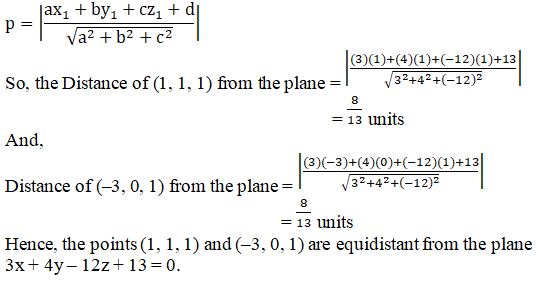
Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 10

EXERCISE 29.10

Q1.

Solution:

Let P(x₁, y₁, z₁) be any point on plane 2x – y + 3z – 4 = 0.

⟹ 2x₁ – y₁ + 3z₁ = 4 …….. (1)

Distance between (x₁, y₁, z₁) and the plane

6x – 3y + 9z + 13 = 0:

We know, the distance of point (x₁, y₁, z₁) from the plane π: ax + by + cz + d = 0 is given by:

Q2.

Solution:

Since the plane is parallel to 2x – 3y + 5z + 7 = 0, it must be of the form:

2x – 3y + 5z + θ = 0

It is given that,

The plane passes through (3, 4, –1)

⟹ 2(3) – 3(4) +5(–1) + θ = 0

θ = -11

So, the equation of the plane is as follows:

2x – 3y + 5z – 11 = 0

Distance of the plane 2x – 3y + 5z + 7 = 0 from (3, 4, –1):

We know, the distance of point (x₁, y₁, z₁) from the plane π: ax + by + cz + d = 0 is given by:

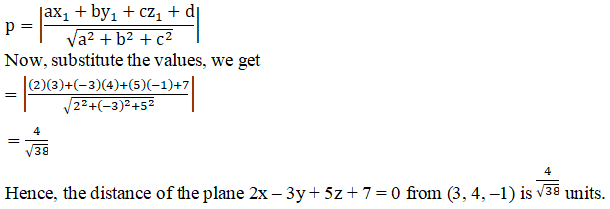
Q3.

Solution:

Given:

Equation of planes: π₁= 2x – 2y + z + 3 = 0

π₂= 2x – 2y + z + 9 = 0

Let the equation of the plane mid–parallel to these planes be:

π₃: 2x – 2y + z + θ = 0

Now,

Let P(x₁, y₁, z₁) be any point on this plane,

⟹ 2(x₁) – 2(y₁) + (z₁) + θ = 0 …… (1)

We know, the distance of point (x₁, y₁, z₁) from the plane π: ax + by + cz + d = 0 is given by:

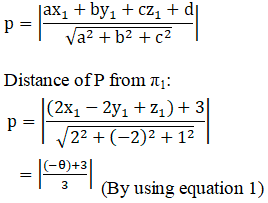
Q4.

Solution:

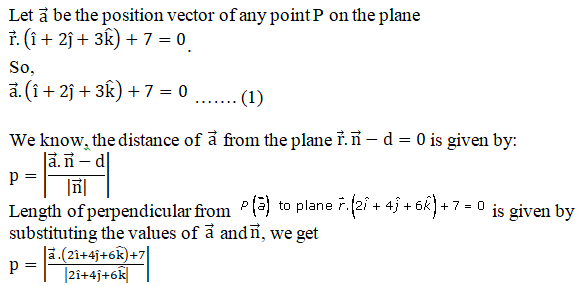
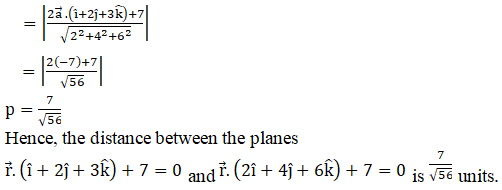
Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 11

EXERCISE 29.11

Q1.

Solution:

Q2.

Solution:

Q3.

Solution:

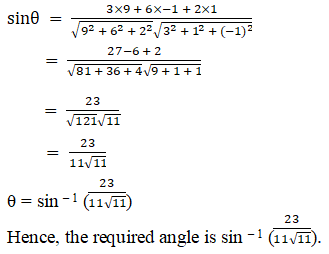
Q4.

Solution:

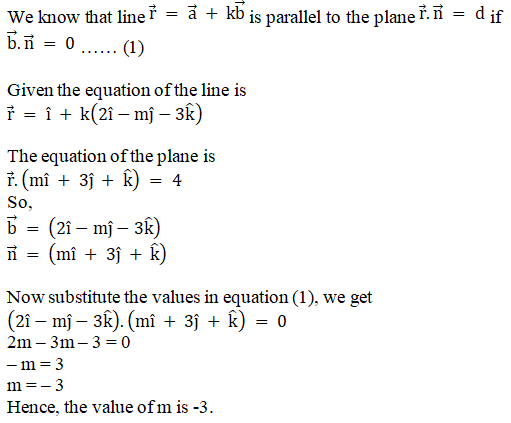
Q5.

Solution:

Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 12

EXERCISE 29.12

Q1.

Solution:

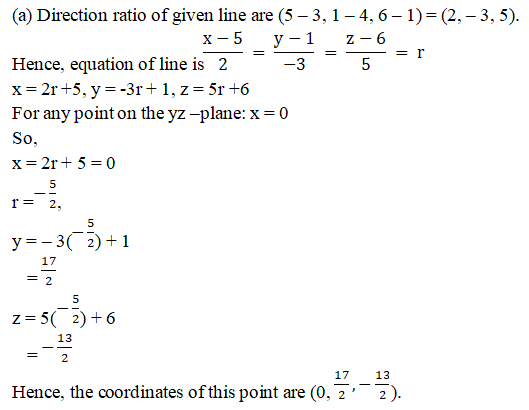
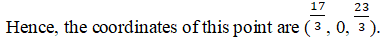
Q2.

Solution:

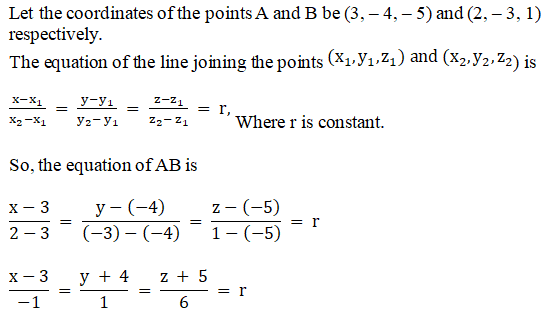
Any point on the line AB is the form:

– r + 3, r – 4, 6r – 5

Let p be the point of intersection of the line AB and the plane 2x + y + z = 7

Thus, we have,

2(– r + 3) + r – 4 + 6r – 5 = 7

– 2r + 6 + r – 4 + 6r – 5 = 7

5r = 10

r = 2

Now substitute the value of r in – r + 3, r – 4, 6r – 5, the coordinates of P are:

(– 2 + 3, 2 – 4, 12 – 5) = (1, – 2, 7).

Q3.

Solution:

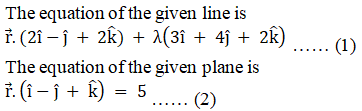
Q4.

Solution:

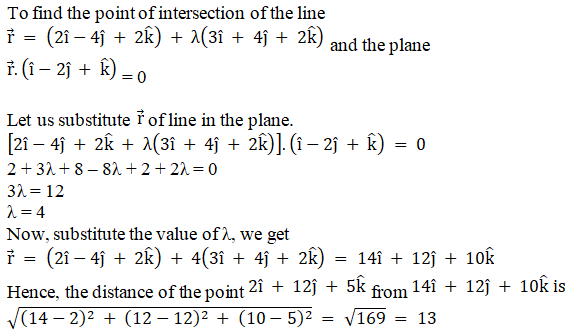
Q5.

Solution:

Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 13

EXERCISE 29.13

Q1.

Solution:

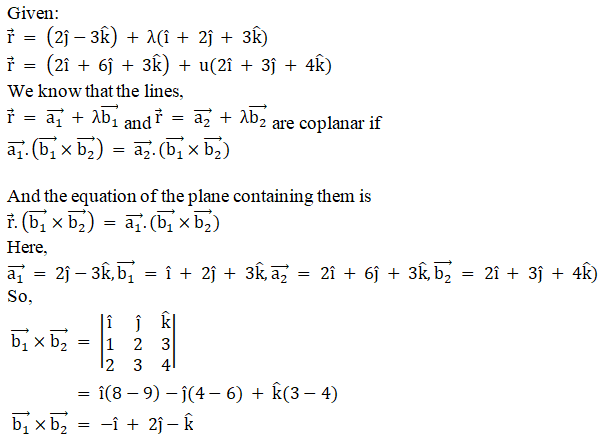
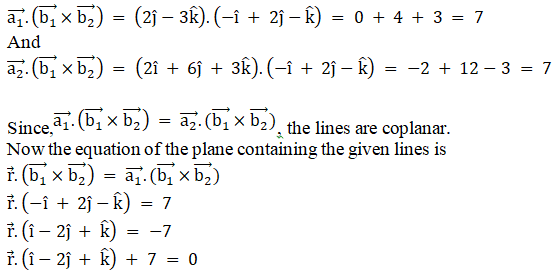
Q2.

Solution:

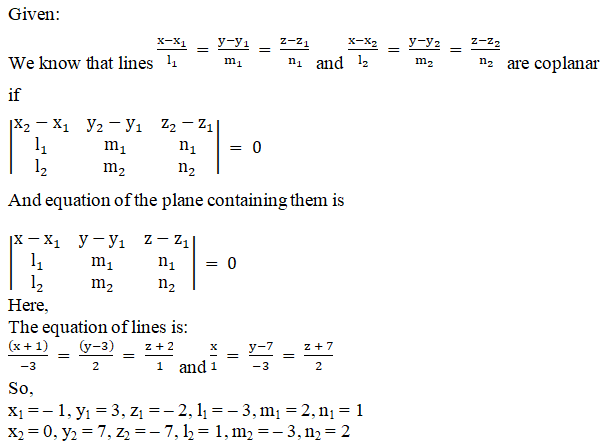
(x + 1) (4 + 3) – (y – 3) (– 6 – 1) + (z + 2) (9 – 2) = 0

7x + 7 + 7y – 21 + 7z + 14 = 0

7x + 7y + 7z = 0

Divide by 7, we get

x + y + z = 0

Hence, the required equation of the plane is x + y + z = 0.

Q3.

Solution:

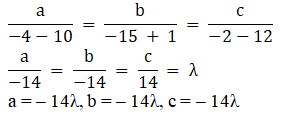
Substitute a, b, c in equation (2), and we get

ax + b(y – 7) + c(z + 7) = 0

(– 14λ)x + (– 14λ) (y – 7) + (– 14λ) (z + 7) = 0

Dividing by (– 14λ) we get

x + y – 7 + z + 7 = 0

x + y + z = 0

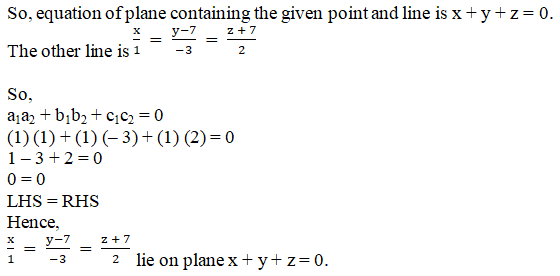
Q4.

Solution:

Given:

We know that equation of the plane passing through (x₁, y₁, z₁) is given by

a(x – x₁) + b(y – y₁) + c(z – z₁) = 0 …… (1)

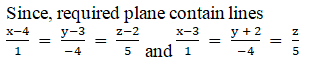
Thus, the required plane passes through points (4, 3, 2) and (3, – 2, 0).

So the equation of the required plane is

a(x – 4) + b(y – 3) + c(z – 2) = 0 …… (2)

Plane (2) also passes through (3, – 2, 0),

So,

a(3 – 4) + b(– 2 – 3) + c(0 – 2)

– a – 5b – 2c = 0

a + 5b + 2c = 0 …… (3)

Now plane (2) is also parallel to the line with direction ratios 1, – 4, 5.

So,

a₁a₂ + b₁b₂ + c₁c₂ = 0

(a) (1) + (b) (– 4) + (c) (5) = 0

a – 4b + 5c = 0 …… (4)

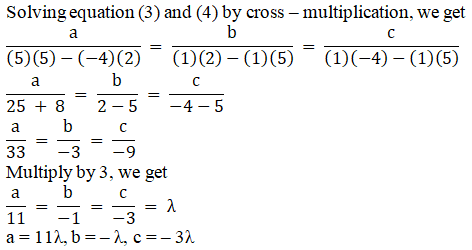
Now substitute the values of a, b, c in equation (2), and we get

a(x – 4) + b(y – 3) + c(z – 2) = 0

(11 λ)(x – 4) + (– λ)(y – 3) + (– 3 λ)(z – 2) = 0

11 λx – 44 λ – λy + 3 λ – 3 λz + 6 λ = 0

11 λx – λy – 3 λz – 35 λ = 0

Divide by λ, we get

11x – y – 3z – 35 = 0

Hence, the required equation of the plane is 11x – y – 3z – 35 = 0.

Q5.

Solution:

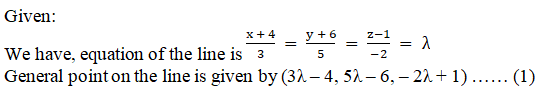
Another equation of line is

3x – 2y + z + 5 = 0

2x + 3y + 4z – 4 = 0

Let a, b, c be the direction ratio of the line so it will be perpendicular to the normal of 3x – 2y + z + 5 = 0 and 2x + 3y + 4z – 4 = 0

So, using a₁a₂ + b₁b₂ + c₁c₂ = 0

(3) (a) + (– 2) (b) + (1) (c) = 0

3a – 2b + c = 0 …… (2)

Again, (2) (a) + (3) (b) + (4) (c) = 0

2a + 3b + 4c = 0 …… (3)

Access RD Sharma Solutions for Class 12 Maths Chapter 29 Exercise 14

EXERCISE 29.14

Q1.

Solution:

Here,

(x₁, y₁, z₁) = (2, 5, 0) and (x₂, y₂, z₂) = (0, –1, 1)

Also

(a₁, b₁, c₁) = (–1, 2, 3) and (a₂, b₂, c₂) = (2, –1, 2)

We shall evaluate the numerator first.

Let

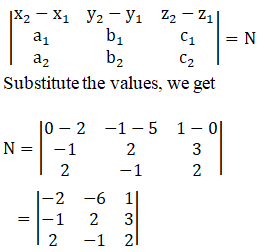
Let us simplify,

N = (–2)[(2)(2) – (–1)(3)] – (–6)[(–1)(2) – (2)(3)] + (1)[(–1)(–1) – (2)(2)]

= –2(4 + 3) + 6(–2 – 6) + (1 – 4)

= –14 – 48 – 3

= –65

Now, we shall evaluate the denominator.

Let

Q2.

Solution:

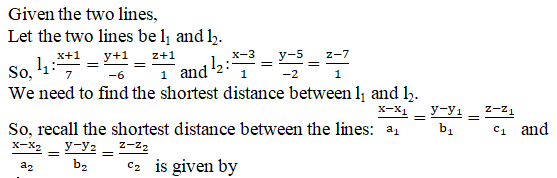
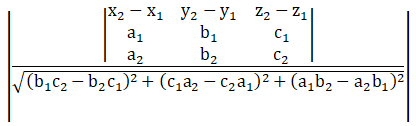
Here,

(x₁, y₁, z₁) = (–1, –1, –1) and (x₂, y₂, z₂) = (3, 5, 7)

Also

(a₁, b₁, c₁) = (7, –6, 1) and (a₂, b₂, c₂) = (1, –2, 1)

We shall evaluate the numerator first.

Let

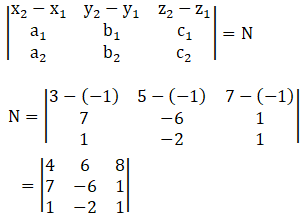
N = (4)[(–6)(1) – (–2)(1)] – (6)[(7)(1) – (1)(1)] + (8)[(7)(–2) – (1)(–6)]

= 4(–6 + 2) – 6(7 – 1) + 8(–14 + 6)

= –16 – 36 – 64

= –116

Now, we shall evaluate the denominator.

Let

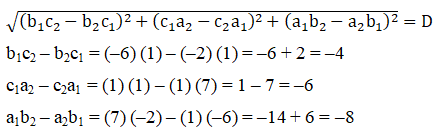
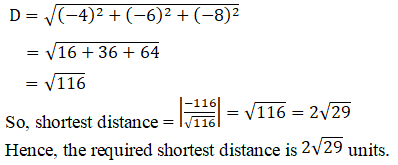
Q3.

Solution:

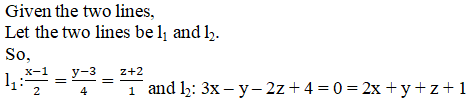
We need to find the shortest distance between l₁ and l₂.

The equation of a plane containing the line l₂ is given by

(3x – y – 2z + 4) + λ(2x + y + z + 1) = 0

(3 + 2λ)x + (λ – 1) y + (λ – 2) z + (4 + λ) = 0

Direction ratios of l₁ are 2, 4, 1, and those of the line containing the shortest distance are proportional to 3 + 2λ, λ – 1 and λ – 2.

We know that if two lines with direction ratios (a₁, b₁, c₁) and (a₂, b₂, c₂) are perpendicular to each other, then a₁a₂ + b₁b₂ + c₁c₂ = 0.

(3 + 2λ)(2) + (λ – 1)(4) + (λ – 2)(1) = 0

6 + 4λ + 4λ – 4 + λ – 2 = 0

9λ = 0

λ = 0

Thus, the plane containing line l₂ is 3x – y – 2z + 4 = 0.

We have

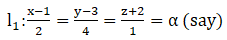
When α = 0, (x, y, z) = (1, 3, –2)

So, the point (1, 3, –2) lies on line l₁.

Hence, the shortest distance between the two lines is the same as the distance of the perpendicular from (1, 3, –2) onto the plane 3x – y – 2z + 4 = 0.

The length of the perpendicular drawn from (x₁, y₁, z₁) to the plane Ax + By + Cz + D = 0 is given by

Access RD Sharma Solutions For Class 12 Maths Chapter 29 Exercise 15

EXERCISE 29.15

Q1.

Solution:

Given:

Let point P = (0, 0, 0), and M be the image of P in the plane

3x + 4y – 6z + 1 = 0.

Direction ratios of PM are proportional to 3, 4, – 6 as PM is normal to the plane.

The equation of the line passing through (x₁, y₁, z₁) and having direction ratios proportional to l, m, n is given by

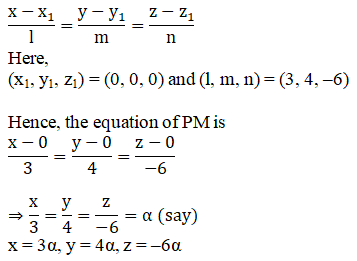
Let M = (3α, 4α, –6α).

As M is the image of P in the given plane, the midpoint of PM lies on the plane.

Using the midpoint formula, we have

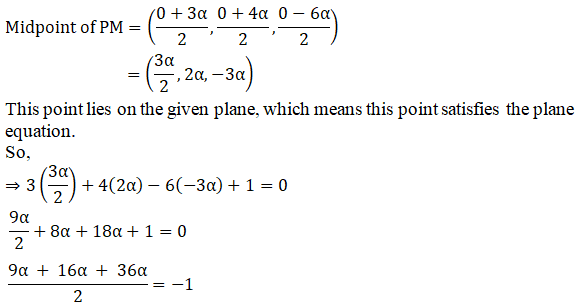
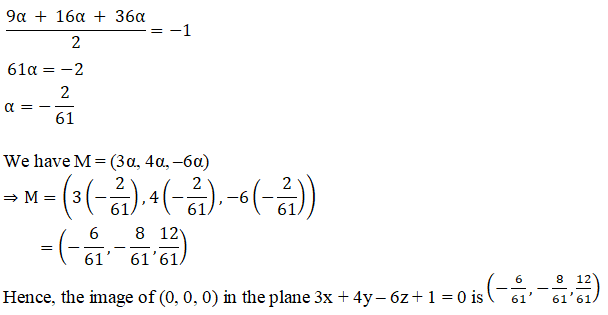
Q2.

Solution:

Given:

Let point P = (1, 2, –1) and M be the image of P in the plane 3x – 5y + 4z = 5.

Direction ratios of PM are proportional to 3, –5, 4 as PM is normal to the plane.

The equation of the line passing through (x₁, y₁, z₁) and having direction ratios proportional to l, m, n is given by

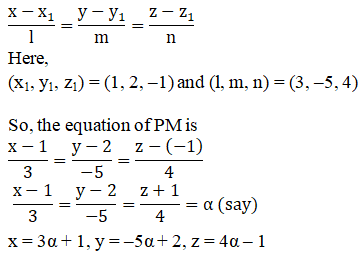
Let M = (3α + 1, –5α + 2, 4α – 1).

As M is the image of P in the given plane, the midpoint of PM lies on the plane.

Using the midpoint formula, we have

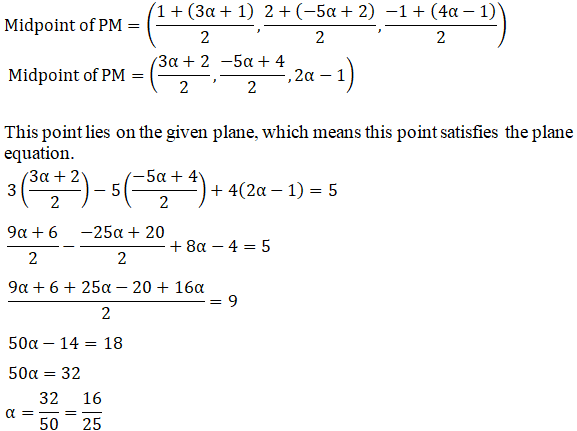
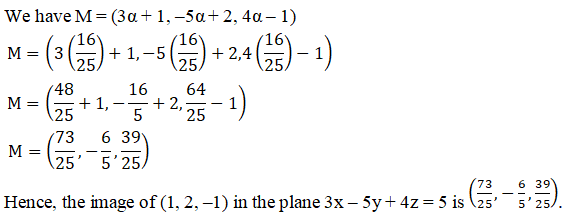
Q3.

Solution:

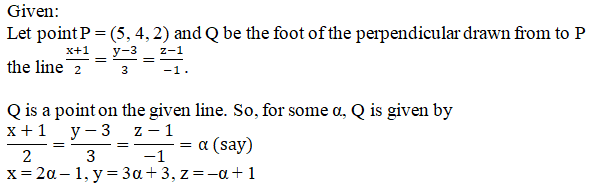
So, Q = (2α – 1, 3α + 3, –α + 1)

Now, let us find the direction ratios of PQ.

The direction ratios of a line joining two points (x₁, y₁, z₁) and (x₂, y₂, z₂) are given by (x₂ – x₁, y₂ – y₁, z₂ – z₁).

Here,

(x₁, y₁, z₁) = (5, 4, 2) and (x₂, y₂, z₂) = (2α – 1, 3α + 3, –α + 1)

Direction Ratios of PQ are ((2α – 1) – (5), (3α + 3) – (4), (–α + 1) – (2))

Direction Ratios of PQ are (2α – 6, 3α – 1, –α – 1)

PQ is perpendicular to the given line, whose direction ratios are (2, 3, –1).

We know that if two lines with direction ratios (a₁, b₁, c₁) and (a₂, b₂, c₂) are perpendicular to each other, then a₁a₂ + b₁b₂ + c₁c₂ = 0.

(2)(2α – 6) + (3)(3α – 1) + (–1)(–α – 1) = 0

4α – 12 + 9α – 3 + α + 1 = 0

14α – 14 = 0

14α = 14

α = 1

We have Q = (2α – 1, 3α + 3, –α + 1)

Q = (2×1 – 1, 3×1 + 3, –1 + 1)

Q = (1, 6, 0)

Using the distance formula, we have

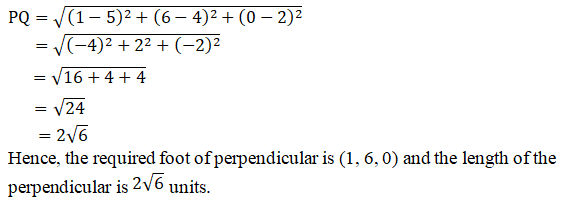
Q4.

Solution:

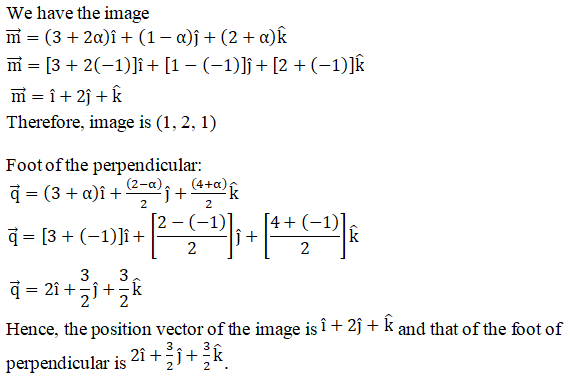
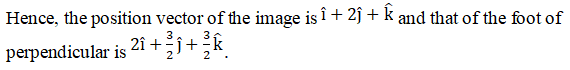
Q5.

Solution:

Given:

Let point P = (1, 1, 2) and Q be the foot of the perpendicular drawn from P to the plane 2x – 2y + 4z + 5 = 0.

Direction ratios of PQ are proportional to 2, –2, 4 as PQ is normal to the plane.

The equation of the line passing through (x₁, y₁, z₁) and having direction ratios proportional to l, m, n is given by

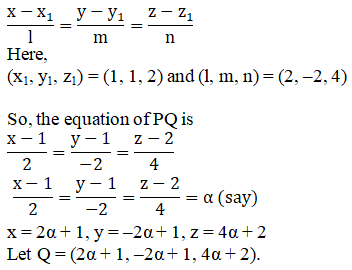
This point lies on the given plane, which means this point satisfies the plane equation.

2(2α + 1) – 2(–2α + 1) + 4(4α + 2) + 5 = 0

4α + 2 + 4α – 2 + 16α + 8 + 5 = 0

24α + 13 = 0

24α = –13