Chapter 28 STRAIGHT LINE IN SPACE

Access Answers to RD Sharma Solution Class 12 Maths Chapter 28 Exercise 1

Q1.

Solution:

Q2.

Solution:

It is given that,

The direction ratios of the line are: (3+1, 4-0, 6-2) = (4, 4, 4)

Since the given line passes through (-1, 0, 2)

We know that the vector equation of a line is given as

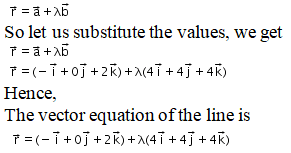
Q3.

Solution:

Let us consider,

The vector equation of the line passing through a fixed point vector a and parallel to vector b is given as

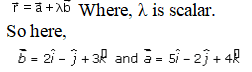
Q4.

Solution:

Let us consider,

The vector equation of the line passing through a fixed point vector a and parallel to vector b is given as

Hence,

The Cartesian form of the equation of the line is

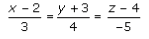
Q5.

Solution:

It is given that ABCD is a parallelogram.

Let us consider AC and BD bisects each other at point O.

So,

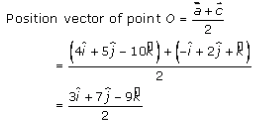
Let us consider position vector of point O and B are represented by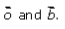

So,

The equation of the line BD is the line passing through O and B is given by

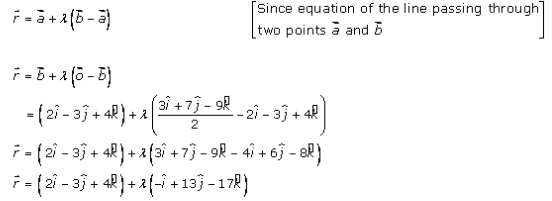
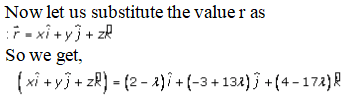
Now, let us compare the coefficients of vector i, j, R

x = 2 – λ, y = -3 – 13λ, z = 4 – 17λ

By equating to λ, we get,

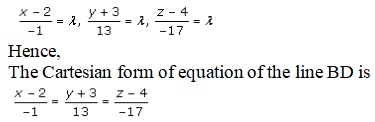
Access Answers to RD Sharma Solution Class 12 Maths Chapter 28 Exercise 2

Q1.

Solution:

Let us consider,

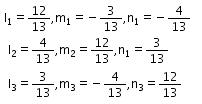
Now let us simplify, we get

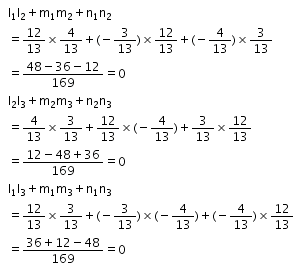
Hence, we can say that the lines are mutually perpendicular.

Q2.

Solution:

Given points are (1, -1, 2) and (3, 4, -2)

The direction ratios of a line passing through the points will be

(3-1, 4+1, -2-2) = (2, 5, -4)

Given points are (0, 3, 2) and (3, 5, 6)

The direction ratios of a line passing through the points will be

(3-0, 5-3, 6-2) = (3, 2, 4)

So,

Now the angle between the lines will be

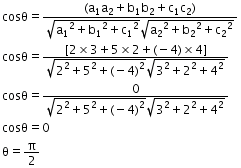
Hence, we can say that the lines are mutually perpendicular.

Q3.

Solution:

Given points are (4, 7, 8) and (2, 3, 4)

The direction ratios of a line passing through the points will be

(4-2, 7-3, 8-4) = (2, 4, 4)

Given points are (-1, -2, 1) and (1, 2, 5)

The direction ratios of a line passing through the points will be

(-1-1, -2-2, 1-5) = (-2, -4, -4)

So,

The direction ratios are proportional.

2/-2 = 4/-4 = 4/-4

Hence, we can say that the lines are mutually perpendicular.

Q4.

Solution:

It is given that,

The Cartesian equation of a line passing through (x₁, y₁, z₁) and with direction ratios (a₁, b₁, c₁) is

Q5.

Solution:

It is given that.

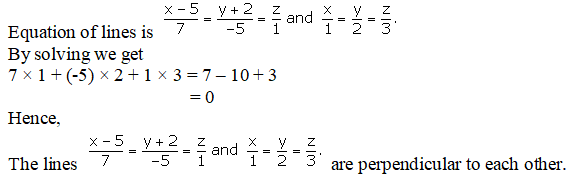
Access Answers to RD Sharma Solution Class 12 Maths Chapter 28 Exercise 3

Q1.

Solution:

Let us consider the equation of the line,

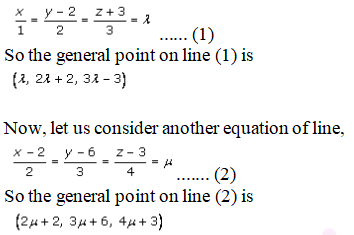
If lines (1) and (2) intersect, we get a common point

So for the same value of λ and μ, must have,

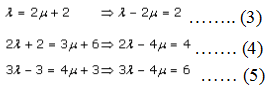
Now, let us solve (3) and (4), we get

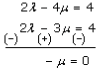
μ = 0

Now, let us substitute μ = 0 in equation (3), we get

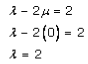
By substituting the values λ and μ in equation (5), we get

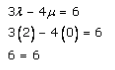
Hence,

LHS = RHS

Q2.

Solution:

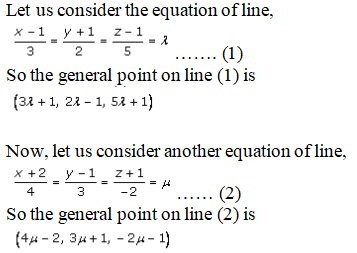
If lines (1) and (2) intersect, we get a common point

So for the same value of λ and μ, must have,

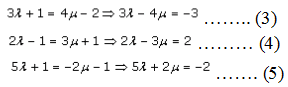
Now, let us solve (3) and (4), we get

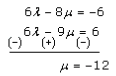
μ = -12

Now, let us substitute μ = -12 in equation (3), we get

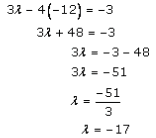
By substituting the values λ and μ in equation (5), we get

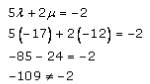
Hence,

LHS ≠ RHS

Q3.

Solution:

If lines (1) and (2) intersect, we get a common point

So for the same value of λ and μ, must have,

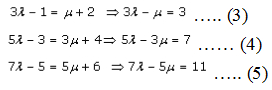
Now, let us solve (3) and (4), we get

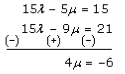
μ = -6/4

Now, let us substitute μ = -6/4 in equation (3), we get

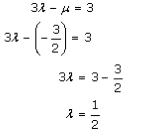
By substituting the values λ and μ in equation (5), we get

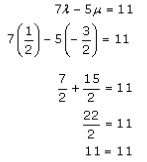
LHS = RHS

Since the value of λ and μ obtained by solving equations (3) and (4) satisfies equation (5).

Hence, the given lines intersect each other.

So,

Q4.

Solution:

Given points A(0, -1, -1) and B(4, 5, 1)

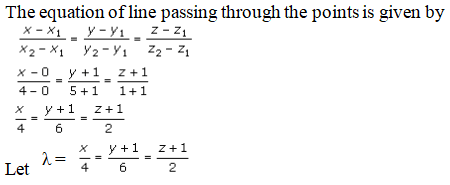
So, the general point on line AB is

(4λ, 4λ, 2λ – 1)

Given points C(3, 9, 4) and D(-4, 4, 4)

The equation of the line passing through the points is given by

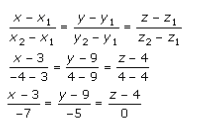
Let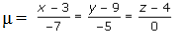

So, the general point on line CD is

(-7μ + 3, -5μ + 9, 0μ + 4)

(-7μ + 3, -5μ + 9, 4)

If lines AB and CD intersect, there exists a common point.

So let us find the value of λ and μ.

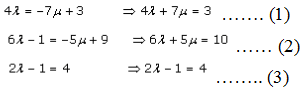
So from equation (3),

2λ = 4 + 1

2λ = 5

λ = 5/2

By substituting the value of λ = 5/2 in equation (2), we get

6(5/2) + 5μ = 10

5μ = 10 – 15

= -5

μ = -1

Now, by substituting the values of λ and μ in equation (1), we get

4λ + 7μ = 3

4(5/2) + 7(-1) = 3

10 – 7 = 3

3 = 3

LHS = RHS

Since the value of λ and μ obtained by solving equations (3) and (4) satisfies equation (1).

Hence, the given lines, AB and CD intersect each other.

So,

The point of intersection of AB and CD = (-7μ+3, -5μ+9, 4)

= (-7(-)+3, -5(-1)+9, 4)

= (7+3, 5+9, 4)

= (10, 14, 4)

Hence, the point of intersection of AB and CD is (10, 14, 4).

Q5.

Solution:

Given:

The equations of lines are

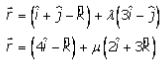
If these lines intersect, there exists a common point.

So for some value of λ and μ, we must have

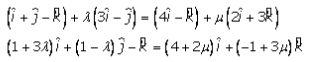
So, the equation of coefficients of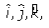
we get

1 + 3λ = 4 + 2μ => 3λ – 2μ = 3 …….. (1)

1 – λ = 0 => λ = 1 …………… (2)

-1 = -1 + 3μ => μ = 0 …………… (3)

By substituting the values of λ and μ in equation (1)

3λ – 2μ = 3

3(1) – 2(0) = 3

3 = 3

LHS = RHS

Since the value of λ and μ satisfies equation (1).

Hence, the given lines intersect each other.

So,

The point of intersection by substituting the value of λ in equation (1), we get

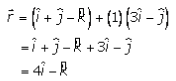
Hence, the point of intersection is (4, 0, -1).

Access Answers to RD Sharma Solution Class 12 Maths Chapter 28 Exercise 4

Q1.

Solution:

So, the Co-ordinates of Q are

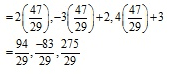
The distance between P and Q is given as

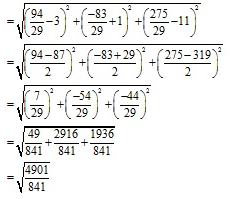
Hence, the required distance is √(4901/841) units.

Q2.

Solution:

So, the Co-ordinates of Q are

(2λ+1, -3λ-1, 8λ-10) = [2(1)+1, -3(1)-1, 8(1)-10]

= [3, 4, -2]

The distance between P and Q is given as

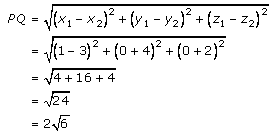
Hence,

The foot of perpendicular = (3, -4, -2)

Length of perpendicular = 2√6 units.

Q3.

Solution:

Let us consider,

The foot of the perpendicular drawn from A(1, 0, 3) to the line joining the points B(4,7,1) and C(3,5,3) be D.

The equation of line passing through points B(4,7,1) and C(3,5,3) is

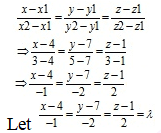
So, the direction ratio of AD is (-λ+4-1), (-2λ+7-0), (2λ+1-3)

= (-λ+3), (-2λ+7), (2λ-2)

Line AD is perpendicular to BC so,

a₁a₂ + b₁b₂ + c₁c₂ = 0

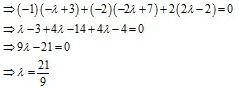
Hence,

Coordinates of D are:

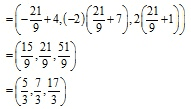
Q4.

Solution:

Given:

D is the foot of the perpendicular from A(1, 0, 4) on BC.

So,

The equation of the line passing through B, and C is

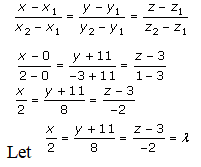
Coordinates of D = (2λ, 8λ-11, -2λ+3)

Direction ratios of AD is (2λ-1), (8λ-11-0), (-2λ+3-4)

= (2λ-1), (8λ-11), (-2λ-1)

Line AD is perpendicular to BC, so,

a₁a₂ + b₁b₂ + c₁c₂ = 0

Hence,

Coordinates of D = (2λ, 8λ-11, -2λ+3)

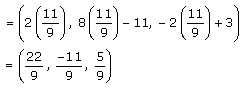
Q5.

Solution:

Let us consider,

Coordinates of Q = (-2λ+4, 6λ, -3λ+1)

Direction ratios of PQ = (-2λ+4-2), (6λ-3), (-3λ+1-4)

= (-2λ+2), (6λ-3), (-3λ-3)

Since PQ is perpendicular to the given line,

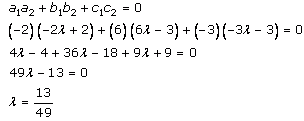
Coordinates of Q = (-2λ+4, 6λ, -3λ+1)

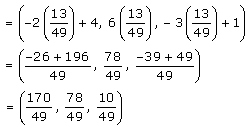
The distance between P and Q is given as

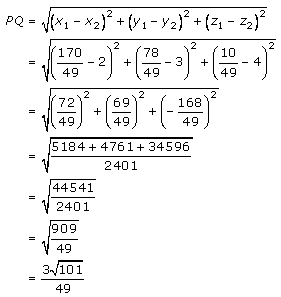
Hence,

The perpendicular distance from (2,3,4) to the given line is (3√101)/49 units.

Access Answers to RD Sharma Solution Class 12 Maths Chapter 28 Exercise 5

Q1.i

Solution:

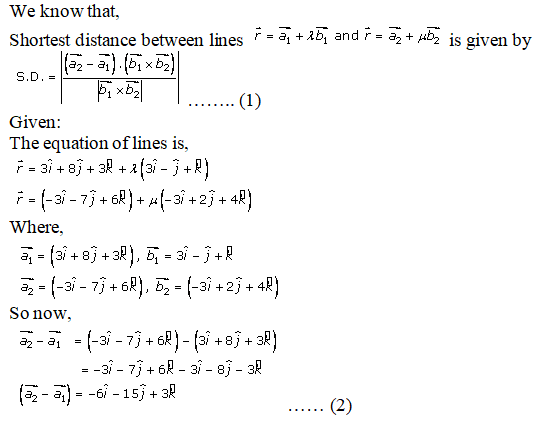
Let us solve for b, we get

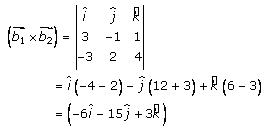……… (3)

By solving (2) and (3), we get

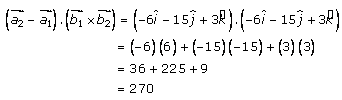
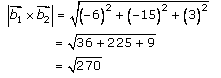
Now let us substitute the above-obtained values in equation (1), to get the shortest distance between given lines,

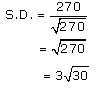
Hence, the shortest distance is 3√30 units.

ii.

Solution:

Given:

The equation of the lines is,

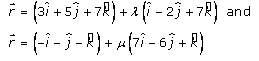
We know that,

Shortest distance between lines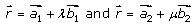
is given by

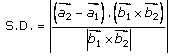…….. (1)

Where,

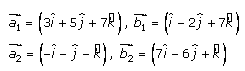
So now,

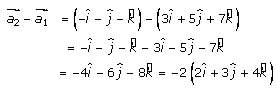……. (2)

Let us solve for b, we get

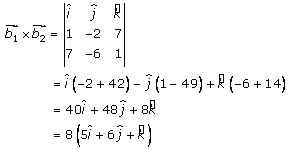…… (3)

By solving (2) and (3), we get

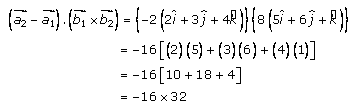
= -512

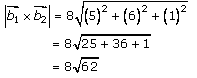
Now let us substitute the above-obtained values in equation (1), to get the shortest distance between given lines,

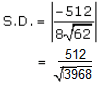
Hence, the shortest distance is 512/√3968 units.

iii.

Solution:

Given:

The equation of the lines is,

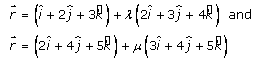
We know that,

Shortest distance between lines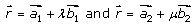
is given by

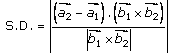…….. (1)

Where,

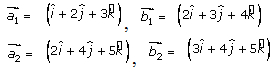
So now,

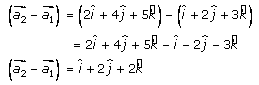…….. (2)

Let us solve for b, we get

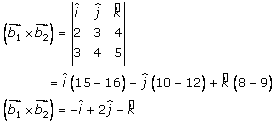……… (3)

By solving (2) and (3), we get

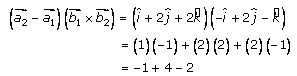
= 1

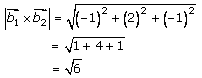
Now let us substitute the above-obtained values in equation (1), to get the shortest distance between given lines,

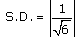
Hence, the shortest distance is 1/√6 units.

iv.

Solution:

Given:

The vector equations are

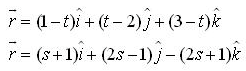
The above equations can be written as

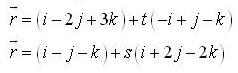
By using the formula,

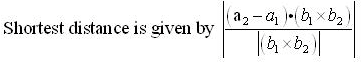
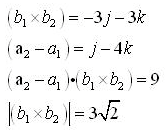
Hence,

The shortest distance is 9/3√2 = 3/√2 units.

v.

Solution:

Given:

The equation of lines is,

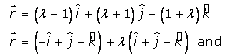
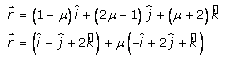
We know that,

Shortest distance between lines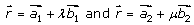
is given by

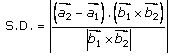…….. (1)

Where,

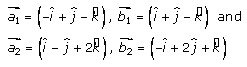
So now,

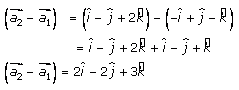……. (2)

Let us solve for b, we get

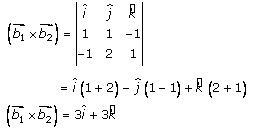
By solving (2) and (3), we get

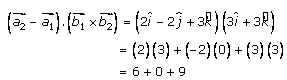
= 15

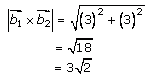
Now let us substitute the above-obtained values in equation (1), to get the shortest distance between given lines,

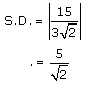
Hence, the shortest distance is 5/√2 units.