Chapter 24 SCALAR OR DOT PRODUCT

Access Answers for Rd Sharma Solution Class 12 Maths Chapter 24 Exercise 1

Exercise 24.1

1.

(i) Solution:

Given,

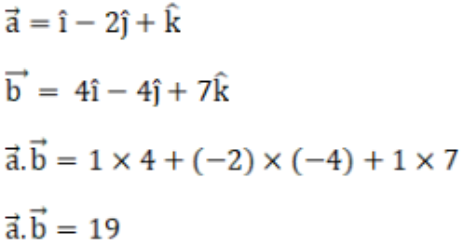
Hence, the dot product is 19.

(ii) Solution:

Given,

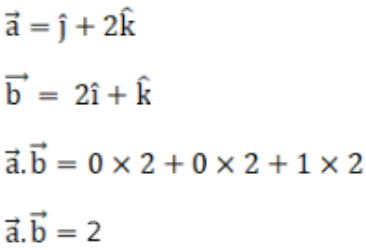
Hence, the dot product is 2.

(iii) Solution:

Given,

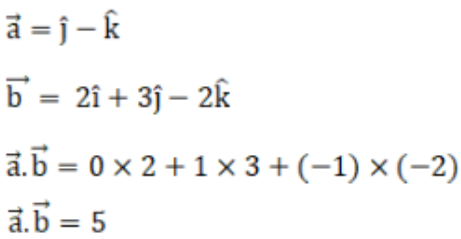
Hence, the dot product is 5.

2.

(i) Solution:

Given,

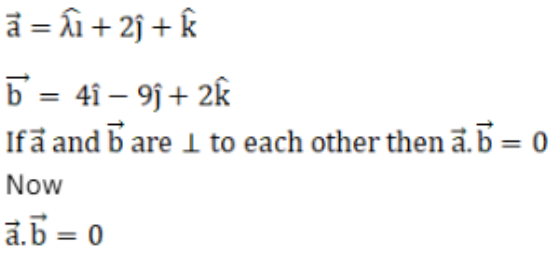
λ (4) + 2 (-9) + 1 (2) = 0

4λ – 18 + 2 = 0

4λ – 16 = 0

4λ = 16

λ = 16/4

∴ λ = 4

(ii) Solution:

Given,

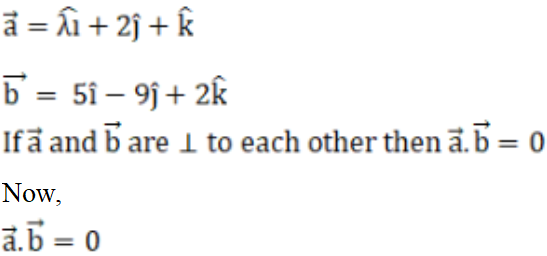
λ (5) + 2 (-9) + 1 (2) = 0

5λ – 18 + 2 = 0

5λ – 16 = 0

5λ = 16

∴ λ = 16/5

(iii) Solution:

Given,

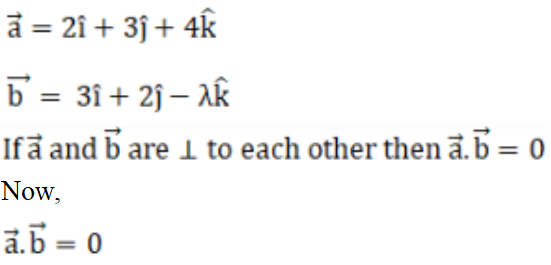
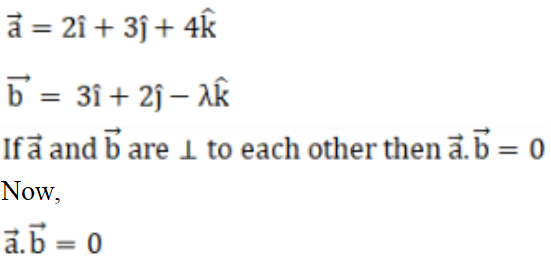
2 (3) + 3 (2) + 4 (-λ) = 0

-4λ + 6 + 6 = 0

-4λ + 12 = 0

-4λ = -12

λ = -12/-4

∴ λ = 3

(iv) Solution:

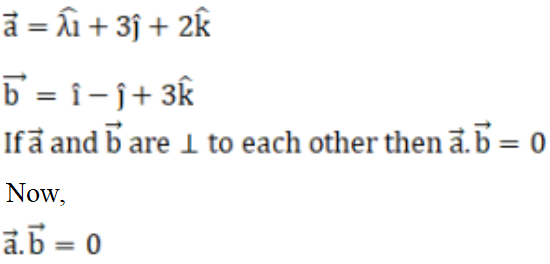
λ (1) + 3 (-1) + 2 (3) = 0

λ – 3 + 6 = 0

λ + 3 = 0

∴ λ = -3

3. Solution:

Given,

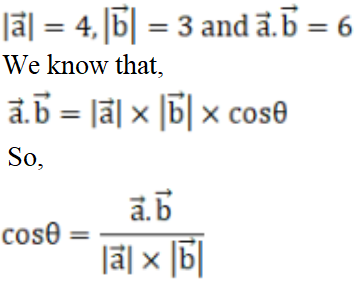
= 6/(4 x 3)

= 6/12

= ½

θ = cos^-1 (½)

∴ θ = π/3

4. Solution:

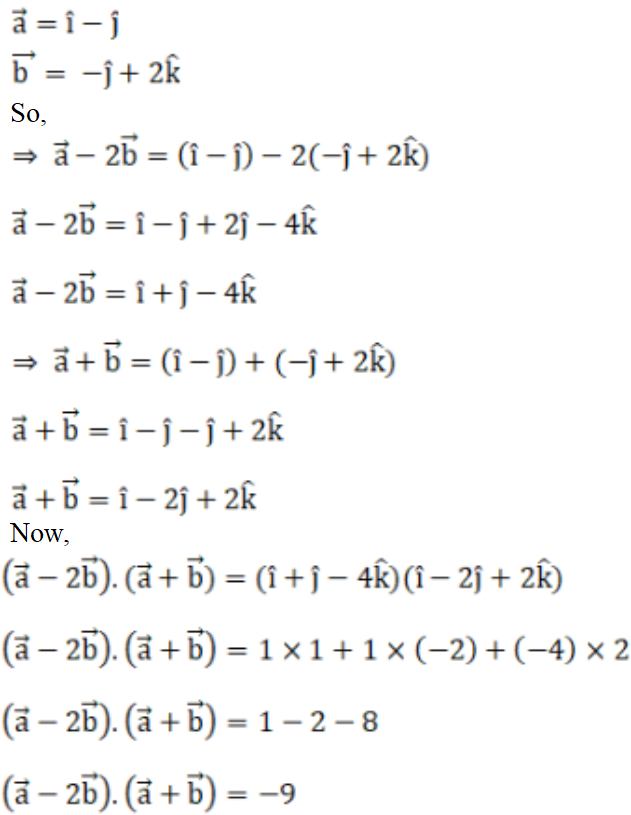
5.

(i) Solution:

Given,

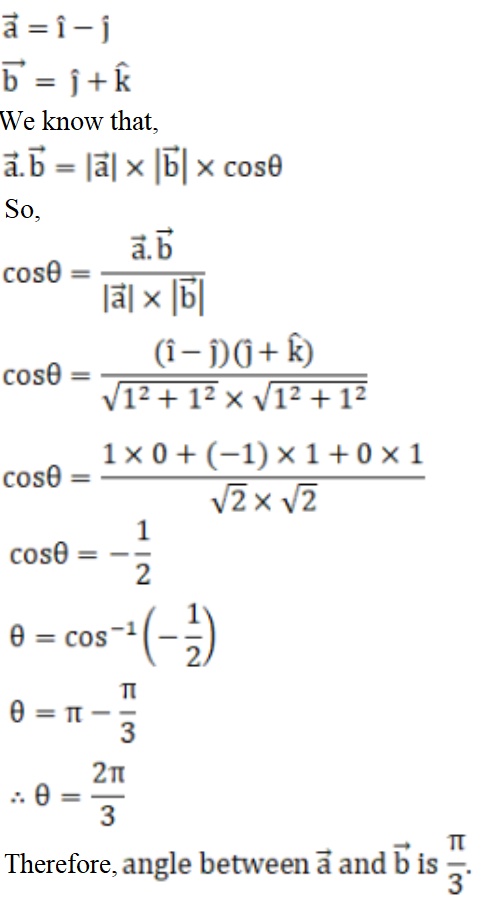
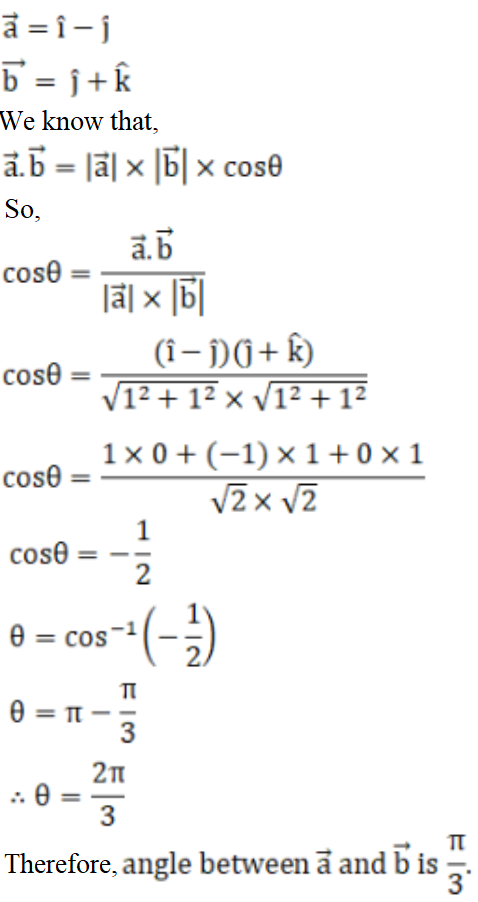
(ii) Solution:

Given,

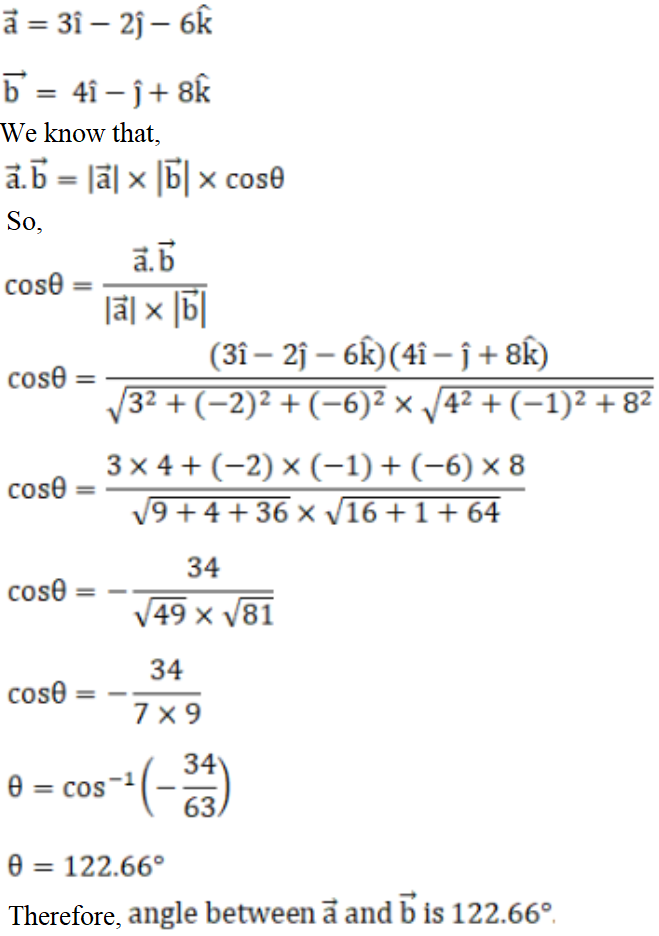
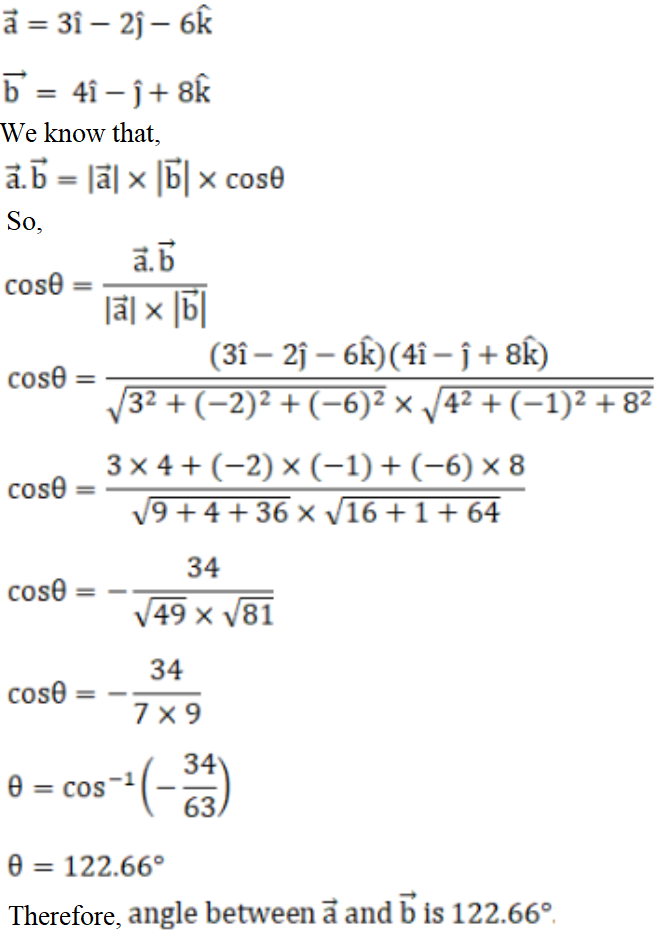
Access Answers for Rd Sharma Solution Class 12 Maths Chapter 24 Exercise 2

Exercise 24.2

1. Solution:

∴ OP² + OQ² = 5/9 AB²

2. Solution:

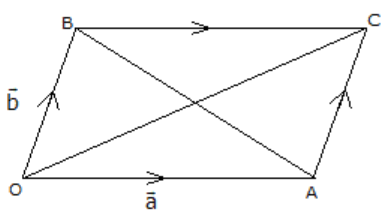
Let OACB be a quadrilateral such that its diagonal bisect each other at right angles.

We know that, if the diagonals of a quadrilateral bisect each other, then it’s a parallelogram.

Thus, OACB is a parallelogram

So,

OA = BC and OB = AC

Now,

Taking O as the origin. Let
be the position vector of A and B

AB and OC be the diagonals of a quadrilateral, which bisect each other at right angles.

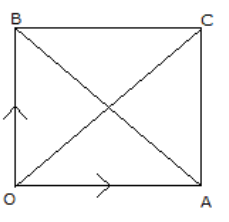
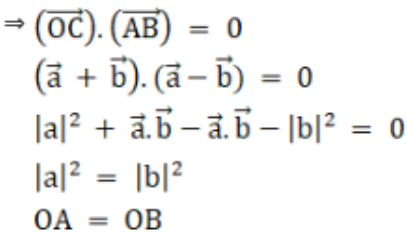
Similarly,

OA = OB = BC = CA

Therefore, OACB is a rhombus.

3. Solution:

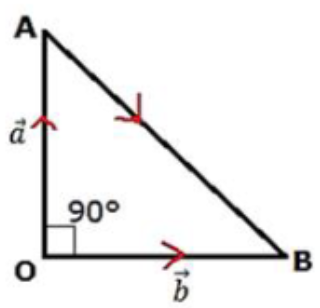
Let ∆AOB be a right-angle triangle with right angle at O.

Required to prove: AB² = OA² + OB²

Taking O as the origin, we have

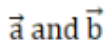
to be the position vector of A and B, respectively.

Now, as OB is perpendicular to OA, their dot product equals zero

So, we have

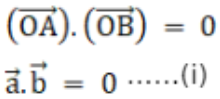
And,

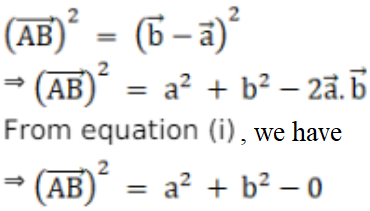
Therefore,

AB² = OA² + OB²

• Hence proved

4. Solution:

Let OAC be a right triangle, right-angled at O.

Now, taking O as the origin

Let
be the position vector of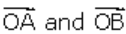
.

• Hence proved

5. Solution:

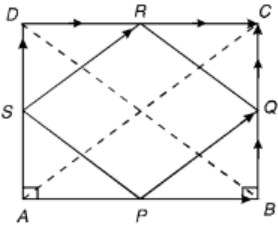
Given, ABCD is a rectangle

Let P, Q, R and S be the midpoints of the sides AB, BC, CD and DA, respectively.

Now,

From (iii) and (iv), we get

(PQ)² = (PS)²

⇒ PQ = PS

So, the adjacent sides of PQRS are equal

Hence, PQRS is a rhombus.

6. Solution:

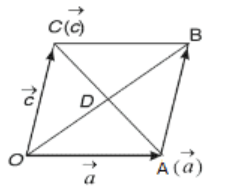
Let OABC be a rhombus whose diagonals OB and AC intersect at point D

And let O be the origin

Let the position vector of A and C be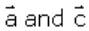
respectively then,

7. Solution:

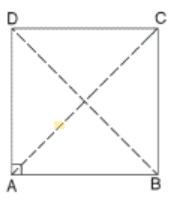
Let ABCD be a rectangle

Taking A as the origin, we have position vectors of points B and D to be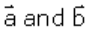
respectively

By parallelogram law,

Hence, ABCD is a square.