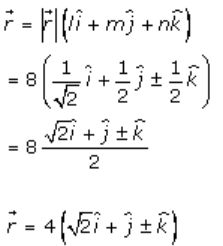Chapter 23 ALGEBRA OF VECTORS

Access Answers for RD Sharma Solution Class 12 Maths Chapter 23 Exercise 1

Exercise 23.1

1.

(i) Solution:

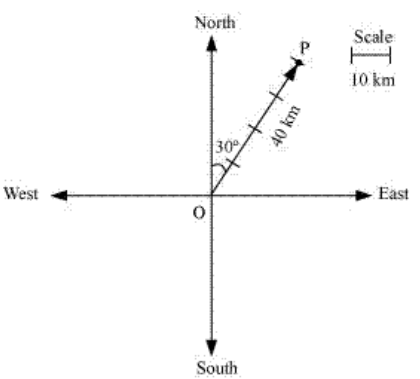
It’s seen that vector represents the displacement of 40 km, 30^o East of North.

(ii) Solution:

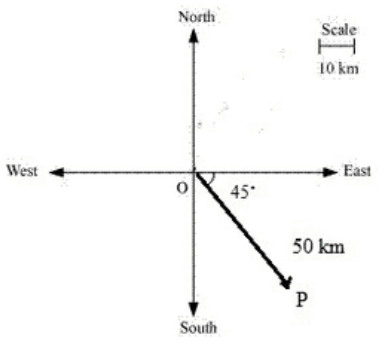
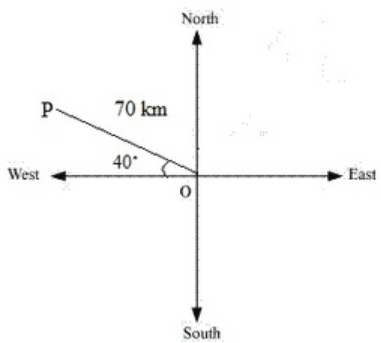
It’s seen that vector 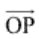represents the displacement of 50 km, South-East.

(iii) Solution:

It’s seen that vector represents the displacement of 70 km, 40^o North of West.

2. Solutions:

(i) 15 kg is a scalar quantity because it involves only mass.

(ii) 20 kg weight is a vector quantity as it involves both magnitude and direction.

(iii) 45^o is a scalar quantity as it involves only magnitude.

(iv) 10 meters southeast is a vector quantity as it involves direction.

(v) 50 m/s² is a scalar quantity as it involves the magnitude of acceleration.

3. Solutions:

(i) Time period is a scalar quantity as it involves only magnitude.

(ii) Distance is a scalar quantity as it involves only magnitude.

(iii) Displacement is a vector quantity as it involves both magnitude and direction.

(iv) Force is a vector quantity as it involves both magnitude and direction.

(v) Work done is a scalar quantity as it involves only magnitude.

(vi) Velocity is a vector quantity as it involves both magnitude as well as direction.

(vii) Acceleration is a vector quantity as it involves both magnitude as well as direction.

4. Solutions:

(i)

Collinear vectors are

(ii)

Equal vectors are

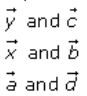
(iii)

Co-initial vectors are

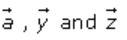
(iv)

Collinear but not equal vectors are

5. Solutions:

(i) True. Vectors a and b are collinear.

(ii) False. Two collinear vectors may not be equal in magnitude.

(iii) False. Zero vector may not be unique.

(iv) False. Two vectors having the same magnitude may not be collinear.

(v) False. Two collinear vectors having the same magnitude may not be equal.

Access Answers for Rd Sharma Solution Class 12 Maths Chapter 23 Exercise 2

Exercise 23.2

1. Solution:

Given that P, Q and R are collinear

Also, given that

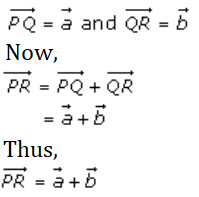
2. Solution:

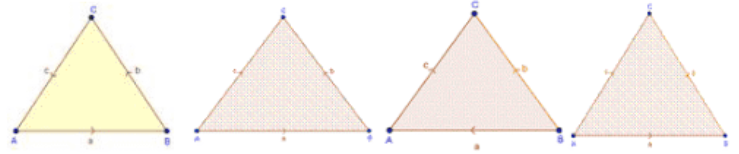
Given that,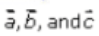
are the three sides of a triangle

So, we have

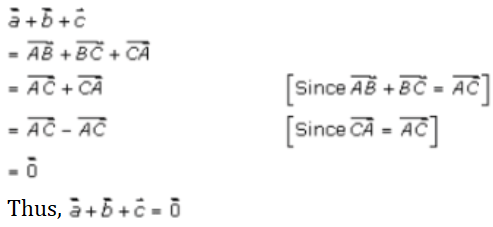
The triangle law says that if vectors are represented in magnitude and direction by the two sides of a triangle taken in the same order, then their sum is represented by the third side taken in reverse order.

Therefore,

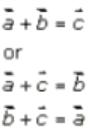
3. Solution:

Given that
are two non-collinear vectors having the same initial point

Let
, so we can draw a parallelogram ABCD as above

By the properties of a parallelogram, we have

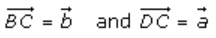
In ∆ABC,

Using triangle law, we have

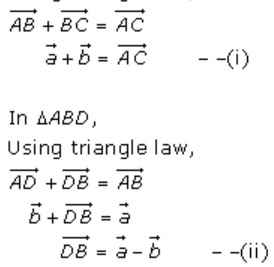
Thus, from equations (i) and (ii), we get that

4. Solution:

Given m is scalar and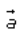
is a vector such that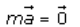

Now,

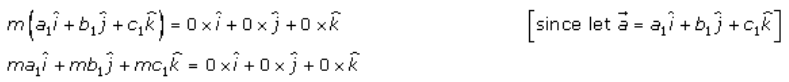
On comparing the coefficients of unit vectors i, j and k of L.H.S and R.H.S, we have

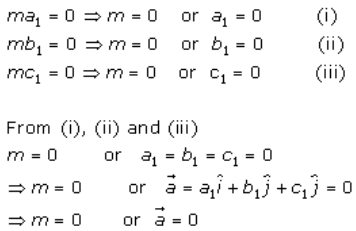
5.(i) Solution:

Let

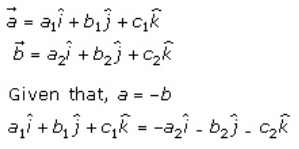
On comparing the coefficients of unit vectors i, j and k in L.H.S and R.H.S, we get

a₁ = -a₂ … (i)

b₁ = – b₂ … (ii)

c₁ = – c₂ … (iii)

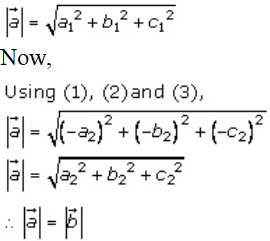
(ii) Solution:

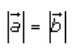
Given that a and b are two vectors such that

It means that the magnitudes of vector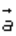
are equal to the magnitude of the vector
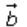, but we cannot conclude anything about the direction of vectors.

So, it is false that

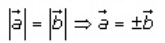
(iii) Solution:

Given that for any vector

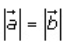
It means that the magnitudes of vector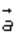
are equal to the magnitude of the vector
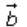, but we cannot conclude anything about the direction of vectors.

Moreover, we know that only when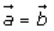
means both the direction and magnitude are the same for both vectors. Hence, the given statement is false.

Access Answers for RD Sharma Solution Class 12 Maths Chapter 23 Exercise 3

Exercise 23.3

1. Solution:

When,

Point R divides the line joining the two points P and Q in the ratio 1: 2 internally.

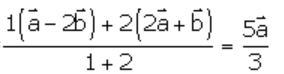
So, the position vector of point R =

And when,

Point R divides the line joining the two points P and Q in the ratio 1: 2 externally.

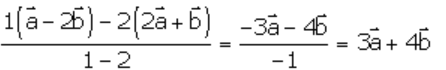
So, the position vector of point R =

2. Solution:

It’s given that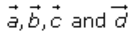
be the position vectors of the four distinct points A, B, C and D such that

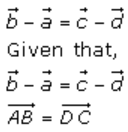
So, AB is parallel and equal to DC (in magnitude).

Therefore, ABCD is a parallelogram.

3. Solution:

It’s given that
are position vectors of A and B, respectively.

Let C be a part of AB produced such that AC = 3AB

Thus, it’s clear that point C divides the line AB in a ratio 3: 2 externally

So,

The position vector of point C is given by

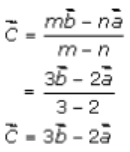
Again, let D be a point in BA produced such that BD = 2BA

Let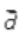
be the position vector of D. It is clear that point D divides the line AB in 1: 2 externally. So, the position vector of D is given by

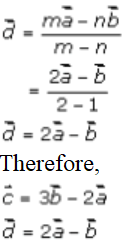
4. Solution:

Given that,

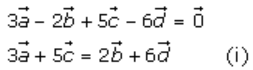
It’s seen that the sum of the coefficients on both sides of equation (i) is 8, so divide equation (i) by 8 on both sides.

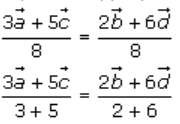
It shows that the position vector of a point P dividing AC in the ratio 3: 5, is the same as that of a point dividing BD in the ratio of 2: 6.

Hence, point P is the common point to AC and BD, and P is the point of intersection of AC and BD.

So, A, B, C and D are coplanar.

Therefore, the position vector of point P is given by

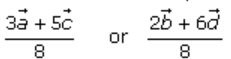
5. Solution:

It’s seen that the sum of the coefficients on both sides of equation (i) is 11, so divide equation (i) by 11 on both sides.

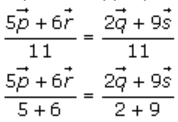
It shows the position vector of point A dividing PR in the ratio 6: 5 and QS in the ratio of 9: 2.

Hence, point A is the common point to PR and QS and it is also the point of intersection of PQ and QS.

So, P, Q, R and S are coplanar.

Therefore, the position vector of point A is given by

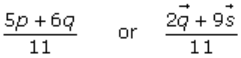
Access Answers for RD Sharma Solution Class 12 Maths Chapter 23 Exercise 4

Exercise 23.4

1. Solution:

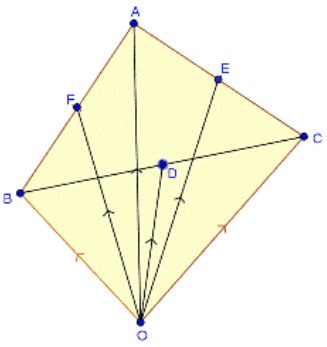
Given,

In ∆ABC, D, E and F are the mid-points of the sides of BC, CA and AB, respectively. And O is any point in space.

Let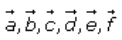
be the position vectors of points A, B, C, D, E and F with respect to O.

So,

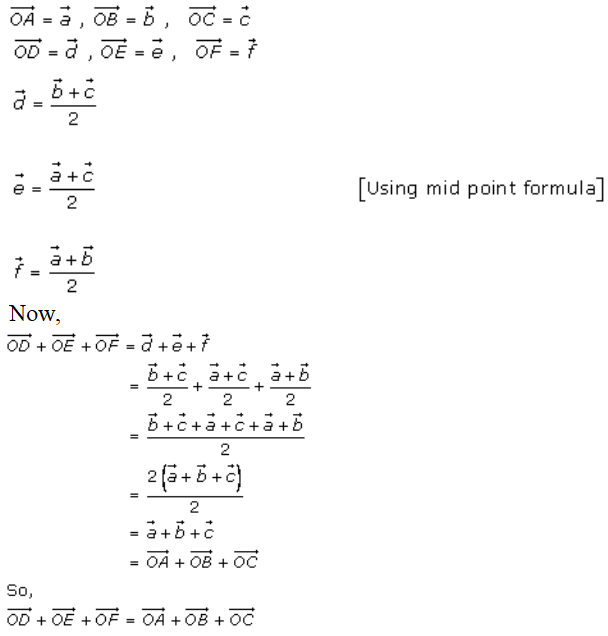
2. Solution:

Required to prove: The sum of the three vectors determined by the medians of a triangle directed from the vertices is zero.

Let ABC be a triangle such the position vector of A, B, and C are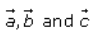
respectively.

As AD, BE, and CF are medians

Then, D, E and F are mid-points

So, we have

3. Solution:

Given, ABCD is a parallelogram and P is the point of intersection of diagonals, and O is the point of reference.

4. Solution:

Let’s consider ABCD to be a quadrilateral and P, Q, R and S to be the mid-points of sides

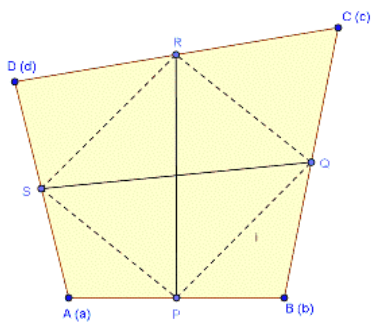
Let ABCD be a quadrilateral and P, Q, R and S be the midpoints of sides AB, BC, CD and DA, respectively.

Let the position vector of A, B, C and D be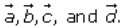

So, these are the position vector of P, Q, R and S, respectively.

 

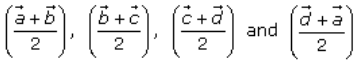
Now,

Thus, PQRS is a parallelogram, and hence, PR bisects QS.

[Since diagonals of a parallelogram bisect each other]

Therefore, the line segment joining the midpoint of opposite sides of a quadrilateral bisect each other.

5. Solution:

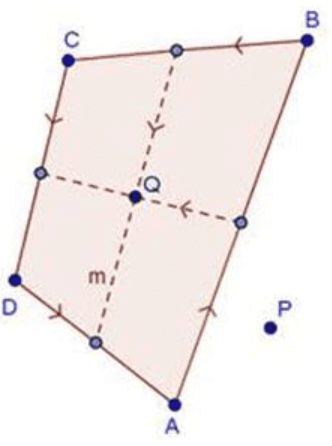
Let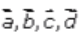
be the position vectors of the points A, B, C and D, respectively.

Then position vector of

Q is the midpoint of the line joining the midpoints of AB and CD.

Hence,

Access Answers for RD Sharma Solution Class 12 Maths Chapter 23 Exercise 5

Exercise 23.5

1. Solution:

Given,

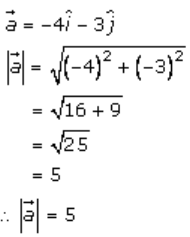
2. Solution:

Given,

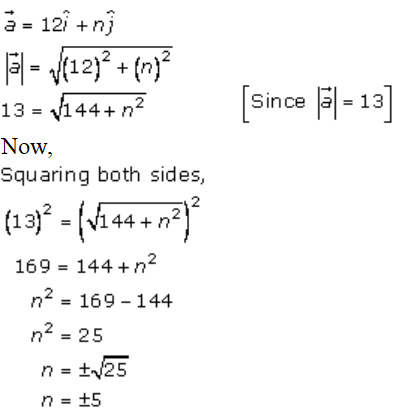
3. Solution:

Given,

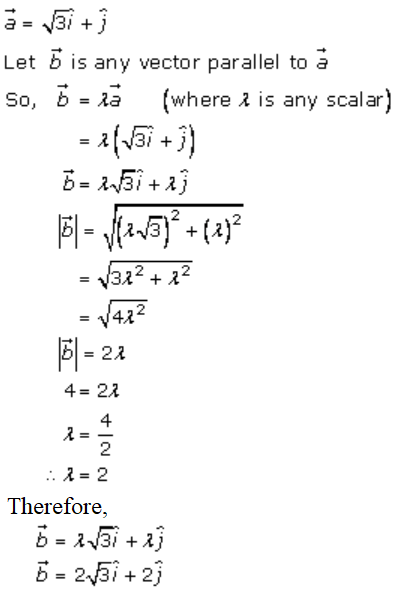
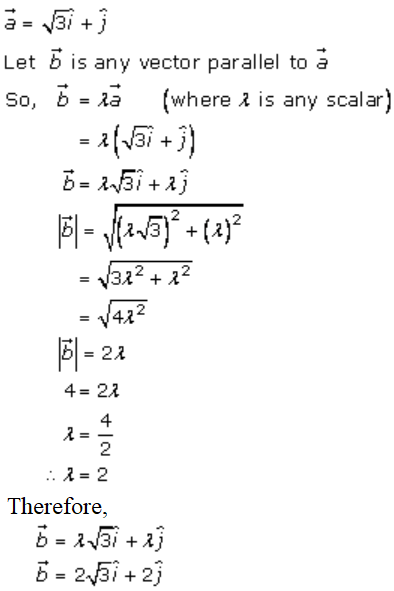
4. (i)

Solution:

Given,

A = (4, -1) and B = (1, 3)

So, the position vector of A and B will be

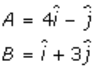
Now, the vector AB is

4. (ii)

Solution:

Given,

A = (-6, 3) and B = (-2, -5)

So, the position vector of A and B will be

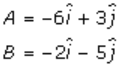
Now, the vector AB is

5. Solution:

Given,

A = (-1, 3) and B = (-2, 1)

So, the position vector of A and B will be

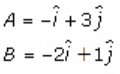
Now, the vector AB is

.

Access Answers for RD Sharma Solution Class 12 Maths Chapter 23 Exercise 6

Exercise 23.6

1. Solution:

We know that

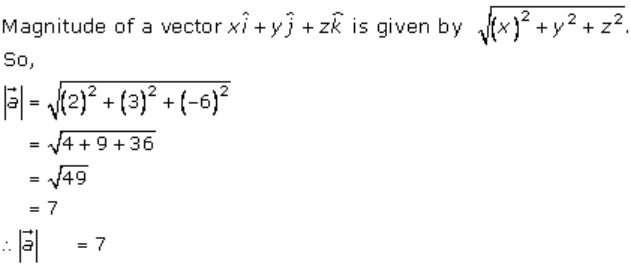
2. Solution:

We know that,

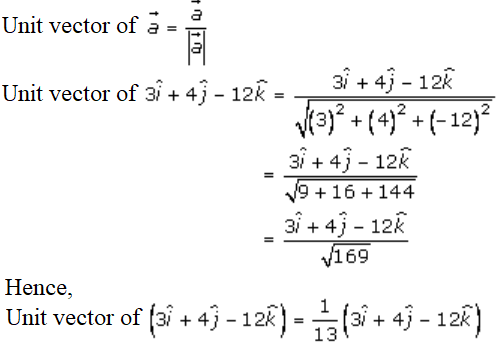
3. Solution:

Let

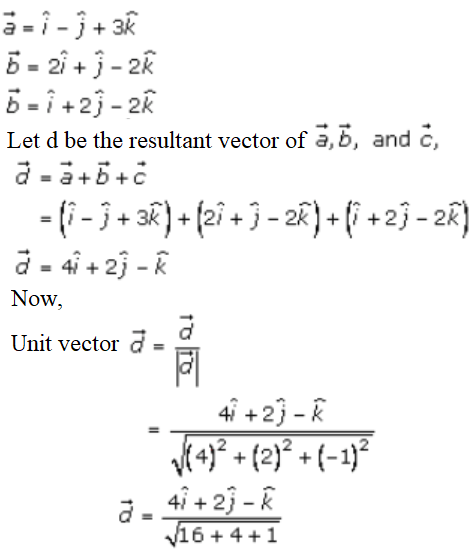
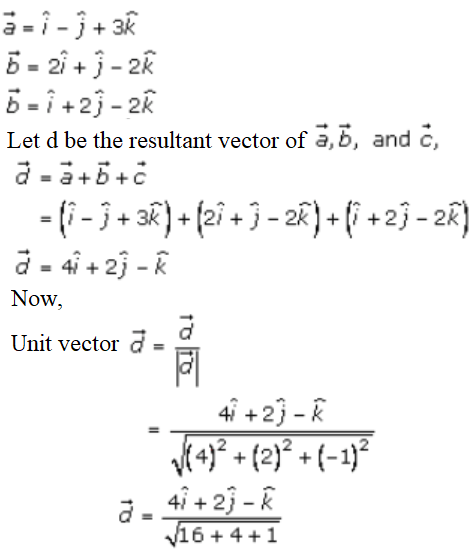
4. Solution:

Let PQRS be a parallelogram such that

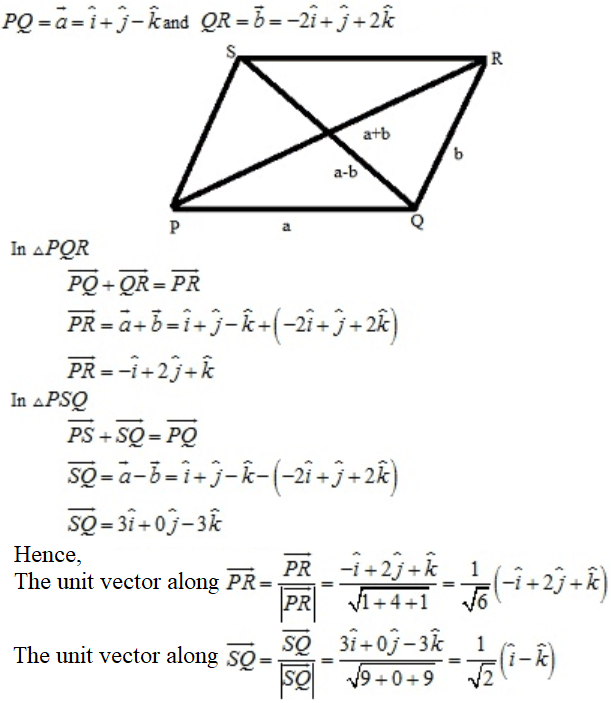
5. Solution:

We have,

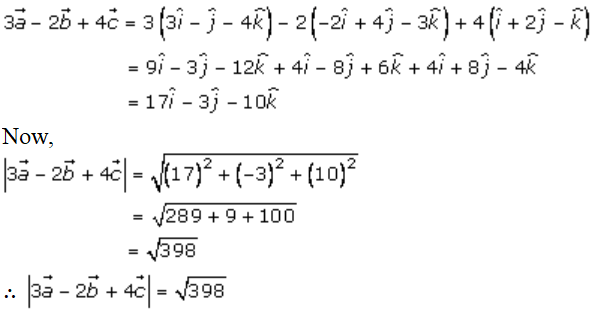
Access Answers for RD Sharma Solution Class 12 Maths Chapter 23 Exercise 7

Exercise 23.7

1. Solution:

Given,

2. (i)

Solution:

Let the points be A, B and C

So,

On comparing the coefficients of LHS and RHS, we get

– λ = 3, λ = -3 and λ = 3

As the values of λ are different, we can conclude that A, B and C are not collinear.

2. (ii)

Solution:

Let the points be A, B and C

Therefore, points A, B C are collinear.

3. Solution:

Let the points be A, B and C

We have,

4. Solution:

Let the points be A, B and C

On comparing the coefficients of L.H.S and R.H.S, we get

λa – 12 λ = 2 … (i)

-8 = 11 λ + 5 λ … (ii)

-8 = 16 λ

λ = -8/16

⇒ λ = -1/2

Now, putting the value of λ in (i) we get

λa – 12 λ = 2

(-1/2)a – 12(-1/2) = 2

-1/2a + 12/2 = 2

-1/2a + 6 = 2

-1/2a = -4

a = (-4) x (-2)

∴ a = 8

5. Solution:

Let A, B and C be the points then

Access Answers for Rd Sharma Solution Class 12 Maths Chapter 23 Exercise 8

Exercise 23.8

1. (i)

Solution:

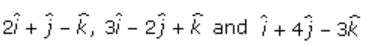
Let P, Q and R be the points whose position vectors are

respectively.

Now,

1. (ii)

Solution:

Let P, Q and R be the points represented by the vectors

2. (i)

Solution:

Given,

2. (ii)

Solution:

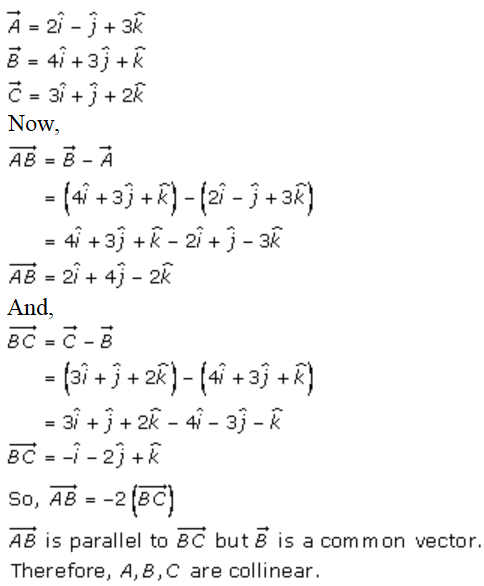
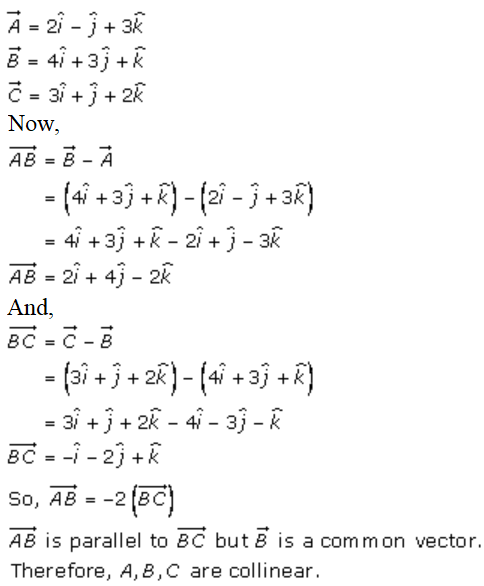
2. (iii)

Solution:

Given,

Therefore, A, B and C are collinear.

2. (iv)

Solution:

Given,

Therefore, A, B and C are collinear.

2. (v)

Solution:

Given,

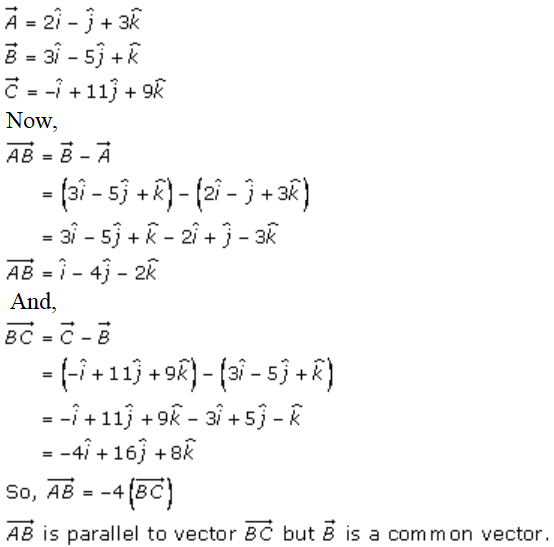
Therefore, A, B and C are collinear.

Access Answers for Rd Sharma Solution Class 12 Maths Chapter 23 Exercise 9

Exercise 23.9

1. Solution:

We know that if l, m and n are the direction cosines of a vector and α, β, γ be the direction angle

Then,

l = cos α

m = cos β

n = cos γ

And, l² + m² + n² = 1 … (i)

Here,

l = 1/√2

m = ½

n = -½

Putting the value of l, m and n in (i), we get

(1/√2)² + (1/2)² + (-1/2)² = 1

½ + ¼ + ¼ = 1

(2 + 1 + 1)/4 = 1

1 = 1

L.H.S = R.H.S

Therefore, a vector can have direction angles as 45^o, 60^o and 120^o.

2. Solution:

Given,

l = 1, m = 1 and n = 1

We know that,

l² + m² + n² = 1

(1)² + (1)² + (1)² = 1

1 + 1 + 1 = 1

3 ≠ 1

L.H.S ≠ R.H.S

Therefore, 1,1,1 cannot be the direction cosines of a straight line.

3. Solution:

We have,

α = π/4 and β = π/4

So,

l = cos α = cos π/4 = 1/ √2

m = cos β = cos π/4 = 1/ √2

And,

n = cos γ

We know that,

l² + m² + n² = 1

(1/√2)² + (1/√2)² + cos² γ = 1

½ + ½ + cos² γ = 1

1 + cos² γ = 1

cos² γ = 0

Taking square root on both sides, we get

cos γ = 0

γ = cos^-1 0

γ = π/2

Therefore, the angle made by the vector with the z-axis is π/2.

4. Solution:

We have,

α = β = γ

So,

cos α = cos β = cos γ

Also,

l = m = n = k (say)

We know that,

l² + m² + n² = 1

k² + k² + k² = 1

3k² = 1

k² = 1/3

Taking square root on both sides, we get

k = ± 1/√3

So,

l = ± 1/√3, m = ± 1/√3 and n = ± 1/√3

Hence, the direction cosines of vector r are ± 1/√3, ± 1/√3, ± 1/√3

Now,

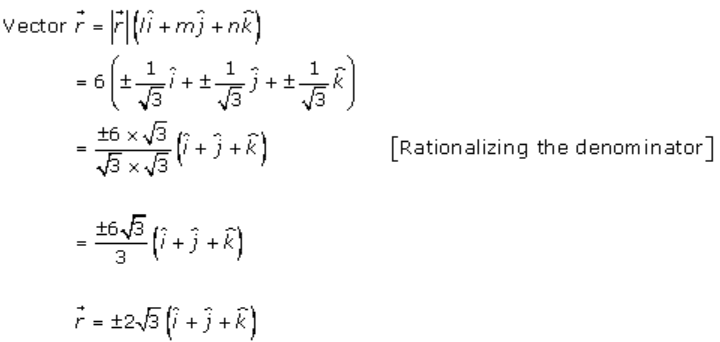
5. Solution:

We have,

α = 45^o, β = 60^o and γ = θ (say)

So,

l = cos α = cos 45^o = 1/√2

m = cos β = cos 60^o = ½

And,

n = cos γ = cos θ

We know that,

l² + m² + n² = 1

Putting values of l, m and n

(1/√2)² + (½)² + cos² θ = 1

½ + ¼ + cos² θ = 1

¾ + cos² θ = 1

cos² θ = 1 – ¾ = (4 – 3)/4

cos² θ = ¼

Taking square root on both sides, we get,

cos θ = ± 1/2

So, the direction cosines of the vector r are ± ½, ± ½, ± ½

Thus, the required vector is given by