Chapter 22 DIFFERENTIAL EQUATIONS

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 1

EXERCISE 22.1

Question. 1

Solution:

From the question, it is given that,

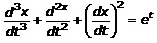
So, it is clear that the highest order of the given differential coefficient is d³x/dt^3, and then its power is 1.

The given differential equation is non-linear with order 3 and degree 1.

Question. 2

Solution:

From the question, it is given that,

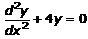
So, it is clear that the highest order of the given differential coefficient is d²y/dx^2, and then its power is 1.

The given differential equation is linear with order 2 and degree 1.

Question. 3

Solution:

From the question, it is given that,

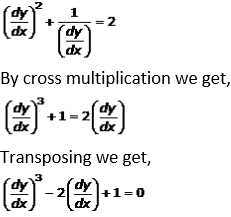
So, it is clear that the highest order of the given differential coefficient is d²y/dx² and then its power is 1.

The given differential equation is linear with order 2 and degree 1.

Question. 4

Solution:

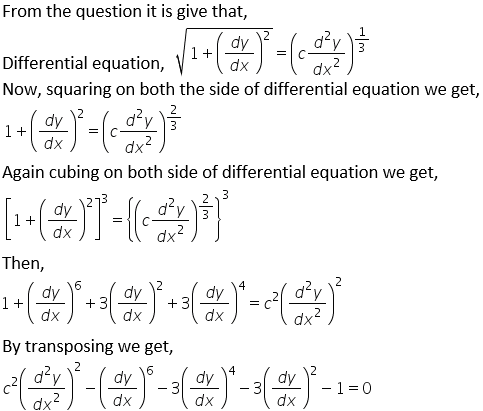
So, it is clear that the highest order of the above differential equation is d²y/dx² and then its power is 2.

The differential equation is non-linear with order 2 and degree 2.

Question. 5

Solution:

From the question, it is given that,

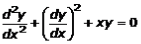
So, it is clear that the highest order of the given differential coefficient is d²y/dx² and then its power is 1.

The given differential equation is non-linear with order 2 and degree 1.

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 2

EXERCISE 22.2

Question. 1

Solution:

From the question, it is given that,

y² = (x – c)³ … [equation (i)]

Now, differentiate the equation (i) with respect x,

2y dy/dx = 3(x – c)²

By cross multiplication, we get,

(x – c)² = (2y/3) (dy/dx)

Transferring the square to Right Hand Side (RHS),

(x – c) = {(2y/3) (dy/dx)}^1/2

Then, substitute the value of (x – c) in equation (i),

y² = [{(2y/3) (dy/dx)}^1/2]³

y² = {(2y/3) (dy/dx)}^3/2

Squaring on both the side we get,

(y²)² = [{(2y/3) (dy/dx)}^3/2]²

y⁴ = [{(2y/3) (dy/dx)}³

y⁴ = (2y/3)³ (dy/dx)³

y⁴= (8y³/27) (dy/dx)³

By cross multiplication, we get,

27y⁴/y³ = 8 (dy/dx)³

27y = 8 (dy/dx)³

Question. 2

Solution:

From the question, it is given that,

y = e^mx … [equation (i)]

Now, differentiate the equation (i) with respect x,

dy/dx = me^mx

We know that, from equation (i) y = e^mx

So, applying log on both sides we get,

log y = mx

m = log y/x

Now, substitute the value of m and e^mx is equation (i) we get,

dy/dx = (log y/x)y

By cross multiplication, we get,

x(dy/dx) = y log y

Question. 3(i)

Solution:

From the question, it is given that,

y² = 4ax … [equation (i)]

Now, differentiate the equation (i) with respect x,

2y (dy/dx) = 4a … [equation (ii)]

From equation (i), a = y²/4x

Then, substitute the value of a in equation (ii),

2y (dy/dx) = 4(y²/4x)

2y (dy/dx) = y²/x

By cross multiplication, we get,

2x (dy/dx) = y²/y

2x (dy/dx) = y

Question. 3(ii)

Solution:

From the question, it is given that,

y = cx + 2c² + c³ … [equation (i)]

Now, differentiate the equation (i) with respect x,

dy/dx = c

Then, substitute the value of c in equation (i),

y = (dy/dx) x + 2(dy/dx)² + (dy/dx)³

Question. 3(iii)

Solution:

From the question, it is given that,

xy = a² … [equation (i)]

Now, differentiate the equation (i) with respect x,

x dy/dx + y(1) = 0

x dy/dx + y = 0

Question. 3(iv)

Solution:

From the question, it is given that,

y = ax² + bx + c … [equation (i)]

Now, differentiate the equation (i) with respect x,

dy/dx = 2ax + b

Then, the above equation is again differentiating with respect to x we get,

d²y/dx² = 2a

The above equation is again differentiating with respect to x we get

d³y/dx³ = 0

Question. 4

Solution:

From the question, it is given that,

y = Ae^2x + Be^-2x … [equation (i)]

Now, differentiate the equation (i) with respect x,

dy/dx = 2Ae^2x – 2Be^-2x

Then, the above equation is again differentiating with respect to x we get,

d²y/dx² = 4Ae^2x + 4Be^-2x

Taking common terms outside,

d²y/dx² = 4 (Ae^2x + Be^-2x)

From equation (i) we have y = Ae^2x + Be^-2x

Therefore, d²y/dx² = 4y

Question. 5

Solution:

From the question, it is given that,

x = A cos nt +B sin nt … [equation (i)]

Now, differentiate the equation (i) with respect t,

dx/dt = – An sin nt + Bn cos nt

Then, the above equation is again differentiating with respect to t we get,

d²x/dt² = – An² cos nt – Bn² sin nt

Taking common terms outside,

d²x/dt² = – n² (A cos nt + B sin nt)

From equation (i) we have x = A cos nt +B sin nt

d²x/dt² = – n²x

By transposing, we get,

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 3

EXERCISE 22.3

Question. 1

Solution:

From the question, it is given that,

y = be^x + ce^2x … [equation (i)]

Now, differentiate the equation (i) with respect x,

dy/dx = be^x + 2ce^2x … [equation (ii)]

Then, the above equation is again differentiating with respect to x we get,

d²y/dx² = be^x + 4ce^2x … [equation (iii)]

The given differential equation is d²y/dx² – 3 (dy/dx) + 2y = 0

Substitute equation (i), equation (ii) and equation (iii) in the given differential equation,

d²y/dx² – 3 (dy/dx) + 2y = 0

(be^x + 4ce^2x) – 3 (be^x + 2ce^2x) + 2(be^x + ce^2x) = 0

be^x + 4ce^2x – 3be^x – 6ce^2x + 2be^x + 2ce^2x = 0

3be^x – 3be^x + 6ce^2x – 6ce^2x = 0

0 = 0

Hence it is proved that, d²y/dx² – 3 (dy/dx) + 2y = 0

Question. 2

Solution:

From the question, it is given that,

y = 4 sin 3x … [equation (i)]

Now, differentiate the equation (i) with respect to x,

dy/dx = 4(3) cos 3x

dy/dx = 12 cos 3x … [equation (ii)]

Then, the above equation is again differentiating with respect to x we get,

d²y/dx² = 12(3) cos 3x

d²y/dx² = – 36 sin 3x … [equation (iii)]

The given differential equation is d²y/dx² + 9y = 0

Substitute equation (i) and equation (iii) in the given differential equation,

d²y/dx² + 9y = 0

– 36 sin 3x + 9 (4 sin 3x) = 0

– 36 sin 3x + 36 sin 3x = 0

0 = 0

Hence it is verified that y = 4 sin 3x is a solution of the differential equation is d²y/dx² + 9y = 0.

Question. 3

Solution:

From the question, it is given that,

y = ae^2x + be^-x … [equation (i)]

Now, differentiate the equation (i) with respect x,

dy/dx = 2 ae^2x – be^-x … [equation (ii)]

Then, the above equation is again differentiated with respect to x, and we get,

d²y/dx² = 4 ae^2x + be^-x … [equation (iii)]

The given differential equation is d²y/dx² – dy/dx – 2y = 0

Substitute equation (i), equation (ii) and equation (iii) in the given differential equation,

d²y/dx² – dy/dx – 2y = 0

(4 ae^2x + be^-x) – (2 ae^2x – be^-x) – 2(ae^2x + be^-x) = 0

4 ae^2x + be^-x – 2ae^2x + be^-x – 2ae^2x – 2be^-x = 0

4 ae^2x – 4ae^2x + 2be^-x – 2be^-x = 0

0 = 0

Hence it is verified that y = ae^2x + be^-x is a solution of the differential equation is d²y/dx² – dy/dx – 2y = 0.

Question. 4

Solution:

From the question, it is given that,

y = A cos x + B sin x … [equation (i)]

Now, differentiate the equation (i) with respect x,

dy/dx = – A sin x + B cos x … [equation (ii)]

Then, the above equation is again differentiating with respect to x we get,

d²y/dx² = – A cos x – B sin x … [equation (iii)]

The given differential equation is d²y/dx² + y = 0

Substitute equation (i) and equation (iii) in the given differential equation,

(- A cos x – B sin x) + (A cos x + B sin x ) = 0

– A cos x – B sin x + A cos x + B sin x = 0

0 = 0

Hence it is verified that y = A cos x + B sin x is a solution of the differential equation is d²y/dx² + y = 0.

Question. 5

Solution:

From the question, it is given that,

y = A cos 2x – B sin 2x … [equation (i)]

Now, differentiate the equation (i) with respect x,

dy/dx = – 2A sin (2x) – 2B cos 2x

Taking common terms outside,

dy/dx = -2 (A sin 2x + B cos 2x) … [equation (ii)]

Then, the above equation is again differentiating with respect to x we get,

d²y/dx² = – 2 [2A cos 2x – 2B sin 2x]

= -4 [A cos 2x – B sin 2x] … [equation (iii)]

The given differential equation is d²y/dx² + 4y = 0

Substitute equation (i) and equation (iii) in the given differential equation,

d²y/dx² + 4y = 0

-4 [A cos 2x – B sin 2x] + 4 (A cos 2x – B sin 2x) = 0

-4A cos 2x + 4B sin 2x + 4A cos 2x – 4B sin 2x = 0

0 = 0

Hence it is verified that y = A cos 2x – B sin 2x is a solution of the differential equation is d²y/dx² + 4y = 0.

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 4

EXERCISE 22.4

Question. 1

Solution:

From the question, it is given that,

Function, y = log x

Now, differentiate with respect x,

dy/dx = 1/x

By cross multiplication, we get,

x (dy/dx) = 1

Therefore, y = log x is a solution of the equation.

Then, x = 1

So, y = log (1) = 0

Hence, y(1) = 0

Question. 2

Solution:

From the question, it is given that,

Function, y = e^x

Now, differentiate with respect x,

dy/dx = e^x

dy/dx = y [given y = e^x]

Therefore, y = e^x is a solution of the equation.

Then, x = 0

So, y = e⁰ = 1

Hence, y(0) = 1

Question. 3

Solution:

From the question, it is given that,

Function, y = sin x … [equation (i)]

Now, differentiate with respect x,

dy/dx = cos x … [equation (ii)]

Then, the above equation is again differentiating with respect to x we get,

d²y/dx² = – sin x

From equation (i) y = sin x

So,

d²y/dx² = – y

Transposing we get,

d²y/dx² + y = 0

Therefore, y = sin x is a solution of the equation.

Then, substitute x = 0 in equation (i)

So, y = sin (0)

y = 0

Hence, y(0) = 0

Now, substitute x = 0 in equation (ii)

dy/dx = cos (0)

dy/dx = 1

Hence, (dy/dx) (0) = 1

Question. 4

Solution:

From the question, it is given that,

Function, y = e^x + 1 … [equation (i)]

Now, differentiate with respect x,

dy/dx = e^x

From equation (i), y = e^x + 1

Then, e^x = y – 1

dy/dx = y – 1 … [equation (ii)]

Then, the above equation is again differentiating with respect to x we get,

d²y/dx² = dy/dx

Transposing we get,

(d²y/dx²) – (dy/dx) = 0

Therefore, y = e^x + 1 is a solution to the equation.

Then, substitute x = 0 in equation (i)

So, y = e⁰ + 1

y = 1 + 1

y = 2

Hence, y(0) = 0

Now, substitute x = 0 in equation (ii)

dy/dx = e⁰ = 1

dy/dx = 1

Hence, (dy/dx) (0) = 1

Question. 5

Solution:

From the question, it is given that,

Function, y = e^-x + 2 … [equation (i)]

Now, differentiate with respect x,

dy/dx = – e^-x

From equation (i), y = e^-x + 2

Then, e^-x = y – 2

dy/dx = – (y – 2)

dy/dx = -y + 2

Transposing we get,

(dy/dx) + y = 2

Then, the above equation is again differentiating with respect to x we get,

d²y/dx² = dy/dx

Transposing we get,

(d²y/dx²) – (dy/dx) = 0

Therefore, y = e^-x + 2 is a solution of the equation.

Then, substitute x = 0 in equation (i)

So, y = e⁰ + 2

y = 1 + 2

y = 3

Hence, y(0) = 3

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 5

EXERCISE 22.5

Question. 1

Solution:

From the question, it is given that,

dy/dx = x² + x – (1/x)

Integrating on both sides, we get,

∫dy = ∫(x² + x – (1/x)) dx

We know that ∫ xⁿ dx = x^{(n + 1)}/(n + 1)

y = (x³/3) + (x²/2) – log x + c

Question. 2

Solution:

From the question, it is given that,

dy/dx = x⁵ + x² – (2/x)

Integrating on both sides, we get,

∫dy = ∫(x⁵ + x² – (2/x)) dx

We know that ∫ xⁿ dx = x^{(n + 1)}/(n + 1)

y = (x⁶/6) + (x³/3) – 2 log x + c

Question. 3

Solution:

From the question, it is given that,

dy/dx + 2x = e^3x

Transposing we get,

dy/dx = e^3x – 2x

Integrating on both sides, we get,

∫dy = ∫(e^3x – 2x) dx

We know that ∫ xⁿ dx = x^{(n + 1)}/(n + 1)

y = (e^3x/3) – (2x²/2) + c

y = (e^3x/3) – x² + c

Therefore, y + x² = 1/3 (e^3x) + c

Question. 4

Solution:

From the question, it is given that,

(x² + 1)dy/dx = 1

By cross multiplication,

dy = dx/(x² + 1)

Integrating on both sides, we get,

∫dy = ∫(dx/(x² + 1)

We know that ∫ dx/(x² + 1) = tan ^-1 x + c

Therefore, y = tan ^-1 x + c

Question. 5

Solution:

From the question, it is given that,

dy/dx = (1 – cos x)/(1 + cos x)

We know that (1 – cos x) = 2 sin² (x/2) and (1 + cos x) = 2 cos² (x/2)

So,

dy/dx = (2 sin² (x/2))/(2 cos² (x/2))

Also, we know that = sin θ/cos θ = tan θ

dy/dx = tan² (x/2)

By cross multiplication,

dy = tan² (x/2) dx

Integrating on both sides, we get,

∫dy = ∫tan² (x/2) dx

We know that, sec² x – 1 = tan² x

∫dy = ∫sec² (x/2) – 1 dx

y = 2 tan (x/2) – x + c

Therefore, y = 2 tan (x/2) – x + c

Question. 6

Solution:

From the question, it is given that,

(x + 2)dy/dx = x² + 3x + 7

By cross multiplication,

dy = [(x² + 3x + 7)/(x + 2)] dx

On dividing, we get,

dy = [x + 1 + (5/(x +2))] dx

Integrating on both sides, we get,

∫dy = ∫[x + 1 + (5/(x +2))] dx

Therefore, y = (x²/2) + x + 5 log (x + 2) + c

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 6

EXERCISE 22.6

Question. 1

Solution:

From the question, it is given that,

(dy/dx) + ((1 + y²)/y) = 0

Transposing we get,

dy/dx = – (1 + y²)/y

By cross multiplication,

(y/(1 + y²)) dy = – dx

Integrating on both sides, we get,

∫(y/(1 + y²)) dy = ∫-dx

∫(2y/(1 + y²)) dy = -2 ∫dx

log (1 + y²) = – 2x + c₁

Therefore, ½log [1 + y²] + x = c

Question. 2

Solution:

From the question, it is given that,

(dy/dx) = ((1 + y²)/y³)

By cross multiplication,

(y³/(1 + y²)) dy = dx

Integrating on both sides, we get,

∫(y – (y/(1 + y²)) dy = ∫dx

∫ydy – ∫(y/(1 + y²)) dy = ∫ dx

∫ydy – ½ ∫(2y/(1 + y²)) dy = ∫ dx

(y²/2) – ½ log [y² + 1] = x + c

Question. 3

Solution:

From the question, it is given that,

(dy/dx) = sin² y

By cross multiplication,

dy/sin² y = dx

We know that, (1/sin x) = cosec x

cosec² y dy = dx

Integrating on both sides, we get,

∫cosec² y dy = ∫dx + c

– cot y = x + c

Question. 4

Solution:

From the question, it is given that,

(dy/dx) = (1 – cos 2y)/(1 + cos 2y)

We know that, 1 – cos 2y = 2 sin²y and 1 + cos 2y = 2 cos² y

So, dy/dx = (2 sin² y)/(2 cos² y)

Also, we know that sin θ/cos θ = tan θ

By cross multiplication,

dy/tan² y = dx

Integrating on both sides, we get,

∫cot² y dy = ∫dx

∫ (cosec² y – 1) dy = ∫dx

– cot y- y + c = x

c = x + y + cot y

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 7

EXERCISE 22.7

Question. 1

Solution:

From the question, it is given that,

(x – 1)dy/dx = 2xy

By cross multiplication,

(1/y) dy = (2x/(x – 1)) dx

Integrating on both sides, we get,

∫(1/y) dy = ∫ (2x/(x – 1)) dx

∫(1/y) dy = ∫ [2 + (2/(x – 1))] dx

Log y = 2x + 2 log [x – 1] + c

Question. 2

Solution:

From the question, it is given that,

(1 + x²)dy = xy dx

By cross multiplication,

(1/y) dy = x/(x² + 1) dx

Integrating on both sides, we get,

∫(1/y) dy = ∫ x/(x² + 1) dx

∫(1/y) dy = ½ ∫ 2x/(x² + 1) dx

Log y = ½ log [x² + 1] + log c

Log y = log [C(√(x² + 1))]

y = C√(x² + 1)

Therefore, y = C √(x² + 1) is the required solution.

Question. 3

Solution:

From the question, it is given that,

dy/dx = (e^x + 1)y

Integrating on both side, we get,

∫(1/y) dy = ∫(e^x + 1) dx

Log y = e^x + x + c

Question. 4

Solution:

From the question, it is given that,

(x – 1)dy/dx = 2x³y

By cross multiplication,

(1/y) dy = (2x³/(x – 1)) dx

dy/y = 2[x² + x + 1 + (1/(x – 1))]dx

Integrating on both sides, we get,

∫(1/y) dy = ∫ 2[x² + x + 1 + (1/(x – 1))]dx

log y = 2[(x³/3) + (x²/2) + x + log (x – 1)] + c

log y = (2/3)x³ + x² + 2x + 2 log (x – 1) + c

Question. 5

Solution:

From the question, it is given that,

xy (y + 1)dy = (x² + 1) dx

By cross multiplication,

y (y + 1)dy = ((x² + 1)/x) dx

(y² + y)dy = ((x + (1/x)) dx

Integrating on both sides, we get,

∫(y² + y)dy = ∫(x + (1/x)) dx

(y³/3) + (y²/2) = (x²/2) + log x + c

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 8

EXERCISE 22.8

Question. 1

Solution:

From the question it is given that, dy/dx = (x + y + 1)² … [equation (i)]

Let us assume that, x + y + 1 = v

Differentiating with respect to x on both sides, we get,

1 + (dy/dx) = dv/dx

Transposing,

dy/dx = (dv/dx) – 1 … [equation (ii)]

Substituting equation (ii) in equation (i),

Then, (dv/dx) – 1 = v²

dv/dx = v² + 1

Now, taking like variables on the same side,

dv/(v² + 1) = dx

Integrating on both sides we get,

∫( dv/(v² + 1)) = ∫dx

We know that, ∫( dx/(a² + x²)) = (1/a) tan^-1 (x/a) + c

tan^-1 (v) + x + c

Substitute value of v we get,

tan^-1 (x + y + 1) = x + c

Question. 2

Solution:

From the question, it is given that (dy/dx) cos (x – y) = 1 … [equation (i)]

Let us assume that x – y = v

Differentiating with respect to x on both sides, we get,

1 – (dy/dx) = dv/dx

Transposing,

dy/dx = 1 – (dv/dx) … [equation (ii)]

Substituting equation (ii) in equation (i),

Then, 1 – (dv/dx) cos v = 1

1 – (dv/dx) = sec v

1 – sec v = dv/dx

Now, taking like variables on the same side,

dx = dv/(1 – sec v)

dx = (cos/(1 – cos v)) dv

dx = [((cos² (v/2)) – (sin² (v/2)))/(2 sin² (v/2))] dv

Integrating on both side we get,

∫dx = ∫[((cos² (v/2)) – (sin² (v/2)))/(2 sin² (v/2))] dv

We know that, ∫cosec² x = – cot x + c

∫dx = ∫(½ cot (v/2)) dv – ∫½ dv

2∫dx = ∫(cosec² (v/2) – 1) dv – ∫ dv

2x = – 2 cot (v/2) dv – v – v + c₁

2(x + v) = – 2 cot (v/2) + c₁

x + x – y = – cot ((x – y)/2) + c

c + y = cot ((x – y)/2)

Question. 3

Solution:

From the question, it is given that (dy/dx) = ((x – y) + 3)/(2(x – y) + 5) … [equation (i)]

Let us assume that x – y = v

Differentiating with respect to x on both sides, we get,

1 – (dy/dx) = dv/dx

Transposing,

dy/dx = 1 – (dv/dx) … [equation (ii)]

Substituting equation (ii) in equation (i),

Then, 1 – (dv/dx) = (v + 3)/(2v + 3)

Transposing we get,

dv/dx = 1 – ((v + 3)/(2v + 5))

dv/dx = (2v + 5 – v – 3)/(2v + 5)

dv/dx = (v + 2)/(2v + 5)

Now, taking like variables on the same side,

((2v + 5)/(v + 2))dv = dx

(((2v + 4) + 1)/(v + 2)) dv = dx

On dividing, we get,

(2 + (1/(v + 2))) dv = dx

Integrating on both side we get,

∫(2 + (1/(v + 2))) dv = ∫dx

We know that, ∫dx/x = log x + c and ∫adx = ax + c

2v + log [v + 2] = x + c

2(x – y) + log [x – y – 2] = x + c

Question. 4

Solution:

From the question, it is given that (dy/dx) = (x + y)² … [equation (i)]

Let us assume that x + y = v

Differentiating with respect to x on both side, we get,

1 + (dy/dx) = dv/dx

Transposing,

dy/dx = (dv/dx) – 1 … [equation (ii)]

Substituting equation (ii) in equation (i),

Then, (dv/dx) – 1 = v²

Transposing we get,

dv/dx = v² + 1

Now, taking like variables on the same side,

dv/(v² + 1) = dx

Integrating on both sides we get,

∫ (1/(v² + 1)) dv = ∫dx

tan^-1 v = x + c

tan^-1 (x + y) = x + c

x + y = tan (x + c)

Question. 5

Solution:

From the question it is given that, (x + y)² (dy/dx) = 1 … [equation (i)]

Let us assume that x + y = v

Differentiating with respect to x on both sides, we get,

1 + (dy/dx) = dv/dx

Transposing,

dy/dx = (dv/dx) – 1 … [equation (ii)]

Substituting equation (ii) in equation (i),

Then, v² ((dv/dx) – 1) = 1

dv/dx = (1/v²) + 1

dv/dx = (v² + 1)/v²

Now, taking like variables on the same side,

(v²/(v² + 1)) dv = dx

((v² + 1 – 1)/(v² + 1)) dv = dx

Integrating on both sides we get,

∫((v² + 1 – 1)/(v² + 1))dv = ∫dx

∫(1 – (1/(v² + 1))) dv = ∫dx

v – tan^-1 v = x + c

x + y – tan^-1 (x + y) = x + c

y – tan^-1 (x + c) = c

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 9

EXERCISE 22.9

Question. 1

Solution:

From the question it is given that, x² dy + y (x + y) dx = 0

The given differential equation can be written in standard form as,

dy/dx = – (y(x + y))/x²

So, it is a homogeneous equation,

Let us assume, y = vx and (dy/dx) = v + x (dv/dx)

Then, v + x (dv/dx) = – (vx (x + vx))/x²

v + x (dv/dx) = – v – v²

Transposing,

x (dv/dx) = – v – v – v²

x (dv/dx) = – 2v – v²

Now, taking like variables on the same side,

dv/(2v + v²) = – dx/x

Integrating on both sides we get,

∫(1/(2v + v²)dv = – ∫dx/x

∫(1/(v² + 2v + 1 – 1)dv = – ∫dx/x

We know that, (a + b)² = a² + 2ab + b²

∫(1/((v + 1)² – 1²)dv = – ∫dx/x

½ log [(v + 1 – 1)/(v + 1 + 1)] = – log x + log c

Log [v/(v + 2)]^1/2 = – log (c/x)

v/(v + 2) = c²/x²

((y/x)/((y/x) + 2)) = c²/x²

By simplification, we get,

y/(y + 2x) = c²/x²

yx² = (y + 2x) c²

Question. 2

Solution:

From the question, it is given that (dy/dx) = (y – x)/(y + x)

The given differential equation is a homogeneous equation,

Let us assume, y = vx and (dy/dx) = v + x (dv/dx)

v + x (dv/dx) = (vx – x)/(vx + x)

Then, v + x (dv/dx) = (v – 1)/(v + 1)

x (dv/dx) = ((v – 1)/(v + 1)) – v

x (dv/dx) = (v – 1 – v² – v)/(v + 1)

On dividing, we get,

x (dv/dx) = – (1 + v²)/(v + 1)

Now, taking like variables on the same side,

((v + 1)/(v² + 1)) = – dx/x

Integrating on both sides we get,

∫((v + 1)/(v² + 1)) dv = – ∫dx/x

∫(v/(v² + 1)) dv + ∫(1/(v² + 1)) dv = – ∫dx/x

½ ∫(2v/(v² + 1)) dv + ∫(1/(v² + 1)) dv = – ∫dx/x

½ log [v² + 1] + tan^-1 v = – log x + log c

Then, log [(y² + x²)/x²] + 2 tan^-1 (y/x) = 2 log (c/x)

log [x² + y²] – 2 log x + 2 tan^-1 (y/x) = 2 log (c/x)

log (x² + y²) + 2 tan^-1 (y/x) = 2 log c

log (x² + y²) + 2 tan^-1 (y/x) = k

Question. 3

Solution:

From the question, it is given that (dy/dx) = (y² – x²)/(2xy)

The given differential equation is a homogeneous equation,

Let us assume, y = vx and (dy/dx) = v + x (dv/dx)

v + x (dv/dx) = (v²x² – x²)/(2xvx)

Then, x (dv/dx) = ((v² – 1)/(2v)) – (v/1)

x (dv/dx) = (v² – 1 – 2v²)/(2v)

x(dv/dx) = (-1 – v²)/2v

Now, taking like variables on the same side,

((2v)/(v² + 1)) dv = – dx/x

Integrating on both sides we get,

∫((2v)/(v² + 1)) dv = – ∫dx/x

log (1 + v²) = – log x + log c

1 + v² = c/x

Now substitute the value of v,

1 + y²/x² = c/x

x² + y² = cx

Question. 4

Solution:

From the question it is given that, x (dy/dx) = (x + y)/x

The given differential equation can be written in standard form as,

dy/dx = (x + y)/x

So, it is a homogeneous equation,

Let us assume, y = vx and (dy/dx) = v + x (dv/dx)

dy/dx = v + x (dv/dx)

Then, v + x (dv/dx) = (x + vx)/x

v + x (dv/dx) = (x/x) + (vx/x)

v + x (dv/dx) = 1 + v

Now, taking like variables on the same side,

dv = dx/x

Integrating on both sides we get,

∫dv = ∫dx/x

v = log x + c

Now substitute the value of v,

y/x = log x + c

y = x log x + cx

Question. 5

Solution:

From the question it is given that, (x² – y²)dx – 2xy dy = 0

The given differential equation can be written in standard form as,

dy/dx = (x² – y²)/2xy

So, it is a homogeneous equation,

Let us assume, y = vx and (dy/dx) = v + x (dv/dx)

v + x (dv/dx) = (x² – v²x²)/(2xvx)

Then, x (dv/dx) = ((1 – v²)/(2v)) – (v/1)

x (dv/dx) = (1 – v² – 2v²)/(2v)

x(dv/dx) = (1 – 3v²)/2v

Now, taking like variables on the same side,

((2v)/(1 – 3v²)) dv = dx/x

Integrating on both sides we get,

∫((2v)/(1 – 3v²)) dv = – ∫dx/x

1/-3∫((-6v)/(1 – 3v²)) dv = – 3∫dx/x

log (1 – 3v²) = -3 log x + log c

1 – 3v² = c/x³

Now substitute the value of v,

x³ (1 – (3y²/x²)) = c/

x³ (x² – 3y²)/x² = c

x(x² – 3y²) = c

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 10

EXERCISE 22.10

Question. 1

Solution:

From the question, it is given that,

(dy/dx) + 2y = e^3x … [equation (i)]

The given linear differential equation is compared with (dy/dx) + py = Q

So, p = 2, Q = e^3x

IF = e^∫pdx

= e^∫2dx

= e^2x

Then, multiplying both sides of equation (i) by IF,

e^2x(dy/dx) + e^2x 2y = e^2x × e^3x

e^2x(dy/dx) + e^2x 2y = e^5x … [because a^m × aⁿ = a^{m + n}]

Now, integrating the above equation with respect to x,

ye^2x = ∫e^5x dx + c

ye^2x = (e^5x/5) + c

y = (e^5x/5) + ce^-2x

Question. 2

Solution:

From the question, it is given that,

4(dy/dx) + 8y = 5e^-3x

Dividing both sides by 4, we get,

dy/dx + 2y = 5e^-3x/4 … [equation (i)]

The given linear differential equation is compared with, (dy/dx) + py = Q

So, p = 2, Q = 5e^-3x/4

IF = e^∫pdx

= e^∫2dx

= e^2x

Then, multiplying both sides of equation (i) by IF,

e^2x(dy/dx) + e^2x 2y = e^2x × 5e^-3x/4

e^2x(dy/dx) + e^2x 2y = 5e^-x/4

Now, integrating the above equation with respect to x,

ye^2x = ∫5e^-x/4 dx+ c

ye^2x = (-5/4) e^-x + c

y = (-5/4) e^-3x + ce^-2x

Question. 3

Solution:

From the question, it is given that,

(dy/dx) + 2y = 6e^x … [equation (i)]

The given linear differential equation is compared with (dy/dx) + py = Q

So, p = 2, Q = 6e^x

IF = e^∫pdx

= e^∫2dx

= e^2x

Then, multiplying both sides of equation (i) by IF,

e^2x(dy/dx) + e^2x 2y = e^2x × 6e^x

e^2x(dy/dx) + e^2x 2y = 6e^3x … [because a^m × aⁿ = a^{m + n}]

Now, integrating the above equation with respect to x,

ye^2x = ∫6e^3x dx + c

ye^2x = (6/3) e^3x + c

y = 2e^3x + ce^-2x

Question. 4

Solution:

From the question, it is given that,

(dy/dx) + y = e^-2x … [equation (i)]

The given linear differential equation is compared with, (dy/dx) + py = Q

So, p = 1, Q = e^-2x

IF = e^∫pdx

= e^∫1dx

= e^x

Then, multiplying both sides of equation (i) by IF,

e^x(dy/dx) + e^x y = e^x × e^-2x

e^x(dy/dx) + e^x y = e^-x … [because a^m × aⁿ = a^{m + n}]

Now, integrating the above equation with respect to x,

ye^x = ∫e^-x dx + c

ye^x = e^-x/-1 + c

y = -e^-2x + ce^-x

Question. 5

Solution:

From the question, it is given that,

x(dy/dx) = x + y

dy/dx = (x + y)/x

dy/dx = 1 + (y/x) … [equation (i)]

The given linear differential equation is compared with (dy/dx) + py = Q

So, p = – 1/x, Q = 1

IF = e^∫pdx

= e^∫-1/xdx

= e^{-log x}

= e^log(1/x)

= 1/x

Then, multiplying both sides of equation (i) by IF,

Y(1/x) = ∫1 (1/x) dx + c

ye^x = log x + c

y = x log x + cx

Access RD Sharma Solutions for Class 12 Maths Chapter 22 Exercise 11

EXERCISE 22.11

Question. 1

Solution:

From the question, it is given that,

Initial radius of balloon = 1 unit

After 3 seconds radius of the balloon = 2 units

So, let us assume A be the surface area of the balloon,

(dA/dt) ∝ t

Then,

dA/dt = λt

d(4πr²)/dt = λt

8πr (dr/dt) = λt

Integrating on both sides we get,

8π ∫rdr = λ ∫t dt

8π (r²/2) = (λt²/2) + c

4πr² = (λt²/2) + c …. … [equation (i)]

From question, r = 1 unit when t = 0,

4π (1)² = 0 + c

4π = c

From equation (i) c = 4πr² – (λt²/2)

Then, 4πr² = (λt²/2) + 4π … [equation (ii)]

And also form question, given r = 2 units when t = 3 sec

4π(2)² = (λ(3)²/2) + 4π

16π = (9/2) λ + 4π

(9/2) λ = 12π

By cross multiplication, we get,

λ = (24/9) π

λ = (8/3) π

So, now equation (ii) becomes,

4πr² = (8π/6) t² + 4π

4π (r² – 1) = (4/3) πt²

By cross multiplication,

r² – 1 = (1/3) t²

r² = 1 + (1/3)t²

r = √(1 + (1/3)t²)

Question. 2

Solution:

From the question, it is given that,

Population grows at the rate of 5% per year.

So, let us assume the population after time t is p and the initial population is P_o,

(dp/dt) = 5% × P

Then,

dP/dt = P/20

By cross multiplication, we get,

20 (dP/P) = dt

Integrating on both sides we get,

20 ∫(dP/P) = ∫ dt

20 log P = t + c …. … [equation (i)]

From question, P = P_o unit when t = 0,

20 log (P_o) = 0 + c

20log(P/P_o) = c

Then, equation (i) becomes,

20 log (P) = t + 20 log (P_o)

By cross multiplication, we get,

20 log (P/P_o) = t

Let time is t, when P = 2P_o,

Then, 20 log (2P/2P_o) = t₁

t₁ = 20 log 2

Therefore, the time period required is 20 log 2 years.

Question. 3

Solution:

From the question, it is given that,

The present population is 1,00,000

Then, the population of the city doubled in the past 25 years,

So, let us assume P be the surface area of the balloon,

(dP/dt) ∝ P

Then,

dP/dt = λP

dP/dt = λ dt

Integrating on both sides, we get,

∫ dP/dt = λ ∫ dt

Log P = λt + c … [equation (i)]

From question, P = P_o t when t = 0,

log (P_o) = 0 + c

c = log (P_o)

Then, equation (i) becomes,

log (P) = λt + log (P_o)

log (P/P_o) = λt … [equation (ii)]

And also form question, given P = 2P_o when t = 25

log (2P_o/P_o) = 25λ

log 2 = 25λ

By cross multiplication, we get,

λ = log2/25

So, now equation (ii) becomes,

log (P/P_o) = (log2/25)t

let us assume that t₁ be the time to become population 5,00,000 from 1,00,000,

Then, log (5,00,000/1,00,000) = (log2/25) t₁

By cross multiplication, we get,

t₁ = 25 log 5/log 2

= 25(1.609)/(0.6931)

= 58

Therefore, the required time is 58 years.

Question. 4

Solution:

From the question, it is given that,

The bacteria count is 1,00,000

The number is increased by 10% in 2 hours.

So, let us assume C be the surface area of the balloon,

(dC/dt) ∝ C

Then,

dC/dt = λC

dC/dt = λ dt

Integrating on both sides we get,

∫ dC/dt = λ ∫ dt

Log C = λt + log k … [equation (i)]

From question, t = 0 when c = 1,00,000,

log (1,00,000) = λ × 0 + log k … [equation (ii)]

log (1,00,000) = log k … [equation (iii)]

And also form question, given t = 2, c = 1,00,000 + 1,00,000 × (10/100) = 110000

So, from equation (i) we have,

log 110000 = λ × 2 + log K … [equation (iv)]

Now, subtracting equation (ii) from equation (iv), we have,

Log 110000 – log 100000 = 2 λ

Then, log 11 × 10000 – log 10 × 10000 = 2 λ

Log ((11 × 10000)/(10 × 10000)) = 2λ

Log (11/10) = 2λ

So, λ = ½ log (11/10) … [equation (v)]

Now we need to find the time ‘t’ in which the count reaches 200000.

Then, substituting the values of λ and k from equations (iii) and (v) in equation (i),

Log 200000 = ½ log (11/10)t + log 100000

½ log (11/10)t = log 200000 – log 100000

½ log (11/10)t = log (200000/100000)

½ log(11/10)t = log 2

Therefore, the required time t = 2log2/log(11/10) hours.

Question. 5

Solution:

From the question, it is given that,

The interest is compounded continuously at 6% per annum

So, let us assume P is the principal,

(dP/dt) = Pr/100

Then,

dP/dt = (r/100) dt

Integrating on both sides, we get,

∫ dP/P = ∫ r/100 dt

Log P = (rt/100) + c … [equation (i)]

Let us assume P_o is the initial principal at t = 0

log (P_o) = 0 + C

C = log (P_o)

Now, substitute the value of C in equation (i)

log (P) = rt/100 + log (P_o)

log (P/P_o) = rt/100

Now in case 1:

P_o = 1000, t = 10 years and r = 6

log (P/1000) = (6 × 10)/100

log P – log 1000 = 0.6

log P = loge^0.6 + log 1000

Taking log common in both terms,

log P = log (e^0.6 + 1000)

log P = log (1.822 + 1000)

log P = log 1822

Then,

P = ₹ 1822

₹ 1000 will be ₹ 1822 after 10 years,

Now in case 2:

Let us assume t₁ is the time to double ₹ 1000,

P = 2000, P_o = 1000, r = 6%

log (P/P_o) = rt/100

log (2000/1000) = 6t₁/100

(100 log2)/6 = t₁

(100 × 0.6931)/6 = t₁

t₁ = 11.55 years

Therefore, it will take approximately 12 years to double