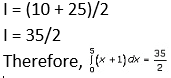Chapter 20 DEFINITE INTEGRALS

Access RD Sharma Solutions for Class 12 Maths Chapter 20 Exercise 1

EXERCISE 20.1

Question. 1

Solution:

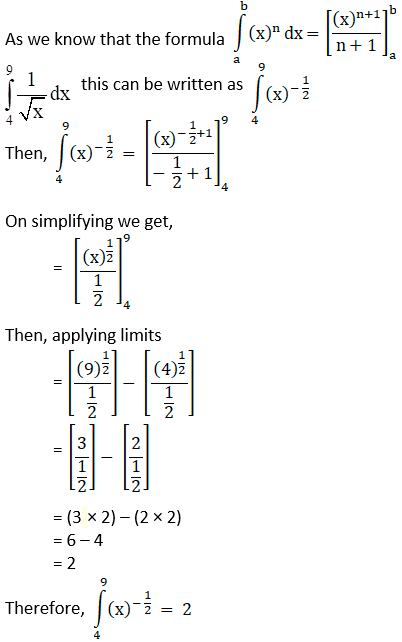
Question. 2

Solution:

Question. 3

Solution:

Let us assume that x = sin θ,

dx = cos θ dθ

Then, substitute x = 0

θ = 0

Again substitute x = ½

θ = π/6

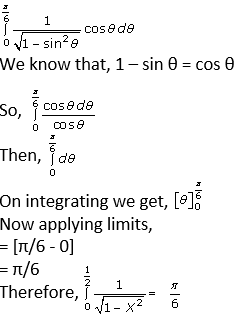
Question. 4

Solution:

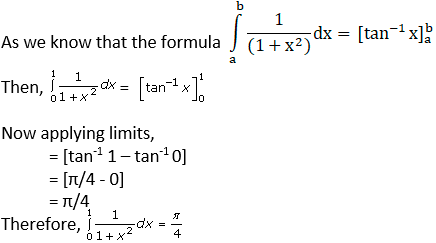
Question. 5

Solution:

Let us assume that x² + 1 = t

Then, 2x dx = dt

x dx = dt/2

Now substitute x = 2

t = 5

Again substitute x = 3

t = 10

Then,

Access RD Sharma Solutions for Class 12 Maths Chapter 20 Exercise 2

EXERCISE 20.2

Question. 1

Solution:

Question. 2

Solution:

Let us assume 1 + log x = t

Then differentiating w.r.t. x, we get

(1/x) dx = dt

Now substitute x = 1

t = 1

Again substitute x = 2

t = 1 + log 2

Then given question becomes,

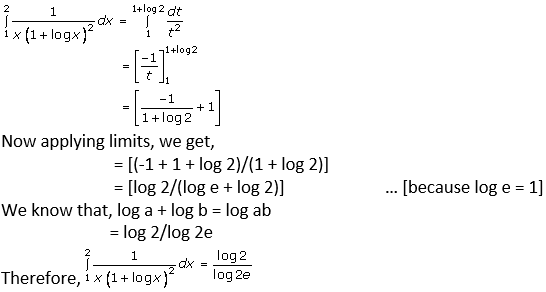
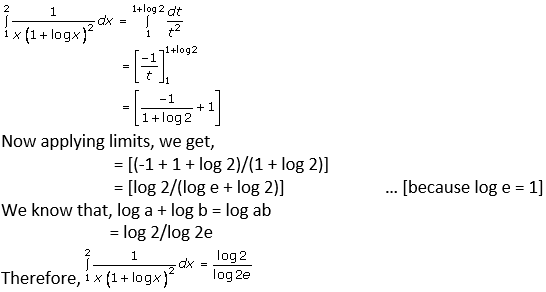
Question. 3

Solution:

Let us assume that 9x² – 1 = t

Then, differentiating w.r.t. x, we get,

18x dx = dt

Dividing both sides by 6, we get

3x dx = dt/6

So, substitute x = 1

t = 8

Again substitute x = 2

t = 35

Then, the given question becomes,

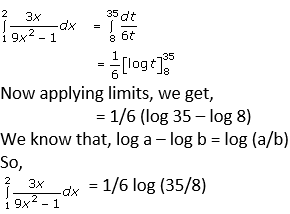
Question. 6

Solution:

Let us assume that, e^x = t

Then, differentiating w.r.t. x, we get,

e^x dx = dt

So, substitute x = 0

t = 1

Again substitute x = 1

t = e

Then, the given question becomes,

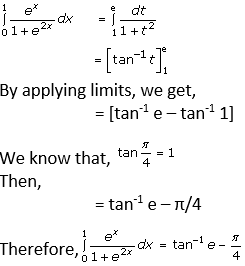
Question. 7

Solution:

Let us assume that x² = t

Then, differentiating w.r.t. x, we get,

2x dx = dt

So, substitute x = 0

t = 0

Again substitute x = 1

t = 1

Then, the given question becomes,

Access RD Sharma Solutions for Class 12 Maths Chapter 20 Exercise 3

EXERCISE 20.3

Question. 1(i)

Solution:

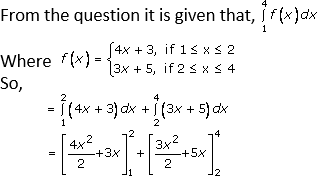
Then, applying limits, we get,

= [((16/2) + 6) – ((4/2) + 3)] + [((48/2) + 20) – ((12/2) + 10)]

= [(8 + 6) – (2 + 3)] + [(24 + 20) – (6 + 10)]

= [14 -5] + [44 – 16]

= 9 + 28

= 37

Question. 1(ii)

Solution:

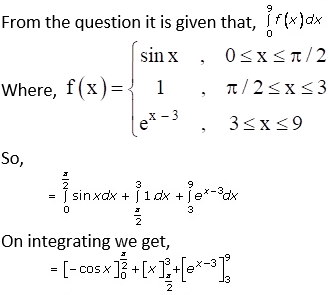
Then, applying limits, we get,

= [- cos (π/2) + cos 0] + [3 – (π/2)] + [e^{9 – 3} – e^{3 – 3}]

= [0 + 1] + [3 – (π/2)] + [e⁶ – e⁰]

= 0 + 1 + 3 – (π/2) + e⁶ – e⁰

= 1 + 3 – (π/2) + e⁶ – 1

= 3 – π/2 + e⁶

Question. 1(iii)

Solution:

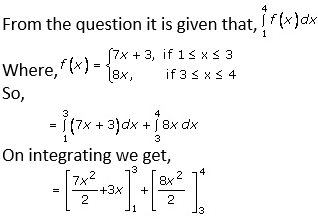
Then, applying limits, we get,

= [(((7 × 9)/2) + (3 × 3)) – (((7 × 1)/2) + (3 × 1))] + [(((8 × 16)/2) – ((8 × 9)/2))]

= [(63/2) + 9 – (7/2) – 3] + [64 – 36]

= 34 + 28

= 62

Question. 2

Solution:

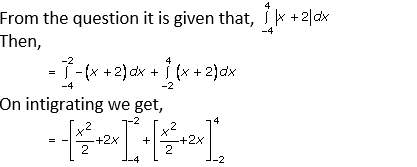
Now, applying limits,

= – [((4/2) – 4) – ((16/2) – 8)] + [((16/2) + 8) – ((4/2) – 4)]

= – [(2 – 4) – (8 – 8)] + [(8 + 8) – (2 – 4)]

= – [- 2 – 0] + [16 – (- 2)]

= – [-2] + [16 + 2]

= 2 + 18

= 20

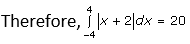
Question. 3

Solution:

Question. 4

Solution:

Question. 5

Solution:

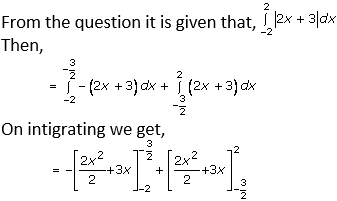
Now, applying limits we get,

= – [((18/8) – (9/2)) – ((8/2) – 6)] + [((8/2) + 6) – ((18/8) – (9/2))]

= – [((9/4) – (9/2)) – ((4/1) – 6)] + [((4/1) + 6) – ((9/4) – (9/2))]

= – [((9/4) – (9/2)) – (- 2)] + [(10) + (9/4)]

= – [(- 9/4) + 2] + [10 + (9/4)]

= 9/4 – 2 + 10 + 9/4

= 18/4 + 8

= 9/2 + 8

= (9 + 16)/2

= 25/2

Access RD Sharma Solutions for Class 12 Maths Chapter 20 Exercise 4

EXERCISE 20.4

Question. 1

Solution:

Question. 2

Solution:

Question. 3

Solution:

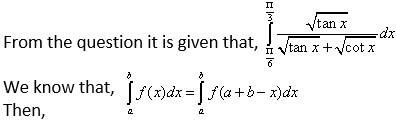
Now applying limits, we get,

2I = π/3 – π/6

2I = (2π – π)/6

2I = π/6

I = π/12

Question. 4

Solution:

Now applying limits, we get,

2I = π/3 – π/6

2I = (2π – π)/6

2I = π/6

I = π/12

Question. 6

Solution:

Access RD Sharma Solutions for Class 12 Maths Chapter 20 Exercise 5

EXERCISE 20.5

Question. 1

Solution:

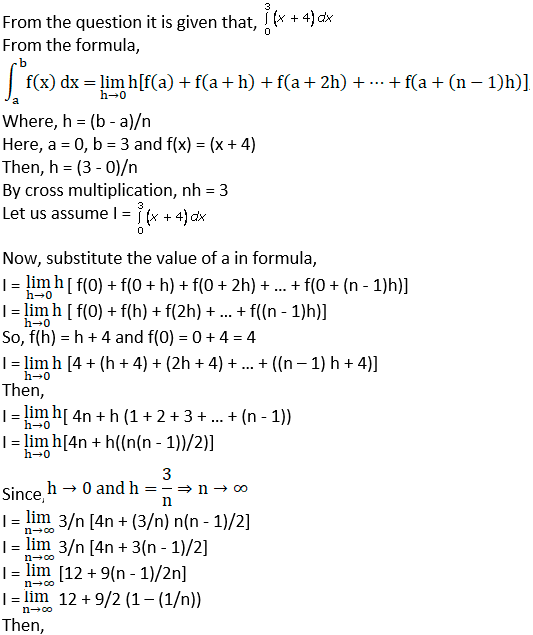
I = 12 + 9/2 (1 – 1/∞)

I = 12 + (9/2) (1 – 0)

I = 12 + (9/2)

I = (24 + 9)/2

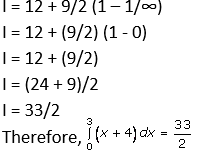
Question. 2

Solution:

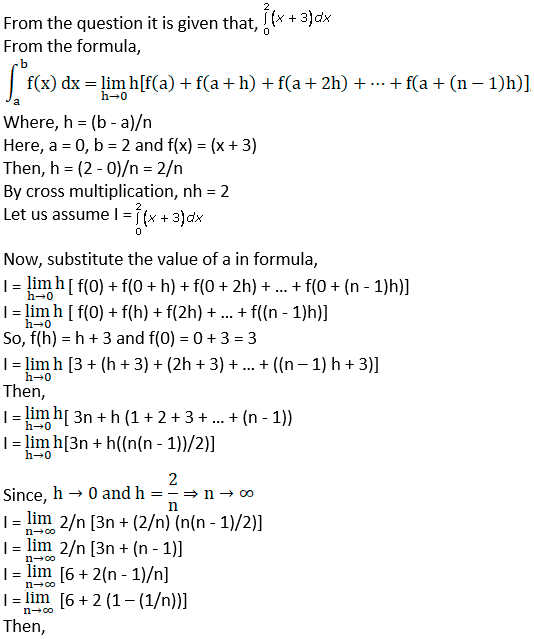
I = 6 + 2 (1 – 1/∞)

I = 6 + 2 (1 – 0)

I = 6 + 2

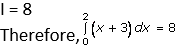
Question. 3

Solution:

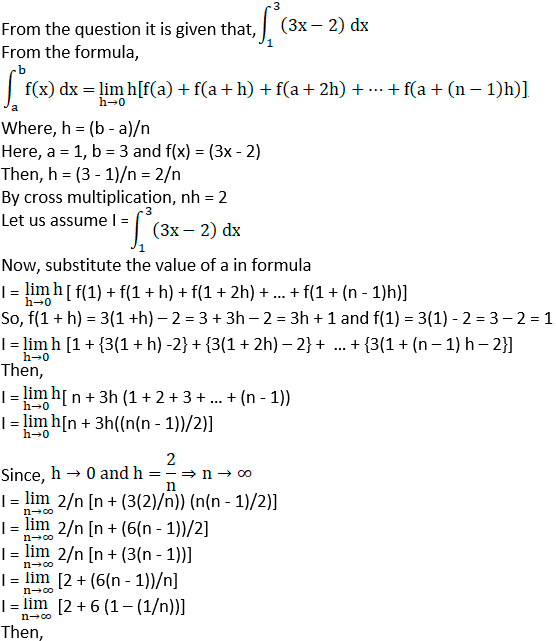
I = 2 + 6 (1 – 1/∞)

I = 2 + 6 (1 – 0)

I = 2 + 6

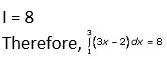
Question. 4

Solution:

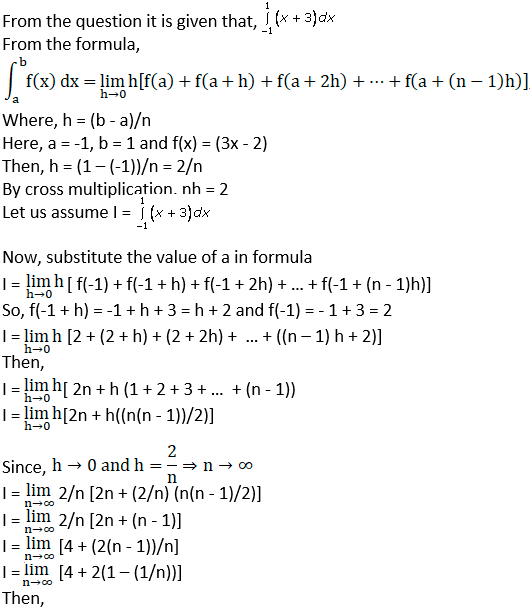
I = 4 + 2 (1 – 1/∞)

I = 4 + 2 (1 – 0)

I = 4 + 2

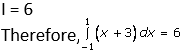
Question. 5

Solution:

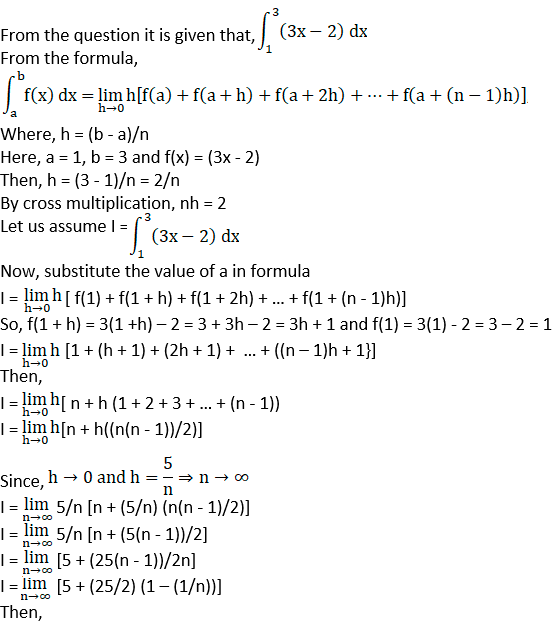
I = 5 + (25/2) (1 – 1/∞)

I = 5 + (25/2) (1 – 0)

I = 5 + 25/2