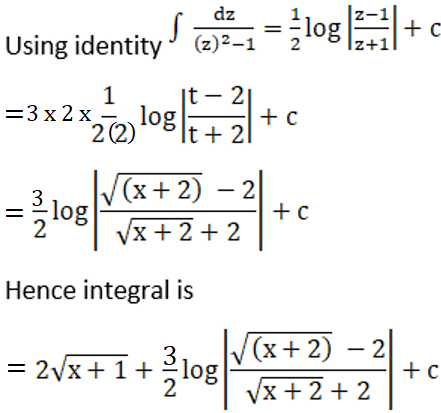Chapter 19 INDEFINITE INTEGRALS
Class 12th Maths R D Sharma Solution
Access answers to Maths RD Sharma Solutions For Class 12 Chapter 19 – Indefinite Integrals
Exercise 19.1 Page No: 19.4
1. Evaluate the following integrals:
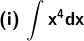
Solution:
Given
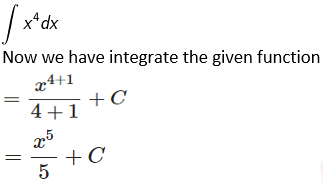
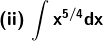
Solution:
Given
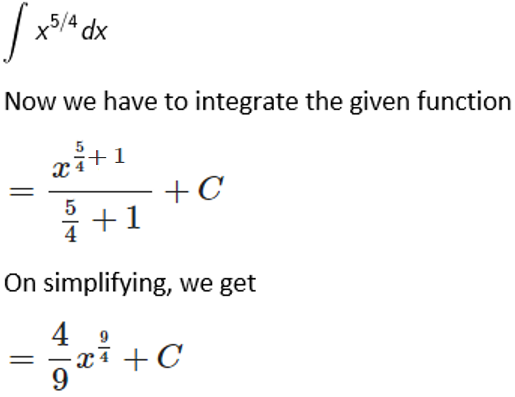
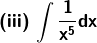
Solution:
Given
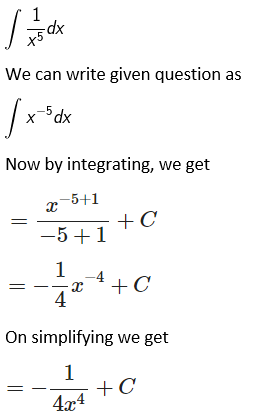
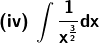
Solution:
Given
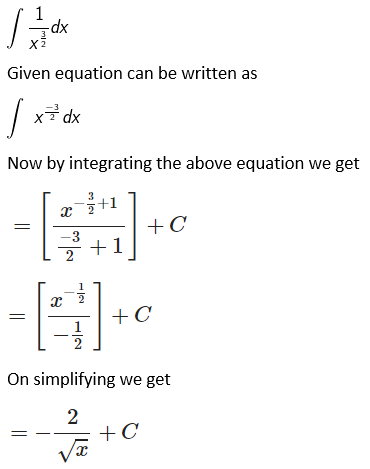
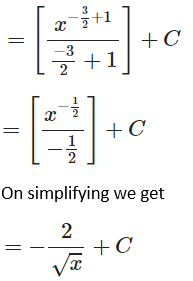
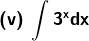
Solution:
Given

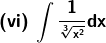
Solution:
Given
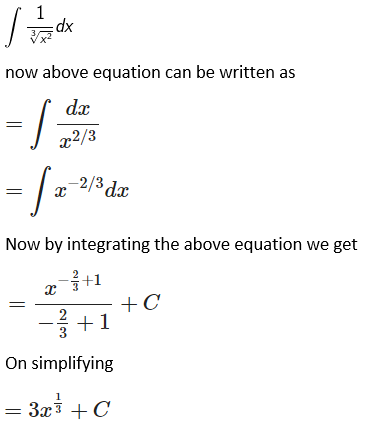
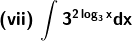
Solution:
Given
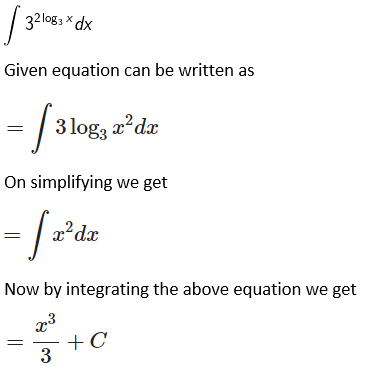

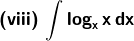
Solution:
Given
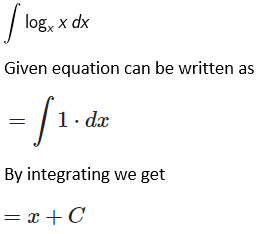
2. Evaluate:
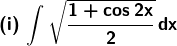
Solution:
Given
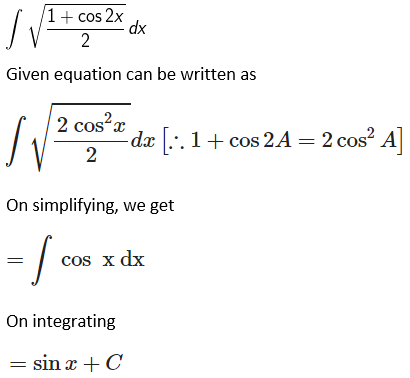
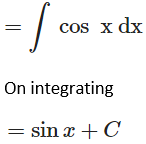
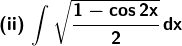
Solution:
Given
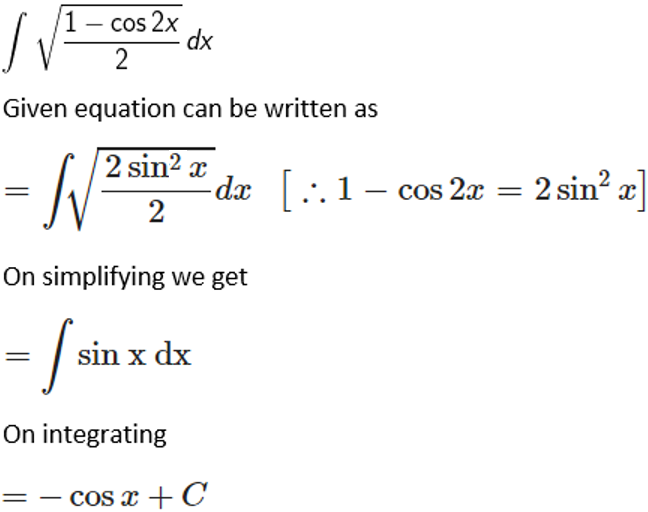
3. Evaluate:
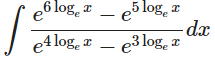
Solution:
Given
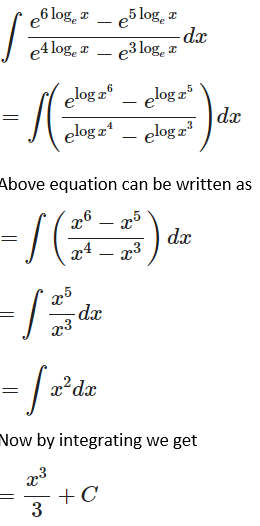
Exercise 19.2 Page No: 19.14
Evaluate the following integrals (1 – 44):
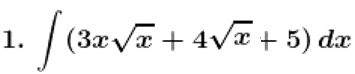
Solution:
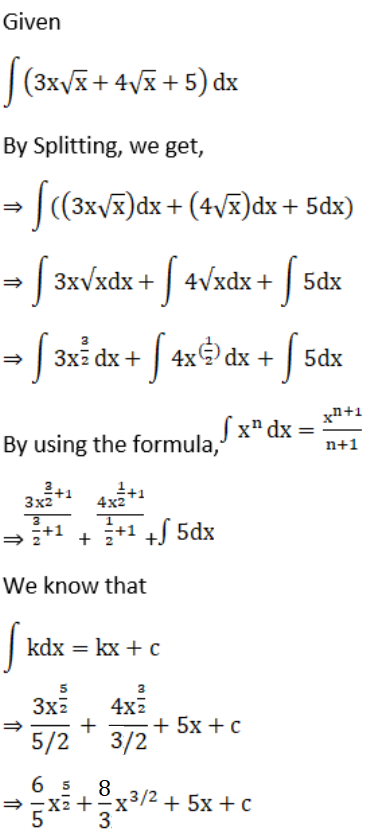
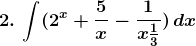
Solution:
Given

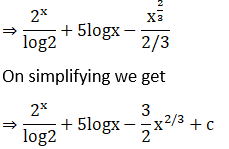
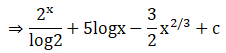
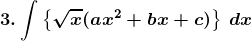
Solution:
Given
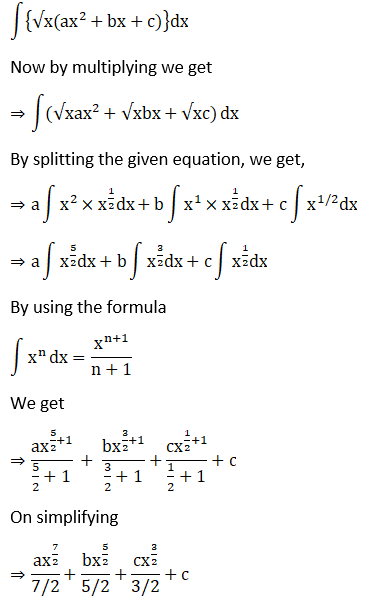
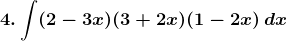
Solution:
Given,
∫(2 – 3x)(3 + 2x)(1 – 2x) dx
= ∫(6 + 4x – 9x – 6x2)(1 – 2x) dx
= ∫(6 – 5x – 6x2)(1 – 2x) dx
= ∫(6 – 5x – 6x2 – 12x + 10x2 + 12x3) dx
= ∫(6 – 17x + 4x2 + 12x3) dx
Upon splitting the above, we have
= ∫6 dx – ∫17x dx + ∫4x2 dx + ∫12x3 dx
On integrating using formula,
∫xn dx = xn+1/n+1
we get
= 6x – 17/(1+1) x1+1 + 4/(2+1) x2+1 + 12/(3+1) x3+1 + c
= 6x – 17x2/2 + 4x3/3 + 3x4 + c
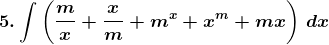
Solution:
Given
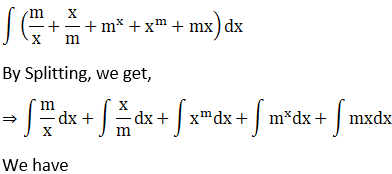

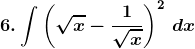
Solution:
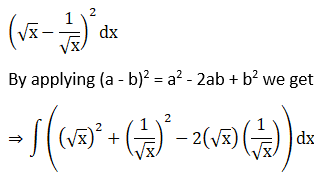

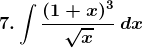
Solution:
Given
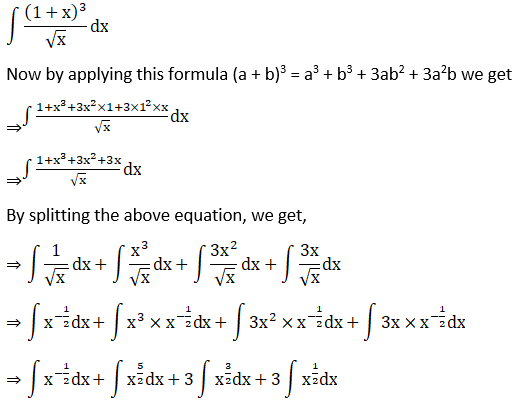
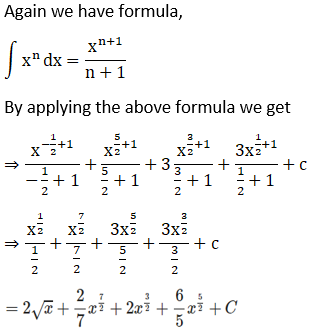
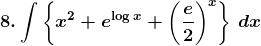
Solution:
Given
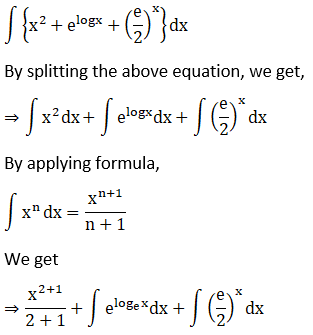
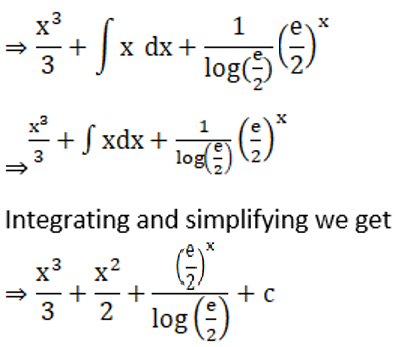
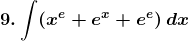
Solution:
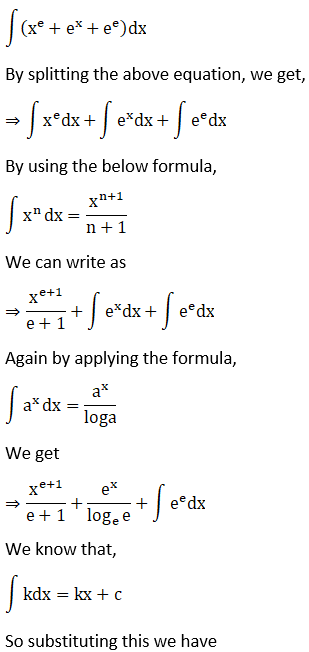
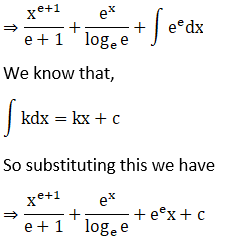
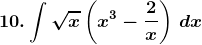
Solution:
Given

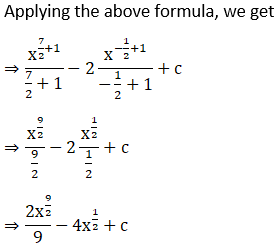
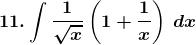
Solution:
Given
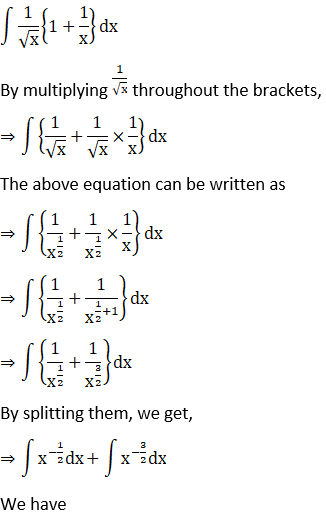
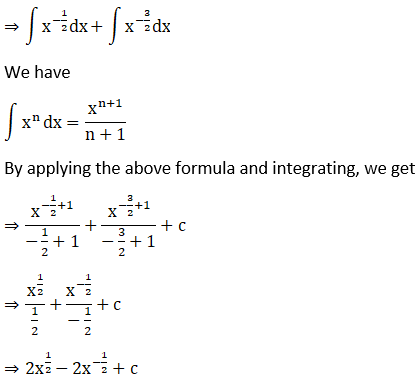
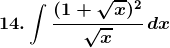
Solution:
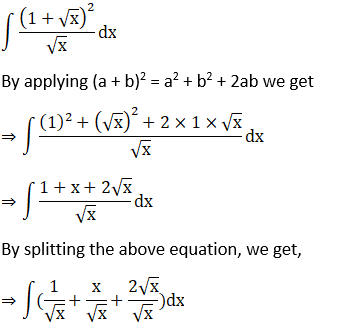
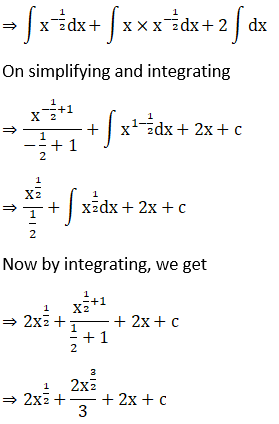
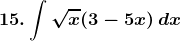
Solution:
Given
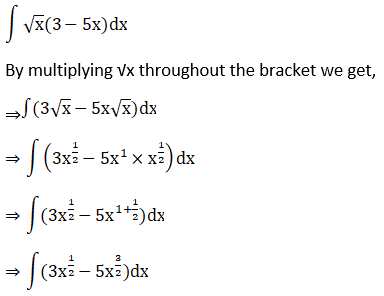

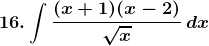
Solution:
Given
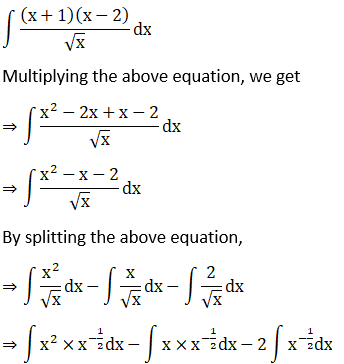
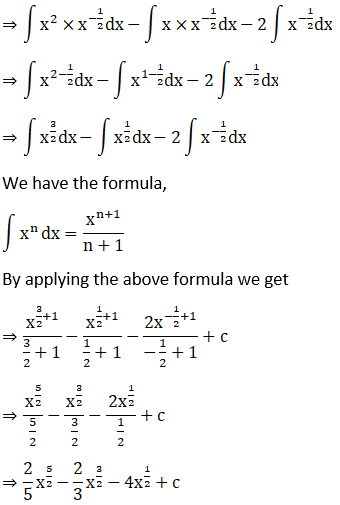
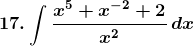
Solution:
Given
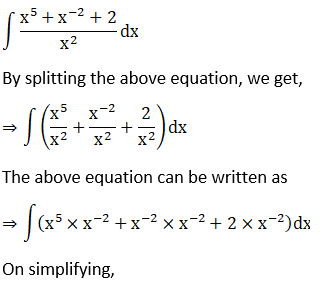

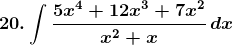
Solution:
Given
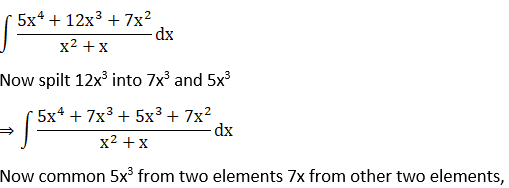
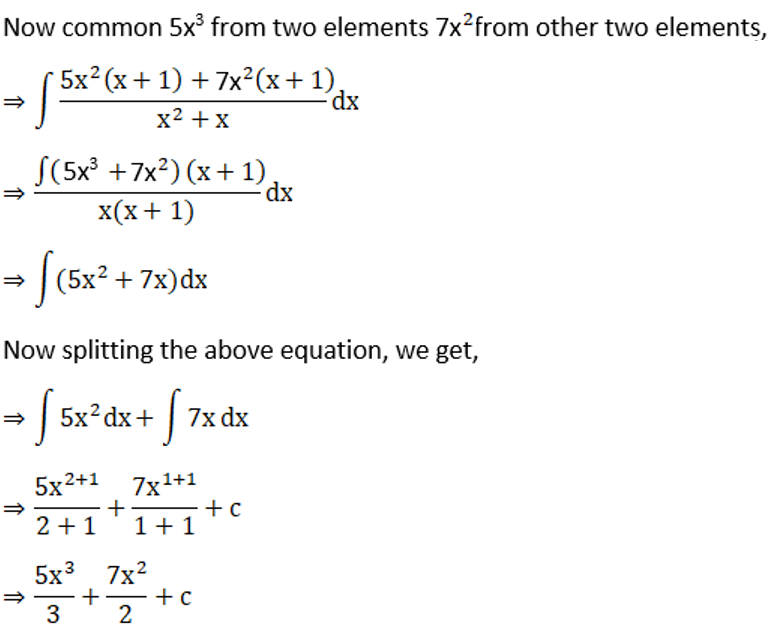
Exercise 19.3 Page No: 19.23
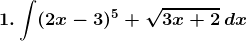
Solution:
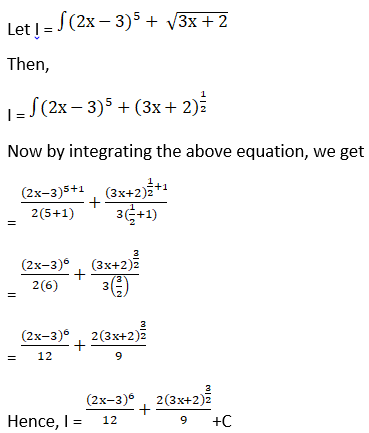
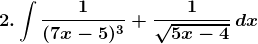
Solution:
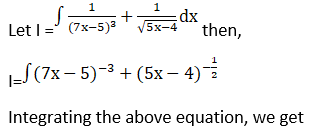
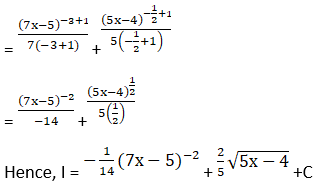
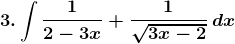
Solution:
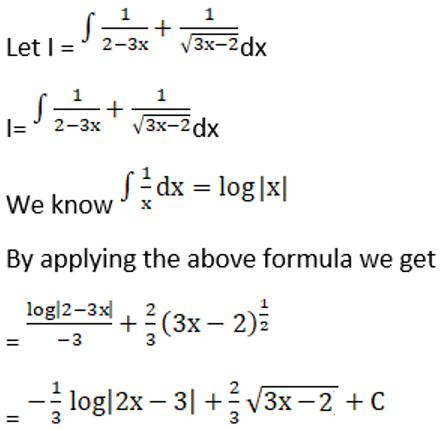
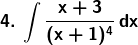
Solution:
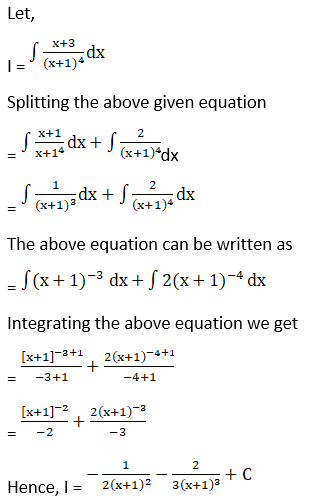
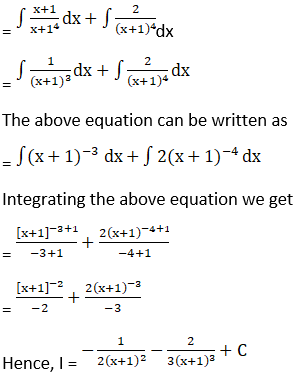
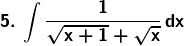
Solution:

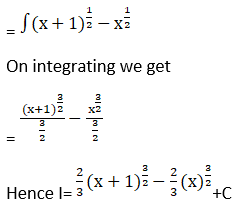
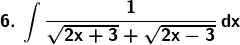
Solution:
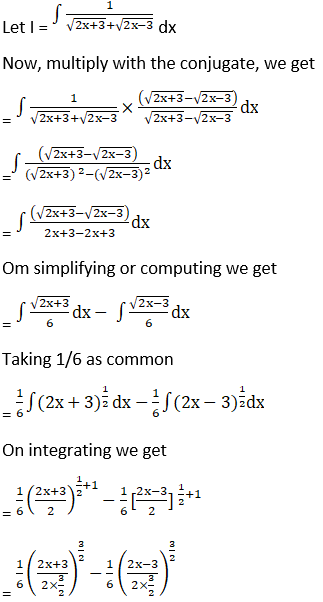
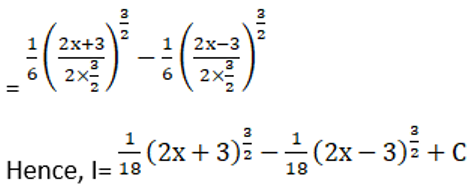
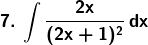
Solution:
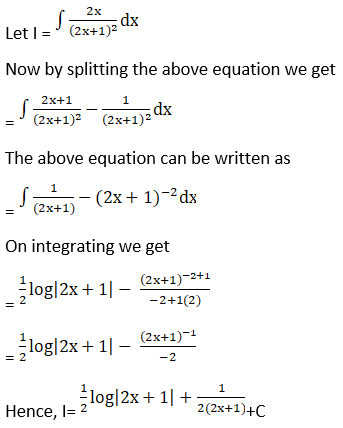
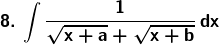
Solution:
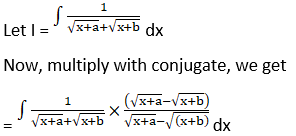
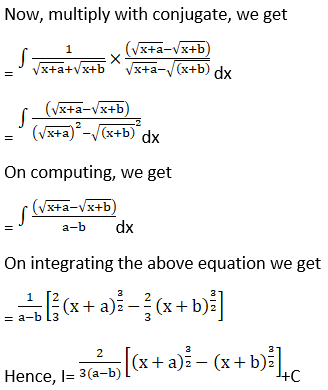
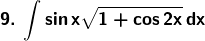
Solution:
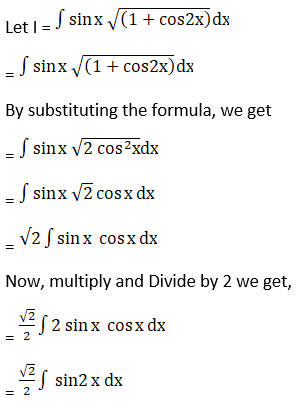
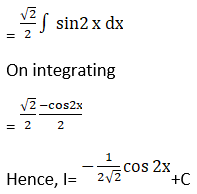
Exercise 19.4 Page No: 19.30
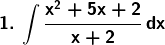
Solution:

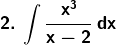
Solution:

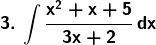
Solution:
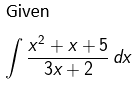

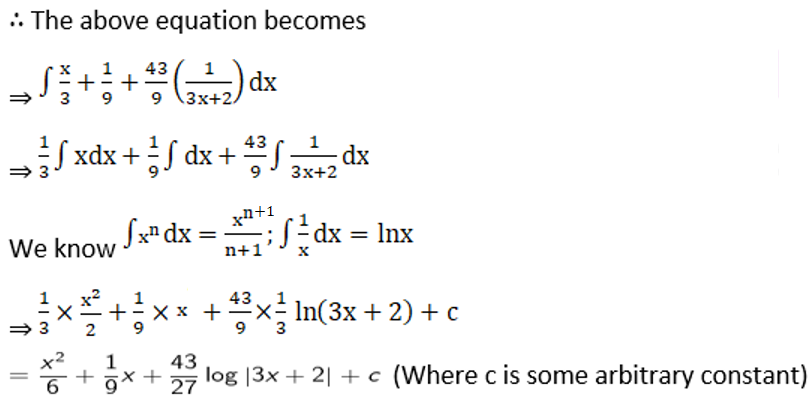
Exercise 19.5 Page No: 19.33
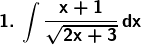
Solution:
Given

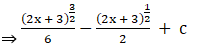
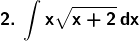
Solution:

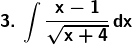
Solution:

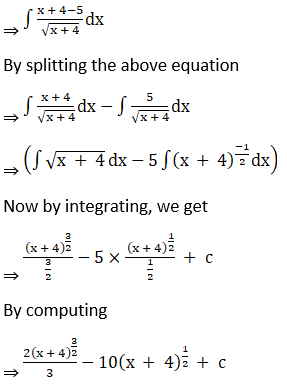
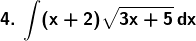
Solution:

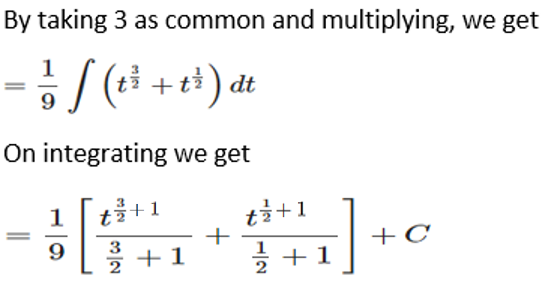

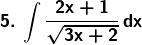
Solution:


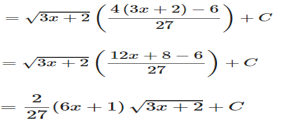
Exercise 19.6 Page No: 19.36
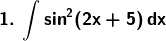
Solution:
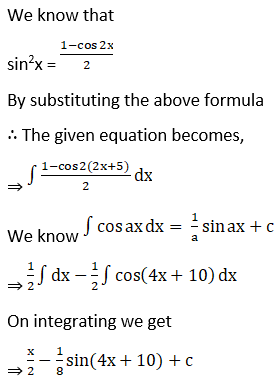
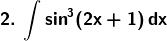
Solution:
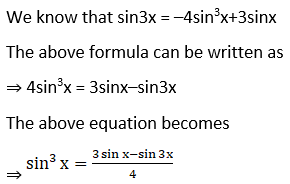
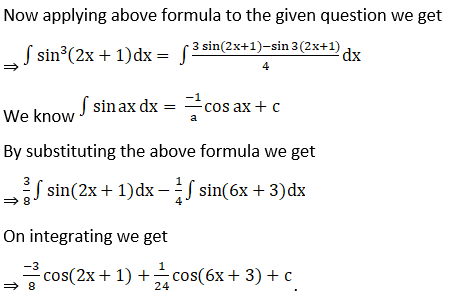
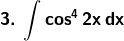
Solution:

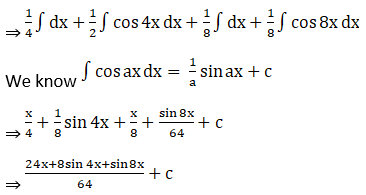
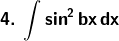
Solution:
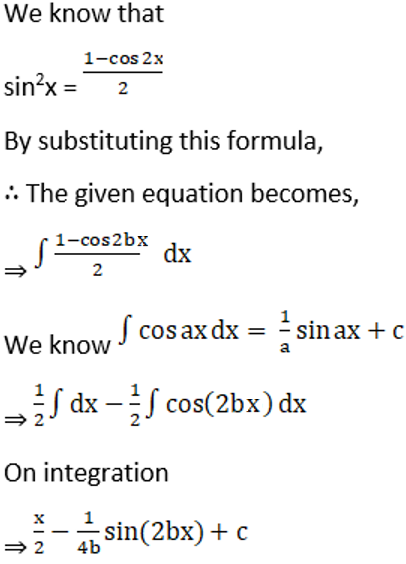
Exercise 19.7 Page No: 19.38
Integrate the following integrals:
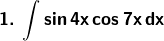
Solution:

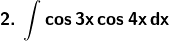
Solution:
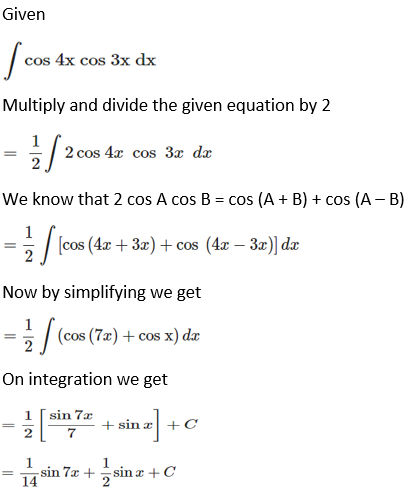
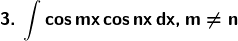
Solution:
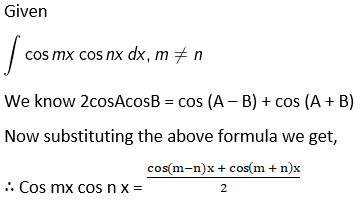
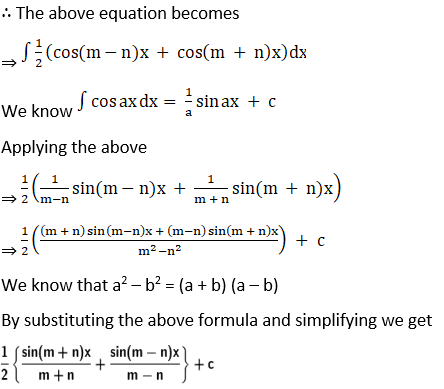
Exercise 19.8 Page No: 19.47
Evaluate the following integrals:
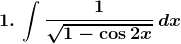
Solution:
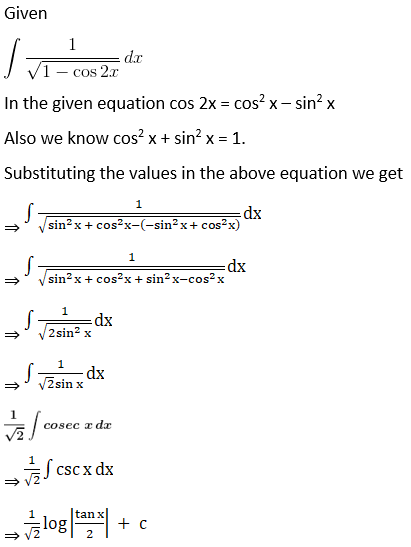
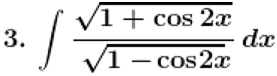
Solution:
Given,
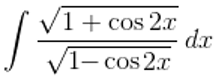

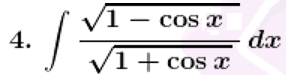
Solution:
Given,
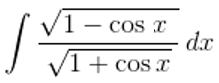
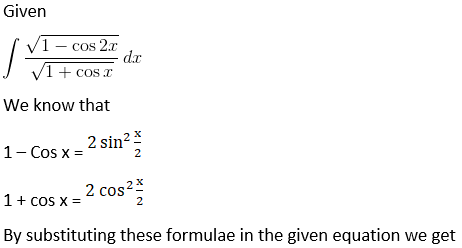
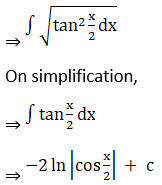
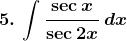
Solution:
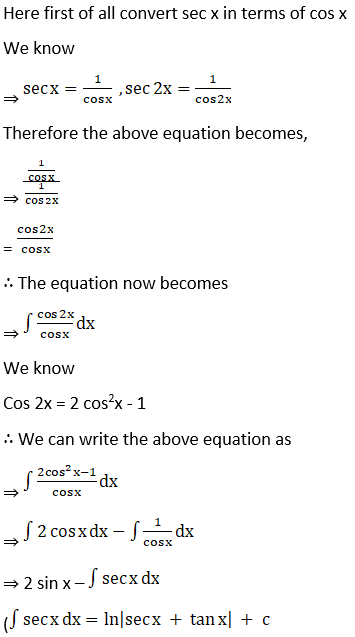
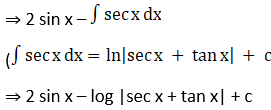
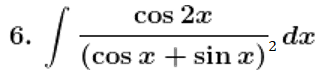
Solution:
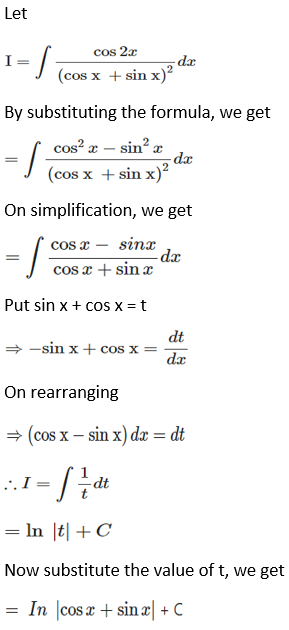
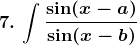
Solution:

Therefore,
= cos (b – a)x + sin(b – a) log |sin(x – b)| + c, where c is an arbitrary constant.
Exercise 19.9 Page No: 19.57
Evaluate the following integrals:
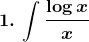 dx
dx
Solution:

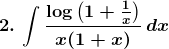
Solution:
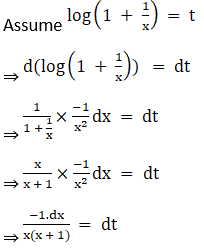
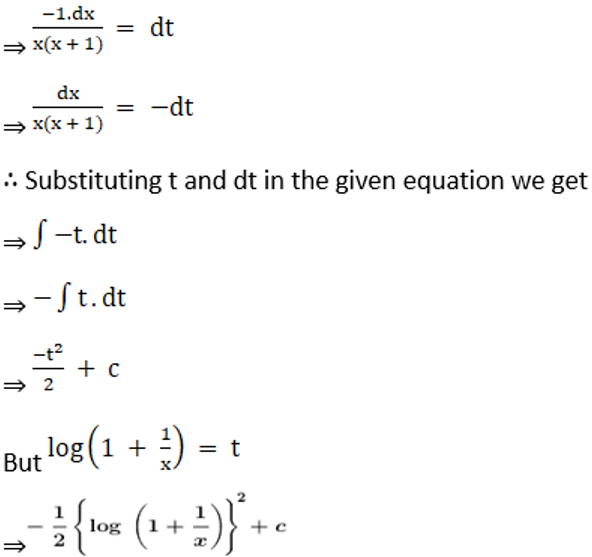
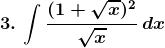
Solution:
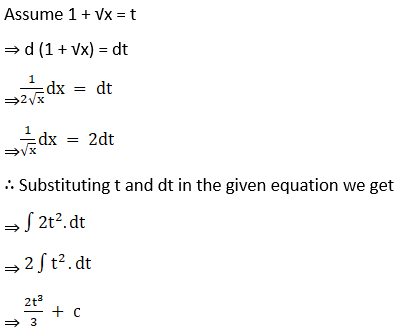
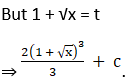
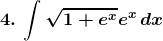
Solution:

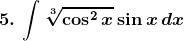
Solution:
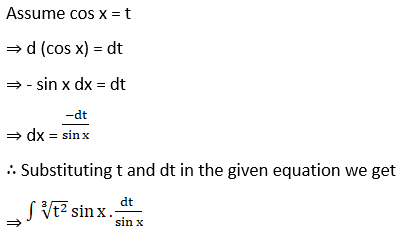
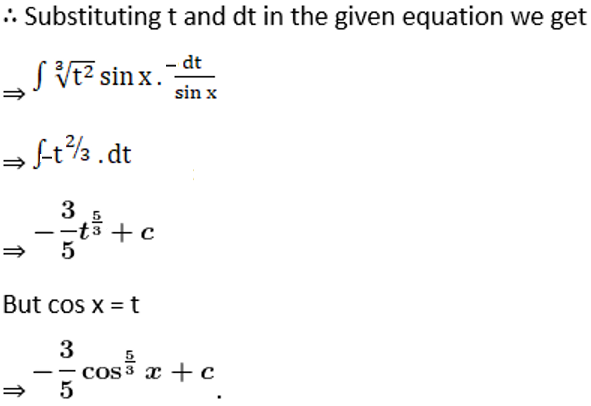
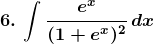
Solution:

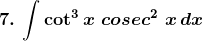
Solution:
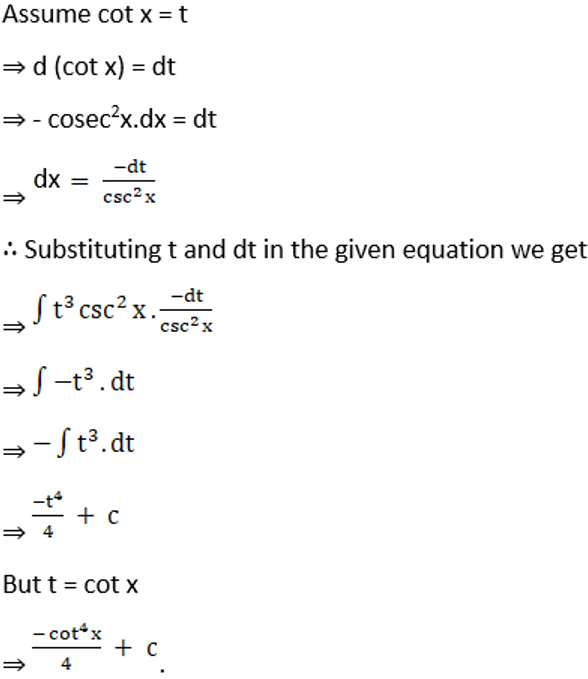
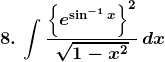
Solution:

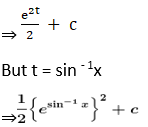
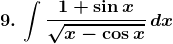
Solution:
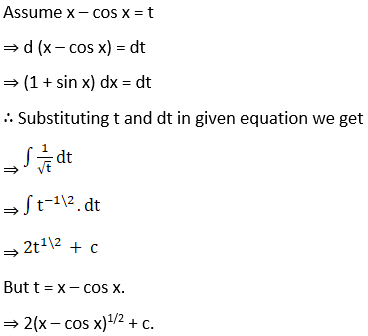
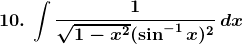
Solution:

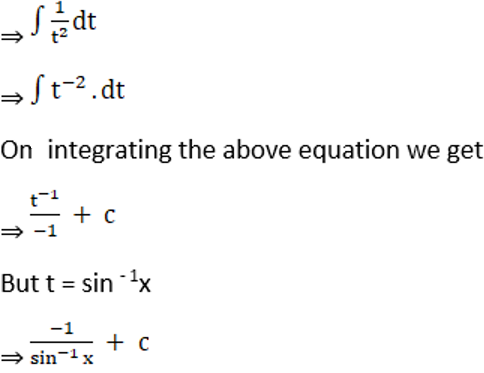
Exercise 19.10 Page No: 19.65
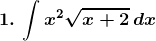
Solution:
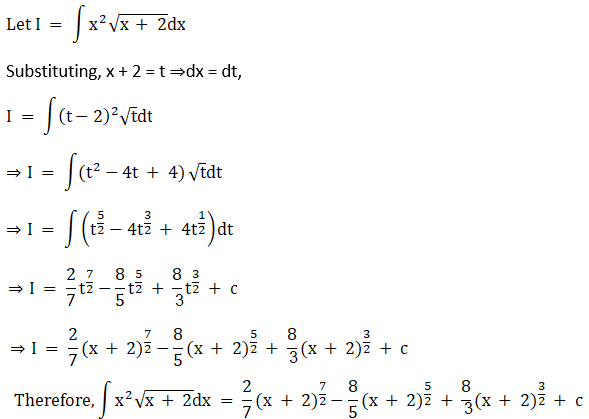
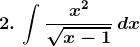
Solution:
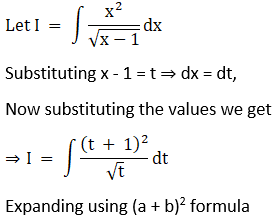

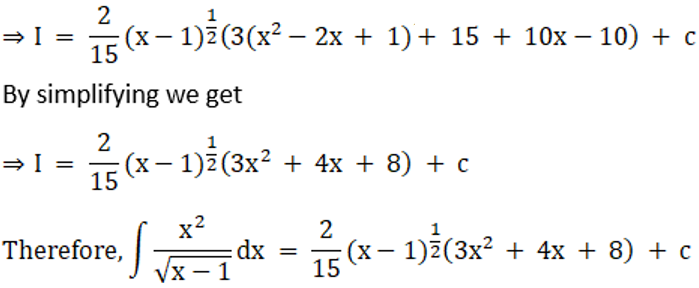
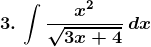
Solution:

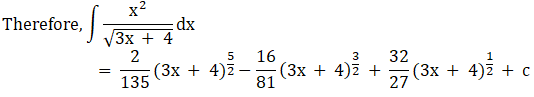
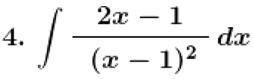
Solution:

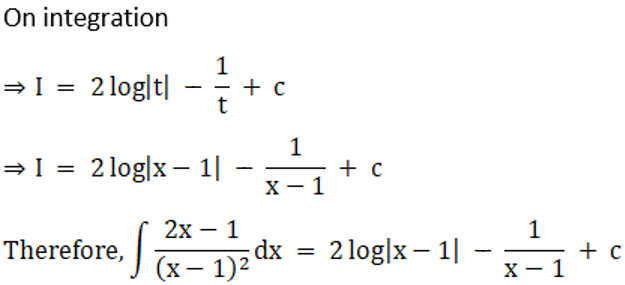
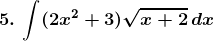
Solution:
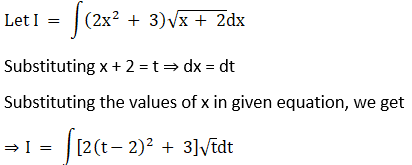

Exercise 19.11 Page No: 19.69
Evaluate the following integrals:
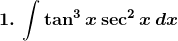
Solution:

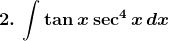
Solution:
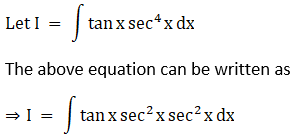

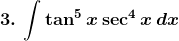
Solution:
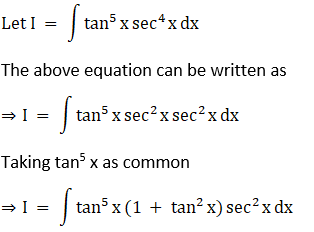

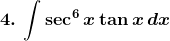
Solution:
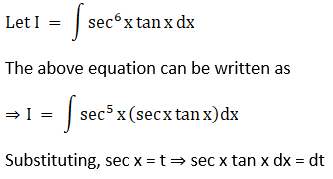
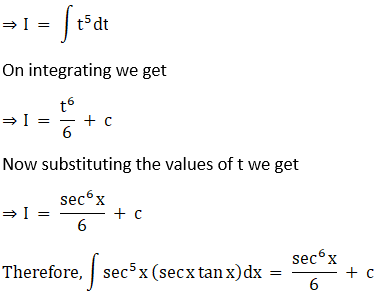
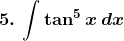
Solution:
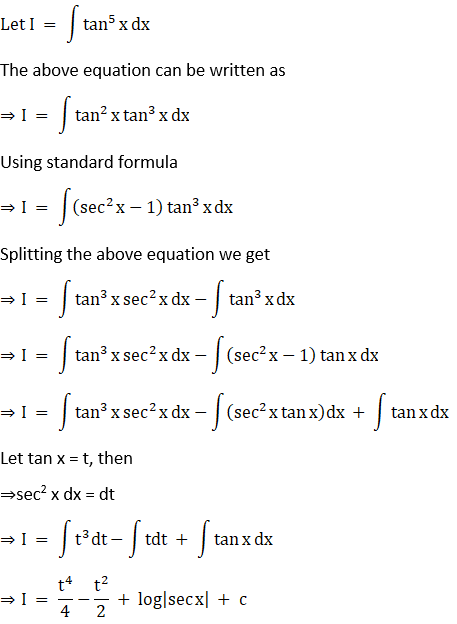
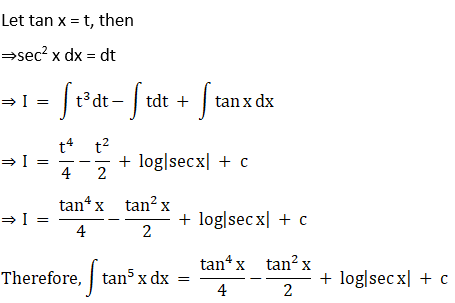
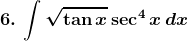
Solution:
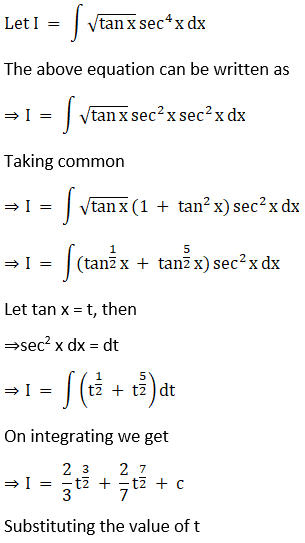
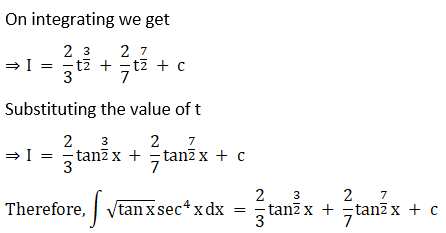
Exercise 19.12 Page No: 19.73
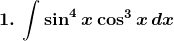
Solution:

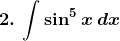
Solution:
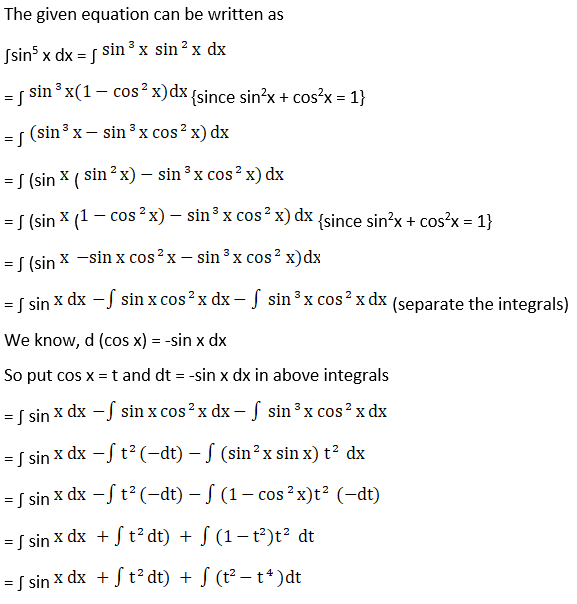
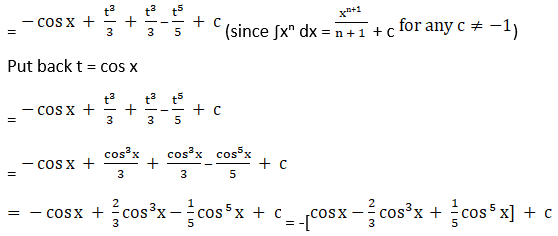
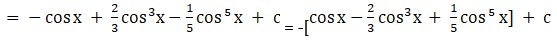
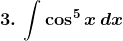
Solution:
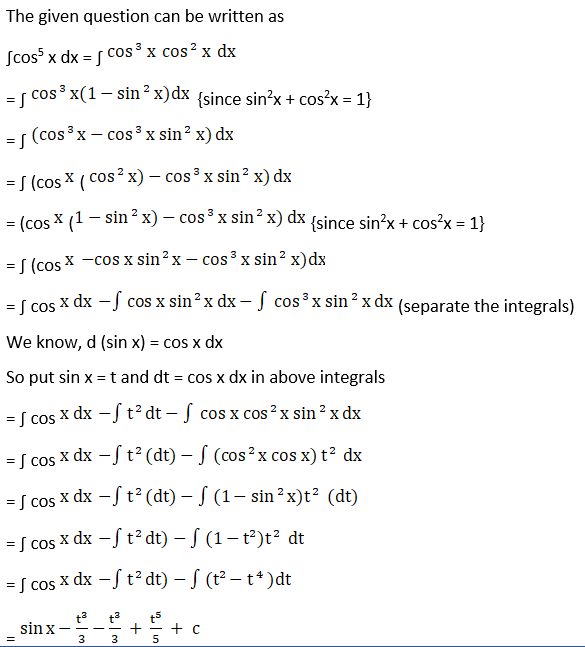
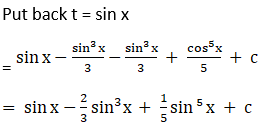
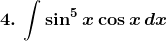
Solution:
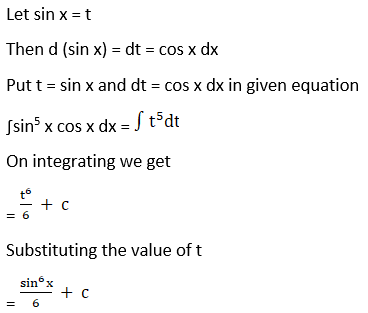
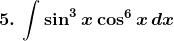
Solution:
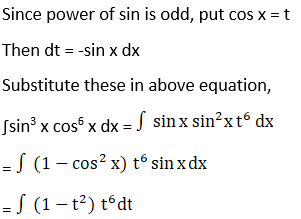
Exercise 19.13 Page No: 19.79
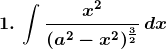
Solution:

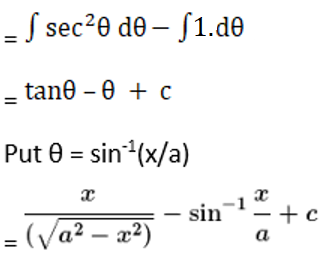
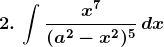
Solution:
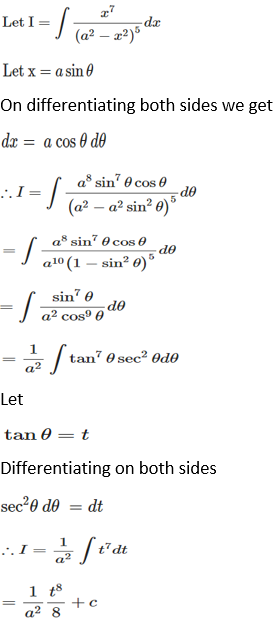
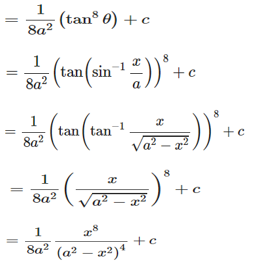
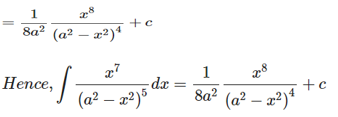
Exercise 19.14 Page No: 19.83
Evaluate the following integrals:
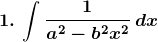
Solution:

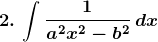
Solution:

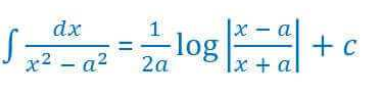
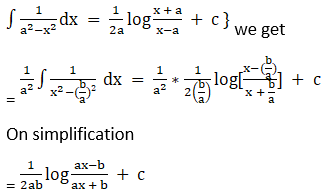
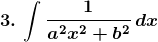
Solution:
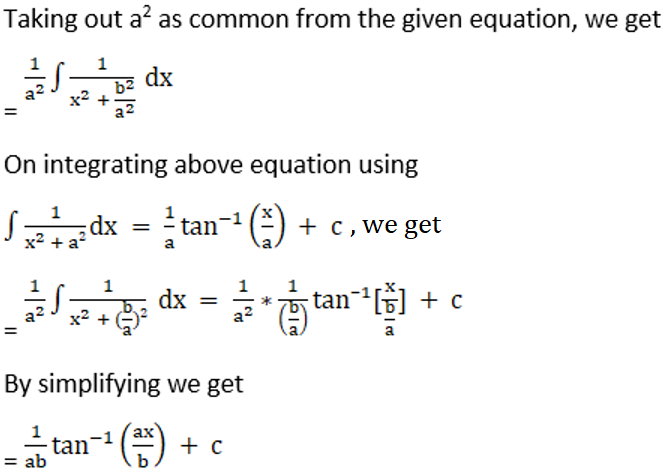
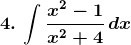
Solution:
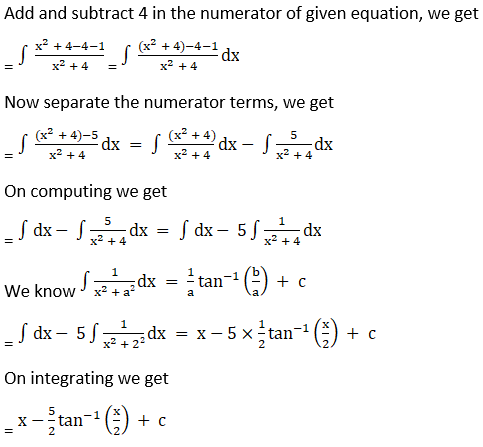

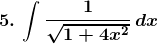
Solution:
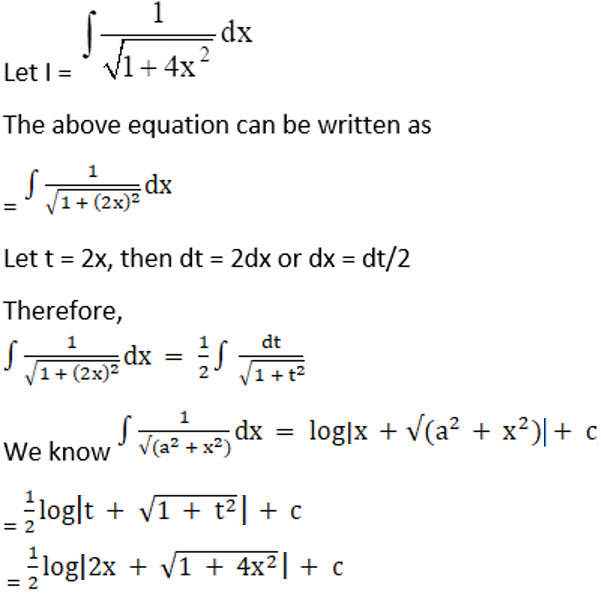
Exercise 19.15 Page No: 19.86
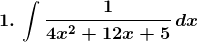
Solution:

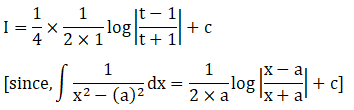
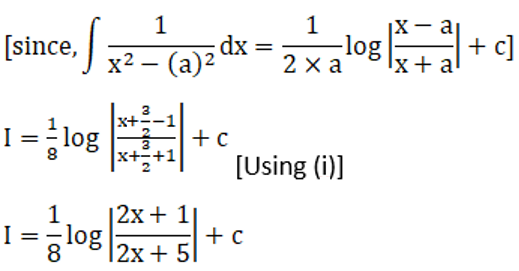
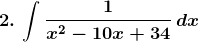
Solution:

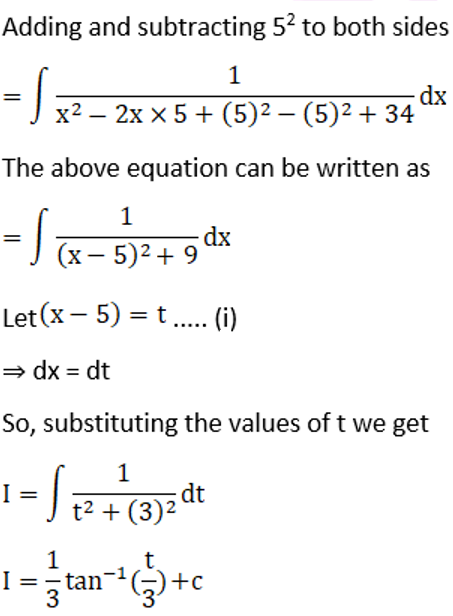
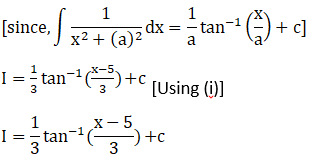
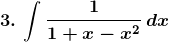
Solution:

By using,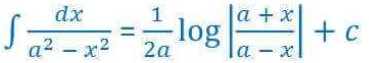
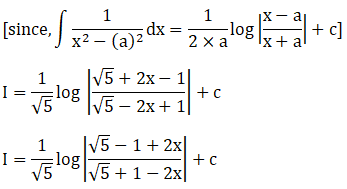
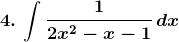
Solution:

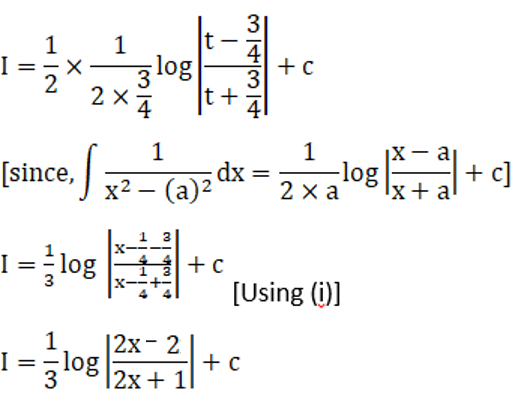
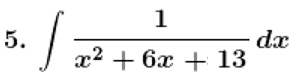
Solution:

Exercise 19.16 Page No: 19.90
Evaluate the following integrals:
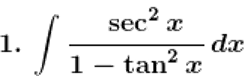
Solution:
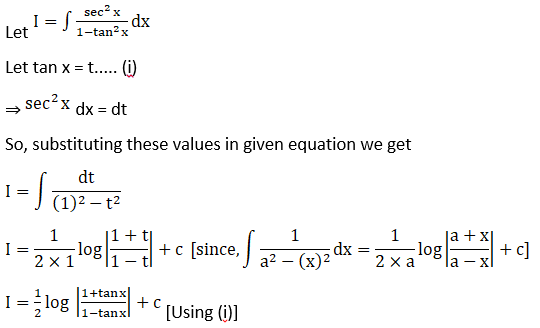
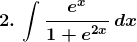
Solution:
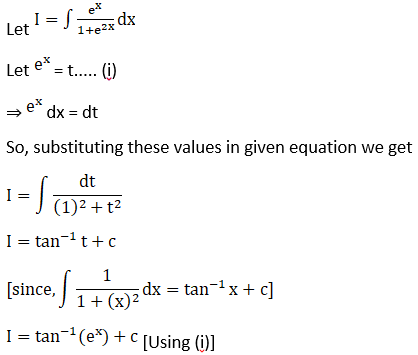
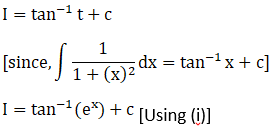
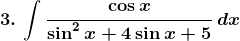
Solution:

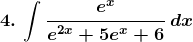
Solution:
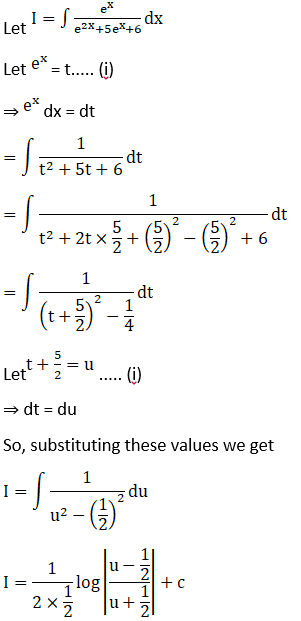
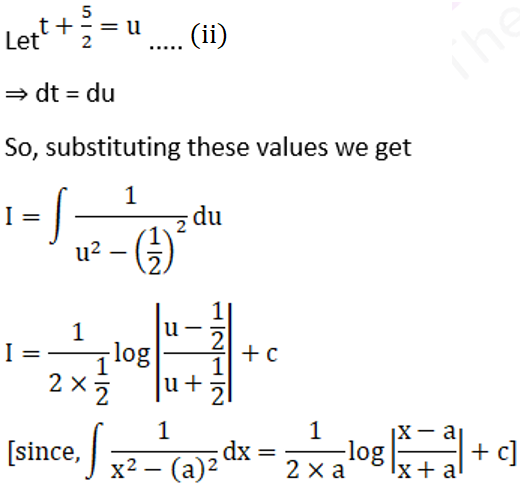
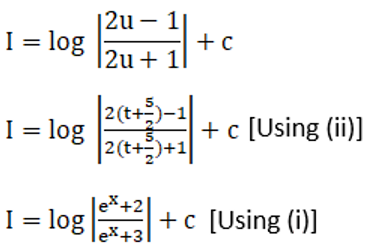
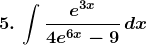
Solution:
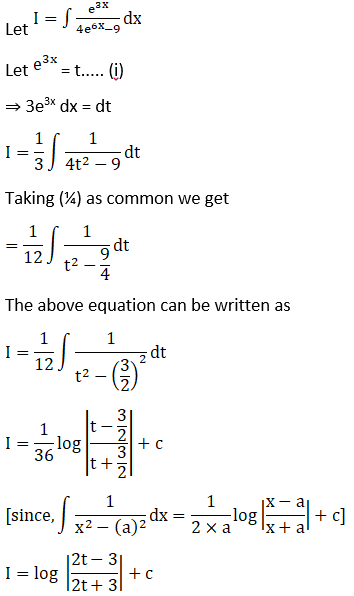
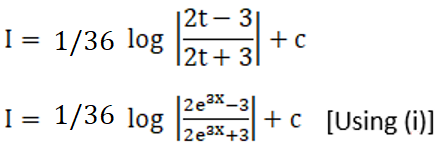
Exercise 19.17 Page No: 19.93
Evaluate the following integrals:
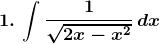
Solution:

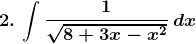
Solution:

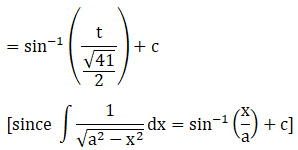
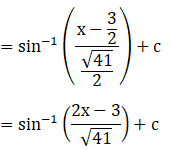
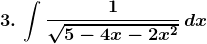
Solution:

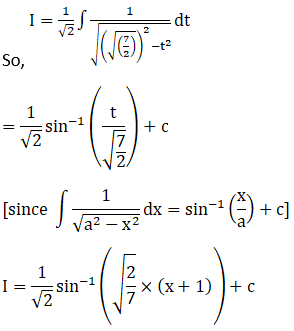
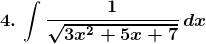
Solution:

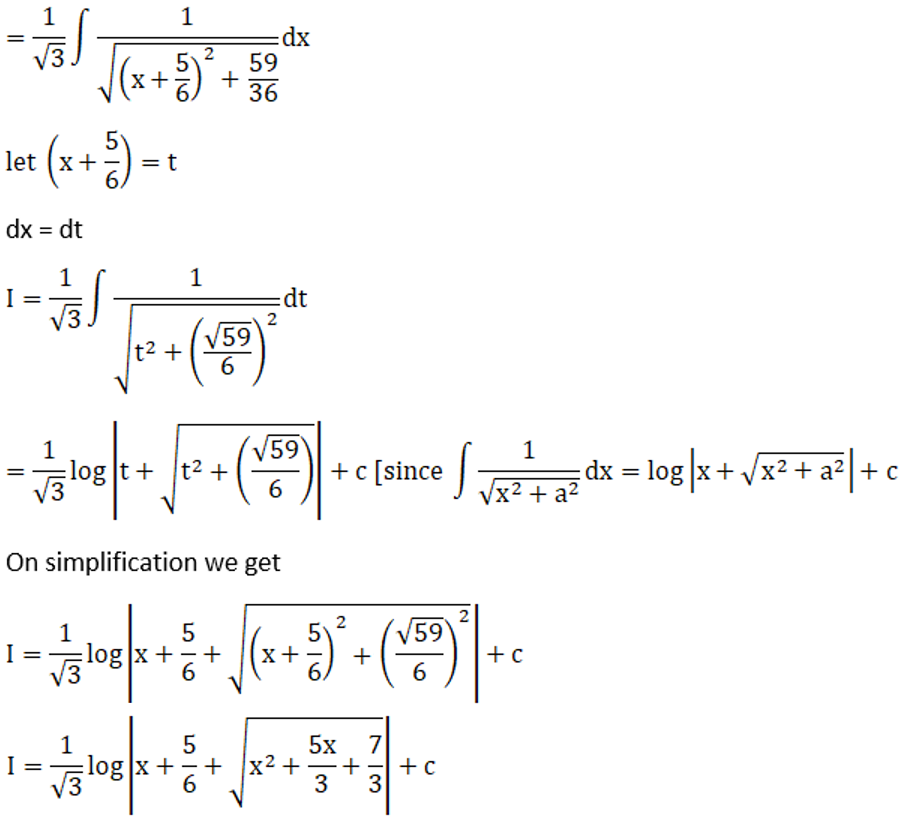
Exercise 19.18 Page No: 19.98
Evaluate the following integrals:
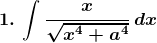
Solution:
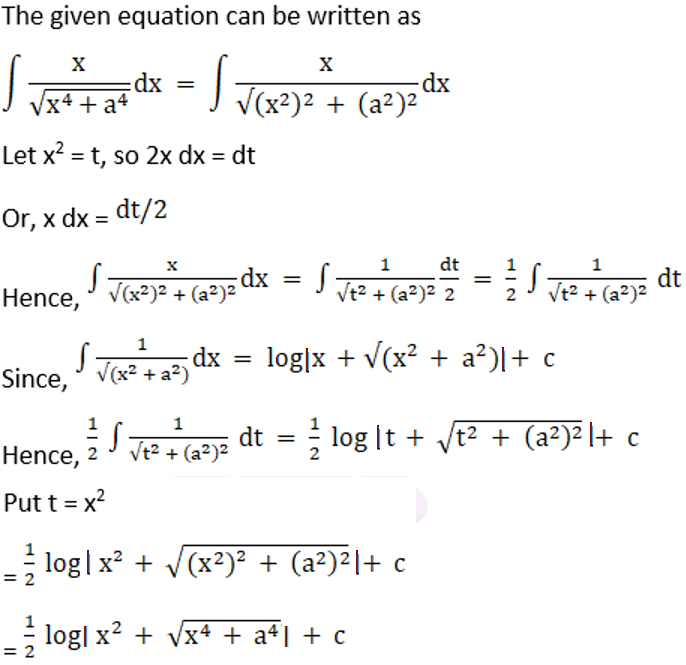
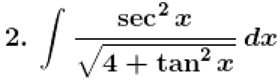
Solution:
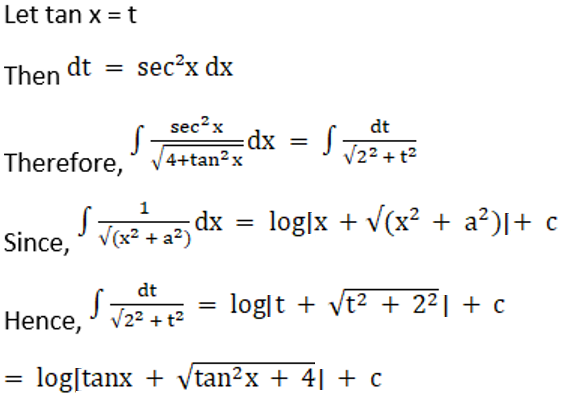
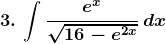
Solution:
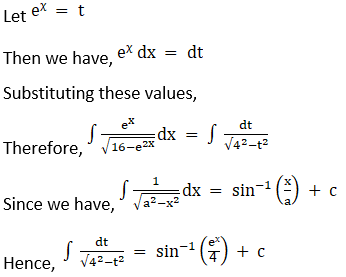
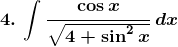
Solution:
Let sin x = t
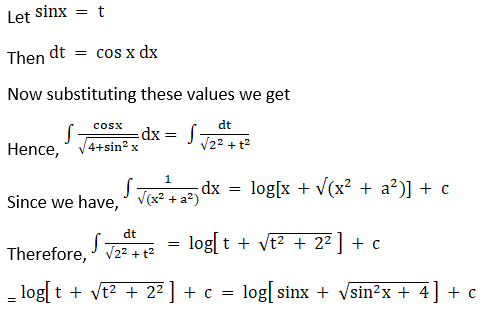
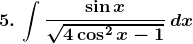
Solution:
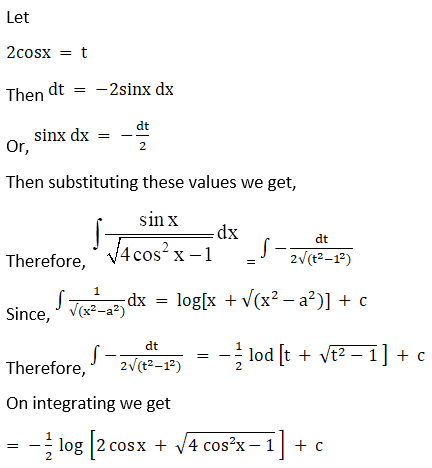
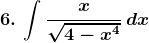
Solution:
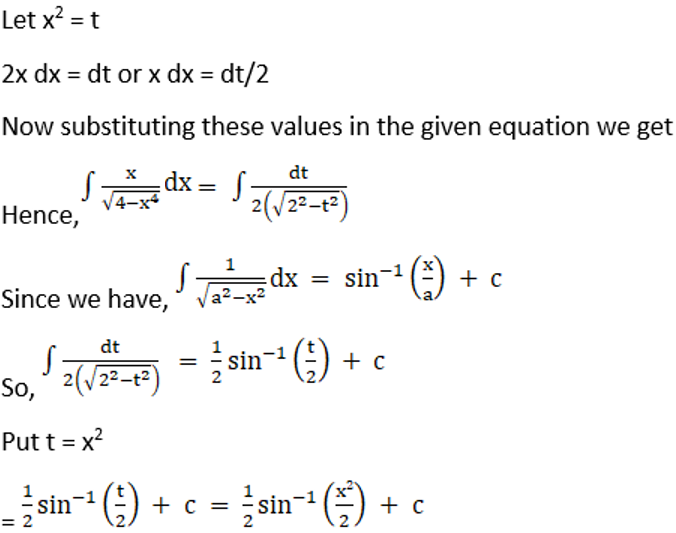
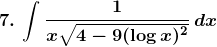
Solution:
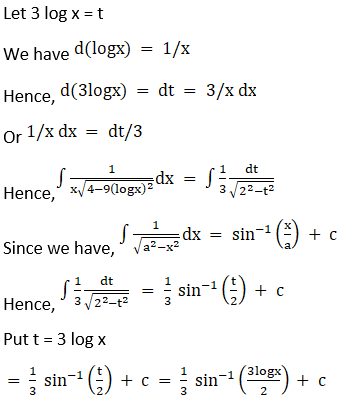
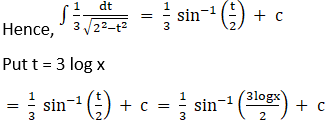
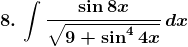
Solution:
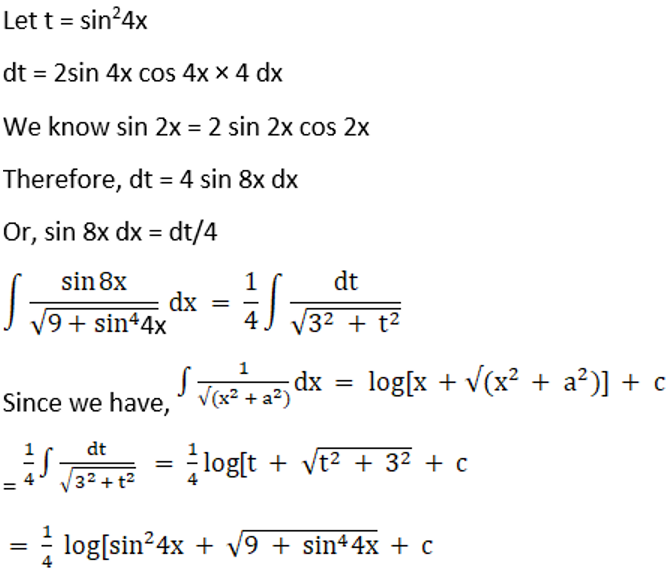
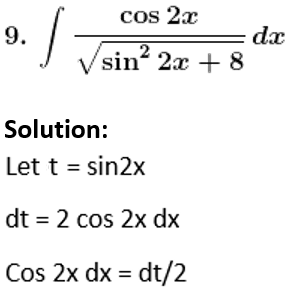
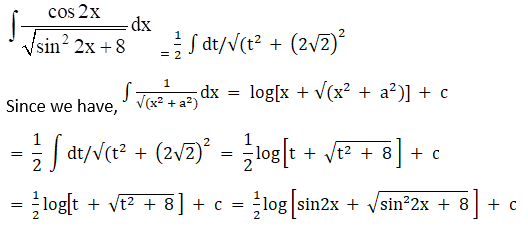
Exercise 19.19 Page No: 19.104
Evaluate the following integrals:
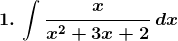
Solution:

We will solve I1 and I2 individually.

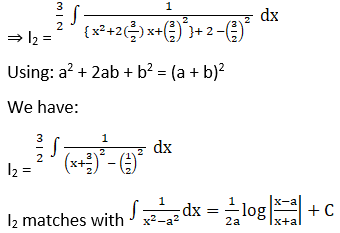
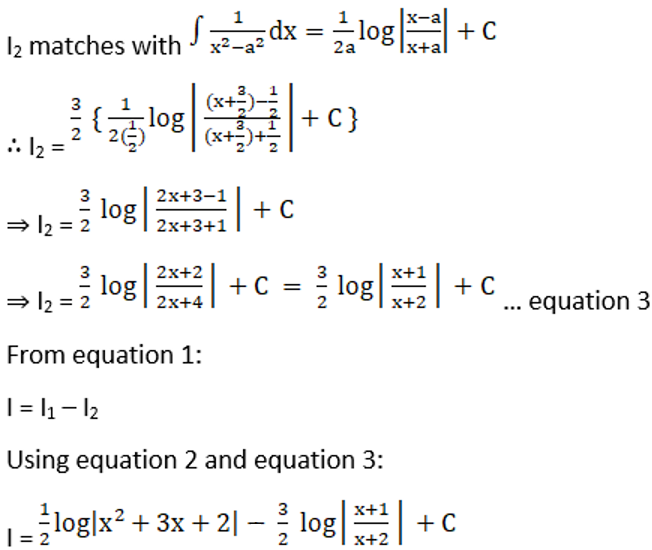
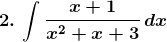
Solution:

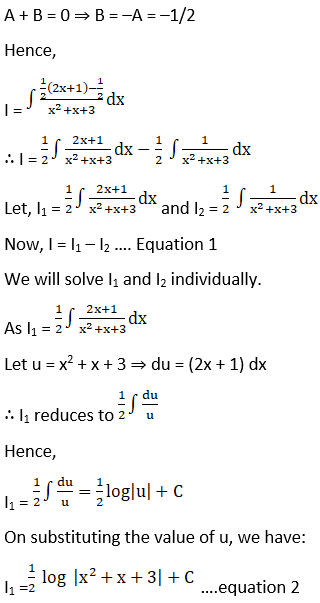


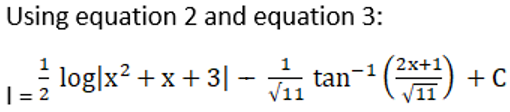
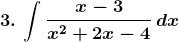
Solution:




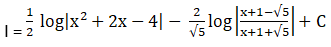
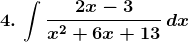
Solution:
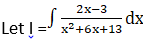



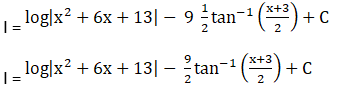
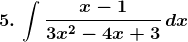
Solution:

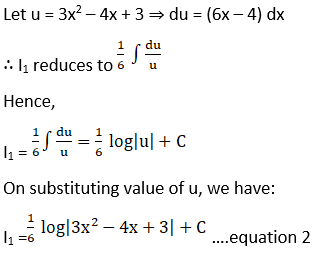

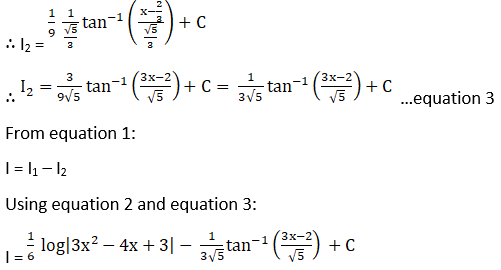
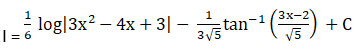
Exercise 19.20 Page No: 19.106
Evaluate the following integrals:
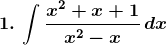
Solution:

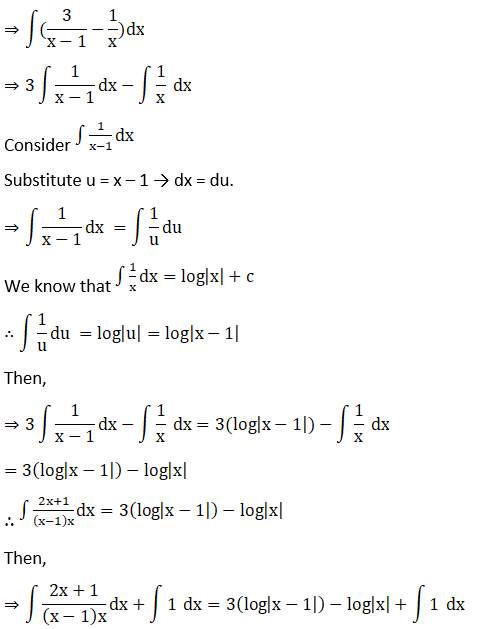
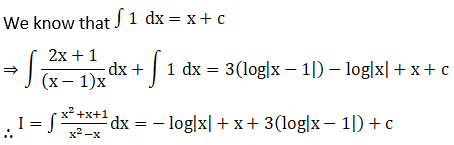
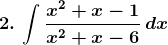
Solution:
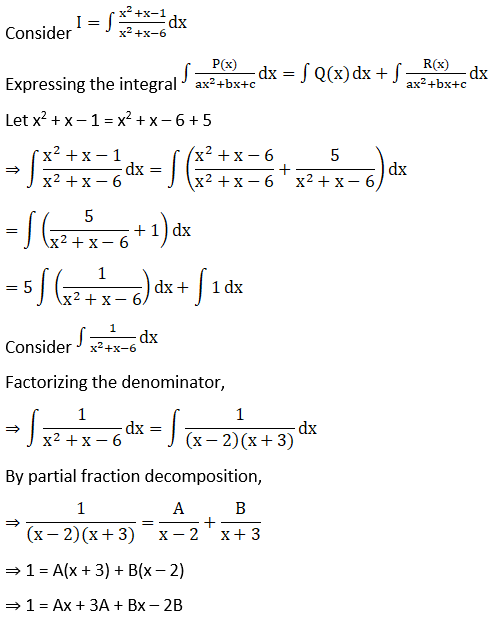
⇒ 1 = (A + B) x + (3A – 2B)
⇒ Then A + B = 0 … (1)
And 3A – 2B = 1 … (2)
Solving (1) and (2),
2 × (1) → 2A + 2B = 0
1 × (2) → 3A – 2B = 1
5A = 1
∴ A = 1/5
Substituting A value in (1),
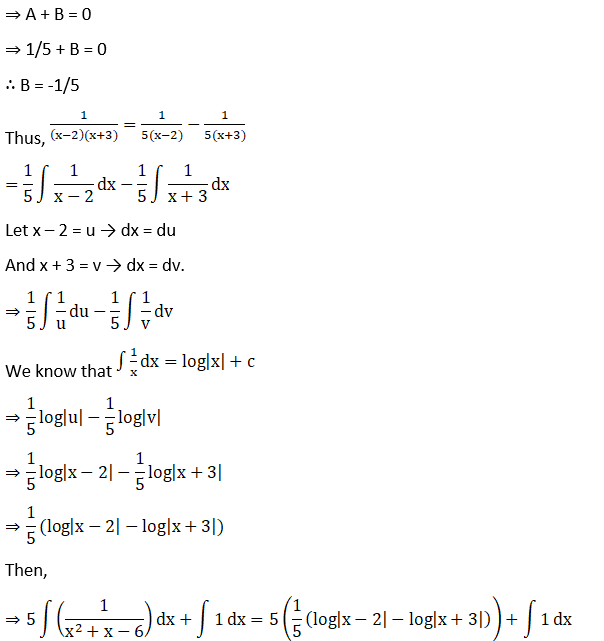
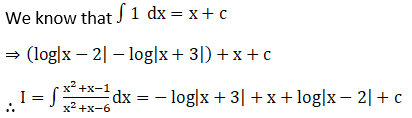
Or I = log|(x – 2)/(x + 3)| + x + c
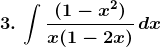
Solution:

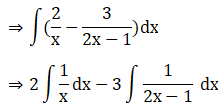
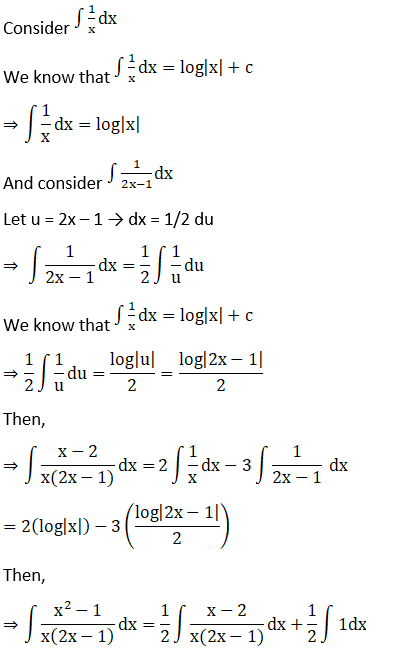
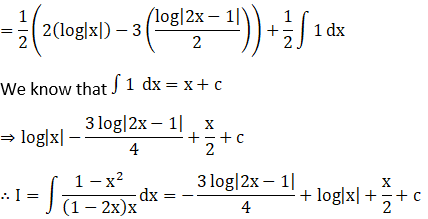
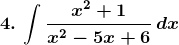
Solution:

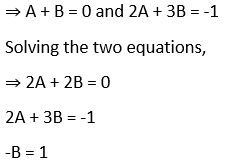
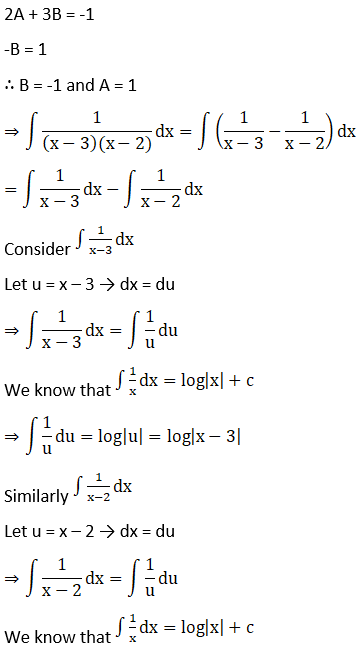
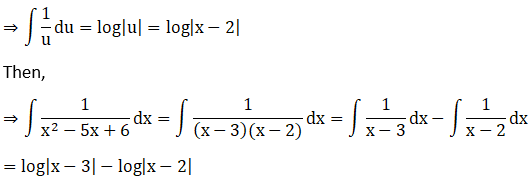
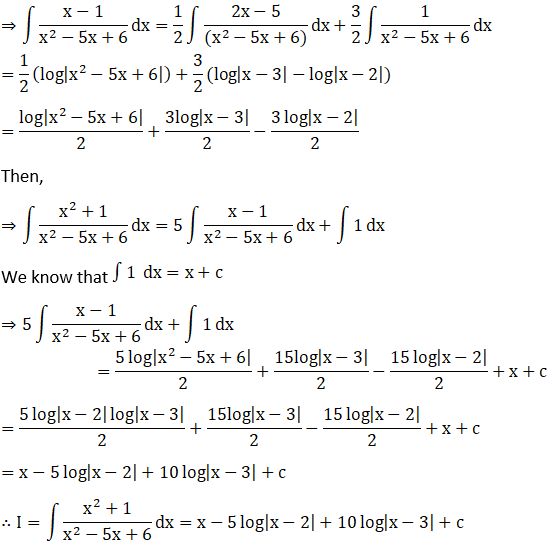
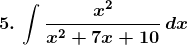
Solution:

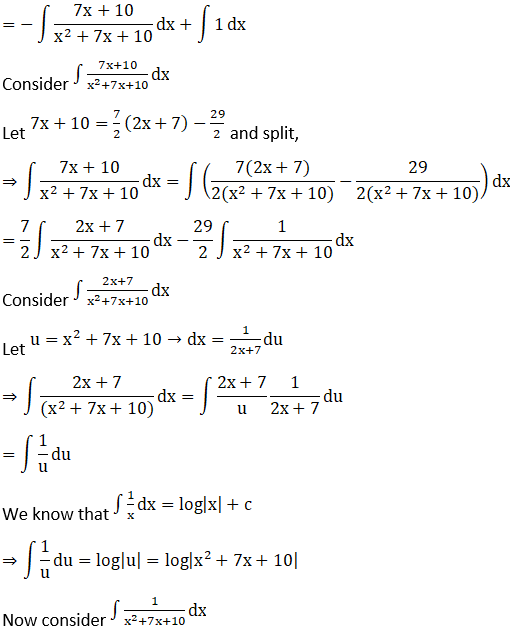
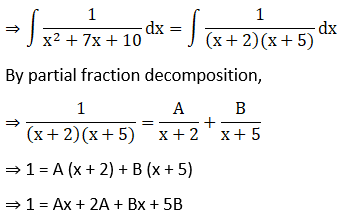
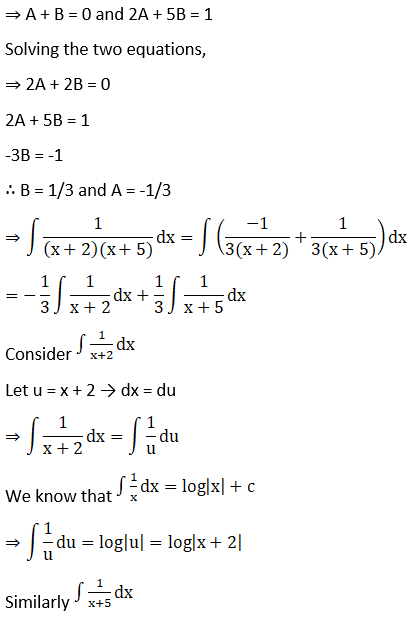
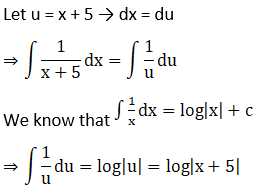
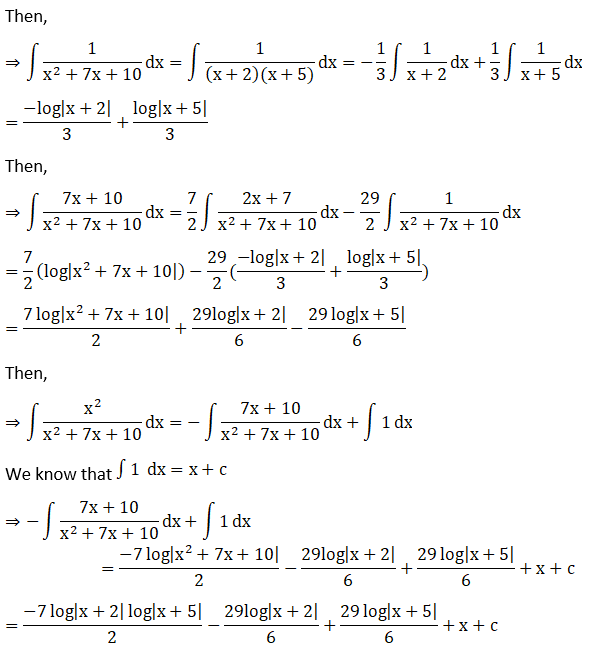
Hence,
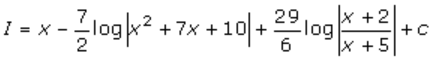
Exercise 19.21 Page No: 19.110
Evaluate the following integrals:
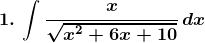
Solution:

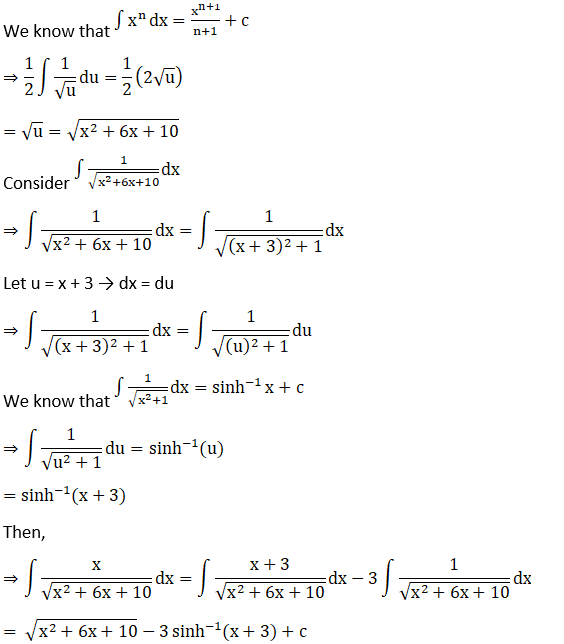
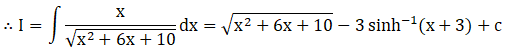
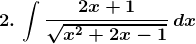
Solution:
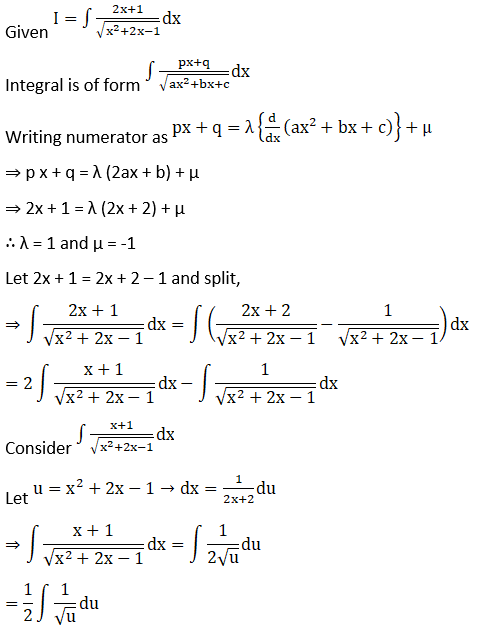
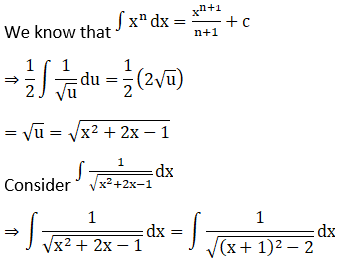
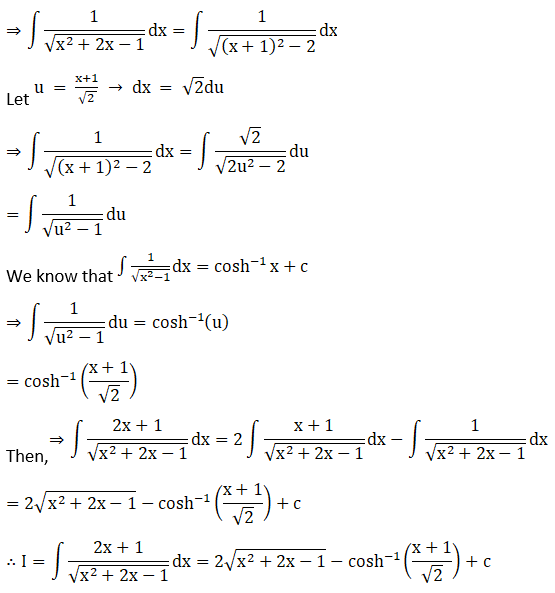
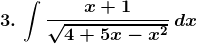
Solution:

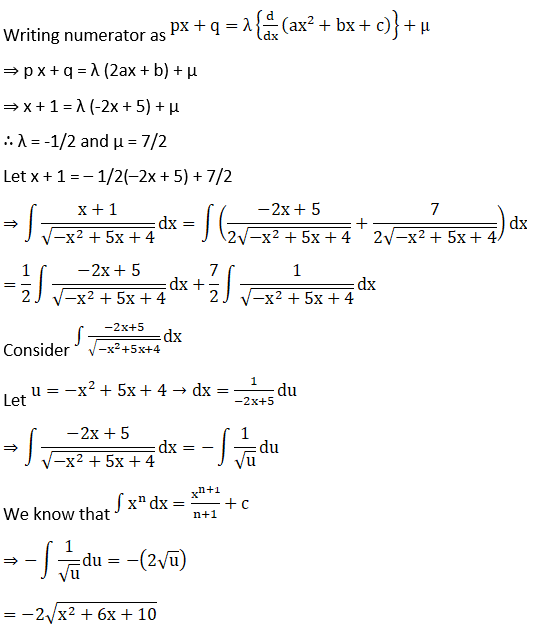
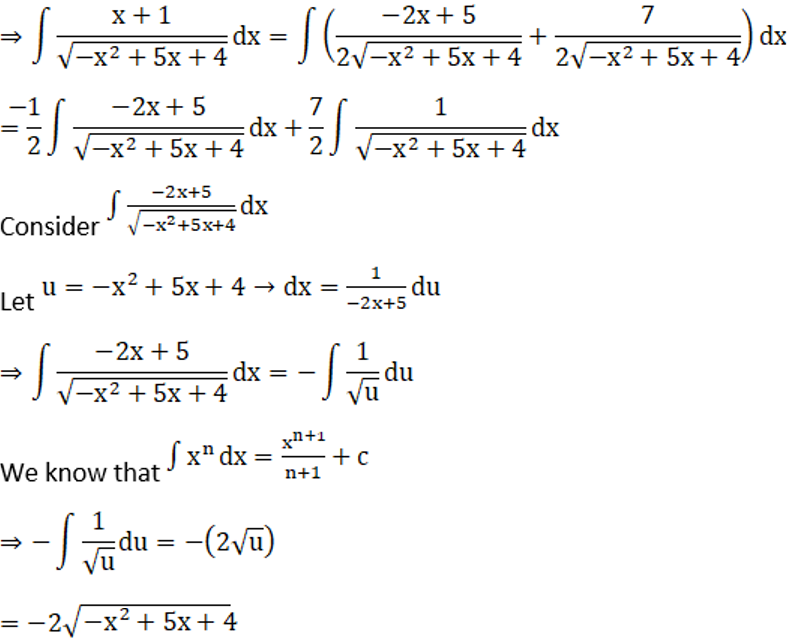
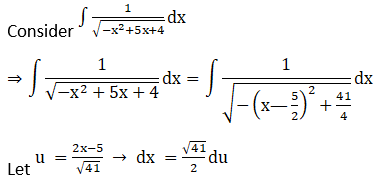
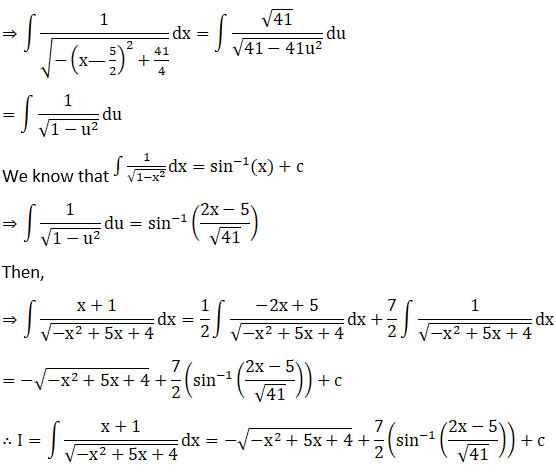
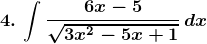
Solution:

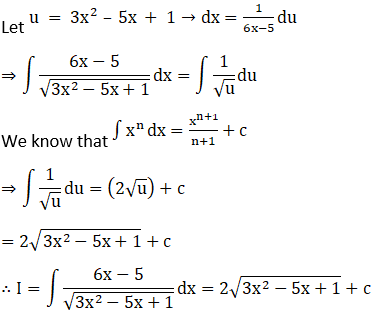
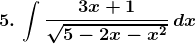
Solution:
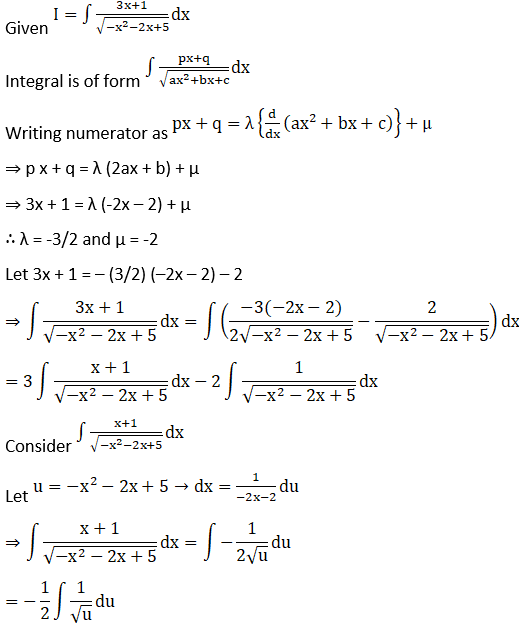
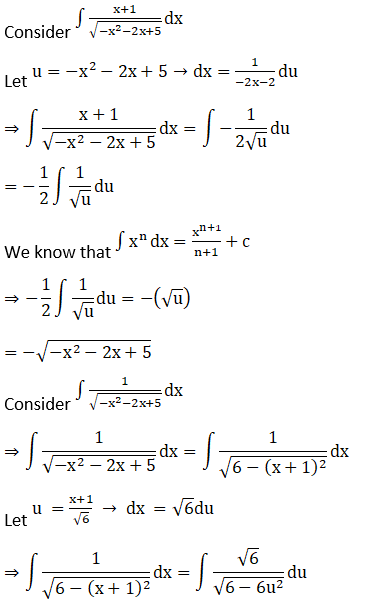
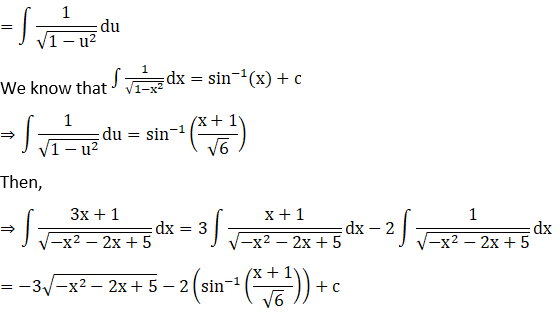
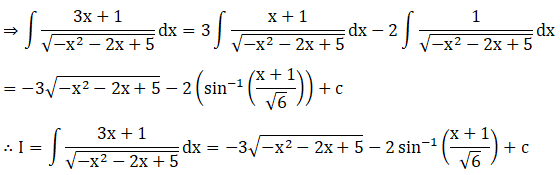
Exercise 19.22 Page No: 19.114
Evaluate the following integrals:
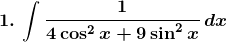
Solution:

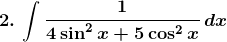
Solution:

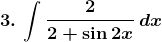
Solution:
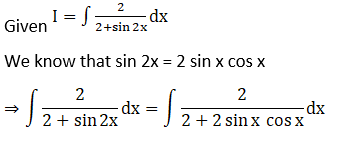
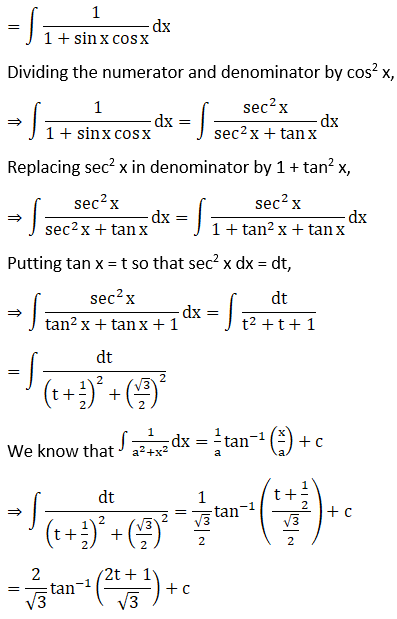
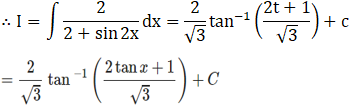
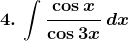
Solution:
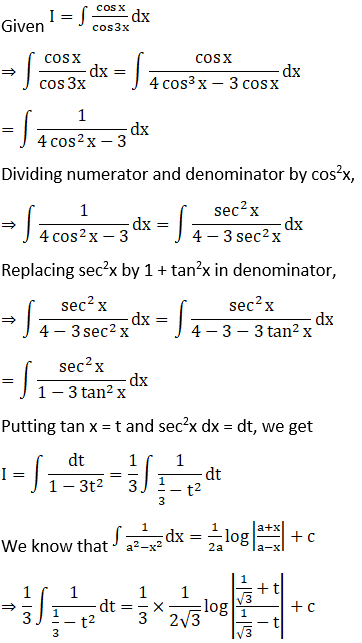
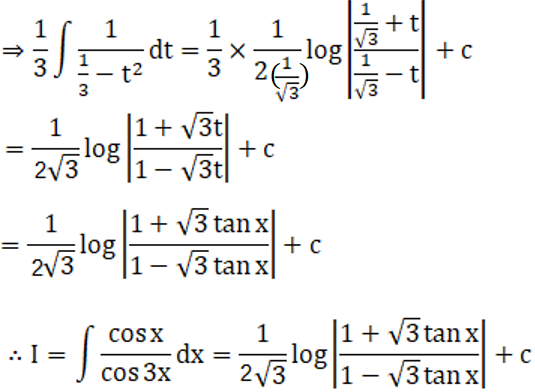
Exercise 19.23 Page No: 19.117
Evaluate the following integrals:
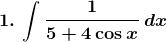
Solution:
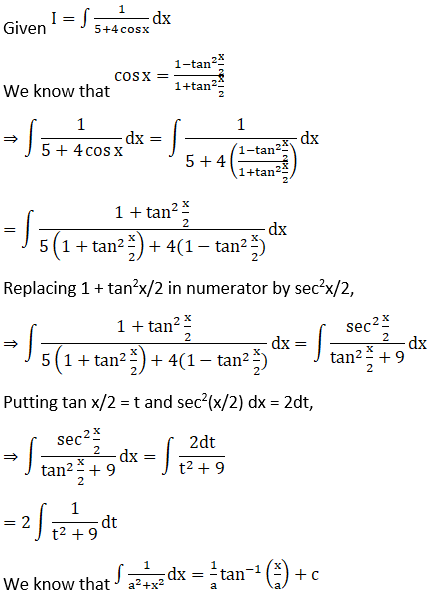
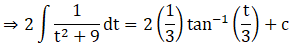
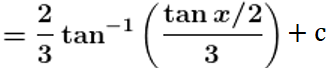
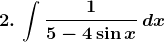
Solution:

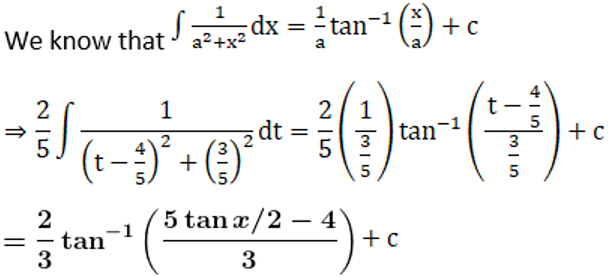
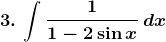
Solution:
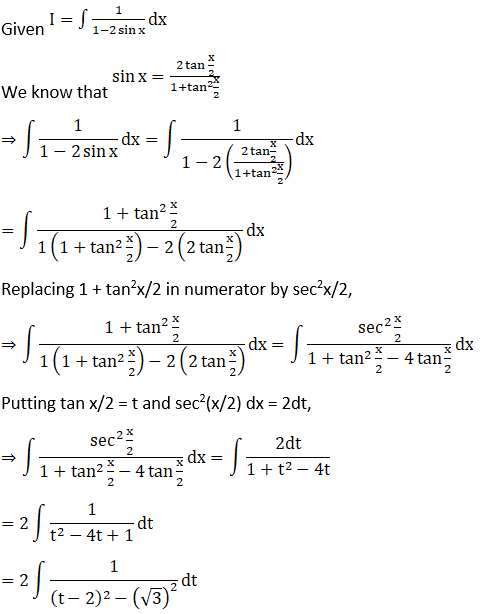
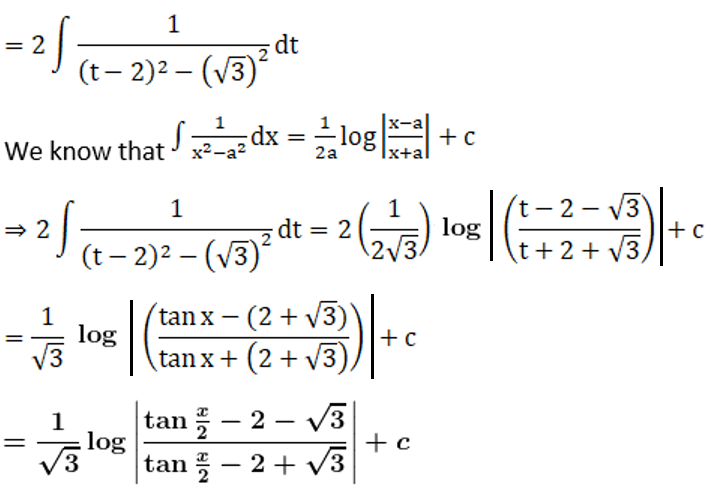
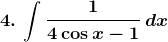
Solution:
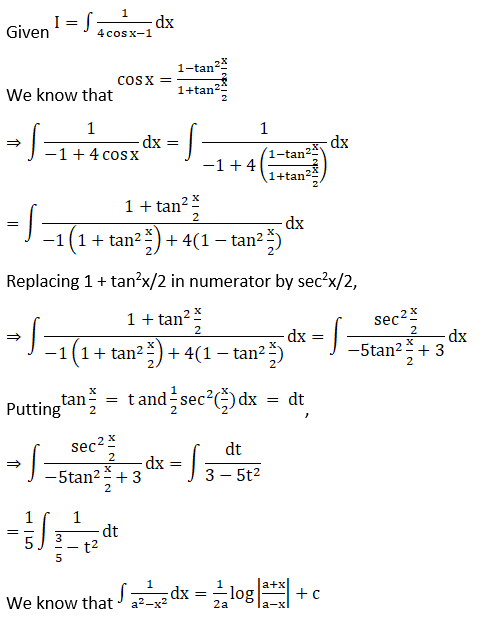
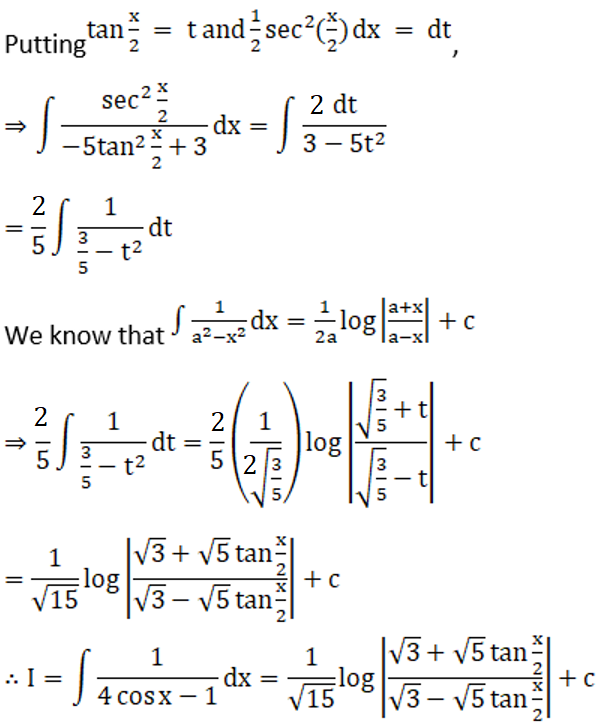
5.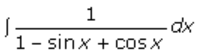
Solution:
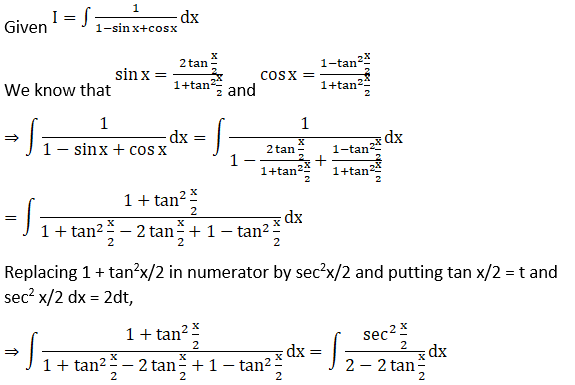
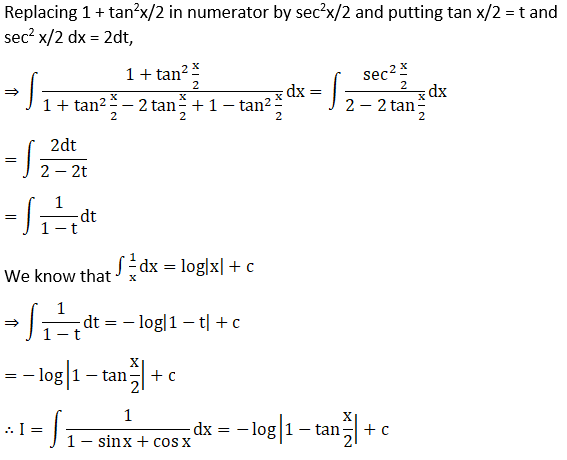
Exercise 19.24 Page No: 19.122
Evaluate the following integrals:
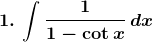
Solution:


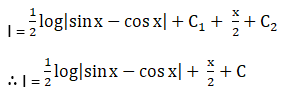
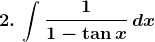
Solution:

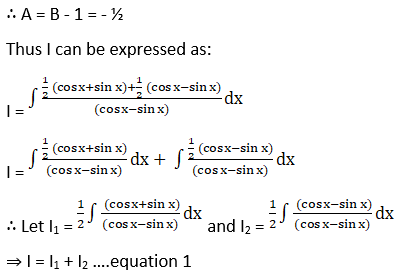
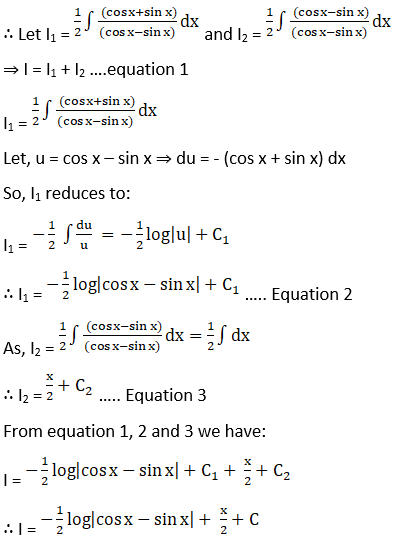
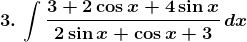
Solution:
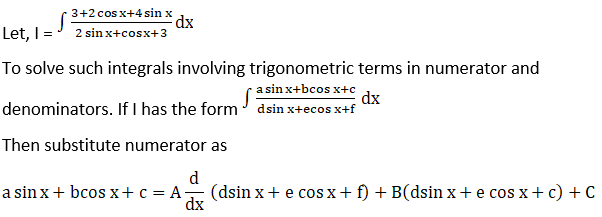

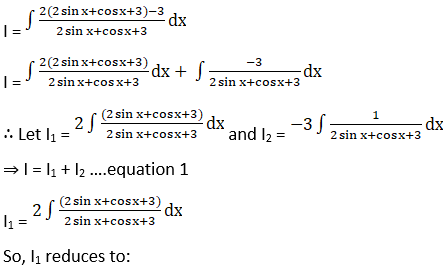

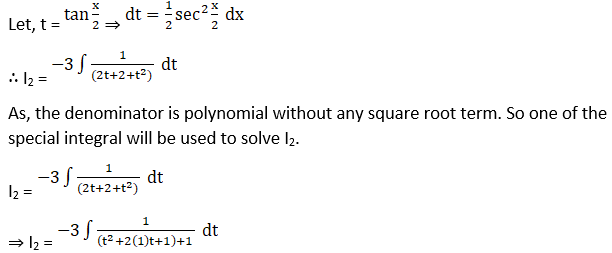

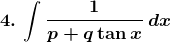
Solution:



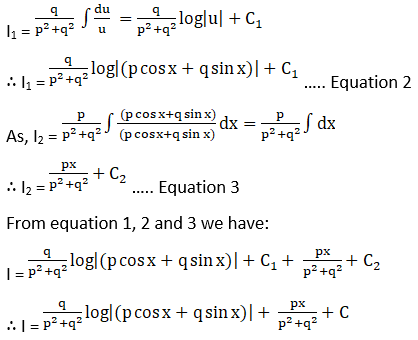
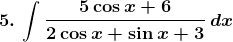
Solution:


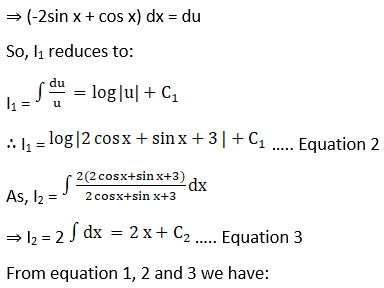
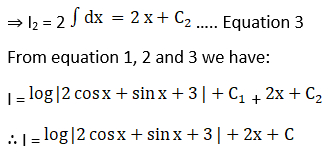
Exercise 19.25 Page No: 19.133
Evaluate the following integrals:
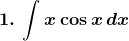
Solution:
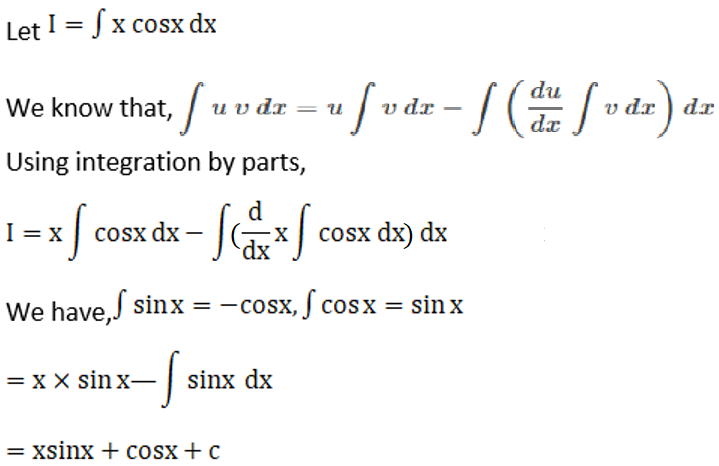
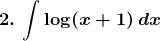
Solution:
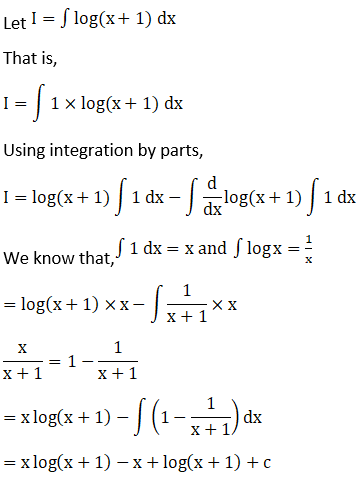
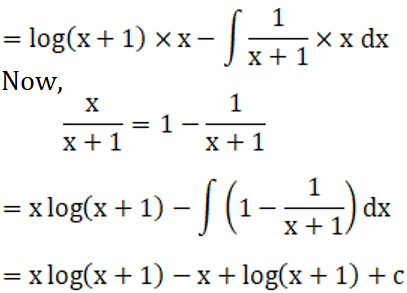
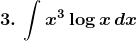
Solution:
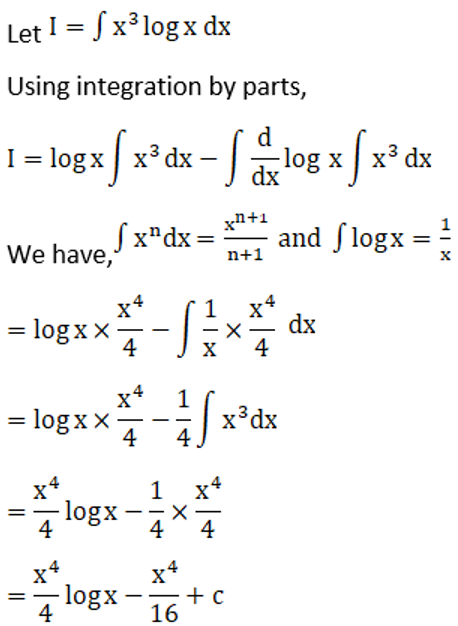
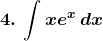
Solution:
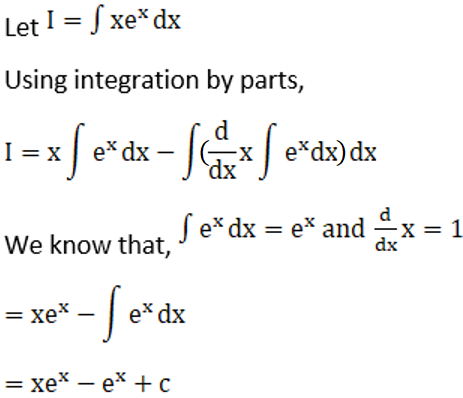
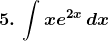
Solution:

Exercise 19.26 Page No: 19.143
Evaluate the following integrals:
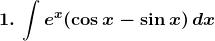
Solution:
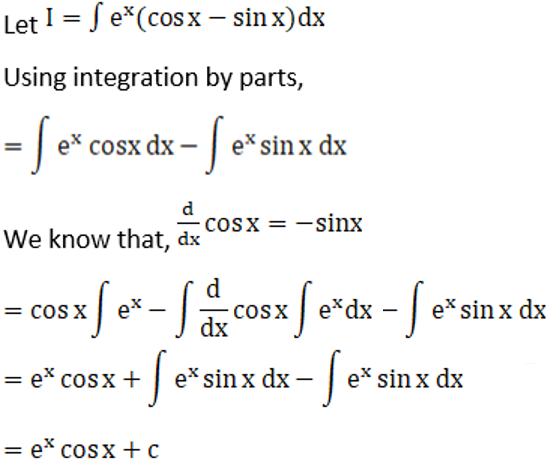
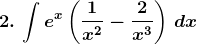
Solution:
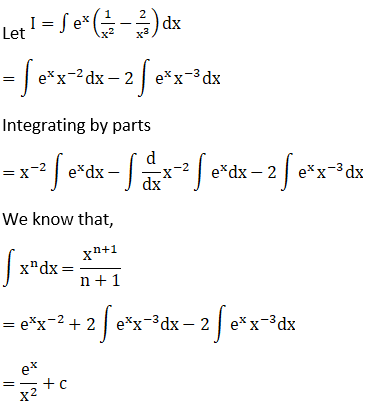
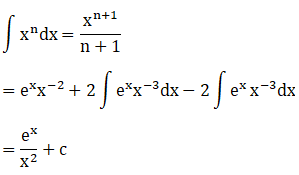
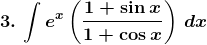
Solution:
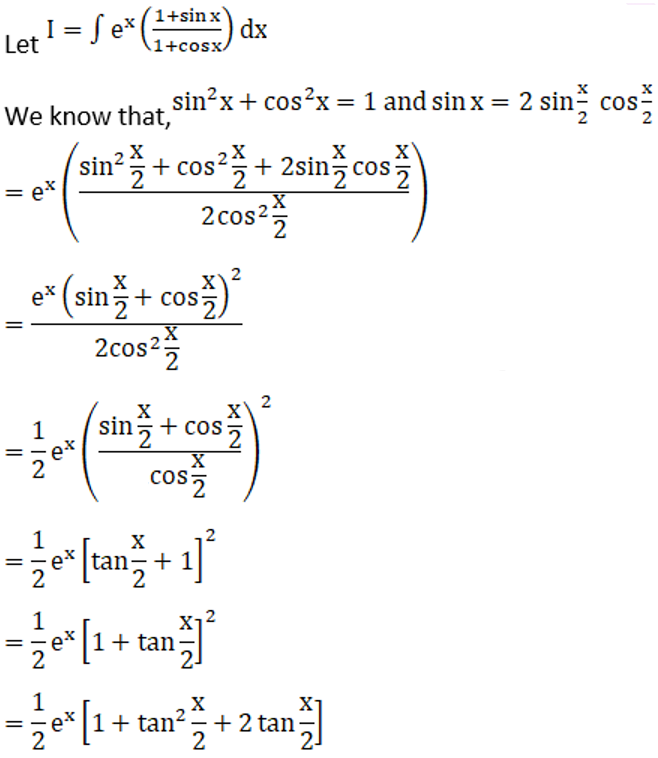
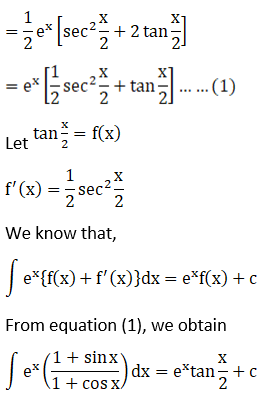
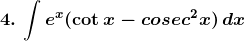
Solution:
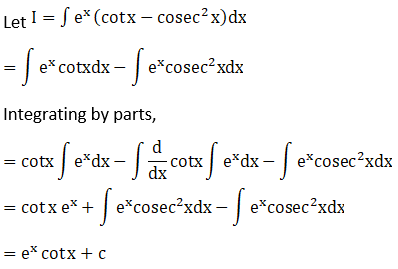
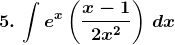
Solution:
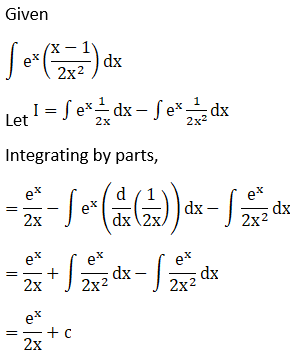
Exercise 19.27 Page No: 19.149
Evaluate the following integrals:
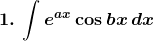
Solution:
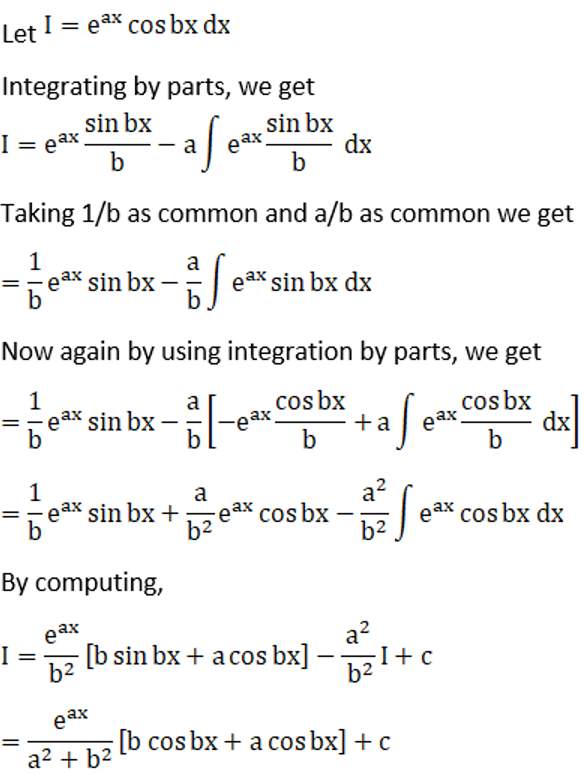
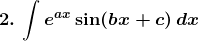
Solution:
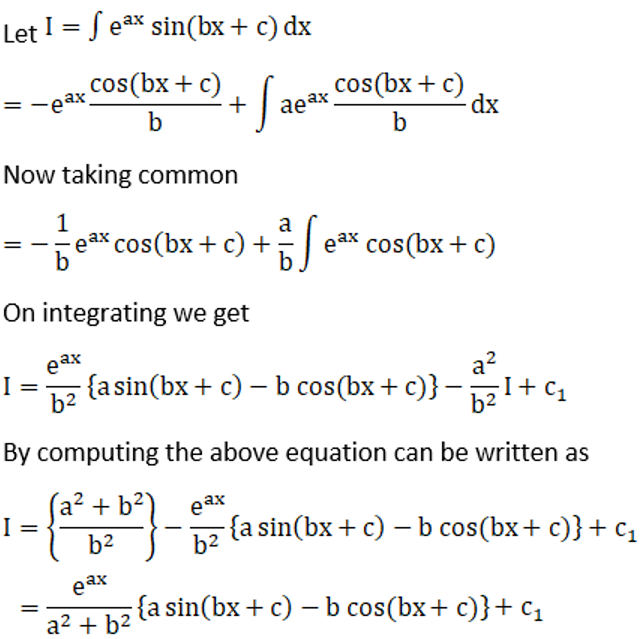
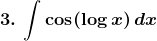
Solution:
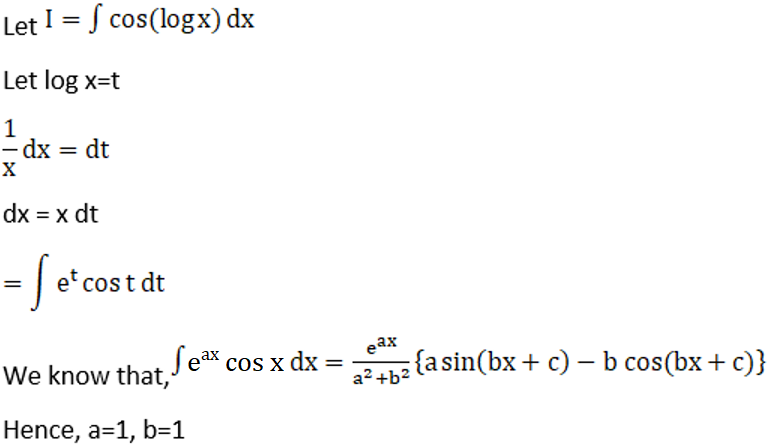
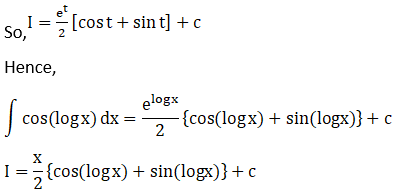
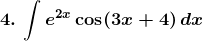
Solution:
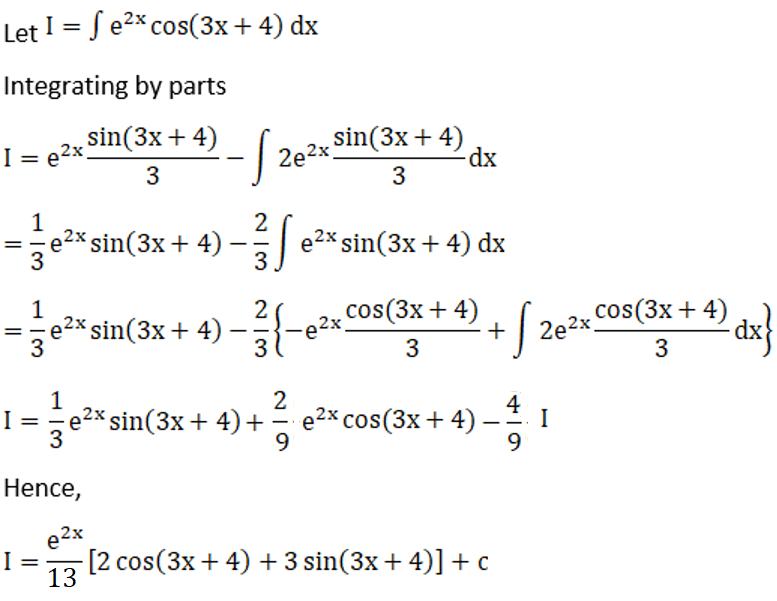
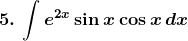
Solution:
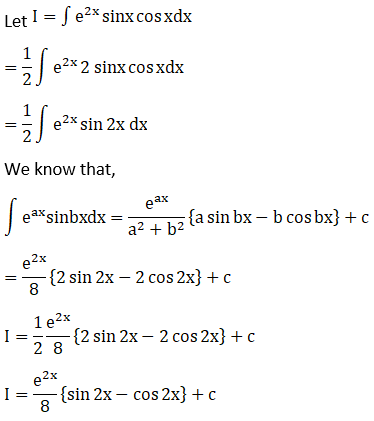
Exercise 19.28 Page No: 19.154
Evaluate the following integrals:
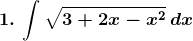
Solution:
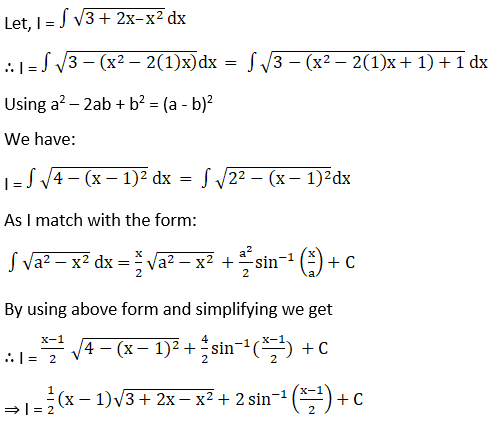
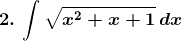
Solution:
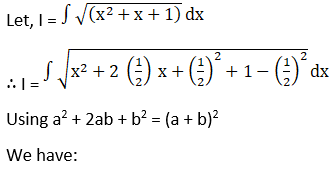
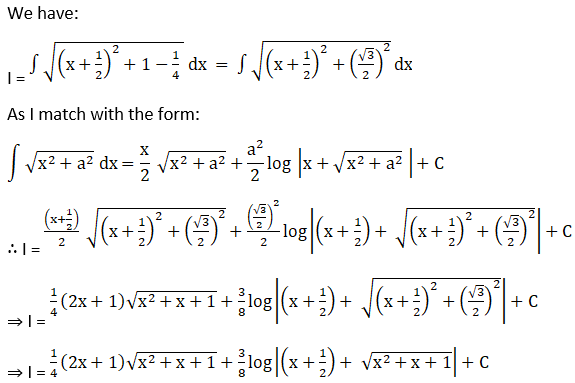
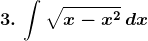
Solution:
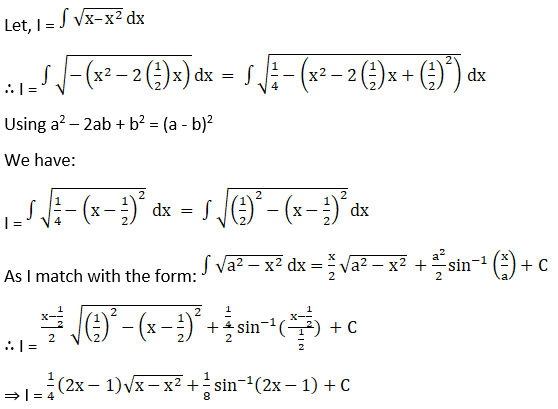
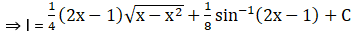
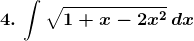
Solution:
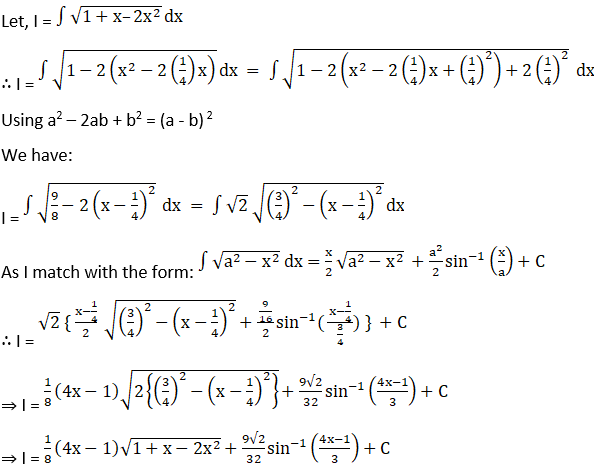
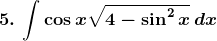
Solution:
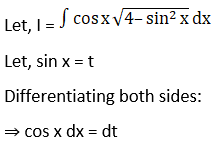
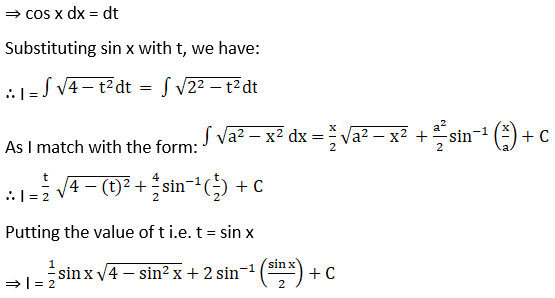
Exercise 19.29 Page No: 19.158
Evaluate the following integrals:
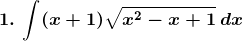
Solution:
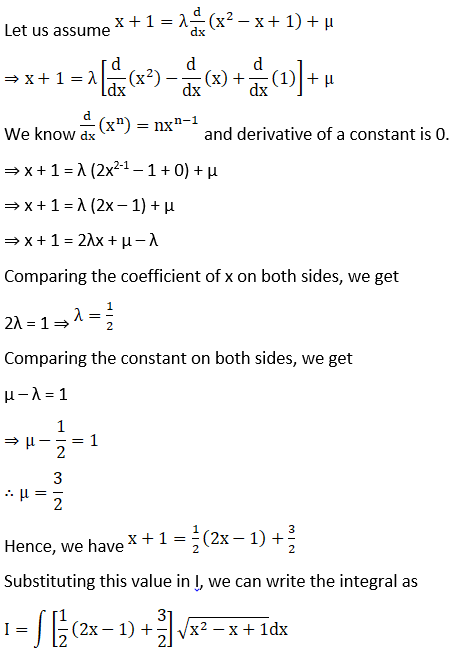
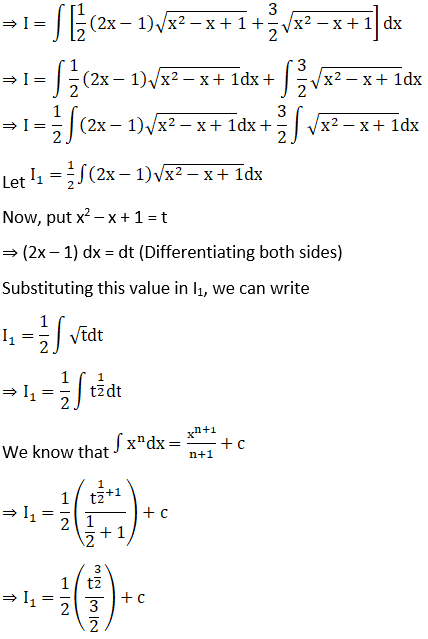
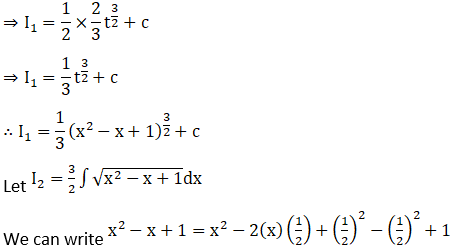
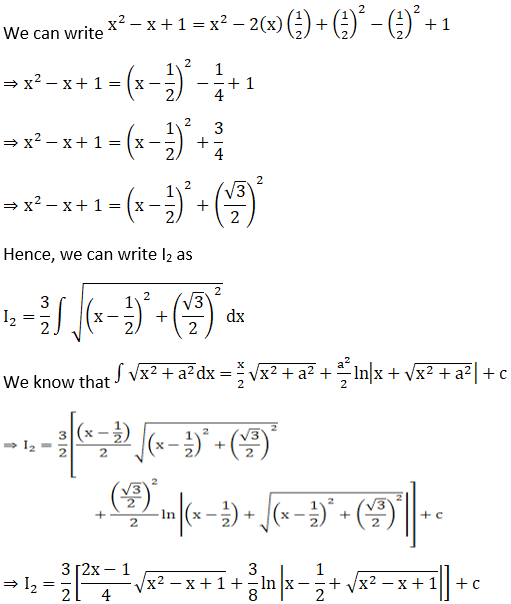
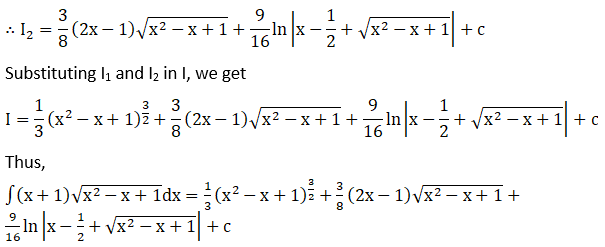
Solution:



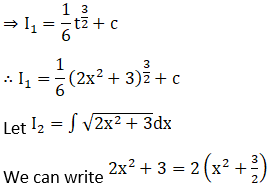

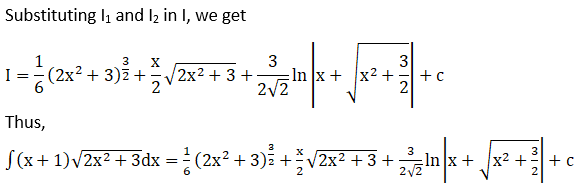
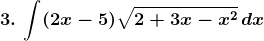
Solution:

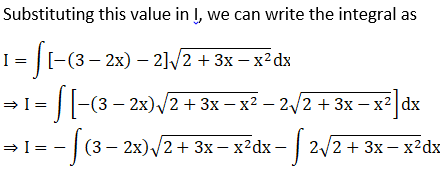

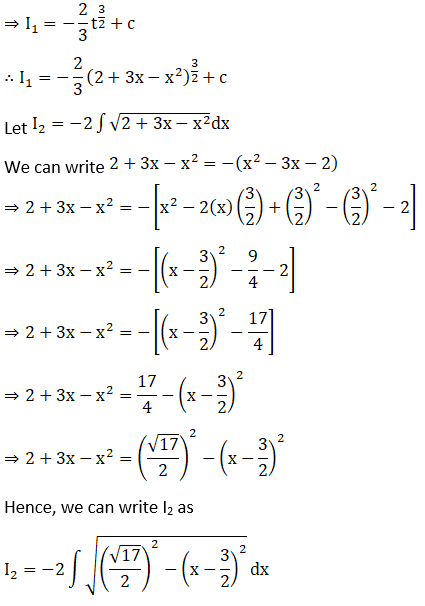
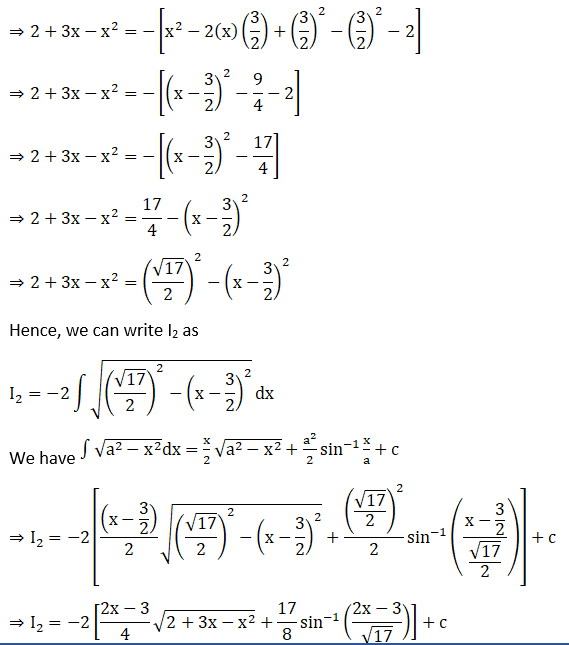
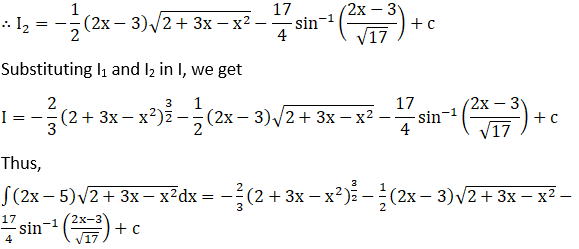
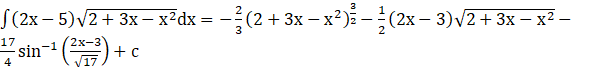
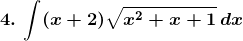
Solution:


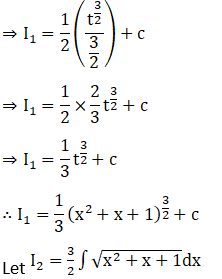
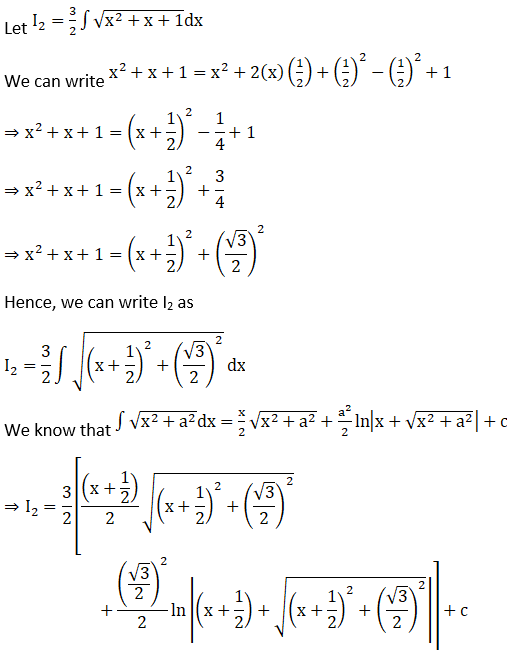
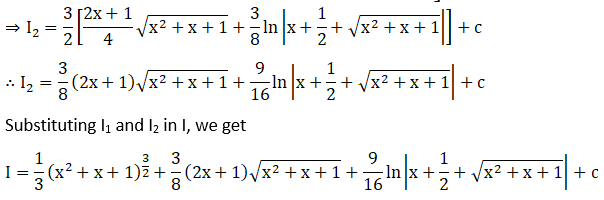
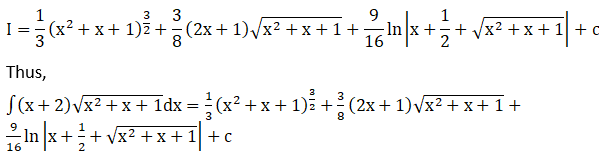
Exercise 19.30 Page No: 19.176
Evaluate the following integrals:
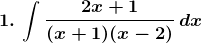
Solution:


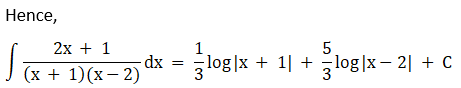
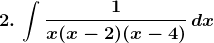
Solution:



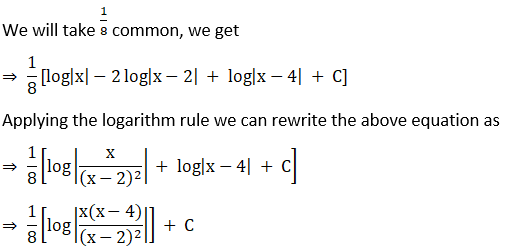


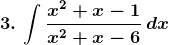
Solution:


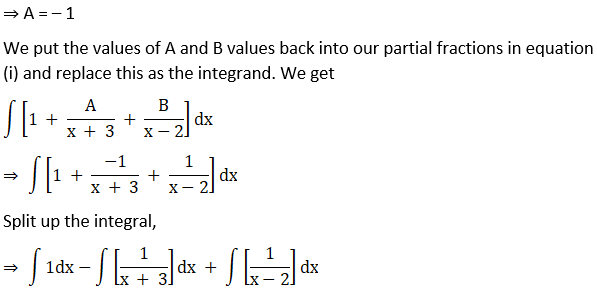

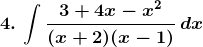
Solution:




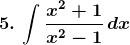
Solution:




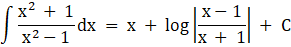
Exercise 19.31 Page No: 19.190
Evaluate the following integrals:
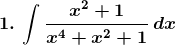
Solution:
The given equation can be written as,
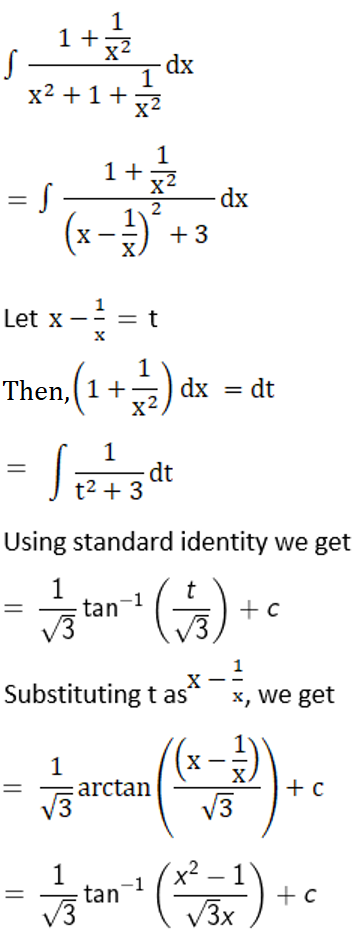
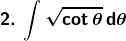
Solution:
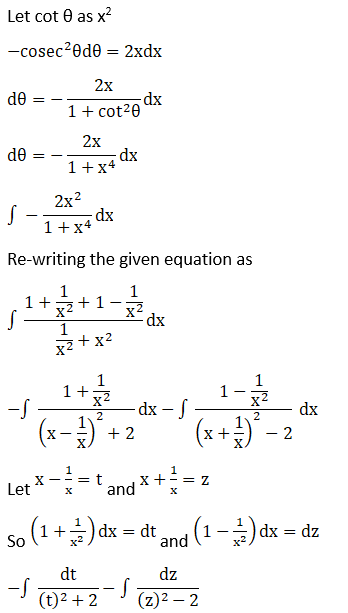
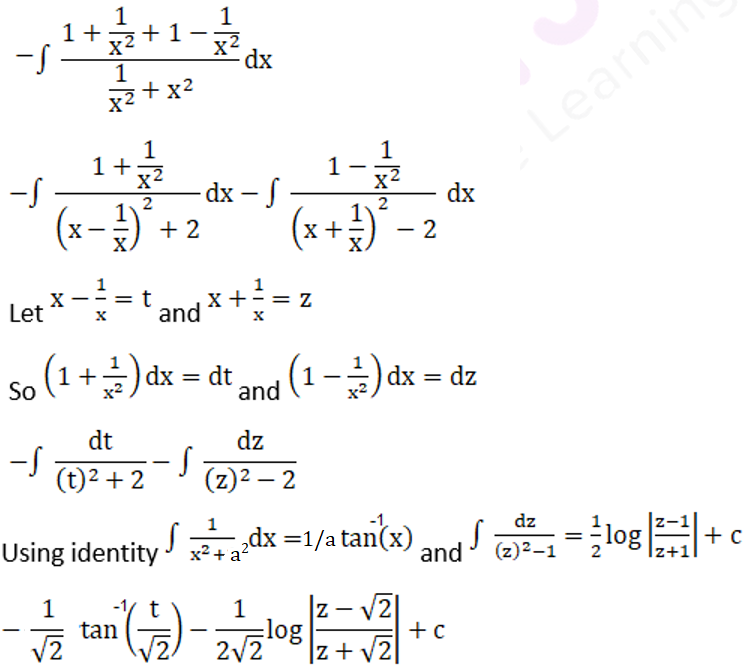
Now, substituting t as x – 1/x and z as x + 1/x we have
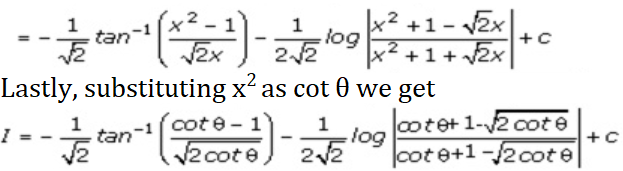
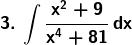
Solution:

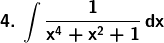
Solution:

We get,
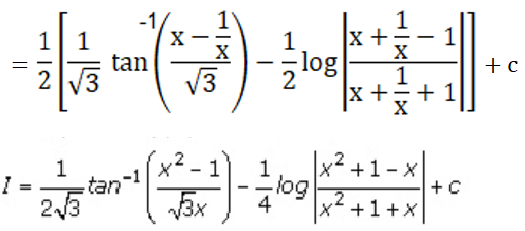
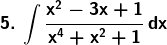
Solution:
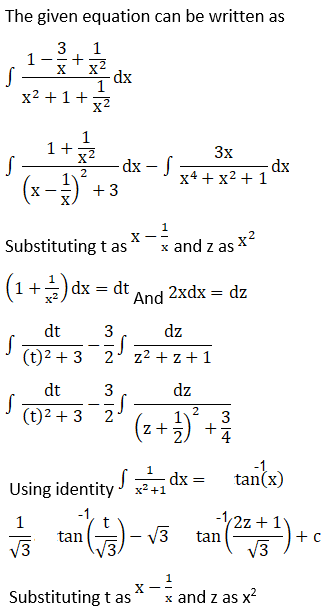
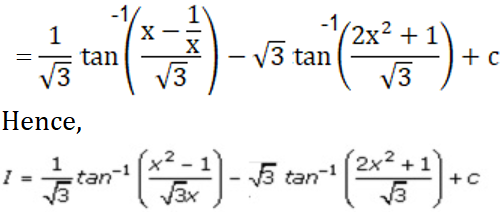
Exercise 19.32 Page No: 19.196
Evaluate the following integrals:
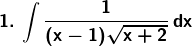
Solution:
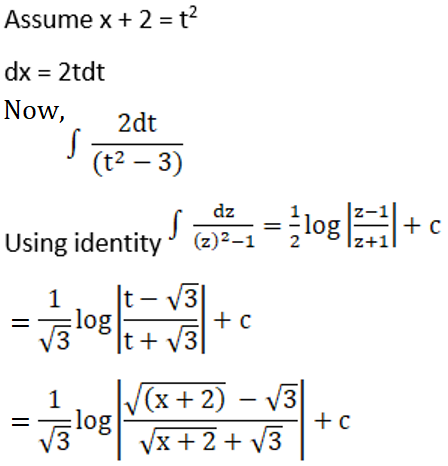
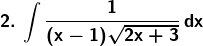
Solution:
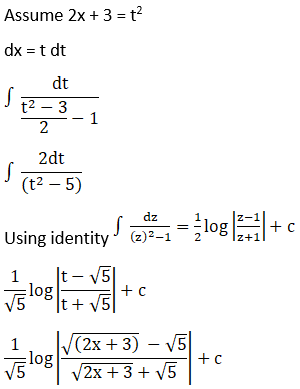
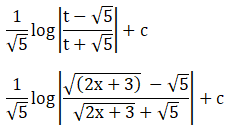
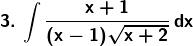
Solution:
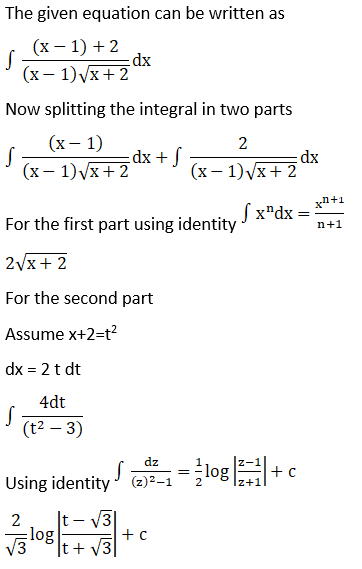
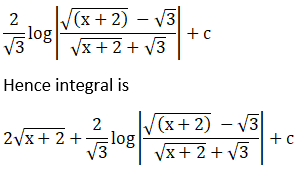
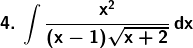
Solution:


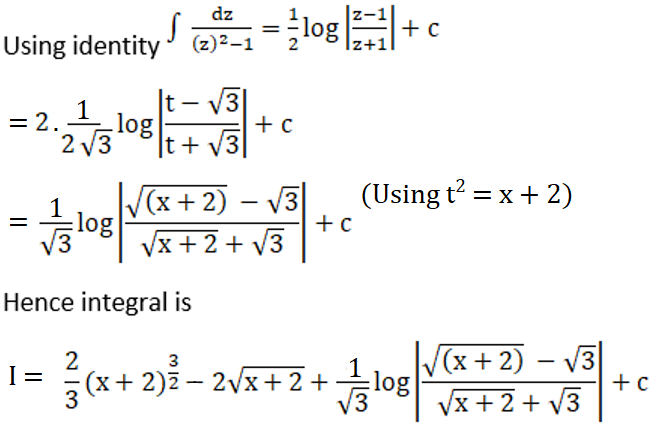
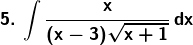
Solution: