Chapter 18 MAXIMA AND MINIMA
Class 12th Maths R D Sharma Solution
Access answers to Maths RD Sharma Solutions For Class 12 Chapter 18 – Maxima and Minima
Exercise 18.1 Page No: 18.7
Find the maximum and the minimum values, if any, without using derivatives of the following functions:
1. f (x) = 4x2 – 4x + 4 on R
Solution:
Given f (x) = 4x2 – 4x + 4 on R
= 4x2 – 4x + 1 + 3
By grouping the above equation we get,
= (2x – 1)2 + 3
Since, (2x – 1)2 ≥ 0
= (2x – 1)2 + 3 ≥ 3
= f(x) ≥ f (½)
Thus, the minimum value of f(x) is 3 at x = ½
Since, f(x) can be made large. Therefore maximum value does not exist.
2. f (x) = –(x – 1)2 + 2 on R
Solution:
Given f(x) = – (x – 1)2 + 2
It can be observed that (x – 1)2 ≥ 0 for every x ∈ R
Therefore, f(x) = – (x – 1)2 + 2 ≤ 2 for every x ∈ R
The maximum value of f is attained when (x – 1) = 0
(x – 1) = 0, x = 1
Since, Maximum value of f = f (1) = – (1 – 1)2 + 2 = 2
Hence, function f does not have minimum value.
3. f (x) = |x + 2| on R
Solution:
Given f (x) = |x + 2| on R
⇒ f(x) ≥ 0 for all x ∈ R
So, the minimum value of f(x) is 0, which attains at x = -2
Hence, f(x) = |x + 2| does not have the maximum value.
4. f (x) = sin 2x + 5 on R
Solution:
Given f (x) = sin 2x + 5 on R
We know that – 1 ≤ sin 2x ≤ 1
⇒ – 1 + 5 ≤ sin2x + 5 ≤ 1 + 5
⇒ 4 ≤ sin 2x + 5 ≤ 6
Hence, the maximum value and minimum value of f are 6 and 4 respectively.
5. f (x) = |sin 4x + 3| on R
Solution:
Given f (x) = |sin 4x + 3| on R
We know that – 1 ≤ sin 4x ≤ 1
⇒ 2 ≤ sin 4x + 3 ≤ 4
⇒ 2 ≤ |sin 4x + 3| ≤ 4
Hence, the maximum value and minimum value of f are 4 and 2 respectively.
Exercise 18.2 Page No: 18.16
Find the points of local maxima or local minima, if any, of the following functions, using the first derivative test. Also, find the local maximum or local minimum values, as the case may be:
1. f (x) = (x – 5)4
Solution:
Given f (x) = (x – 5)4
Differentiate with respect to x
f’(x) = 4(x – 5)3
For local maxima and minima
f‘(x) = 0
= 4(x – 5)3 = 0
= x – 5 = 0
x = 5
f‘(x) changes from negative to positive as passes through 5.
So, x = 5 is the point of local minima
Thus, local minima value is f (5) = 0
2. f (x) = x3 – 3x
Solution:
Given, f (x) = x3 – 3x
Differentiate with respect to x then we get,
f’ (x) = 3x2 – 3
Now, f‘(x) =0
3x2 = 3 ⇒ x = ±1
Again differentiate f’(x) = 3x2 – 3
f’’(x)= 6x
f’’(1)= 6 > 0
f’’ (– 1)= – 6 < 0
By second derivative test, x = 1 is a point of local minima and local minimum value of f at
x = 1 is f (1) = 13 – 3 = 1 – 3 = – 2
However, x = – 1 is a point of local maxima and local maxima value of f at
x = – 1 is
f (– 1) = (– 1)3 – 3(– 1)
= – 1 + 3
= 2
Hence, the value of minima is – 2 and maxima is 2.
3. f (x) = x3 (x – 1)2
Solution:
Given, f(x) = x3(x – 1)2
Differentiate with respect to x, we get,
f ‘(x) = 3x2(x – 1)2 + 2x3(x – 1)
= (x – 1) (3x2(x – 1) + 2x3)
= (x – 1) (3x3 – 3x2 + 2x3)
= (x – 1) (5x3 – 3x2)
= x2 (x – 1) (5x – 3)
For all maxima and minima,
f ’(x) = 0
= x2(x – 1) (5x – 3) = 0
By solving the above equation we get
x =0, 1, 3/5
At x = 3/5, f’(x) changes from negative to positive
Since, x = 3/5 is a point of Minima
At x =1, f‘(x) changes from positive to negative
Since, x =1 is point of maxima.
4. f (x) = (x – 1) (x + 2)2
Solution:
Given, f(x) = (x – 1) (x + 2)2
Differentiate with respect to x, we get,
f‘(x) = (x + 2)2 + 2(x – 1)(x + 2)
= (x + 2) (x + 2 + 2x – 2)
= (x + 2) (3x)
For all maxima and minima,
f’(x) = 0
(x + 2) (3x) = 0
By solving the above equation we get
x = 0, – 2
At x = – 2, f’(x) changes from positive to negative
Since, x = – 2 is a point of Maxima
At x = 0, f‘(x) changes from negative to positive
Since, x = 0 is point of Minima.
Hence, local min value = f (0) = – 4
Local max value = f (– 2) = 0.

Therefore x = 0, now for the values close to x = 0 and to the left of 0, f'(x) > 0
Also for values x = 0 and to the right of 0, f’(x) < 0
Therefore, by first derivative test, x = 0 is a point of local maxima and local minima value of f (x) is ½.
6. f (x) = x3 – 6x2 + 9x +15
Solution:
Given, f(x) = x3 – 6x2 + 9x + 15
Differentiate with respect to x, we get, f‘(x) = 3x2 – 12x + 9 = 3(x2 – 4x + 3)
= 3 (x – 3) (x – 1)
For all maxima and minima,
f’(x) = 0
= 3(x – 3) (x – 1) = 0
= x = 3, 1
At x = 1, f’(x) changes from positive to negative
Since, x = 1 is a point of Maxima
At x = 3, f‘(x) changes from negative to positive
Since, x = 3 is point of Minima.
Hence, local maxima value f (1) = (1)3 – 6(1)2 + 9(1) + 15 = 19
Local minima value f (3) = (3)3 – 6(3)2 + 9(3) + 15 = 15
7. f (x) = sin 2x, 0 < x < π
Solution:
Given f (x) = sin 2x
Differentiate w.r.t x, we get
f'(x) = 2 cos 2x, 0 < x < π
For the point of local maxima and minima, f’(x) = 0
2 cos 2x = 0
cos 2x = 0
2x = π/2, 3π/2
x = π/4, 3π/4
Now, at x = π/4, f’(x) changes from positive to negative

Exercise 18.3 Page No: 18.31
Find the points of local maxima or local minima and corresponding local maximum and local minimum values of each of the following functions. Also, find the points of inflection, if any:
(i) f(x) = x4 – 62x2 + 120x + 9
Solution:
Given f (x) = x4 – 62x2 + 120x + 9
∴ f'(x) = 4x3 – 124x + 120 = 4(x3 – 31x + 30)
f”(x) = 12x2 – 124 = 4(3x2 – 31)
For maxima and minima, f'(x) = 0
4(x3 – 31x + 30) = 0
So roots will be x = 5, 1, – 6
Now, f”(5) = 176 > 0
x = 5 is point of local minima
f”(1) = – 112 < 0
x = 1 is point of local maxima
f”(– 6) = 308 > 0
x = – 6 is point of local minima
Local max value = f (1) = 68
Local min value = f (5) = – 316 and f (– 6) = – 1647
(ii) f (x) = x3 – 6x2 + 9x + 15
Solution:
Given f (x) = x3 – 6x2 + 9x + 15
Differentiating f with respect to x
∴ f'(x) = 3x2 – 12x + 9 = 3(x2 – 4x + 3)
f” (x) = 6x – 12 = 6(x – 2)
For maxima and minima, f'(x) = 0
3(x2 – 4x + 3) = 0
So roots will be x = 3, 1
Now, f” (3) = 6 > 0
x = 3 is point of local minima
f”(1) = – 6 < 0
x = 1 is point of local maxima
Local max value = f (1) = 19 and local min value = f (3) = 15
(iii) f(x) = (x – 1) (x + 2)2
Solution:
Given f (x) = (x – 1) (x + 2)2
∴ f'(x) = (x + 2)2 + 2 (x – 1) (x + 2)
= (x + 2) (x + 2 + 2x – 2)
= (x + 2) (3x)
And f”(x) = 3(x + 2) + 3x
= 6x + 6
For maxima and minima, f'(x) = 0
(x + 2) (3x) = 0
So roots will be x = 0, – 2
Now, f” (0) = 6 > 0
x = 0 is point of local minima
f”(– 2) = – 6 < 0
x = -2 is point of local maxima
Local maxima value = f (– 2) = 0 and local minima value = f (0) = – 4
(iv) f (x) = 2/x – 2/x2, x > 0
Solution:
Given f (x) = 2/x – 2/x2, x > 0
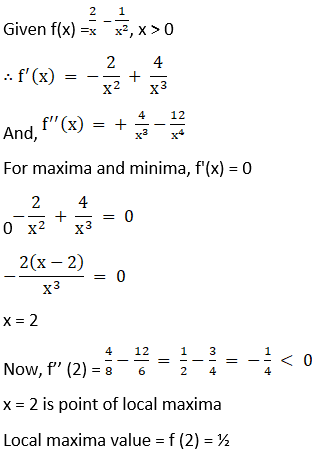
-2/x2 + 4/x3 = 0
-2(x – 2)/x3 = 0
⇒ (x – 2) = 0
⇒ x = 2
Now,
f’’(2) = 4/8 – 12/16 = ½ – ¾ = – ¼ < 0
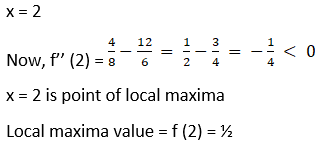
(v) f (x) = x ex
Solution:
Given f(x) = x ex
f'(x) = ex + x ex = ex(x + 1)
f”(x) = ex(x + 1) + ex
= ex(x + 2)
For maxima and minima,
f'(x) = 0
ex(x + 1) = 0
x = – 1
Now f’’ (– 1) = e – 1 = 1/e > 0
x = – 1 is point of local minima
Hence, local min = f (– 1) = – 1/e
2. Find the local extremum values of the following functions:
(i)
f(x) = (x – 1) (x – 2)2
Solution:
Given f(x) = (x – 1)(x – 2)2
f’(x) = (x – 2)2 + 2(x – 1)(x – 2)
= (x – 2) (x – 2 + 2x – 2)
= (x – 2) (3x – 4)
f’’(x) = (3x – 4) + 3(x – 2)
For maxima and minima, f'(x) = 0
(x – 2)(3x – 4) = 0
x = 2, 4/3
Now f’’ (2) > 0
x = 2 is point of local minima
f’’(4/3) = – 2 < 0
x = 4/3 is point of local maxima
Hence local maxima value = f (4/3) = 4/27
Local minima value = f (2) = 0
Solution:
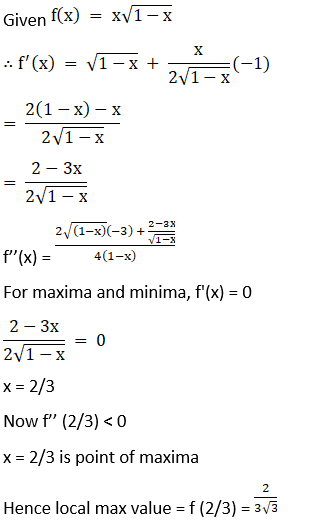
(iii) f (x) = – (x – 1)3(x + 1)2
Solution:
Given f (x) = – (x – 1)3(x + 1)2
f’(x) = – 3(x – 1)2(x + 1)2 – 2(x – 1)3(x + 1)
= – (x – 1)2(x + 1) (3x + 3 + 2x – 2)
= – (x – 1)2(x + 1) (5x + 1)
f’’(x) = – 2(x – 1)(x + 1)(5x + 1) – (x – 1)2(5x + 1) – 5(x – 1)2(x + 1)
For maxima and minima, f'(x) = 0
– (x – 1)2(x + 1) (5x + 1) = 0
x = 1, – 1, – 1/5
Now f’’ (1) = 0
x = 1 is inflection point
f’’(– 1) = – 4× – 4 = 16 > 0
x = – 1 is point of minima
f’’ (– 1/5) = – 5(36/25) × 4/5 = – 144/25 < 0
x = – 1/5 is point of maxima
Hence local max value = f (– 1/5) = 3456/3125
Local min value = f (– 1) = 0
3. The function y = a log x + bx2 + x has extreme values at x = 1 and x = 2. Find a and b.
Solution:
Given y = a log x + bx2 + x
On differentiating we get
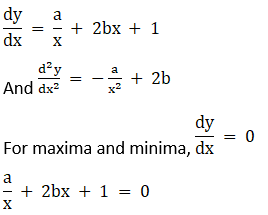
Given that extreme values exist at x = 1, 2
a + 2b = – 1 …… (1)
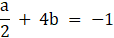
a + 8b = – 2 …… (2)
Solving (1) and (2) we get
a = – 2/3 b = – 1/6
4. Show that log x/x has a maximum value at x = e.
Solution:
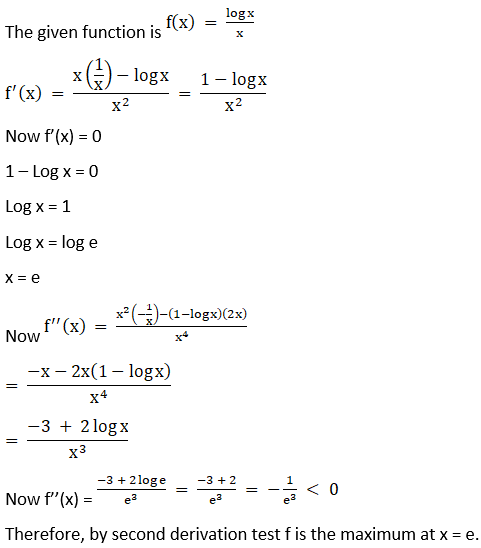 at
x = e
at
x = e
Therefore, by second derivative test f attains the maximum value at x = e
Exercise 18.4 Page No: 18.37
1. Find the absolute maximum and the absolute minimum values of the following functions in the given intervals:
(i) f (x) = 4x – x2/2 in [–2, 9/2]
Solution:

(ii) f (x) = (x – 1)2 + 3 on [–3, 1]
Solution:
Given function is f(x) = (x – 1)2 + 3
On differentiation we get
⇒ f'(x) = 2(x – 1)
Now, for local minima and local maxima we have f'(x) = 0
2(x – 1) = 0
x = 1
Then, we evaluate of f at critical point x = 1 and at the interval [– 3, 1]
f (1) = (1 – 1)2 + 3 = 3
f (– 3) = (– 3 – 1)2 + 3 = 19
Hence, we can conclude that the absolute maximum value of f on [– 3, 1] is 19 occurring at x = – 3 and the minimum value of f on [– 3, 1] is 3 occurring at x = 1
(iii) f (x) = 3x4 – 8x3 + 12x2 – 48x + 25 on [0, 3]
Solution:
Given function is f(x) = 3x4 – 8x3 + 12x2 – 48x + 25 on [0, 3]
On differentiating we get
f’ (x) = 12x3 – 24x2 + 24 x – 48
f’ (x) = 12 (x3 – 2x2 + 2x – 4)
f’ (x) = 12 (x – 2) (x2 + 2)
Now, for local minima and local maxima we have f'(x) = 0
x = 2 or x2 + 2 = 0 for which there are no real roots.
Therefore, we consider only x = 2 ∈ [0, 3].
Then, we evaluate of f at critical point x = 2 and at the interval [0, 3]
f (2) = 3 (2)4 – 8 (2)3 + 12 (2)2 – 48 (2) + 25
f (2) = 48 – 64 + 48 – 96 + 25 = – 39
f (0) = 3 (0)4 – 8 (0)3 + 12 (0)2 – 48 (0) + 25 = 25
f (3) = 3 (3)4 – 8 (3)3 + 12 (3)2 – 48 (3) + 25 = 16
Hence, we can conclude that the absolute maximum value of f on [0, 3] is 25 occurring at x = 0 and the minimum value of f on [0, 3] is – 39 occurring at x = 2
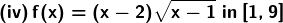
Solution:
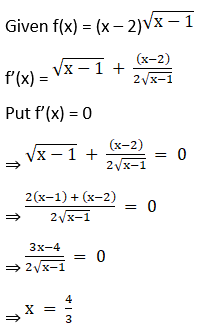

And,
f(9) = (9 – 2) √(9 – 1) = 7√8 = 14√2
Hence, we can conclude that the absolute maximum value of f is 14√2 occurring at x = 9 and the minimum value of f is -2 √3/9 occurring at x = 4/3.
2. Find the maximum value of 2x3 – 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [–3, –1].
Solution:
Let f(x) = 2x3 – 24 x + 107
∴ f'(x) = 6 x2 – 24 = 6(x2 – 4)
Now, for local maxima and local minima we have f'(x) = 0
⇒ 6(x2 – 4) = 0
⇒ x2 = 4
⇒ x = ±2
We first consider the interval [1, 3].
Then, we evaluate the value of f at the critical point x = 2 ∈ [1, 3] and at the end points of the interval [1, 3].
f (2) = 2 (23)– 24 (2) + 107 = 75
f (1) = 2(1)3 – 24(1) + 107 = 85
f (3) = 2(3)3– 24 (3) + 107 = 89
Hence, the absolute maximum value of f(x) in the interval [1, 3] is 89 occurring at x = 3,
Next, we consider the interval [– 3, – 1].
Evaluate the value of f at the critical point x = – 2 ∈ [-3, -1]
f (-3) = 2 (-3)3 – 24 (-3) + 107 = 125
f (-2) = 2 (-2)3 – 24 (-3) + 107 = 139
f (-1) = 2 (-1)3 – 24 (-2) + 107 = 129
Hence, the absolute maximum value of f is 139 and occurs when x = -2.
Exercise 18.5 Page No: 18.72
1. Determine two positive numbers whose sum is 15 and the sum of whose squares is minimum.
Solution:

Which implies S is minimum when a = 15/2 and b = 15/2.
2. Divide 64 into two parts such that the sum of the cubes of two parts is minimum.
Solution:
Let the two positive numbers be a and b.
Given a + b = 64 … (1)
We have, a3 + b3 is minima
Assume, S = a3 + b3
(From equation 1)
S = a3 + (64 – a)3
 of
S
of
S
Hence, the two number will be 32 and 32.
3. How should we choose two numbers, each greater than or equal to –2, whose sum is ½ so that the sum of the first and the cube of the second is minimum?
Solution:

dS/da = 0
1 + 3(½ – a)2 (-1) = 0
1 – 3(½ – a)2 = 0
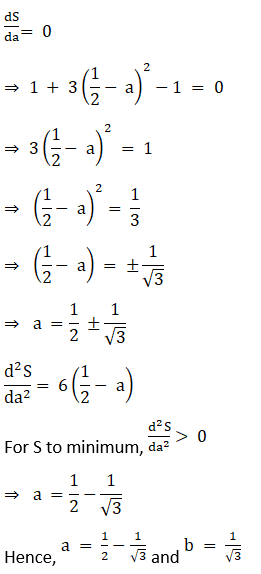
4. Divide 15 into two parts such that the square of one multiplied with the cube of the other is minimum.
Solution:
Let the given two numbers be x and y. Then,
x + y = 15 ….. (1)
y = (15 – x)
Now we have, z = x2 y3
z = x2 (15 – x)3 (from equation 1)
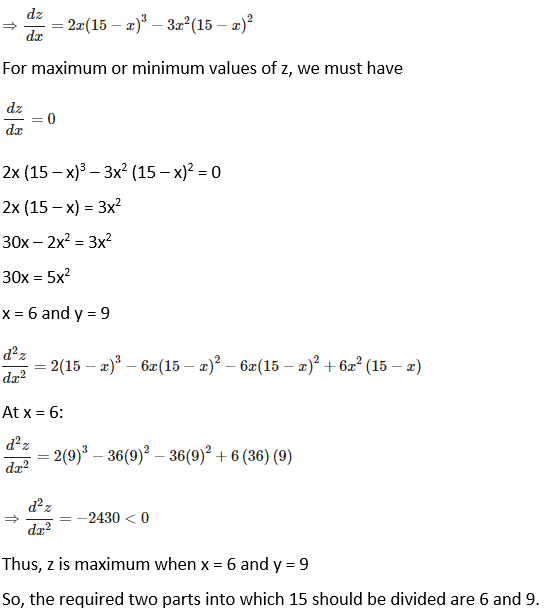
5. Of all the closed cylindrical cans (right circular), which enclose a given volume of 100 cm3, which has the minimum surface area?
Solution:
Let r and h be the radius and height of the cylinder, respectively. Then,
Volume (V) of the cylinder = πr2 h
⟹ 100 = πr2 h
⟹ h = 100/ πr2
Surface area (S) of the cylinder = 2 πr2 + 2 πr h = 2 πr2 + 2 πr × 100/ πr2
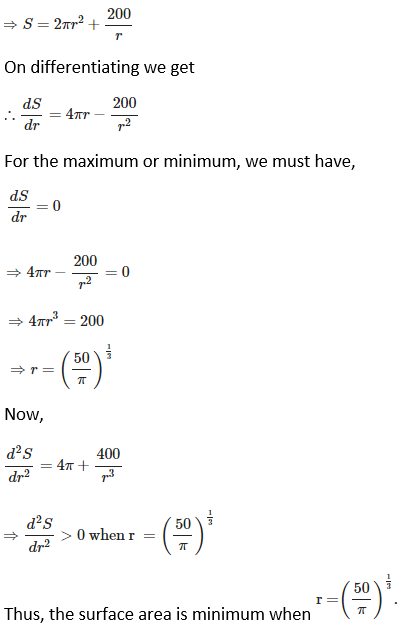
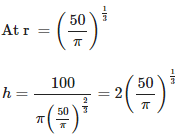
6. A beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by
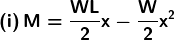
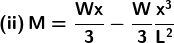
Find the point at which M is maximum in each case.
Solution:
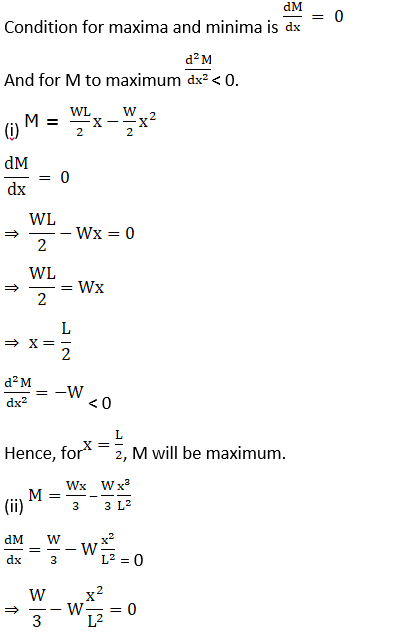
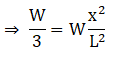

7. A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the circle and the square is minimum?
Solution:
Suppose the given wire, which is to be made into a square and a circle, is cut into two pieces of length x and y m respectively. Then,
x + y = 28 ⇒ y = (28 – x)
We know that perimeter of square, 4 (side) = x
Side = x/4
Area of square = (x/4)2 = x2/16
Circumference of circle, 2 π r = y
r = y/ 2 π
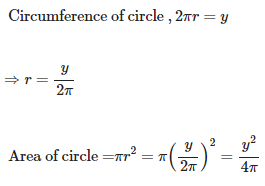
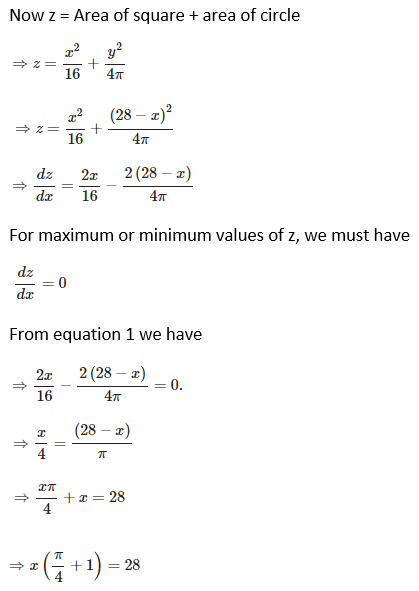
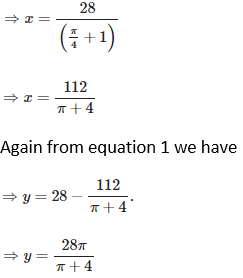
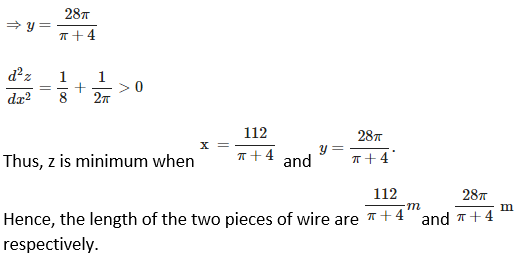
8. A wire of length 20 m is to be cut into two pieces. One of the pieces will be bent into shape of a square and the other into shape of an equilateral triangle. Where the wire should be cut so that the sum of the areas of the square and triangle is minimum?
Solution:
Suppose the wire, which is to be made into a square and a triangle, is cut into two pieces of length x and y respectively. Then,
x + y = 20 ⇒ y = (20 – x) …… (1)
We know that perimeter of square, 4 (side) = x
Side = x/4
Area of square = (x/4)2 = x2/16
Again we know that perimeter of triangle, 3 (side) = y.
Side = y/3
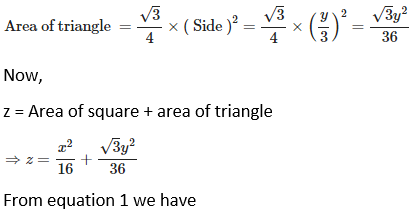
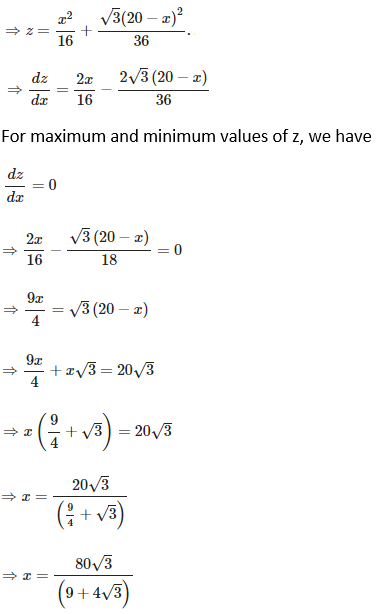

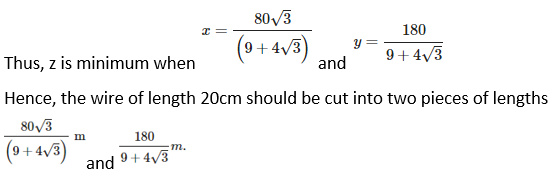
Hence, the wire of length 20 m should be cut into two pieces of lengths
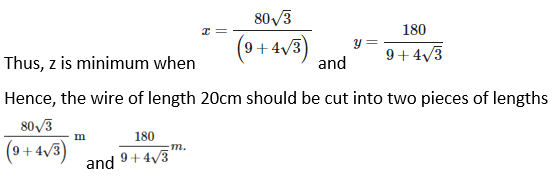
9. Given the sum of the perimeters of a square and a circle, show that the sum of their areas is least when one side of the square is equal to diameter of the circle.
Solution:
Let us say the sum of perimeter of square and circumference of circle be L
Given sum of the perimeters of a square and a circle.
Assuming, side of square = a and radius of circle = r
Then, L = 4a + 2πr ⇒ a = (L – 2πr)/4… (1)
Let the sum of area of square and circle be S
So, S = a2 + πr2
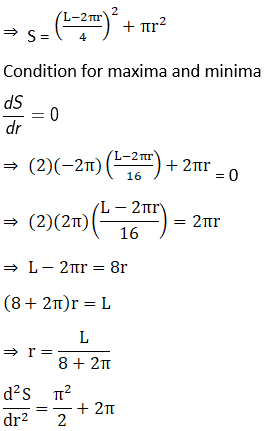
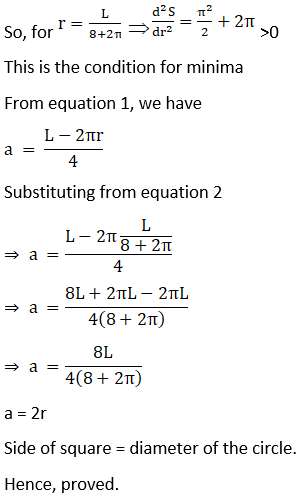
10. Find the largest possible area of a right angled triangle whose hypotenuse is 5 cm long.
Solution:
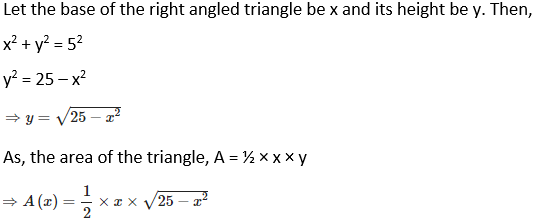

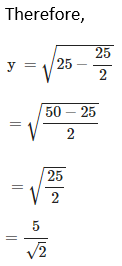
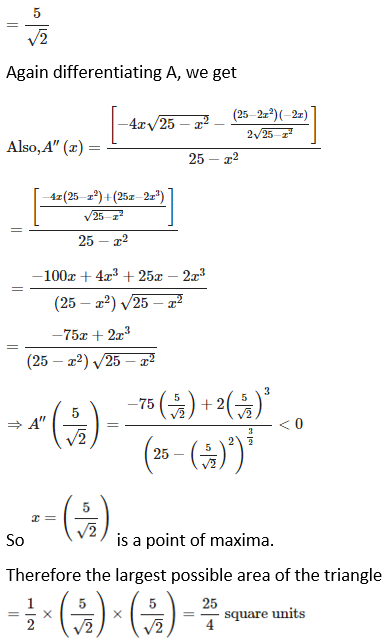
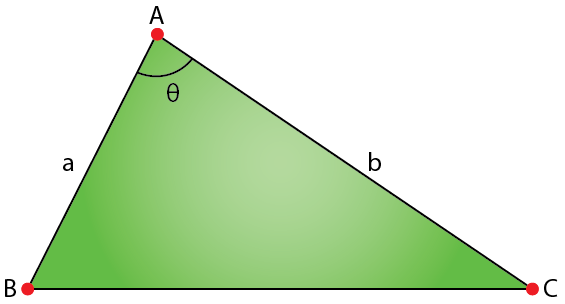
11. Two sides of a triangle have lengths ‘a’ and ‘b’ and the angle between them is θ. What value of θ will maximize the area of the triangle? Find the maximum area of the triangle also.
Solution:
It is given that two sides of a triangle have lengths a and b and the angle between them is θ.
Let the area of triangle be A

12. A square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each corner and folding up the flaps to form a box. What should be the side of the square to be cut off so that the volume of the box is maximum? Also, find this maximum volume
Solution:
Given side length of big square is 18 cm
Let the side length of each small square be a.
If by cutting a square from each corner and folding up the flaps we will get a cuboidal box with
Length, L = 18 – 2a
Breadth, B = 18 – 2a and
Height, H = a
Assuming, volume of box, V = LBH = a (18 – 2a)2
Condition for maxima and minima is
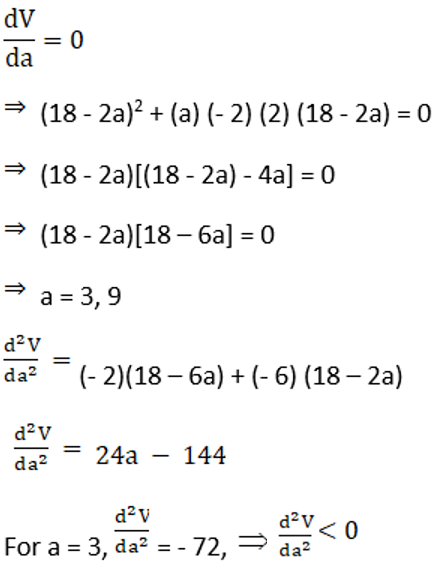
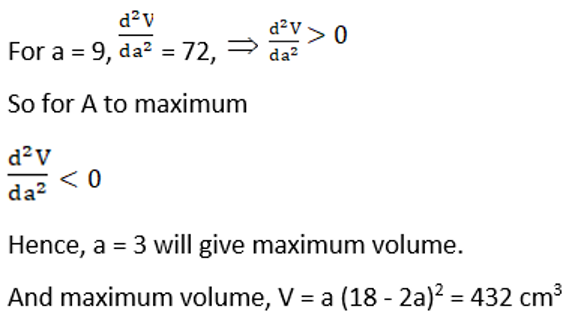
13. A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off squares from each corners and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum possible?
Solution:
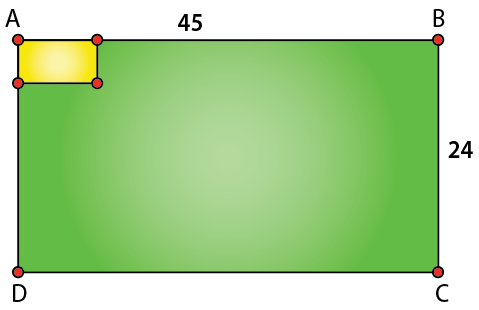
Given length of rectangle sheet = 45 cm
Breath of rectangle sheet = 24 cm
Let the side length of each small square be a.
If by cutting a square from each corner and folding up the flaps we will get a cuboidal box with
Length, L = 45 – 2a
Breadth, B = 24 – 2a and
Height, H = a
Assuming, volume of box, V = LBH = (45 – 2a)(24 – 2a)(a)
Condition for maxima and minima is
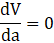
(45 – 2a) (24 – 2a) + (- 2) (24 – 2a) (a) + (45 – 2a) (- 2)(a) = 0
4a2 – 138a + 1080 + 4a2 – 48a + 4a2 – 90a = 0
12a2 – 276a + 1080= 0
a2 – 23a + 90= 0
a = 5, 18
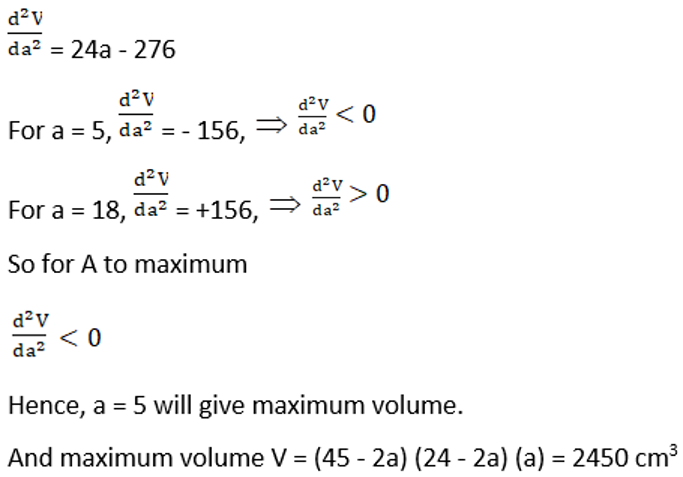
14. A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If building of tank cost Rs 70 per square metre for the base and Rs 45 per square metre for sides, what is the cost of least expensive tank?
Solution:
Let the length, breath and height of tank be l, b and h respectively.
Also, assume volume of tank as V
h = 2 m (given)
V = 8 m3
l b h = 8
2lb = 8 (given)
lb = 4
b = 4/l … (1)
Cost for building base = Rs 70/m2
Cost for building sides = Rs 45/m2
Cost for building the tank, C = Cost for base + cost for sides
C = lb × 70 + 2(l + b) h × 45
C = l(4/l) × 70 + 2(l + 4/l) (2) × 45 [Using (1)]
= 280 + 180 (l + 4/l)
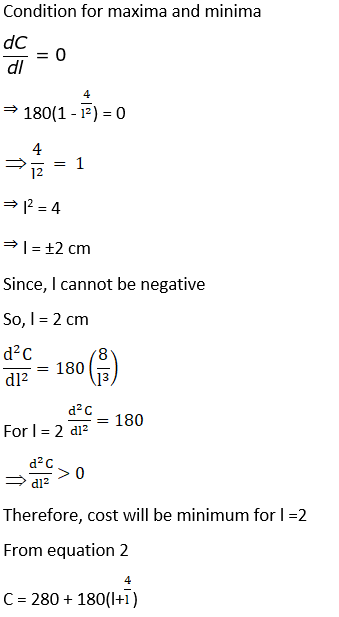
C = Rs 1000
15. A window in the form of a rectangle is surmounted by a semi-circular opening. The total perimeter of the window is 10 m. Find the dimensions of the rectangular part of the window to admit maximum light through the whole opening.
Solution:
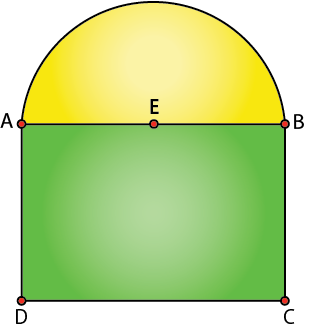
Let the radius of semicircle, length and breadth of rectangle be r, x and y respectively
AE = r
AB = x = 2r (semicircle is mounted over rectangle) …1
AD = y
Given Perimeter of window = 10 m
x + 2y + πr = 10
2r + 2y + πr = 10
2y = 10 – (π + 2).r

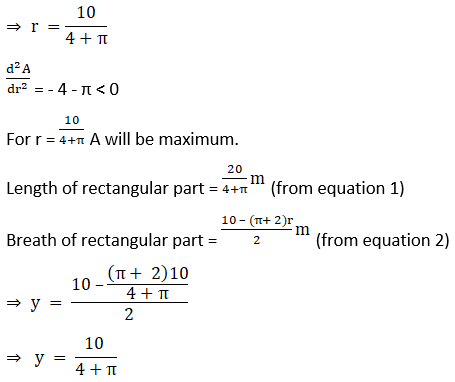
16. A large window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 metres find the dimensions of the rectangle that will produce the largest area of the window.
Solution:
Let the dimensions of the rectangle be x and y.
Therefore, the perimeter of window = x + y + x + x + y = 12
3x + 2y = 12
y = (12 – 3x)/2 …. (1)
Now,

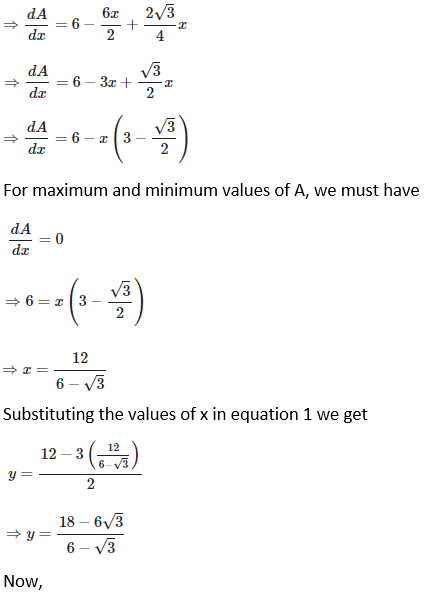
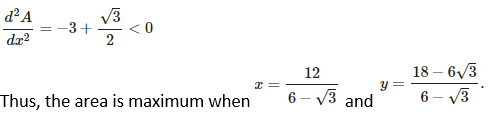
17. Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R/√3.
Solution:
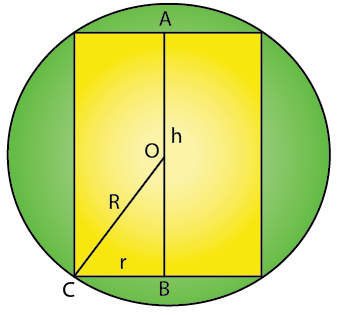

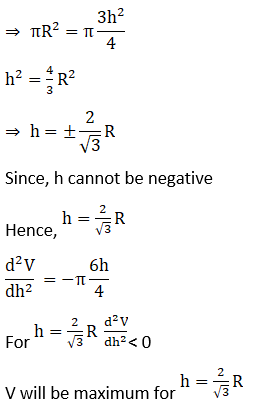
18. A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimensions of the rectangle so that its area is maximum. Find also the area.
Solution:
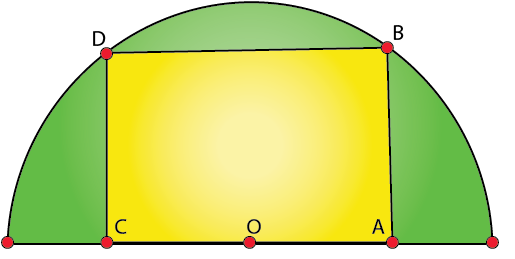
Let the length and breadth of rectangle ABCD be 2x and y respectively
Radius of semicircle = r (given)
In triangle OBA, where is the centre of the circle and mid-point of the side AC
r2 = x2 + y2 (Pythagoras theorem)
y2 = r2 – x2
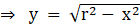 …
(1)
…
(1)
Let us say, area of rectangle = A = xy
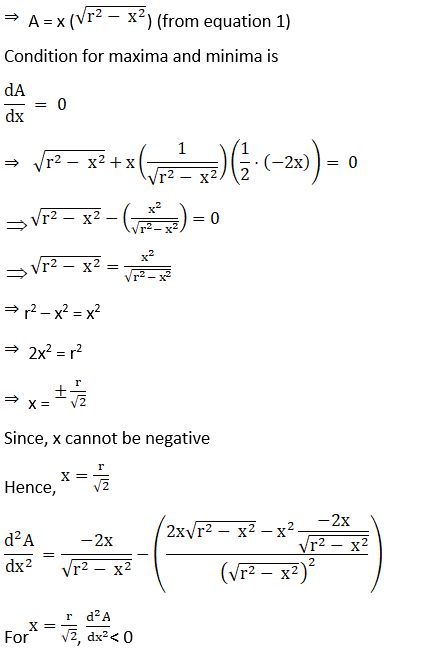
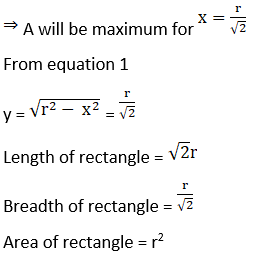 [Since,
l = 2x]
[Since,
l = 2x]
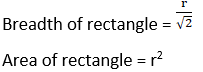
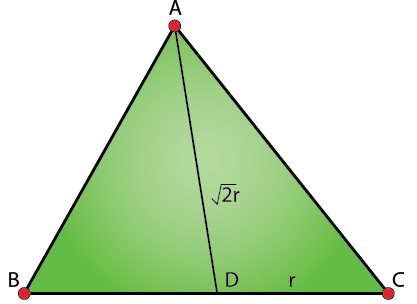
19. Prove that a conical tent of given capacity will require the least amount of canvas when the height is √2 times the radius of the base.
Solution:


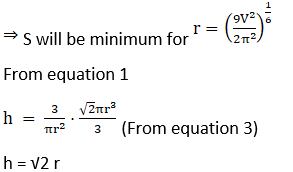
20. Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to 2/3 of the diameter of the sphere.
Solution:
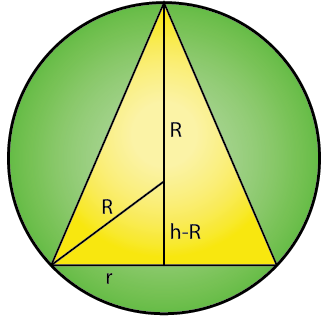
Let the radius and height of cone be r and h respectively
Radius of sphere = R
R2 = r2 + (h – R)2
R2 = r2 + h2 + R2 – 2hR
r2 = 2hR – h2 … (1)
Assuming volume of cone be V

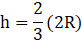
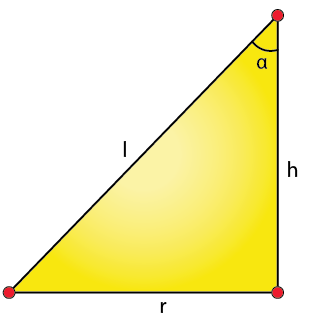
21. Prove that the semi – vertical angle of the right circular cone of given volume and least curved surface is cot-1√2
Solution:





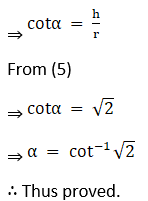
22. An isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a. Show that the area of the triangle is maximum when θ = π/6.
Solution:
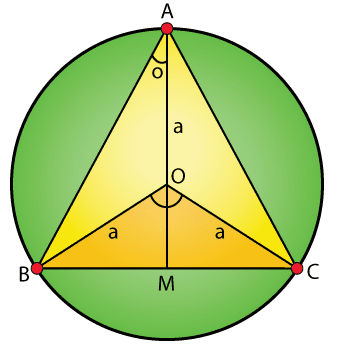
Δ ABC is an isosceles triangle such that AB = AC.
The vertical angle BAC = 2θ
Triangle is inscribed in the circle with center O and radius a.
Draw AM perpendicular to BC.
Since, Δ ABC is an isosceles triangle, the circumcenter of the circle will lie on the perpendicular from A to BC.
Let O be the circumcenter.
BOC = 2 × 2θ = 4θ (Using central angle theorem)
COM = 2θ (Since, Δ OMB and Δ OMC are congruent triangles)
OA = OB = OC = a (radius of the circle)
In Δ OMC,
CM = asin2θ
OM = acos2θ
BC = 2CM (Perpendicular from the center bisects the chord)
BC = 2asin2θ
Height of Δ ABC = AM = AO + OM
AM = a + acos2θ

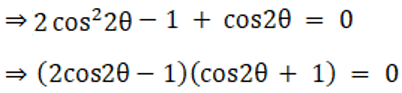

23. Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is 6√3r.
Solution:
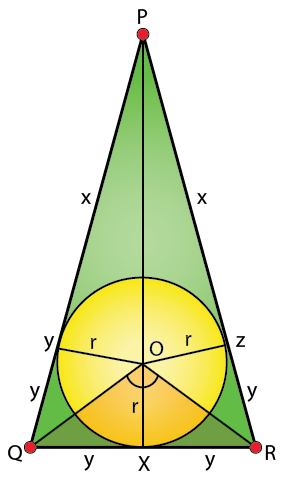
QR at X and PR at Z.
OZ, OX, OY are perpendicular to the sides PR, QR, PQ.
Here PQR is an isosceles triangle with sides PQ = PR and also from the figure,
⇒ PY = PZ = x
⇒ YQ = QX = XR = RZ = y
From the figure we can see that,
⇒ Area (ΔPQR) = Area (ΔPOR) + Area (ΔPOQ) + Area (ΔQOR)
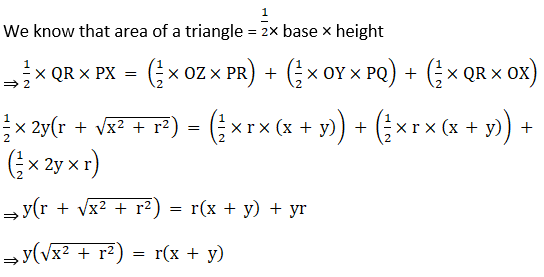



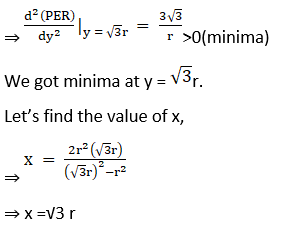
⇒ PER = 2(√3r) + 4(√3r)
⇒ PER = 6√3r
∴ Thus proved