Chapter 17 INCREASING AND DECREASING

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 17 – Increasing and Decreasing Functions

Exercise 17.1 Page No: 17.10

1. Prove that the function f(x) = log_e x is increasing on (0, ∞).

Solution:

Let x₁, x₂ ∈ (0, ∞)

We have, x₁ < x₂

⇒ log_e x₁ < log_e x₂

⇒ f (x₁) < f (x₂)

So, f(x) is increasing in (0, ∞)

2. Prove that the function f(x) = log_a x is increasing on (0, ∞) if a > 1 and decreasing on (0, ∞), if 0 < a < 1.

Solution:

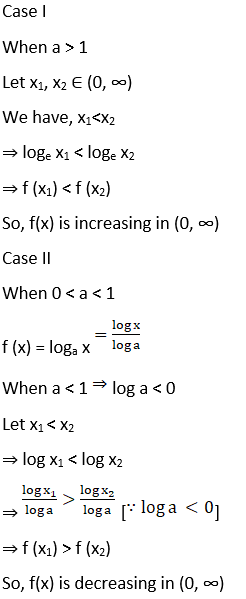
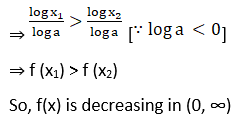
3. Prove that f(x) = ax + b, where a, b are constants and a > 0 is an increasing function on R.

Solution:

Given,

f (x) = ax + b, a > 0

Let x₁, x₂ ∈ R and x₁ > x₂

⇒ ax₁ > ax₂ for some a > 0

⇒ ax₁ + b> ax₂ + b for some b

⇒ f (x₁) > f(x₂)

Hence, x₁ > x₂ ⇒ f(x₁) > f(x₂)

So, f(x) is increasing function of R

4. Prove that f(x) = ax + b, where a, b are constants and a < 0 is a decreasing function on R.

Solution:

Given,

f (x) = ax + b, a < 0

Let x₁, x₂ ∈ R and x₁ > x₂

⇒ ax₁ < ax₂ for some a > 0

⇒ ax₁ + b < ax₂ + b for some b

⇒ f (x₁) < f(x₂)

Hence, x₁ > x₂⇒ f(x₁) < f(x₂)

So, f(x) is decreasing function of R

Exercise 17.2 Page No: 17.33

1. Find the intervals in which the following functions are increasing or decreasing.

(i) f (x) = 10 – 6x – 2x²

Solution:

(ii) f (x) = x² + 2x – 5

Solution:

(iii) f (x) = 6 – 9x – x²

Solution:

(iv) f(x) = 2x³ – 12x² + 18x + 15

Solution:

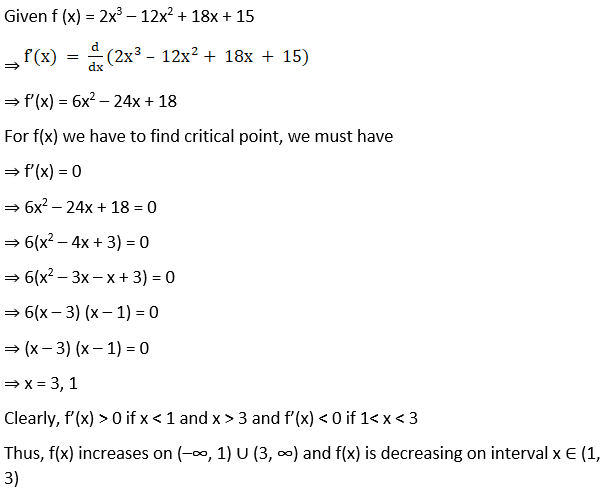
(v) f (x) = 5 + 36x + 3x² – 2x³

Solution:

Given f (x) = 5 + 36x + 3x² – 2x³

⇒

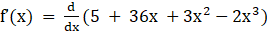
⇒ f’(x) = 36 + 6x – 6x²

For f(x) now we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 36 + 6x – 6x² = 0

⇒ 6(–x² + x + 6) = 0

⇒ 6(–x² + 3x – 2x + 6) = 0

⇒ –x² + 3x – 2x + 6 = 0

⇒ x² – 3x + 2x – 6 = 0

⇒ (x – 3) (x + 2) = 0

⇒ x = 3, – 2

Clearly, f’(x) > 0 if –2< x < 3 and f’(x) < 0 if x < –2 and x > 3

Thus, f(x) increases on x ∈ (–2, 3) and f(x) is decreasing on interval (–∞, –2) ∪ (3, ∞)

(vi) f (x) = 8 + 36x + 3x² – 2x³

Solution:

Given f (x) = 8 + 36x + 3x² – 2x³

Now differentiating with respect to x

⇒

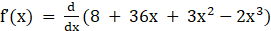
⇒ f’(x) = 36 + 6x – 6x²

For f(x) we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 36 + 6x – 6x² = 0

⇒ 6(–x² + x + 6) = 0

⇒ 6(–x² + 3x – 2x + 6) = 0

⇒ –x² + 3x – 2x + 6 = 0

⇒ x² – 3x + 2x – 6 = 0

⇒ (x – 3) (x + 2) = 0

⇒ x = 3, – 2

Clearly, f’(x) > 0 if –2 < x < 3 and f’(x) < 0 if x < –2 and x > 3

Thus, f(x) increases on x ∈ (–2, 3) and f(x) is decreasing on interval (–∞, 2) ∪ (3, ∞)

(vii) f(x) = 5x³ – 15x² – 120x + 3

Solution:

Given f(x) = 5x³ – 15x² – 120x + 3

Now by differentiating above equation with respect x, we get

⇒

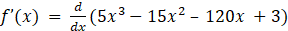
⇒ f’(x) = 15x² – 30x – 120

For f(x) we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 15x² – 30x – 120 = 0

⇒ 15(x² – 2x – 8) = 0

⇒ 15(x² – 4x + 2x – 8) = 0

⇒ x² – 4x + 2x – 8 = 0

⇒ (x – 4) (x + 2) = 0

⇒ x = 4, – 2

Clearly, f’(x) > 0 if x < –2 and x > 4 and f’(x) < 0 if –2 < x < 4

Thus, f(x) increases on (–∞,–2) ∪ (4, ∞) and f(x) is decreasing on interval x ∈ (–2, 4)

(viii) f(x) = x³ – 6x² – 36x + 2

Solution:

Given f (x) = x³ – 6x² – 36x + 2

⇒

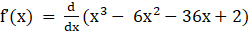
⇒ f’(x) = 3x² – 12x – 36

For f(x) we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 3x² – 12x – 36 = 0

⇒ 3(x² – 4x – 12) = 0

⇒ 3(x² – 6x + 2x – 12) = 0

⇒ x² – 6x + 2x – 12 = 0

⇒ (x – 6) (x + 2) = 0

⇒ x = 6, – 2

Clearly, f’(x) > 0 if x < –2 and x > 6 and f’(x) < 0 if –2< x < 6

Thus, f(x) increases on (–∞,–2) ∪ (6, ∞) and f(x) is decreasing on interval x ∈ (–2, 6)

(ix) f(x) = 2x³ – 15x² + 36x + 1

Solution:

Given f (x) = 2x³ – 15x² + 36x + 1

Now by differentiating above equation with respect x, we get

⇒

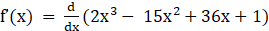
⇒ f’(x) = 6x² – 30x + 36

For f(x) we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 6x² – 30x + 36 = 0

⇒ 6 (x² – 5x + 6) = 0

⇒ 6(x² – 3x – 2x + 6) = 0

⇒ x² – 3x – 2x + 6 = 0

⇒ (x – 3) (x – 2) = 0

⇒ x = 3, 2

Clearly, f’(x) > 0 if x < 2 and x > 3 and f’(x) < 0 if 2 < x < 3

Thus, f(x) increases on (–∞, 2) ∪ (3, ∞) and f(x) is decreasing on interval x ∈ (2, 3)

(x) f (x) = 2x³ + 9x² + 12x + 20

Solution:

Given f (x) = 2x³ + 9x² + 12x + 20

Differentiating above equation we get

⇒

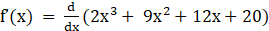
⇒ f’(x) = 6x² + 18x + 12

For f(x) we have to find critical point, we must have

⇒ f’(x) = 0

⇒ 6x² + 18x + 12 = 0

⇒ 6(x² + 3x + 2) = 0

⇒ 6(x² + 2x + x + 2) = 0

⇒ x² + 2x + x + 2 = 0

⇒ (x + 2) (x + 1) = 0

⇒ x = –1, –2

Clearly, f’(x) > 0 if –2 < x < –1 and f’(x) < 0 if x < –1 and x > –2

Thus, f(x) increases on x ∈ (–2,–1) and f(x) is decreasing on interval (–∞, –2) ∪ (–2, ∞)

2. Determine the values of x for which the function f(x) = x² – 6x + 9 is increasing or decreasing. Also, find the coordinates of the point on the curve y = x² – 6x + 9 where the normal is parallel to the line y = x + 5.

Solution:

Given f(x) = x² – 6x + 9

⇒

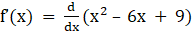
⇒ f’(x) = 2x – 6

⇒ f’(x) = 2(x – 3)

For f(x) let us find critical point, we must have

⇒ f’(x) = 0

⇒ 2(x – 3) = 0

⇒ (x – 3) = 0

⇒ x = 3

Clearly, f’(x) > 0 if x > 3 and f’(x) < 0 if x < 3

Thus, f(x) increases on (3, ∞) and f(x) is decreasing on interval x ∈ (–∞, 3)

Now, let us find coordinates of point

Equation of curve is f(x) = x² – 6x + 9

Slope of this curve is given by

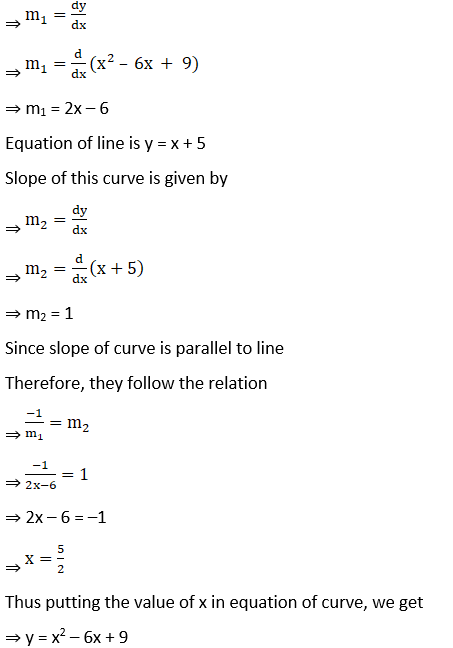
3. Find the intervals in which f(x) = sin x – cos x, where 0 < x < 2π is increasing or decreasing.

Solution:

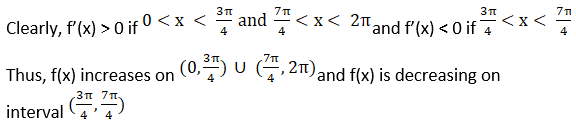
4. Show that f(x) = e^2x is increasing on R.

Solution:

Given f (x) = e^2x

⇒

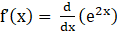
⇒ f’(x) = 2e^2x

For f(x) to be increasing, we must have

⇒ f’(x) > 0

⇒ 2e^2x > 0

⇒ e^2x > 0

Since, the value of e lies between 2 and 3

So, whatever be the power of e (that is x in domain R) will be greater than zero.

Thus f(x) is increasing on interval R

5. Show that f (x) = e^1/x, x ≠ 0 is a decreasing function for all x ≠ 0.

Solution:

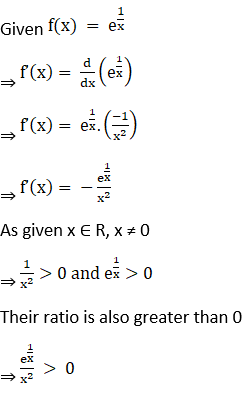
6. Show that f(x) = log_a x, 0 < a < 1 is a decreasing function for all x > 0.

Solution:

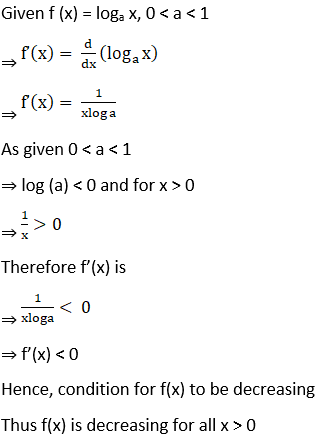
7. Show that f(x) = sin x is increasing on (0, π/2) and decreasing on (π/2, π) and neither increasing nor decreasing in (0, π).

Solution:

8. Show that f(x) = log sin x is increasing on (0, π/2) and decreasing on (π/2, π).

Solution:

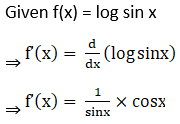
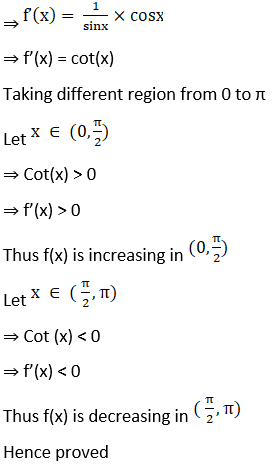
9. Show that f(x) = x – sin x is increasing for all x ϵ R.

Solution:

Given f (x) = x – sin x

⇒

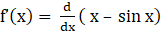
⇒ f’(x) = 1 – cos x

Now, as given x ϵ R

⇒ –1 < cos x < 1

⇒ –1 > cos x > 0

⇒ f’(x) > 0

Hence, condition for f(x) to be increasing

Thus f(x) is increasing on interval x ∈ R

10. Show that f(x) = x³ – 15x² + 75x – 50 is an increasing function for all x ϵ R.

Solution:

Given f(x) = x³ – 15x² + 75x – 50

⇒

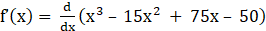
⇒ f’(x) = 3x² – 30x + 75

⇒ f’(x) = 3(x² – 10x + 25)

⇒ f’(x) = 3(x – 5)²

Now, as given x ϵ R

⇒ (x – 5)² > 0

⇒ 3(x – 5)² > 0

⇒ f’(x) > 0

Hence, condition for f(x) to be increasing

Thus f(x) is increasing on interval x ∈ R

11. Show that f(x) = cos² x is a decreasing function on (0, π/2).

Solution:

Given f (x) = cos² x

⇒

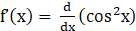
⇒ f’(x) = 2 cos x (–sin x)

⇒ f’(x) = –2 sin (x) cos (x)

⇒ f’(x) = –sin2x

Now, as given x belongs to (0, π/2).

⇒ 2x ∈ (0,
π)

⇒ Sin (2x)> 0

⇒ –Sin (2x) < 0

⇒ f’(x) < 0

Hence, condition for f(x) to be decreasing

Thus f(x) is decreasing on interval (0, π/2).

Hence proved

12. Show that f(x) = sin x is an increasing function on (–π/2, π/2).

Solution:

Given f (x) = sin x

⇒

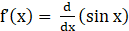
⇒ f’(x) = cos x

Now, as given x ∈ (–π/2, π/2).

That is 4^th quadrant, where

⇒ Cos x> 0

⇒ f’(x) > 0

Hence, condition for f(x) to be increasing

Thus f(x) is increasing on interval (–π/2, π/2).

13. Show that f(x) = cos x is a decreasing function on (0, π), increasing in (–π, 0) and neither increasing nor decreasing in (–π, π).

Solution:

Given f(x) = cos x

⇒

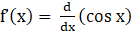
⇒ f’(x) = –sin x

Taking different region from 0 to 2π

Let x ∈ (0, π).

⇒ Sin(x) > 0

⇒ –sin x < 0

⇒ f’(x) < 0

Thus f(x) is decreasing in (0, π)

Let x ∈ (–π, o).

⇒ Sin (x) < 0

⇒ –sin x > 0

⇒ f’(x) > 0

Thus f(x) is increasing in (–π, 0).

Therefore, from above condition we find that

⇒ f (x) is decreasing in (0, π) and increasing in (–π, 0).

Hence, condition for f(x) neither increasing nor decreasing in (–π, π)

14. Show that f(x) = tan x is an increasing function on (–π/2, π/2).

Solution:

Given f (x) = tan x

⇒

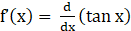
⇒ f’(x) = sec²x

Now, as given

x ∈ (–π/2, π/2).

That is 4^th quadrant, where

⇒ sec²x > 0

⇒ f’(x) > 0

Hence, Condition for f(x) to be increasing

Thus f(x) is increasing on interval (–π/2, π/2).

15. Show that f(x) = tan^–1 (sin x + cos x) is a decreasing function on the interval (π/4, π /2).

Solution:

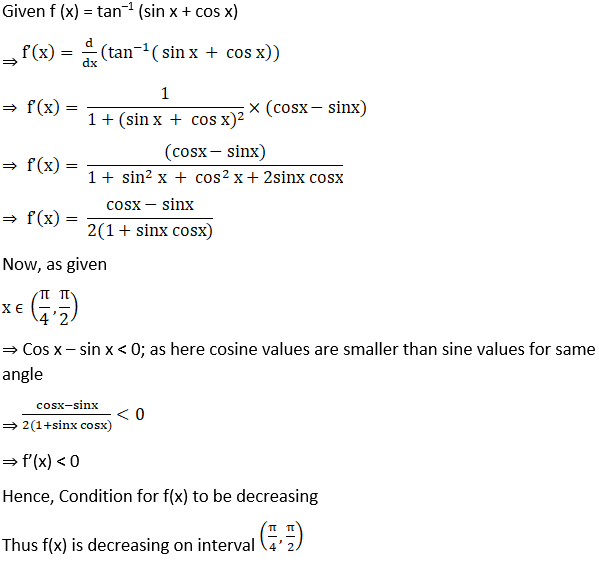
16. Show that the function f (x) = sin (2x + π/4) is decreasing on (3π/8, 5π/8).

Solution:

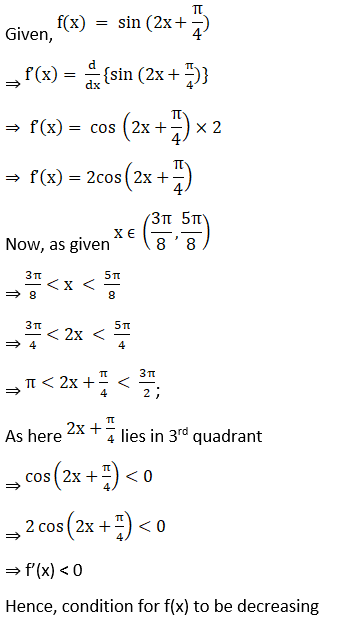
Thus f (x) is decreasing on the interval (3π/8, 5π/8).

17. Show that the function f(x) = cot^–1 (sin x + cos x) is decreasing on (0, π/4) and increasing on (π/4, π/2).

Solution:

Given f(x) = cot^–1 (sin x + cos x)

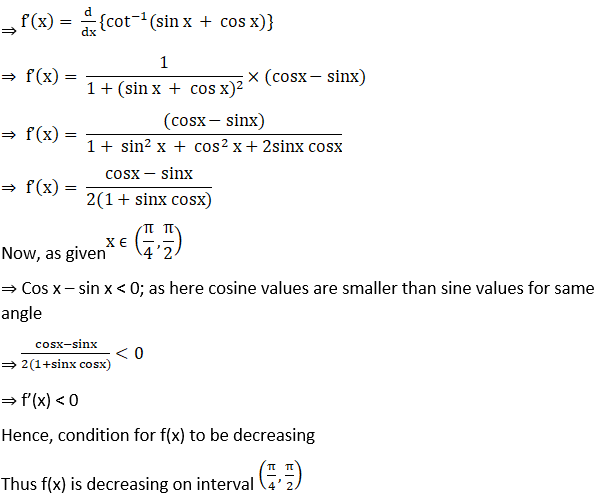
18. Show that f(x) = (x – 1) e^x + 1 is an increasing function for all x > 0.

Solution:

Given f (x) = (x – 1) e^x + 1

Now differentiating the given equation with respect to x, we get

⇒

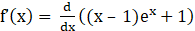
⇒ f’(x) = e^x + (x – 1) e^x

⇒ f’(x) = e^x(1+ x – 1)

⇒ f’(x) = x e^x

As given x > 0

⇒ e^x > 0

⇒ x e^x > 0

⇒ f’(x) > 0

Hence, condition for f(x) to be increasing

Thus f(x) is increasing on interval x > 0

19. Show that the function x² – x + 1 is neither increasing nor decreasing on (0, 1).

Solution:

Given f(x) = x² – x + 1

Now by differentiating the given equation with respect to x, we get

⇒

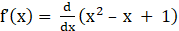
⇒ f’(x) = 2x – 1

Taking different region from (0, 1)

Let x ∈ (0, ½)

⇒ 2x – 1 < 0

⇒ f’(x) < 0

Thus f(x) is decreasing in (0, ½)

Let x ∈ (½, 1)

⇒ 2x – 1 > 0

⇒ f’(x) > 0

Thus f(x) is increasing in (½, 1)

Therefore, from above condition we find that

⇒ f (x) is decreasing in (0, ½)  and increasing in (½, 1)

Hence, condition for f(x) neither increasing nor decreasing in (0, 1)

20. Show that f(x) = x⁹ + 4x⁷ + 11 is an increasing function for all x ϵ R.

Solution:

Given f (x) = x⁹ + 4x⁷ + 11

Now by differentiating above equation with respect to x, we get

⇒

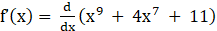
⇒ f’(x) = 9x⁸ + 28x⁶

⇒ f’(x) = x⁶(9x² + 28)

As given x ϵ R

⇒ x⁶ > 0 and 9x² + 28 > 0

⇒ x⁶ (9x² + 28) > 0

⇒ f’(x) > 0

Hence, condition for f(x) to be increasing

Thus f(x) is increasing on interval x ∈ R