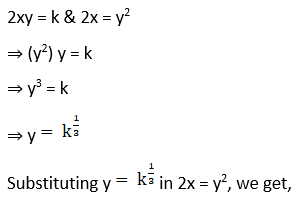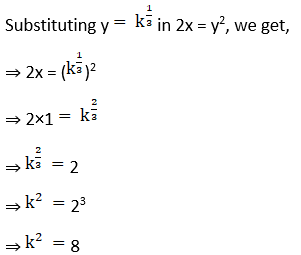Chapter 16 TANGENTS AND NORMALS

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 16 – Tangents and Normals

Exercise 16.1 Page No: 16.10

1. Find the Slopes of the tangent and the normal to the following curves at the indicated points:

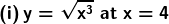
Solution:

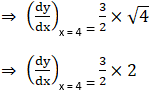
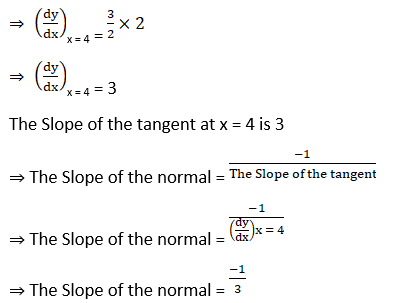
(ii) y = √x at x = 9

Solution:

⇒ The Slope of the normal = – 6

(iii) y = x³ – x at x = 2

Solution:

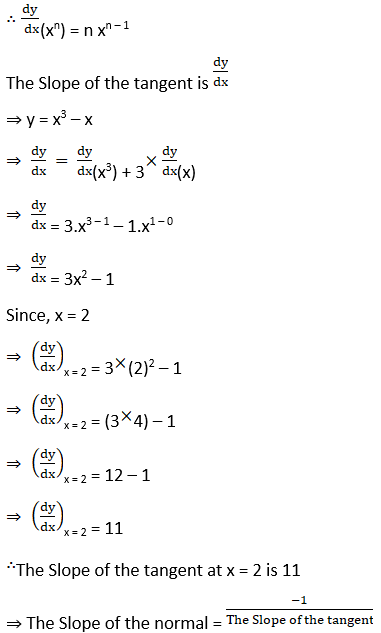
(iv) y = 2x² + 3 sin x at x = 0

Solution:

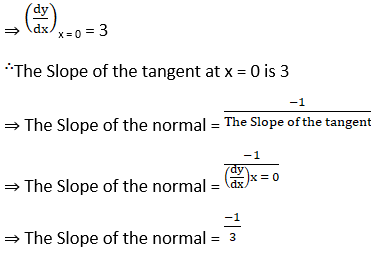
(v) x = a (θ – sin θ), y = a (1 + cos θ) at θ = -π /2

Solution:

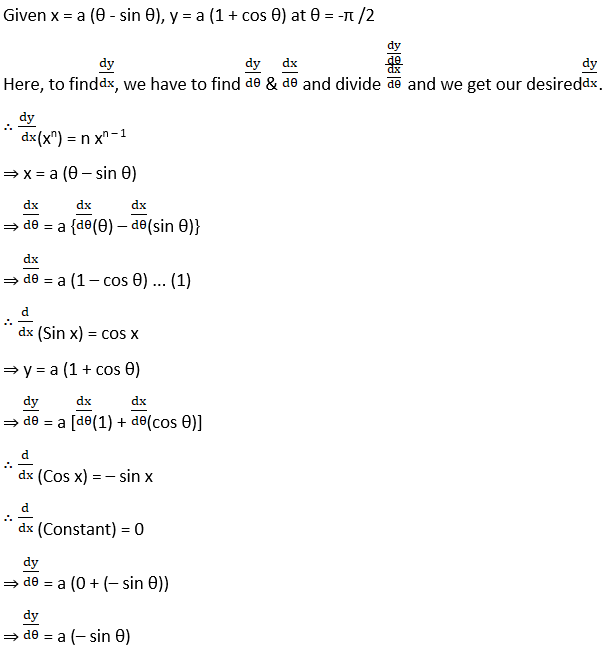
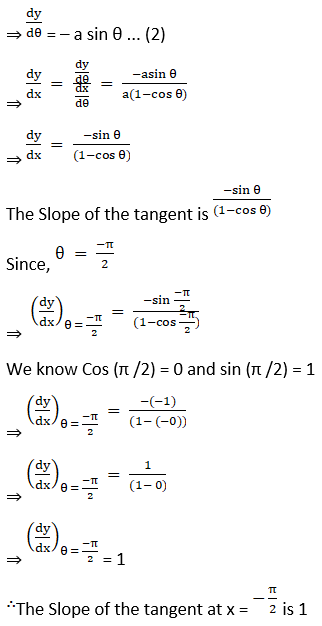
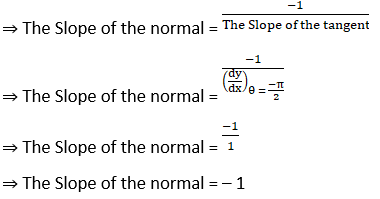
(vi) x = a cos³ θ, y = a sin³ θ at θ = π /4

Solution:

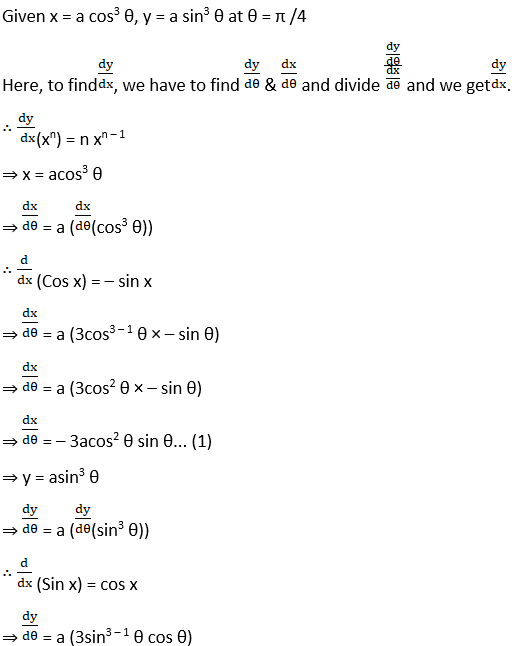
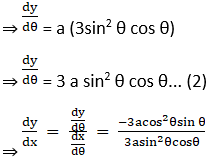
(vii) x = a (θ – sin θ), y = a (1 – cos θ) at θ = π /2

Solution:

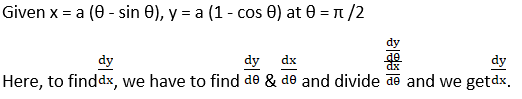
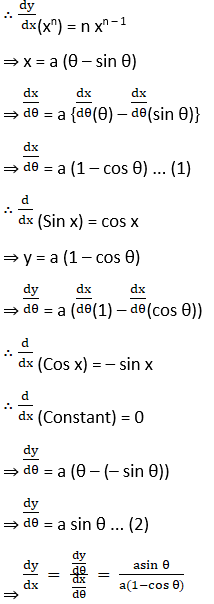
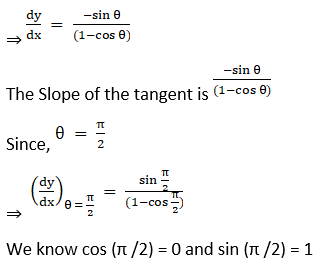
(viii) y = (sin 2x + cot x + 2)² at x = π /2

Solution:

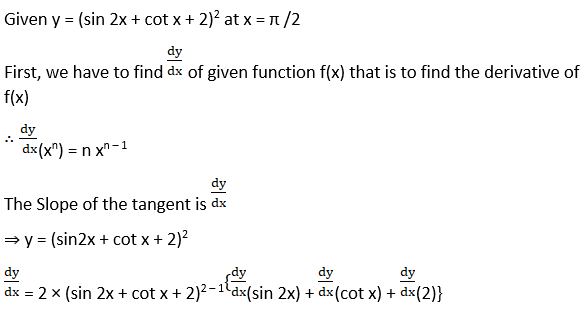
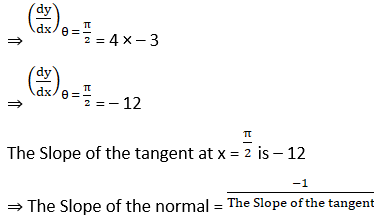
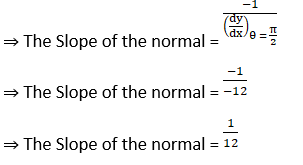
(ix) x² + 3y + y² = 5 at (1, 1)

Solution:

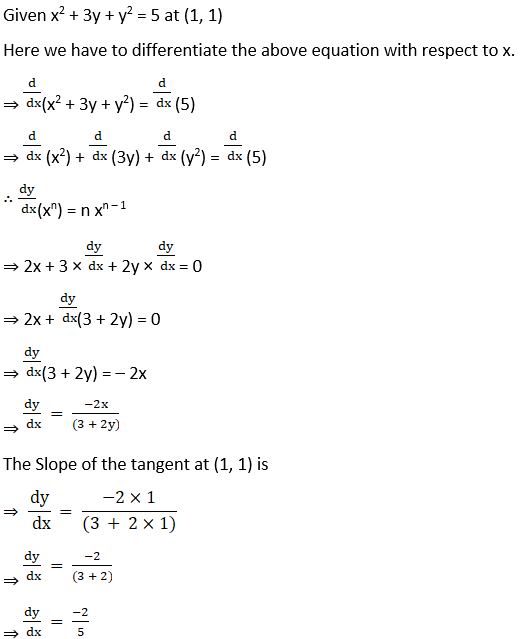
(x) x y = 6 at (1, 6)

Solution:

2. Find the values of a and b if the Slope of the tangent to the curve x y + a x + by = 2 at (1, 1) is 2.

Solution:

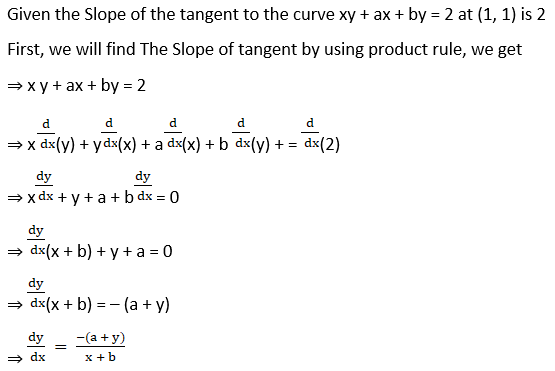
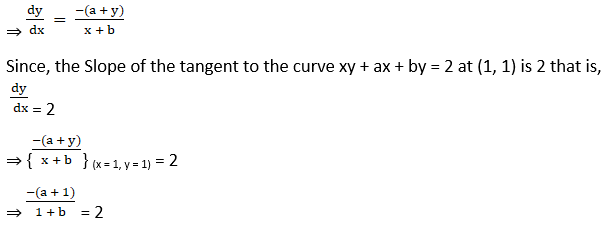
⇒ – a – 1 = 2(1 + b)

⇒ – a – 1 = 2 + 2b

⇒ a + 2b = – 3 … (1)

Also, the point (1, 1) lies on the curve xy + ax + by = 2, we have

1 × 1 + a × 1 + b × 1 = 2

⇒ 1 + a + b = 2

⇒ a + b = 1 … (2)

From (1) & (2), we get b = -4

Substitute b = – 4 in a + b = 1

a – 4 = 1

⇒ a = 5

So the value of a = 5 & b = – 4

3. If the tangent to the curve y = x³ + a x + b at (1, – 6) is parallel to the line x – y + 5 = 0, find a and b

Solution:

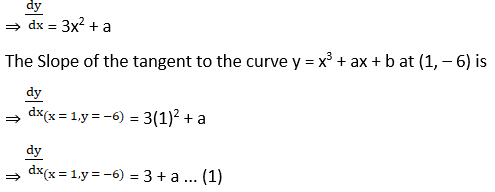
The given line is x – y + 5 = 0

y = x + 5 is the form of equation of a straight line y = mx + c, where m is the Slope of the line.

So the slope of the line is y = 1 × x + 5

So the Slope is 1. … (2)

Also the point (1, – 6) lie on the tangent, so

x = 1 & y = – 6 satisfies the equation, y = x³ + ax + b

– 6 = 1³ + a × 1 + b

⇒ – 6 = 1 + a + b

⇒ a + b = – 7 … (3)

Since, the tangent is parallel to the line, from (1) & (2)

Hence, 3 + a = 1

⇒ a = – 2

From (3)

a + b = – 7

⇒ – 2 + b = – 7

⇒ b = – 5

So the value is a = – 2 & b = – 5

4. Find a point on the curve y = x³ – 3x where the tangent is parallel to the chord joining (1, – 2) and (2, 2).

Solution:

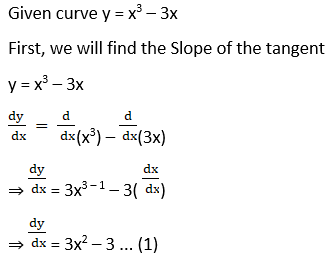
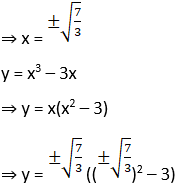
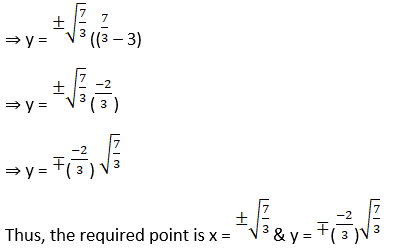
5. Find a point on the curve y = x³ – 2x² – 2x at which the tangent lines are parallel to the line y = 2x – 3.

Solution:

Given the curve y = x³ – 2x² – 2x and a line y = 2x – 3

First, we will find the slope of tangent

y = x³ – 2x² – 2x

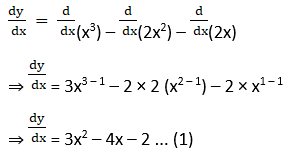
y = 2x – 3 is the form of equation of a straight line y = mx + c, where m is the Slope of the line.

So the slope of the line is y = 2 × (x) – 3

Thus, the Slope = 2. … (2)

From (1) & (2)

⇒ 3x² – 4x – 2 = 2

⇒ 3x² – 4x = 4

⇒ 3x² – 4x – 4 = 0

We will use factorization method to solve the above Quadratic equation.

⇒ 3x² – 6x + 2x – 4 = 0

⇒ 3 x (x – 2) + 2 (x – 2) = 0

⇒ (x – 2) (3x + 2) = 0

⇒ (x – 2) = 0 & (3x + 2) = 0

⇒ x = 2 or

x = -2/3

Substitute x = 2 & x = -2/3 in y = x³ – 2x² – 2x

When x = 2

⇒ y = (2)³ – 2 × (2)² – 2 × (2)

⇒ y = 8 – (2 × 4) – 4

⇒ y = 8 – 8 – 4

⇒ y = – 4

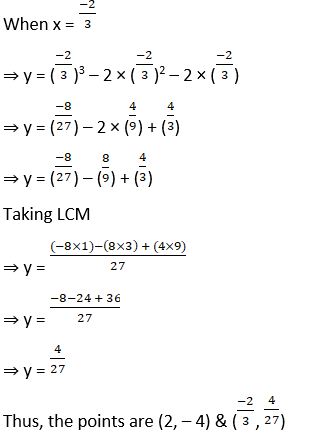
6. Find a point on the curve y² = 2x³ at which the Slope of the tangent is 3

Solution:

Given the curve y² = 2x³ and the Slope of tangent is 3

y² = 2x³

Differentiating the above with respect to x

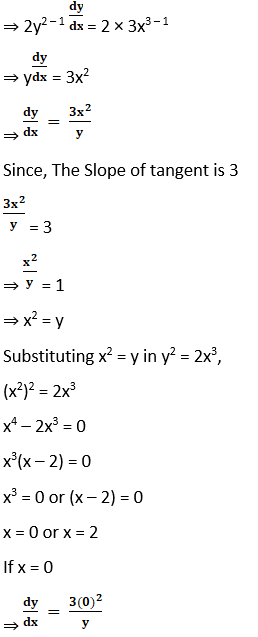
dy/dx = 0 which is not possible.

So we take x = 2 and substitute it in y² = 2x³, we get

y² = 2(2)³

y² = 2 × 8

y² = 16

y = 4

Thus, the required point is (2, 4)

7. Find a point on the curve x y + 4 = 0 at which the tangents are inclined at an angle of 45^o with the x–axis.

Solution:

Substitute in xy + 4 = 0, we get

⇒ x (– x) + 4 = 0

⇒ – x² + 4 = 0

⇒ x² = 4

⇒ x =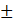
2

So when x = 2, y = – 2

And when x = – 2, y = 2

Thus, the points are (2, – 2) & (– 2, 2)

8. Find a point on the curve y = x² where the Slope of the tangent is equal to the x – coordinate of the point.

Solution:

Given the curve is y = x²

y = x²

Differentiating the above with respect to x

From (1) & (2), we get,

2x = x

⇒ x = 0.

Substituting this in y = x², we get,

y = 0²

⇒ y = 0

Thus, the required point is (0, 0)

9. At what point on the circle x² + y² – 2x – 4y + 1 = 0, the tangent is parallel to x – axis.

Solution:

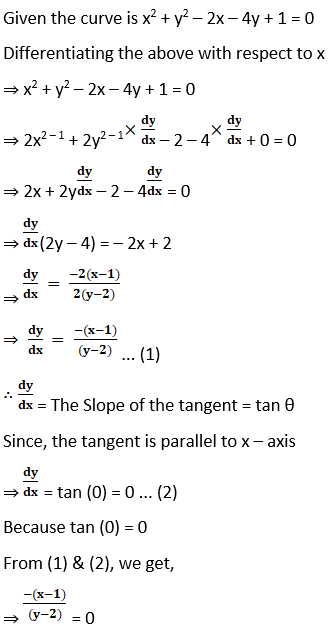
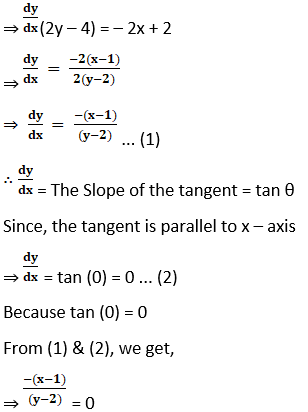
⇒ – (x – 1) = 0

⇒ x = 1

Substituting x = 1 in x² + y² – 2x – 4y + 1 = 0, we get,

⇒ 1² + y² – 2(1) – 4y + 1 = 0

⇒ 1 – y² – 2 – 4y + 1 = 0

⇒ y² – 4y = 0

⇒ y (y – 4) = 0

⇒ y = 0 and y = 4

Thus, the required point is (1, 0) and (1, 4)

10. At what point of the curve y = x² does the tangent make an angle of 45^o with the x–axis?

Solution:

Given the curve is y = x²

Differentiating the above with respect to x

⇒ y = x²

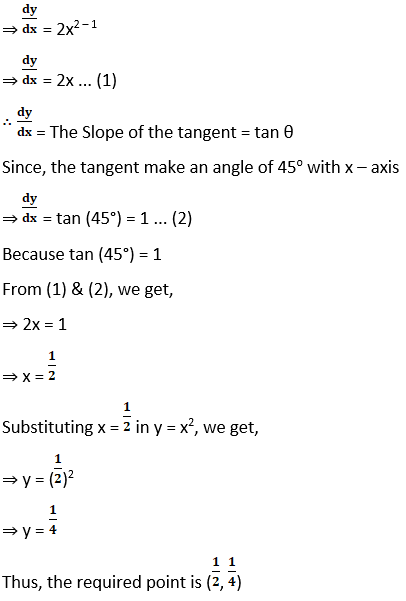
Exercise 16.2 Page No: 15.27

1. Find the equation of the tangent to the curve √x + √y = a, at the point (a²/4, a²/4).

Solution:

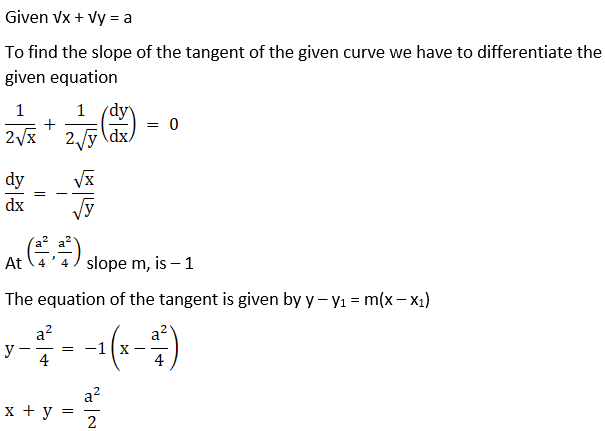
2. Find the equation of the normal to y = 2x³ – x² + 3 at (1, 4).

Solution:

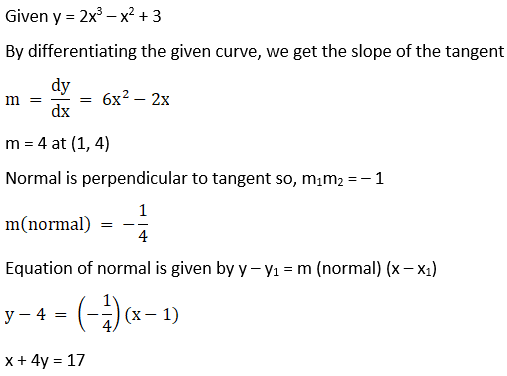
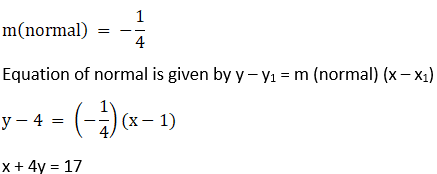
3. Find the equation of the tangent and the normal to the following curves at the indicated points:

(i) y = x⁴ – 6x³ + 13x² – 10x + 5 at (0, 5)

Solution:

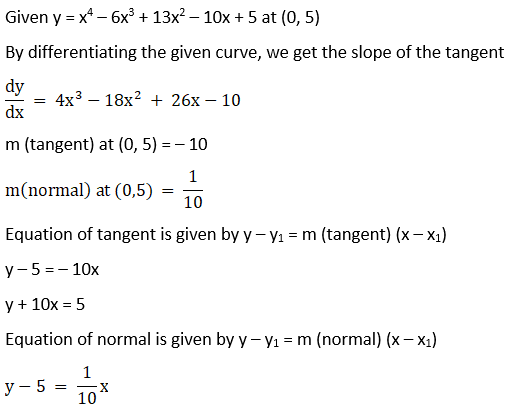
(ii) y = x⁴ – 6x³ + 13x² – 10x + 5 at x = 1 y = 3

Solution:

(iii) y = x² at (0, 0)

Solution:

Given y = x² at (0, 0)

By differentiating the given curve, we get the slope of the tangent

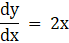
m (tangent) at (x = 0) = 0

Normal is perpendicular to tangent so, m₁m₂ = – 1

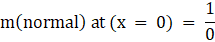
We can see that the slope of normal is not defined

Equation of tangent is given by y – y₁ = m (tangent) (x – x₁)

y = 0

Equation of normal is given by y – y₁ = m (normal) (x – x₁)

x = 0

(iv) y = 2x² – 3x – 1 at (1, – 2)

Solution:

Given y = 2x² – 3x – 1 at (1, – 2)

By differentiating the given curve, we get the slope of the tangent

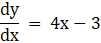
m (tangent) at (1, – 2) = 1

Normal is perpendicular to tangent so, m₁m₂ = – 1

m (normal) at (1, – 2) = – 1

Equation of tangent is given by y – y₁ = m (tangent) (x – x₁)

y + 2 = 1(x – 1)

y = x – 3

Equation of normal is given by y – y₁ = m (normal) (x – x₁)

y + 2 = – 1(x – 1)

y + x + 1 = 0

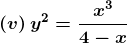
Solution:

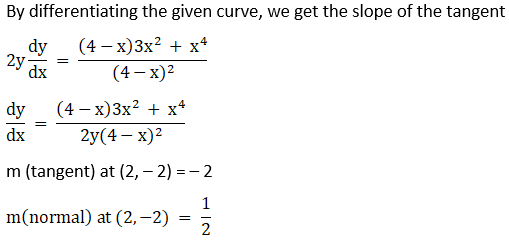
Equation of tangent is given by y – y₁ = m (tangent) (x – x₁)

y + 2 = – 2(x – 2)

y + 2x = 2

Equation of normal is given by y – y₁ = m (normal) (x – x₁)

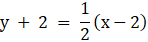
2y + 4 = x – 2

2y – x + 6 = 0

4. Find the equation of the tangent to the curve x = θ + sin θ, y = 1 + cos θ at θ = π/4.

Solution:

5. Find the equation of the tangent and the normal to the following curves at the indicated points:

(i) x = θ + sin θ, y = 1 + cos θ at θ = π/2

Solution:

Given x = θ + sin θ, y = 1 + cos θ at θ = π/2

By differentiating the given equation with respect to θ, we get the slope of the tangent

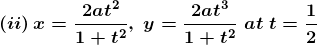
Solution:

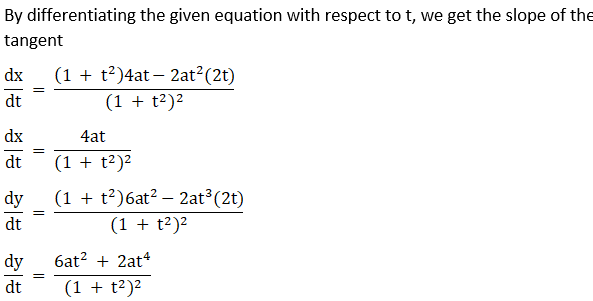
(iii) x = at², y = 2at at t = 1.

Solution:

(iv) x = a sec t, y = b tan t at t.

Solution:

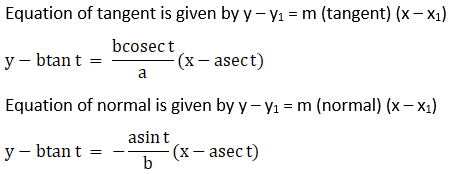
(v) x = a (θ + sin θ), y = a (1 – cos θ) at θ

Solution:

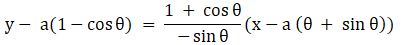
(vi) x = 3 cos θ – cos³ θ, y = 3 sin θ – sin³θ

Solution:

6. Find the equation of the normal to the curve x² + 2y² – 4x – 6y + 8 = 0 at the point whose abscissa is 2.

Solution:

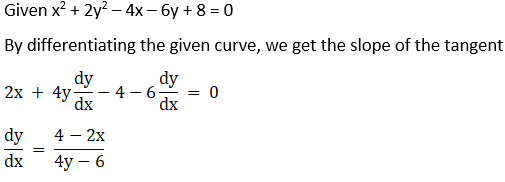
Finding y co – ordinate by substituting x in the given curve

2y² – 6y + 4 = 0

y² – 3y + 2 = 0

y = 2 or y = 1

m (tangent) at x = 2 is 0

Normal is perpendicular to tangent so, m₁m₂ = – 1

m (normal) at x = 2 is 1/0, which is undefined

Equation of normal is given by y – y₁ = m (normal) (x – x₁)

x = 2

7. Find the equation of the normal to the curve ay² = x³ at the point (am², am³).

Solution:

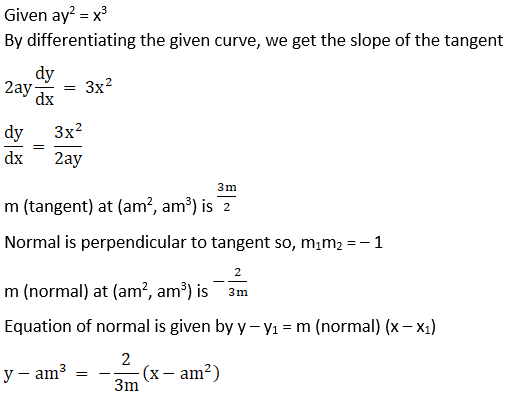
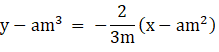
8. The equation of the tangent at (2, 3) on the curve y² = ax³ + b is y = 4x – 5. Find the values of a and b.

Solution:

Given y² = ax³ + b is y = 4x – 5

By differentiating the given curve, we get the slope of the tangent

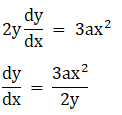
m (tangent) at (2, 3) = 2a

Equation of tangent is given by y – y₁ = m (tangent) (x – x₁)

Now comparing the slope of a tangent with the given equation

2a = 4

a = 2

Now (2, 3) lies on the curve, these points must satisfy

3² = 2 × 2³ + b

b = – 7

9. Find the equation of the tangent line to the curve y = x² + 4x – 16 which is parallel to the line 3x – y + 1 = 0.

Solution:

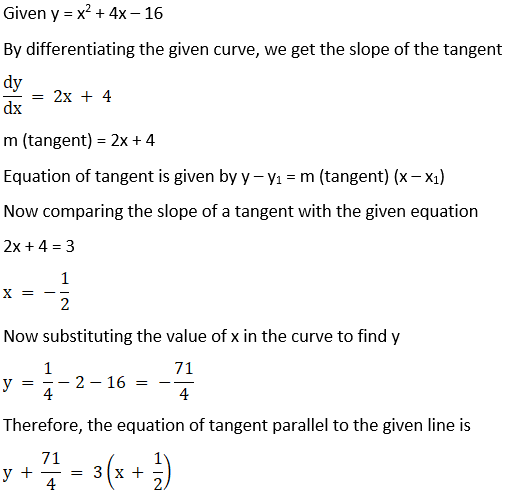
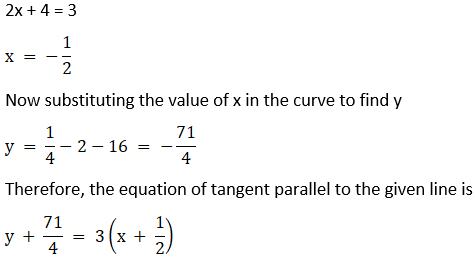
10. Find the equation of normal line to the curve y = x³ + 2x + 6 which is parallel to the line x + 14y + 4 = 0.

Solution:

 

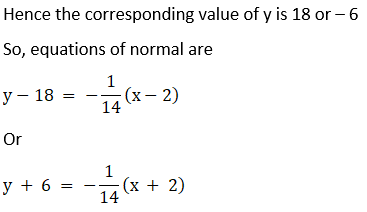
Exercise 16.3 Page No: 16.40

1. Find the angle to intersection of the following curves:

(i) y² = x and x² = y

Solution:

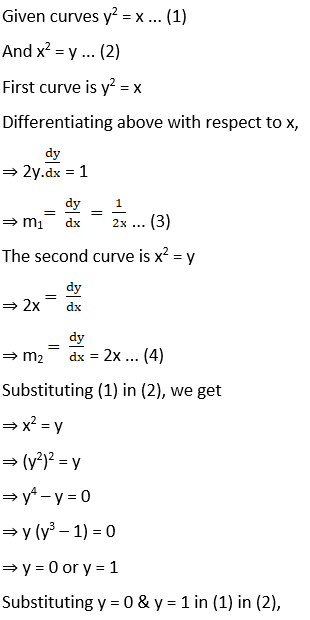
x = y²

When y = 0, x = 0

When y = 1, x = 1

Substituting above values for m₁ & m_2, we get,

When x = 0,

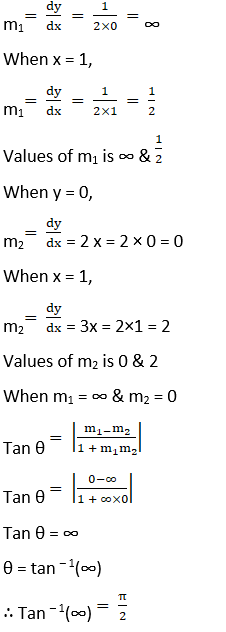
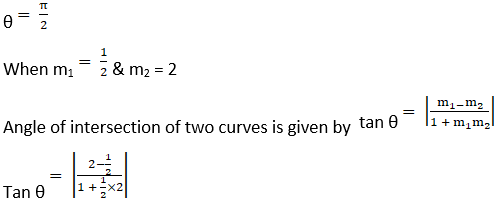
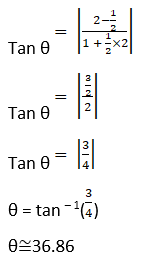
(ii) y = x² and x² + y² = 20

Solution:

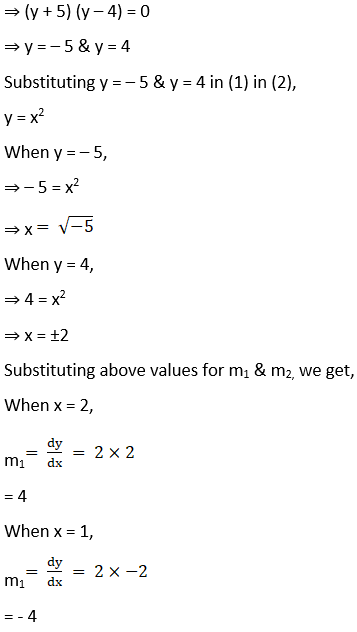
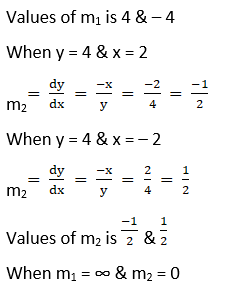
(iii) 2y² = x³ and y² = 32x

Solution:

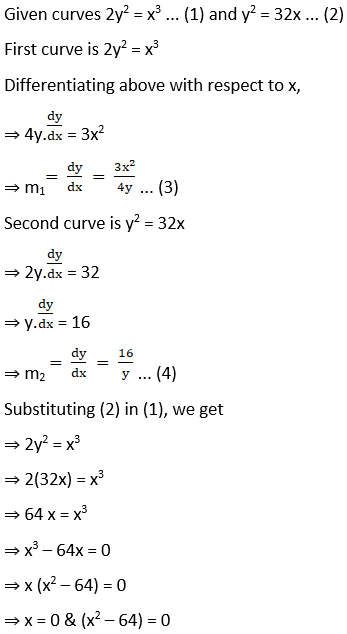
Substituting (2) in (1), we get

⇒ 2y² = x³

⇒ 2(32x) = x³

⇒ 64 x = x³

⇒ x³ – 64x = 0

⇒ x (x² – 64) = 0

⇒ x = 0 & (x² – 64) = 0

⇒ x = 0 & ±8

Substituting x = 0 & x = ±8 in (1) in (2),

y² = 32x

When x = 0, y = 0

When x = 8

⇒ y² = 32 × 8

⇒ y² = 256

⇒ y = ±16

Substituting above values for m₁ & m_2, we get,

When x = 0, y = 16

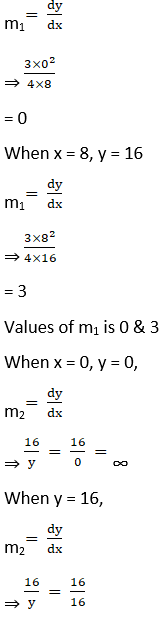
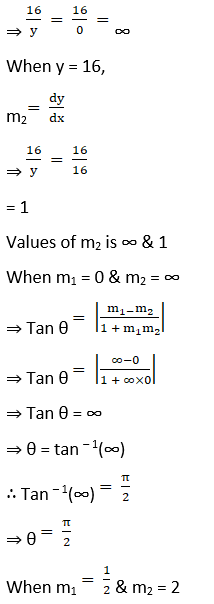
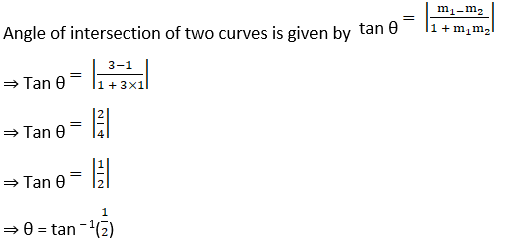
(iv) x² + y² – 4x – 1 = 0 and x² + y² – 2y – 9 = 0

Solution:

Given curves x² + y² – 4x – 1 = 0 … (1) and x² + y² – 2y – 9 = 0 … (2)

First curve is x² + y² – 4x – 1 = 0

⇒ x² – 4x + 4 + y² – 4 – 1 = 0

⇒ (x – 2)² + y² – 5 = 0

Now, Subtracting (2) from (1), we get

⇒ x² + y² – 4x – 1 – ( x² + y² – 2y – 9) = 0

⇒ x² + y² – 4x – 1 – x² – y² + 2y + 9 = 0

⇒ – 4x – 1 + 2y + 9 = 0

⇒ – 4x + 2y + 8 = 0

⇒ 2y = 4x – 8

⇒ y = 2x – 4

Substituting y = 2x – 4 in (3), we get,

⇒ (x – 2)² + (2x – 4)² – 5 = 0

⇒ (x – 2)² + 4(x – 2)² – 5 = 0

⇒ (x – 2)²(1 + 4) – 5 = 0

⇒ 5(x – 2)² – 5 = 0

⇒ (x – 2)² – 1 = 0

⇒ (x – 2)² = 1

⇒ (x – 2) = ±1

⇒ x = 1 + 2 or x = – 1 + 2

⇒ x = 3 or x = 1

So, when x = 3

y = 2×3 – 4

⇒ y = 6 – 4 = 2

So, when x = 3

y = 2 × 1 – 4

⇒ y = 2 – 4 = – 2

The point of intersection of two curves are (3, 2) & (1, – 2)

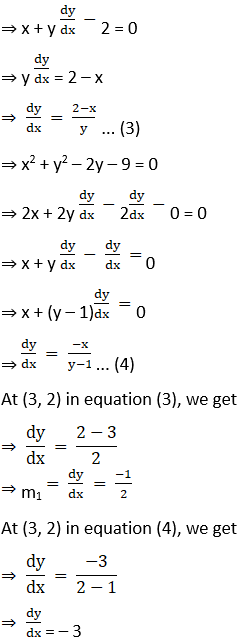
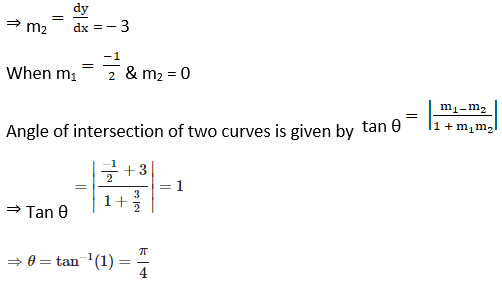
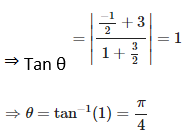
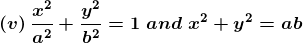
Solution:

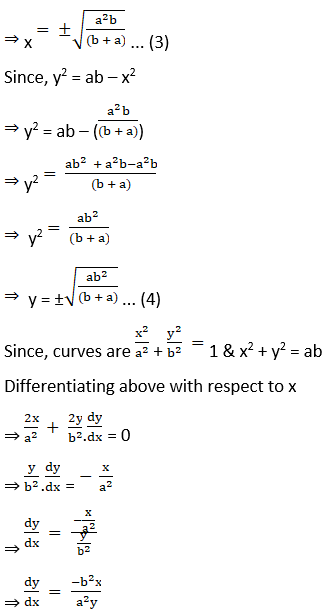
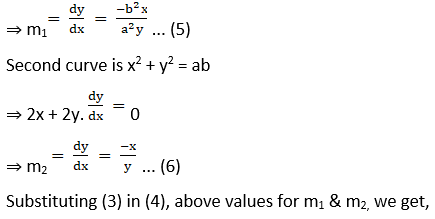
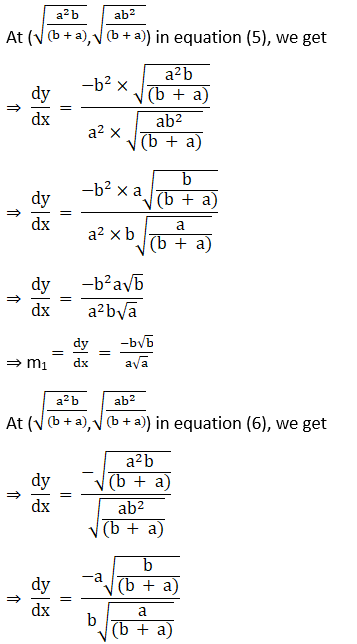
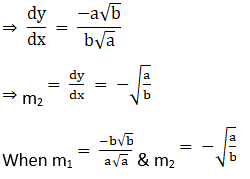
2. Show that the following set of curves intersect orthogonally:
(i) y = x³ and 6y = 7 – x²

Solution:

Given curves y = x³ … (1) and 6y = 7 – x² … (2)

Solving (1) & (2), we get

⇒ 6y = 7 – x²

⇒ 6(x³) = 7 – x²

⇒ 6x³ + x² – 7 = 0

Since f(x) = 6x³ + x² – 7,

We have to find f(x) = 0, so that x is a factor of f(x).

When x = 1

f (1) = 6(1)³ + (1)² – 7

f (1) = 6 + 1 – 7

f (1) = 0

Hence, x = 1 is a factor of f(x).

Substituting x = 1 in y = x³, we get

y = 1³

y = 1

The point of intersection of two curves is (1, 1)

First curve y = x³

Differentiating above with respect to x,

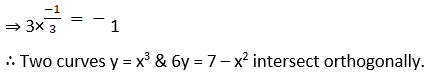
(ii) x³ – 3xy² = – 2 and 3x² y – y³ = 2

Solution:

Given curves x³ – 3xy² = – 2 … (1) and 3x²y – y³ = 2 … (2)

Adding (1) & (2), we get

⇒ x³ – 3xy² + 3x²y – y³ = – 2 + 2

⇒ x³ – 3xy² + 3x²y – y³ = – 0

⇒ (x – y)³ = 0

⇒ (x – y) = 0

⇒ x = y

Substituting x = y on x³ – 3xy² = – 2

⇒ x³ – 3 × x × x² = – 2

⇒ x³ – 3x³ = – 2

⇒ – 2x³ = – 2

⇒ x³ = 1

⇒ x = 1

Since x = y

y = 1

The point of intersection of two curves is (1, 1)

First curve x³ – 3xy² = – 2

Differentiating above with respect to x,

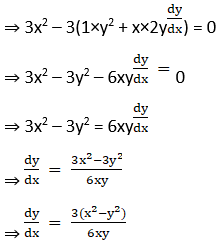
(iii) x² + 4y² = 8 and x² – 2y² = 4.

Solution:

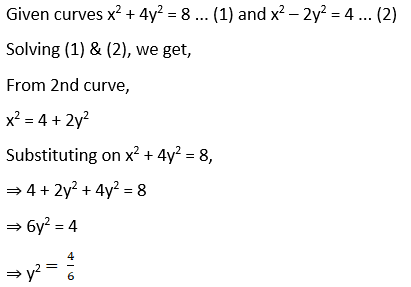
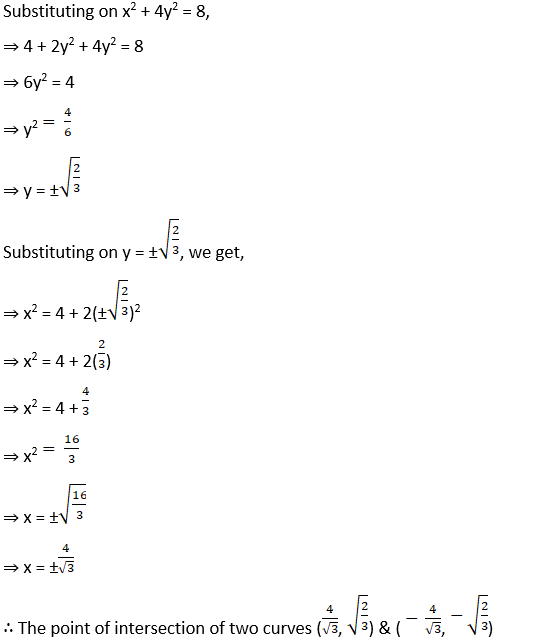
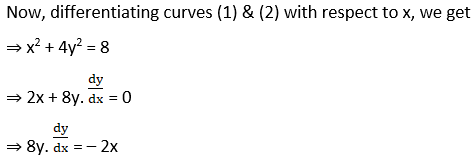
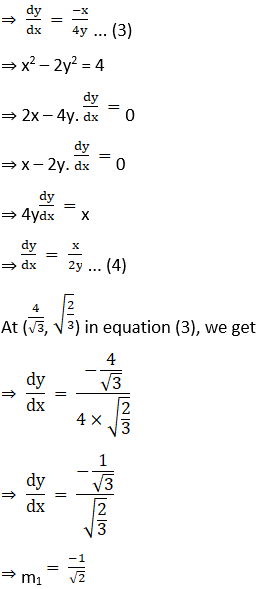
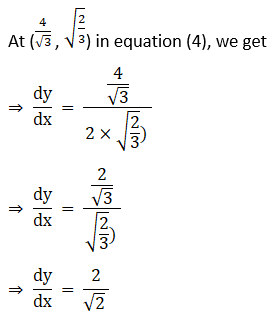
3. x² = 4y and 4y + x² = 8 at (2, 1)

Solution:

(ii) x² = y and x³ + 6y = 7 at (1, 1)

Solution:

Given curves x² = y … (1) and x³ + 6y = 7 … (2)

The point of intersection of two curves (1, 1)

Solving (1) & (2), we get,

First curve is x² = y

Differentiating above with respect to x,

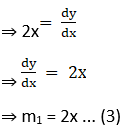
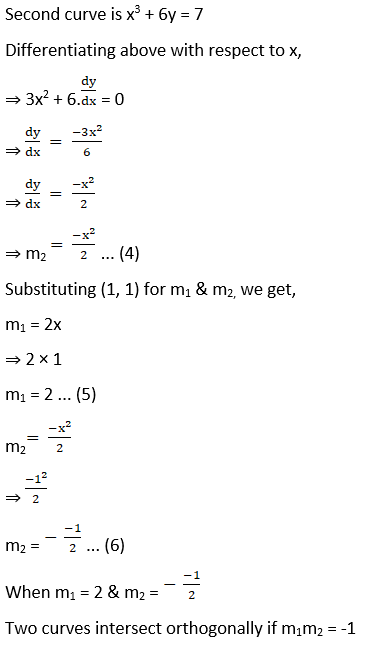
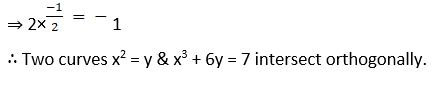
(iii) y² = 8x and 2x² + y² = 10 at (1, 2√2)

Solution:

Given curves y² = 8x … (1) and 2x² + y² = 10 … (2)

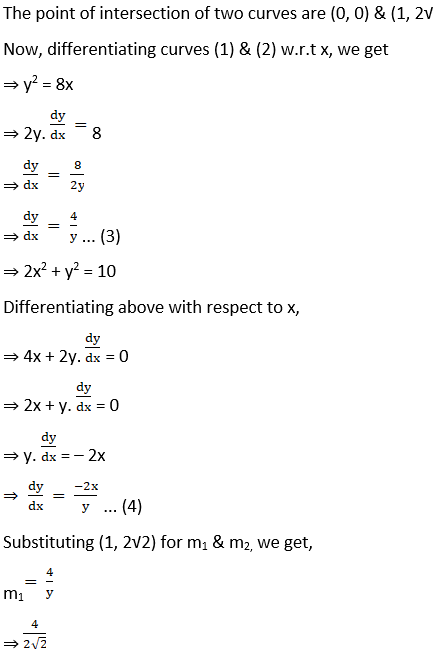
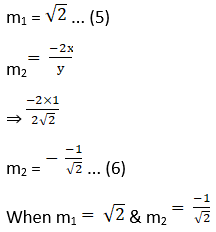
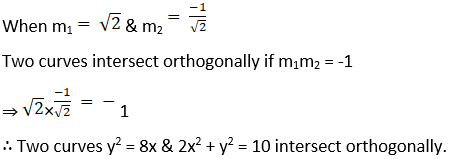
4. Show that the curves 4x = y² and 4xy = k cut at right angles, if k² = 512.

Solution:

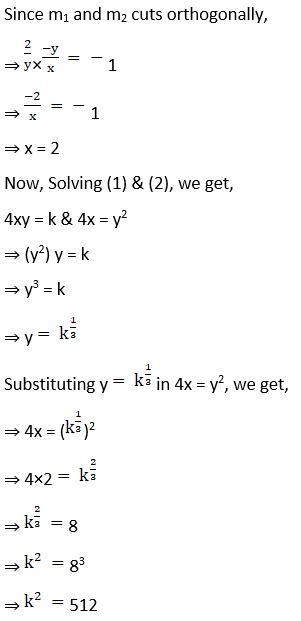
5. Show that the curves 2x = y² and 2xy = k cut at right angles, if k² = 8.

Solution:

Given curves 2x = y² … (1) and 2xy = k … (2)

We have to prove that two curves cut at right angles if k² = 8

Now, differentiating curves (1) & (2) with respect to x, we get

⇒ 2x = y²