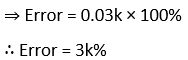Chapter 14 DIFFERENTIALS,ERRORS AND APPOROXIMATIONS

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 14 – Differentials, Errors and Approximations

Exercise 14.1 Page No: 14.9

1. If y = sin x and x changes from π/2 to 22/14, what is the approximate change in y?

Solution:

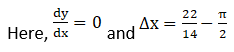
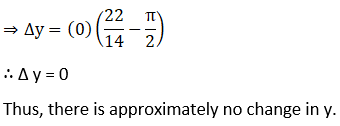
2. The radius of a sphere shrinks from 10 to 9.8 cm. Find approximately the decrease in its volume.

Solution:

Given the radius of a sphere changes from 10 cm to 9.8 cm.

Let x be the radius of the sphere and Δ x be the change in the value of x.

Hence, we have x = 10 and x + Δ x = 9.8

⇒ 10 + Δ x = 9.8

⇒ Δ x = 9.8 – 10

∴ Δ x = – 0.2

The volume of a sphere of radius x is given by

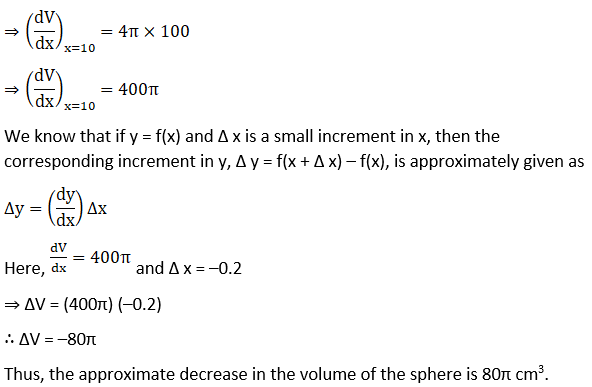
3. A circular metal plate expands under heating so that its radius increases by k%. Find the approximate increase in the area of the plate, if the radius of the plate before heating is 10 cm.

Solution:

4. Find the percentage error in calculating the surface area of a cubical box if an error of 1% is made in measuring the lengths of the edges of the cube.

Solution:

5. If there is an error of 0.1% in the measurement of the radius of a sphere, find approximately the percentage error in the calculation of the volume of the sphere.

Solution:

6. The pressure p and the volume v of a gas are connected by the relation pv^1.4 = const. Find the percentage error in p corresponding to a decrease of ½ % in v.

Solution:

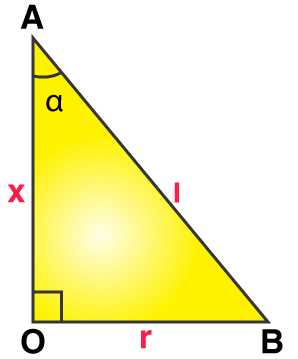
7. The height of a cone increases by k%, its semi-vertical angle remaining the same. What is the approximate percentage increase in (i) in total surface area, and (ii) in the volume, assuming that k is small.

Solution:

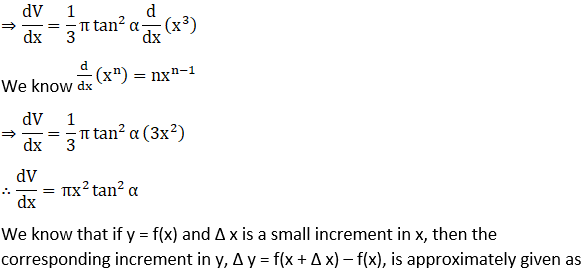
8. Show that the relative error in computing the volume of a sphere, due to an error in measuring the radius, is approximately equal to three times the relative error in the radius.

Solution: