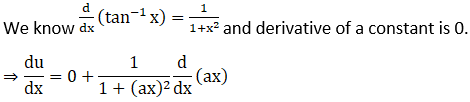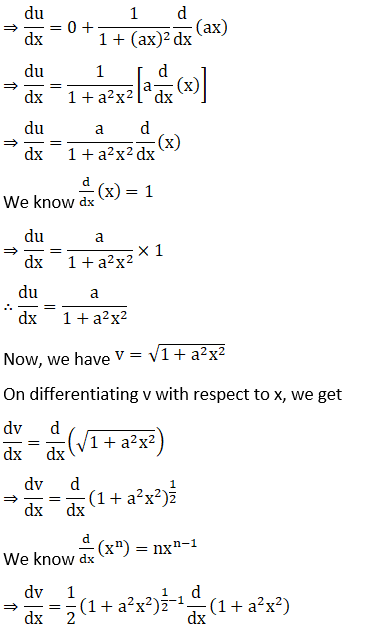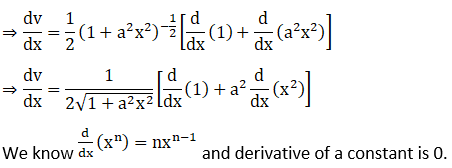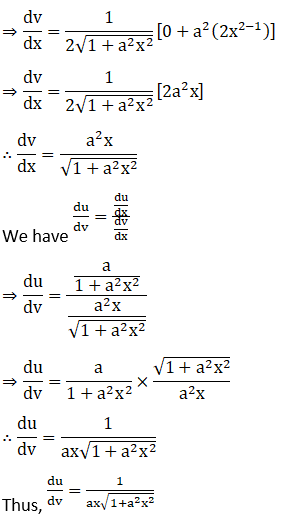Chapter 11 DIFFRENTIATION

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 11 – Differentiation

Exercise 11.1 Page No: 11.17

Differentiate the following functions from the first principles:

1. e^-x

Solution:

2. e^3x

Solution:

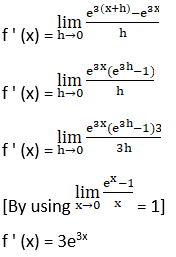
3. e^{ax + b}

Solution:

4. e^{cos x}

Solution:

We have to find the derivative of e^cos x with the first principle method,

So, let f (x) = e^cos x

By using the first principle formula, we get,

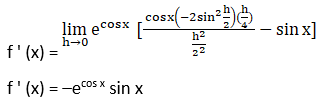
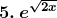
Solution:

Exercise 11.2 Page No: 11.37

Differentiate the following functions with respect to x:

1. Sin (3x + 5)

Solution:

Given Sin (3x + 5)

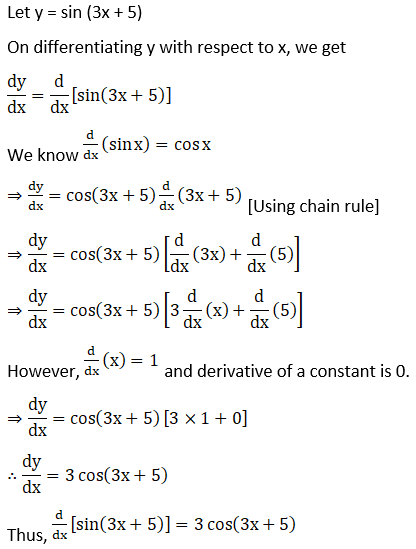
2. tan² x

Solution:

Given tan² x

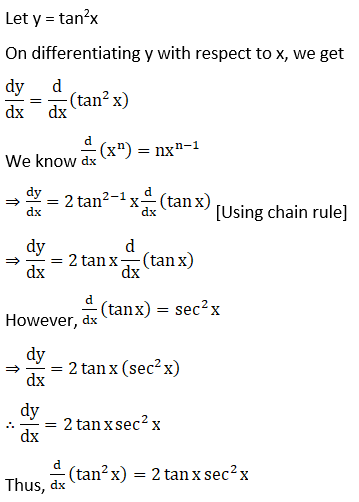
3. tan (x^o + 45^o)

Solution:

Let y = tan (x° + 45°)

First, we will convert the angle from degrees to radians.

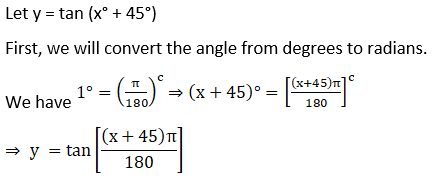
4. Sin (log x)

Solution:

Given sin (log x)

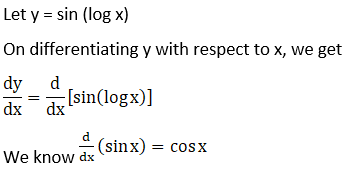
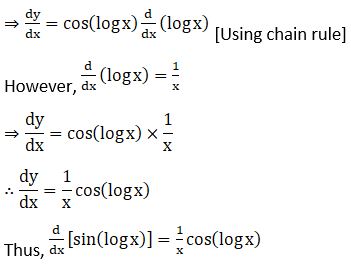
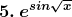
Solution:

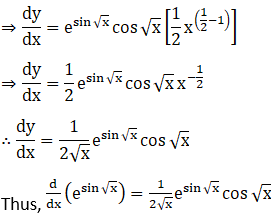
6. e^{tan x}

Solution:

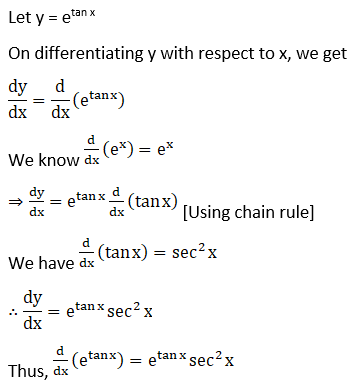
7. Sin² (2x + 1)

Solution:

Let y = sin² (2x + 1)

On differentiating y with respect to x, we get

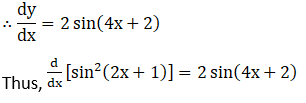
8. log₇ (2x – 3)

Solution:

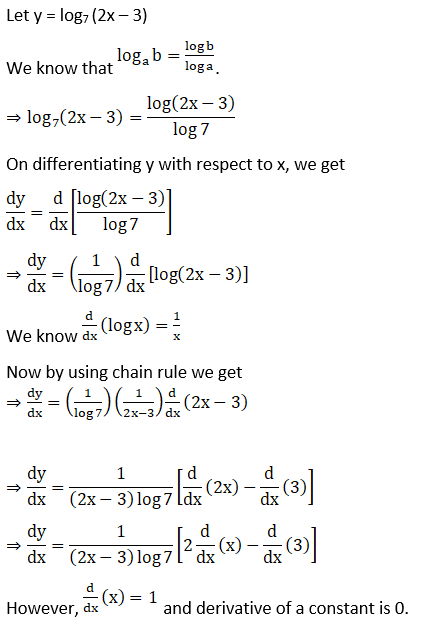
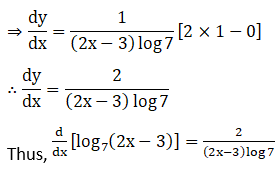
9. tan 5x^o

Solution:

Let y = tan (5x°)

First, we will convert the angle from degrees to radians. We have

Solution:

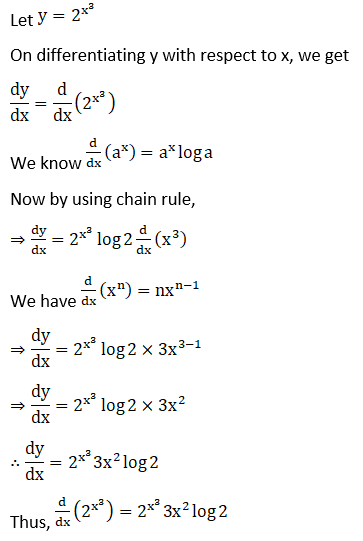
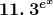
Solution:

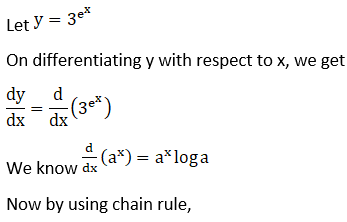
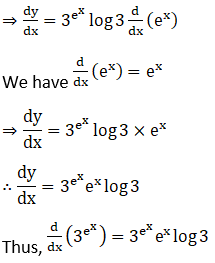
12. log_x 3

Solution:

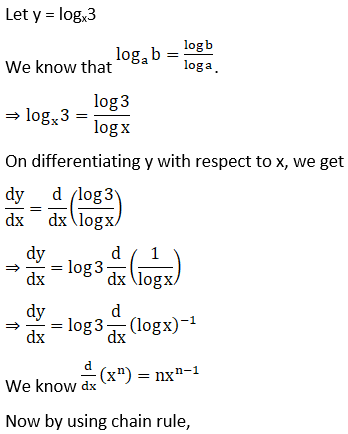
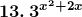
Solution:

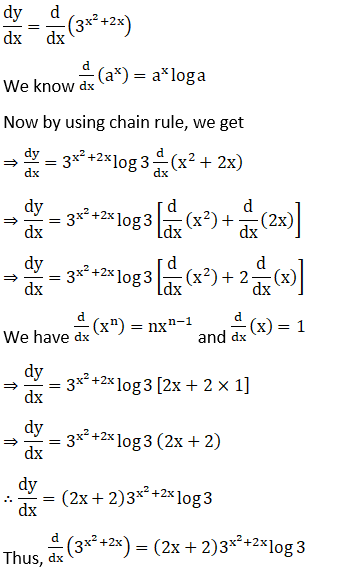
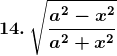
Solution:

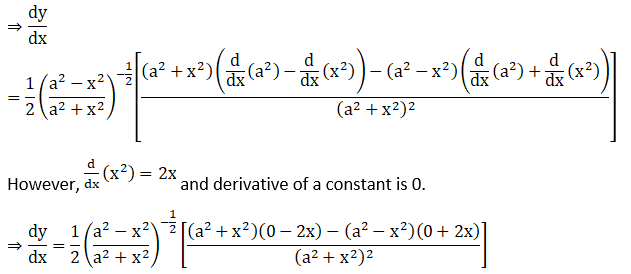
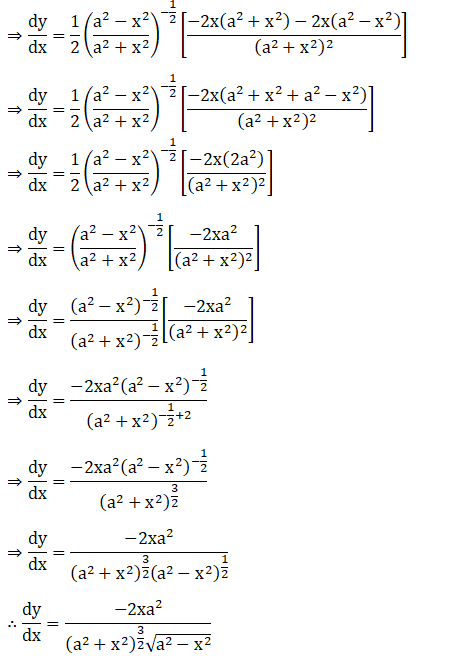
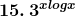
Solution:

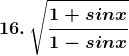
Solution:

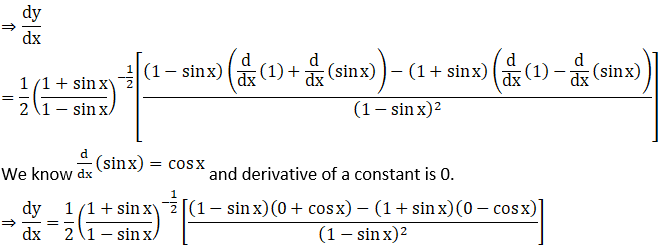
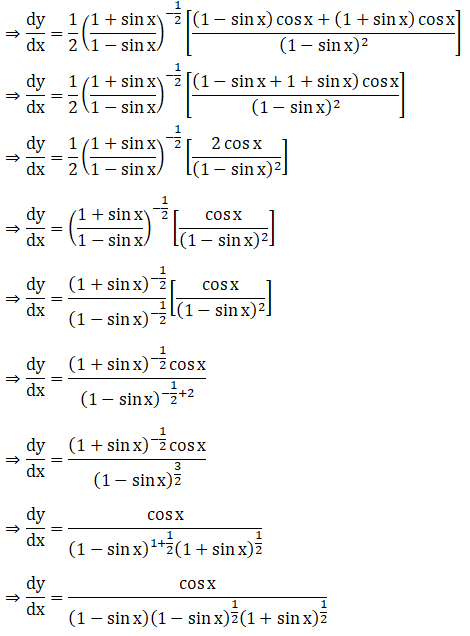
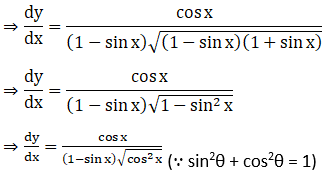
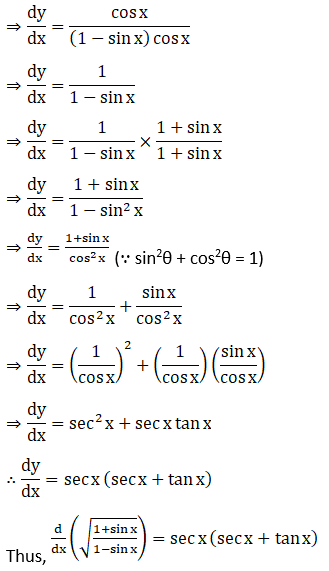
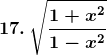
Solution:

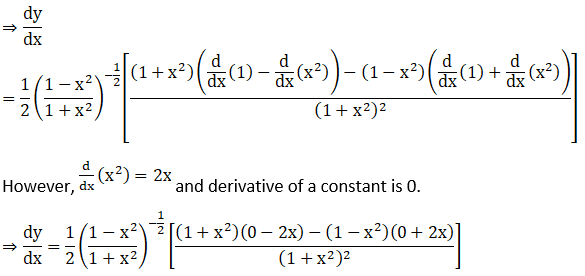
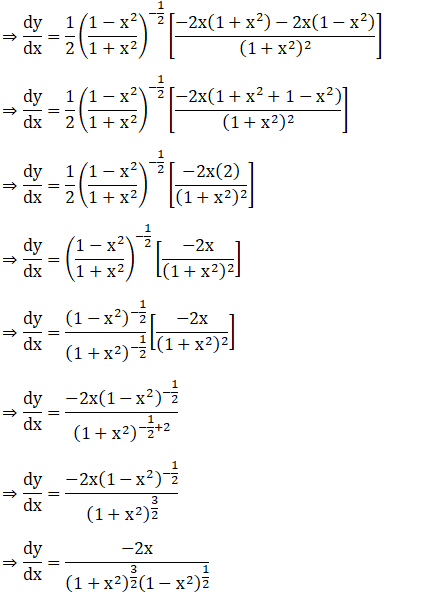
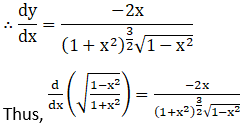
18. (log sin x)²

Solution:

Let y = (log sin x)²

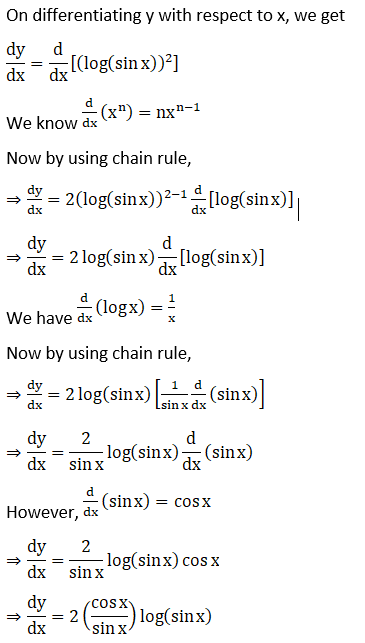
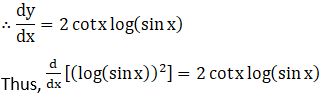
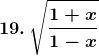
Solution:

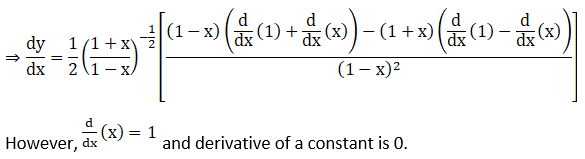
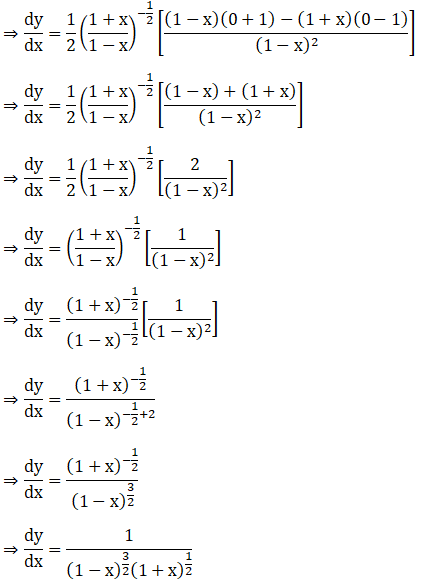
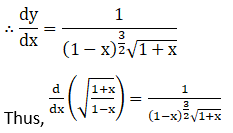
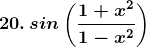
Solution:

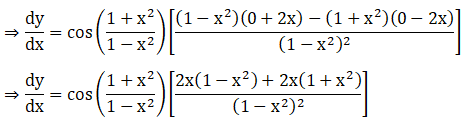
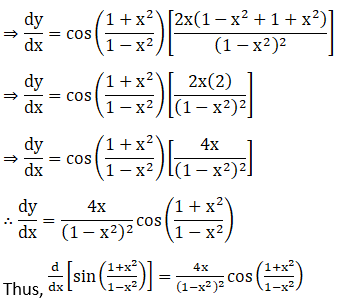
21. e^3x cos 2x

Solution:

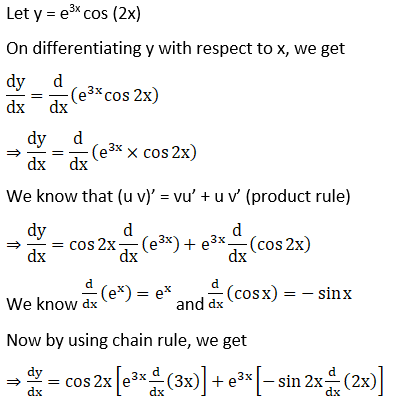
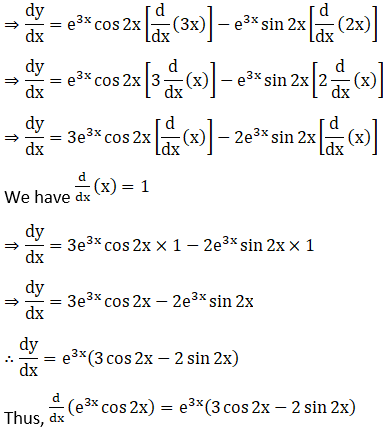
22. Sin (log sin x)

Solution:

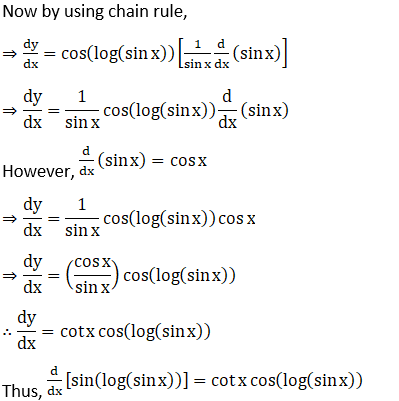
23. e^{tan 3x}

Solution:

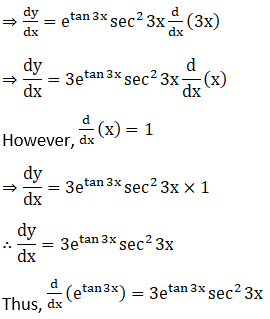
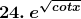
Solution:

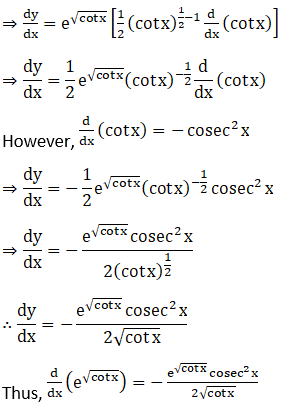
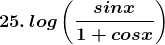
Solution:

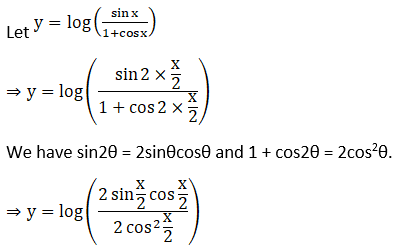
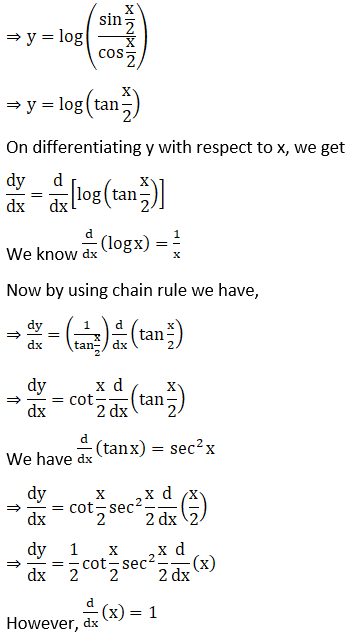
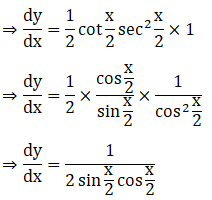
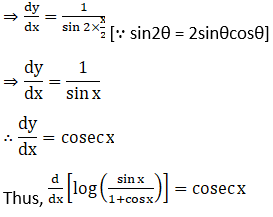
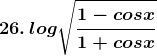
Solution:

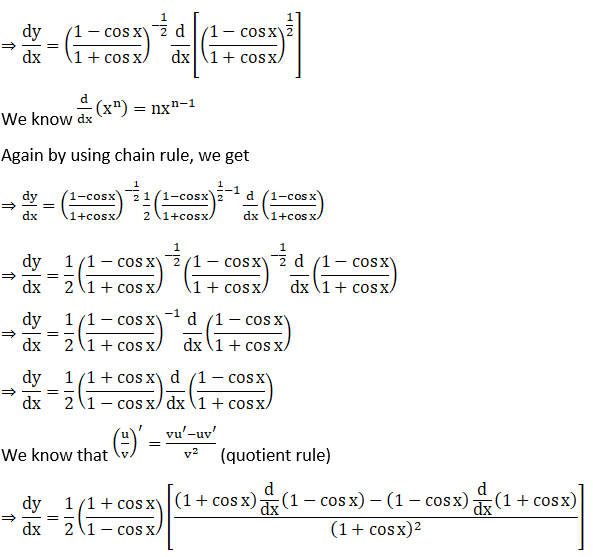
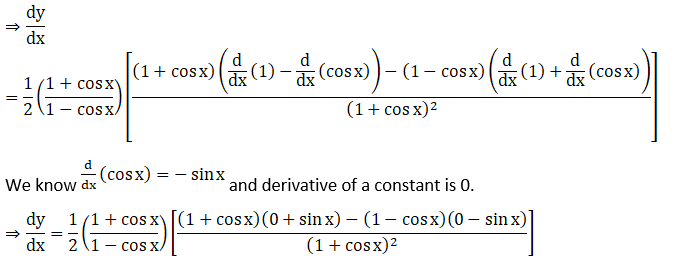
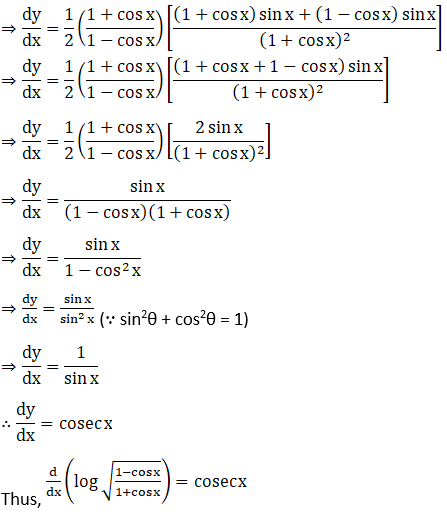
27. tan (e^{sin x})

Solution:

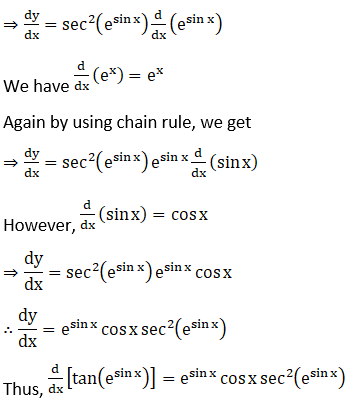
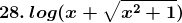
Solution:

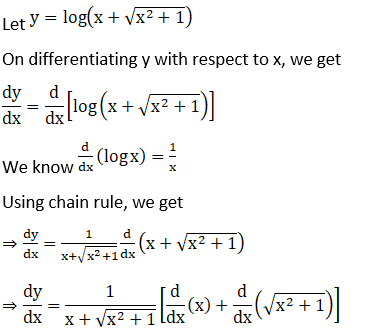
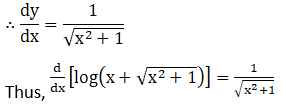
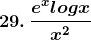
Solution:

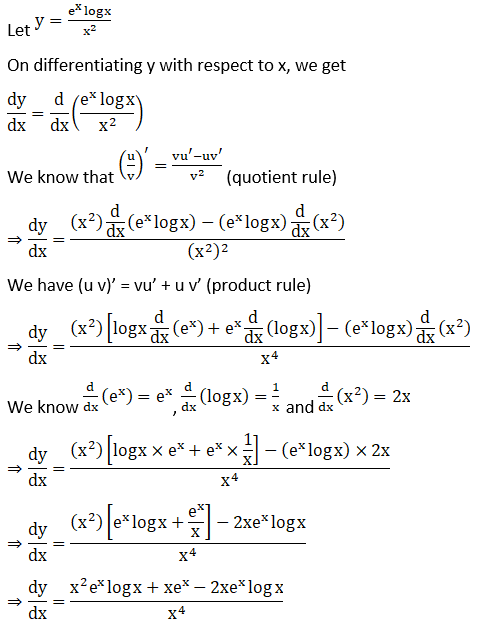
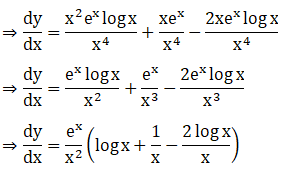
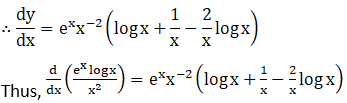
30. log (cosec x – cot x)

Solution:

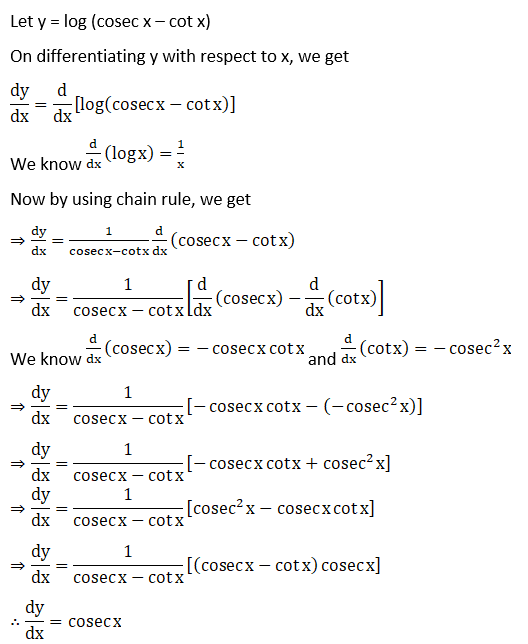
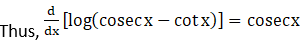
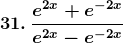
Solution:

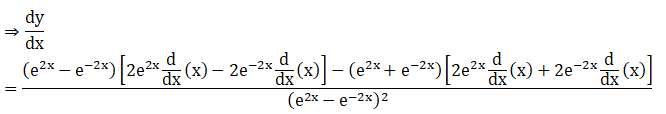
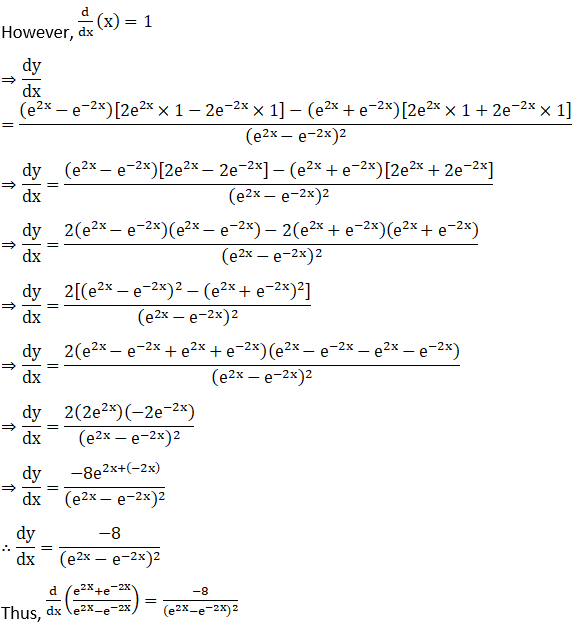
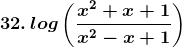
Solution:

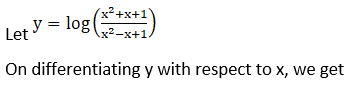
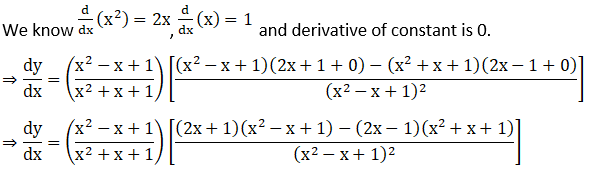
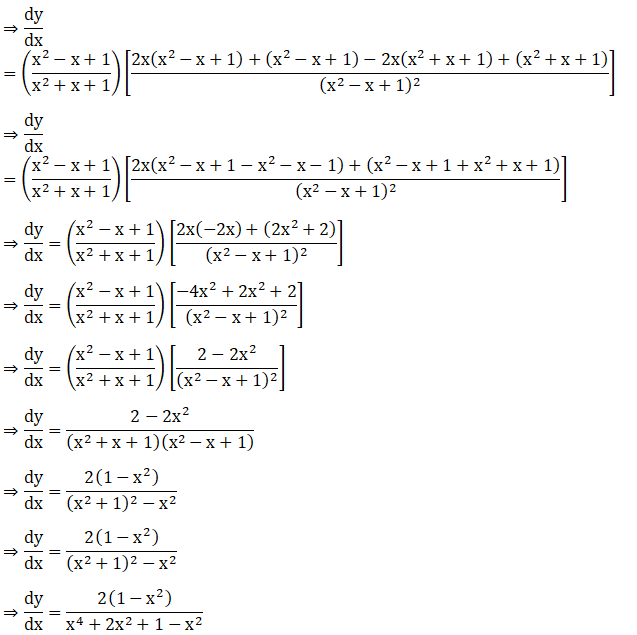
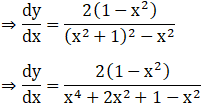
33. tan^-1 (e^x)

Solution:

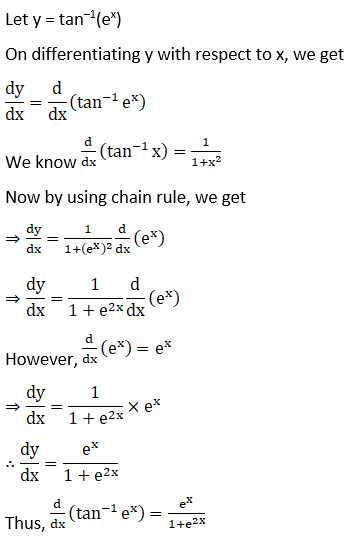
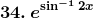
Solution:

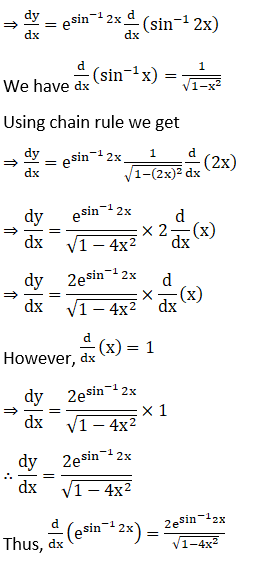
35. sin (2 sin^-1 x)

Solution:

Let y = sin (2sin^–1x)

On differentiating y with respect to x, we get

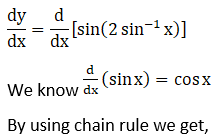
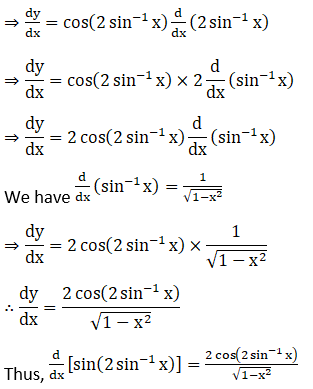
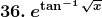
Solution:

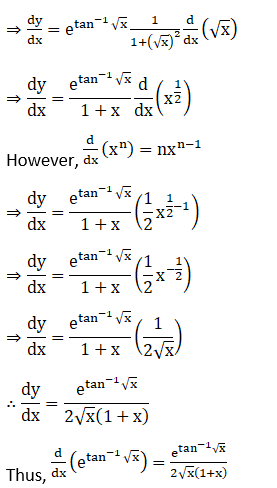
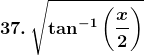
Solution:

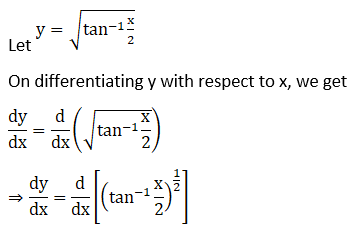
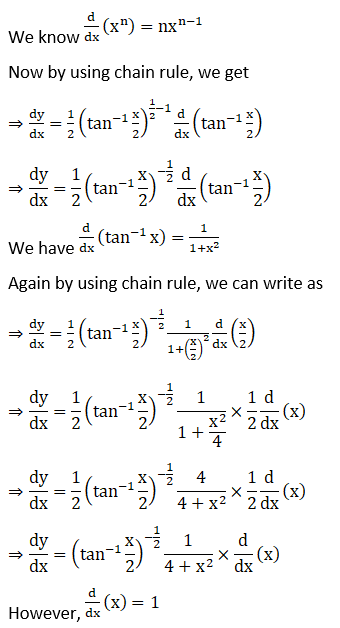
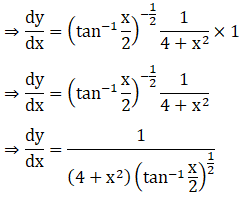
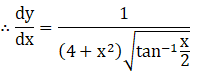
Exercise 11.3 Page No: 11.62

Differentiate the following functions with respect to x:

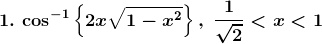
Solution:

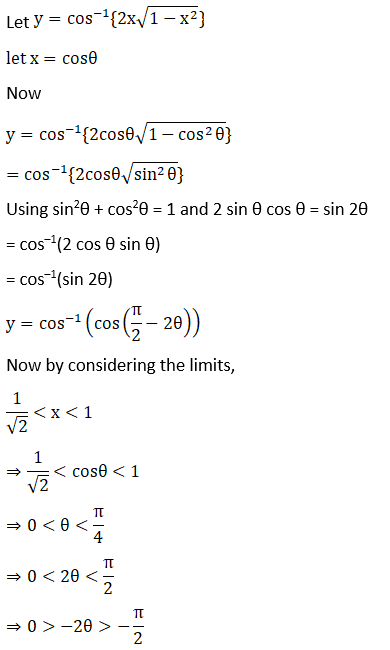
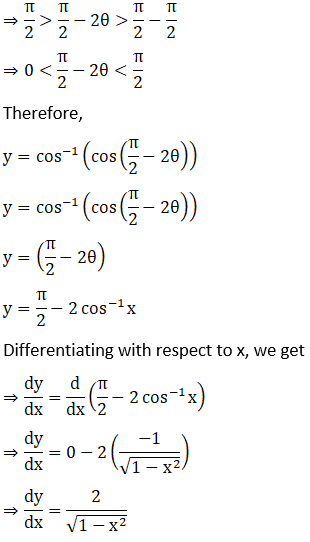
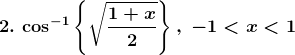
Solution:

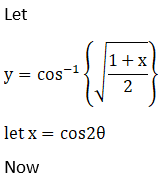
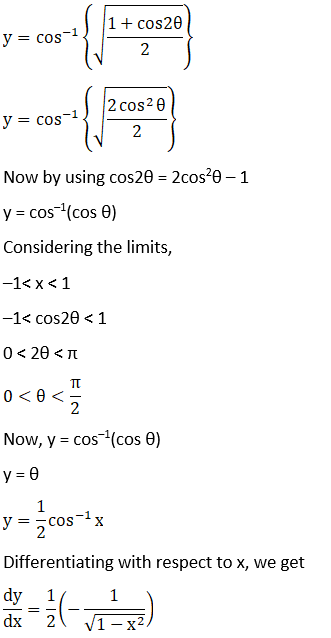
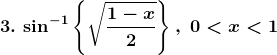
Solution:

Let,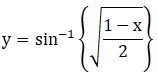

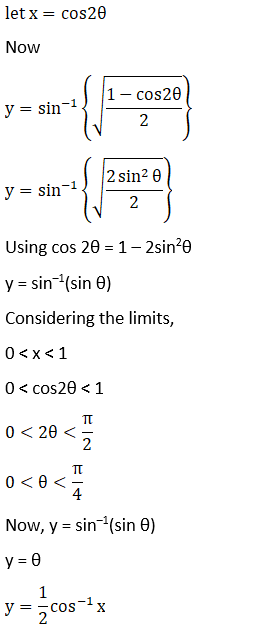
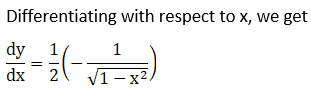
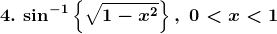
Solution:

Let,

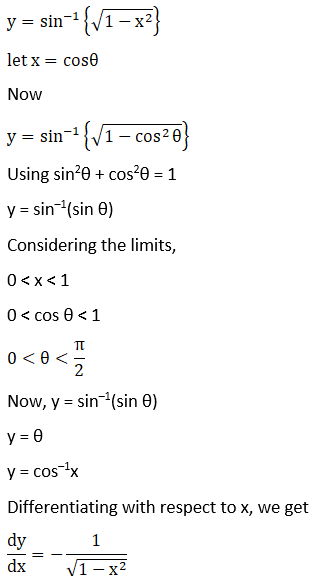
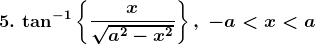
Solution:

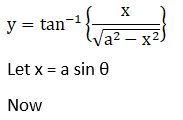
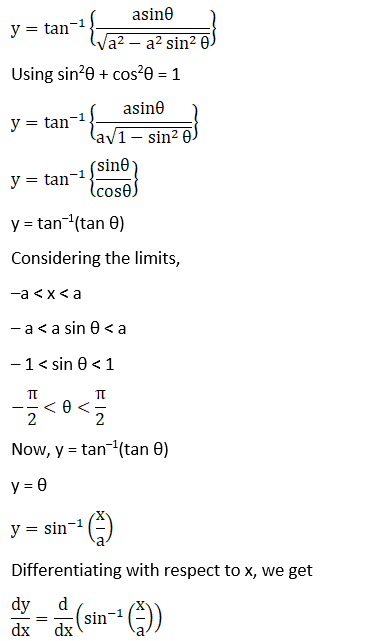
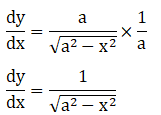
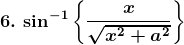
Solution:

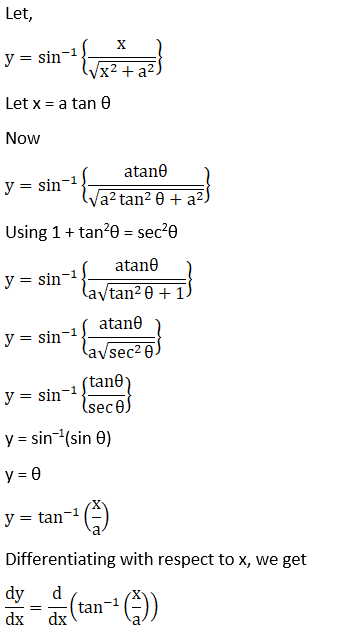
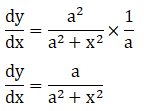
7. Sin^-1 (2x² – 1), 0 < x < 1

Solution:

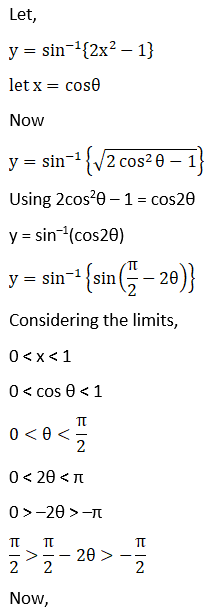
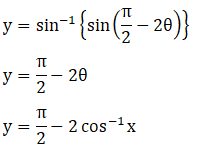
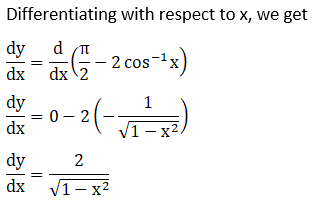
8. Sin^-1 (1 – 2x²), 0 < x < 1

Solution:

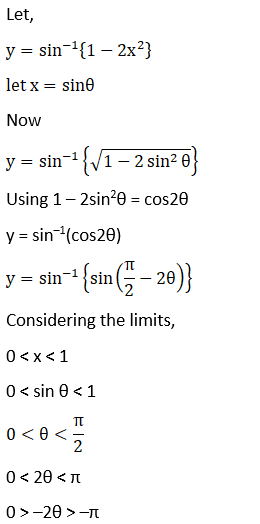
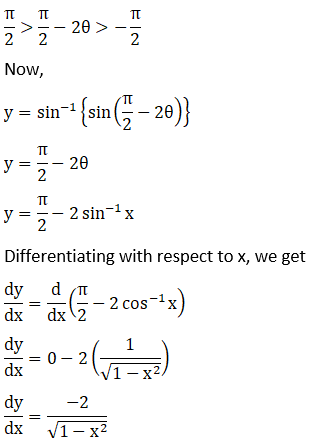
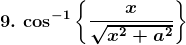
Solution:

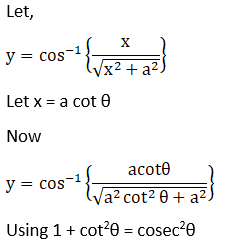
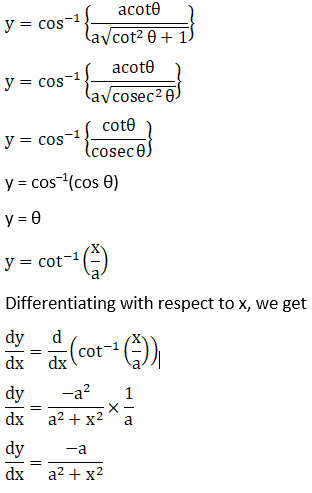
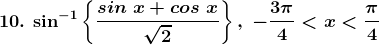
Solution:

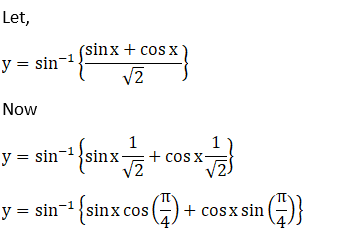
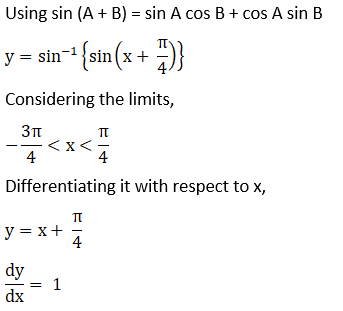
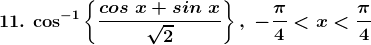
Solution:

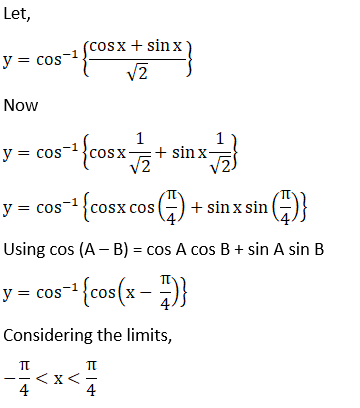
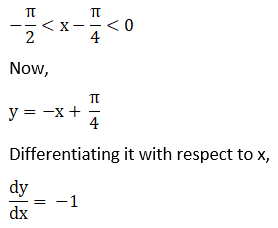
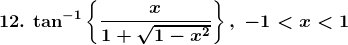
Solution:

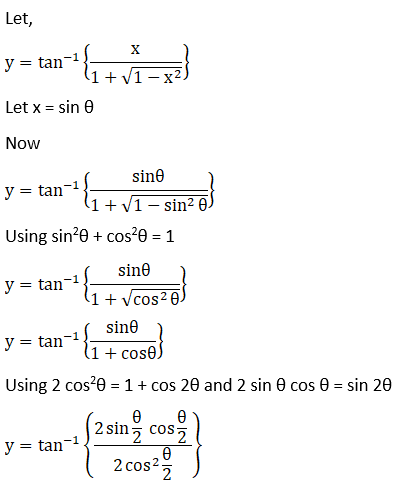
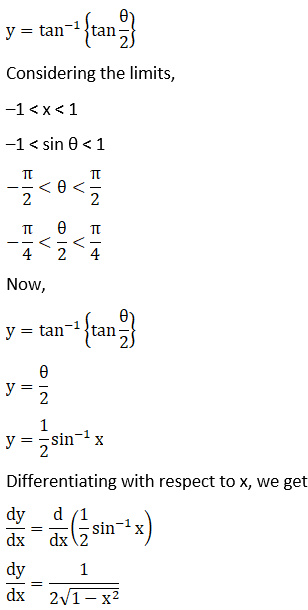
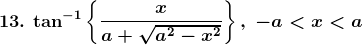
Solution:

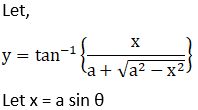
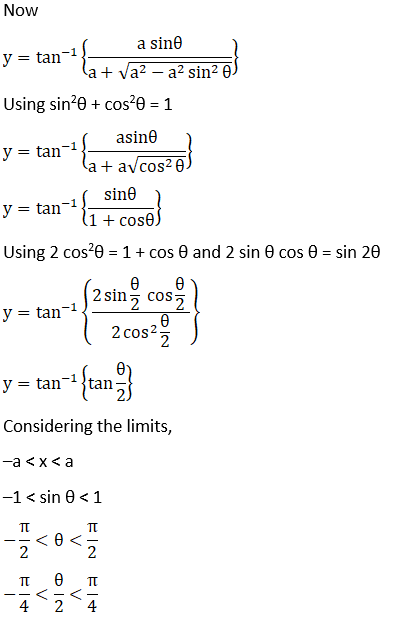
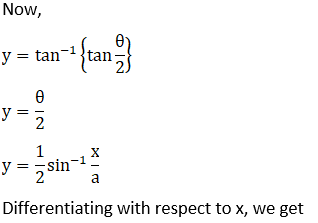
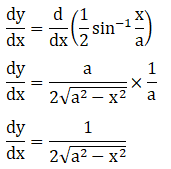
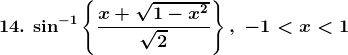
Solution:

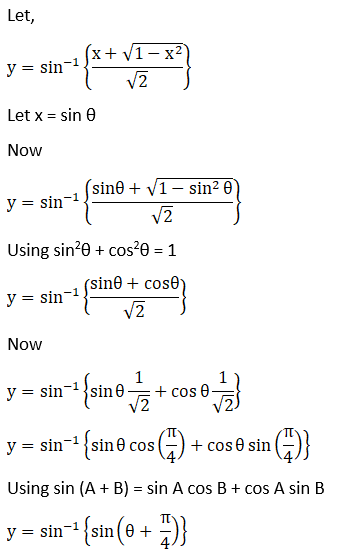
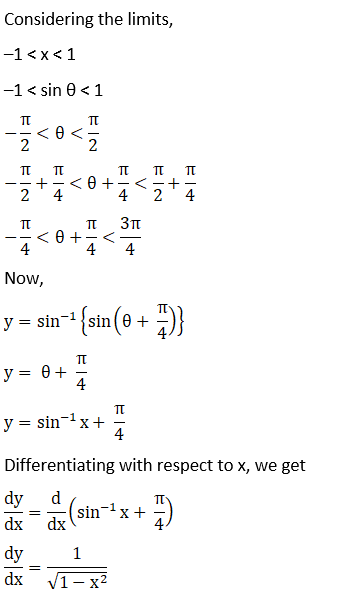
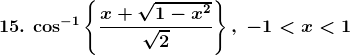
Solution:

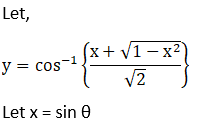
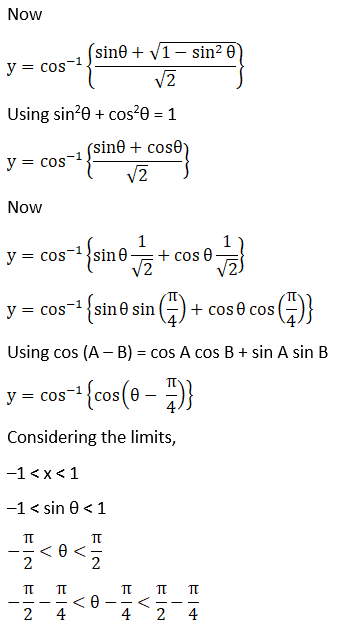
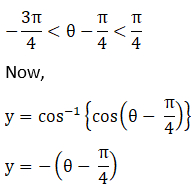
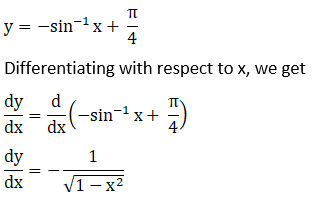
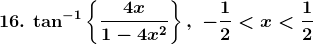
Solution:

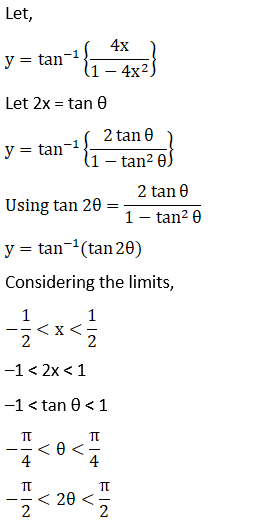
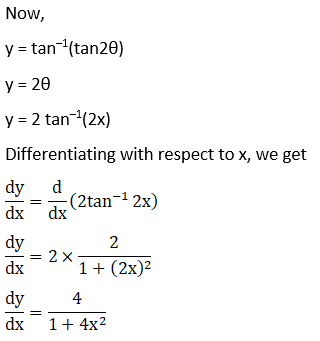
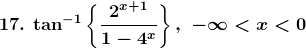
Solution:

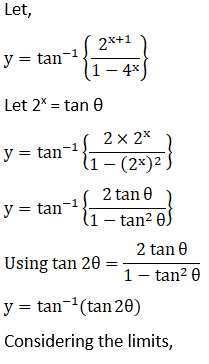
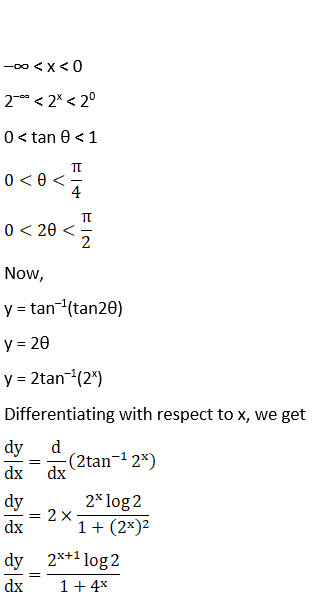
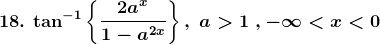
Solution:

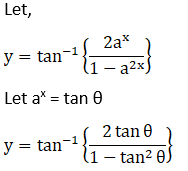
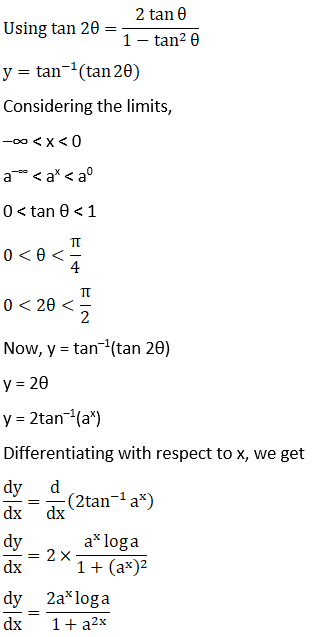
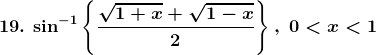
Solution:

Let,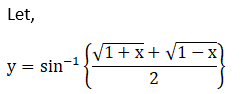

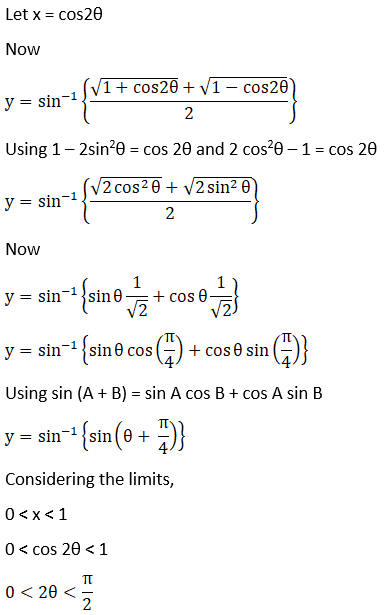
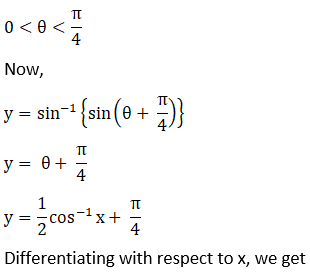
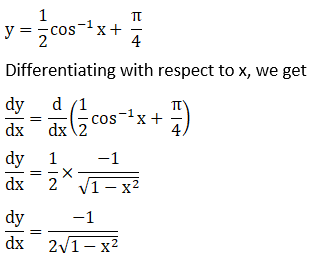
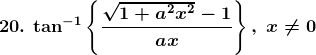
Solution:

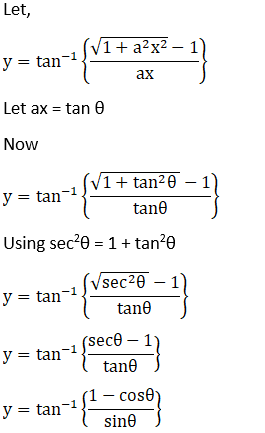
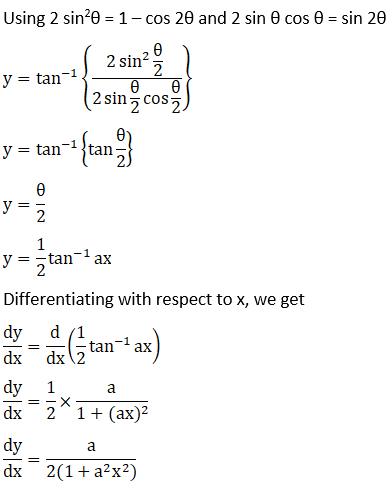
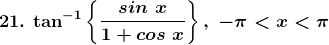
Solution:

Solution:

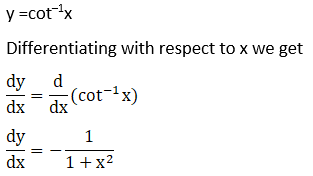
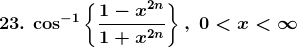
Solution:

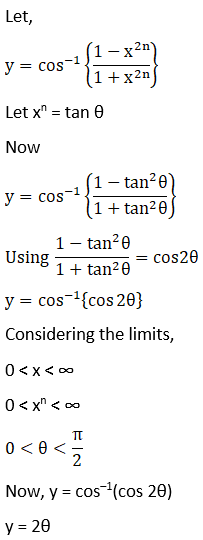
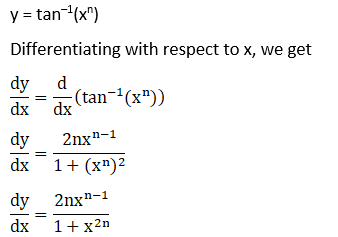
Exercise 11.4 Page No: 11.74

Find dy/dx in each of the following:

1. xy = c²

Solution:

2. y³ – 3xy² = x³ + 3x²y

Solution:

Given y³ – 3xy² = x³ + 3x²y,

Now we have to find dy/dx of given equation, so by differentiating the equation on both sides with respect to x, we get,

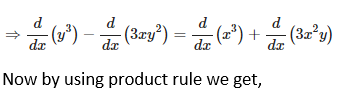
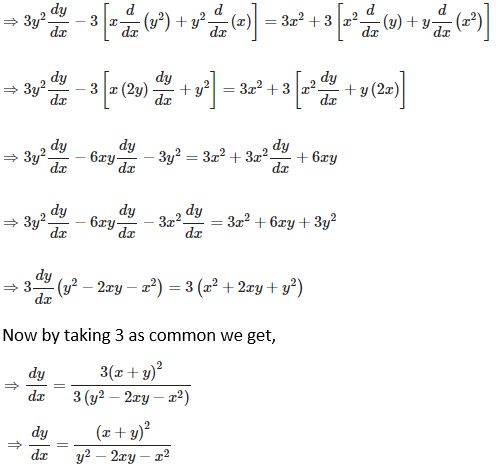
3. x^2/3 + y^2/3 = a^2/3

Solution:

Given x^2/3 + y^2/3 = a^2/3,

Now we have to find dy/dx of given equation, so by differentiating the equation on both sides with respect to x, we get,

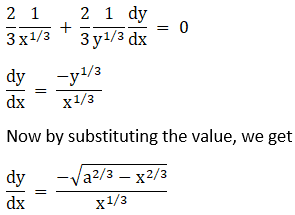
4. 4x + 3y = log (4x – 3y)

Solution:

Given 4x + 3y = log (4x – 3y),

Now we have to find dy/dx of it, so by differentiating the equation on both sides with respect to x, we get,

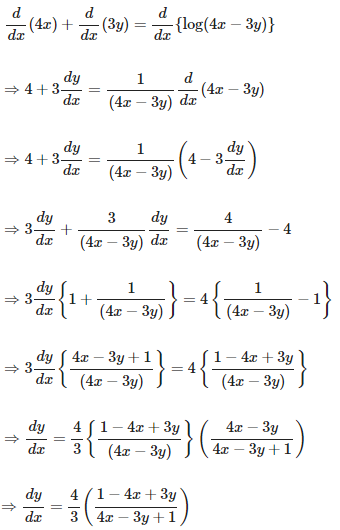
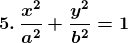
Solution:

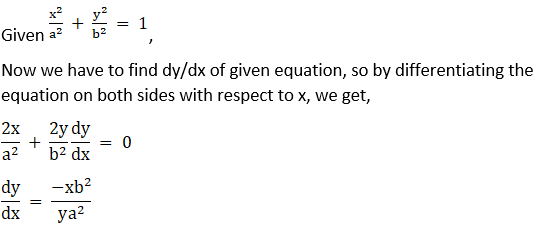
6. x⁵ + y⁵ = 5xy

Solution:

Given x⁵ + y⁵ = 5xy

Now we have to find dy/dx of given equation, so by differentiating the equation on both sides with respect to x, we get,

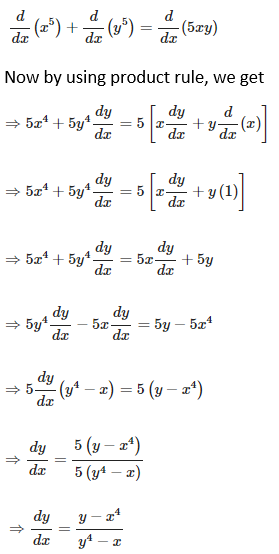
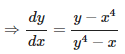
7. (x + y)² = 2axy

Solution:

Given (x + y)² = 2axy

Now we have to find dy/dx of given equation, so by differentiating the equation on both sides with respect to x, we get,

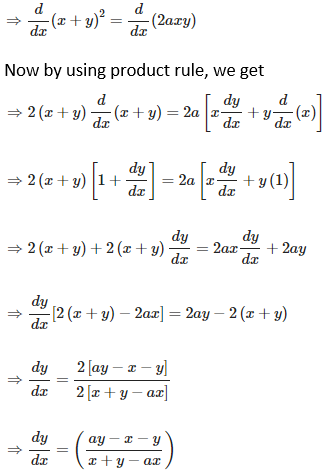
8. (x² + y²)² = xy

Solution:

Given (x + y)² = 2axy

Now we have to find dy/dx of given equation, so by differentiating the equation on both sides with respect to x, we get,

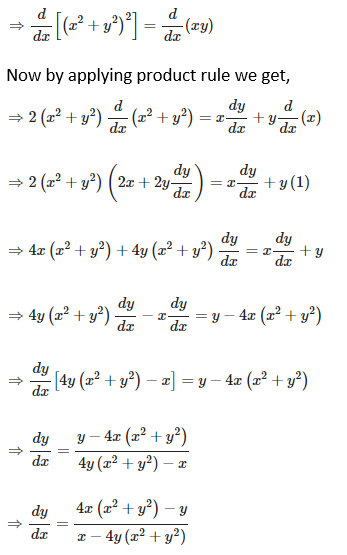
9. Tan^-1 (x² + y²)

Solution:

Given tan ^{– 1}(x² + y²) = a,

Now we have to find dy/dx of given function, so by differentiating the equation on both sides with respect to x, we get,

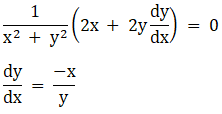
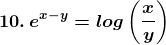
Solution:

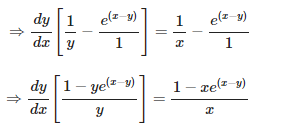
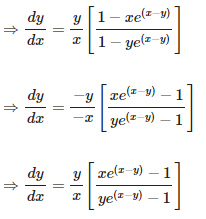
11. Sin xy + cos (x + y) = 1

Solution:

Given Sin x y + cos (x + y) = 1

Now we have to find dy/dx of given function, so by differentiating the equation on both sides with respect to x, we get,

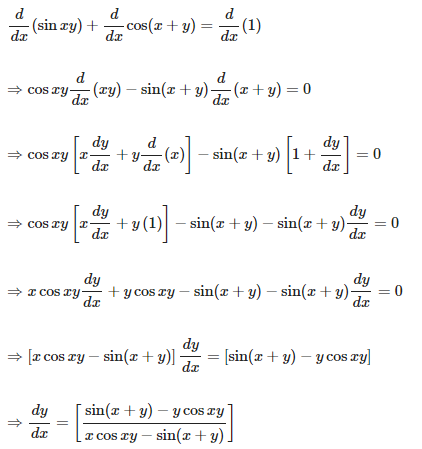
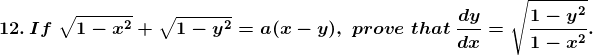
Solution:

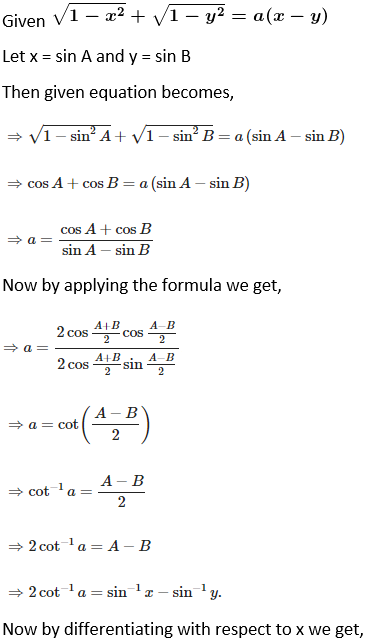
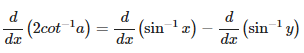
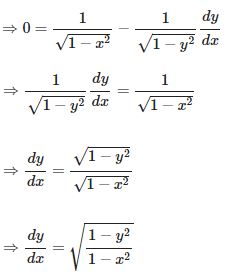
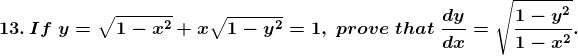
Solution:

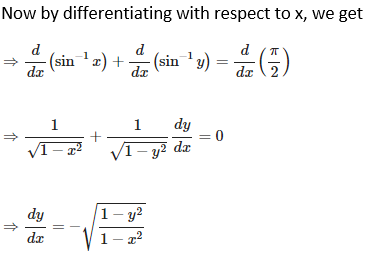
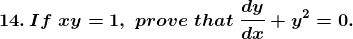
Solution:

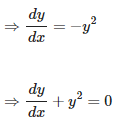
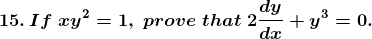
Solution:

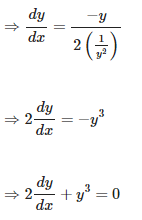
Exercise 11.5 Page No: 11.88

Differentiate the following functions with respect to x:

1. x^1/x

Solution:

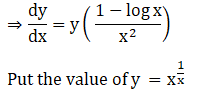
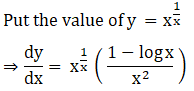
2. x^{sin x}

Solution:

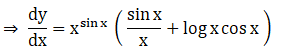
3. (1 + cos x)^x

Solution:

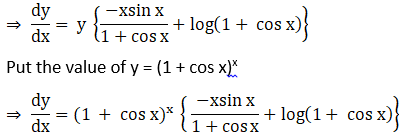
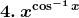
Solution:

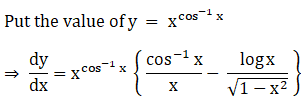
5. (log x)^x

Solution:

6. (log x)^{cos x}

Solution:

Let y = (log x)^{cos x}

Taking log both the sides, we get

7. (Sin x)^{cos x}

Solution:

8. e^{x log x}

Solution:

9. (Sin x)^{log x}

Solution:

10. 10^{log sin x}

Solution:

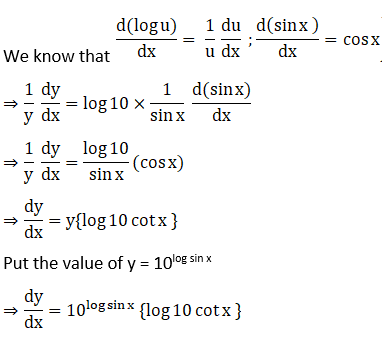
11. (log x)^{log x}

Solution:

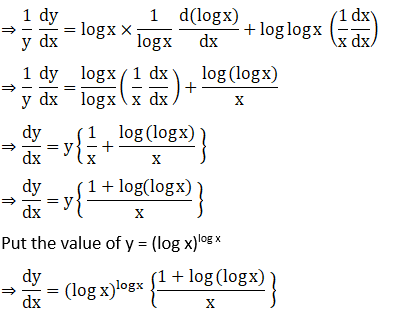
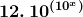
Solution:

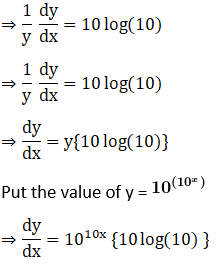
13. Sin (x^x)

Solution:

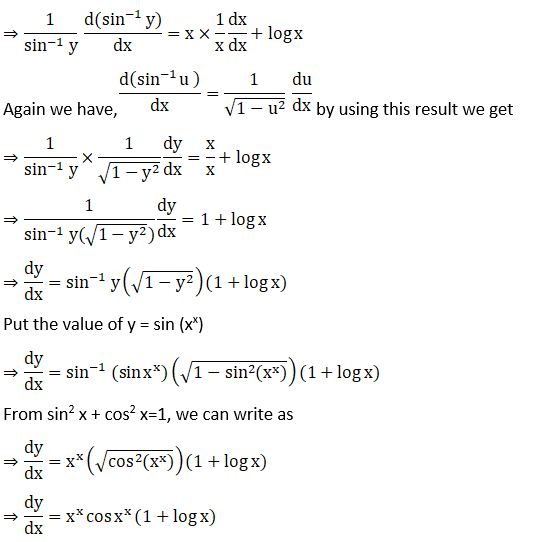
14. (Sin^-1 x)^x

Solution:

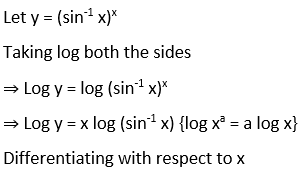
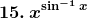
Solution:

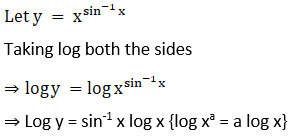
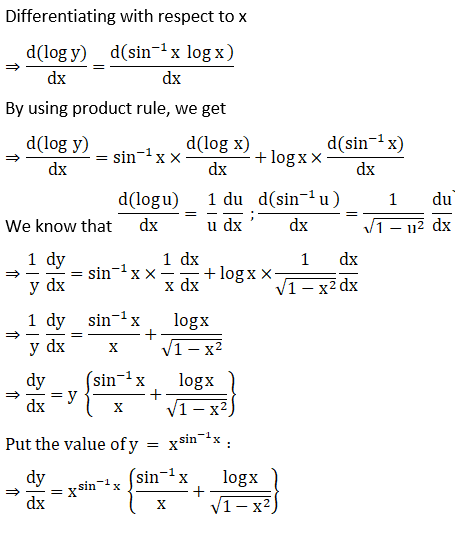
16. (tan x)^1/x

Solution:

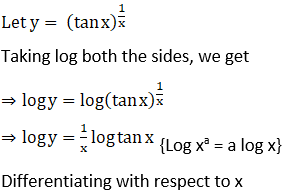
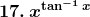
Solution:

18. (i) (x^x) √x

Solution:

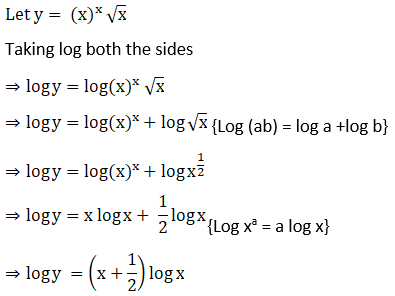
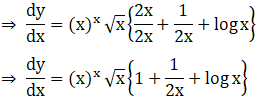
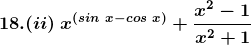
Solution:

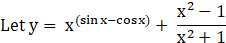
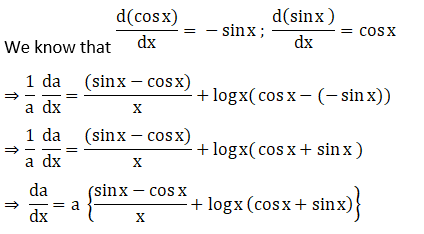
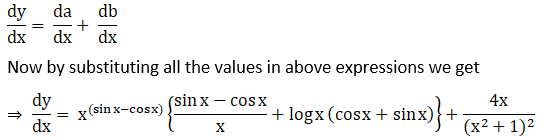
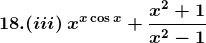
Solution:

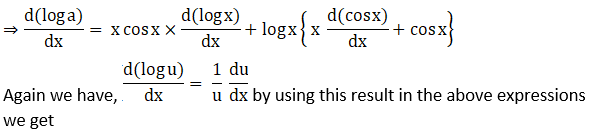
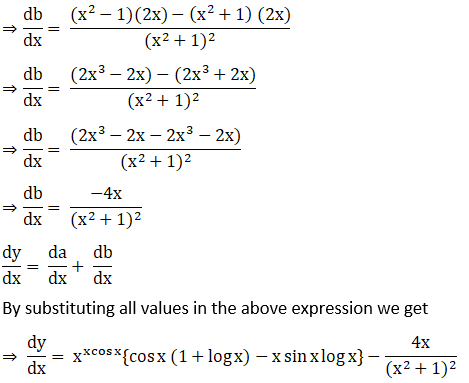
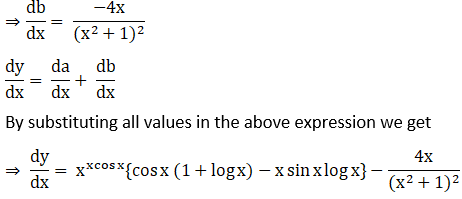
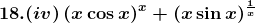
Solution:

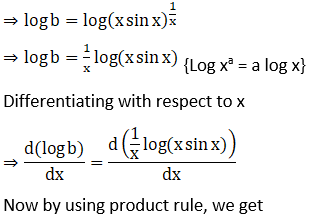
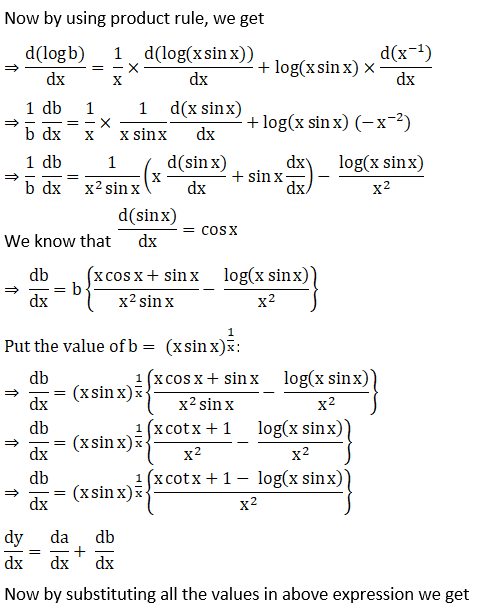
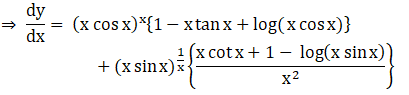
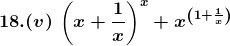
Solution:

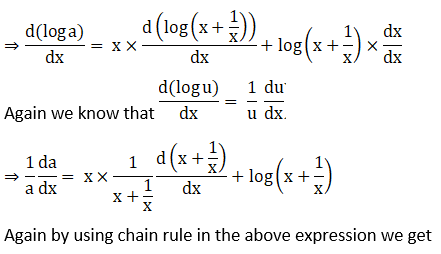
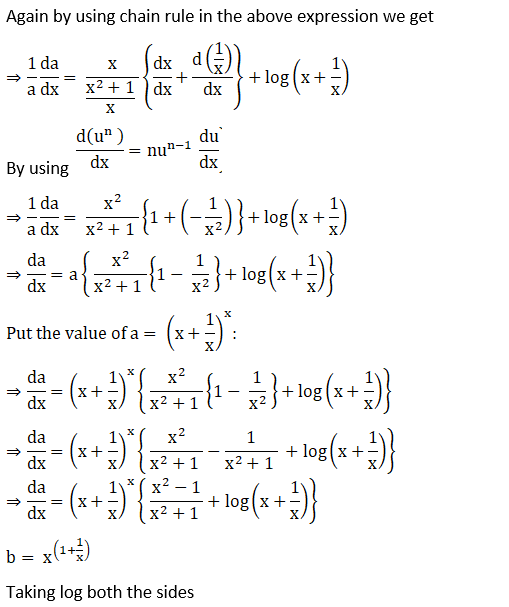
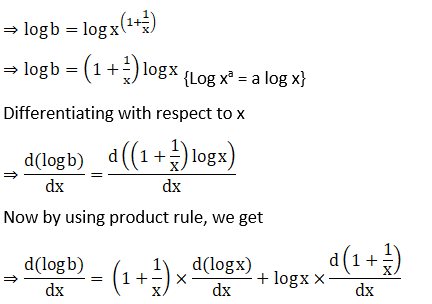
18. (vi) e^{sin x} + (tan x)^x

Solution:

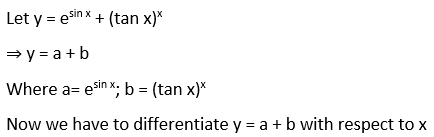
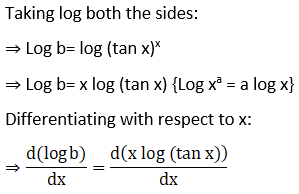
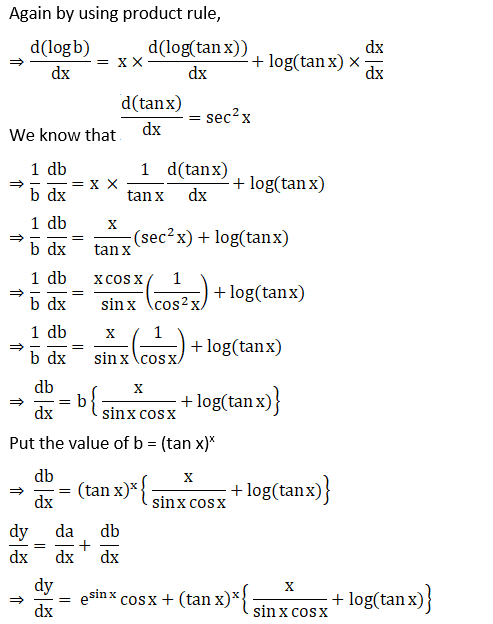
18. (vii) (cos x)^x + (sin x)^1/x

Solution:

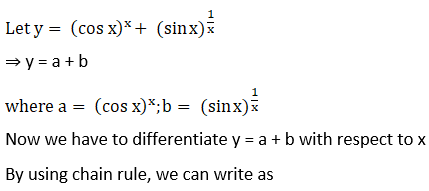
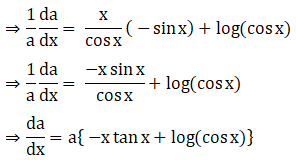
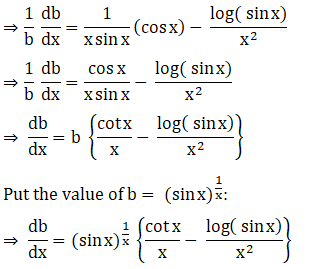
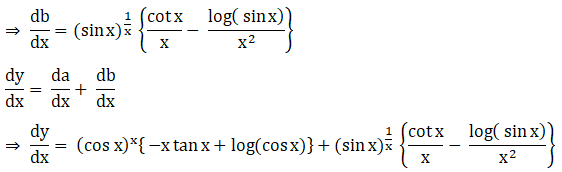
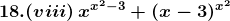
Solution:

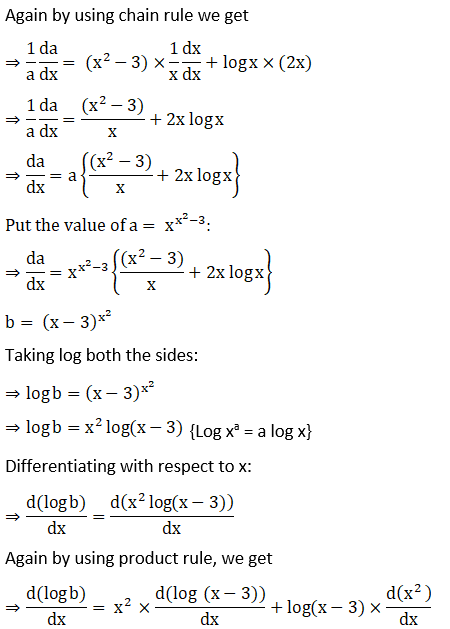
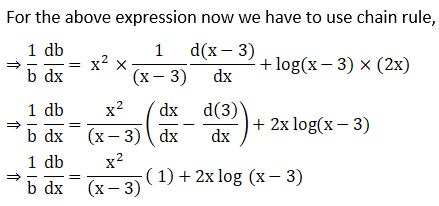
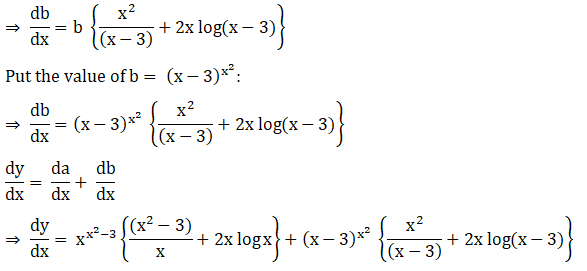
19. y = e^x + 10^x + x^x

Solution:

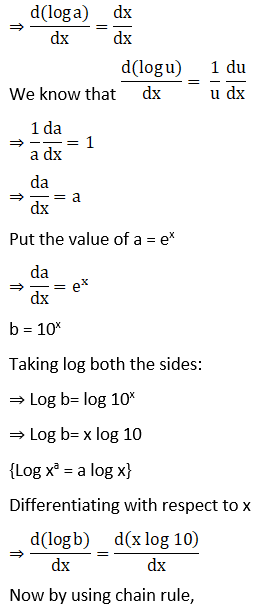
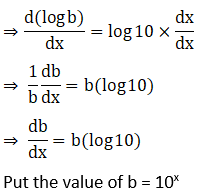
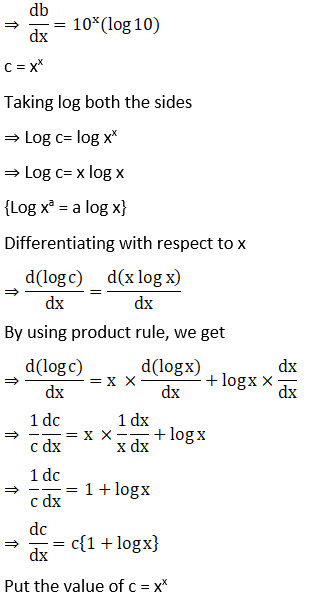
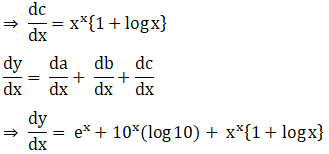
20. y = xⁿ + n^x + x^x + nⁿ

Solution:

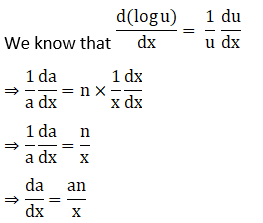
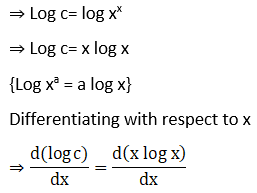
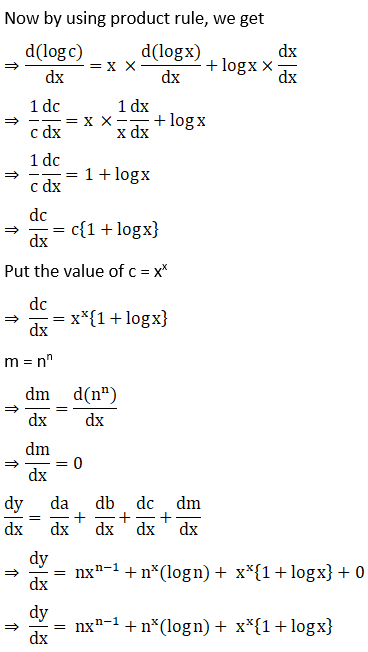
Exercise 11.6 Page No: 11.98

Solution:

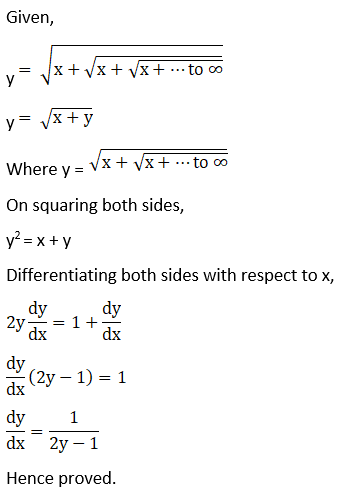
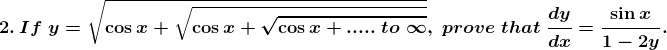
Solution:

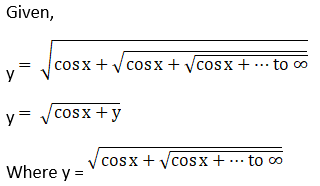
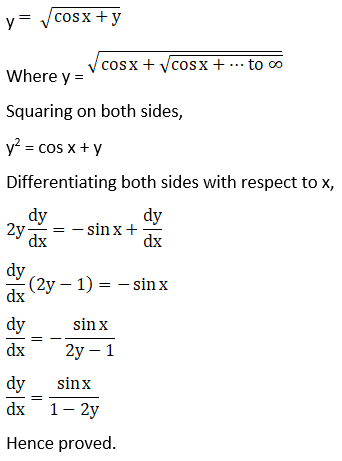
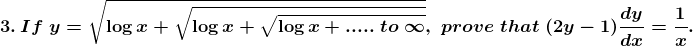
Solution:

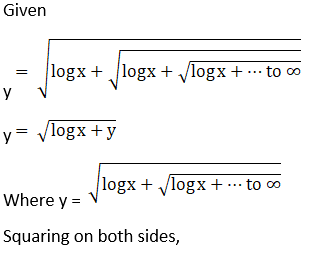
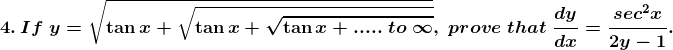
Solution:

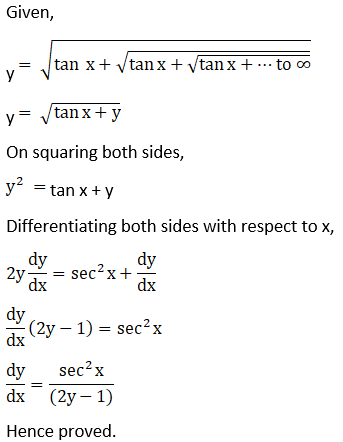
Exercise 11.7 Page No: 11.103

Find dy/dx, when

1. x = at² and y = 2 at

Solution:

2. x = a (θ + sin θ) and y = a (1 – cos θ)

Solution:

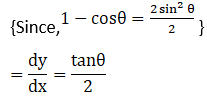
3. x = a cos θ and y = b sin θ

Solution:

Given x = a cos θ and y = b sin θ

4. x = a e^θ (sin θ – cos θ), y = a e^θ (sin θ + cos θ)

Solution:

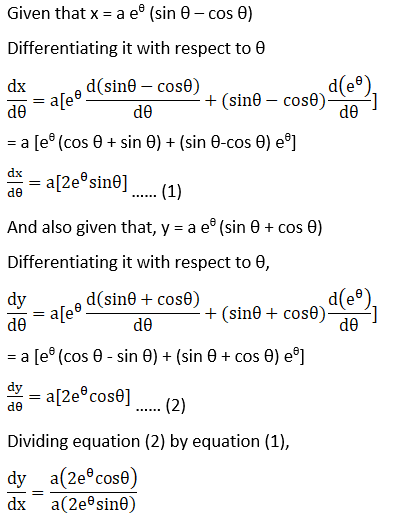
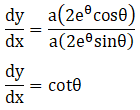
5. x = b sin² θ and y = a cos² θ

Solution:

6. x = a (1 – cos θ) and y = a (θ + sin θ) at θ = π/2

Solution:

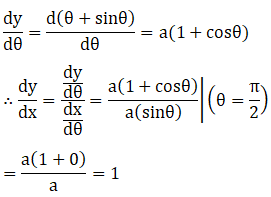
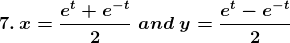
Solution:

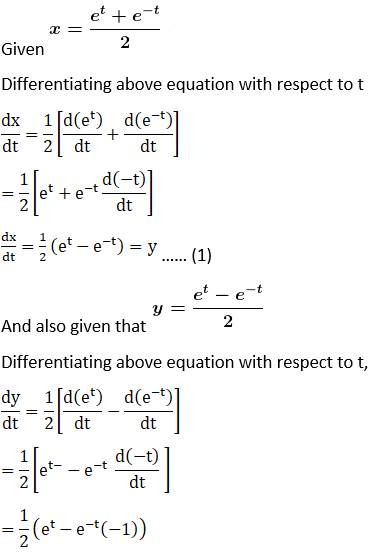
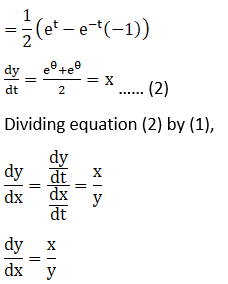
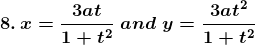
Solution:

9. x = a (cos θ + θ sin θ) and y = a (sin θ – θ cos θ)

Solution:

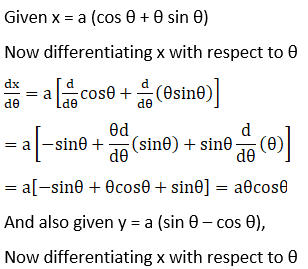
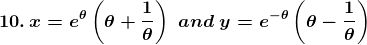
Solution:

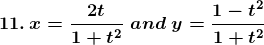
Solution:

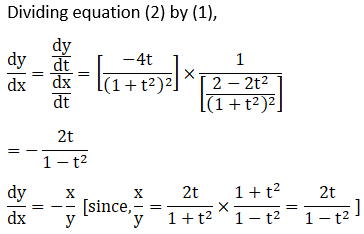
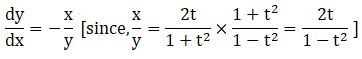
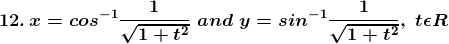
Solution:

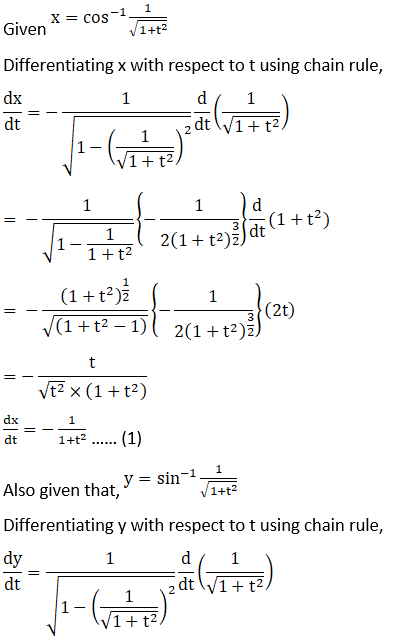
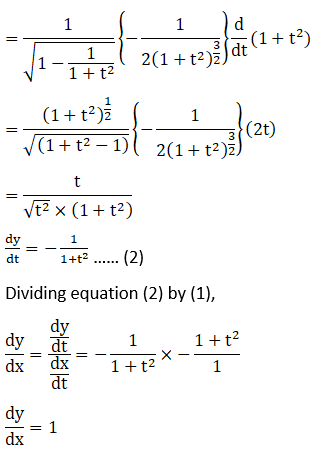
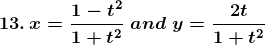
Solution:

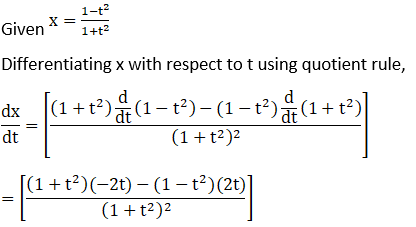
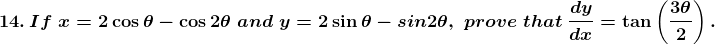
Solution:

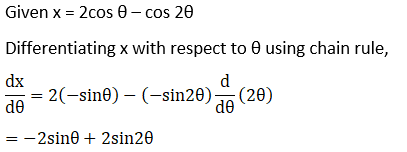
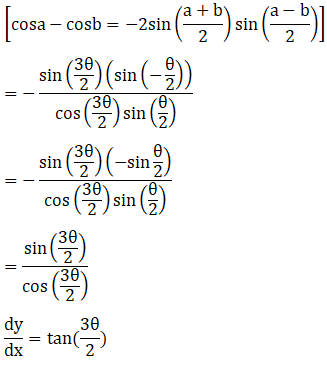
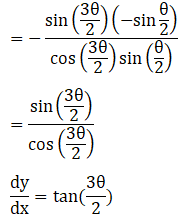
Exercise 11.8 Page No: 11.112

1. Differentiate x² with respect to x³.

Solution:

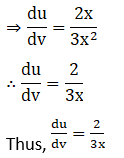
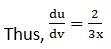
2. Differentiate log (1 +x²) with respect to tan^-1 x.

Solution:

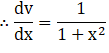
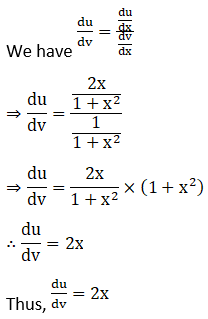
3. Differentiate (log x)^x with respect to log x.

Solution:

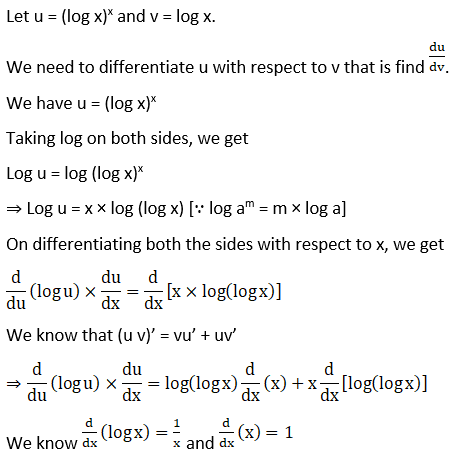
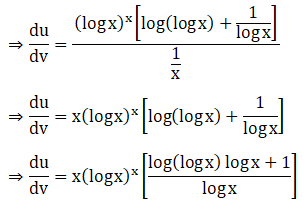
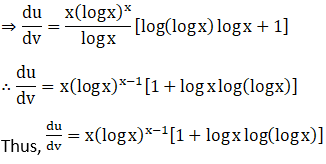
4. Differentiate sin^-1 √ (1-x²) with respect to cos^-1x, if

(i) x ∈ (0, 1)

(ii) x ∈ (-1, 0)

Solution:

(i) Given sin^-1 √ (1-x²)

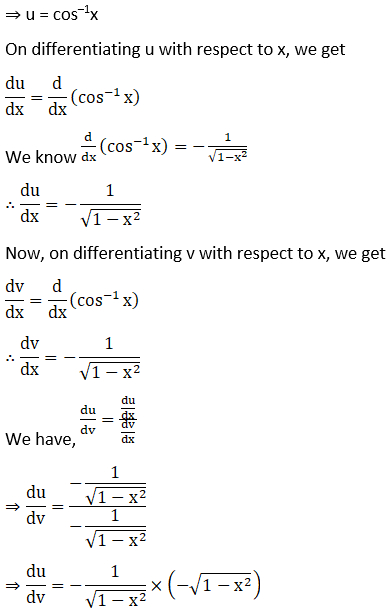
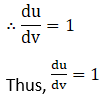
(ii) Given sin^-1 √ (1-x²)

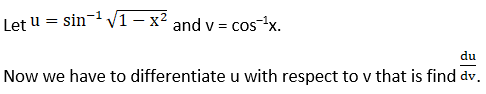
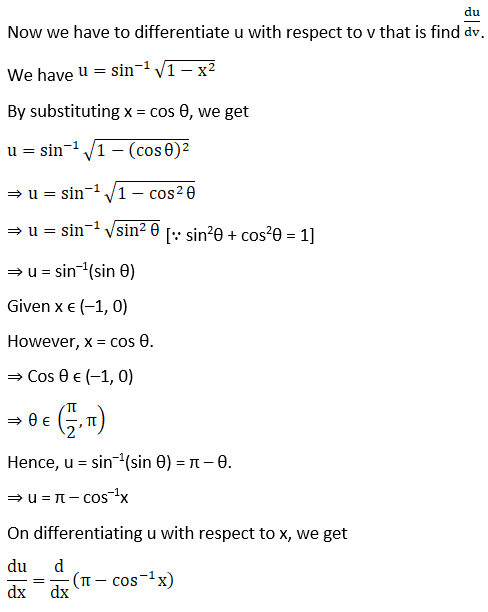
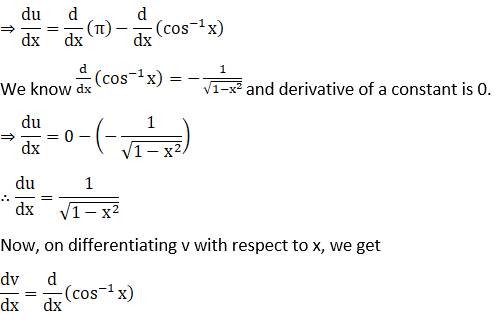
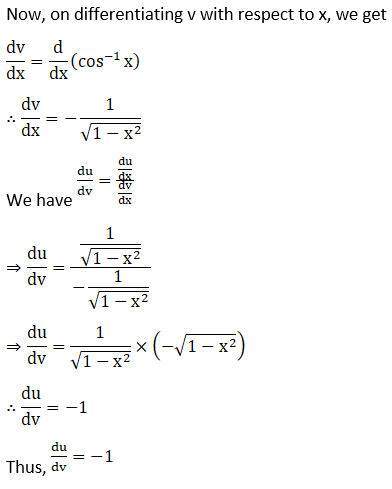
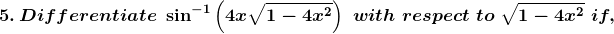
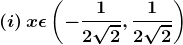
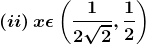
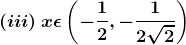
Solution:

(i) Let

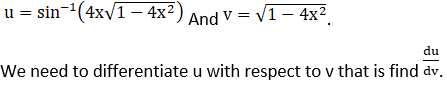
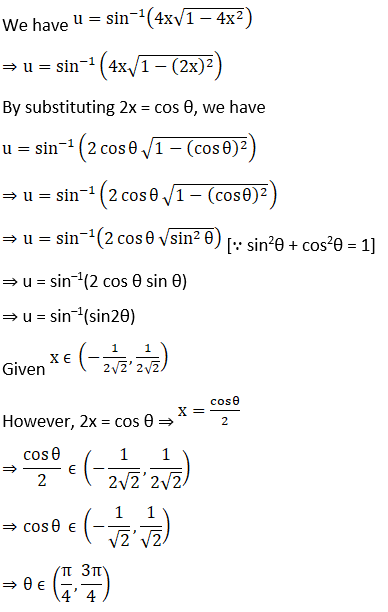
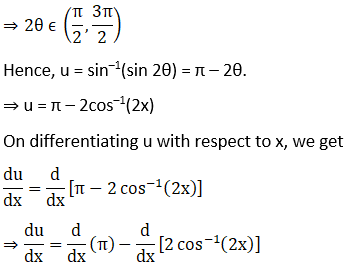
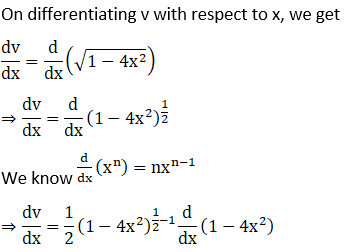
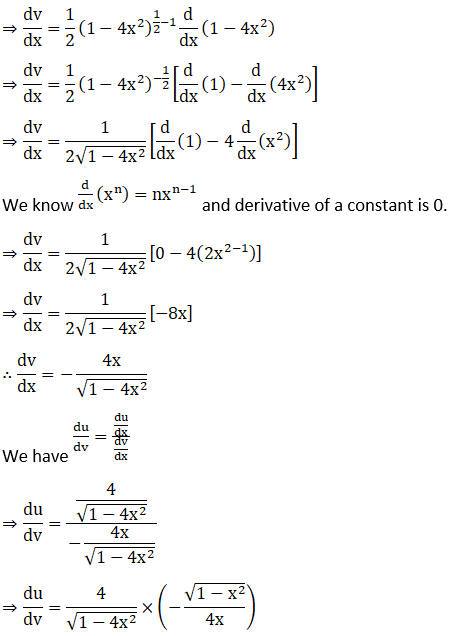
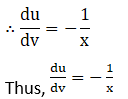
(ii) Let

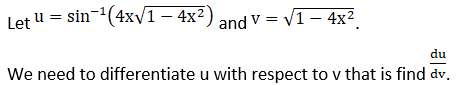
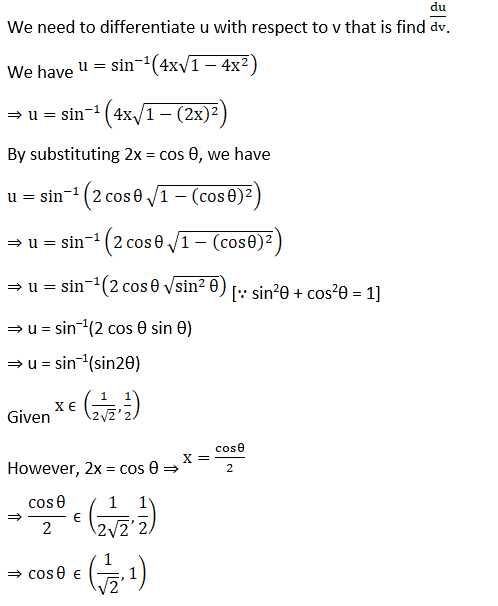
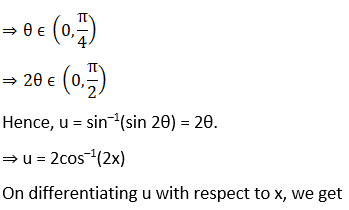
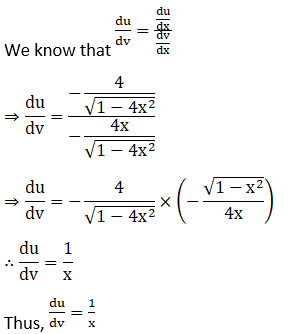
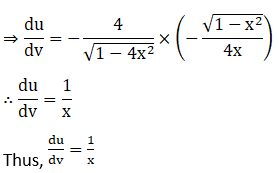
(iii) Let

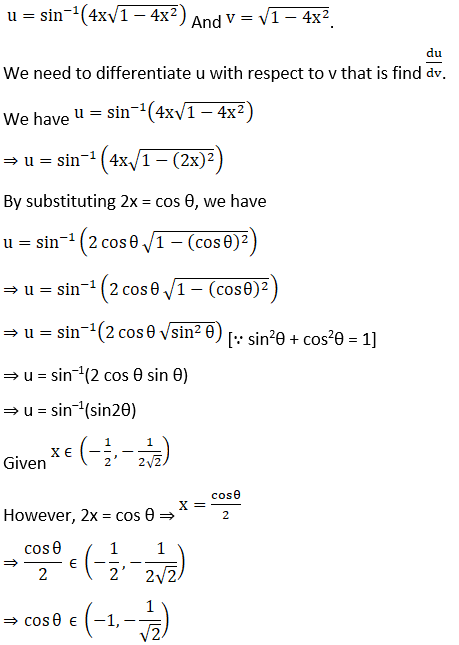
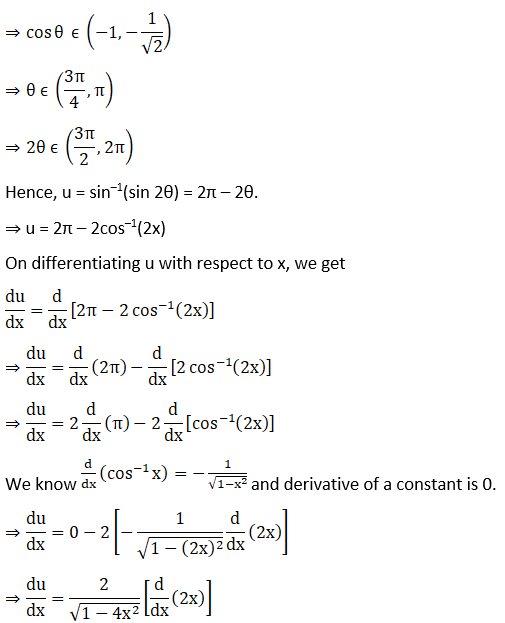
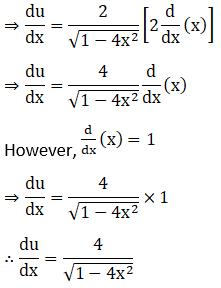
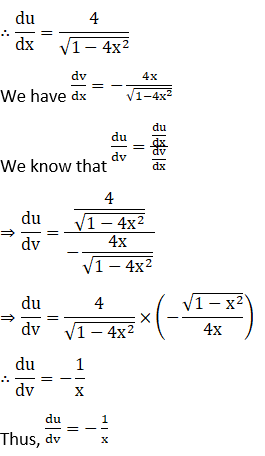
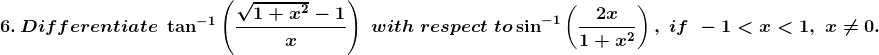
Solution:

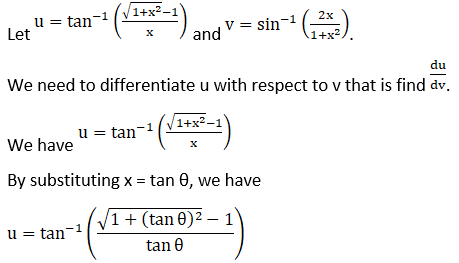
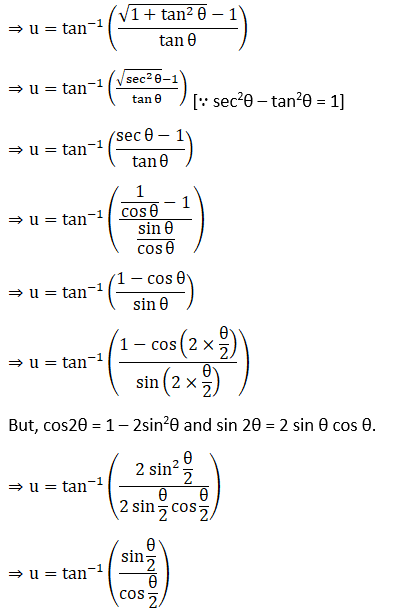
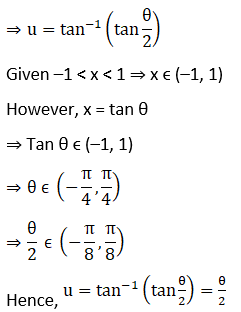
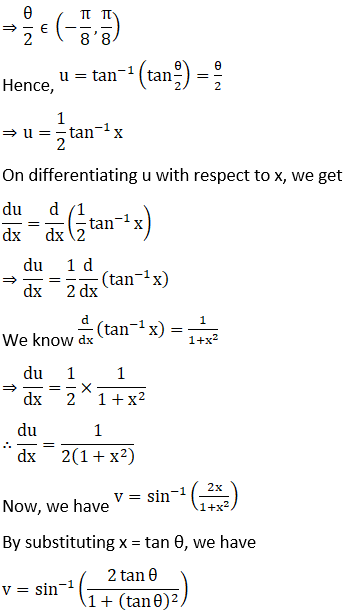
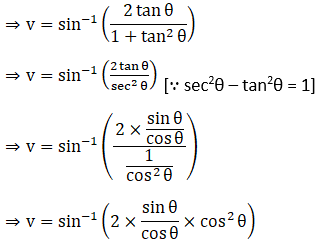
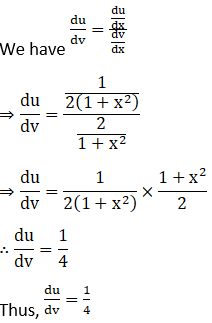
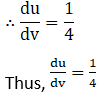
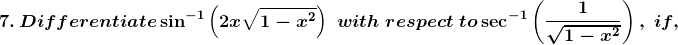
(i) x ∈ (0, 1/ √2)

(ii) x ∈ (1/√2, 1)

Solution:

(i) Let

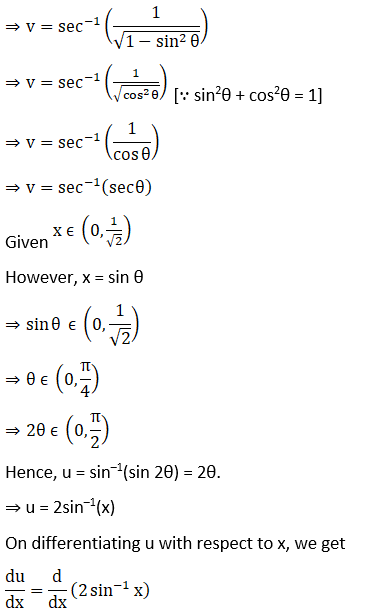
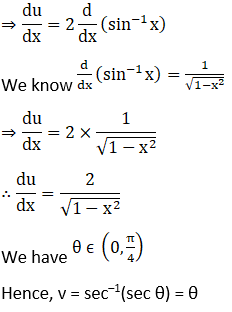
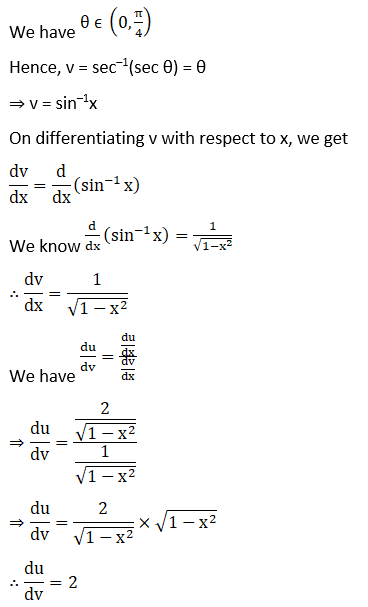
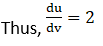
(ii) Let

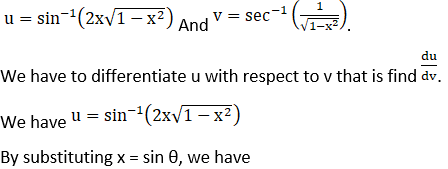
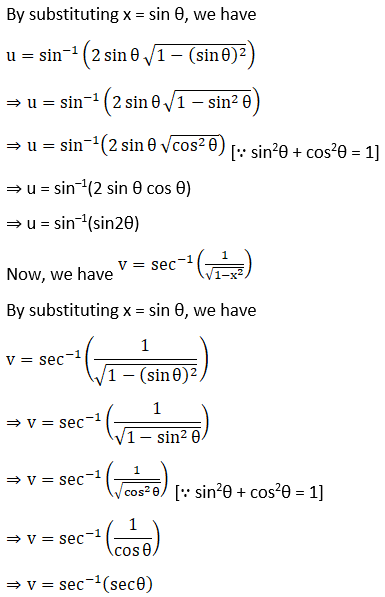
8. Differentiate (cos x)^{sin x} with respect to (sin x)^{cos x}.

Solution:

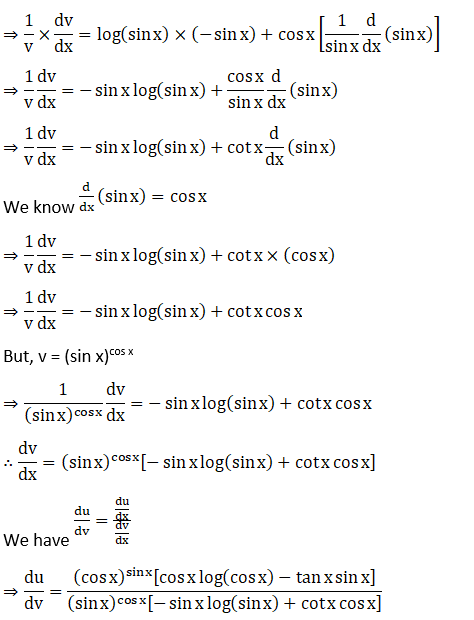
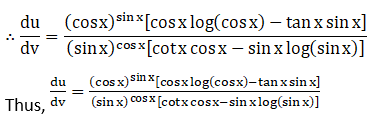
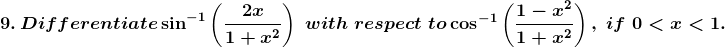
Solution:

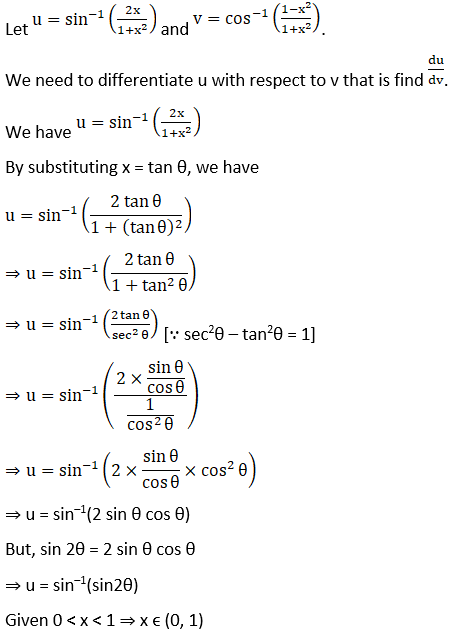
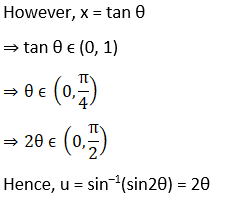
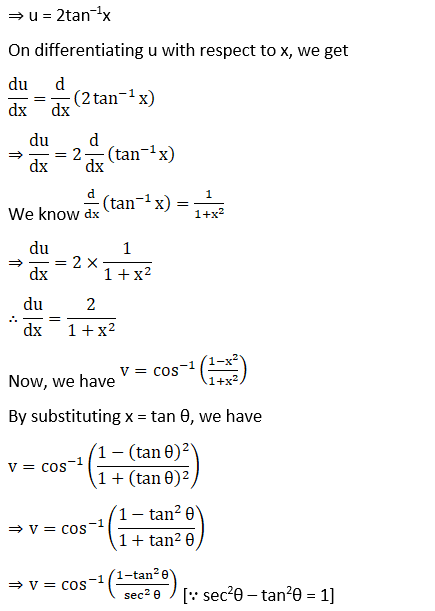
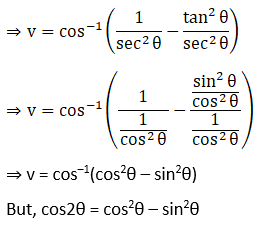
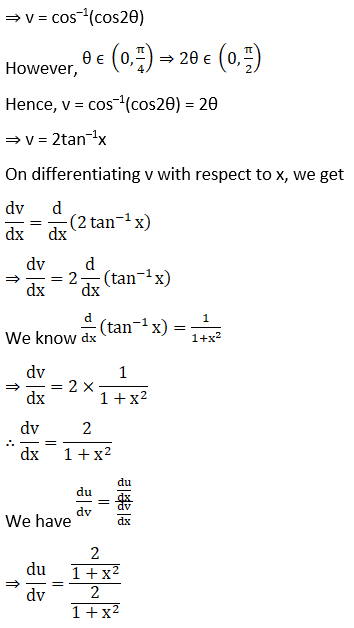
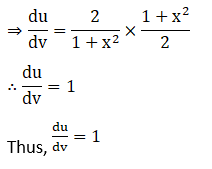
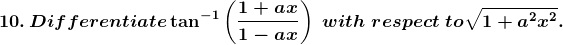
Solution: