Chapter 10 DIFFRENTIABILITY

Access Answers to Maths RD Sharma Solutions for Class 12 Chapter 10 – Differentiability

Exercise 10.1 Page No: 10.10

1. Show that f (x) = |x – 3| is continuous but not differentiable at x = 3.

Solution:

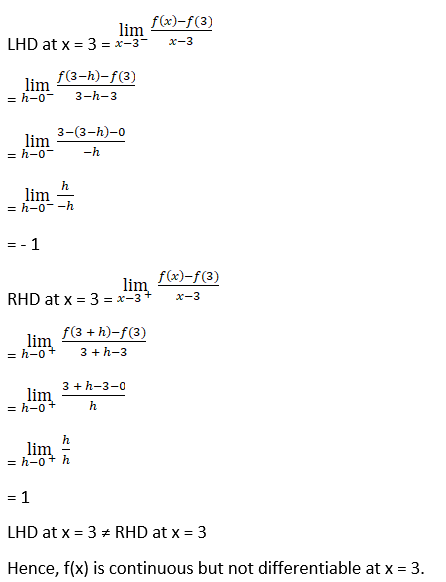
2. Show that f (x) = x ^1/3 is not differentiable at x = 0.

Solution:

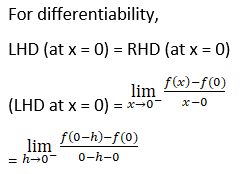
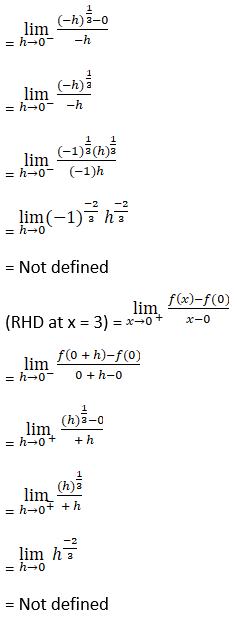
Since, LHD and RHD does not exist at x = 0

Hence, f(x) is not differentiable at x = 0

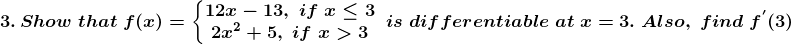
Solution:

Now we have to check differentiability of given function at x = 3

That is LHD (at x = 3) = RHD (at x = 3)

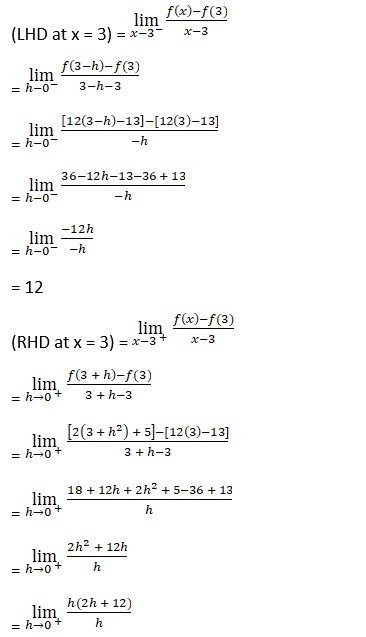
= 12

Since, (LHD at x = 3) = (RHD at x = 3)

Hence, f(x) is differentiable at x = 3.

4. Show that the function f is defined as follows

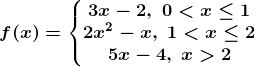
Is continuous at x = 2, but not differentiable thereat.

Solution:

Since, LHL = RHL = f (2)

Hence, F(x) is continuous at x = 2

Now we have to differentiability at x = 2

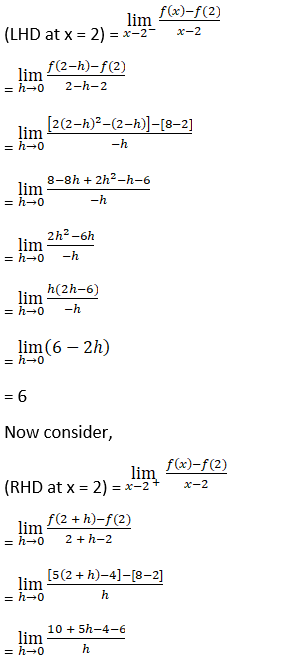
= 5

Since, (RHD at x = 2) ≠ (LHD at x = 2)

Hence, f (2) is not differentiable at x = 2.

5. Discuss the continuity and differentiability of the function f (x) = |x| + |x -1| in the interval of (-1, 2).

Solution:

We know that a polynomial and a constant function is continuous and differentiable everywhere. So, f(x) is continuous and differentiable for x ∈

(-1, 0) and x ∈ (0, 1) and (1, 2).

We need to check continuity and differentiability at x = 0 and x = 1.

Continuity at x = 0

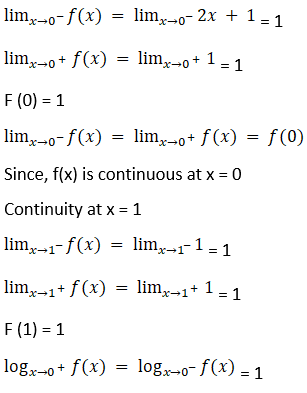
Since, f(x) is continuous at x = 1

Now we have to check differentiability at x = 0

For differentiability, LHD (at x = 0) = RHD (at x = 0)

Differentiability at x = 0

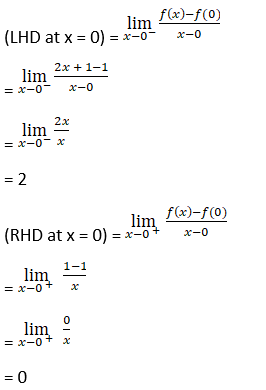
Since, (LHD at x = 0) ≠ (RHD at x = 0)

So, f(x) is differentiable at x = 0.

Now we have to check differentiability at x = 1

For differentiability, LHD (at x = 1) = RHD (at x = 1)

Differentiability at x = 1

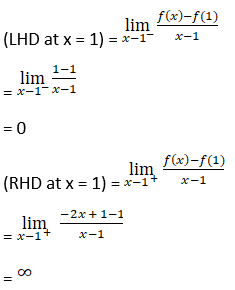
Since, f(x) is not differentiable at x = 1.

So, f(x) is continuous on (- 1, 2) but not differentiable at x = 0, 1

Exercise 10.2 Page No: 10.16

1. If f is defined by f (x) = x², find f’ (2).

Solution:

2. If f is defined by f (x) = x² – 4x + 7, show that f’ (5) = 2 f’ (7/2)

Solution:

Hence the proof.

3. Show that the derivative of the function f is given by f (x) = 2x³ – 9x² + 12 x + 9, at x = 1 and x = 2 are equal.

Solution:

We are given with a polynomial function f(x) = 2x³ – 9x² + 12x + 9, and we have

4. If for the function Ø (x) = λ x² + 7x – 4, Ø’ (5) = 97, find λ.

Solution:

We have to find the value of λ given in the real function and we are given with the differentiability of the function f(x) = λx² + 7x – 4 at x = 5 which is f ‘(5) = 97, so we will adopt the same process but with a little variation.

5. If f (x) = x³ + 7x² + 8x – 9, find f’ (4).

Solution:

We are given with a polynomial function f(x) = x³ + 7x² + 8x – 9, and we have to find whether it is derivable at x = 4 or not,

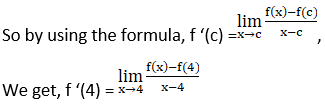
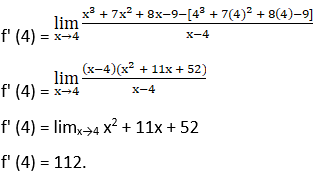
6. Find the derivative of the function f defined by f (x) = mx + c at x = 0.

Solution:

We are given with a polynomial function f(x) = mx + c, and we have to find whether it is derivable at x = 0 or not,

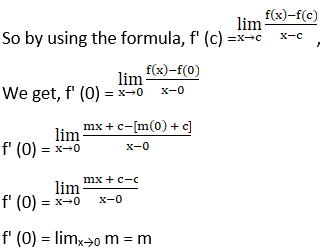
This is the derivative of a function at x = 0, and also this is the derivative of this function at every value of x.