Chapter 9 Some Applications of Trigonometry
Class 10th Maths Chapter MCQs
Class 10 Maths MCQs Chapter 9 Application of Trigonometry
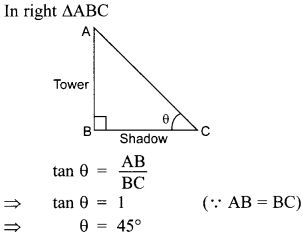
Question 1. The shadow of a tower
is equal to its height at 10-45 a.m. The sun’s altitude is
(a) 30°
(b)
45°
(c) 60°
(d) 90°
Answer/ Explanation
Answer: b
Explaination: Reason: Let the height of tower BC = rm and sun’s
altitude = θ
Then Length of its shadow, AB = x m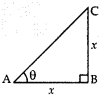
In rt. ∆ABC, tan θ = \(\frac{BC}{AB}\) = \(\frac{x}{x}\) =
1
⇒ tan θ = tan 450
∴ θ = 45°
2. In given figure, the value of CE is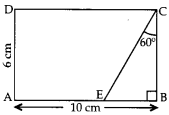
(a) 12 cm
(b) 6 cm
(c) 9 cm
(d) 6√3 cm
Answer/ Explanation
Answer: a
Explaination: Reason: In rt. ∆EBC, cos 60° =
\(\frac{BC}{CE}\)
⇒ \(\frac{1}{2}\) = \(\frac{6}{CE}\)
⇒ CE = 12
cm
Question 3. In given figure,
the value of ZC is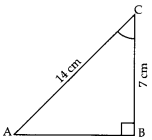
(a) 90°
(b) 45°
(c) 30°
(d) 60°
Answer/ Explanation
Answer: d
Explaination: Reason: In rt. ∆ABC, cos C = \(\frac{BC}{AB}\) =
\(\frac{7}{14}\) = \(\frac{1}{2}\)
⇒ cos C = cos 60°
∴ C =
60°
Question 4. In given Fig., the angle of
depression from the observing position D and E of the object at A are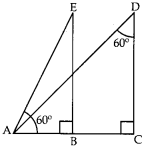
(a) 60°, 60°
(b) 30°, 30°
(c) 30°, 60°
(d) 60°,
30°
Answer/ Explanation
Answer: c
Explaination: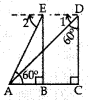
Reason: ∵ APD, ∠1 = 90° – 60° = 30°
∴ APE, ∠2 = ∠EAB …[alt
Zs]
∴ ∠2 = 60°
Hence the angles of depression at D and E are 30° and 60°
respectively.
Question 5. In given figure,
the length of AP is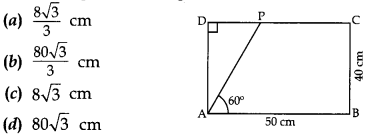
Answer/ Explanation
Answer: b
Explaination:
Question 6. In given figure,
the value of AE is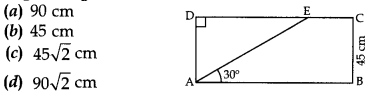
Answer/ Explanation
Answer: a
Explaination: Reason: ∠AED = ∠EAB = 30°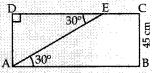
In rt. ∆AED, sin 30° = \(\frac{AD}{AP}\)
⇒ \(\frac{1}{2}\)
= \(\frac{45}{AE}\)
⇒ AE = 90 cm
Question 7. In given figure, AD = 4 cm, BD = 3 cm
and CB = 12 cm. The value of tan θ is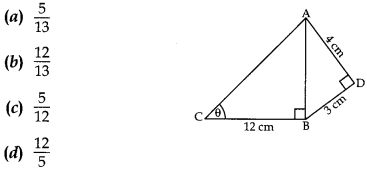
Answer/ Explanation
Answer: c
Explaination: Reason: In rt ∆ADB,
AB² = AD² + BD² = (4)² +
(3)² = 16 + 9 = 25
∴ AB = √25 = 5
∴ In rt ∆ABC, tan θ \(\frac{AB}{BC}\) =
\(\frac{5}{12}\)
Question 8. In figure given ABCD is a rectangle, the value of CE is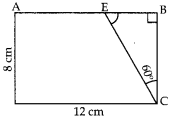
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4
cm
Answer/ Explanation
Answer: d
Explaination: Reason: Since ABCD is a rectangle
∴ BC = AD = 8
cm and B = 90°
In rt ∆CBE, cos 60° = \(\frac{CE}{BC}\)
⇒ \(\frac{1}{2}\) =
\(\frac{CE}{8}\)
∴ CE = \(\frac{8}{2}\) = 4 cm
Question 9. In given figure, ABCD is a || gm. The
lenght of AP is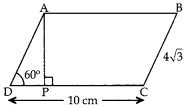
(a) 2 cm
(b) 4 cm
(c) 6 cm
(d) 8
cm
Answer/ Explanation
Answer: c
Explaination: Reason: Since ABCD is a || gm
∴ AD = BC =
4√3
In rt ∆APD, sin 60° = \(\frac{AP}{AD}\)
⇒
\(\frac{\sqrt{3}}{2}=\frac{\mathrm{AP}}{4 \sqrt{3}}\)
⇒ 2AP = 4 × 3 = 12
∴
AP = 6 cm
Question 10. When the length
of shadow of a vertical pole is equal to √3 times of its height, the angle of
elevation of the Sun’s altitude is
(a) 30°
(b) 45°
(c) 60°
(d)
15°
Answer/ Explanation
Answer: a
Explaination: Reason: Let the height of the vertical pole, BC =
h m
∴ Shadow AB = √3 h m and the angle of elevation ZBAC = θ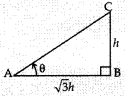
In rt ∆ABC, tan θ = \(\frac{B C}{A B}=\frac{h}{\sqrt{3}
h}=\frac{1}{\sqrt{3}}\) = tan 30°
∴ θ = 30°
Hence the Sun’s altitude is
30°
Question 11. The angle of elevation of top of a
tower from a point on the ground, which is 30 m away from the foot of the tower
is 30°. The length of the tower is
(a) √3 m
(b) 2√3 m
(c) 5√3m
(d)
10√3 m
Answer/ Explanation
Answer: d
Explaination: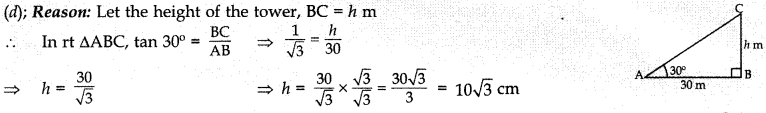
Question 12. A plane is observed
to be approaching the airport. It is at a distance of 12 km from the point of
observation and makes an angle of elevation of 60°. The height above the ground
of the plane is
(a) 6√3 m
(b) 4√3 m
(c) 3√3 m
(d) 2√3
m
Answer/ Explanation
Answer: a
Explaination: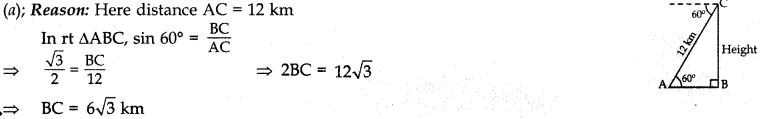
Question 13. The upper
part of a tree is broken by the wind and makes an angle of 30° with the ground.
The distance from the foot of the tree to the point where the top touches the
ground is 5 m. The height of the tree is
(a) 10√33 m
(b) 5√33 m
(c) √3
m
(d) √3/5 m
Answer/ Explanation
Answer: b
Explaination: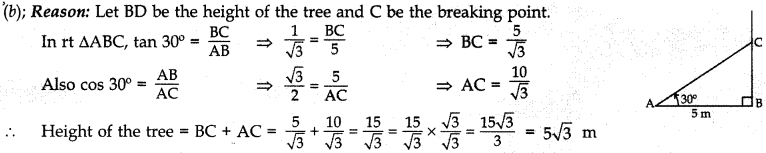
Question 14. The angles of elevation of the top of a
rock from the top and foot of 100 m high tower are respectively 30° and 45°. The
height of the rock is
(a) 50 m
(b) 150 m
(c) 5o√3m
(d) 50(3 +
√3)
Answer
Answer: d
Question 15. The tops of two poles of height 20 m and 14 m
are connected by a wire. If the wire makes an angle of 30° with horizontal, the
length of the wire is
(a) 6 m
(b) 10 m
(c) 12 m
(d) 20
m
Answer
Answer: c
Question 16. The angle of depression
of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The
distance of the car from the base of the tower (in m) is:
(a) 25√3
(b)
50√3
(c) 75√3
(d) 150
Answer/Explanation
Answer: c
Explaination: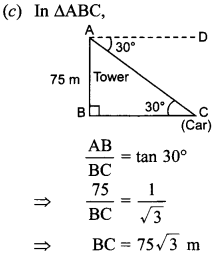
Question 17. A ladder 15 m long just reaches the
top of a vertical wall. If the ladder makes an angle of 60° with the wall, then
the height of the wall is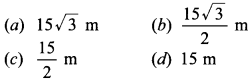
Answer/Explanation
Answer: b
Explaination: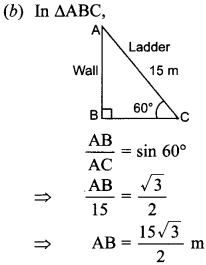
Question 18. The line drawn from the eye of an observer
to the point in the object viewed by the observer is known as
(a) horizontal
line
(b) vertical line
(c) line of sight
(d) transversal
line
Answer
Answer: c
Question 19. The tops of two poles of heights 20
m and 14 m are connected by a wire. If the wire makes an angle of 30° with the
horizontal, then the length of the wire is
(a) 8 m
(b) 10 m
(c) 12
m
(d) 14 m
Answer/Explanation
Answer: c
Explaination: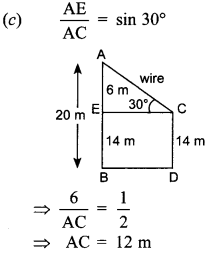
Question 20. If two towers of heights
h1 and h2 subtend angles of 60° and 30° respectively at
the mid-point of the line joining their feet, then h1 : h2
=
(a) 1 : 2
(b) 1 : 3
(c) 2 : 1
(d) 3 : 1
Answer/Explanation
Answer: d
Explaination: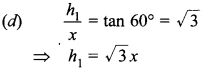
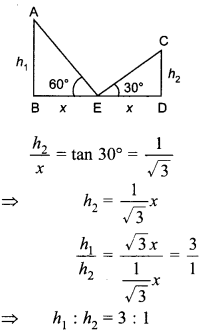
Question 21. The angle of elevation of the
top of a tower from a point 20 metres away from its base is 45°. The height of
the tower is
(a) 10 m
(b) 20 m
(c) 30 m
(d) 20√3
m
Answer/Explanation
Answer: b
Explaination: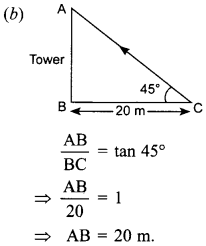
Question 22. Two poles are 25 m and 15 m
high and the line joining their tops makes an angle of 45° with the horizontal.
The distance between these poles is
(a) 5 m
(b) 8 m
(c) 9 m
(d) 10
m
Answer/Explanation
Answer: c
Explaination: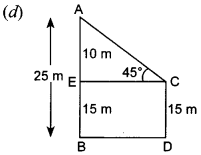

Question 23. A portion of a 60 m
long tree is broken by tornado and the top struck up the ground making an angle
of 30° with the ground level. The height of the point where the tree is broken
is equal to
(a) 30 m
(b) 35 m
(c) 40 m
(d) 20
m
Answer/Explanation
Answer:
Explaination: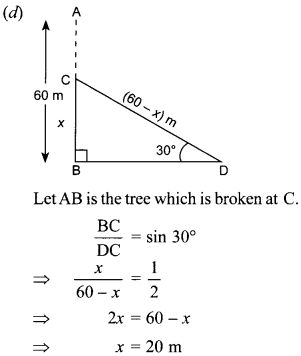
Question 24. The angle of elevation of the top of a 15m high tower at a point 15m away from the base of the tower is ____ .
Answer/Explanation
Answer:
Explaination:
Hints:
∵ Height of tower = distance of point
from the base
∴ Angle of elevation = 45°.
Question 25. The ratio of the height of a tower and the length of its shadow on the ground is √3 : 1. What is the angle of elevation of the sun?
Answer/Explanation
Answer:
Explaination: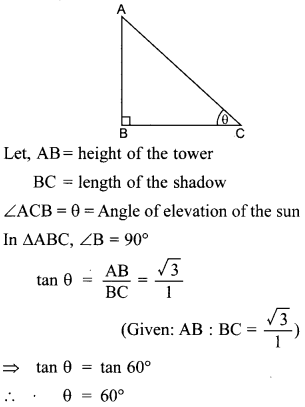
Question 26. An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
Answer/Explanation
Answer:
Explaination: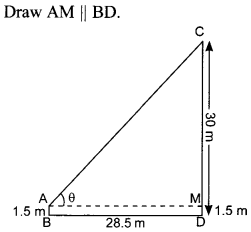
Here, AB = DM = 1.5 m
CM = CD – DM
= 30 – 1.5 = 28.5
m
Let 0 be the angle of elevation of the top of the tower from the eye of the
observer.
∴ In ∆ACM
tan θ = \(\frac{C M}{A M}=\frac{28.5}{28.5}\)
tan θ
= 1
tan θ = tan 45°
θ = 45°
Question 27. If a tower 30 m high, casts a shadow 10√3 m long on the ground, then what
is the angle of elevation of the sun?
Answer/Explanation
Answer:
Explaination:
Question 28. If two towers of height h1 and h2 subtends angles of 60° and 30° respectively at the mid points of line joining their feet, find h1 : h2
Answer/Explanation
Answer:
Explaination: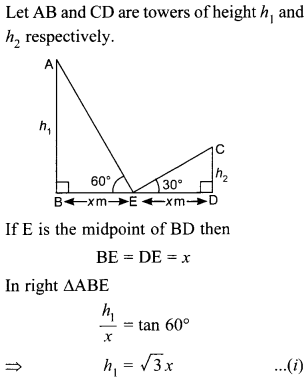
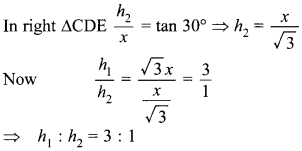
Question 29. At some time of the day the length of the shadow of a tower is equal to its height. Find the sun’s altitude at that time.
Answer/Explanation
Answer:
Explaination: