Chapter 8 Introduction to Trigonometry

Class 10 Maths MCQs Chapter 8 Introduction to Trigonometry

1. The value of cos 0°. cos 1°. cos 2°. cos 3°… cos 89° cos 90° is
(a) 1
(b) -1
(c) 0
(d) \(\frac{1}{\sqrt{2}}\)

Answer

Answer: c

---

2. If x tan 45° sin 30° = cos 30° tan 30°, then x is equal to
(a) √3
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{\sqrt{2}}\)
(d) 1

Answer

Answer: d

---

3. If x and y are complementary angles, then
(a) sin x = sin y
(b) tan x = tan y
(c) cos x = cos y
(d) sec x = cosec y

Answer

Answer: d

---

4. sin 2B = 2 sin B is true when B is equal to
(a) 90°
(b) 60°
(c) 30°
(d) 0°

Answer

Answer: d

---

5. If A, B and C are interior angles of a ΔABC then \(\cos \left(\frac{\mathrm{B}+\mathrm{C}}{2}\right)\) is equal to

Answer

Answer: a

---

6. If A and (2A – 45°) are acute angles such that sin A = cos (2A – 45°), then tan A is equal to
(a) 0
(b) \(\frac{1}{\sqrt{3}}\)
(c) 1
(d) √3

Answer

Answer: c

---

7. If y sin 45° cos 45° = tan2 45° – cos2 30°, then y = …
(a) –\(\frac{1}{2}\)
(b) \(\frac{1}{2}\)
(c) -2
(d) 2

Answer

Answer: b

---

8. If sin θ + sin² θ = 1, then cos² θ + cos⁴ θ = ..
(a) -1
(b) 0
(c) 1
(d) 2

Answer

Answer: c

---

9. 5 tan² A – 5 sec² A + 1 is equal to
(a) 6
(6) -5
(c) 1
(d) -4

Answer

Answer: d

---

10. If sec A + tan A = x, then sec A =

Answer

Answer: d

---

11. If sec A + tan A = x, then tan A =

Answer

Answer: b

---

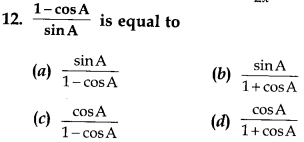
Answer

Answer: b

---

13. If x = a cos 0 and y = b sin 0, then b2x2 + a2y2 =
(a) ab
(b) b² + a²
(c) a²b²
(d) a⁴b⁴

Answer

Answer: c

---

14. What is the maximum value of \(\frac{1}{\csc A}\)?
(a) 0
(b) 1
(c) \(\frac{1}{2}\)
(d) 2

Answer

Answer: b

---

15. What is the minimum value of sin A, 0 ≤ A ≤ 90°
(a) -1
(b) 0
(c) 1
(d) \(\frac{1}{2}\)

Answer

Answer: b

---

16. What is the minimum value of cos θ, 0 ≤ θ ≤ 90°
(a) -1
(b) 0
(c) 1
(d) \(\frac{1}{2}\)

Answer

Answer: b

---

17. Given that sin θ = \(\frac{a}{b}\) , then tan θ =

Answer

Answer: c

---

18. If cos 9A = sin A and 9A < 90°, then the value of tan 5A is
(a) 0
(b) 1
(c) \(\frac{1}{\sqrt{3}}\)
(d) √3

Answer

Answer: b

---

19. If in ΔABC, ∠C = 90°, then sin (A + B) =
(a) 0
(b) 1/2
(c) \(\frac{1}{\sqrt{2}}\)
(d) 1

Answer

Answer: d

---

20. If sin A – cos A = 0, then the value of sin⁴ A + cos⁴ A is
(a) 2
(b) 1
(c) \(\frac{3}{4}\)
(d) \(\frac{1}{2}\)

Answer

Answer: d

---

21. Ratios of sides of a right triangle with respect to its acute angles are known as
(a) trigonometric identities
(b) trigonometry
(c) trigonometric ratios of the angles
(d) none of these

Answer/Explanation

Answer: c
Explaination: (c) trigonometric ratios of the angles

---

22. If tan θ = \(\frac{a}{b}\) then the value of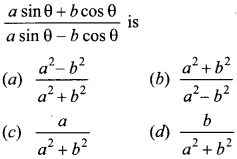

Answer/Explanation

Answer: b
Explaination: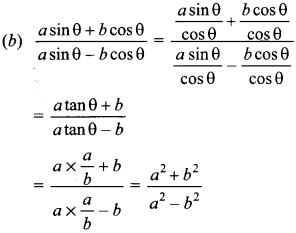

---

23. Match the Columns:

(a) 1 – A, 2 – C, 3 – B
(b) 1 – B, 2 – C, 3 – A
(c) 1 – B, 2 – C, 3 – D
(d) 1 – D, 2 – B, 3 – A

Answer/Explanation

Answer: b
Explaination:

---

24. In the given figure, if AB = 14 cm, then the value of tan B is: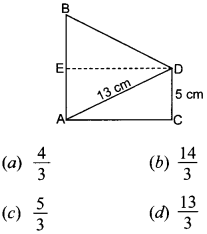

Answer/Explanation

Answer: a
Explaination: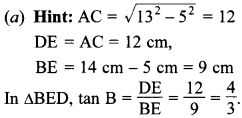

---

25. Match the Columns:

(a) 1 – A, 2 – C, 3 – B
(b) 1 – C, 2 – A, 3 – D
(c) 1 – B, 2 – A, 3 – E
(d) 1 – B, 2 – D, 3 – A

Answer/Explanation

Answer: d
Explaination: (d) definition of trigonometric ratios.

---

26. The value of sin² 30° – cos² 30° is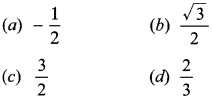

Answer/Explanation

Answer:
Explaination: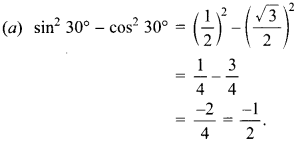

---

27. If 3 cot θ = 2, then the value of tan θ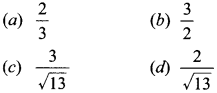

Answer/Explanation

Answer: b
Explaination:
3 cot θ = 2
⇒ cot θ \(\frac{2}{3}\)
tan θ = \(\frac{3}{2}\)

---

28. If ∆ABC is right angled at C, then the value of cos (A + B) is [NCERT Exemplar Problems]

Answer/Explanation

Answer: a
Explaination:
(a) ∆ ABC is right angled at C,
∴ A + B + C = 180°
A + B = 180° – 90° = 90° (∵ ∠C = 90°)
cos (A + B) = cos 90° = 0

---

29. If 0° < θ < 90°, then sec 0 is (a) >1
(b) < 1
(c) =1
(d) 0

Answer/Explanation

Answer: a
Explaination:
(a) ∵ sec θ = \(\frac{1}{\cos \theta}\)
∵ sce θ > 1.

---

30. If sin 0 = √3 cos θ, 0° < θ < 90°, then θ is equal to
(a) 30°
(b) 45°
(c) 60°
(d) 90°

Answer/Explanation

Answer: c
Explaination: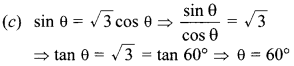

---

31. If cos (α + β) = 0, then sin (α – β) can be reduced to [NCERT Exemplar Problems]
(a) cos β
(b) cos 2β
(c) sin α
(d) sin 2α

Answer/Explanation

Answer: b
Explaination:
(b) cos (α + β) = 0 = cos 90°
⇒ α + β = 90°
sin (α – β) = sin (α – β + β – β)
= sin (α + β – 2β)
= sin (90° – 2β) = cos 2β

---

32. If cos 9α = sin a and 9α < 90°, then the value of tan 5α is [NCERT Exemplar Problems]
(a) \(\frac{1}{\sqrt{3}}\)
(b) √3
(c) 1
(d) 0

Answer/Explanation

Answer: c
Explaination:
cos 9α = sin α
⇒ cos 9α = cos (90° – α)
⇒ 9α = 90° – α
⇒ 10α = 90°
⇒ α = 9°
∴ tan 5α = tan 5 × 9°
= tan 45° = 1

---

33. sin (45° + θ) – cos (45° – θ) is equal to
(a) 2 cos θ
(b) 0
(c) 2 sin θ
(d) 1

Answer/Explanation

Answer: b
Explaination:
sin (45° + θ) – cos (45° – θ)
= sin {90° – (45° – θ)} – cos (45° – θ)
= cos (45° – θ) – cos (45° – θ) = 0

---

34. The value of sin² 5° + sin² 10° + sin² 15° + … + sin² 90° is equal to
(a) 8
(b) 8.5
(c) 9
(d) 9.5

Answer/Explanation

Answer: d
Explaination:
sin² 5° + sin² 10° + sin² 15° + ….. + sin² 90°
= (sin² 5° + sin² 85°) + (sin² 10° + sin² 80°) + … + (sin² 40° + sin² 50°) + sin² 45° + sin² 90°
= (sin² 5° + cos² 5°) + (sin 10° + cos² 10°) + … + (sin² 40° + cos² 40°) + \(\left(\frac{1}{\sqrt{2}}\right)^{2}\) + 1
= 1 + 1 + 1 + … 8 times + \(\frac{1}{2}\) + 1
= 9\(\frac{1}{2}\) = 9.5

---

35. The value of the expression [cosec (75° + θ) – sec (15° – θ) – tan (55° + θ) + cot (35° – θ)] is [NCERT Exemplar Problems]
(a) -1
(b) 0
(c) 1
(d) \(\frac{3}{2}\)

Answer/Explanation

Answer: b
Explaination:
cosec (75° + θ) – sec (15° – θ) – tan (55° + θ) + cot (35° – θ)
= cosec {90° – (15° – θ)} – sec (15° – θ) – tan {90° – (35° – θ)} + cot (35° – θ)
= sec (15° – θ) – sec (15° – θ) – cot (35° – θ) + cot (35° – θ) = 0

---

36. sin (90° – A) =
(a) sin A
(b) tan A
(c) cos A
(d) cosec A

Answer

Answer: c

---

37. tan A =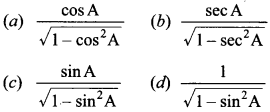

Answer/Explanation

Answer: c
Explaination:

---

38. If cosec A – cot A = —, then cosec A =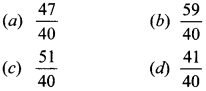

Answer/Explanation

Answer: d
Explaination:
cosec A – cot A = \(\frac{4}{5}\) ……(i)
Also cosec² A – cot² A = 1
⇒ (cosec A – cot A) (cosec A + cot A) = 1
⇒ \(\frac{4}{5}\)(cosec A + cot A) = 1
⇒ cosec A + cot A = \(\frac{4}{5}\) …(ii)
From (i) and (ii), cosec A = \(\frac{41}{40}\)

---

39. If sin x + cosec x = 2, then sin¹⁹x + cosec²⁰x =
(a) 2¹⁹
(b) 2²⁰
(c) 2
(d) 2³⁹

Answer/Explanation

Answer: c
Explaination:
(c) sin x + cosec x = 2
⇒ sin x + \(\frac{1}{sin x}\) = 2
⇒ sin² x + 1 = 2 sin x
⇒ (sin x – 1)² = 0 => sin x = 1 => cosec x = 1
∴ sin¹⁹ x + cosec²⁰ x = 1 + 1 = 2

---

40. If sin θ – cos θ = 0, then the value of (sin⁴ θ + cos⁴ θ) is

Answer/Explanation

Answer: c
Explaination:
sin θ – cos θ = 0
⇒ (sin θ – cos θ)² = 0
⇒ sin2²θ + cos²θ – 2 sin θ cos θ = 0
⇒ – 2 sin θ cos θ = – 1
⇒ 2 sin θ cos θ=1
⇒ sin θ cos θ = \(\frac{1}{2}\)
⇒ sin²θ cos²θ = \(\frac{1}{4}\)
sin⁴θ + cos⁴θ = sin⁴θ + cos⁴θ + 2 sin²θ cos²θ – 2 sin²θ cos²θ
= (sin²θ + cos² θ)² – 2 sin²θ cos²θ
= (1)² – 2 × \(\frac{1}{4}\) = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)

---

41. sec A =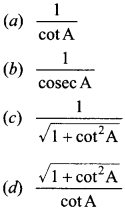

Answer/Explanation

Answer: d
Explaination:

---

42.
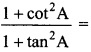
(a) tan² A
(b) sec² A
(c) cosec² A – 1
(d) 1 – sin² A

Answer/Explanation

Answer: c
Explaination: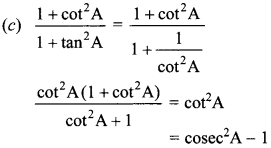

---

43. If sec A + tan A = x, then tan A =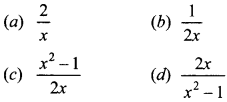

Answer/Explanation

Answer: c
Explaination:
secA + tanA = x … (i)
Also sec² A – tan² A = 1
⇒ (sec A – tan A) (sec A + tan A) = 1
⇒ x (sec A – tan A)
∴ sec A – tan A = \(\frac{1}{x}\) ….. (ii)
Now, subtracting (ii) from (i), we have
tan A = \(\frac{x^{2}-1}{2 x}\)

---

44. Reciprocal of cot A is _____ .

Answer/Explanation

Answer:
Explaination: tan A

---

45. Reciprocal of cosec A is _____ .

Answer/Explanation

Answer:
Explaination: sin A

---

46. In ∆ABC, right angled at B, AB = 5 cm and sin C = \(\frac{1}{2}\). Determine the length of side AC.

Answer/Explanation

Answer:
Explaination: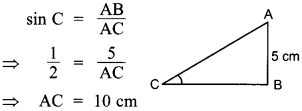

---

47. If sec θ = \(\frac{25}{7}\), find the values of tan θ and cosec θ.

Answer/Explanation

Answer:
Explaination: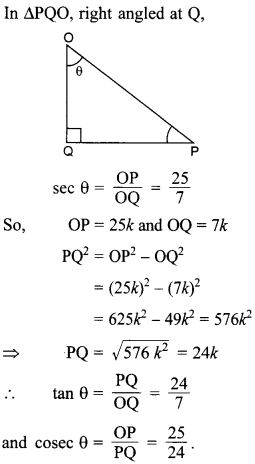

---

48. In ∆ABC, right angled at B, if AB = 12 cm and BC = 5 cm, find
(i) sin A and tan A, (ii) sin C and cot C.

Answer/Explanation

Answer:
Explaination: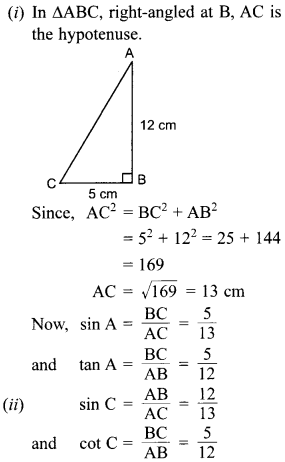

---

49. If sin A = cos A, 0° < A < 90°, then A is equal to _____ .

Answer/Explanation

Answer:c
Explaination:
sin A = cos A sin A
⇒ \(\frac{\sin A}{\cos A}\) = 1
⇒ tan A = 1
⇒ A = 45°

---

50. If sin θ₁ + sin θ₂ + sin θ₃ = 3, 0° < θ₁ θ₂, θ₃ ≤ 90°, then cos θ₁, + cos θ₂, + cos θ₃ = _____ .

Answer/Explanation

Answer:
Explaination:
Hint: Maximum value of sin 0 = 1
sin θ₁ + sin θ₂ + sin θ₃ = 3
⇒ sin θ₁ = 1, sin θ₂ = 1 and sin θ₃ = 1
⇒ θ₁ = 90°, θ₂ = 90° and θ₃ = 90°
∴ cos θ₁ + cos θ₂ + cos θ₃ = 0

---

51. Evaluate:
sin² 60° + 2 tan 45° – cos² 30° [Allahabad 2019]

Answer/Explanation

Answer:
Explaination: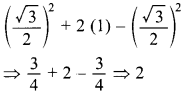

---

52. Given A = 30°, verify sin 2A = 2 sin A cos A.

Answer/Explanation

Answer:
Explaination: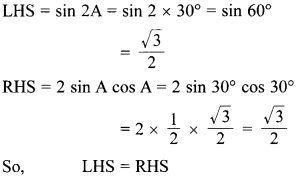

---

53. If tan θ = \(\frac{1}{\sqrt{3}}\) =r, then evaluate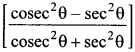

Answer/Explanation

Answer:
Explaination: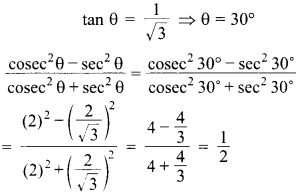

---

54. If sin (A – B) = \(\frac{1}{2}\), cos (A + B) = \(\frac{1}{2}\), find A and B.

Answer/Explanation

Answer:
Explaination:
sin (A – B) = \(\frac{1}{2}\)
⇒ A – B = 30° ……(i)
and cos (A + B) = \(\frac{1}{2}\)
⇒ A + B = 60 °…..(ii)
Solving equation (i) and (ii),
we get A = 45° and B = 15°

---

55. Value of \(\frac{\tan 65^{\circ}}{\cot 25^{\circ}}\) = _____.

Answer/Explanation

Answer:
Explaination: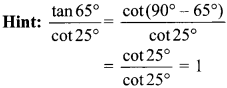

---

56. If cos (40° + A) = sin 30°, the value of A is _____ .

Answer/Explanation

Answer:
Explaination:
Hint: cos (40° + A) = sin 30°
⇒ cos (40° + A) = cos (90° – 30°)
⇒ 40° + A = 60° => A = 20°

---

57. If tan θ = cot (30° + θ), find the value of θ.

Answer/Explanation

Answer:
Explaination:
tan θ = cot (30° + θ)
⇒ cot (90° – θ)
= cot (30° + θ)
⇒ 90° – θ = 30° + θ
⇒ 2θ = 60°
⇒ θ = 30°

---

58. Find the value of (sin²33° + sin²57°) [Delhi 2019]

Answer/Explanation

Answer:
Explaination:
sin²33° + sin²57°
⇒ sin²33° + sin²(90° – 33°)
⇒ sin²33° + cos²33° [Using sin(90° – θ) = cos θ]
⇒ 1 [Using sin²θ + cos² θ=1]

---

59. Express cot 85° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.

Answer/Explanation

Answer:
Explaination:
cot 85° + cos 75° = tan (90° – 85°) + sin (90° – 75°)
= tan 5° + sin 15°

---

60. If sec A = \(\frac{15}{7}\) and A + B = 90°, find the value of cosec B.

Answer/Explanation

Answer:
Explaination:
sec A = \(\frac{15}{7}\)
⇒ sec(90° – B) = \(\frac{15}{7}\) [∵ A + B = 90° ⇒ A = 90°-B]
⇒ cosec B = \(\frac{15}{7}\) [∵ sec (90° – θ) = cosec θ]

---

61. If tan A + cot A = 4, then tan⁴ A + cot⁴ A =

Answer/Explanation

Answer:
Explaination:
Hint: (tan A + cot A)2 = 42
⇒ tan² A + cot² A + 2 = 16
⇒ tan² A + cot² A = 14
⇒ (tan² A + cot² A)² = (14)²
⇒ tan⁴ A + cot⁴ A + 2 = 196
tan⁴ A + cot⁴ A = 194

---

62. If sin x + sin²x = 1, then value of cos² x + cos⁴ x

Answer/Explanation

Answer:
Explaination:
Hint: sin x + sin² x = 1
⇒ sin x = 1 – sin² x
⇒ sin x = cos² x
cos² x + cos⁴ x = cos² x (1 + cos² x)
= sin x (1 + sin x)
= sin x + sin² x = 1

---

63. If tan A = \(\frac{5}{12}\), find the value of 12 (sin A + cos A).sec A.

Answer/Explanation

Answer:c
Explaination: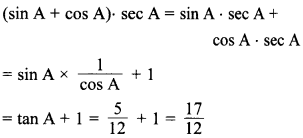

---

64. If cot θ = \(\frac{7}{8}\), evaluate

Answer/Explanation

Answer:
Explaination: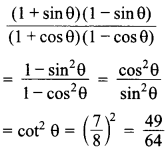

---

65. If sin θ = \(\frac{1}{3}\), then find the value of (2 cot² θ + 2)

Answer/Explanation

Answer:
Explaination:

---