Chapter 7 Coordinate Geometry
Class 10th Maths Chapter MCQs
Class 10 Maths MCQs Chapter 7 Coordinate Geometry
1. The distance of the point P(2, 3) from the x-axis is
(a) 2
(b) 3
(c) 1
(d) 5
Answer/ Explanation
Answer: b
Explaination: Reason: The distance from x-axis is equal to its
ordinate i.e., 3
2. The distance between the point P(1, 4) and Q(4, 0) is
(a) 4
(b)
5
(c) 6
(d) 3√3
Answer/ Explanation
Answer: b
Explaination: Reason: The required distance =
\(\sqrt{(4-1)^{2}+(0-4)^{2}}=\sqrt{9+16}=\sqrt{25}=5\)
3. The points (-5, 1), (1, p) and (4, -2) are collinear if
the value of p
is
(a) 3
(b) 2
(c) 1
(d) -1
Answer/ Explanation
Answer: d
Explaination: Reason: The points are collinear if area of Δ =
0
= \(\frac{1}{2}\)[-5(p + 2) +l(-2 -1) + 4(1 – p)] – 0
⇒ -5 p -10-3 +
4-4p = 0
⇒ -9p = +9
∴ p = -1
4. The area of the triangle ABC with the vertices A(-5, 7), B(-4, -5) and
C(4, 5) is
(a) 63
(b) 35
(c) 53
(d) 36
Answer/ Explanation
Answer: c
Explaination: Reason: Area of ΔABC = \(\frac{1}{2}\)
[x1(y2 – y3) + x2(y3 –
y1) + x3(y1 – y2)]
=
\(\frac{1}{2}\)[-5(-5 – 5) -4(5 – 7) + 4(7 – (-5))] = \(\frac{1}{2}\)[-5(-10)
-4(-2) + 4(12)]
= \(\frac{1}{2}\)[50 + 8 + 48] = \(\frac{1}{2}\) × 106 = 53
sq. units
5. The distance of the point (α, β) from the origin is
(a) α + β
(b) α²
+ β²
(c) |α| + |β|
(d)
\(\sqrt{\alpha^{2}+\beta^{2}}\)
Answer/ Explanation
Answer: d
Explaination: Reason: Distance of (α, β) from origin (0, 0) =
\(\sqrt{(\alpha-0)^{2}+(\beta-0)^{2}}=\sqrt{\alpha^{2}+\beta^{2}}\)
6. The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3,
-4) is
(a) 11
(b) 22
(c) 33
(d) 21
Answer/ Explanation
Answer: a
Explaination: Reason: Required area= \(\frac{1}{2}\)[1(3 + 4)
-2(-4 – 2) -3(2 – 3)]
= \(\frac{1}{2}\)[7 + 12 + 3]
= \(\frac{1}{2}\) × 22
= 11
7. The line segment joining the points (3, -1) and (-6, 5) is trisected. The
coordinates of point of trisection are
(a) (3, 3)
(b) (- 3, 3)
(c) (3,
– 3)
(d) (-3,-3)
Answer/ Explanation
Answer: b
Explaination: Reason: Since the line segment AB is
trisected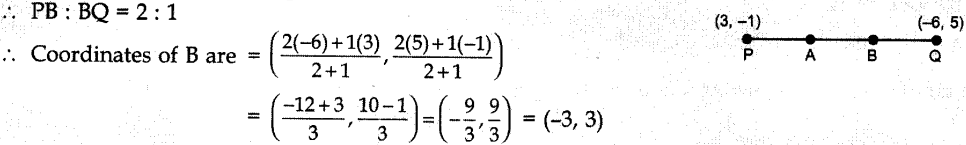
8. The line 3x + y – 9 = 0 divides the line joining the points (1, 3) and (2,
7) internally in the ratio
(a) 3 : 4
(b) 3 : 2
(c) 2 : 3
(d) 4 :
3
Answer/ Explanation
Answer: a
Explaination: Reason: Let the line 3x + y – 9 = 0 divide the
line segment joining A(l, 3) ad B(2, 7) in the ratio K : 1 at point C.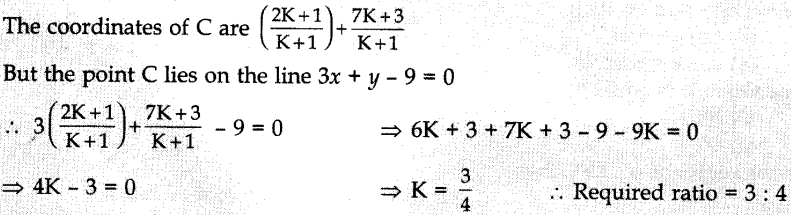
9. The distance between A (a + b, a – b) and B(a – b, -a – b) is
Answer/ Explanation
Answer: c
Explaination: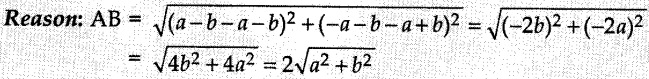
10. If (a/3, 4) is the mid-point of the segment joining the points P(-6, 5)
and R(-2, 3), then the value of ‘a’ is
(a) 12
(b) -6
(c) -12
(d)
-4
Answer/ Explanation
Answer: c
Explaination: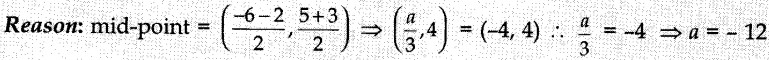
11. If the distance between the points (x, -1) and (3, 2) is 5, then the
value of x is
(a) -7 or -1
(b) -7 or 1
(c) 7 or 1
(d) 7 or
-1
Answer/ Explanation
Answer: d
Explaination: Reason: We have
\(\sqrt{(x-3)^{2}+(-1-2)^{2}}=5\)
⇒ (x – 3)² + 9 = 25
⇒ x² – 6x + 9 + 9 =
25
⇒ x² -6x – 7 = 0
⇒ (x – 7)(x + 1) = 0
⇒ x = 7 or x =
-1
12. The points (1,1), (-2, 7) and (3, -3) are
(a) vertices of an
equilateral triangle
(b) collinear
(c) vertices of an isosceles
triangle
(d) none of these
Answer/ Explanation
Answer: b
Explaination: Reason: Let A(1, 1), B(-2, 7) and C(3, 3) are the
given points, Then, we have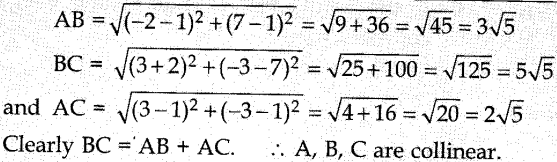
13. The coordinates of the centroid of a triangle whose vertices are (0, 6),
(8,12) and (8, 0) is
(a) (4, 6)
(b) (16, 6)
(c) (8, 6)
(d) (16/3,
6)
Answer/ Explanation
Answer: d
Explaination: Reason: The co-ordinates of the centroid of the
triangle is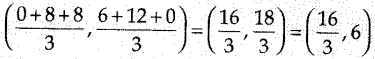
14. Two vertices of a triangle are (3, – 5) and (- 7,4). If its centroid is
(2, -1), then the third vertex is
(a) (10, 2)
(b) (-10,2)
(c)
(10,-2)
(d) (-10,-2)
Answer/ Explanation
Answer: c
Explaination: Reason: Let the coordinates of the third vertex be
(x, y)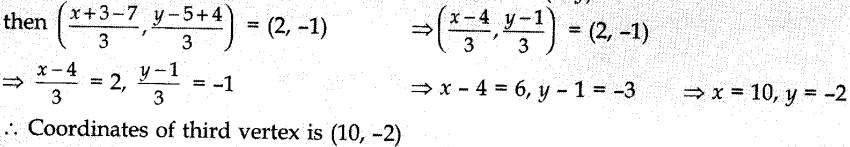
15. The area of the triangle formed by the points A(-1.5, 3), B(6, -2) and
C(-3, 4) is
(a) 0
(b) 1
(c) 2
(d) 3/2
Answer/ Explanation
Answer: a
Explaination: Reason: Area of ΔABC = \(\frac{1}{2}\) [-1.5(-2 –
4) + 6(4 – 3) + (-3) (3 + 2)] = \(\frac{1}{2}\) [9 + 6 – 15] = 0. It is a
straight line.
16. If the points P(1, 2), B(0, 0) and C(a, b) are collinear, then
(a) 2a
= b
(b) a = -b
(c) a = 2b
(d) a = b
Answer/ Explanation
Answer: a
Explaination: Reason: Area of ΔPBC = 0
⇒ \(\frac{1}{2}\)[1(0
– b) + 0(6 – 1) + a(2 – 0)] = 0
⇒ \(\frac{1}{2}\)[-6 + 2a] = 0
⇒ -b + 2a =
0
∴ 2a = b