Chapter 6 Triangles
Class 10th Maths Chapter MCQs
Class 10 Maths MCQs Chapter 6 Triangles
1. O is a point on side PQ of a APQR such that PO = QO = RO, then
(a) RS²
= PR × QR
(b) PR² + QR² = PQ²
(c) QR² = QO² + RO²
(d) PO² + RO² =
PR²
Answer
Answer: b
2. In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal
to
(a) 7.5 cm
(b) 3 cm
(c) 4.5 cm
(d) 6
cm
Answer
Answer: c
3. AABC is an equilateral A of side a. Its area will be…
Answer
Answer: a
4. In a square of side 10 cm, its diagonal = …
(a) 15 cm
(b) 10√2
cm
(c) 20 cm
(d) 12 cm
Answer
Answer: b
5. In a rectangle Length = 8 cm, Breadth = 6 cm. Then its diagonal = …
(a)
9 cm
(b) 14 cm
(c) 10 cm
(d) 12 cm
Answer
Answer: c
6. In a rhombus if d1 = 16 cm, d2 = 12 cm, its area
will be…
(a) 16 × 12 cm²
(b) 96 cm²
(c) 8 × 6 cm²
(d) 144
cm²
Answer
Answer: b
7. In a rhombus if d1 = 16 cm, d2 = 12 cm, then the
length of the side of the rhombus is
(a) 8 cm
(b) 9 cm
(c) 10 cm
(d)
12 cm
Answer
Answer: c
8. If in two As ABC and DEF,
\(\frac{\mathrm{AB}}{\mathrm{DF}}=\frac{\mathrm{BC}}{\mathrm{FE}}=\frac{\mathrm{CA}}{\mathrm{ED}}\),
then
(a) ∆ABC ~ ∆DEF
(b) ∆ABC ~ ∆EDF
(c) ∆ABC ~ ∆EFD
(d) ∆ABC ~
∆DFE
Answer
Answer: d
9. It is given that ∆ABC ~ ∆DEF and
\(\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{1}{5}\). Then
\(\frac{\operatorname{ar}(D E F)}{\operatorname{ar}(A B C)}\) is equal to
(а)
5
(b) 25
(c) \(\frac{1}{25}\)
(d)
\(\frac{1}{5}\)
Answer
Answer: b
10. In ∠BAC = 90° and AD ⊥ BC. A Then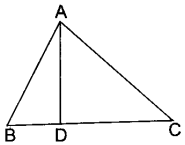
(а) BD.CD = BC²
(б) AB.AC = BC²
(c) BD.CD = AD²
(d)
AB.AC = AD²
Answer
Answer: c
11. D and E are respectively the points on the sides AB and AC of a triangle
ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE
(in cm) is
(a) 2.5
(b) 3
(c) 5
(d) 6
Answer
Answer: b
12. If ΔABC ~ ΔDEF and ΔABC is not similar to ΔDEF then which of the
following is not true?
(a) BC.EF = AC.FD
(b) AB.ED = AC.DE
(c) BC.DE =
AB.EE
(d) BC.DE = AB.FD
Answer
Answer: c
13. If in two triangles DEF and PQR, ZD = ZQ and ZR = ZE, then which of the
following is not true?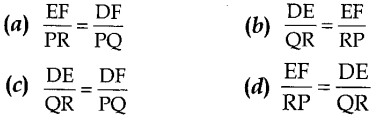
Answer
Answer: b
14. If ΔABC ~ ΔPQR, \(\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{1}{3}\) then
\(\frac{\operatorname{ar}(PQR)}{\operatorname{ar}(BCA)}\) is
(a) 9
(b)
3
(c) 1/3
(d) 1/9
Answer
Answer: a
15. If ΔABC ~ ΔQRP,
\(\frac{\operatorname{ar}(\mathrm{ABC})}{\operatorname{ar}(\mathrm{PQR})}=\frac{9}{4}\),
AB = 18 cm and BC = 15 cm, then PR is equal to
(a) 10 cm
(b) 12 cm
(c)
\(\frac{20}{3}\)cm
(d) 8 cm
Answer
Answer: a
16. If in triangles ABC and
DEF,\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{FD}}\) , then
they will be similar, if
(a) ∠B = ∠E
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠A
= ∠F
Answer
Answer: c