Chapter 5 Arithmetic Progressions
Class 10th Maths Chapter MCQs
Class 10 Maths MCQs Chapter 5 Arithmetic Progressions
1. The nth term of an A.P. is given by an = 3 + 4n. The
common difference is
(a) 7
(b) 3
(c) 4
(d)
1
Answer/Explanation
Answer: c
Explaination:Reason: We have an = 3 + 4n
∴ an+1 =
3 + 4(n + 1) = 7 + 4n
∴ d = an+1 – an
= (7 + 4n) –
(3 + 4n)
= 7 – 3
= 4
2. If p, q, r and s are in A.P. then r – q is
(a) s – p
(b) s – q
(c) s – r
(d) none of these
Answer/Explanation
Answer: c
Explaination:Reason: Since p, q, r, s are in A.P.
∴ (q – p) =
(r – q) = (s – r) = d (common difference)
3. If the sum of three numbers in an A.P. is 9 and their product is 24, then
numbers are
(a) 2, 4, 6
(b) 1, 5, 3
(c) 2, 8, 4
(d) 2, 3, 4
Answer/Explanation
Answer: d
Explaination:Reason: Let three numbers be a – d, a, a + d
∴ a
– d +a + a + d = 9
⇒ 3a = 9
⇒ a = 3
Also (a – d) . a . (a + d) = 24
⇒ (3 -d) .3(3 + d) = 24
⇒ 9 – d² = 8
⇒ d² = 9 – 8 = 1
∴ d = ± 1
Hence numbers are 2, 3, 4 or 4, 3, 2
4. The (n – 1)th term of an A.P. is given by 7,12,17, 22,… is
(a) 5n + 2
(b) 5n + 3
(c) 5n – 5
(d) 5n – 3
Answer/Explanation
Answer: d
Explaination:Reason: Here a = 7, d = 12-7 = 5
∴
an-1 = a + [(n – 1) – l]d = 7 + [(n – 1) -1] (5) = 7 + (n – 2)5 = 7 +
5n – 10 = 5M – 3
5. The nth term of an A.P. 5, 2, -1, -4, -7 … is
(a) 2n + 5
(b) 2n – 5
(c) 8 – 3n
(d) 3n – 8
Answer/Explanation
Answer: c
Explaination:Reason: Here a = 5, d = 2 – 5 = -3
an
= a + (n – 1)d = 5 + (n – 1) (-3) = 5 – 3n + 3 = 8 – 3n
6. The 10th term from the end of the A.P. -5, -10, -15,…, -1000
is
(a) -955
(b) -945
(c) -950
(d) -965
Answer/Explanation
Answer: a
Explaination:Reason: Here l = -1000, d = -10 – (-5) = -10 + 5 =
– 5
∴ 10th term from the end = l – (n – 1 )d = -1000 – (10 – 1)
(-5) = -1000 + 45 = -955
7. Find the sum of 12 terms of an A.P. whose nth term is given by
an = 3n + 4
(a) 262
(b) 272
(c) 282
(d)
292
Answer/Explanation
Answer: a
Explaination:Reason: Here an = 3n + 4
∴
a1 = 7, a2 – 10, a3 = 13
∴ a= 7, d = 10 – 7
= 3
∴ S12 = \(\frac{12}{2}\)[2 × 7 + (12 – 1) ×3] = 6[14 + 33] = 6
× 47 = 282
8. The sum of all two digit odd numbers is
(a) 2575
(b) 2475
(c)
2524
(d) 2425
Answer/Explanation
Answer: b
Explaination:Reason: All two digit odd numbers are 11,13,15,…
99, which are in A.P.
Since there are 90 two digit numbers of which 45
numbers are odd and 45 numbers are even
∴ Sum = \(\frac{45}{2}\)[11 + 99] =
\(\frac{45}{2}\) × 110 = 45 × 55 = 2475
9. The sum of first n odd natural numbers is
(a) 2n²
(b) 2n + 1
(c)
2n – 1
(d) n²
Answer/Explanation
Answer: d
Explaination:Reason: Required Sum = 1 + 3 + 5 + … + upto n
terms.
Here a = 1, d = 3 – 1 = 2
Sum = \(\frac{n}{2}\)[2 × 1 + (n – 1) ×
2] = \(\frac{n}{2}\)[2 + 2n – 2] = \(\frac{n}{2}\) × 2n = n²Reason: All two
digit odd numbers are 11,13,15,… 99, which are in A.P.
Since there are 90 two
digit numbers of which 45 numbers are odd and 45 numbers are even
∴ Sum =
\(\frac{45}{2}\)[11 + 99] = \(\frac{45}{2}\) × 110 = 45 × 55 =
2475
10. If (p + q)th term of an A.P. is m and (p – q)tn
term is n, then pth term is
Answer/Explanation
Answer: d
Explaination:Reason: Let a is first term and d is common
difference
∴ ap + q = m
ap – q = n
⇒ a + (p + q –
1)d = m = …(i)
⇒ a + (p – q – 1)d = m = …(ii)
On adding (i) and (if), we
get
2a + (2p – 2)d = m + n
⇒ a + (p -1)d = \(\frac{m+n}{2}\) …[Dividing by
2
∴ an = \(\frac{m+n}{2}\)
11. If a, b, c are in A.P. then \(\frac{a-b}{b-c}\) is equal to
Answer/Explanation
Answer: a
Explaination:Reason: Since a, b, c are in A.P.
∴ b – a = c –
b
⇒ \(\frac{b-a}{c-b}\) = 1
⇒ \(\frac{a-b}{b-c}\) = 1
12. The number of multiples lie between n and n² which are divisible by n
is
(a) n + 1
(b) n
(c) n – 1
(d) n – 2
Answer/Explanation
Answer: d
Explaination:Reason: Multiples of n from 1 to n² are n × 1,
n × 2, n × 3, …, m× n
∴ There are n numbers
Thus, the number of mutiples
of n which lie between n and n² is (n – 2) leaving first and last in the given
list: Total numbers are (n – 2).
13. If a, b, c, d, e are in A.P., then the value of a – 4b + 6c – 4d + e
is
(a) 0
(b) 1
(c) -1.
(d) 2
Answer/Explanation
Answer: a
Explaination:Reason: Let common difference of A.P. be x
∴ b =
a + x, c = a + 2x, d = a + 3x and e = a + 4x
Given equation n-4b + 6c-4d +
c
= a – 4(a + x) + 6(A + 2r) – 4(n + 3x) + (o + 4.v)
= a – 4a – 4x + 6a +
12x – 4a – 12x + a + 4x = 8a – 8a + 16x – 16x = 0
14. The next term of the sequence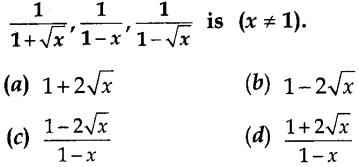
Answer/Explanation
Answer: a
Explaination: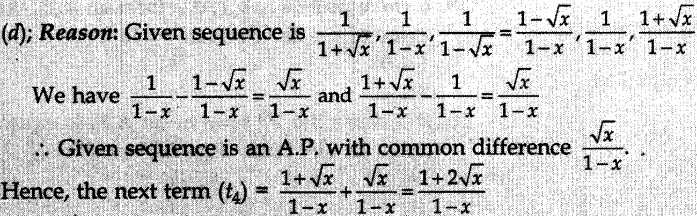
15. nth term of the sequence a, a + d, a + 2d,… is
(a) a +
nd
(b) a – (n – 1)d
(c) a + (n – 1)d
(d) n +
nd
Answer/Explanation
Answer: a
Explaination:Reason: an = a + (n – 1)d
16. The 10th term from the end of the A.P. 4, 9,14, …, 254 is
(a) 209
(b) 205
(c) 214
(d) 213
Answer/Explanation
Answer: a
Explaination:Reason: Here l – 254, d = 9-4 = 5
∴
10th term from the end = l – (10 – 1 )d = 254 -9d = 254 = 9(5) = 254
– 45 = 209
17. If 2x, x + 10, 3x + 2 are in A.P., then x is equal to
(a) 0
(b)
2
(c) 4
(d) 6
Answer/Explanation
Answer: d
Explaination:Reason: Since 2x, x + 10 and 3x + 2 are in A.P.
∴ 2(x + 10) = 2x + (3x + 2)
⇒ 2x + 20 – 5x + 2
⇒ 2x – 5x = 2 – 20
⇒ 3x
= 18
⇒ x = 6
18. The sum of all odd integers between 2 and 100 divisible by 3 is
(a)
17
(b) 867
(c) 876
(d) 786
Answer/Explanation
Answer: b
Explaination:Reason: The numbers are 3, 9,15, 21, …, 99
Here
a = 3, d = 6 and an = 99
∴ an = a + (n – 1 )d
⇒ 99 =
3 + (n – 1) x 6
⇒ 99 = 3 + 6n – 6
⇒ 6n = 102
⇒ n = 17
Required Sum =
\(\frac{n}{2}\)[a + an] = \(\frac{17}{2}\)[3 + 99] = \(\frac{17}{2}\)
× 102 = 867
19. If the numbers a, b, c, d, e form an A.P., then the value of a – 4b + 6c
– 4d + e is
(a) 0
(b) 1
(c) -1
(d) 2
Answer/Explanation
Answer: a
Explaination:Reason: Let x be the common difference of the given
AP
∴ b = a + x, c = a + 2x, d = a + 3x and e = a + 4x
∴ a – 4b + 6c – 4d +
e = a – 4 (a + x) + 6(a + 2x) – 4(a + 3x) + (a + 4x)
= a – 4a – 4x + 6a + 12x
– 4a – 12x + a + 4x = 8a – 8a + 16x – 16x = 0
20. If 7 times the 7th term of an A.P. is equal to 11 times its
11th term, then 18th term is
(a) 18
(b) 9
(c)
77
(d) 0
Answer/Explanation
Answer: d
Explaination:Reason: We have 7a7 =
11a11
⇒ 7[a + (7 – 1)d] = 11[a + (11 – 1 )d]
⇒ 7(a + 6d) = 11(a
+ 10d)
⇒ 7a + 42d = 11a + 110d
⇒ 4a = -68d
⇒ a = -17d
∴
a18 = a + (18 – 1)d = a + 17d = -17d + 17d = 0