Chapter 3 Pair of Linear Equations in Two Variables
Class 10th Maths Chapter MCQs
Class 10 Maths MCQs Chapter 3 Pair of Linear Equations in Two Variables
1. A pair of linear equations a1x + b1y + c1
= 0; a2x + b2y + c2 = 0 is said to be
inconsistent, if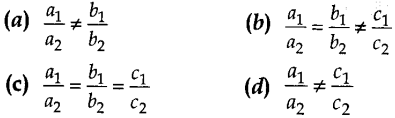
Answer
Answer: b
2. Graphically, the pair of equations 7x – y = 5; 21x – 3y = 10 represents
two lines which are
(a) intersecting at one point
(b) parallel
(c)
intersecting at two points
(d) coincident
Answer
Answer: b
3. The pair of equations 3x – 5y = 7 and – 6x + 10y = 7 have
(a) a unique
solution
(b) infinitely many solutions
(c) no solution
(d) two
solutions
Answer
Answer: c
4. If a pair of linear equations is consistent, then the lines will be
(a)
always coincident
(b) parallel
(c) always intersecting
(d) intersecting
or coincident
Answer
Answer: d
5. The pair of equations x = 0 and x = 5 has
(a) no solution
(b)
unique/one solution
(c) two solutions
(d) infinitely many
solutions
Answer
Answer: c
6. The pair of equation x = – 4 and y = – 5 graphically represents lines
which are
(a) intersecting at (- 5, – 4)
(b) intersecting at (- 4, –
5)
(c) intersecting at (5, 4)
(d) intersecting at (4,
5)
Answer
Answer: b
7. For what value of k, do the equations 2x – 3y + 10 = 0 and 3x + ky + 15 =
0 represent coincident lines
Answer
Answer: a
8. If the lines given by 2x + ky = 1 and 3x – 5y = 7 are parallel, then the
value of k is
Answer
Answer: a
9. One equation of a pair of dependent linear equations is 2x + 5y = 3. The
second equation will be
(a) 2x + 5y = 6
(b) 3x + 5y = 3
(c) -10x – 25y
+ 15 = 0
(d) 10x + 25y = 15
Answer
Answer: c
10. If x = a, y = b is the solution of the equations x + y = 5 and 2x – 3y =
4, then the values of a and b are respectively
(a) 6, -1
(b) 2, 3
(c)
1, 4
(d) 19/5, 6/5
Answer
Answer: d
11. The graph of x = -2 is a line parallel to the
(a) x-axis
(b)
y-axis
(c) both x- and y-axis
(d) none of
these
Answer
Answer: b
12. The graph of y = 4x is a line
(a) parallel to x-axis
(b) parallel
to y-axis
(c) perpendicular to y-axis
(d) passing through the
origin
Answer
Answer: d
13. The graph of y = 5 is a line parallel to the
(a) x-axis
(b)
y-axis
(c) both axis
(d) none of these
Answer
Answer: a
14. Two equations in two variables taken together are called
(a) linear
equations
(b) quadratic equations
(c) simultaneous equations
(d) none
of these
Answer
Answer: c
15. If am bl then the system of equations ax + by = c, lx + my = n, has
(a) a unique solution
(b) no solution
(c) infinitely many solutions
(d)
none of these
Answer
Answer: a
16. If in the equation x + 2y = 10, the value of y is 6, then the value of x
will be
(a) -2
(b) 2
(c) 4
(d) 5
Answer
Answer: a
17. The graph of the equation 2x + 3y = 5 is a
(a) vertical line
(b)
straight line
(c) horizontal line
(d) none of
these
Answer
Answer: b
18. The value of k, for which equations 3x + 5y = 0 and kx + lOy = 0 has a
non-zero solution is
(a) 6
(b) 0
(c) 2
(d)
5
Answer
Answer: a
19. The value of k, for which the system of equations x + (k + l)y = 5 and (k
+ l)x + 9y = 8k – 1 has infinitely many solutions is
(a) 2
(b) 3
(c)
4
(d) 5
Answer
Answer: a
20. The value of k for which the equations (3k + l)x + 3y = 2; (k2 + l)x + (k
– 2)y = 5 has no solution, then k is equal to
(a) 2
(b) 3
(c) 1
(d)
-1
Answer
Answer: d
21. The pair of equations x = a and y = b graphically represents lines which
are
(a) parallel
(b) intersecting at (b, a)
(c) coincident
(d)
intersecting at (a, b)
Answer
Answer: d
22. Asha has only ₹1 and ₹2 coins with her. If the total number of coins that
she has is 50 and the amount of money with her is ₹75, then the number of ₹1 and
₹2 coins are, respectively
(a) 35 and 15
(b) 15 and 35
(c) 35 and
20
(d) 25 and 25
Answer
Answer: d
23. The father’s age is six times his son’s age. Four years hence, the age of
the father will be four times his son’s age. The present ages of the son and the
father are, respectively
(a) 4 and 24
(b) 5 and 30
(c) 6 and 36
(d)
3 and 24
Answer
Answer: c
24. The sum of the digits of a two-digit number is 9. If 27 is added to it,
the digits of the number get reversed. The number is
(a) 27
(b) 72
(c)
45
(d) 36
Answer
Answer: d