Chapter 10 Circles

1. A circle has a number of tangents equal to

(a) 0

(b) 1

(c) 2

(d) Infinite

Answer: (d) Infinite

Explanation: A circle has infinitely many tangents, touching the circle at infinite points on its circumference.

2. A tangent intersects the circle at:

(a) One point

(b) Two distinct point

(c) At the circle

(d) None of the above

Answer: (a) One point

Explanation: A tangent touches the circle only on its boundary and do not cross through it.

3. A circle can have _____parallel tangents at a single time.

(a) One

(b) Two

(c) Three

(d) Four

Answer: (b) Two

Explanation: A circle can have two parallel tangents at the most.

4. If the angle between two radii of a circle is 110º, then the angle between the tangents at the ends of the radii is:

(a) 90º

(b) 50º

(c) 70º

(c) 40º

Answer: (c) 70º

Explanation: If the angle between two radii of a circle is 110º, then the angle between tangents is 180º − 110º = 70º. (By circles and tangents properties)

5. The length of the tangent from an external point A on a circle with centre O is

(a) always greater than OA

(b) equal to OA

(c) always less than OA

(d) cannot be estimated

Answer: (c) always less than OA

Explanation: Since the tangent is perpendicular to the radius of the circle, then the angle between them is 90º. Thus, OA is the hypotenuse for the right triangle OAB, which is right-angled at B. As we know, for any right triangle, the hypotenuse is the longest side. Therefore the length of the tangent from an external point is always less than the OA.

6. AB is a chord of the circle and AOC is its diameter such that angle ACB = 50°. If AT is the tangent to the circle at the point A, then BAT is equal to

(a) 65°

(b) 60°

(c) 50°

(d) 40°

Answer: (c) 50°

Explanation: As per the given question:

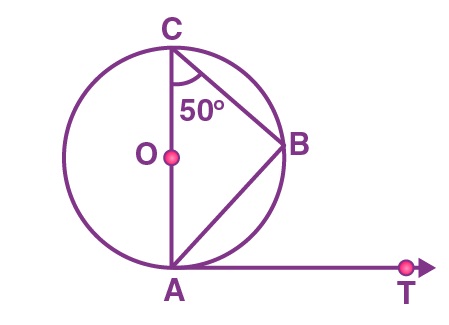
∠ABC = 90° (angle in Semicircle is right angle)

In ∆ACB

∠A + ∠B + ∠C = 180°

∠A = 180° – (90° + 50°)

∠A = 40°

Or ∠OAB = 40°

Therefore, ∠BAT = 90° – 40° = 50°

7. If TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to

(a) 60°

(b) 70°

(c) 80°

(d) 90°

Answer: (b) 70°

Explanation: As per the given question:

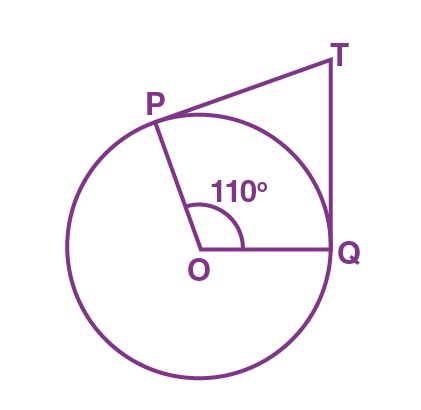
We can see, OP is the radius of the circle to the tangent PT and OQ is the radius to the tangents TQ.

So, OP ⊥ PT and TQ ⊥ OQ

∴ ∠OPT = ∠OQT = 90°

Now, in the quadrilateral POQT, we know that the sum of the interior angles is 360°

So, ∠PTQ + ∠POQ + ∠OPT + ∠OQT = 360°

Now, by putting the respective values, we get,

⇒ ∠PTQ + 90° + 110° + 90° = 360°

⇒ ∠PTQ = 70°

8. The length of a tangent from a point A at a distance 5 cm from the centre of the circle is 4 cm. The radius of the circle is:

(a) 3 cm

(b) 5 cm

(c) 7 cm

(d) 10 cm

Answer: (a) 3 cm

Explanation: As per the given question:

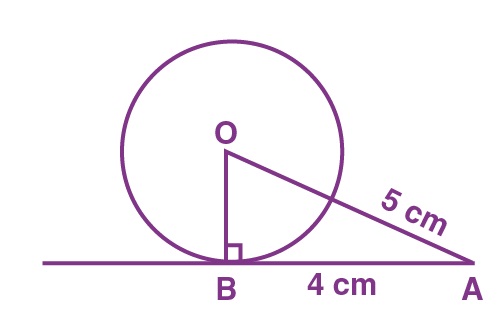
AB is the tangent, drawn on the circle from point A.

So, OB ⊥ AB

Given, OA = 5cm and AB = 4 cm

Now, In △ABO,

OA² = AB² + BO² (Using Pythagoras theorem)

⇒ 5² = 4² + BO²

⇒ BO² = 25 – 16

⇒ BO² = 9

⇒ BO = 3

9. If a parallelogram circumscribes a circle, then it is a:

(a) Square

(b) Rectangle

(c) Rhombus

(d) None of the above

Answer: (c) Rhombus

If a parallelogram circumscribes a circle, then it is a Rhombus.

10. Two concentric circles are of radii 5 cm and 3 cm. The length of the chord of the larger circle which touches the smaller circle is:

(a) 8 cm

(b) 10 cm

(c) 12 cm

(d) 18 cm

Answer: (a) 8 cm

Explanation: As per the given question:

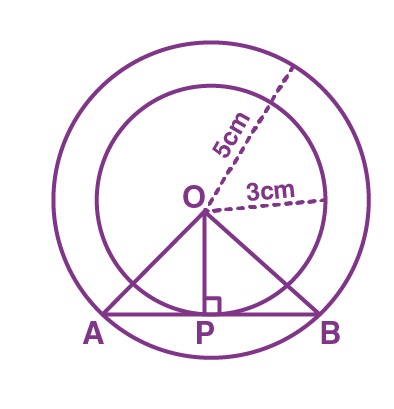
From the above figure, AB is tangent to the smaller circle at point P.

∴ OP ⊥ AB

By Pythagoras theorem, in triangle OPA

OA² = AP² + OP²

⇒ 5² = AP² + 3²

⇒ AP² = 25 – 9

⇒ AP = 4

Now, as OP ⊥ AB,

Since the perpendicular from the center of the circle bisects the chord, AP will be equal to PB

So, AB = 2AP = 2 × 4 = 8 cm

11. If angle between two radii of a circle is 130°, the angle between the tangents at the ends of the radii is

(a) 90°

(b) 50°

(c) 70°

(d) 40°

Answer: (b) 50°

Explanation:

We know that the sum of the angle between two radii of a circle and the angle between the tangents at the ends of the radii is 180°.

Therefore, the angle between the tangents at the ends of the radii = 180° – 130° = 50°

12. A line intersecting a circle in two points is called a _______.

(a) Secant

(b) Chord

(c) Diameter

(d) Tangent

Answer: (a) Secant

A line intersecting a circle in two points is called a Secant.

13. In the figure below, the pair of tangents AP and AQ drawn from an external point A to a circle with centre O are perpendicular to each other and length of each tangent is 5 cm. Then the radius of the circle is

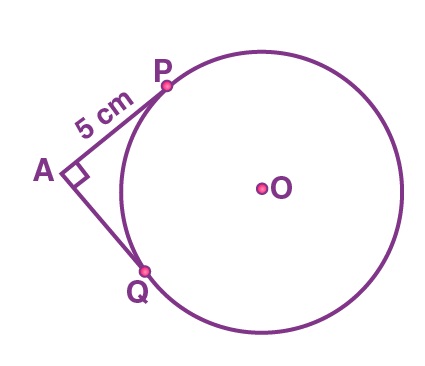
(a) 10 cm

(b) 7.5 cm

(c) 5 cm

(d) 2.5 cm

Answer: (c) 5 cm

Explanation:

Join OP and OQ.

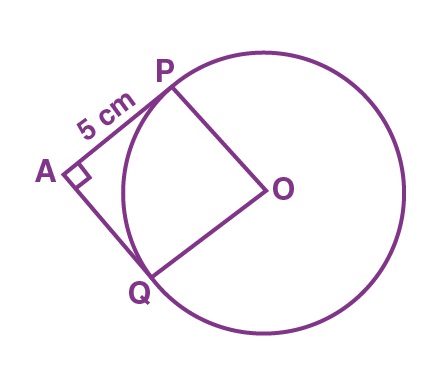
Tangents AP = AQ

In triangle APO and AQO,

AP = AQ

AO = AO (Common)

OP = OQ (radius of same circle)

Thus, ΔAPO ~ ΔAQO.

POQA is a square

OP = OQ = AP = AQ

So, AP = AQ = 5 Cm

And AP = OP (Proved)

Therefore, radius = OP = 5 cm

14. If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then length of each tangent is equal to

(a) (3/2)√3 cm

(b) 6 cm

(c) 3 cm

(d) 3√3 cm

Answer: (d) 3√3 cm

Explanation:

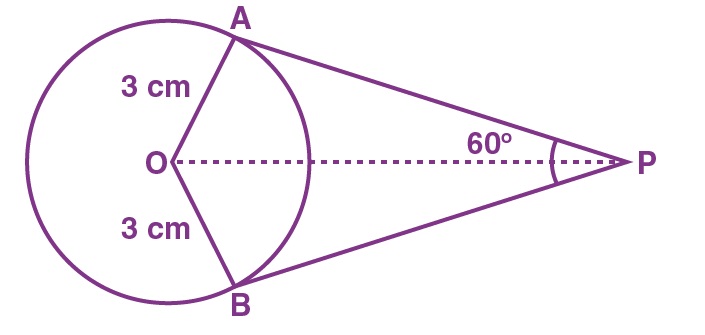
ΔAOP and ΔBOP are congruent.

Therefore, ∠APO = ∠BPO = 60°/2 = 30°

OA is perpendicular to AP.

In right triangle AOP,

tan 30° = OA/AP

1/√3 = 3/AP

AP = 3√3

Hence, the length of the tangent is 3√3 cm.

15. The tangent to a circle is ___________ to the radius through the point of contact.

(a) parallel

(b) perpendicular

(c) perpendicular bisector

(d) bisector

Answer: (b) perpendicular

The tangent to a circle is perpendicular to the radius through the point of contact.

16. In the figure below, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT = 60°. Then ∠PRQ is equal to

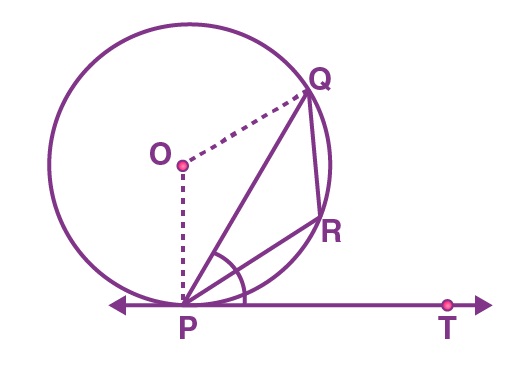
(a) 135°

(b) 150°

(c) 120°

(d) 110°

Answer: (c) 120°

Explanation:

From the given,

∠QPT = 60°

∠OPT = 90°

Thus, ∠OPQ = ∠OQP = 30°, i.e., ∠POQ = 120°.

Also, ∠PRQ = (1/2) reflex ∠POQ

reflex ∠POQ = 360° – 120° = 240°

Therefore, ∠PRQ = (1/2) × 240° = 120°

17. In the below figure, if ∠AOB = 125°, then ∠COD is equal to

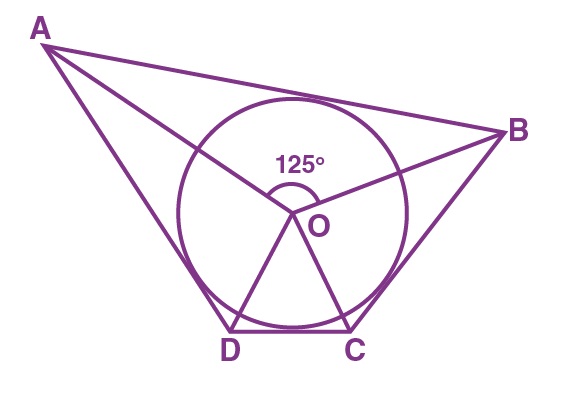
(a) 62.5°

(b) 45°

(c) 35°

(d) 55°

Answer: (d) 55°

ABCD is a quadrilateral circumscribing the circle.

Thus, the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.

∠AOB + ∠COD = 180°

125° + ∠COD = 180°

∠COD = 180° – 125° = 55°

18. In the figure, PQL and PRM are tangents to the circle with centre O at the points Q and R, respectively and S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°. Then ∠QSR is equal to

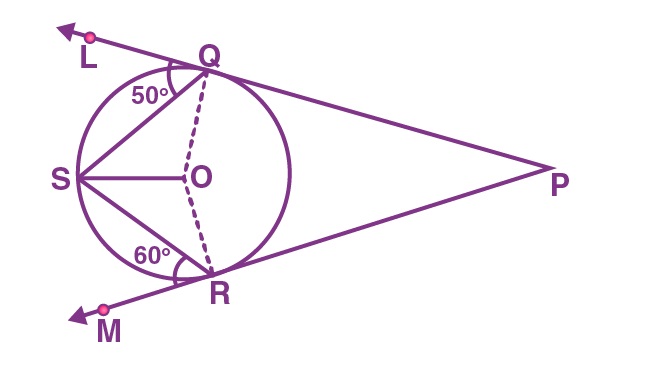
(a) 40°

(b) 60°

(c) 70°

(d) 80°

Answer: (c) 70°

From the given,

∠OSQ = ∠OQS = 90°–50° = 40°

and

∠RSO = ∠SRO = 90° – 60° = 30°

Therefore, ∠QSR = 40° + 30° = 70°.

19. Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. The radius of the inner circle will be

(a) 3 cm

(b) 4 cm

(c) 2.5 cm

(d) 2 cm

Answer: (a) 3 cm

OA = 5 cm and AC = 8 cm

AC is a chord which touches the inner circle at point B.

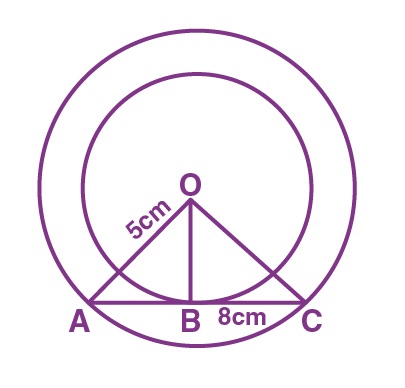
Join OB.

So, OB ⊥ AC

AD = DC = 4 cm {perpendicular line OB bisects the chord}

Thus, in right angled ∆AOB,

OA² = AB² + BO²

BO² = 5² – 4² = 25 – 16 = 9

BO = 3 cm

Hence, the radius of the inner circle will be 3 cm.

20. The distance between two parallel tangents of a circle is 18 cm, then the radius of the circle is

(a) 8 cm

(b) 10 cm

(c) 9 cm

(d) 7.5 cm

Answer: (c) 9 cm

Given,

Distance between two parallel tangents = 18 cm

That means, diameter = 18 cm

Therefore, radius of the circle = 18/2 = 9 cm