Chapter 8 Circles
Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution
Circles Exercise Ex. 8A
Solution 1
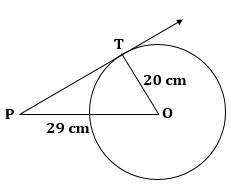
Let O be the centre of the circle and PT be the length of tangent from P to the circle.
Then, OT = 20 cm and OP = 29 cm
Since tangent to a circle is always perpendicular to the radius through the point of contact.
∴ ∠OTP = 90o
In right ΔOTP,
OP2 = OT2 + PT2
⇒ 292 = 202 + PT2
⇒ PT2 = 292 - 202 = (29 - 20)(29 + 20) = 9 × 49 = 441
⇒ PT = 21 cm
Hence, the length of the tangent drawn from P to the circle is 21 cm.
Solution 2
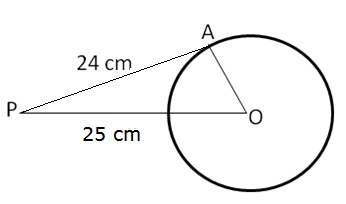
PA is the tangent to the circle with centre O and radius, such that PO = 25 cm, PA = 24 cm
In ![]() PAO,
PAO,
![]() A
= 90,
A
= 90,
By Pythagoras theorem:
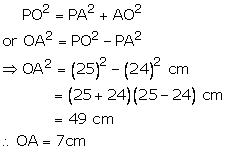
Hence, the radius of the circle is 7 cm.
Solution 3
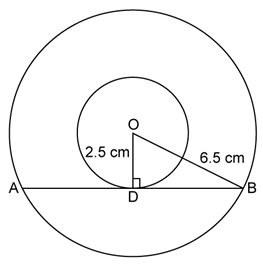

Solution 4

Solution 5
Given AP is a tangent at A and OA is radius through A and PA and PB are the tangent segments to circle with centre O.
Therefore, OA is perpendicular to AP, similarly, OB is perpendicular to BP.
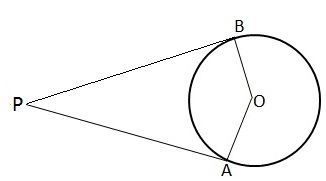
![]()
![]() OAP
= 90
OAP
= 90
And ![]() OBP
= 90
OBP
= 90
So, ![]() OAP
=
OAP
= ![]() OBP
= 90
OBP
= 90
![]()
![]() OBP
+
OBP
+ ![]() OAP
= (90 + 90) = 180
OAP
= (90 + 90) = 180
Thus, the sum of opposite angles of quad. AOBP is 180
![]() AOBP
is a cyclic quadrilateral
AOBP
is a cyclic quadrilateral
Solution 6
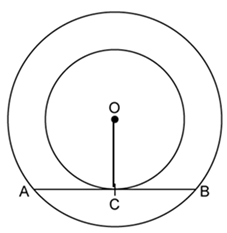

Solution 7
Given: From an external point P, tangent PA and PB are drawn to a circle with centre O. CD is the tangent to the circle at a point E and PA = 14cm.
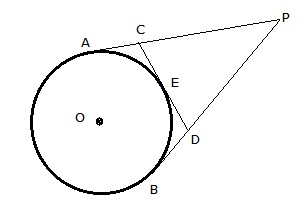
Since the tangents from an external point are equal, we have
PA = PB,
Also, CA = CE and DB = DE
Perimeter of ![]() PCD
= PC + CD + PD
PCD
= PC + CD + PD
=(PA - CA) + (CE + DE) +(PB - DB)
= (PA - CE) + (CE + DE) + (PB - DE)
= (PA + PB) = 2PA = 2(14) cm
= 28 cm
Hence, the Perimeter of ![]() PCD
= 28 cm
PCD
= 28 cm
Solution 8
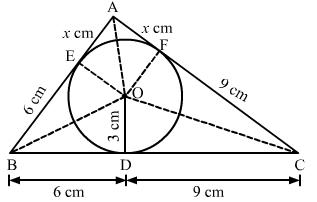
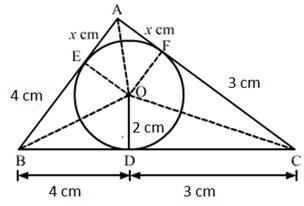
A circle is inscribed in a triangle ABC touching AB, BC and CA at P, Q and R respectively.
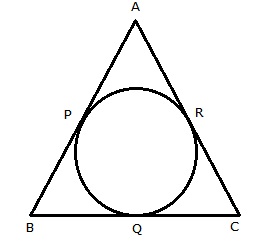
Also, AB = 10 cm, AR = 7cm, CR = 5cm
AR, AP are the tangents to the circle
![]() AP
= AR = 7cm
AP
= AR = 7cm
AB = 10 cm
![]() BP
= AB - AP = (10 - 7)= 3 cm
BP
= AB - AP = (10 - 7)= 3 cm
Also, BP and BQ are tangents to the circle
![]() BP
= BQ = 3 cm
BP
= BQ = 3 cm
Further, CQ and CR are tangents to the circle
![]() CQ
= CR = 5cm
CQ
= CR = 5cm
BC = BQ + CQ = (3 + 5) cm = 8 cm
Hence, BC = 8 cm
Solution 9
Let the circle touches the sides AB, BC, CD and DA at P, Q, R, S respectively
We know that the length of tangents drawn from an exterior point to a circle are equal
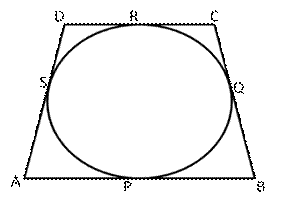
AP = AS ----(1) {tangents from A}
BP = BQ ---(2) {tangents from B}
CR = CQ ---(3) {tangents from C}
DR = DS----(4) {tangents from D}
Adding (1), (2) and (3) we get
![]() AP
+ BP + CR + DR = AS + BQ + CQ + DS
AP
+ BP + CR + DR = AS + BQ + CQ + DS
![]() (AP
+ BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
(AP
+ BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
![]() AB
+ CD = AD + BC
AB
+ CD = AD + BC
![]() AD
= (AB + CD) - BC = {(6 + 4) - 7} cm = 3 cm
AD
= (AB + CD) - BC = {(6 + 4) - 7} cm = 3 cm
Hence, AD = 3 cm
Solution 10
Solution 11
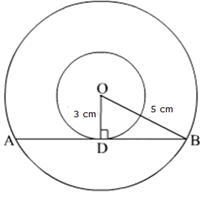
Given O is the centre of two concentric circles of radii 4 cm and 6 cm respectively. PA and PB are tangents to the outer and inner circle respectively. PA = 10cm. Join OA, OB and OP.
Then, OB = 4 cm, OA= 6 cm and PA = 10 cm
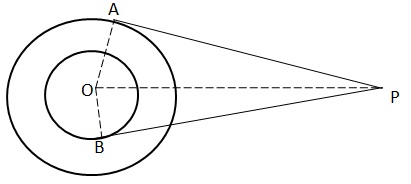
In triangle OAP,
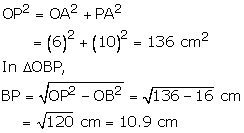
Hence, BP = 10.9 cm
Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Circles Exercise Ex. 8B
Solution 1
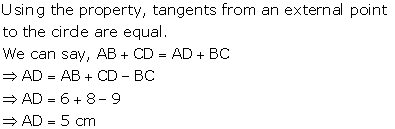
Solution 2

Solution 3

Solution 4
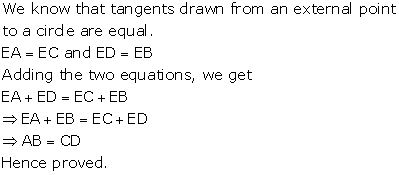
Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12
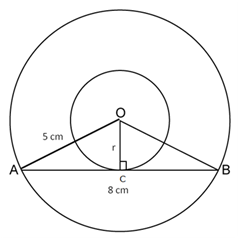

Solution 13

Solution 14

Solution 15
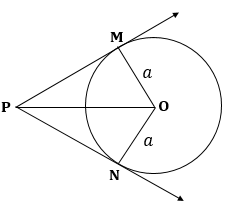
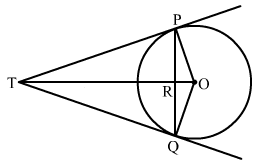
PM and PN are tangents to a circle.
∴ OM ⏊ PM and ON ⏊ PN
⇒ ∠OMP = 90o and ∠ONP = 90o
In ΔOMP and ΔONP,
OM = ON (radii of same circle)
∠OMP = ∠ONP = 90o
OP = OP (common)
∴ ΔOMP ≌ ΔONP (RHS congruency)
∴ ∠OPM = ∠OPN (CACT)
⇒ ∠OPM ![]()
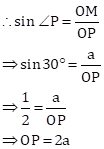
Hence, the length of OP is ![]() .
.
Circles Exercise MCQ
Solution 1
Correct option : (b)
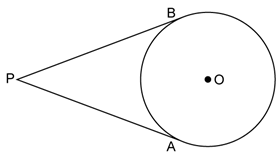
We can draw only 2 tangents from an external point to a circle.
Solution 2

Solution 3

Solution 4
Correct option: (d)
The diameter of the circle always passes through the centre. This means all the diameters of a given circle will intersect at the centre, and hence they cannot be parallel.
Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
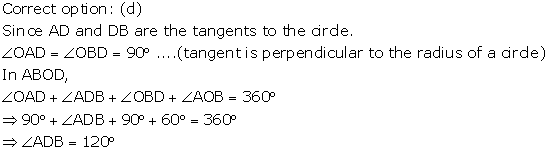
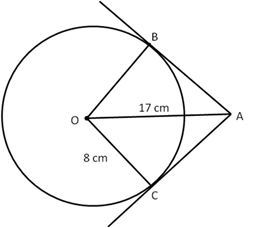
Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

Solution 21
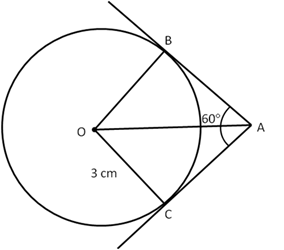

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27

Solution 28

Solution 29

Solution 30

Solution 31
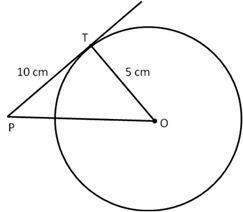

Solution 32

Solution 33

Solution 34
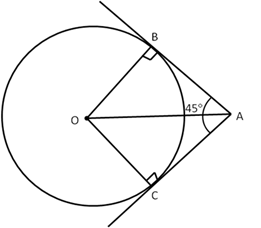

Solution 35

Solution 36
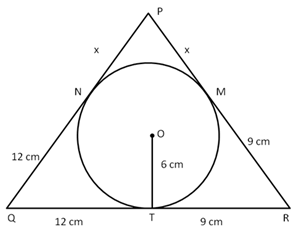

Solution 37

Solution 38

Solution 39

Solution 40

Solution 41

Solution 42

Solution 43

Solution 44
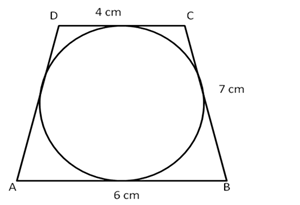
Solution 45

Solution 46

Solution 47

Solution 48

Solution 49

Solution 50
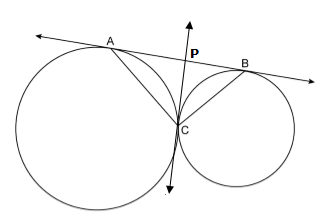
Correct option: (d)
Options (a), (b) and (c) are all true.
However, option (d) is false since we can draw only parallel tangents on either side of the diameter, which would be parallel to a given line.
Solution 51
Correct option: (d)
Options (a), (b) and (c) are all true.
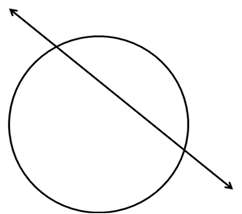
However, option (d) is false since a straight line can meet a circle at two points even as shown below.
Solution 52
Correct option: (d)
Options (a), (b) and (c) are true.
However, option (d) is false since it is not possible to draw a tangent from a point inside a circle.
Solution 53
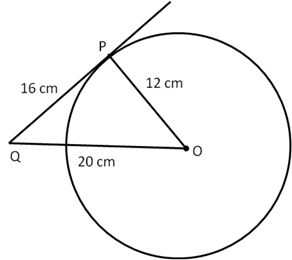

Solution 54
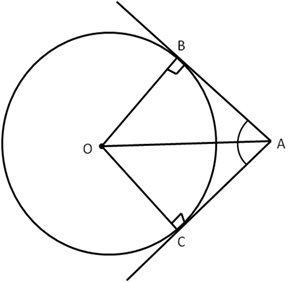

Solution 55

Circles Exercise Test Yourself
Solution 1

Solution 2
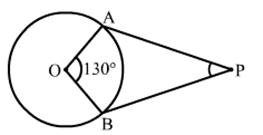
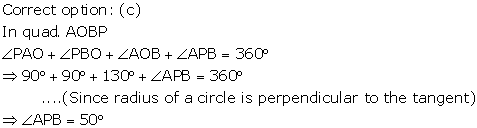
Solution 3

Solution 4
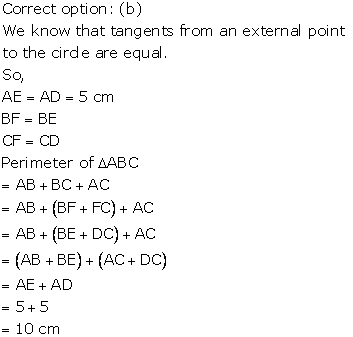
Solution 5

Solution 6

Solution 7

Solution 8

Solution 9
- A line intersecting a circle in two distinct points is called a secant.
- A circle can have two parallel tangents at the most.
- The common point of a tangent to a circle and the circle is called the point of contact.
- A circle can have infinitely many tangents.
Solution 10
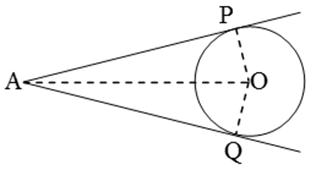

Solution 11
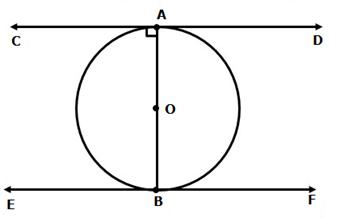

Solution 12
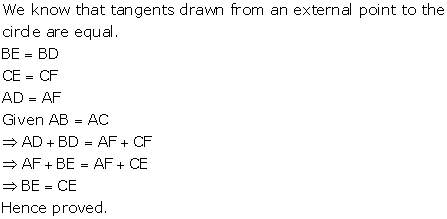
Solution 13
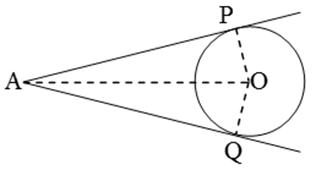

Solution 14
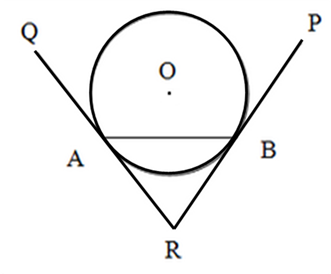

Solution 15
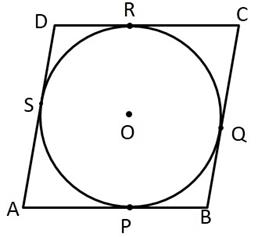

Solution 16
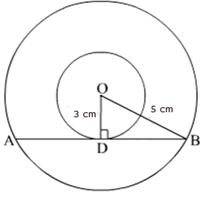

Solution 17
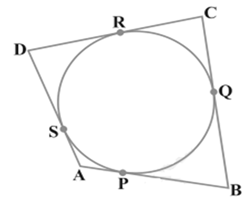

Solution 18
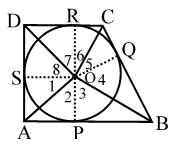

Solution 19
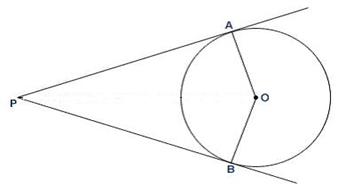

Solution 20