Chapter 5 Arithmetic Progression
Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution
Arithmetic Progression Exercise Ex. 5A
Solution 1(i)
Solution 1(ii)
Solution 1(iii)
Solution 1(iv)
Solution 1(v)
Solution 2(i)
Solution 2(ii)
Solution 2(iii)
Solution 2(iv)
Solution 2(v)
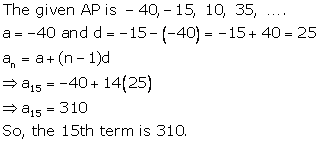
Solution 3(i)
The given AP is 
First term = 6, common difference = 
a
= 6, d = 
The nth term is given by
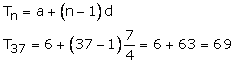
Hence, 37th term is 69.
Solution 3(ii)
The given AP is 
The first term = 5,
common difference = 
a
= 5, 
The nth term is given by
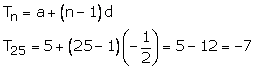
Hence, the 25th term is -7.
Solution 4
Since the numbers 
are
in AP,
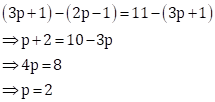
Therefore,
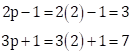
Hence, P = 2 and the numbers are 3, 7, 11.
Solution 5(i)
Solution 5(ii)
Given AP is 16, 9, 2, -5.
First term, a = 16
Common difference, d = 9 - 16 = -7
The nth term of the AP is given by
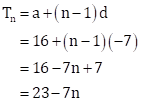
Solution 6
(given)
Then,
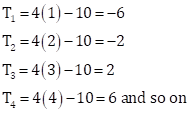
Now,
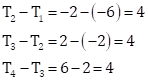
Since 
, the given progression is in AP.
Thus, we have
(i) first term = -6
(ii) common difference = 4
(iii) 16th term = 
Solution 7
In the given AP, we have a = 6 and d = (10 - 6) = 4
Suppose there are n terms in the given AP,.
Then,
Hence, there are 43 terms in the given AP.
Solution 8
In the given AP we have a = 41 and d = 38 - 41 = - 3
Suppose there are n terms in AP.
Then,
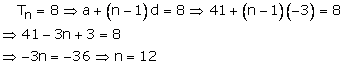
Hence, there are 12 terms in the given AP.
Solution 9
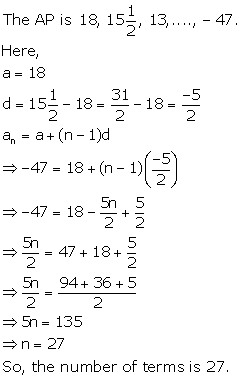
Solution 10
In the given AP, we have a = 3 and d = 8 - 3 = 5
Suppose there are n terms in given AP.
Then,
Hence, the 18th term of given AP is 88.
Solution 11
In the given AP, we have a = 72 and d = 68 - 72 = - 4
Suppose there are n terms in given AP.
Then,
Hence, the 19th term in the given AP is 0.
Solution 12
In the given AP, we have 
Suppose there are n terms in given AP, we have
Then,
Thus, the 14th term in the given AP is 3.
Solution 13
Solution 14
Here, a = 8 and d = 14 - 8 = 6
Therefore, 41st term is given by
Required term = 248 + 72 = 320
Let it be nth term.
Then,
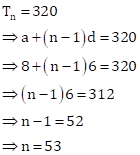
Hence, 53rd is the required term.
Solution 15
The given AP is 5, 15, 25....
a
= 5, d = 15 - 5 = 10
Thus, the required term is 44th term.
Solution 16
In the given AP let the first term = a,
And common difference = d
Then, Tn = a + (n - 1)d
T10= a + (10 - 1)d, T17 = a + (17 - 1)d and T13 = a + (13 - 1)d
T10 = a + 9d, T17 = a + 16d and T13 = a + 12d
Now, T10 = 52 ⇒ a + 9d = 52.....(1)
and T17 = T13 + 20 ⇒ a + 16d = a + 12d + 20
⇒ 4d = 20 ⇒ d = 5
Putting d = 5 in (1), we get
a + 9 x 5 = 52 ⇒ a = 52 - 45 ⇒ a = 7
Thus, a = 7 and d = 5
So the required AP is 7, 12, 17, 22....
Solution 17
Solution 18
Solution 19
Solution 20
Here a = 7, d = (10 - 7) = 3, l = 184
And n = 8
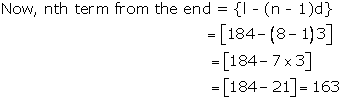
Hence, the 8th term from the end is 163.
Solution 21
Here a = 17, d = (14 - 17) = -3, l = -40
And n = 6
Now, nth term from the end = [l - (n - 1)d]
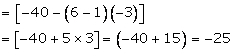
Hence, the 6th term from the end is -25.
Solution 22
Solution 23
Solution 24
Solution 25
Solution 26
In the given AP, let the first term = a common difference = d
So the required AP is 8, 6, 4, 2, 0......
Solution 27
Let the first term of given AP = a and common difference = d
Hence 25th term is triple its 11th term.
Solution 28
Let 'a' be the first term and 'd' be the common difference of the given AP.
Then, nth term, 
Now,
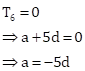
Now,
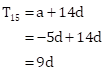
And,
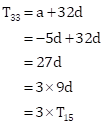
Hence, proved.
Solution 29
Solution 30
Solution 31
Solution 32
Solution 33
Let a be the first term and d be the common difference
Solution 34
Solution 35
Solution 36
First AP is 63, 65, 67....
First term = 63, common difference = 65 - 63 = 2
nthterm
= 63 + (n - 1) 2 = 63 + 2n - 2 = 2n + 61
Second AP is 3, 10, 17 ....
First term = 3, common difference = 10 - 3 = 7
nth term = 3 + (n - 1) 7 = 3 + 7n - 7 = 7n - 4
The two nth terms are equal
2n
+ 61 = 7n - 4 or 5n = 61 + 4 = 65
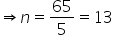
Solution 37
Solution 38
Solution 39
Solution 40
Let a be the first term and d be the common difference.
pth term = a +(p - 1)d = q (given)-----(1)
qth term = a +(q - 1) d = p (given)-----(2)
Subtracting (2) from (1),
(p - q)d = q - p
(p - q)d = -(p - q)
d = -1
Putting d = -1 in (1)
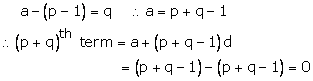
Solution 41
Let a be the first term and d be the common difference
nth
term from the beginning = a + (n - 1)d-----(1)
nth term from end= l - (n - 1)d ----(2)
adding (1) and (2),
sum of the nth term from the beginning and nth term from the end = [a + (n - 1)d] + [l - (n - 1)d] = a + l
Solution 42
Solution 43
Solution 44
The three-digit numbers divisible by 9 are 108, 117, 126, 135,......, 999.
Here,
a = 108 and d = 9
Now,
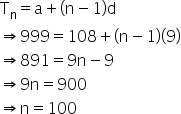
Hence, 100 three-digit numbers are divisible by 9.
Solution 45
Solution 46
Number of rose plants in first, second, third rows.... are 43, 41, 39... respectively.
There are 11 rose plants in the last row
So, it is an AP . viz. 43, 41, 39 .... 11
a = 43, d = 41 - 43 = -2, l = 11
Let nth term be the last term
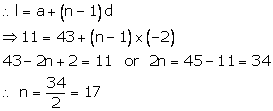
Hence, there are 17 rows in the flower bed.
Solution 47
Solution 48
Integers between 200 and 500 divisible by 8 are 208, 216, 224, 232, ……, 496.
Clearly, these numbers form an AP with
a = 208, d = 8 and l = 496.
Let it contain n terms.
Then,
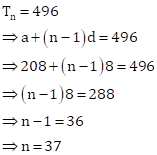
Hence, there are 37 integers between 200 and 500 which are divisible by 8.
Arithmetic Progression Exercise Ex. 5B
Solution 1
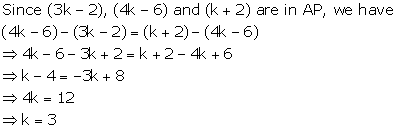
Solution 2
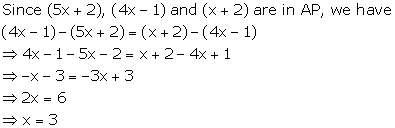
Solution 3
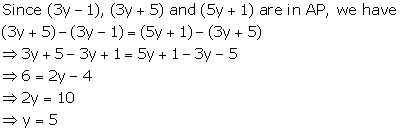
Solution 4
If
are
consecutive terms of an AP, then
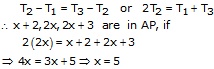
Solution 5
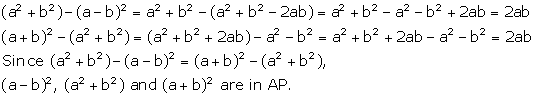
Solution 6
Let the three numbers in AP be 
.
Then, sum of these numbers 
And, product of these numbers
Given, sum = 15 and product = 105
Then,
And,
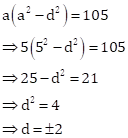
Hence, the required numbers are (3, 5, 7) or (7, 5, 3).
Solution 7
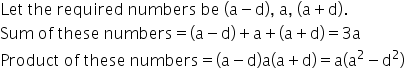
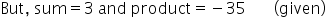
Solution 8
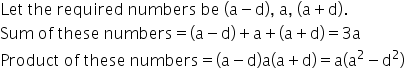
But sum = 24 and product = 440
Solution 9
Let the required numbers be (a - d), a, (a + d)
Sum of these numbers = (a - d) + a + (a + d) = 3a
sum
of squares of these numbers = 
Sum of numbers = 21, sum of squares of numbers = 165
3a
= 21
a = 7
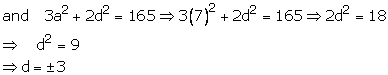
Thus, a = 7 and d = 
Hence, the required numbers are (4, 7, 10) or (10, 7, 4).
Solution 10
Let the required angles be (a - 3d)°, (a - d) °, (a + d) ° and (a + 3d) °
Common difference = (a - d) - (a- 3d) = a - d - a + 3d = 2d
Common difference = 10°
2d
= 10° = d =
5°
Sum of four angles of quadrilateral = 360°
First angle = (a - 3d)° = (90 - 3 × 5) ° = 75°
Second angle = (a - d)° = (90 - 5) ° = 85°
Third angle = (a + d)° = (90 + 5°) = 95°
Fourth angle = (a + 3d)° = (90 + 3 × 5)° = 105°
Solution 11
Let the required number be (a - 3d), (a - d), (a + d) and (a + 3d).
Sum of these numbers = (a - 3d) + (a - d)+ (a + d) + (a + 3d)
4a
= 28 
a = 7
Sum of the squares of these numbers
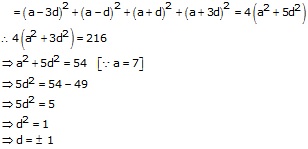
Hence, the required numbers are (4, 6, 8, 10) or (10, 8, 6, 4).
Solution 12
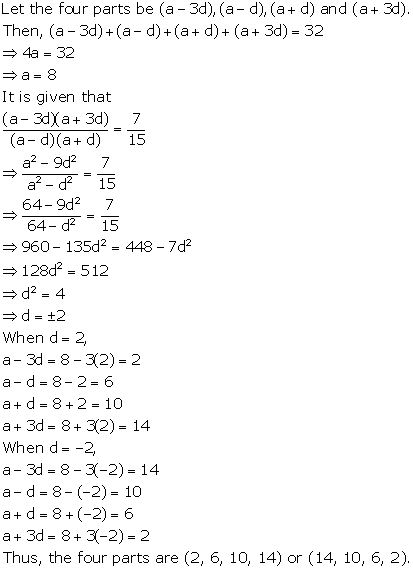
Solution 13
Solution 14
Let the three numbers in AP be .
Then, sum of these numbers
Given, sum = 18
And,
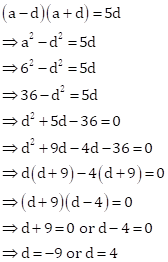
When d = -9, the numbers are 15, 6, -3.
When d = 4, the numbers are 2, 6, 10.
Solution 15
Since the numbers a, 7, b, 23, c are in AP,
7 - a = b - 7 = 23 - b = c - 23
Consider b - 7 = 23 - b
⇒ 2b = 30
⇒ b = 15
Consider 7 - a = b - 7
⇒ a + b = 14
⇒ a + 15 = 14
⇒ a = -1
Consider 23 - b = c - 23
⇒ b + c = 46
⇒ 15 + c = 46
⇒ c = 31
Hence, a = -1, b = 15 and c = 31.
Arithmetic Progression Exercise Ex. 5C
Solution 1(i)
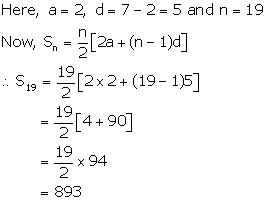
Solution 1(ii)
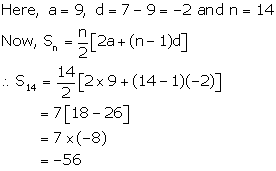
Solution 1(iii)
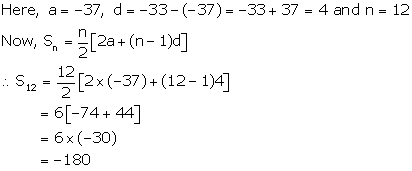
Solution 1(iv)
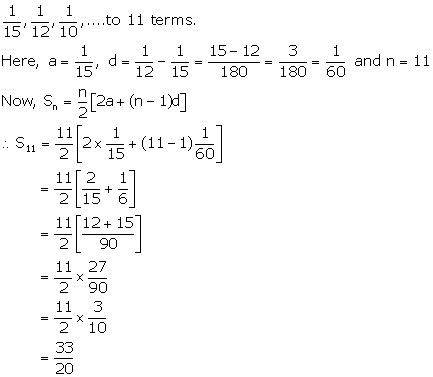
Solution 1(v)
Solution 2(i)
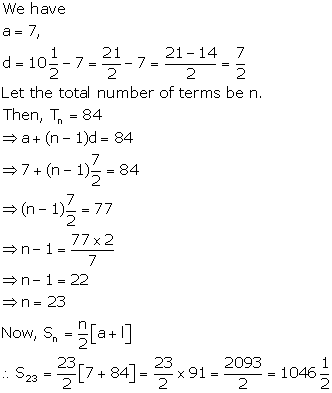
Solution 2(ii)
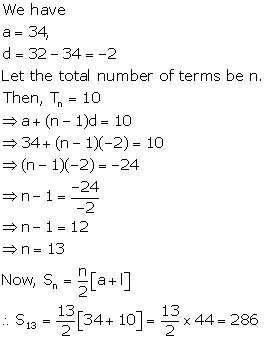
Solution 2(iii)
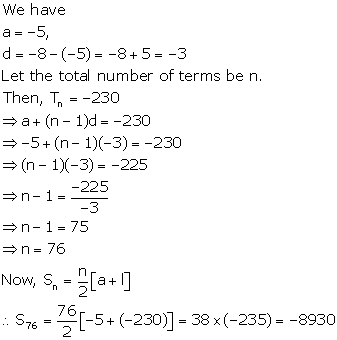
Solution 2(iv)
Given arithmetic series is as follows:
5 + (-41) + 9 + (-39) + 13 + (-37) + 17 + … + (-5) + 81 + (-3)
= (5 + 9 + 13 + 17 + … + 81) + [(-41) + (-39) + (-37) + … + (-5) + (-3)] …..(i)
Let A1 = 5 + 9 + 13 + + 17 + … + 81
Here,
a = 5, l = 81 and d = 9 - 5 = 4
Let A1 series contain n1 terms. Then,
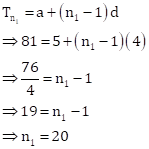
Let A2 = (-41) + (-39) + (-37) + … + (-5) + (-3)
Here,
a = -41, l = -3 and d = -39 - (-41) = 2
Let A2 series contain n2 terms. Then,
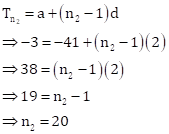
Thus, we have
5 + (-41) + 9 + (-39) + 13 + (-37) + 17 + … + (-5) + 81 + (-3)
= (5 + 9 + 13 + + 17 + … + 81) + [(-41) + (-39) + (-37) + … + (-5) + (-3)]
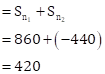
Solution 3
Solution 4
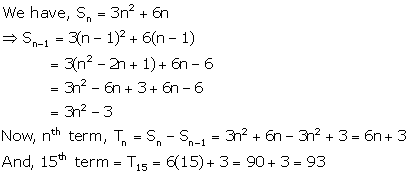
Solution 5
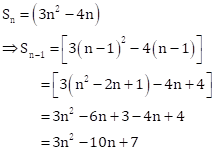
(i) The nth term is given by
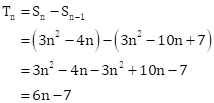
(ii) Putting n = 1 in 
,
we have
(iii) Putting n = 1 in ,
we have
Now, common difference, d = 
Solution 6(i)
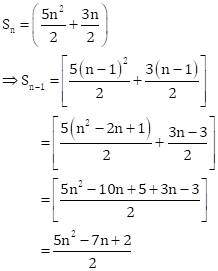
The nth term is given by
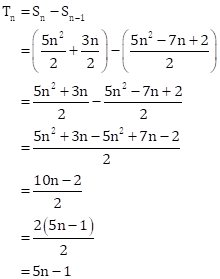
Putting n = 20 in 
,
we have
Solution 6(ii)
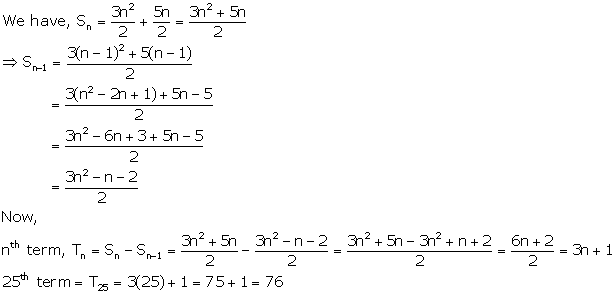
Solution 7
Let 'a' be the first term and 'd' be the common difference of given AP.
Then,
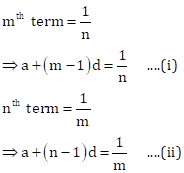
Subtracting (ii) from (i),
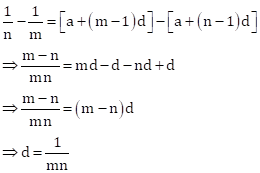
Substituting the value of 'd' in (i),
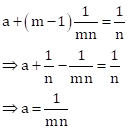
Sum of first mn terms is given by
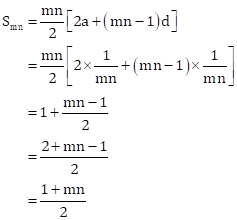
Solution 8
Here a = 21, d = (18 - 21) = -3
Let the required number of terms be n, then
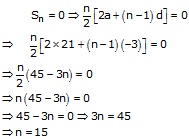
sum
of first 15 terms = 0
Solution 9
Solution 10
Solution 11
Solution 12
Odd numbers between 0 and 50 are 1, 3, 5, 7, ……, 49.
Clearly, these numbers form an AP with
a = 1, d = 2 and l = 49.
Let it contain n terms.
Then,
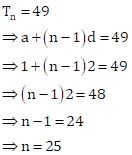
Required sum is given by
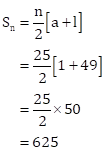
Solution 13
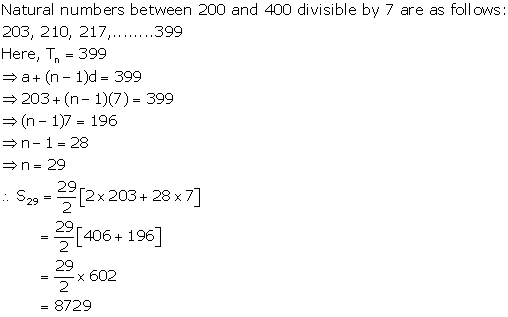
Solution 14
Solution 15
First 15 multiples of 8 are 8, 16, 24, ……, 120.
Clearly, these numbers form an AP with
a = 8, d = 8, l = 120 and n = 15
Required sum is given by
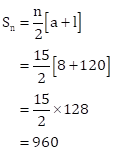
Solution 16
All numbers between 300 and 700 that are multiples of 9 are 306, 315, 324, 333, ..., 693
This is an AP in which a = 306, d = (315 - 306) = 9, l = 693
Let the number of these terms be n, then
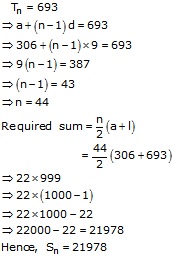
Solution 17
Three-digit numbers divisible by 13 are 104, 117, 130, ……, 988.
Clearly, these numbers form an AP with
a = 104, d = 13 and l = 988.
Let it contain n terms.
Then,
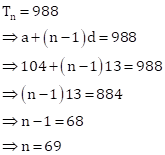
Required sum is given by
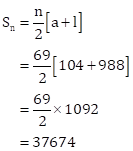
Solution 18
First 100 even natural numbers divisible by 5 are 10, 20, 30, ……, 100 terms.
Clearly, these numbers form an AP with
a = 10, d = 10 and n = 100
Required sum is given by
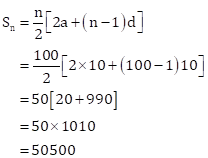
Solution 19
Required sum of n terms is given by
Solution 20
Solution 21
First term 'a' of an AP = 2
The last term l = 29
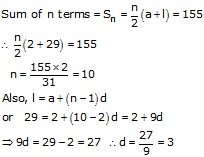
common
difference = 3
Solution 22
Solution 23
Solution 24
Solution 25
First term of an AP, a = 22
Last term = nth term = - 11
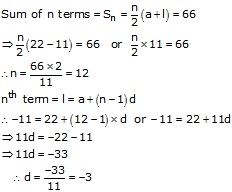
Thus, n = 12, d = -3
Solution 26
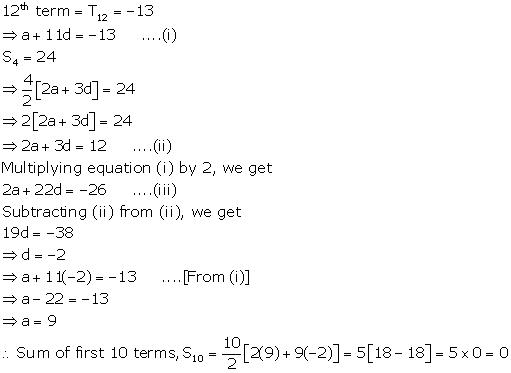
Solution 27
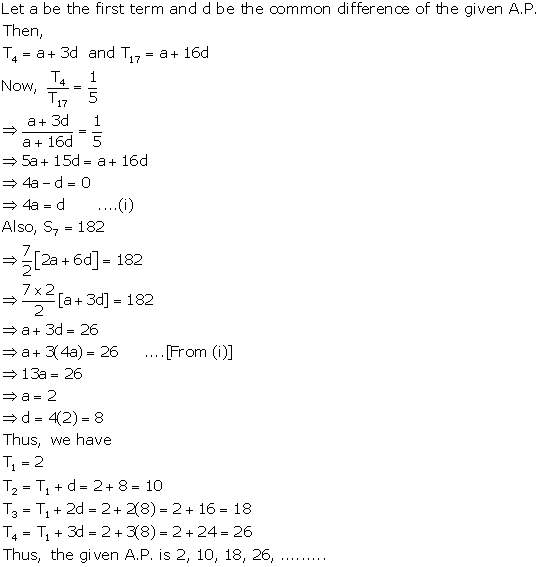
Solution 28
Solution 29
Solution 30
Solution 31
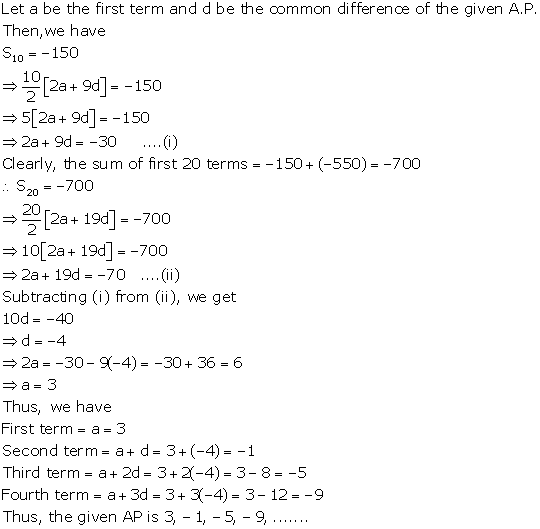
Solution 32
Solution 33
Solution 34(i)
Solution 34(ii)
Solution 35
Let the first term and common difference of 1st AP be 'a' and 'd' respectively.
And, let the first term and common difference of 2nd AP be 'A' and 'D' respectively.
Then
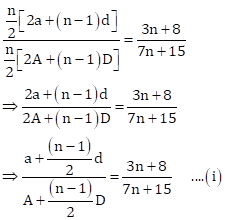
Ratio of 12th terms
Putting n = 23 in (i),
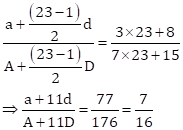
Solution 36
Solution 37
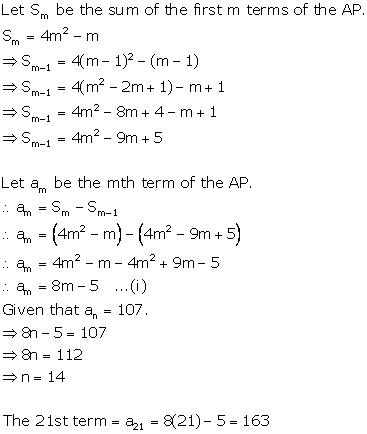
Solution 38
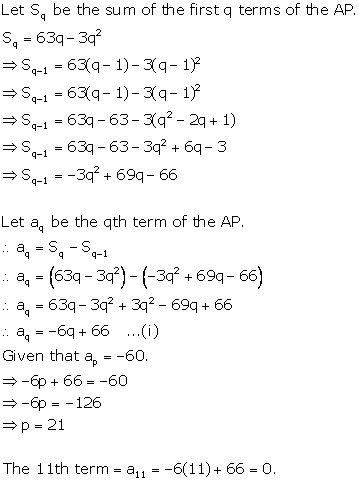
Solution 39
Solution 40
Solution 41
Solution 42
Solution 43
Solution 44
Solution 45
The values of four prizes form an AP with common difference d = -20.
Let the value of first prize = a
And, n = 7
Now, sum of values of prizes = Rs. 700
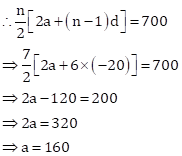
Hence, the values of 7 prizes are Rs. 160, Rs. 140, Rs. 120, Rs. 100, Rs. 80, Rs. 60 and Rs. 40.
Solution 46
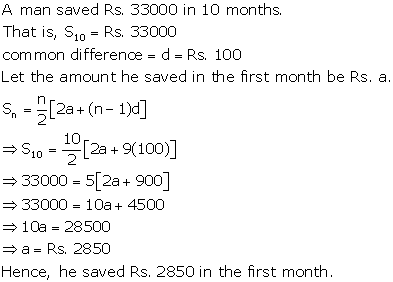
Solution 47
Let the first instalment be Rs. a and let the common difference be d.
Now, for n = 40, S40 = 36000
When 30 instalments are paid, one-third is unpaid.
That means, two-rhird is paid.
So, for n = 30, S30 =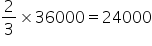 
Now,
Hence, the value of first instalment is Rs. 510.
Solution 48
Solution 49
Saving done by a child on 1st day = Rs. 5
Saving done by a child on 2nd day = Rs. 5 + Rs. 5 = Rs. 10
Saving done by a child on 3rd day = Rs. 10 + Rs. 5 = Rs. 15 and so on
We observe that the savings done by a child form an AP a = 5 and d = 5.
Let the child contributes five-rupee coins in a piggy bank for n days.
Total number of five-rupee coins in the piggy bank = 190
Therefore, total money saved by a child in n days = Rs. 5 × 190 = Rs. 950
Then,
Hence, a child put the five-rupee coins into piggy bank for 19 days and she saved Rs. 950.
Solution 50
For an AP,
First term = a
Second term = b
Then, common difference = b - a
Last term, l = c
Let 'c' be the nth term.
Then, nth term = 
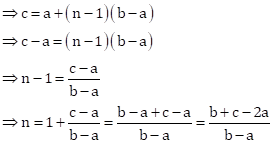
Now, required sum is given by
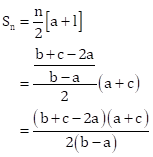
Hence, proved.
Arithmetic Progression Exercise Ex. 5D
Solution 1
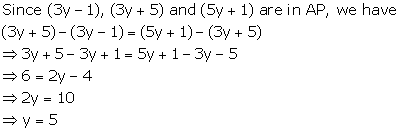
Solution 2
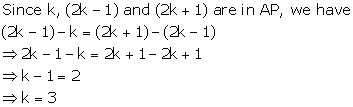
Solution 3
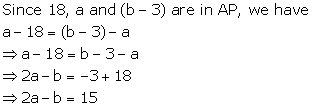
Solution 4
Solution 5
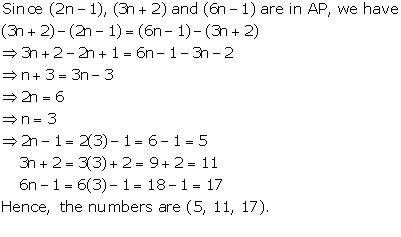
Solution 6
Solution 7
Solution 8
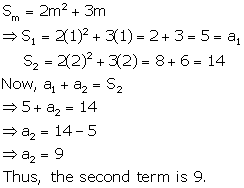
Solution 9
Solution 10
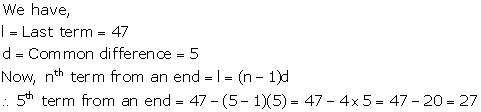
Solution 11
Solution 12
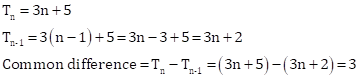
Solution 13
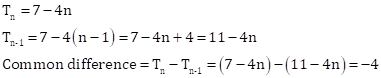
Solution 14
Given AP is 
First term 
Common difference
Therefore, next term of AP
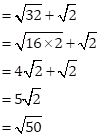
Solution 15
Given AP is 
First term 
Common difference
Therefore, next term of AP
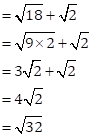
Solution 16
The given AP is 21, 18, 15, ....
First term = 21, common difference = 18 - 21= - 3
Let nth term be zero 
a
+ (n - 1)d = 0or 21 + (n - 1)(-3) = 0
21
- 3n + 3 = 0
3n = 24
or 
Hence, 8th term of given AP is 0.
Solution 17
Sum of n natural numbers = 1 + 2 + 3 + ... + n
Here a = 1, d = 2 - 1 = 1
Solution 18
Sum of even natural numbers = 2 + 4 + 6 + ... to n terms
a = 2, d = 4 - 2 = 2
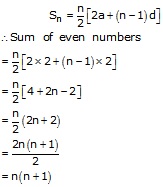
Solution 19
First term of AP = a = p
Common difference = d = q
nth term = a + (n 1)d
10th term = p + (10 1)q
= p + 9q
Solution 20
Solution 21
Solution 22
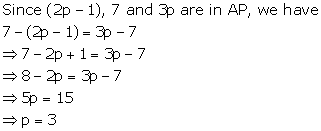
Solution 23
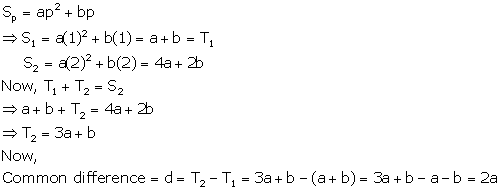
Solution 24
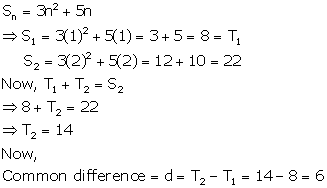
Solution 25
Solution 26
Let 'a' be the first term and 'd' be the common difference of given AP.
Given,
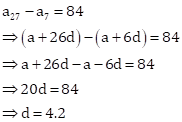
Solution 27
Given,
1 + 4 + 7 + 10 + ….. + x = 287
This forms an AP with
first term, a = 1
and common difference = 4 - 1 = 3
Let x be the nth term.
Now,
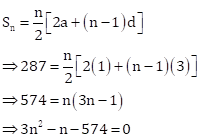
Solving the quadratic equation,
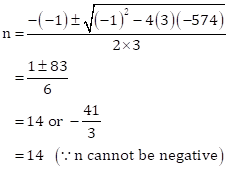
Arithmetic Progression Exercise MCQ
Solution 1
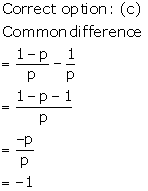
Solution 2
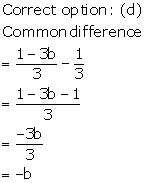
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
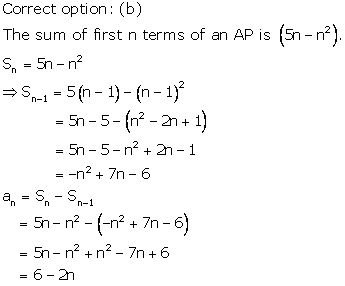
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
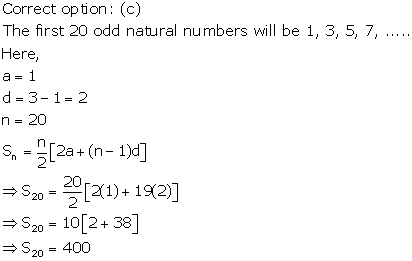
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
Solution 25
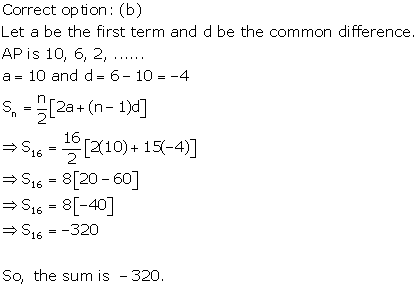
Solution 26
Solution 27
Solution 28
Solution 29
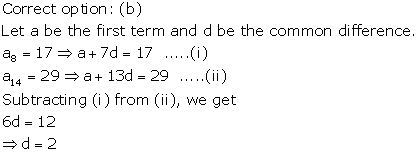
Solution 30
Solution 31
Correct option: (d)
Here,
First term, a = 5
Common difference, d = 9 - 5 = 4
Let 185 be the nth term.
Then,
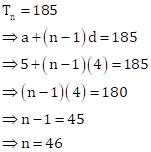
Solution 32
Correct option: (d)
Given,
(2p + 1), 10 and (5p + 5) are three consecutive terms of an AP.
Therefore,
10 - (2p + 1) = (5p + 5) - 10
⇒ 9 - 2p = 5p - 5
⇒ 7p = 14
⇒ p = 2