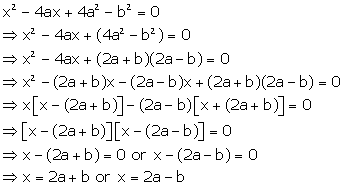Chapter 4 Quadratic Equations
Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution
Quadratic Equations Exercise Ex. 4A
Solution 1(i)
(i)
is
a quadratic polynomial
=
0 is a quadratic equation
Solution 1(ii)
Clearly 
is
a quadratic polynomial
is a
quadratic equation.
Solution 1(iii)
is
a quadratic polynomial
=
0 is a quadratic equation
Solution 1(iv)
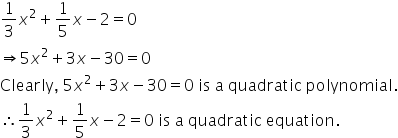
Solution 1(v)
is not
a quadratic polynomial since it contains
in
which power 
of
x is not an integer.
is
not a quadratic equation
Solution 1(vi)
And 
Being
a polynomial of degree 2, it is a quadratic polynomial.
Hence, 
is
a quadratic equation.
Solution 1(vii)
Solution 1(viii)
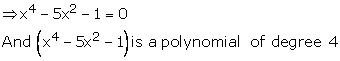
is
not a quadratic equation
Solution 1(ix)
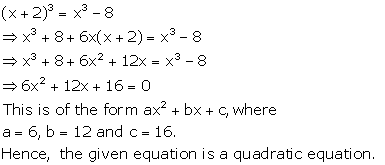
Solution 1(x)
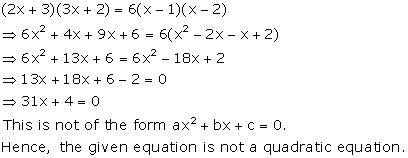
Solution 1(xi)
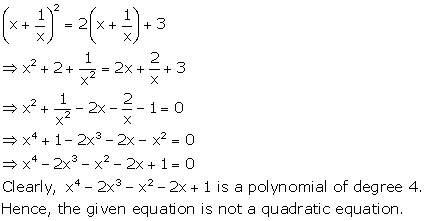
Solution 2
The given
equation is 
(i)On substituting x = -1 in the equation, we get
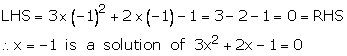
(ii)On substituting 
in
the equation, we get
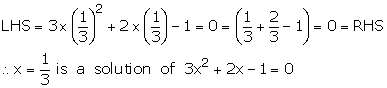
(iii)On substituting 
in
the equation ,
we get
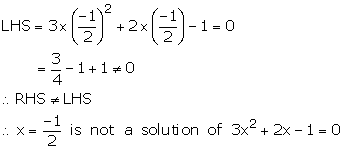
Solution 3(i)
Since x =1 is a root of the equation 
, it must satisfy the equation.
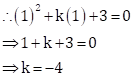
Substituting 
in
,
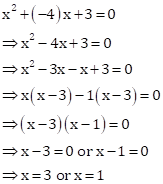
Hence k=-4 and other root is 3.
Solution 3(ii)
Since
is
a root of 
,
we have
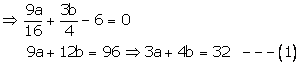
Again x = -2 being a root of ,
we have
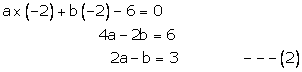
Multiplying (2) by 4 adding the result from (1), we get
11a = 44 
a
= 4
Putting a = 4 in (1), we get
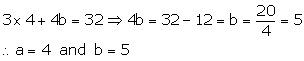
Solution 4
Given equation is 
.
Substituting 
in LHS of the given equation,
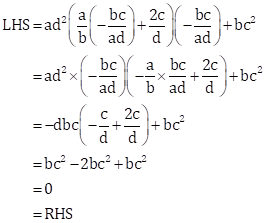
is a solution of the quadratic equation
.
Solution 5
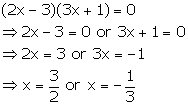
Solution 6
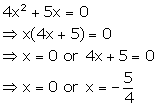
Solution 7
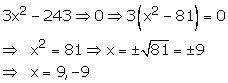
Hence, 9 and -9 are the roots of the equation 
Solution 8
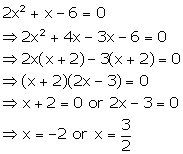
Solution 9
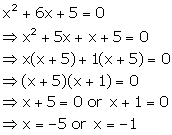
Solution 10
Solution 11
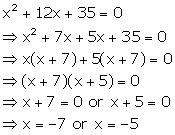
Solution 12
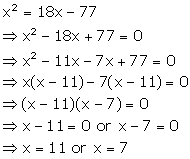
Solution 13
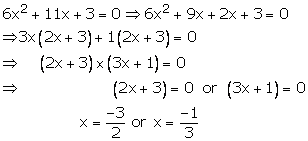
Hence, 
are
the roots of 
Solution 14
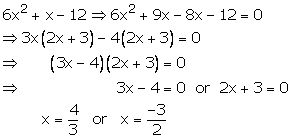
Hence, 
are
the roots of equation
Solution 15
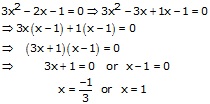
Hence, 
and
1 are the roots of the equation 
.
Solution 16
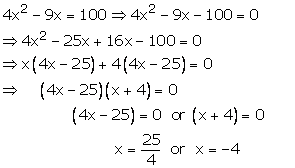
are
the roots of the equation 
Solution 17
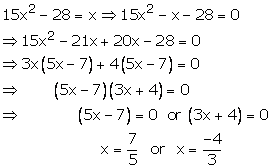
Hence, 
are
the roots of the given equation 
Solution 18
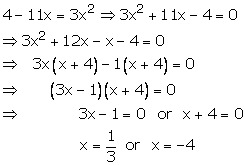
Hence, 
are
the roots of given equation
Solution 19
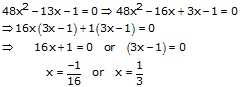
Hence, 
are
the roots of 
Solution 20
Solution 21
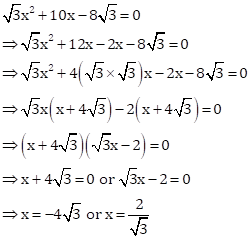
Solution 22
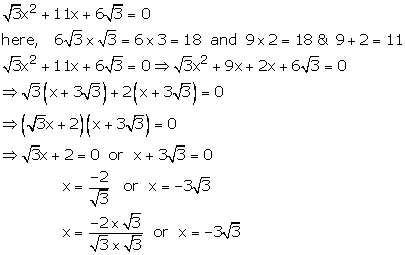
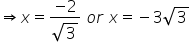
Solution 23
Hence, 
are
the roots of the given equation
Solution 24
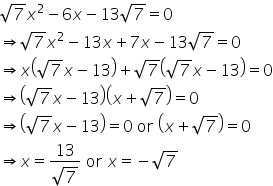
Solution 25
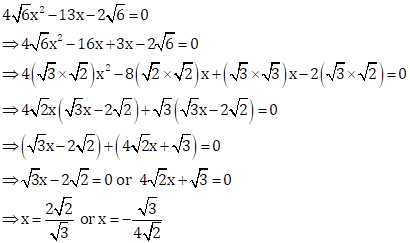
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
Solution 31
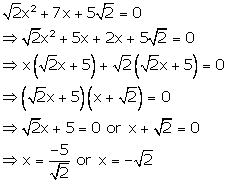
Solution 32
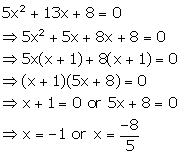
Solution 33
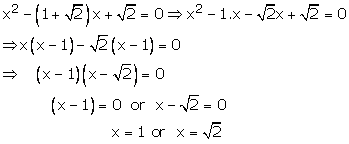
Hence, 1 and 
are
the roots of the given equation
Solution 34
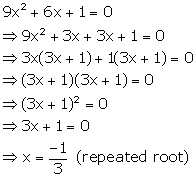
Solution 35
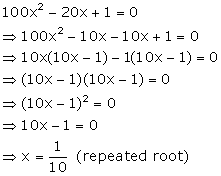
Solution 36
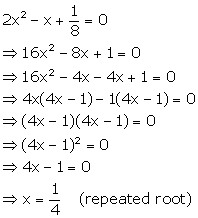
Solution 37
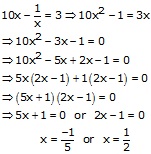
Hence, 
are
the roots of the given equation
Solution 38
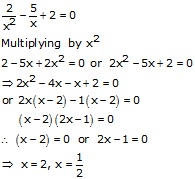
Hence, 2 and 
are
the roots of given equation
Solution 39
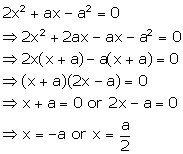
Solution 40
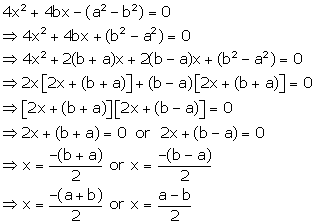
Solution 41
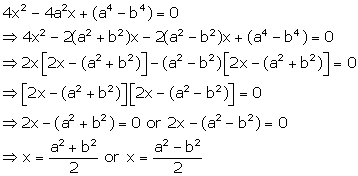
Solution 42
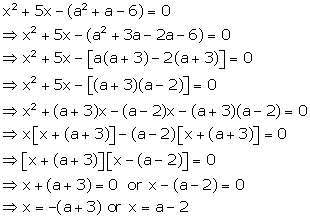
Solution 43
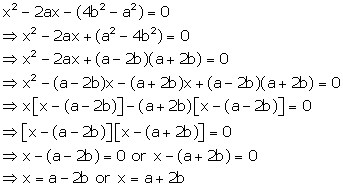
Solution 44
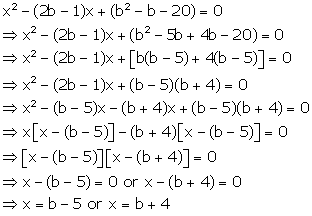
Solution 45
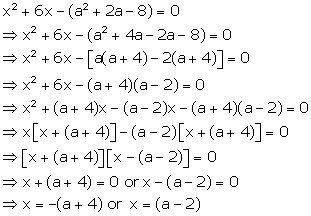
Solution 46
Hence, 
are
the roots of the given equation
Solution 47
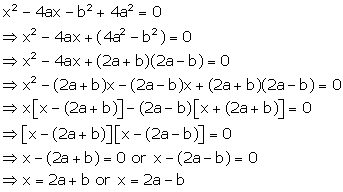
Solution 48
Hence, 
are
the roots of given equation
Solution 49
Hence, 
are
the roots of given equation
Solution 50
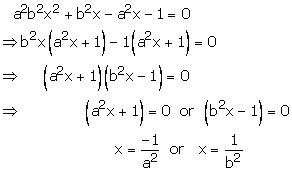
Hence, 
are
the roots of given equation
Solution 51
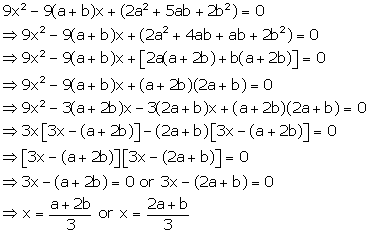
Solution 52
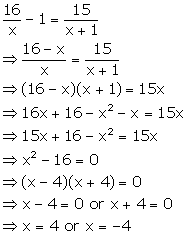
Solution 53
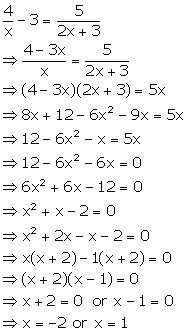
Solution 54
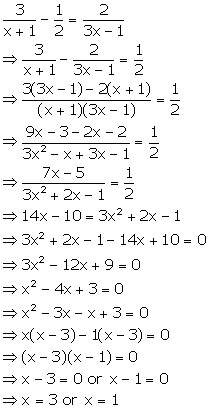
Solution 55(i)
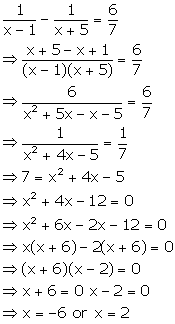
Solution 55(ii)
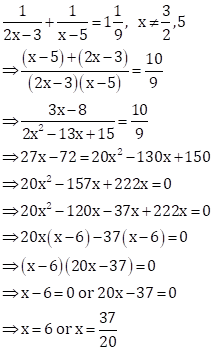
Solution 56
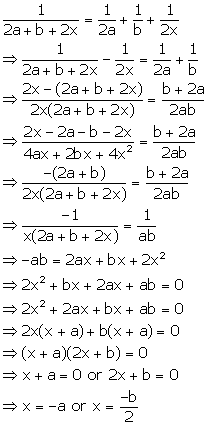
Solution 57
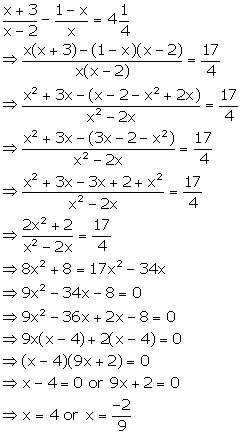
Solution 58
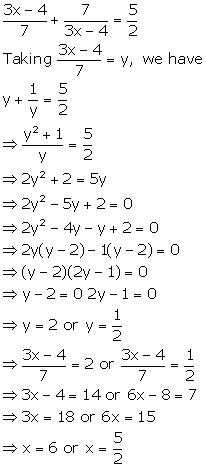
Solution 59(i)
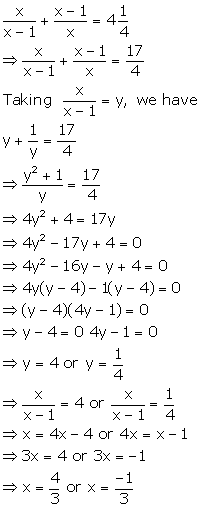
Solution 59(ii)
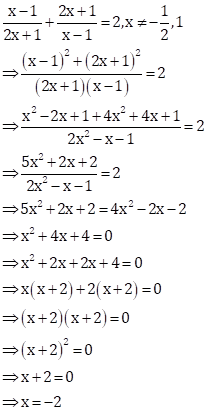
Solution 60
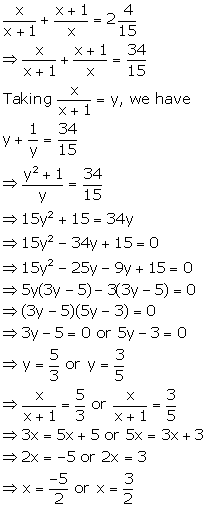
Solution 61
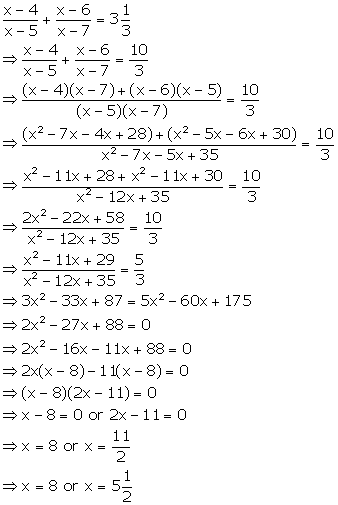
Solution 62
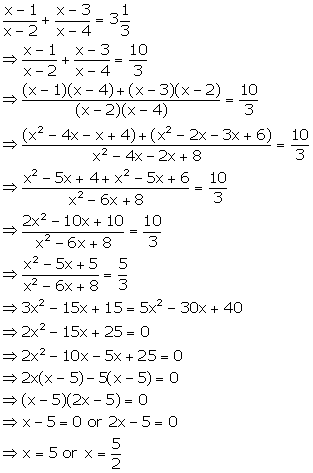
Solution 63
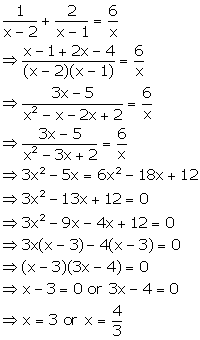
Solution 64(i)
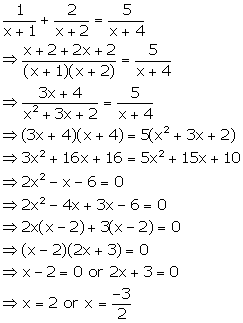
Solution 64(ii)
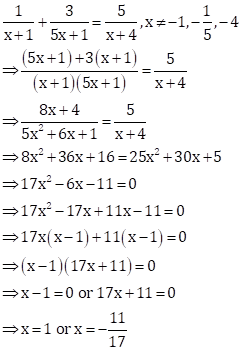
Solution 65
Solution 66
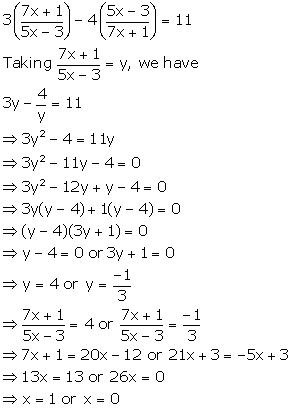
Solution 67
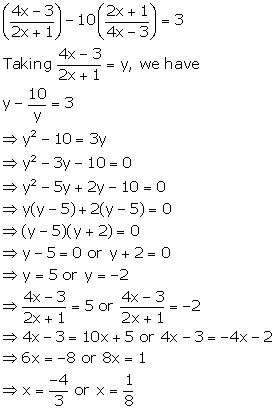
Solution 68
Putting
the
given equation become
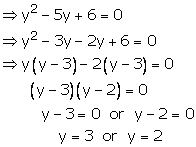
Case I:
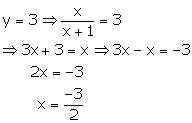
Case II:
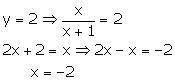
Hence, 
are
the roots of the given equation
Solution 69
The given equation
Hence, 
is
the roots of the given equation
Solution 70
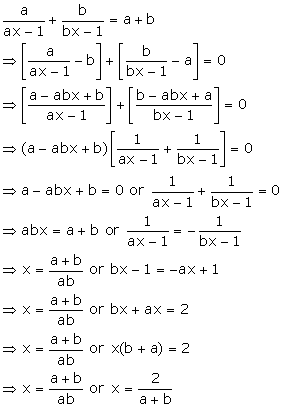
Solution 71
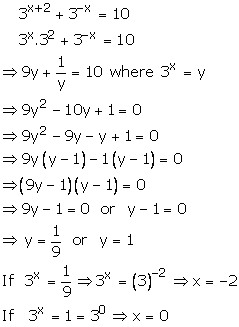
Hence, -2,0 are the roots of given equation
Solution 72
Hence, 
are
the roots of given equation
Solution 73
Hence, 3 and 2 are roots of the given equation
Quadratic Equations Exercise Ex. 4B
Solution 1(i)
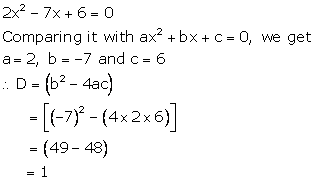
Solution 1(ii)
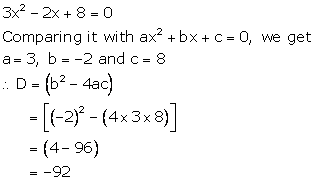
Solution 1(iii)
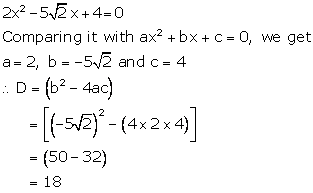
Solution 1(iv)
Solution 1(v)
Solution 1(vi)
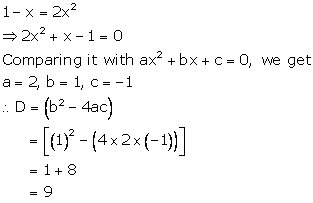
Solution 2
Solution 3
Solution 4
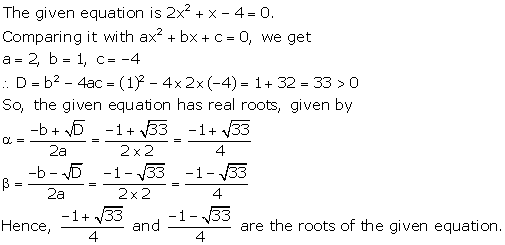
Solution 5
Solution 6
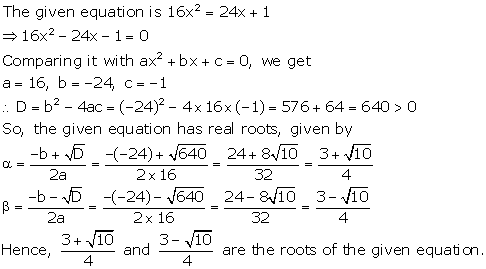
Solution 7
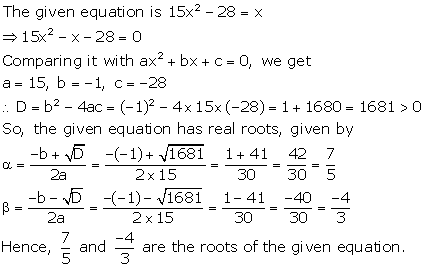
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
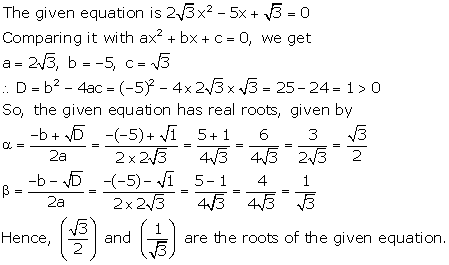
Solution 16
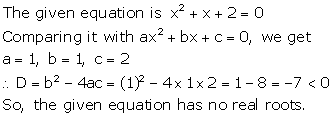
Solution 17
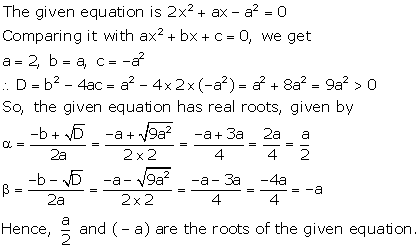
Solution 18
Solution 19
Solution 20
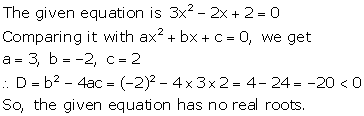
Solution 21
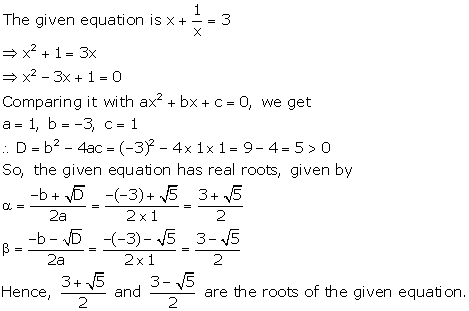
Solution 22
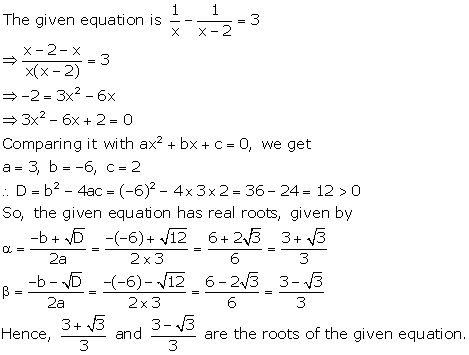
Solution 23
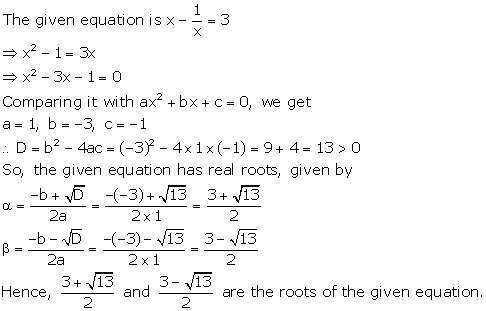
Solution 24
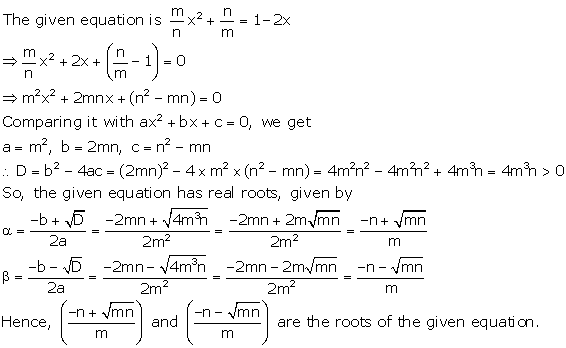
Solution 25
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
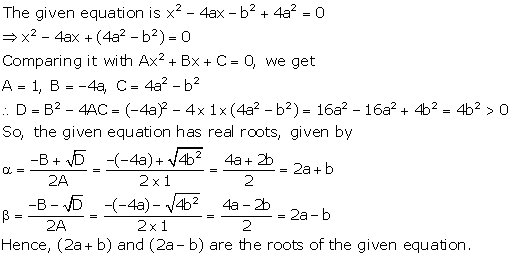
Solution 31
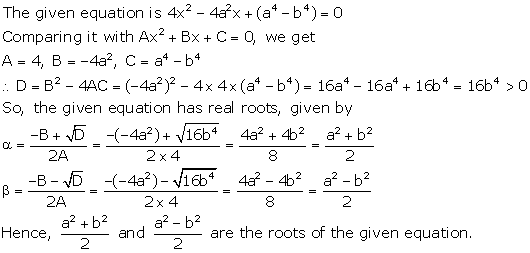
Solution 32
Solution 33
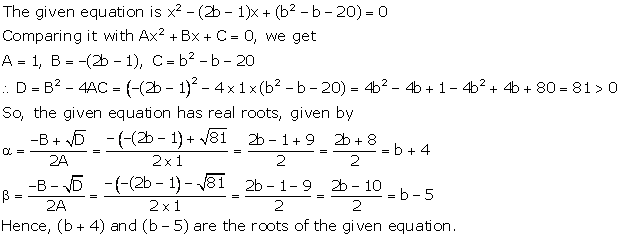
Solution 34
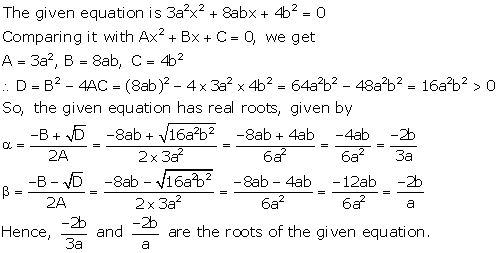
Solution 35
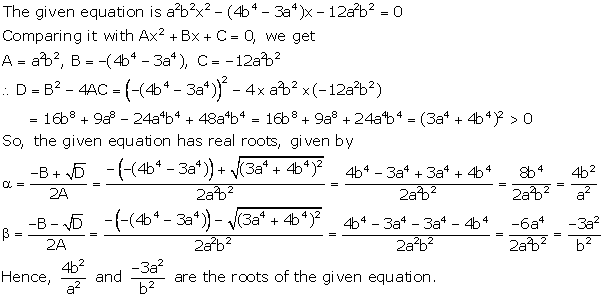
Solution 36
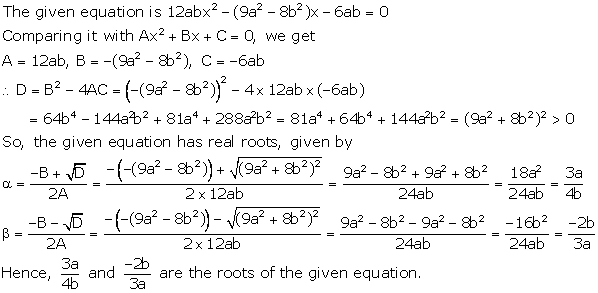
Quadratic Equations Exercise Ex. 4C
Solution 1(i)
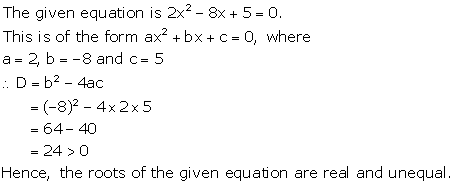
Solution 1(ii)
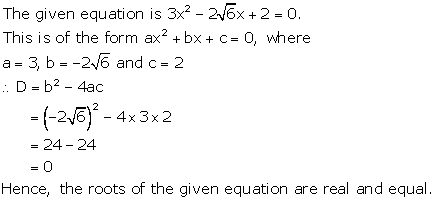
Solution 1(iii)
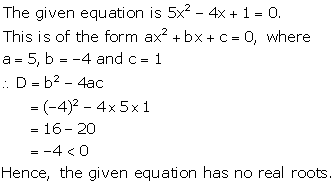
Solution 1(iv)
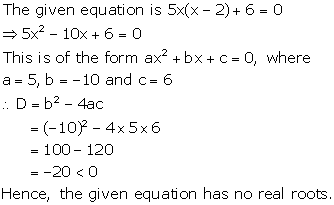
Solution 1(v)
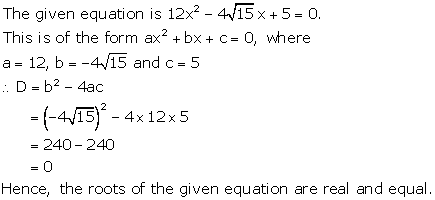
Solution 1(vi)
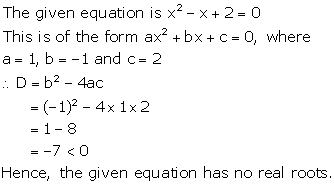
Solution 2
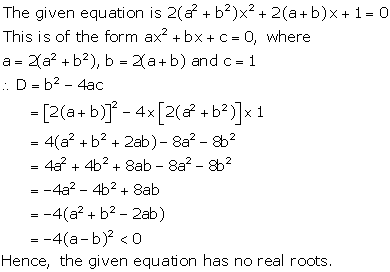
Solution 3
The given equation is 
This is the form of 
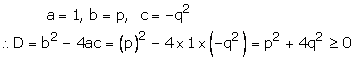
Now 
.
So, the roots of the given equation are real for all real values of p and q.
Solution 4
Solution 5
Solution 6
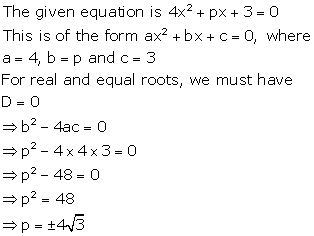
Solution 7
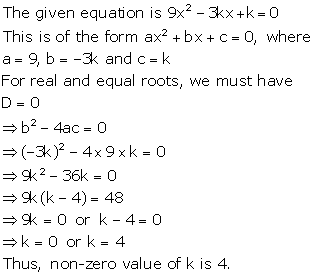
Solution 8(i)
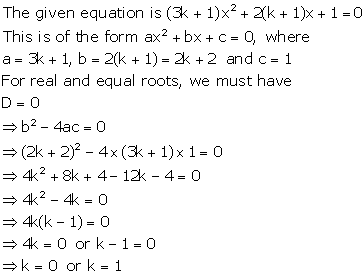
Solution 8(ii)
The given equation is 
This is of the form 
, where
For real and equal roots, we must have
Discriminant, D = 0
Solution 9
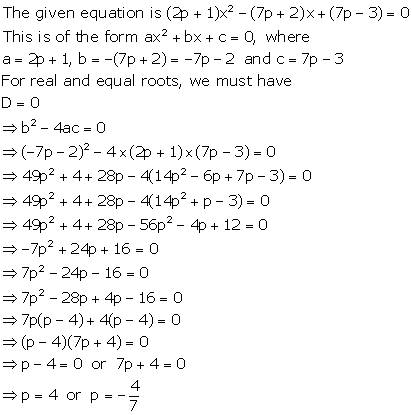
Solution 10
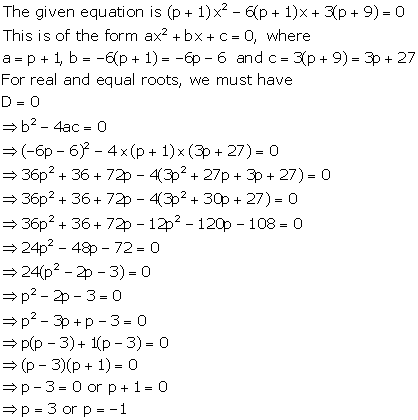
Solution 11
Since -5 is a root of the quadratic equation 
, it must satisfy the equation.
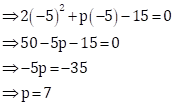
The other quadratic equation is 
(i)
Substituting p = 7 in (i),
This is of the form , where
For equal roots, we must have
Discriminant, D = 0
Solution 12
Solution 13
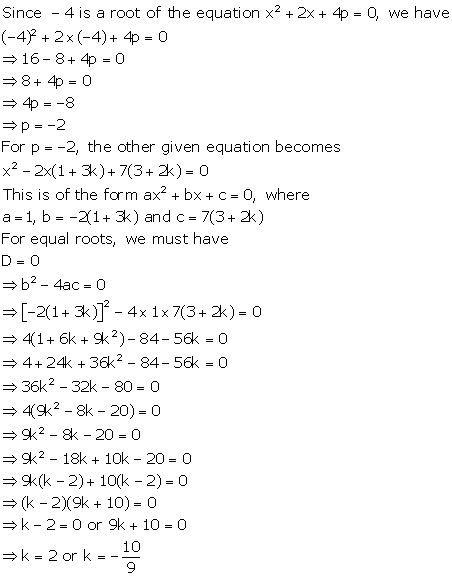
Solution 14
The given equation is 
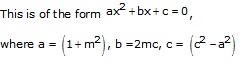
For real and equal roots, we must have D = 0
Solution 15
The given
equation is 
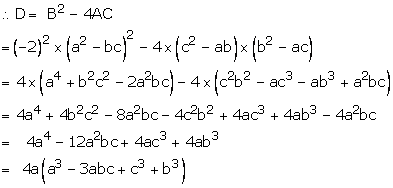
For real and equal roots , we must have D =0
Solution 16
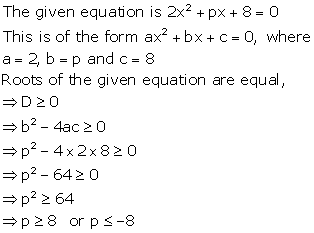
Solution 17
Solution 18
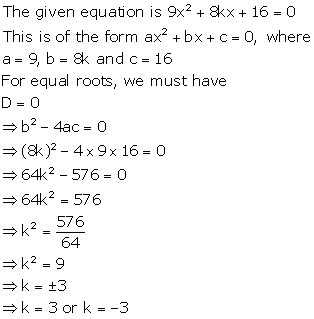
Solution 19(i)
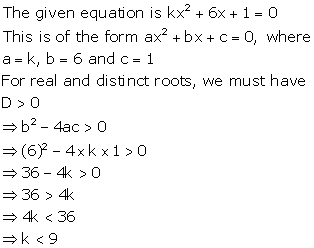
Solution 19(ii)
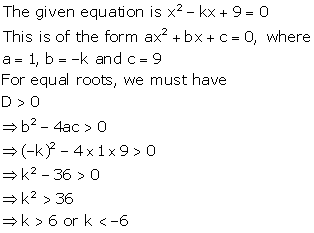
Solution 19(iii)
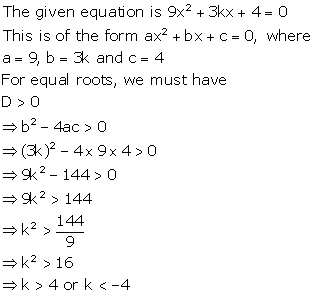
Solution 19(iv)
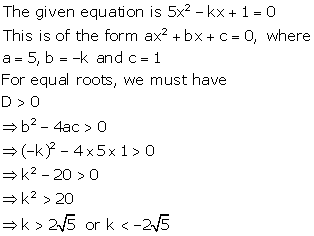
Solution 20
Solution 21
The given equation is 
This is of the form 
, where
For equal roots, Discriminant, D = 0
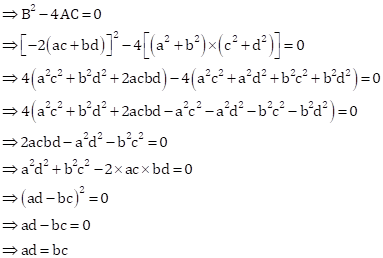
Solution 22
The given equation is 
This is of the form , where
Now, Discriminant
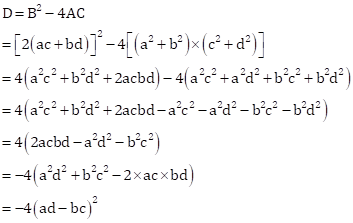
Now,
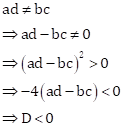
Hence, the given equation has no real roots.
Solution 23
Solution 24
Since 
is
a root of the quadratic equation 
, it must satisfy the equation.
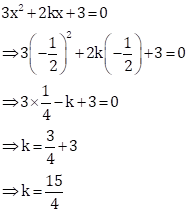
Solution 25
Since 
is a root of the quadratic equation 
, it must satisfy the equation.
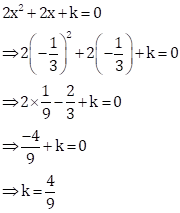
Solution 26
Given quadratic equation is 
.
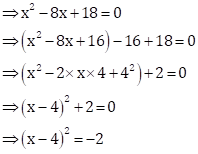
But, square of a number cannot be negative.
Hence, the given equation has no solution.
Solution 27
The given equation is 
This is of the form 
, where
For no real roots,
Discriminant, D <0
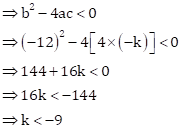
Solution 28
The given equation is 
This is of the form , where
Let the roots of the equation be 
Then,
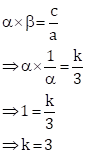
Solution 30
The given equation is 
This is of the form , where
For real and equal roots, we must have
Discriminant, D = 0
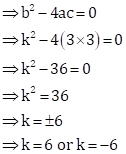
Solution 31
The given equation is 
This is of the form 
, where
For real and equal roots, we must have
Discriminant, D = 0
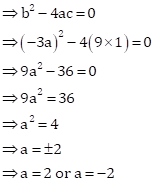
Solution 32
The given equation is 
This is of the form 
, where
For real and equal roots, we must have
Discriminant, D = 0
Solution 29
The given equation is 5x2 + 13x + k = 0
This is of the form ax2 + bx + c = 0, where a = 5, b = 13 and c = k
Let the roots of the equation be α and β.
Then,
α × β = c/a
α × 1/α = k/5
1 = k/5
k = 5
Quadratic Equations Exercise Ex. 4D
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Let the required natural number be x and x - 3.
Then,
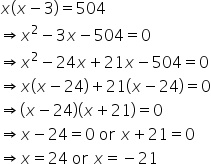
But, x is a natural number.
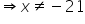
Hence,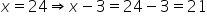 
Therefore, the required numbers are 24 and 21.
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
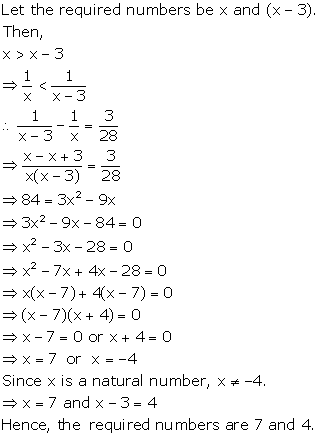
Solution 15
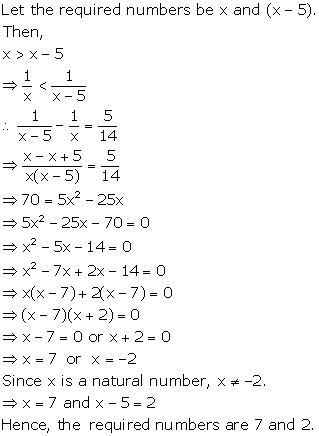
Solution 16
Solution 17
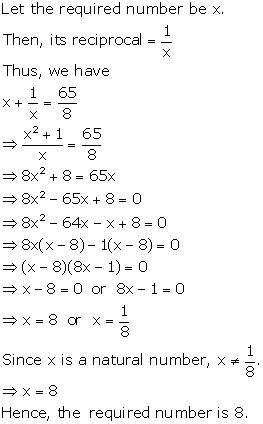
Solution 18
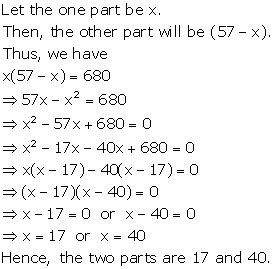
Solution 19
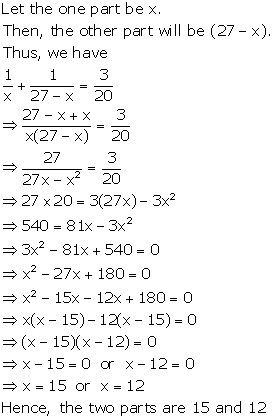
Solution 20
Let the smaller part and larger part be x, 16 - x
Then,
-42 is not a positive part.
Hence, the larger part is 10 and the smaller part is 6.
Solution 21
Let the required natural number be x and y.
Then
Therefore, the required natural numbers are 30 and 10 respectively.
Solution 22
Let x, y be the two natural numbers and x > y
------(1)
Also, square of smaller number = 4 larger number
---------(2)
Putting value of 
from
(1), we get
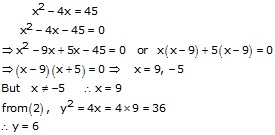
Thus, the two required numbers are 9 and 6.
Solution 23
Let the three consecutive numbers be x, x + 1, x + 2
Sum of square of first and product of the other two
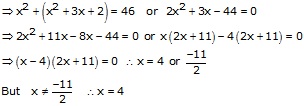
Required
numbers are 4, 5 and 6.
Solution 24
Let the tens digit be x and units digit be y
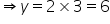
Hence, the tens digit is 3 and units digit is 6.
Hence, the required number is 36.
Solution 25
Let the tens and units digits of the required number be x and y respectively.
Then,
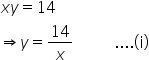
Now, the number is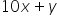 
.
So,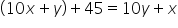 
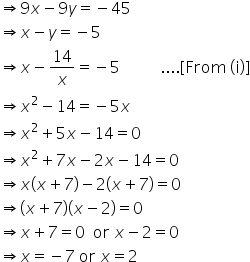
But, digit cannot be negative.
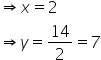
Hence, the required number is 27.
Solution 26
Let the numerator and denominator be x, x + 3
Then,
Hence, numerator and denominator are 2 and 5 respectively and fraction
is 
Solution 27
Solution 28
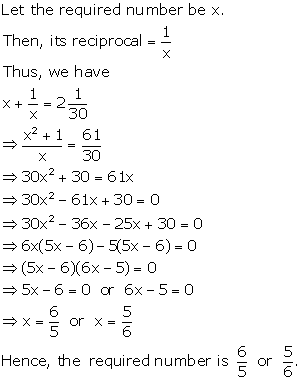
Solution 29
Let there be x rows and number of students in each row be x.
Then, total number of students = 
Hence, total number of students
Therefore, total number of students is 600.
Solution 30
Let the number of students be x.
Then,
Hence, the number of students is 50.
Solution 31
Let the marks obtained by Kamal in Mathematics and English be x and y respectively.
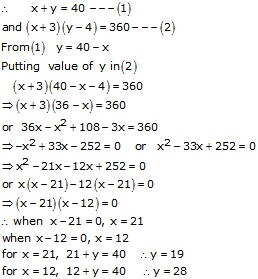
Therefore, the marks obtained by Kamal in Mathematics and English respectively are (21,19) or (12,28).
Solution 32
Solution 33
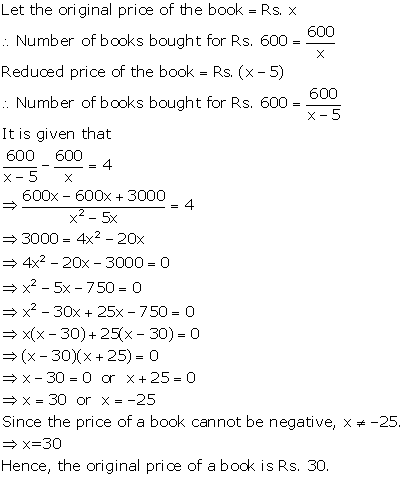
Solution 34
Solution 35
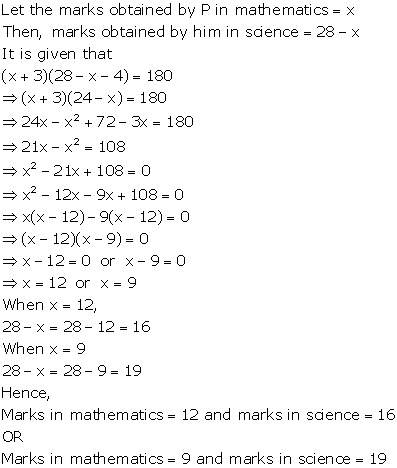
Solution 36
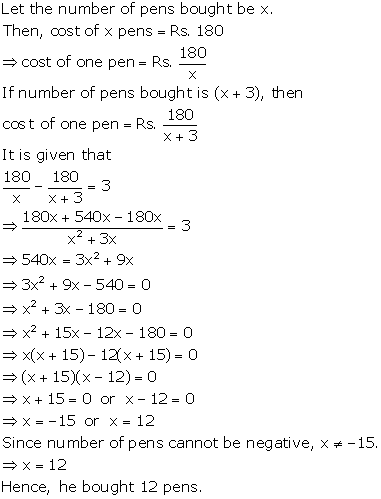
Solution 37
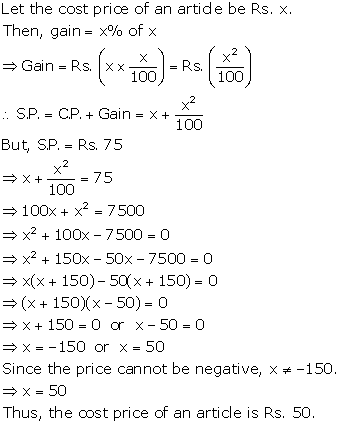
Solution 38(i)
Let the age of son be x years and that of man be y years.
1 year ago,
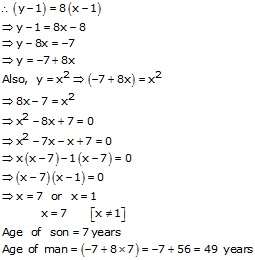
Solution 38(ii)
Let the ages of son and father be x years and y years respectively.
Then, 
Now, sum of the squares of their ages = 1325
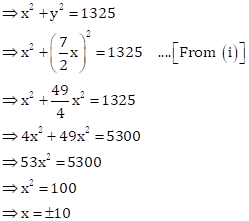
But, age cannot be negative.
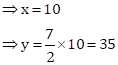
Therefore, the age of father is 35 years and that of son is 10 years.
Solution 39
Solution 40
Solution 41
Let the present age of Tanvi be x years.
Then,
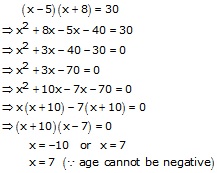
Hence, the present age of Tanvi is 7 years.
Solution 42
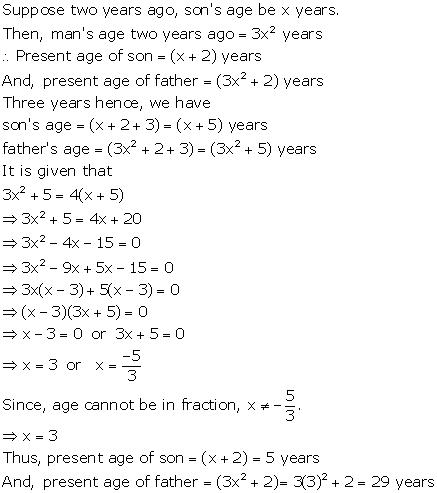
Solution 43
Solution 44
Solution 45
Solution 46
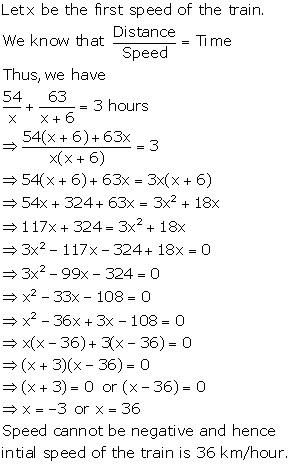
Solution 47
Solution 48
Let the original speed of the train be 
km/hr.
Then, increased speed = (x+5)km/hr
Time taken at original speed = 
hours
Time taken at increased speed = 
hours
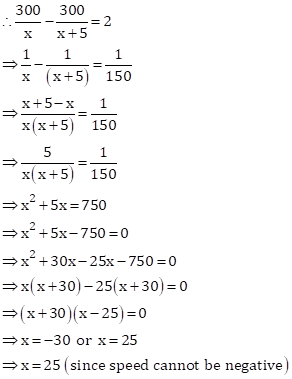
Hence, the original speed of the train is 25 km/hr.
Solution 49
Solution 50
Let the speed of the Deccan Queen = x kmph
The, speed of other train = (x - 20)kmph
Then, time taken by Deccan Queen =
Time taken by other train = 
Difference of time taken by two trains is 
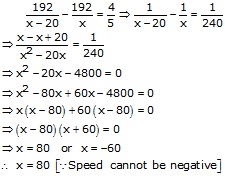
Hence, speed of Deccan Queen = 80km/h
Solution 51
Let the speed of stream be x km/h
Speed of boat in still stream = 18 km/h
Speed of boat up the stream = 18 - x km/h
Time
taken by boat to go up the stream 24 km = 
Time
taken by boat to go down the stream = 
Time taken by the boat to go up the stream is 1 hour more that the time taken down the stream
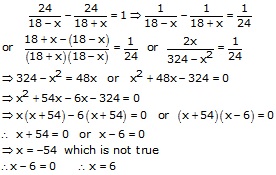
Speed
of the stream = 6 km/h
Solution 52
Let the speed of the stream be = x km/h
Speed of boat in still water = 15 km/hr
Speed of boat upstream = (15-x) km/hr
∴ Time taken by the boat to go
30 km upstream 
hours
Speed of boat downstream = 
km/hr
∴ Time taken by the boat to go
30 km downstream 
Total time taken by the boat 
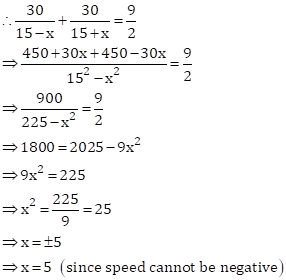
Hence, the speed of the stream is 5 km/hr.
Solution 53
Let the speed of the stream be = x km/h
Speed of boat in still waters = 9 km/h
Speed of boat down stream = 9 + x
time
taken by boat to go 15 km downstream = 
Speed of boat upstream = 9 - x
time
taken by boat to go 15 km of stream = 
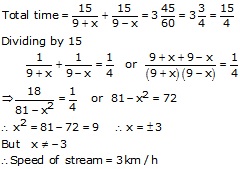
Solution 54
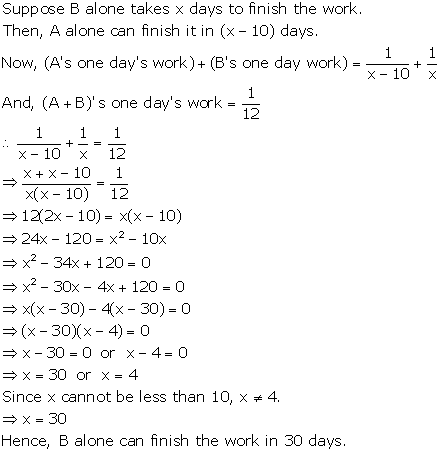
Solution 55
Let one tap takes x minutes to fill the tank.
Then, the other tap will take (x + 3) hours to fill tank.
Total time taken to fill the tank by two taps =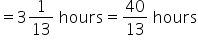 
Part filled by one tap in 1 hour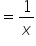 
Part filled by other tap in 1 hour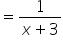 
Part filled by both the taps in 1 hour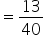 
Therefore, one tap takes 5 hours to fill the tank and other tap takes (5 + 3) 8 hours to fill the tank.
Solution 56
Solution 57
Solution 58
Let the breadth of a rectangle = x cm
Then, length of the rectangle = 2x cm
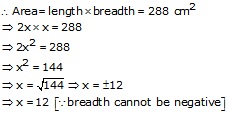
Thus, breadth of rectangle = 12 cm
And length of rectangle = (2 x 12) = 24 cm
Solution 59
Let the breadth of a rectangle = x meter
Then, length of rectangle = 3x meter
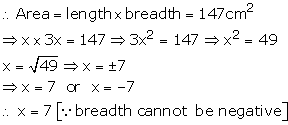
Thus, breadth of rectangle = 7 m
And length of rectangle = (3 x 7)m = 21 m
Solution 60
Let the breadth of hall = x meters
Then, length of the hall = (x + 3) meters
Area
= length breadth = 
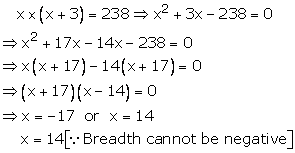
Thus, the breadth of hall is 14 m
And length of the hall is (14 + 3) = 17 m
Solution 61
We know that,
Perimeter of a rectangle = 2(length + breadth)
⇒ 60 = 2(length + breadth)
⇒ length + breadth = 30 m
Let the length of a rectangular plot be x m.
Then, breadth of a rectangular plot = (30-x) m
Now,
Area of a rectangular plot = 200 sq. m
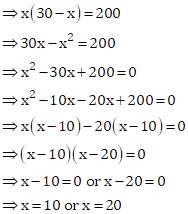
Hence, the length and breadth of a rectangular plot are 20 m and 10 m respectively.
Solution 62
Let the width of the path be x m.
Length of the field including the
path = 
m
Breadth of the field including the path = 
m
Area of the field including the path = 
Area of the field excluding the path = 
Therefore, area of the path 
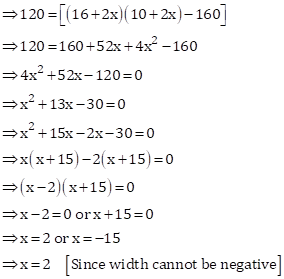
Hence, the width of the path is 2 m.
Solution 63
Let x and y be the lengths of the two square fields.
4x - 4y = 64
x
- y = 16------(2)
From (2),
x = y + 16,
Putting value of x in (1)
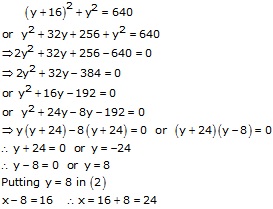
Sides
of two squares are 24 m and 8 m respectively.
Solution 64
Let the side of square be x cm
Then, length of the rectangle = 3x cm
Breadth of the rectangle = (x - 4) cm
Area
of rectangle = Area of square x
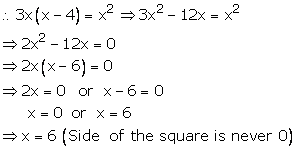
Thus, side of the square = 6 cm
And length of the rectangle = (3 6) = 18 cm
Then, breadth of the rectangle = (6 - 4) cm = 2 cm
Solution 65
Let the length = x meter
Area = length breadth = 
If ength of the rectangle = 15 m
Also, if length of rectangle = 24 m
Solution 66
Let the altitude of triangle be x cm.
Then, base of triangle is (x + 10) cm.
Hence, altitude of triangle is 30 cm and base of triangle 40 cm.
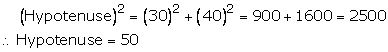
Therefore, the dimensions of the triangle are 30 cm, 40 cm and 50 cm.
Solution 67
Let the altitude of triangle be x meter.
Hence, base = 3x meter
Hence, altitude of triangle is 8 m.
And base of triangle = 3x = (3 x 8) cm = 24 m
Solution 68
Let the base of triangle be x meter
Then, altitude of triangle = (x + 7) meter
Thus, the base of the triangle = 15 m
And the altitude of triangle = (15 + 7) = 22 m
Solution 69
Let the other sides of triangle be x and (x - 4) meters.
By Pythagoras theorem, we have
Thus, height of triangle = 16 m
And the base of the triangle = (16 - 4) = 12 m
Solution 70
Let the base of the triangle be x
Then, hypotenuse = (x + 2) cm
Thus, base of triangle = 15 cm
Then, hypotenuse of triangle = (15 +2 )= 17 cm
And altitude of triangle = 
Solution 71
Let the shorter side of triangle be x meter
Then, its hypotenuse = (2x - 1)meter
And let the altitude = (x + 1) meter
Solution 72
Let the speed of the fast train be x kmph.
Then, the speed of the slow train = 
kmph
Time taken by fast train to cover 200 km 
hours
Time taken by slow train to cover 200 km 
hours
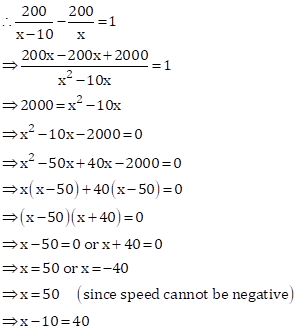
Hence, the speeds of two trains are 50 kmph and 40 kmph respectively.
Solution 73
Let the speed of the stream be = x kmph
Speed of boat in still water = 18 kmph
Speed of boat upstream = (18-x) km/hr
∴ Time taken by the boat to go
36 km upstream 
hours
Speed of boat downstream = (18+x) km/hr
∴ Time taken by boat to go 36
km downstream 
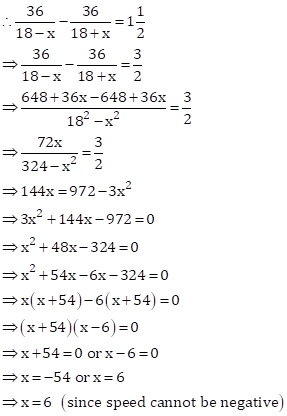
Hence, the speed of the stream is 6 kmph.
Solution 74
Let the time taken by the second pipe to fill the tank = x hours
Then, the time taken by the first pipe to fill the tank = (x-10) hours
Total time taken by both pipes to fill the tank = 12 hours
Part filled by second pipe in 1 hour = 
Part filled by first pipe in 1 hour = 
Part filled by both pipes together in 1 hour =
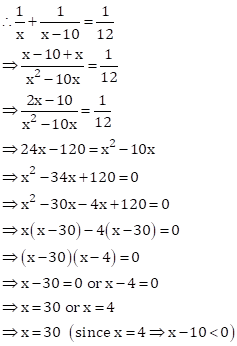
Hence, the time taken by second pipe to fill the tank is 30 hours.
Solution 75
Let the time taken by smaller tap to fill the tank = x hours
Then, the time taken by larger tap to fill the tank = (x-2) hours
Total time taken by both pipes to fill the tank = 
Part filled by smaller tap in 1 hour = 
Part filled by larger tap in 1 hour = 
Part filled by both taps together in 1 hour =
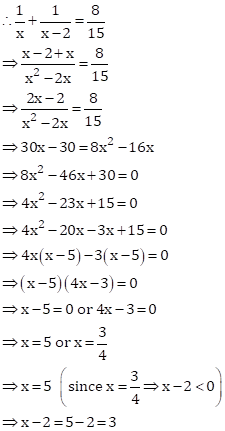
Hence, the smaller tap will take 3 hours and the larger tap will take 5 hours to fill the tank separately.
Solution 76
Let the original speed of the aircraft be x kmph.
Then, time taken to cover 600 km = 
hours
Reduced speed = (x-200) kmph
Time taken to cover 600 km at this speed = 
hours
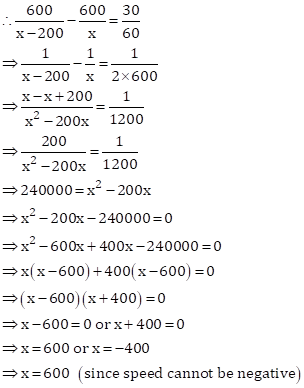
Therefore, original speed of the aircraft = 600 kmph
And, original duration of the flight
Solution 77
Let the time taken by larger pipe and the smaller pipe to
fill the pool be 
hours and 
hours respectively.
Total time taken by both pipes to fill the tank = 12 hours
In 4 hours, part of pool filled by the larger pipe
In 9 hours, part of pool filled by the smaller pipe
Multiplying (i) by 4,
Subtracting (iii) from (ii),
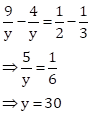
Substituting y=30 in (i),
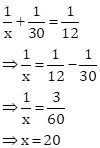
Hence, the larger pipe will take 20 hours and the smaller pipe will take 30 hours to fill the pool separately.
Quadratic Equations Exercise Test Yourself
Solution 1
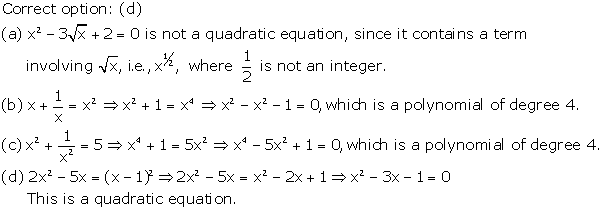
Solution 2
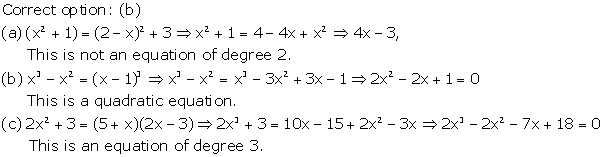
Solution 3
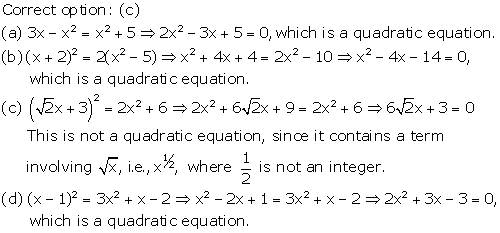
Solution 4
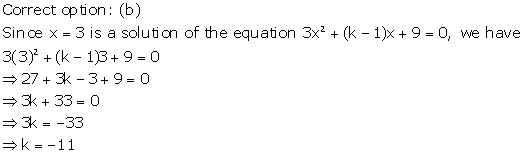
Solution 5
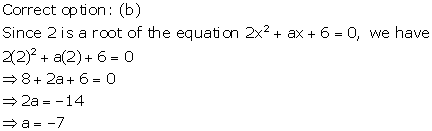
Solution 6
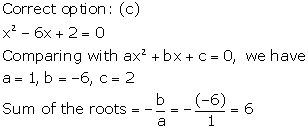
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
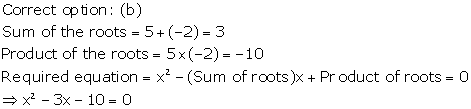
Solution 13
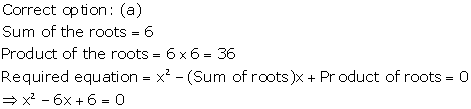
Solution 14
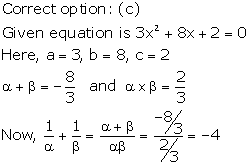
Solution 15
Solution 16
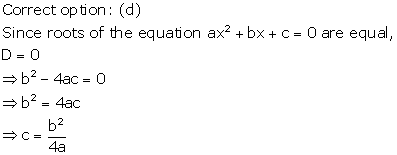
Solution 17
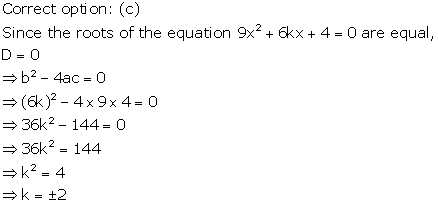
Solution 18
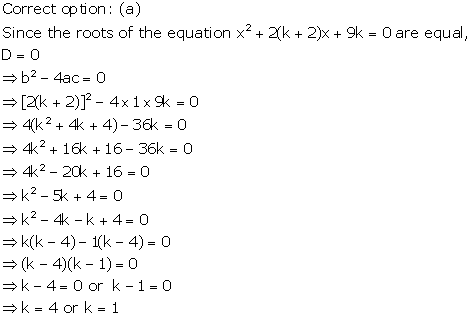
Solution 19
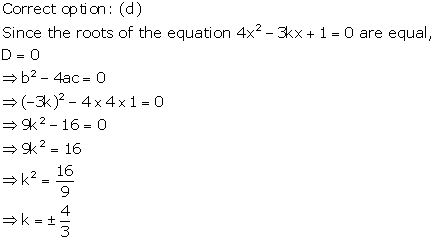
Solution 20
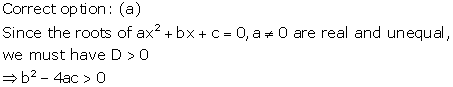
Solution 21
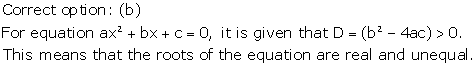
Solution 22
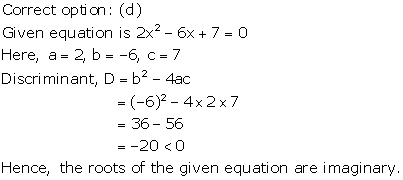
Solution 23
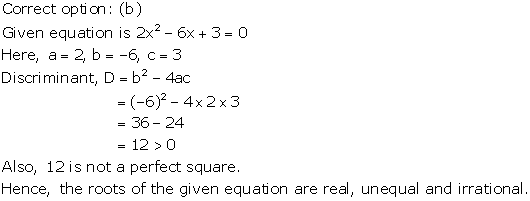
Solution 24
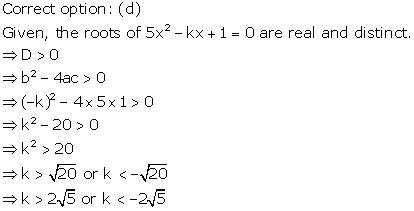
Solution 25
Solution 26
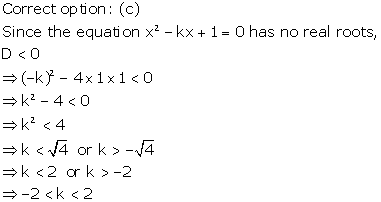
Solution 27
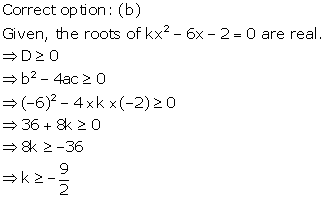
Solution 28
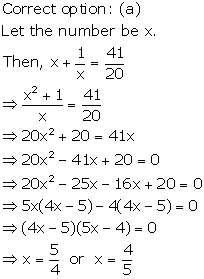
Solution 29
Solution 30
Solution 31
Correct option: (b)
Given equation is 
.
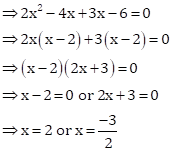
Solution 32
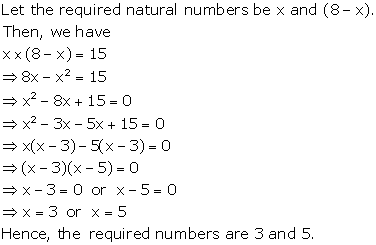
Solution 33
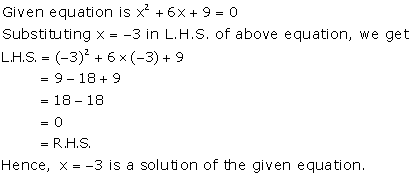
Solution 34
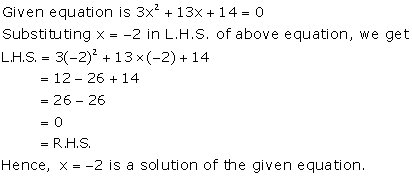
Solution 35
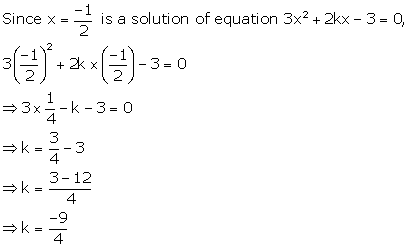
Solution 36
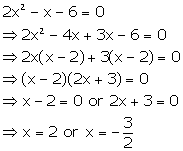
Solution 37
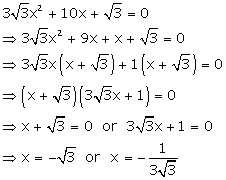
Solution 38
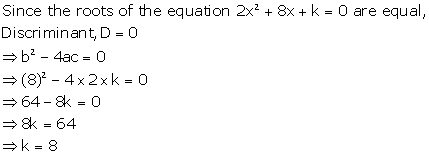
Solution 39
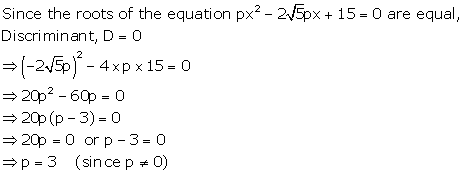
Solution 40
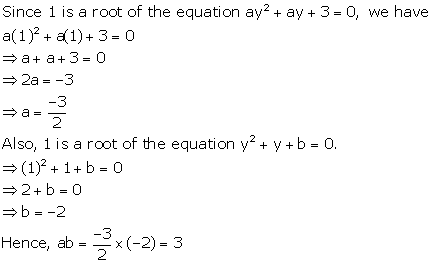
Solution 41
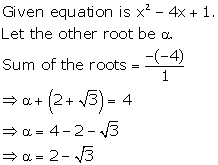
Solution 42
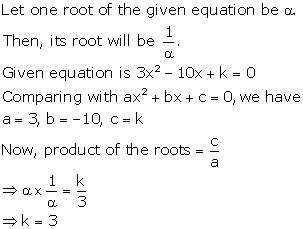
Solution 43
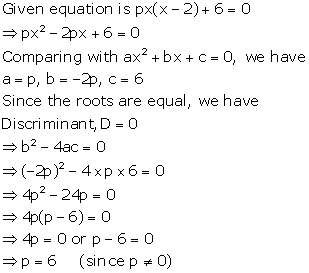
Solution 44
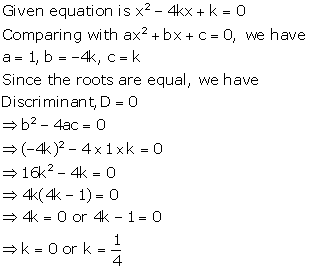
Solution 45
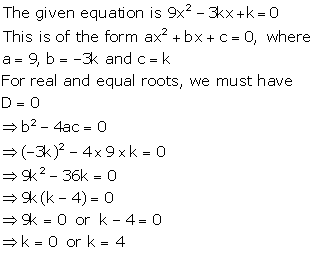
Solution 46
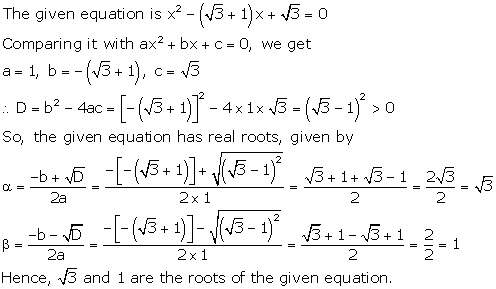
Solution 47
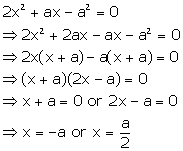
Solution 48
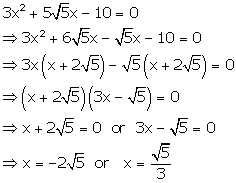
Solution 49
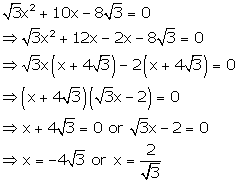
Solution 50
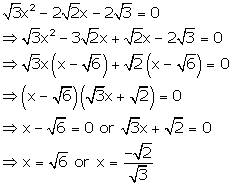
Solution 51
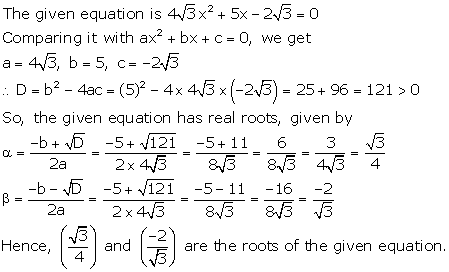
Solution 52
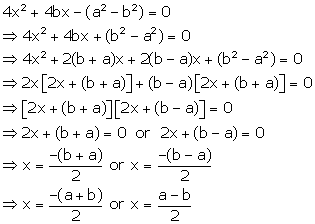
Solution 53
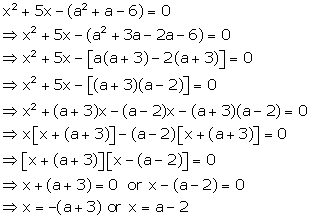
Solution 54
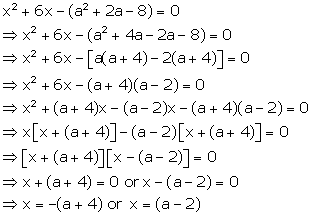
Solution 55
