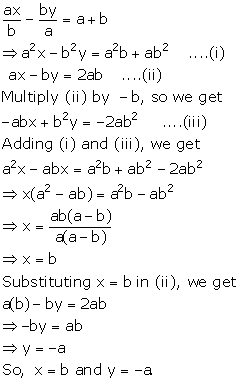Chapter 3 Linear Equations in Two Variables
Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution
Linear Equations in Two Variables Exercise Ex. 3A
Solution 1
Solution 2
Given equations are 
and 
.
On a graph paper, draw X-axis and Y-axis respectively.
Graph of 
:
Thus, we have the following table:
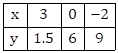
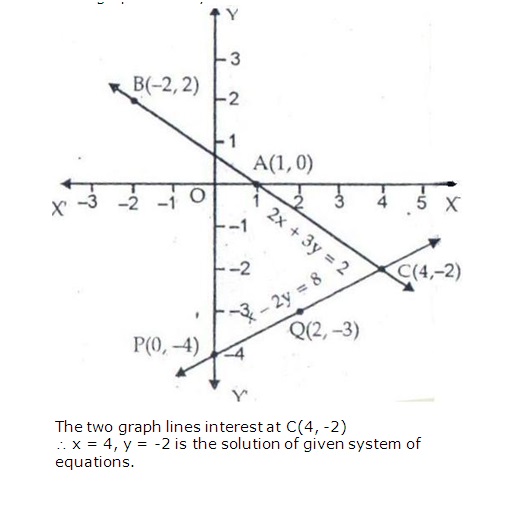
On the graph paper, plot the points A(3, 1.5), B(0, 6), C(-2, 9) and join them.
Graph of :
Thus, we have the following table:
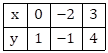
On the graph paper, plot the points P(0, 1), Q(-2, -1), R(3, 4) and join them.
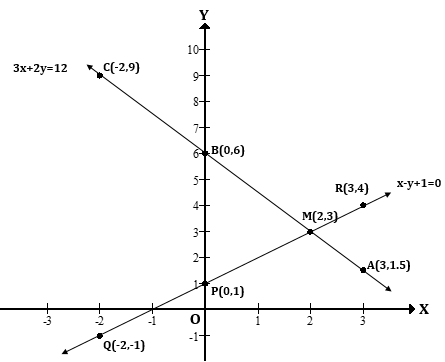
The two graphs intersect at point M (2,3).
Therefore, 
is the solution of the given equations.
Solution 3
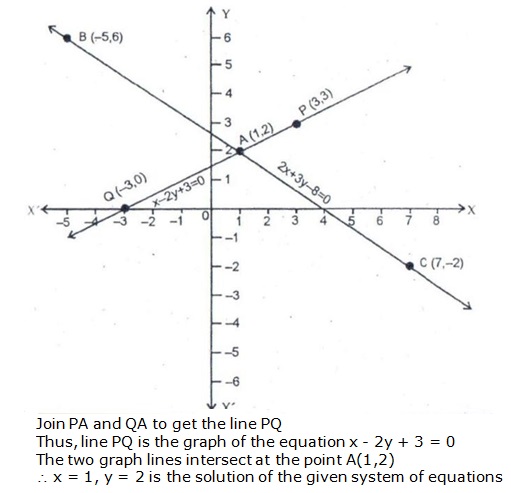
Solution 4
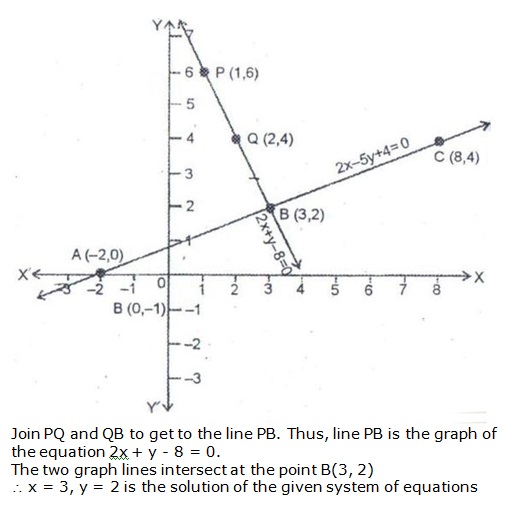
Solution 5
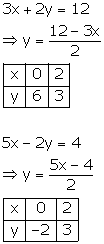
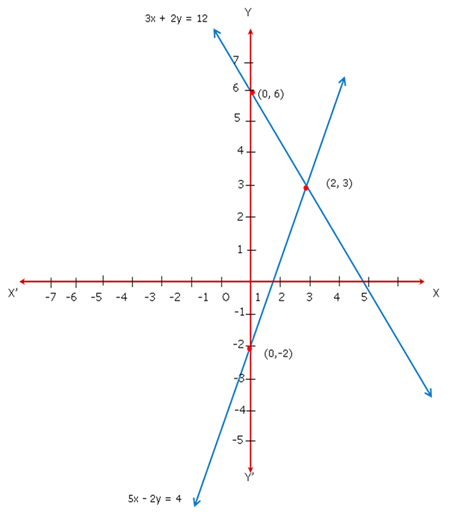
Since the two graphs intersect at (2, 3),
x = 2 and y = 3.
Solution 6
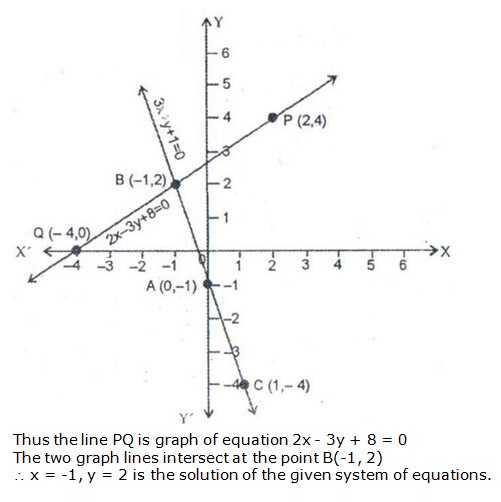
Solution 7
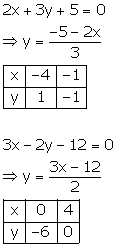
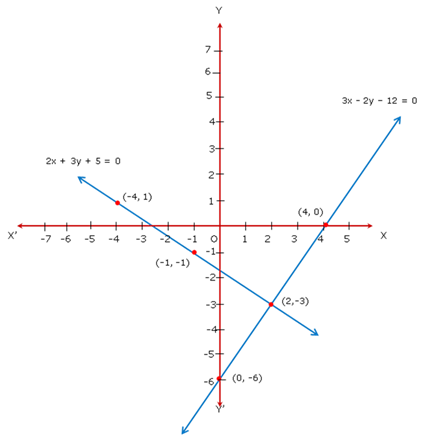
Since the two graphs intersect at (2, -3),
x = 2 and y = -3.
Solution 8
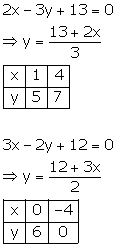
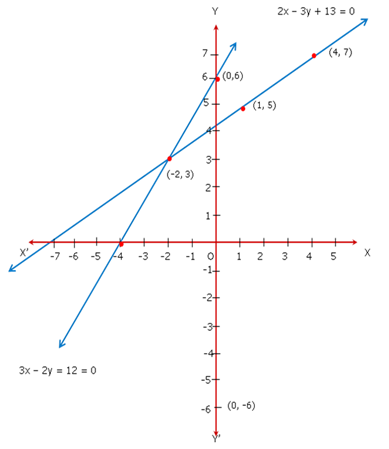
Since the two graphs intersect at (-2, 3),
x = -2 and y = 3.
Solution 9
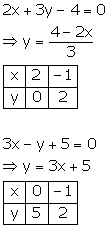
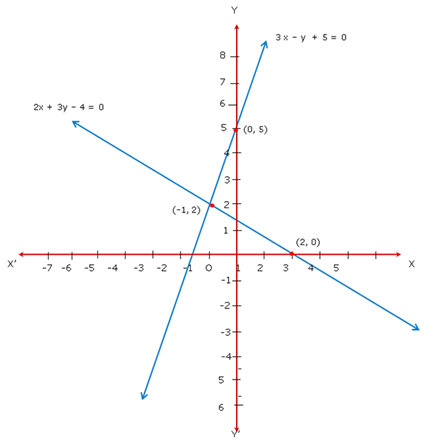
Since the two graphs intersect at (-1, 2),
x = -1 and y = 2.
Solution 10
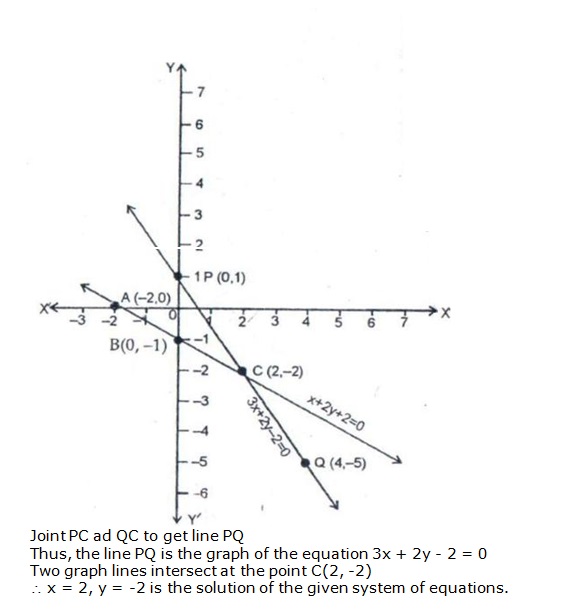
Solution 11
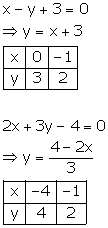
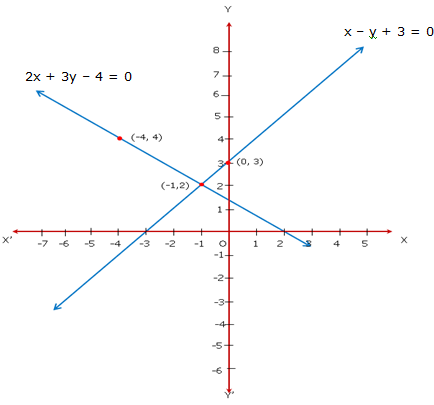
Solution 12
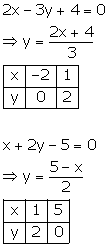
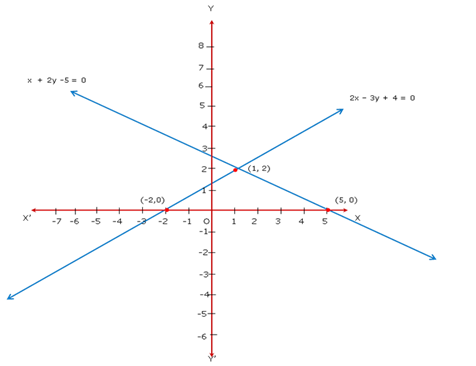
Since the two graphs intersect at (1, 2), x = 1, y = 2 is the solution of the given system of equations.
The vertices of the triangle formed by these lines and the X-axis are (1, 2), (-2, 0) and (5, 0).
So, height of the triangle = distance of (1, 2) from the X-axis = 2 units
And, base = 7 units
Therefore,
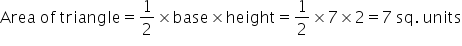
Solution 13
Solution 14
Solution 15
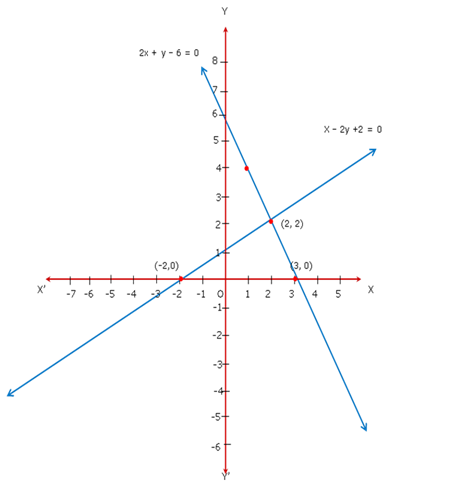
Solution 16
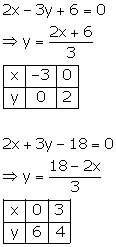
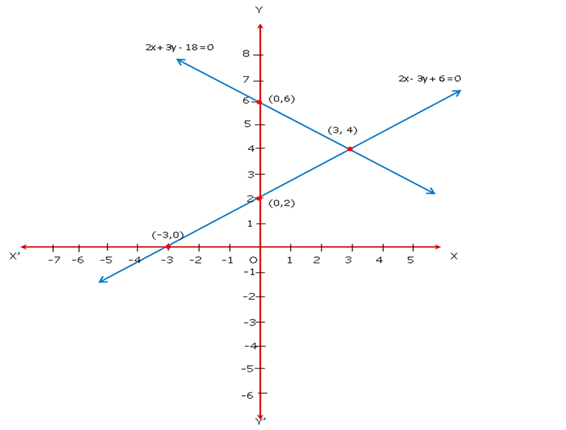
Solution 17
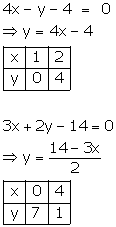
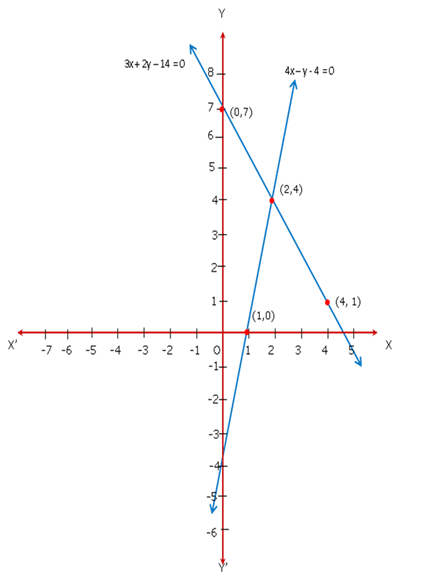
Solution 18
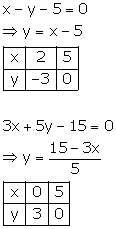
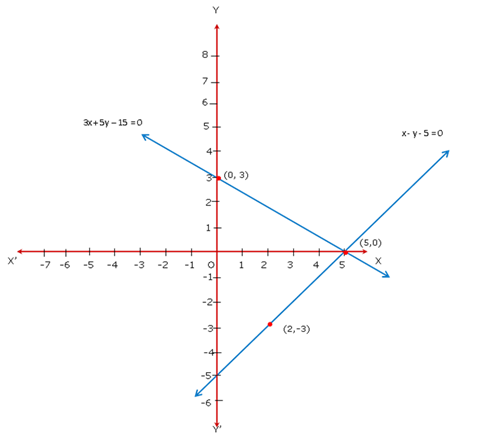
Solution 19
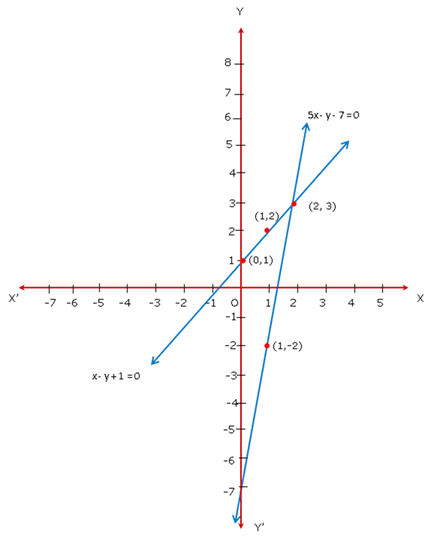
SInce the two lines intersect at A(3,2), x = 3, y = 2 is the solution of system of given equations.
Height of triangle ARS = 3 units
Base of triangle ARS = 7.2 units
Therefore,
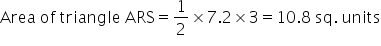
Solution 20
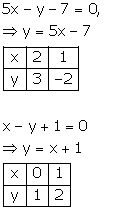
Solution 21
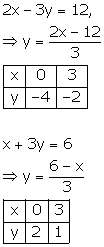
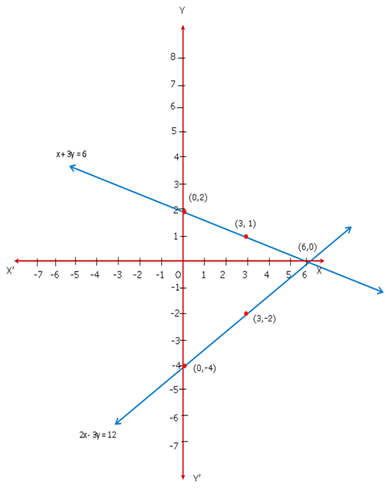
Solution 22
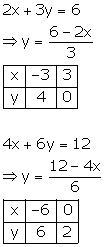
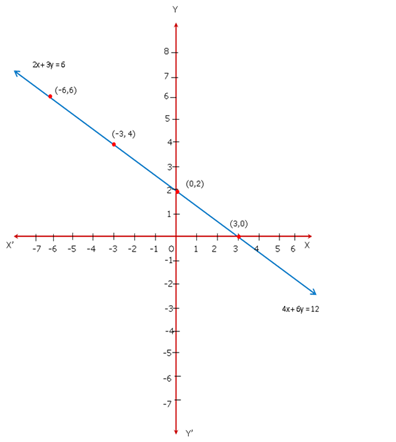
Since the graph of the system of equations is coincident lines, the system has infinitely many solutions.
Solution 23
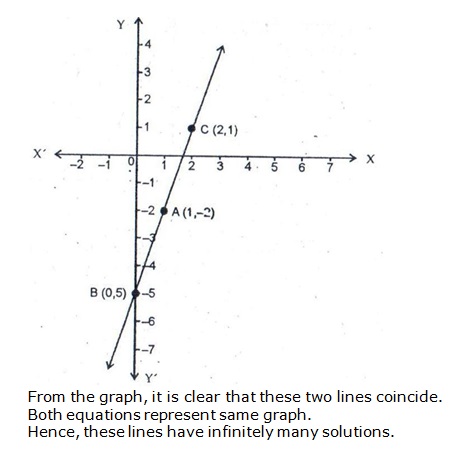
Solution 24
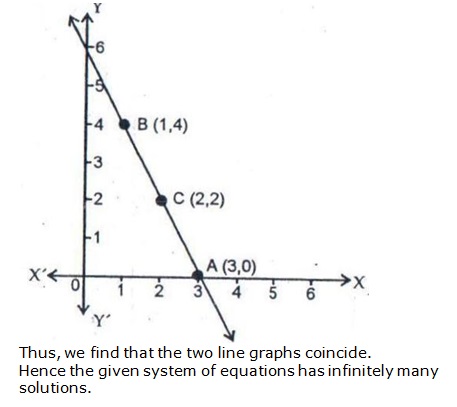
Solution 25
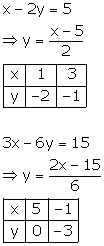
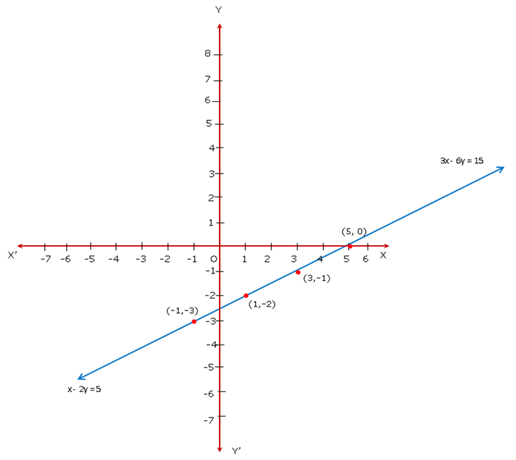
Since the graph of the system of equations is coincident lines, the system has infinitely many solutions.
Solution 26
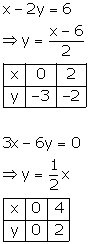
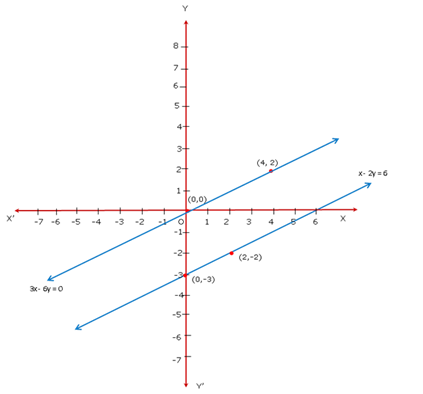
Since the graph of the system of equations is parallel lines, the system has no solution and hence is inconsistent.
Solution 27
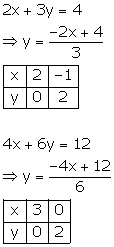
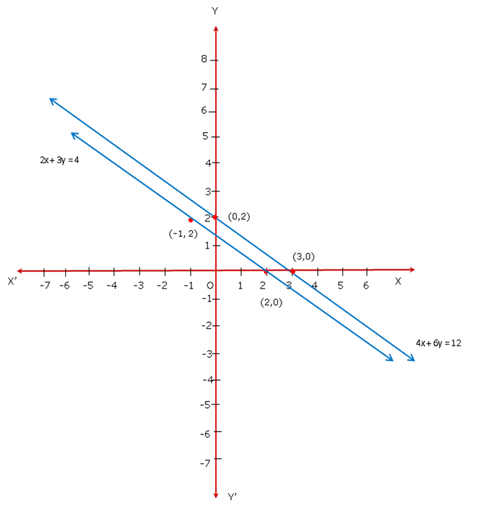
Since the graph of the system of equations is parallel lines, the system has no solution and hence is inconsistent.
Solution 28
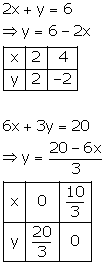
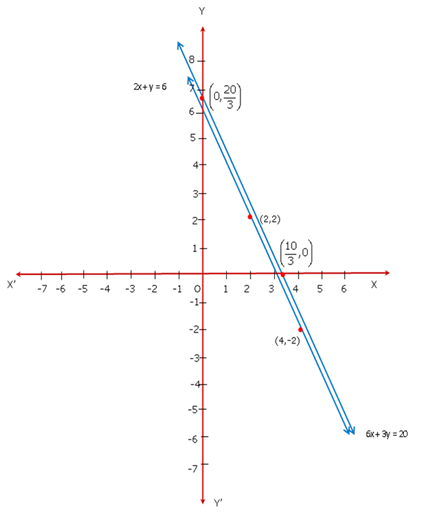
Since the graph of the system of equations is parallel lines, the system has no solution and hence is inconsistent.
Solution 29
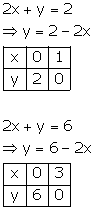
The coordinates of the vertices of the trapezium formed by these lines are (0,6), (3,0), (1,0) and (0,2).
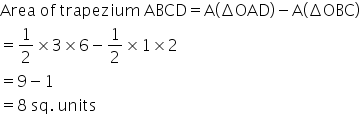
Linear Equations in Two Variables Exercise Ex. 3B
Solution 1
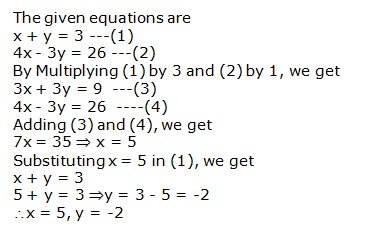
Solution 2
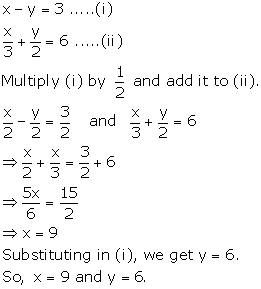
Solution 3
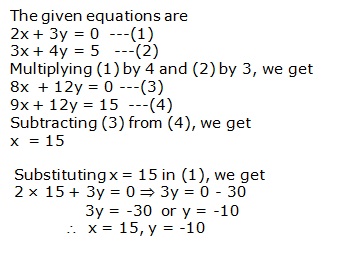
Solution 4
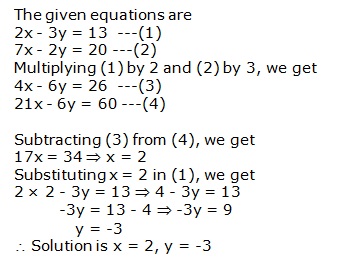
Solution 5
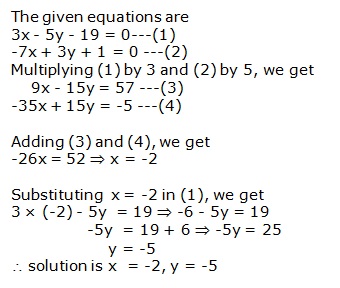
Solution 6
The given equations are
Multiplying equation (i) by 3, we get
Subtracting equation (ii) from equation (iii),
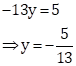
Substituting 
in equation (i),
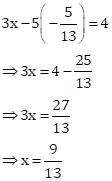
Therefore, solution is 
.
Solution 7
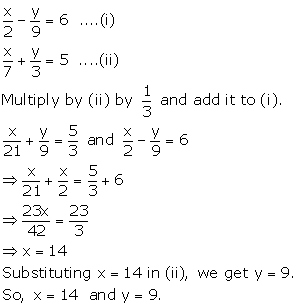
Solution 8
Solution 9
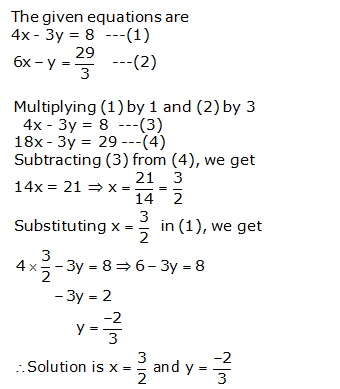
Solution 10
Solution 11
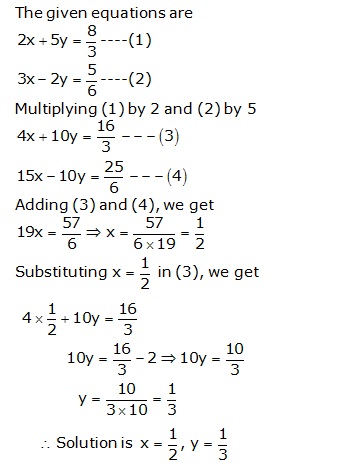
Solution 12
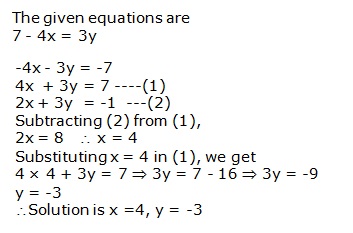
Solution 13
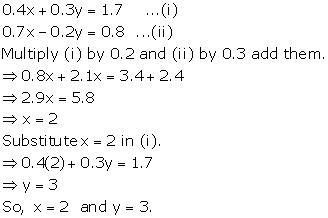
Solution 14
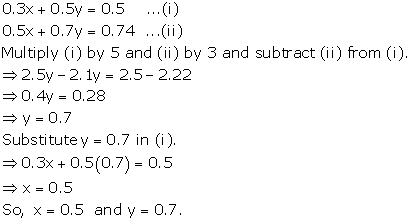
Solution 15
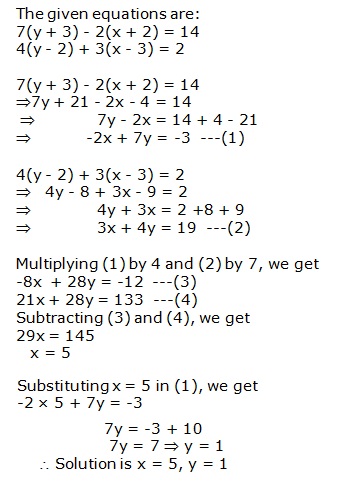
Solution 16
The given equations are:
6x + 5y = 7x + 3y + 1 = 2(x + 6y - 1)
Solution 17
Solution 18
Putting
the
given equations become
5u + 6y = 13---(1)
3u + 4y = 7 ----(2)
Multiplying (1) by 4 and (2) by 6, we get
20u + 24y = 52---(3)
18u + 24y = 42---(4)
Subtracting (4) from (3), we get
2u = 10 
u
= 5
Putting u = 5 in (1), we get
5 × 5 + 6y = 13
6y = 13 - 25
6y = -12
y = -2
Solution 19
The given
equations are 
and
Putting 
x + 6v = 6 ----(1)
3x - 8v = 5---(2)
Multiplying (1) by 4 and (2) by 3
4x + 24v = 24---(3)
9x - 24v = 15 ---(4)
Adding (3) and (4)
13x = 24 + 15 = 39
Puttingx = 3 in (1)
3 + 6v = 6
6v
= 6 - 3 = 3
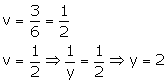
solution
is x = 3, y = 2
Solution 20
Putting 
in
the given equation
2x - 3v = 9 ---(1)
3x + 7v = 2 ---(2)
Multiplying (1) by7 and (2) by 3
14x - 21v = 63 ---(3)
9x + 21v = 6 ---(4)
Adding (3) and (4), we get
Putting x= 3 in (1), we get
2 × 3 - 3v = 9
-3v = 9 - 6
-3v= 3
v = -1
the
solution is x = 3, y = -1
Solution 21
The given equations are
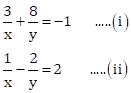
Putting 
in the given equations,
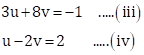
Multiplying equation (iv) by 4, we get
Adding equations (iii) and (v),
Putting 
in
equation (ii),
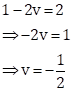
Now,
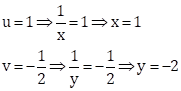
Therefore, solution is 
.
Solution 22
Putting
in
the equation
9u - 4v = 8 ---(1)
13u + 7v = 101---(2)
Multiplying (1) by 7 and (2) by 4, we get
63u - 28v = 56---(3)
52u + 28v = 404---(4)
Adding (3) and (4), we get
Putting u = 4 in (1), we get
9 × 4 - 4v = 8
36 - 4v = 8
-4v = 8 - 36
-4v = -28
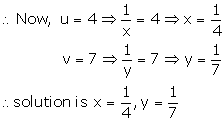
Solution 23
Putting
in
the given equation, we get
5u - 3v = 1 ---(1)
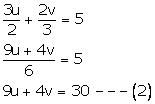
Multiplying (1) by 4 and (2) by 3, we get
20u - 12v = 4----(3)
27u + 12v = 90---(4)
Adding (3) and (4), we get
Putting u = 2 in (1), we get
(5 × 2) - 3v = 1
10 - 3v = 1
-3v = 1 - 10 
-3v
= -9
v = 3
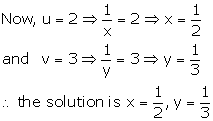
Solution 24
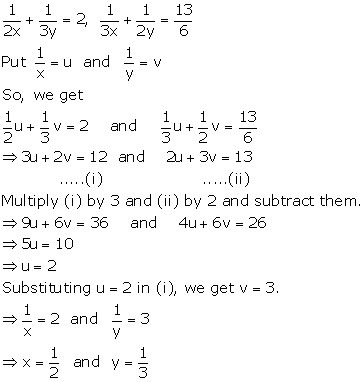
Solution 25
4x + 6y = 3xy
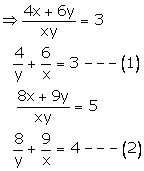
Putting 
in
(1) and (2), we get
4v + 6u = 3---(3)
8v + 9u = 5---(4)
Multiplying (3) by 9 and (4) by 6, we get
36v + 54u = 27 ---(5)
48v + 54u = 30 ---(6)
Subtracting (3) from (4), we get
12v = 3
Putting 
in
(3), we get
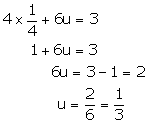
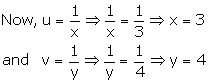
the
solution is x = 3, y = 4
Solution 26
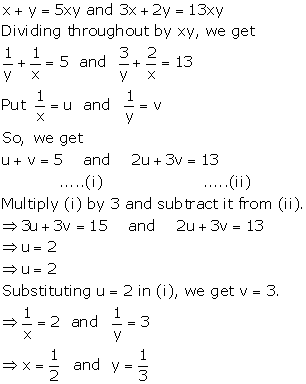
Solution 27
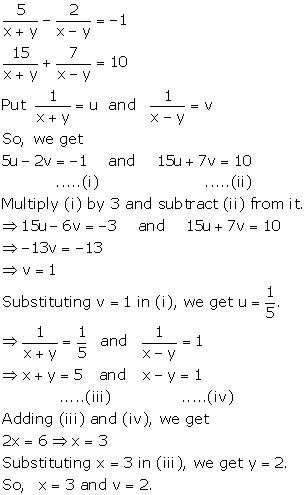
Solution 28
Putting
3u + 2v = 2----(1)
9u - 4v = 1----(2)
Multiplying (1) by 2 and (2) by 1. We get
6u + 4v = 4----(3)
9u - 4v = 1----(4)
Adding (3) and (4), we get
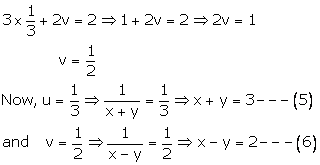
Adding (5) and (6), we get
Putting 
in
(5). We get
the
solution is 
Solution 29
The given equations are
Putting 
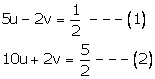
Adding (1) and (2)
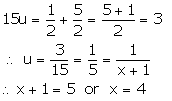
Putting value of u in (1)
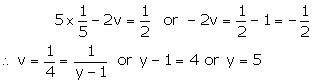
Hence the required solution isx = 4, y = 5
Solution 30
Putting
in
the equation, we get
44u + 30v = 10----(1)
55u + 40v = 13----(2)
Multiplying (1) by 4 and (2) by 3, we get
176u + 120v = 40---(3)
165u + 120v = 39---(4)
Subtracting (4) from (3), we get
Putting 
in
(1) we get
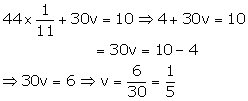
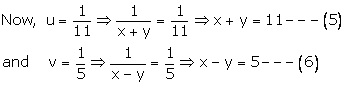
Adding (5) and (6), we get
Putting x = 8 in (5), we get
8 + y = 11 
y
= 11 - 8 = 3
the
solution is x = 8, y = 3
Solution 31
Substituting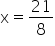 
in
(iii), we get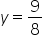 
Therefore, 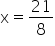and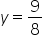
Solution 32
The given equations are
71x + 37y = 253---(1)
37x + 71y = 287---(2)
Adding (1) and (2)
108x + 108y = 540
108(x + y) = 540
----(3)
Subtracting (2) from (1)
34x - 34y = 253 - 287 = -34
34(x - y) = -34
---(4)
Adding (3) and (4)
2x = 5 - 1= 4
Subtracting (4) from (3)
2y = 5 + 1 = 6
solution
is x = 2, y = 3
Solution 33
217x + 131y = 913---(1)
131x + 217y = 827---(2)
Adding (1) and (2), we get
348x + 348y = 1740
348(x + y) = 1740
x + y = 5----(3)
Subtracting (2) from (1), we get
86x - 86y = 86
86(x
- y) = 86
x - y = 1---(4)
Adding (3) and (4), we get
2x = 6
x = 3
putting x = 3 in (3), we get
3 + y = 5
y = 5 - 3 = 2
solution
is x = 3, y = 2
Solution 34
The given equations are
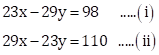
Adding equations (i) and (ii),
Subtracting equation (i) from (ii),
Adding equation (iii) and (iv),
Substituting 
in
equation (iv),
Therefore, solution is 
.
Solution 35
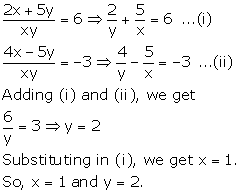
Solution 36
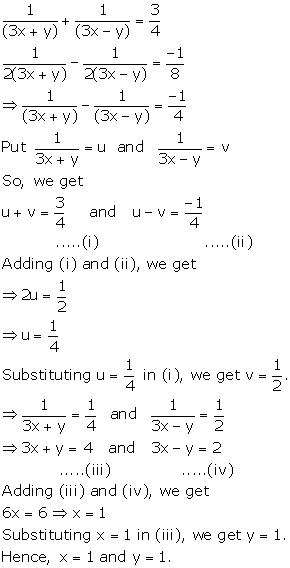
Solution 37
The given equations are
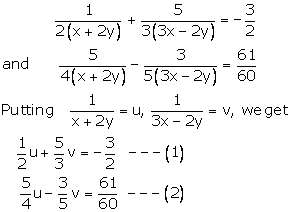
Multiplying (1) by 6 and (2) by 20, we get
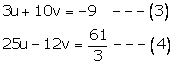
Multiplying (3) by 6 and (4) by 5, we get
18u + 60v = -54---(5)
125u - 60v = 
---(6)
Adding (5) and (6), we get
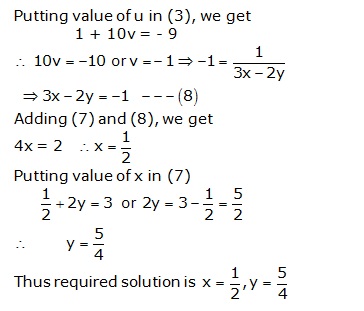
Solution 38
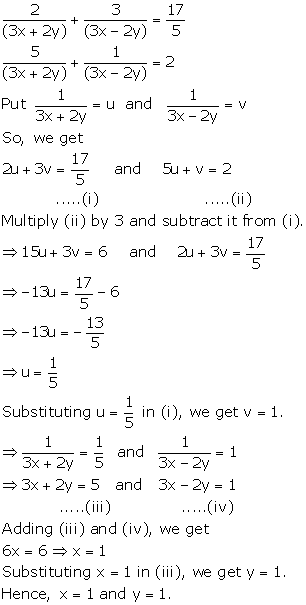
Solution 39
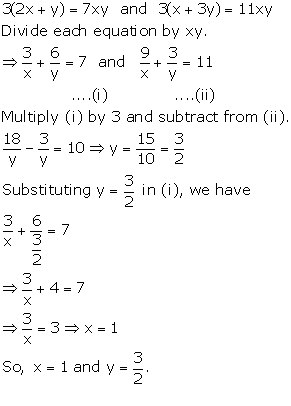
Solution 40
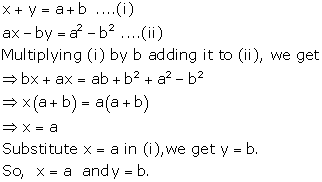
Solution 41
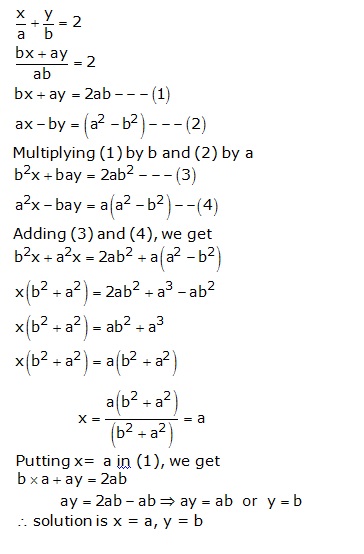
Solution 42
Given equations are as follows:
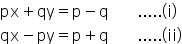
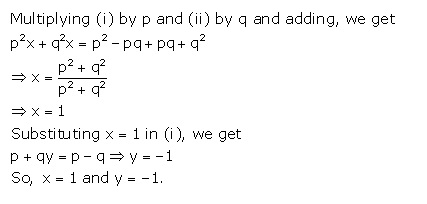
Solution 43
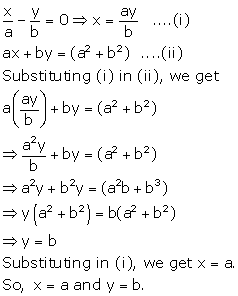
Solution 44
6(ax + by) = 3a + 2b
6ax + 6by = 3a + 2b ---(1)
6(bx - ay) = 3b - 2a
6bx - 6ay = 3b- 2a ---(2)
6ax + 6by = 3a + 2b ---(1)
6bx - 6ay = 3b - 2a ---(2)
Multiplying (1) by a and (2) by b
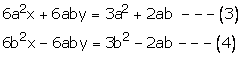
Adding (3) and (4), we get
Substituting 
in(1),
we get
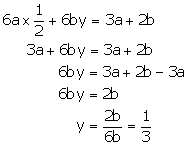
Hence, the solution is 
Solution 45
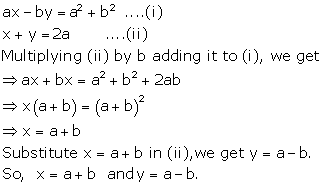
Solution 46
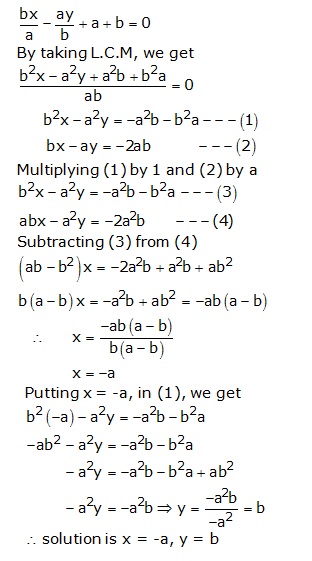
Solution 47
Taking L.C.M, we get
Multiplying (1) by 1 and (2) by 
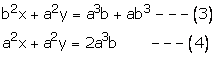
Subtracting (4) from (3), we get
Substituting x = ab in (3), we get
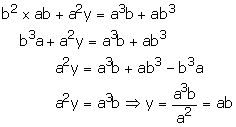
solution
is x = ab, y = ab
Solution 48
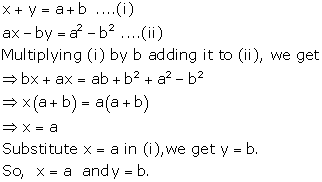
Solution 49
The given equations are
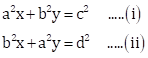
Multiplying equation (i) by
and
equation (ii) by 
,
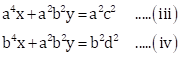
Subtracting equations (iv) from equation (iii),
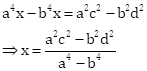
Multiplying equation (i) by
b2 and equation (ii) by 
,
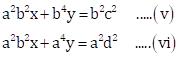
Subtracting equations (v) from equation (vi),
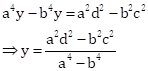
Therefore, solution is 
.
Solution 50
Solution 51
The given equations are
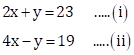
Adding equations (i) and (ii),
Substituting x=7 in equation (i),
Therefore,
And,
Linear Equations in Two Variables Exercise Ex. 3C
Solution 1
x + 2y + 1 = 0 ---(1)
2x - 3y - 12 = 0 ---(2)
By cross multiplication, we have
Hence, x = 3 and y = -2 is the solution
Solution 2
3x - 2y + 3 = 0
4x + 3y - 47 = 0
By cross multiplication we have
the
solution is x = 5, y = 9
Solution 3
6x - 5y - 16 = 0
7x - 13y + 10 = 0
By cross multiplication we have
the
solution is x = 6, y = 4
Solution 4
3x + 2y + 25 = 0
2x + y + 10 = 0
By cross multiplication, we have
the
solution is x = 5,y = -20
Solution 5
2x + 5y - 1 = 0 ---(1)
2x + 3y - 3 = 0---(2)
By cross multiplication we have
the
solution is x = 3, y = -1
Solution 6
2x + y - 35 = 0
3x + 4y - 65 = 0
By cross multiplication, we have
Solution 7
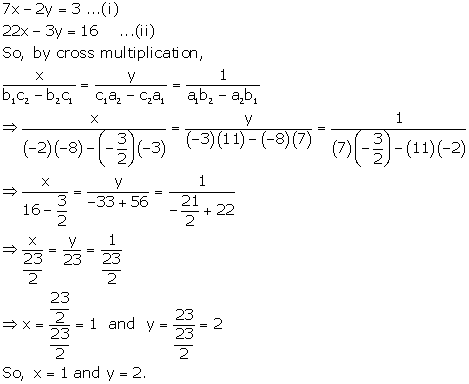
Solution 8
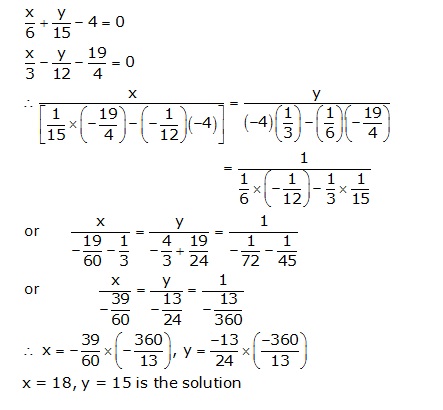
Solution 9
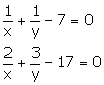
Taking 
u + v - 7 = 0
2u + 3v - 17 = 0
By cross multiplication, we have
the
solution is 
Solution 10
Let
in
the equation
5u - 2v + 1 = 0
15u + 7v - 10 = 0
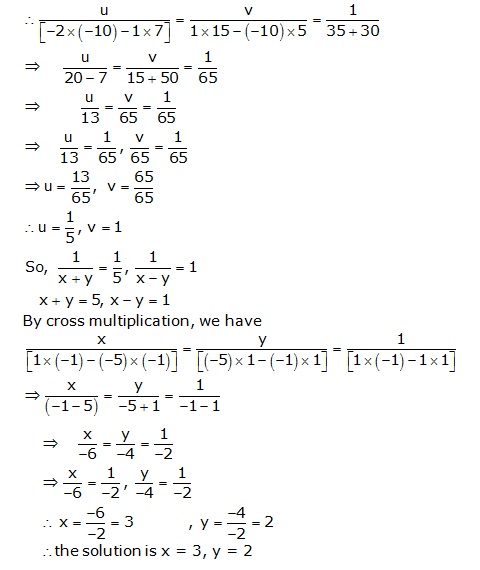
Solution 11
Solution 12
2ax + 3by - (a + 2b) = 0
3ax+ 2by - (2a + b) = 0
By cross multiplication, we have
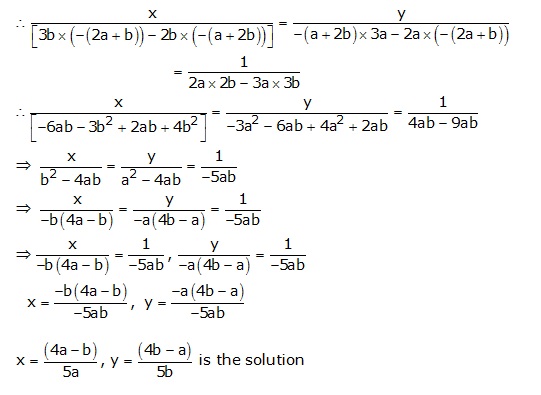
Solution 13
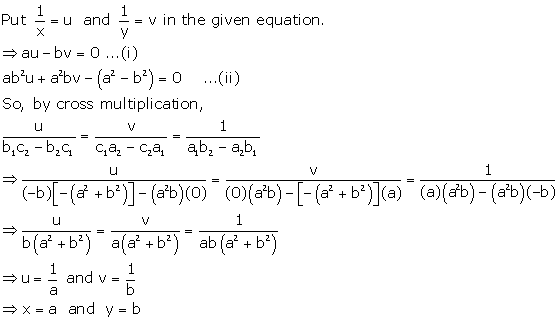
Linear Equations in Two Variables Exercise Ex. 3D
Solution 1
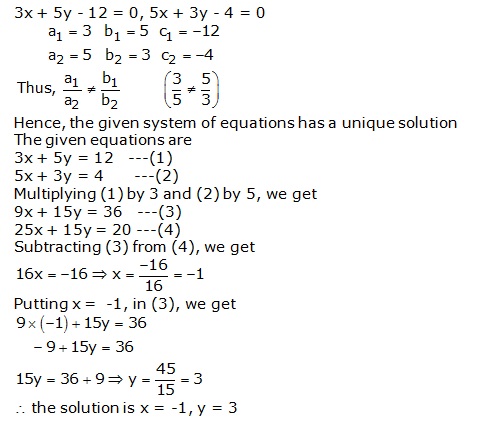
Solution 2
Solution 3
Solution 4
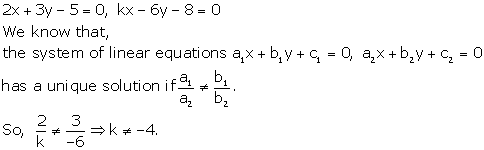
Solution 5
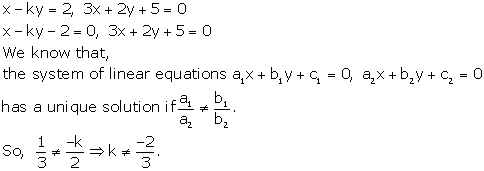
Solution 6
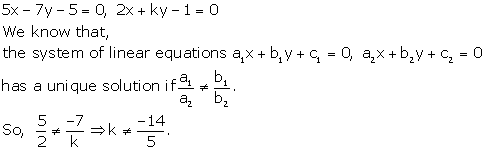
Solution 7
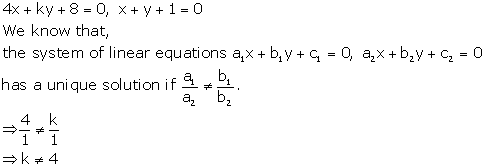
Solution 8
4x - 5y - k = 0, 2x - 3y - 12 = 0
These equations are of the form
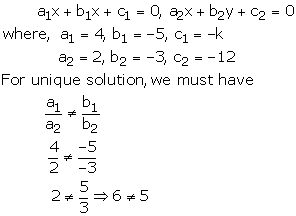
Thus, for all real value of k the given system of equations will have a unique solution
Solution 9
kx + 3y - (k - 3) = 0
12x + ky - k = 0
These equations are of the form
Thus, for all real value of k other than 
,
the given system of equations will have a unique solution
Solution 10
2x - 3y - 5 = 0, 6x - 9y - 15 = 0
These equations are of the form
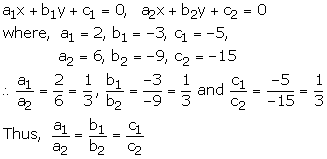
Hence the given system of equations has infinitely many solutions
Solution 11
Solution 12
kx + 2y - 5 = 0
3x - 4y - 10 = 0
These equations are of the form
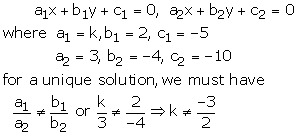
This happens when 
Thus, for all real value of k other that 
,
the given system equations will have a unique solution
(ii) For no solution we must have 
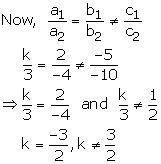
Hence, the given system of equations has no solution if 
Solution 13
x + 2y - 5= 0
3x + ky + 15 = 0
These equations are of the form of
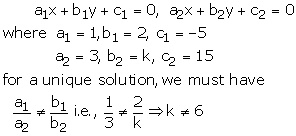
Thus for all real value of k other than 6, the given system ofequation will have unique solution
(ii) For no solution we must have
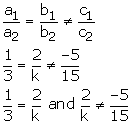
k
= 6
Hence the given system will have no solution when k = 6.
Solution 14
x + 2y - 3 = 0, 5x + ky + 7 = 0
These equations are of the form
(i)For a unique solution we must have
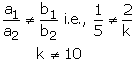
Thus, for all real value of k other than 10
The given system of equation will have a unique solution.
(ii)For no solution we must have
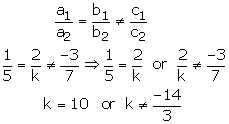
Hence the given system of equations has no solution if 
For infinite number of solutions we must have
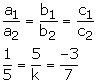
This is never possible since 
There is no value of k for which system of equations has infinitely many solutions
Solution 15
2x + 3y - 7 = 0
(k - 1)x + (k + 2)y - 3k = 0
These are of the form
This hold only when
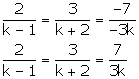
Now the following cases arises
Case : I
Case: II
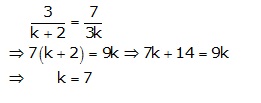
Case III
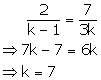
For k = 7, there are infinitely many solutions of the given system of equations
Solution 16
2x + (k - 2)y - k = 0
6x + (2k - 1)y - (2k + 5) = 0
These are of the form
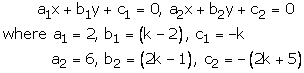
For infinite number of solutions, we have
This hold only when
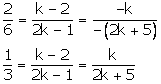
Case (1)
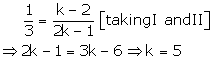
Case (2)
Case (3)
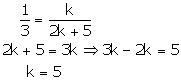
Thus, for k = 5 there are infinitely many solutions
Solution 17
kx + 3y - (2k +1) = 0
2(k + 1)x + 9y - (7k + 1) = 0
These are of the form
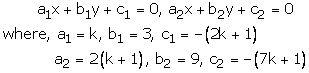
For infinitely many solutions, we must have
This hold only when
Now, the following cases arise
Case - (1)
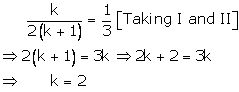
Case (2)
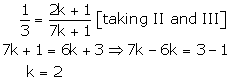
Case (3)
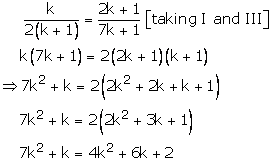
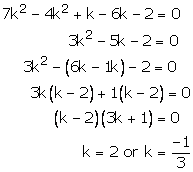
Thus, k = 2, is the common value for which there are infinitely many solutions
Solution 18
5x + 2y - 2k = 0
2(k +1)x + ky - (3k + 4) = 0
These are of the form
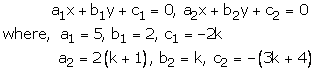
For infinitely many solutions, we must have
These hold only when
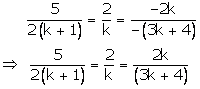
Case I
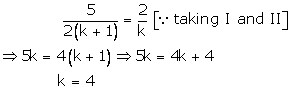
Thus, k = 4 is a common value for which there are infinitely by many solutions.
Solution 19
(k - 1)x - y - 5 = 0
(k + 1)x + (1 - k)y - (3k + 1) = 0
These are of the form
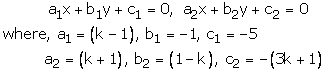
For infinitely many solution, we must now
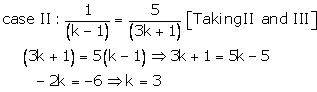
k = 3 is common value for which the number of solutions is infinitely many
Solution 20
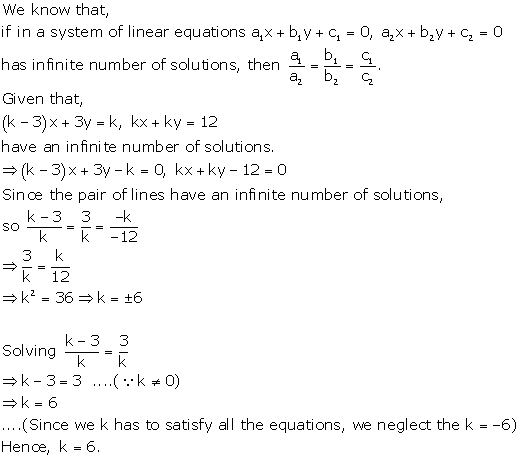
Solution 21
(a - 1)x + 3y - 2 = 0
6x + (1 - 2b)y - 6 = 0
These equations are of the form
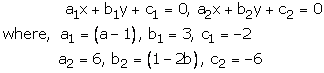
For infinite many solutions, we must have
Hence a = 3 and b = -4
Solution 22
The given equations are
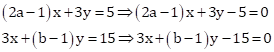
These equations are of the form
Where
If system of equations have infinite number of solutions, then
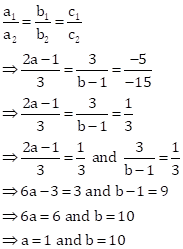
Solution 23
2x - 3y - 7 = 0
(a + b)x + (a + b - 3)y - (4a + b) = 0
These equation are of the form
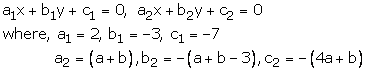
For infinite number of solution
Putting a = 5b in (2), we get
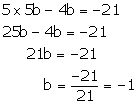
Putting b = -1 in (1), we get
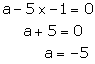
Thus, a = -5, b = -1
Solution 24
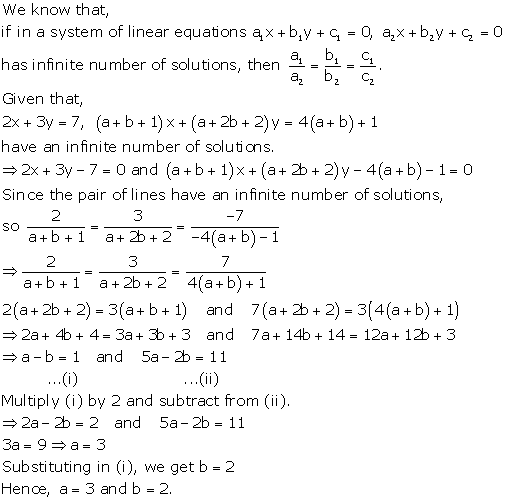
Solution 25
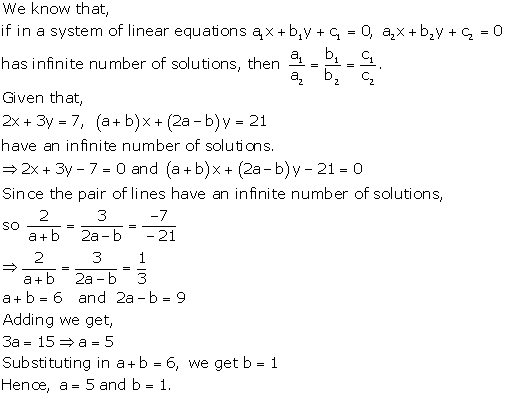
Solution 26
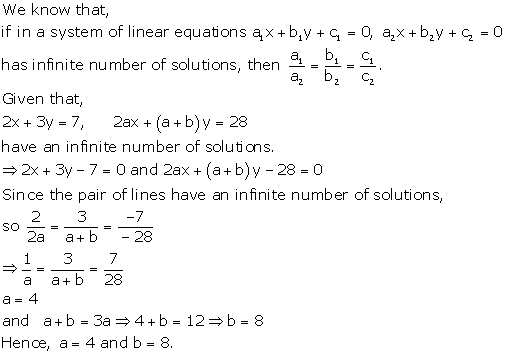
Solution 27
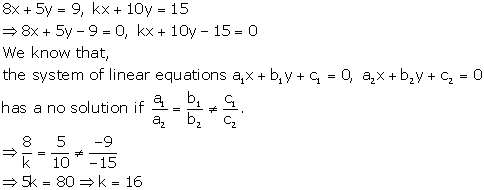
Solution 28
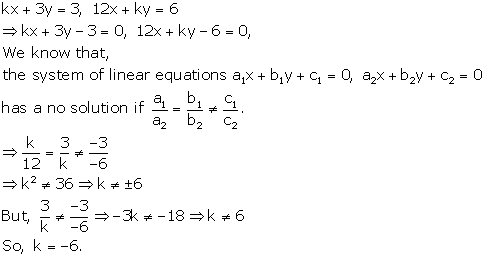
Solution 29
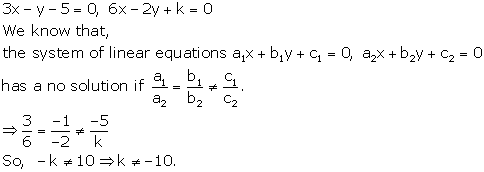
Solution 30
The given equations are
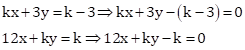
These equations are of the form
Where
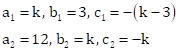
If system of equations have no solution, then
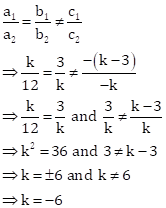
Solution 31
We have 5x - 3y = 0 ---(1)
2x + ky = 0---(2)
Comparing the equation with
These equations have a non - zero solution if 
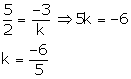
Linear Equations in Two Variables Exercise Ex. 3E
Solution 1
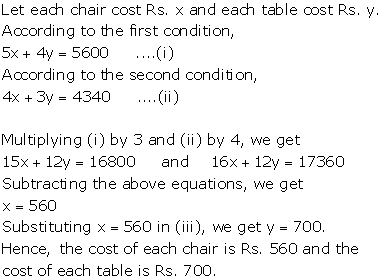
Solution 2
Solution 3
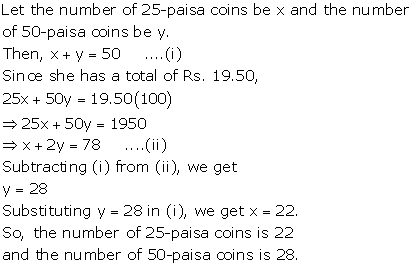
Solution 4
Let the two numbers be x and y respectively.
Given:
x + y = 137---(1)
x - y = 43---(2)
Adding (1) and (2), we get
2x = 180
Putting x = 90 in (1), we get
90 + y = 137
y = 137 - 90
= 47
Hence, the two numbers are 90 and 47.
Solution 5
Let the first and second number be x and y respectively.
According to the
question:
2x + 3y = 92---(1)
4x - 7y = 2 ---(2)
Multiplying (1) by 7 and (2) by 3, we get
14 x+ 21y = 644---(3)
12x - 21y = 6---(4)
Adding (3) and (4), we get
Putting x = 25 in (1), we get
2 × 25 + 3y = 92
50 + 3y = 92
3y = 92 - 50
y = 14
Hence, the first number is 25 and second is 14
Solution 6
Let the first and second numbers be x and y respectively.
According to the
question:
3x + y = 142---(1)
4x - y = 138---(2)
Adding (1) and (2), we get
Putting x = 40 in (1), we get
3 × 40 + y = 142
y = 142 - 120
y = 22
Hence, the first and second numbers are 40 and 22.
Solution 7
Let the
greater number be x and smaller be y respectively.
According to the question:
2x - 45 = y
2x
- y = 45---(1)
and
2y - x = 21
-x
+ 2y = 21---(2)
Multiplying (1) by 2 and (2) by 1
4x - 2y = 90---(3)
-x + 2y = 21 ---(4)
Adding (3) and (4), we get
3x = 111
Putting x = 37 in (1), we get
2 × 37 - y = 45
74
- y = 45
y
= 29
Hence, the greater and the smaller numbers are 37 and 29.
Solution 8
Let the larger number be x and smaller be y respectively.
We know,
Dividend = Divisor × Quotient + Remainder
3x = y × 4 + 8
3x - 4y = 8---(1)
And
5y = x × 3 + 5
-3x + 5y = 5---(2)
Adding (1) and (2), we get
y = 13
putting y = 13 in (1)
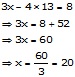
Hence, the larger and smaller numbers are 20 and 13 respectively.
Solution 9
Let the required numbers be x and y respectively.
Then,
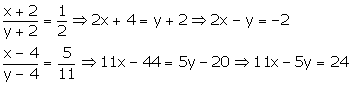
Therefore,
2x - y =-2---(1)
11x - 5y = 24 ---(2)
Multiplying (1) by 5 and (2) by 1
10x - 5y = -10---(3)
11x - 5y = 24---(4)
Subtracting (3) and (4) we get
x = 34
putting x = 34 in (1), we get
2 × 34 - y = -2
68
- y = -2
-y
= -2 - 68
y
= 70
Hence, the required numbers are 34 and 70.
Solution 10
Let the numbers be x and y respectively.
According to the
question:
x - y = 14 ---(1)
From (1), we get
x = 14 + y---(3)
putting x = 14 + y in (2), we get
Putting y = 9 in (1), we get
x - 9 = 14
x = 14 + 9 =
23
Hence the required numbers are 23 and 9
Solution 11
Let the ten's digit be x and units digit be y respectively.
Then,
x + y = 12---(1)
Required
number = 10x + y
Number
obtained on reversing digits = 10y + x
According to the question:
10y + x - (10x + y) = 18
10y + x - 10x - y = 18
9y - 9x = 18
y - x = 2 ----(2)
Adding (1) and (2), we get
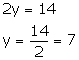
Putting y = 7 in (1), we get
x
+ 7 = 12
x
= 5
Number=
10x + y
= 10 × 5 + 7
= 50 + 7
= 57
Hence, the number is 57.
Solution 12
Let the
ten's digit of required number be x and its unit's digit be y
respectively
Required number = 10x + y
10x
+ y = 7(x + y)
10x + y = 7x + 7y
3x - 6y = 0---(1)
Number found on reversing the digits = 10y + x
(10x
+ y) - 27 = 10y + x
10x - x + y - 10y = 27
9x - 9y = 27
(x - y) = 27
x - y = 3---(2)
Multiplying (1) by 1 and (2) by 6
3x - 6y = 0---(3)
6x - 6y = 18 ---(4)
Subtracting (3) from (4), we get
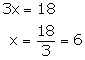
Putting x = 6 in(1), we get
3 × 6 - 6y = 0
18 - 6y = 0
Number = 10x + y
= 10 × 6 + 3
= 60 + 3
= 63
Hence the number is 63.
Solution 13
Let the ten's digit and unit's digits of required number be x and y respectively.
Then,
x + y = 15---(1)
Required number = 10x + y
Number obtained by interchanging the digits = 10y + x
10y
+ x - (10x + y) = 9
10y
+ x - 10x - y = 9
9y - 9x = 9
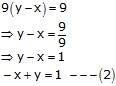
Add (1) and (2), we get
Putting y = 8 in (1), we get
x + 8 = 15
x = 15 - 8 = 7
Required number = 10x + y
= 10 × 7 + 8
= 70 + 8
= 78
Hence the required number is 78.
Solution 14
Let the
ten's and unit's of required number be x and y respectively.
Then,required number =10x + y
According to the given question:
10x + y = 4(x + y) + 3
10x
+ y = 4x + 4y + 3
6x
- 3y = 3
2x
- y = 1 ---(1)
And
10x + y + 18 = 10y + x
9x
- 9y = -18
x
- y = -2---(2)
Subtracting (2) from (1), we get
x
= 3
Putting x = 3 in (1), we get
2 × 3 - y = 1
y
= 6 - 1 = 5
x
= 3, y = 5
Required number = 10x + y
= 10 × 3 + 5
= 30 + 5
= 35
Hence, required number is 35.
Solution 15
Let the ten's digit and unit's digit of required number be x and y respectively.
We know,
Dividend = (divisor × quotient) + remainder
According to the given questiion:
10x + y = 6 × (x + y) + 0
10x
- 6x + y - 6y = 0
4x
- 5y = 0 ---(1)
Number obtained by reversing the digits is 10y + x
10x
+ y - 9 = 10y + x
9x
- 9y = 9
9(x
- y) =9
(x
- y) = 1---(2)
Multiplying (1) by 1 and (2) by 5, we get
4x - 5y = 0 ---(3)
5x - 5y = 5 ---(4)
Subtracting (3) from (4), we get
x
= 5
Putting x = 5 in (1), we get
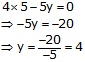
x
=5 and y= 4
Hence, required number is 54.
Solution 16
Let the ten's and unit's digits of the required number be x and y respectively.
Then, xy = 35
Required number = 10x + y
Also,
(10x + y) + 18 = 10y + x
9x
- 9y = -18
9(y
- x) = 18---(1)
y
- x = 2
Now,
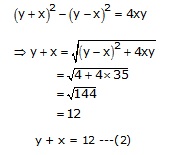
Adding
(1) and (2),
2y = 12 + 2 = 14
y
= 7
Putting y = 7 in (1),
7 - x = 2
x
= 5
Hence, the required number = 5 × 10 + 7
= 57
Solution 17
Let the ten's and unit's digits of the required number be x and y respectively.
Then, xy = 18
Required number = 10x + y
Number obtained on reversing its digits = 10y + x
(10x
+ y) - 63 = (10y + x)
9x
- 9y = 63
x
- y = 7---(1)
Now,
Adding (1) and (2), we get
Putting x = 9 in (1), we get
9 - y = 7
y
= 9 - 7
y
=2
x
= 9, y = 2
Hence, the required number = 9 × 10 + 2
= 92.
Solution 18
Solution 19
Let the numerator and denominator of fraction be x and y respectively.
According to the question:
x + y = 8---(1)
And
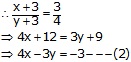
Multiplying (1) be 3 and (2) by 1
3x + 3y = 24---(3)
4x - 3y = -3 ---(4)
Add (3) and (4), we get
Putting x = 3 in (1), we get
3 + y= 8
y
= 8 - 3
y
= 5
x
= 3, y = 5
Hence, the fraction is 
Solution 20
Let the numerator and denominator be x and y respectively.
Then the fraction is 
.
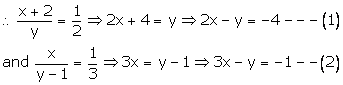
Subtracting (1) from (2), we get
x = 3
Putting x = 3 in (1), we get
2 × 3 - 4
-y
= -4 -6
y
= 10
x
= 3 and y = 10
Hence the fraction is
Solution 21
Let the numerator and denominator be x and y respectively.
Then the fraction is 
.
According to the given question:
y = x + 11
y- x = 11---(1)
and
-3y
+ 4x = -8 ---(2)
Multiplying (1) by 4 and (2) by 1
4y - 4x = 44---(3)
-3y + 4x = -8---(4)
Adding (3) and (4), we get
y = 36
Putting y = 36 in (1), we get
y - x = 11
36
- x = 11
x
= 25
x
= 25, y = 36
Hence the fraction is 
Solution 22
Let the numerator and denominator be x and y respectively.
Then the fraction is 
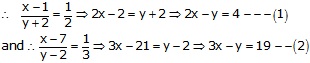
Subtracting (1) from (2), we get
x = 15
Putting x = 15 in (1), we get
2 × 15 - y = 4
30
- y = 4
y = 26
x
= 15 and y = 26
Hence the given fraction is 
Solution 23
Solution 24
Let the two numbers be x and y respectively.
According to the given question:
x
+ y = 16---(1)
And
---(2)
From (2),
xy
= 48
We know,
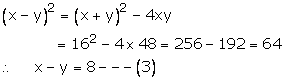
Adding (1) and (3), we get
2x = 24
x
= 12
Putting x = 12 in (1),
y = 16 - x
= 16 - 12
= 4
The
required numbers are 12 and 4
Solution 25
Let the number of student in class room A and B be x and y respectively.
When 10 students are transferred from A to B:
x - 10 = y + 10
x - y = 20---(1)
When 20 students are transferred from B to A:
2(y - 20) = x + 20
2y
- 40 = x + 20
-x
+ 2y = 60---(2)
Adding (1) and (2), we get
y = 80
Putting y = 80 in (1), we get
x - 80 = 20
x
= 100
Hence, number of students of A and B are 100 and 80 respectively.
Solution 26
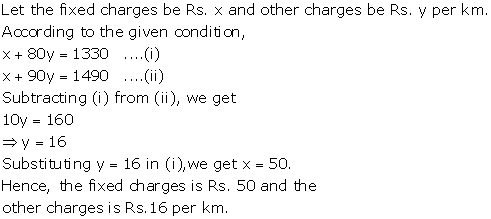
Solution 27
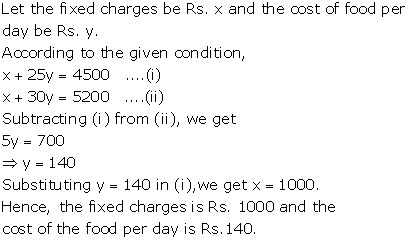
Solution 28
Solution 29
Solution 30
Solution 31
Let P and Q be the cars starting from A and B respectively and let their speeds be x km/hr and y km/hr respectively.
Case- I
When the cars P and Q move in the same direction.
Distance covered by the car P in 7 hours = 7x km
Distance covered by the car Q in 7 hours = 7y km
Let the cars meet at point M.
AM
= 7x km and BM = 7y km
AM
- BM = AB
7x
- 7y = 70
7(x
- y) = 70
x
- y = 10 ----(1)
Case II
When the cars P and Q move in opposite directions.
Distance covered by P in 1 hour = x km
Distance covered by Q in 1 hour = y km
In this case let the cars meet at a point N.
AN
= x km and BN = y km
AN
+ BN = AB
x
+ y = 70---(2)
Adding (1) and (2), we get
2x = 80
x
= 40
Putting x = 40 in (1), we get
40 - y = 10
y
= (40 - 10) = 30
x
= 40, y = 30
Hence, the speeds of these cars are 40 km/ hr and 30 km/ hr respectively.
Solution 32
Let the original speed be x km/h and time taken be y hours
Then, length of journey = xy km
Case I:
Speed = (x + 5)km/h and time taken = (y - 3)hour
Distance covered = (x + 5)(y - 3)km
(x
+ 5) (y - 3) = xy
xy + 5y -3x -15 = xy
5y
- 3x = 15 ---(1)
Case II:
Speed (x - 4)km/hr and time taken = (y + 3)hours
Distance covered = (x - 4)(y + 3) km
(x
- 4)(y + 3) = xy
xy -4y + 3x -12 = xy
3x
- 4y = 12 ---(2)
Multiplying (1) by 4 and (2) by 5, we get
20y - 12x = 60 ---(3)
-20y + 15x = 60 ---(4)
Adding (3) and (4), we get
3x = 120
or x = 40
Putting x = 40 in (1), we get
5y - 3 × 40 = 15
5y
= 135
y = 27
Hence, length of the journey is (40 × 27) km = 1080 km
Solution 33
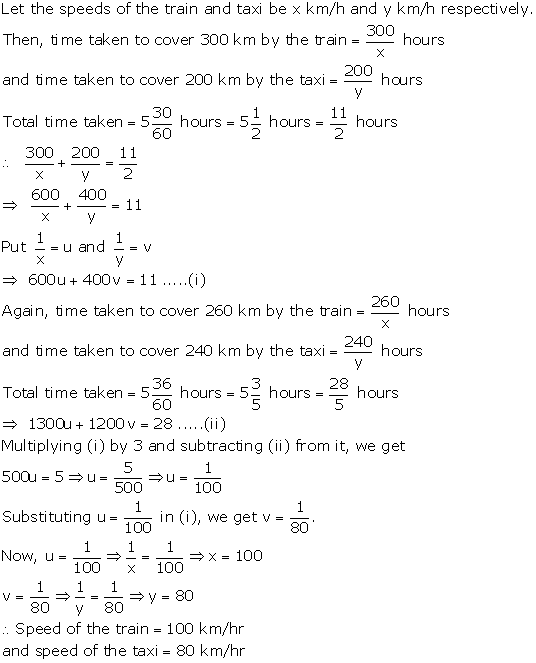
Solution 34
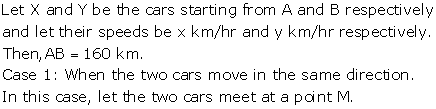
Solution 35
Solution 36
Let the speed of the boat in still water be 
km/hr and the speed of the stream be 
km/hr.
Then,
speed upstream = (x-y) km/hr
speed downstream = (x+y) km/hr
Time taken to cover 30 km upstream = 
hours
Time taken to cover 44 km downstream = 
hours
Total time taken = 10 hours
(i)
Again,
Time taken to cover 40 km upstream = 
hours
Time taken to cover 55 km downstream = 
hours
Total time taken = 13 hours
(ii)
Putting 
in (i) and (ii), we
get
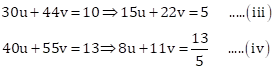
On multiplying (iv) by 2 and subtracting (iii) from the result, we get
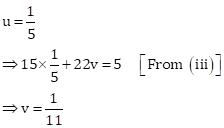
Then,
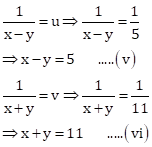
Adding equations (v) and (vi),
Therefore, speed of the stream is 3 km/hr and speed of the boat in still water is 8 km/hr.
Solution 37
Let man's
1 day's work be 
and
1 boy's day's work be 
Also let 
and 
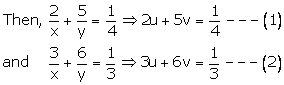
Multiplying (1) by 6 and (2) by 5 we get
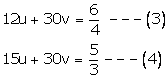
Subtracting (3) from (4), we get
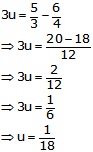
Putting 
in
(1), we get
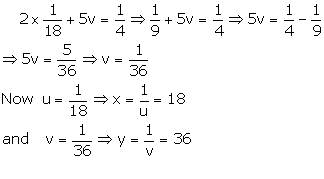
x
= 18, y = 36
The man will finish the work in 18 days and the boy will finish the work in 36 days when they work alone.
Solution 38
Let the length = x meters and breadth = y meters
Then,
x = y + 3
x - y = 3 ----(1)
Also,
(x + 3)(y - 2) = xy
3y
- 2x = 6 ----(2)
Multiplying (1) by 2 and (2) by 1
-2y + 2x = 6 ---(3)
3y - 2x = 6 ---(4)
Adding (3) and (4), we get
y = 12
Putting y = 12 in (1), we get
x - 12 = 3
x= 15
x
= 15, y = 12
Hence length = 15 metres and breadth = 12 metres
Solution 39
Let the length of a rectangle be x meters and breadth be y meters.
Then, area = xy sq.m
Now,
xy - (x - 5)(y + 3) = 8
xy - [xy - 5y + 3x -15] = 8
xy
- xy + 5y - 3x + 15 = 8
3x - 5y = 7 ---(1)
And
(x + 3)(y + 2) - xy = 74
xy + 3y +2x + 6 - xy = 74
2x
+ 3y = 68---(2)
Multiplying (1) by 3 and (2) by 5, we get
9x - 15y = 21---(3)
10x + 15y = 340---(4)
Adding (3) and (4), we get
Putting x = 19 in (3) we get
x
= 19 meters, y = 10 meters
Hence, length = 19m and breadth = 10m
Solution 40
Solution 41
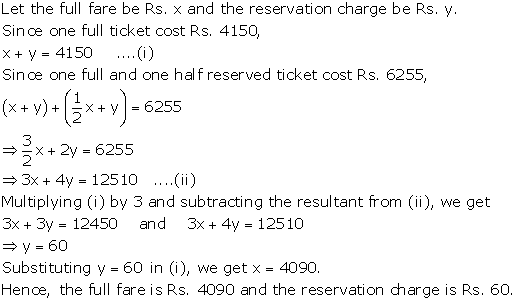
Solution 42
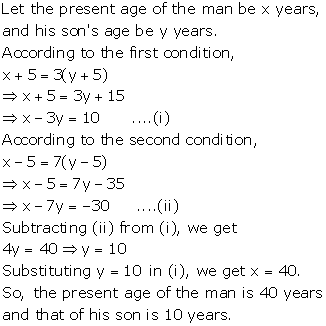
Solution 43
Let the present ages of the man and his son be x years and y years respectively.
Then,
Two years ago:
(x - 2) = 5(y - 2)
x
- 2 = 5y - 10
x - 5y = -8 ---(1)
Two years later:
(x + 2) = 3(y + 2) + 8
x
+ 2 = 3y + 6 + 8
x - 3y = 12 ---(2)
Subtracting (2) from (1), we get
-2y = -20
y = 10
Putting y = 10 in (1), we get
x - 5 10 = -8
x
- 50 = -8
x = 42
Hence the present ages of the man and the son are 42 years and 10 respectively.
Solution 44
Let the present ages of father and his son be x and y respectively.
According to given information
x + 2y = 70 ....(i)
And
2x + y = 95 ....(ii)
Multiplying equation (ii) by 2, we get
4x + 2y = 190 ....(iii)
Subtracting (i) from (iii), we get
Putting x = 40 in (i), we get
40 + 2y = 70
2y
= 30
y
= 15
x
= 40, y = 15
Hence, the ages of father and son are 40 years and 15 years respectively.
Solution 45
Let the present ages of woman and daughter be x and y respectively.
Then,
Their present ages:
x = 3y + 3
x
- 3y = 3---(1)
Three years later:
(x + 3) = 2(y + 3) + 10
x
+ 3 = 2y + 6 + 10
x
- 2y = 13---(2)
Subtracting (2) from (1), we get
y = 10
Putting y = 10 in (1), we get
x - 3 × 10 = 3
x
= 33
x
= 33, y = 10
Hence, present ages of woman and daughter are 33 and 10 years.
Solution 46
Solution 47
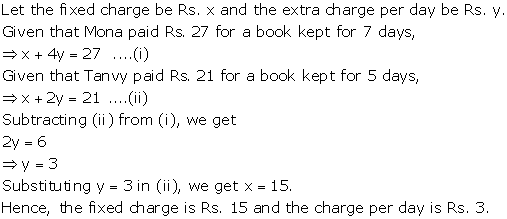
Solution 48
Let the ten's and unit's digits of the required number be
and
respectively.
Then, required number = (10x+y).
Now,
Number obtained on reversing the digits = (10y+x)
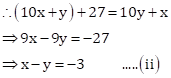
Adding equations (i) and (ii),
Hence, the required number is 36.
Solution 49
Let the required fraction be 
.
Then,
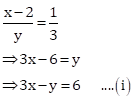
Also,
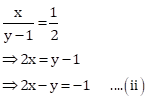
Subtracting equations (ii) from (i), we get
Hence, the required fraction is 
.
Solution 50
Let the present age of father be years
and the sum of the ages of his two children be years.
Then,
.
After 5 years,
father's age = (x+5) years
sum of the ages of two children = 
years
Then,
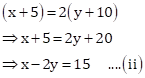
Subtracting equations (i) from (ii), we get
Hence, the present age of the father is 45 years.
Solution 51
Let the sides of two squares be m
and 
m
respectively.
Then,
And,
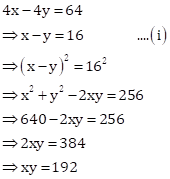
Now,
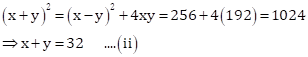
Adding equations (i) and (ii), we get
Hence, the sides of the squares are 24 m and 8 m respectively.
Solution 52
Let the sides of two squares be m
and m
respectively.
Then,
And,
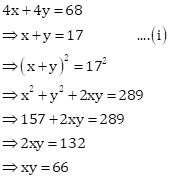
Now,
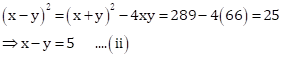
Adding equations (i) and (ii), we get
Hence, the sides of the squares are 11 m and 6 m respectively.
Solution 53
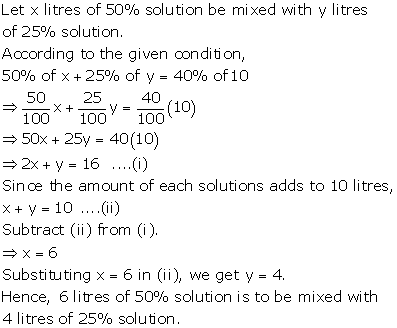
Solution 54
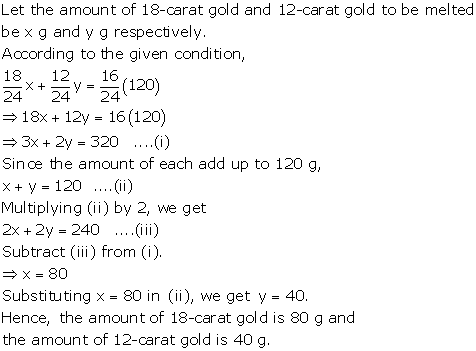
Solution 55
Solution 56
Solution 57
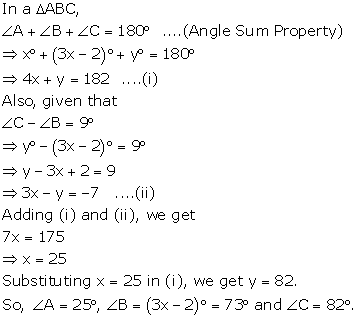
Solution 58
Linear Equations in Two Variables Exercise Ex. 3F
Solution 1
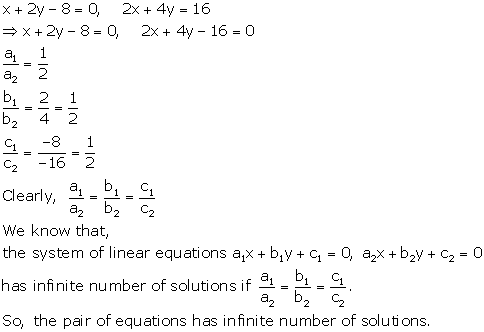
Solution 2
Solution 3
Solution 4
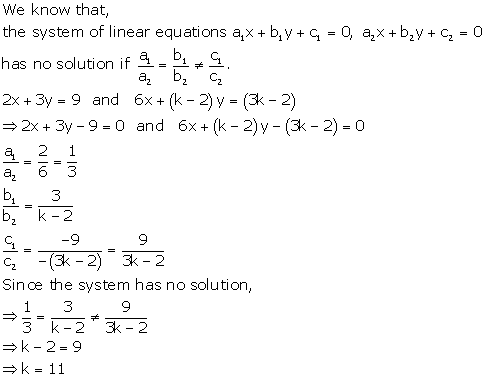
Solution 5
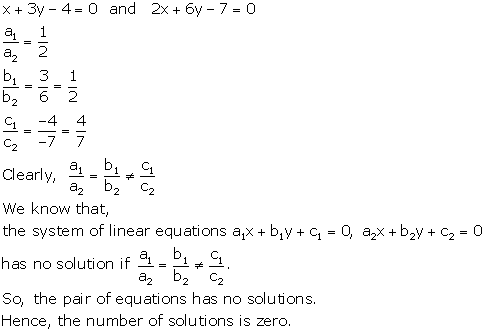
Solution 6
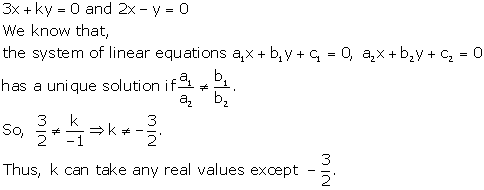
Solution 7
Solution 8
Solution 9
Solution 10
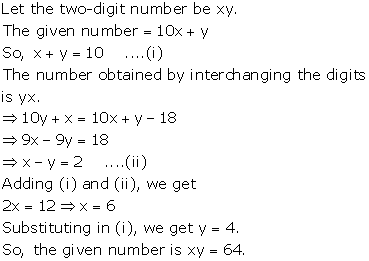
Solution 11
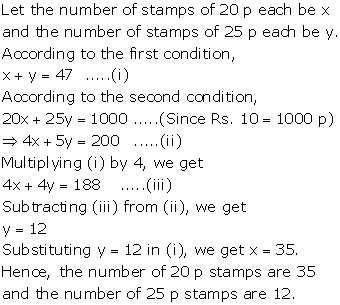
Solution 12
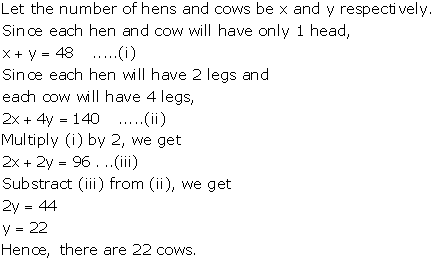
Solution 13
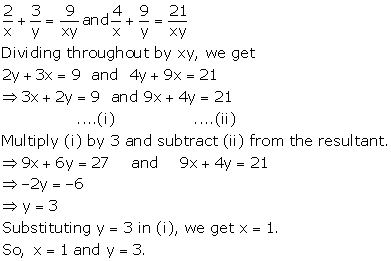
Solution 14
Solution 15
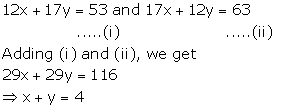
Solution 16
Solution 17
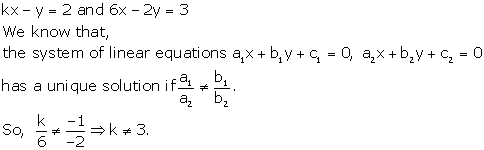
Solution 18
Solution 19
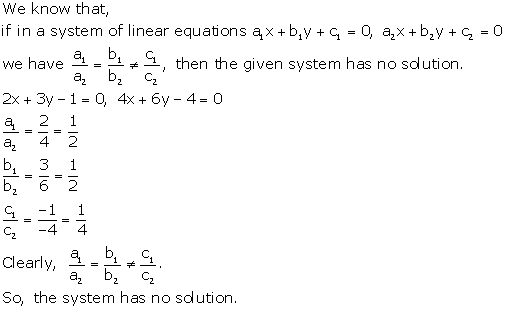
Solution 20
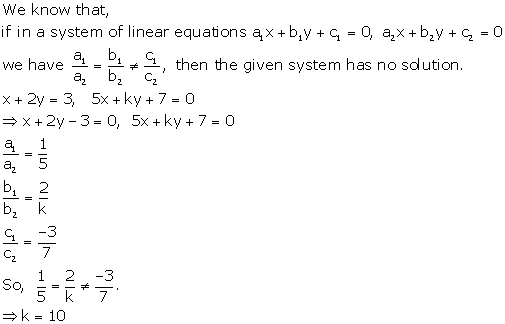
Solution 21
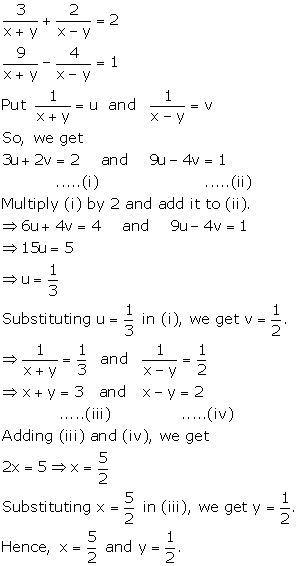
Linear Equations in Two Variables Exercise MCQ
Solution 1
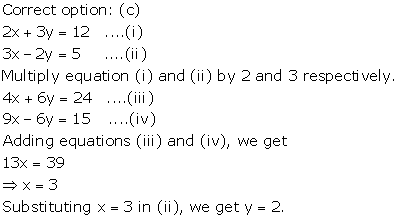
Solution 2
Solution 3
Solution 4
Correct option: (d)
Given equations are
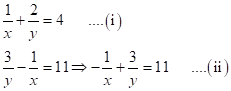
Adding equations (i) and (ii),
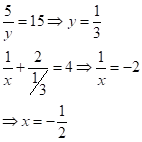
Solution 5
Solution 6
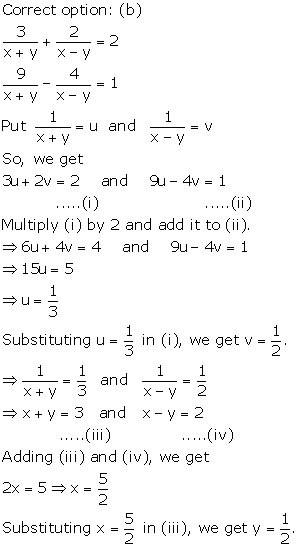
Solution 7
Solution 8
Correct option: (a)
The given equations are
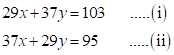
Adding equations (i) and (ii),
Subtracting equation (ii) from (i),
Adding equation (iii) and (iv),
Substituting 
in
equation (iii),
Solution 9
Correct option: (c)
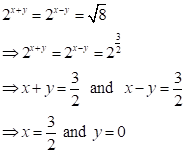
Solution 10
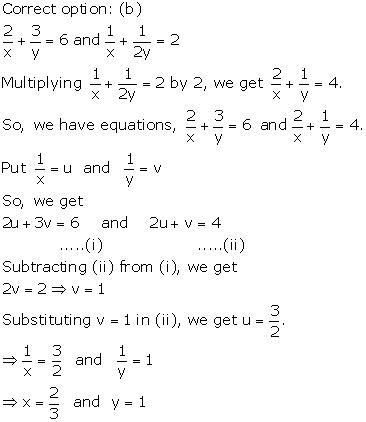
Solution 11
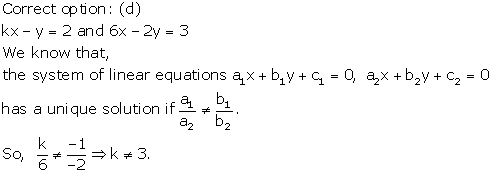
Solution 12
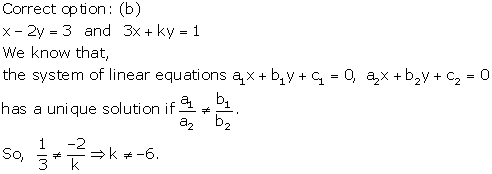
Solution 13
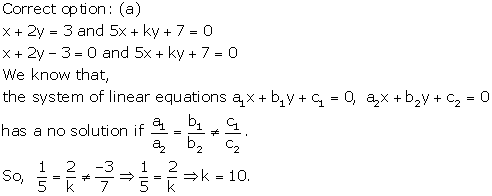
Solution 14
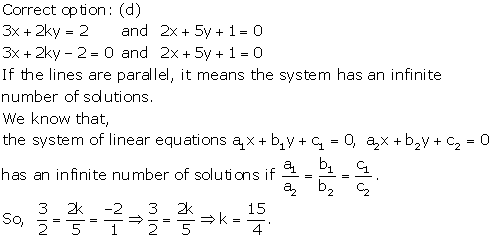
Solution 15
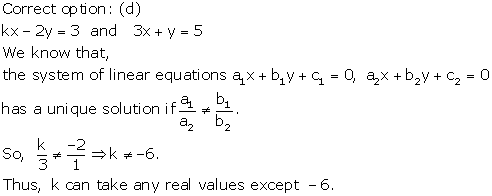
Solution 16
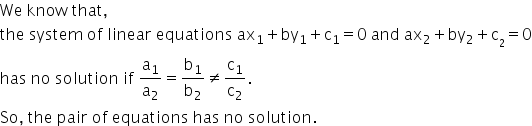
Solution 17
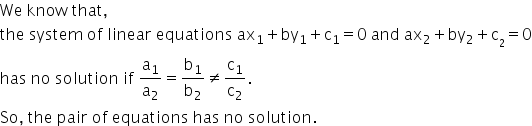
Solution 18
Solution 19
Solution 20
Correct option: (b)
Now,
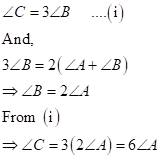
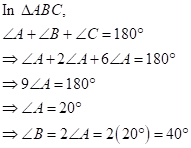
Solution 21
Solution 22
Solution 23
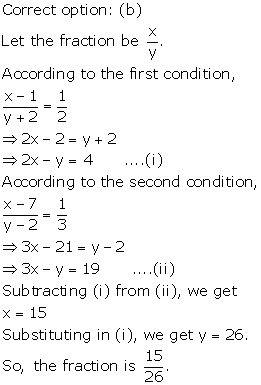
Solution 24
Solution 25
Solution 26
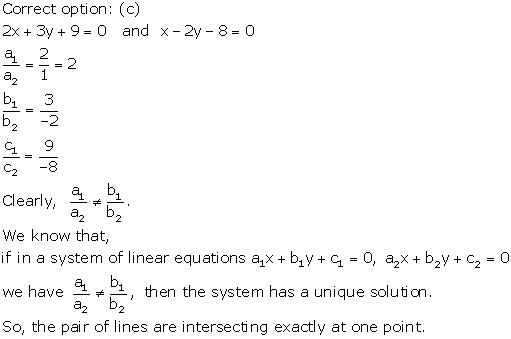
Solution 27
Linear Equations in Two Variables Exercise Test Yourself
Solution 1
Solution 2
Solution 3
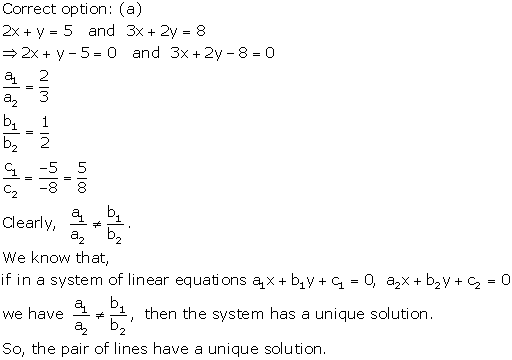
Solution 4
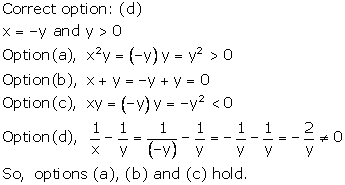
Solution 5
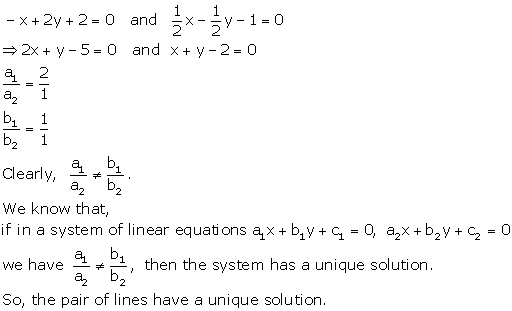
Solution 6
Solution 7
Solution 8
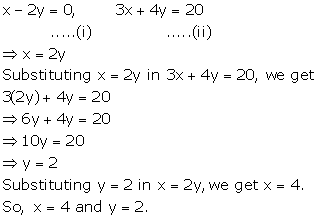
Solution 9
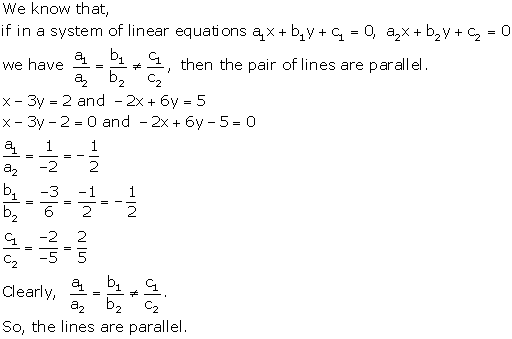
Solution 10
Solution 11
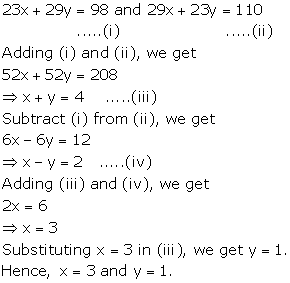
Solution 12
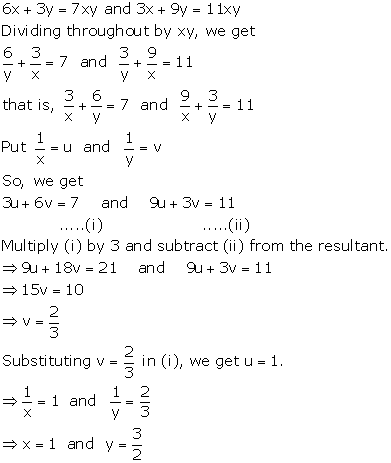
Solution 13
The given system of equations are
These equations are of the form
Where
(i) If system of equations have unique solution, then
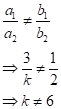
Hence, the given system of equations will have a unique
solution when 
.
(ii) If system of equations have no solution, then
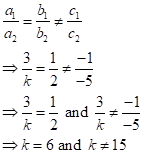
Clearly, 
also satisfies the condition
.
Hence, the given system of equations will have no
solution when .
Solution 14
Solution 15
Solution 16
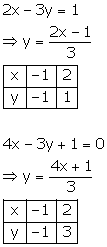
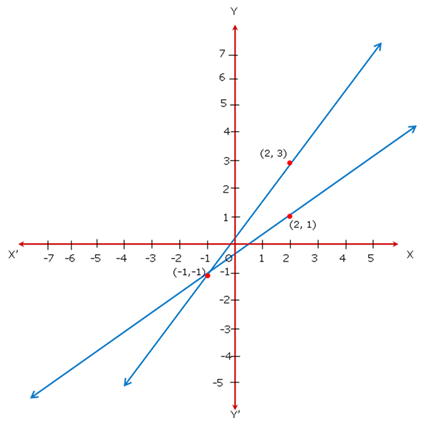
Since the intersection of the lines is the point with coordinates (-1, -1), x = -1 and y = -1.
Solution 17
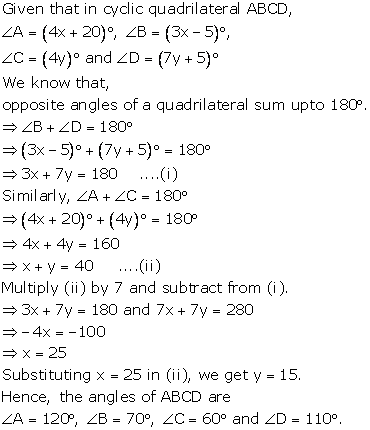
Solution 18
Solution 19
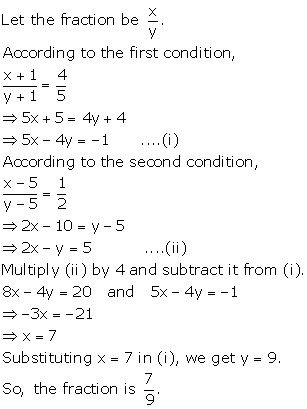
Solution 20
