Chapter 19 Probability
Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution
Probability Exercise Ex. 19
Solution 1
(i) The probability of an impossible event is zero.
(ii) The probability of a sure event is one.
(iii) For any event E, P(E) + P(not E)= one .
(iv) The probability of a possible but not a sure event lies between zero and one.
(v) The sum of probabilities of all the outcomes of an experiment is one.
Solution 2
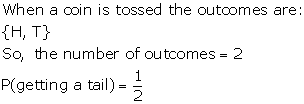
Solution 3

Solution 4
In a throw of a dice, all possible outcomes are 1, 2, 3, 4, 5, 6
Total number of possible outcomes = 6
(i)Let E be event of getting even number
Then, the favorable outcomes are 2, 4, 6
Number of favorable outcomes= 3
∴ P(getting
a even number)= P(E) = ![]()
(ii)Let R be the number less than 5
Then, the favorable outcomes are 1, 2, 3, 4
Number of favorable outcomes = 4
∴ P(getting
a number less than 5)= P(R) = ![]()
(iii)Let M be the event of getting a number greater than 2
Then, the favorable outcomes are 3, 4, 5, 6
Number of favorableoutcomes = 4
∴ P(getting
a number greater than 2)= P(M) ![]()
(iv)Let N be the number lying between 3 and 6
Then the favorable outcomes are 4, 5
Number of favorable outcomes = 2
∴ P(getting
a number 3 and 6)= P(N) = ![]()
(v)Let G be event of getting a number other than 3
Then the favorable outcomes are 1, 2, 4, 5, 6
Number of favorable outcomes = 5
∴ P(getting
a number other than 5)=P(G) = ![]()
(vi)Let T be event of getting a number 5
Then the favorable outcome is 5
Number of favorable outcomes = 1
∴ P(getting
a number 5)=P(T) ![]()
Solution 5

Solution 6
Outcomes are A, B, C, A, A, B
Total number of outcomes = 6
(i) Let E1 be the event of getting a letter 'A'.
Then, the number of favourable outcomes = 3
![]()
(ii) Let E2 be the event of getting a letter 'B'.
Then, the number of favourable outcomes = 2
![]()
Solution 7
Number of defective pens = 12
Number of good pens = 132
Then, total number of pens = 12 + 132 = 144
(i) Let E1 be the event of getting a good pen.
Then, the number of favourable outcomes = 132
![]()
(ii) Let E2 be the event of getting a defective pen.
Then, the number of favourable outcomes = 12
![]()
Solution 8
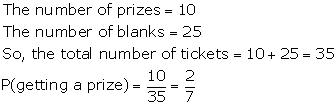
Solution 9
Total number of tickets sold = 250
Number of prizes = 5
Let E be the event getting a prize
Number of favorable outcomes = 5
![]() P(getting a prize) =
P(getting a prize) = ![]()
Solution 10

Solution 11
Since the arrow can come to rest at any one of the numbers 1, 2, 3, 4, ……, 12.
∴ Total number of outcomes = 12
(i) Let E1 be the event of pointing at number 6.
Then, the number of favourable outcomes = 1
∴ P(E1) =
![]()
(ii) Let E2 be the event of pointing at an even number.
Then, favourable outcomes are 2, 4, 6, 8, 10, 12.
So, number of favourable outcomes = 6
∴ P(E2) =
![]()
(iii) Let E3 be the event of pointing at a prime number.
Then, favourable outcomes are 2, 3, 5, 7, 11
So, number of favourable outcomes = 5
∴ P(E3) =
![]()
(iv) Let E4 be the event of pointing at a number which is a multiple of 5.
Then, favourable outcomes are 5, 10
So, number of favourable outcomes = 2
∴ P(E4) =
![]()
(v) Let E5 be the event of pointing at a number which is a factor of 8.
Then, favourable outcomes are 1, 2, 4, 8
So, number of favourable outcomes = 4
∴ P(E5) =
![]()
Solution 12
Outcomes are 1, 2, 3, ....., 17
Total number of outcomes = 17
(i) Let E1 be the event of getting an odd numbers.
Then, favourable outcomes are 1, 3, 5, 7, 9, 11, 13, 15, 17.
So, number of favourable outcomes = 9
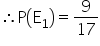
(ii) Let E2 be the event of getting a number divisible by 5.
Then, favourable outcomes are 5, 10, 15.
So, number of favourable outcomes = 3
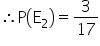
Solution 13

Solution 14
Number of white balls = 5
Number of red balls = 7
Number of black balls = 4
Number of blue balls = 2
Then, total number of balls = 5 + 7 + 4 + 2 = 18
(i) Let E1 be the event of drawing a white or blue ball.
Then, the number of favourable outcomes = 5 + 2 = 7
∴ P(E1) =
![]()
(ii) Let E2 be the event of drawing neither white nor black.
Then, the number of balls which are neither white nor black = 7 + 2 = 9
∴ P(E2) ![]()
Solution 15
Total number of marbles = 24
Given,
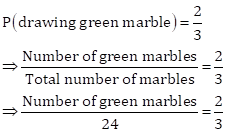
⇒ Number of green marbles = 16
⇒ Number of blue marbles = 24 - 16 = 8
Solution 16
Total number of marbles = 54
Given,
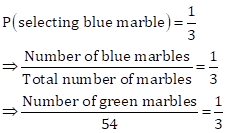
⇒ Number of blue marbles = 18
Also,
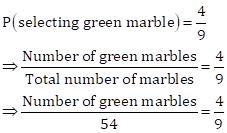
⇒ Number of green marbles = 24
Therefore, number of white marbles in the jar = 54 - 18 - 24 = 12
Solution 17

Solution 18

Solution 19
Let the number of black balls in the bag = x
Number of white balls in the bag = 15
So, total number of balls in the bag = x + 15
Given,
P(drawing a black ball) = 3 × P(drawing a white ball)
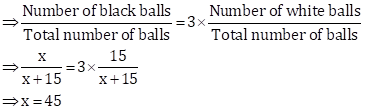
Hence, the number of black balls in the bag is 45.
Solution 20

Solution 21
Number of white balls in the bag = x
Number of black balls in the bag = 2x
Number of red balls in the bag = 3x
So, total number of balls in the bag = x + 2x + 3x = 6x
(i) Let E1 be the event of not drawing a red ball.
Then, the number of balls which are not red = 6x - 3x = 3x
∴ P(E1) ![]()
(ii) Let E2 be the event of drawing a white ball.
Then, the number of favourable outcomes = x
∴ P(E2) ![]()
Solution 22

Solution 23
Total number of cards = 20
(i) Let E1 be the event of drawing a prime number card.
Then, the favourable outcomes are 2, 3, 5, 7, 11, 13, 17, 19
So, number of favourable outcomes = 8
∴ P(E1) ![]()
(ii) Let E2 be the event of drawing a composite number card.
Then, the favourable outcomes are 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20
So, number of favourable outcomes = 11
∴ P(E2) ![]()
(iii) Let E3 be the event of drawing a number card that is divisible by 3.
Then, the favourable outcomes are 3, 6, 9, 12, 15, 18
So, number of favourable outcomes = 6
∴ P(E3) ![]()
Solution 24

Solution 25

Solution 26

Solution 27

Solution 28

Solution 29

Solution 30
Total number of tickets = 100
(i)Even numbers are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100
Total number of even number = 50
P(getting a even number) = ![]()
(ii)Numbers less than 16 are 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
Total number of numbers less than 16 is 14
P(getting a number less than 16) =
![]()
(iii)Numbers which are perfect square are 4, 9, 16, 25, 36, 49, 64, 81, 100
Total number of perfect squares = 9
P(getting a perfect square) = ![]()
(iv)Prime numbers less than 40 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37
Total number of prime numbers =12
P(getting a prime number less 40) =
![]()
Solution 31

Solution 32
When two dice are thrown, the outcomes are as follows:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6).
So, total number of outcomes = 36
(i) Let E1 be the event of obtaining numbers giving even sum.
Then, the favourable outcomes are as follows:
(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6),
(3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (4, 6),
(5, 1), (5, 3), (5, 5), (6, 2), (6, 4), (6, 6).
So, number of favourable outcomes = 18
∴ P(E1) ![]()
(ii) Let E2 be the event of obtaining numbers giving even product.
Then, the favourable outcomes are as follows:
(1, 2), (1, 4), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 2), (3, 4), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 2), (5, 4), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6).
So, number of favourable outcomes = 27
∴ P(E2) ![]()
Solution 33
When two dice are thrown, the outcomes are as follows:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6).
So, total number of outcomes = 36
(i) Let E1 be the event of obtaining numbers having sum less than 7.
Then, the favourable outcomes are as follows:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4),
(3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (5, 1),
So, number of favourable outcomes = 15
∴ P(E1) ![]()
(ii) Let E2 be the event of obtaining numbers having product less than 16.
Then, the favourable outcomes are as follows:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (4, 1),
(4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (6, 1), (6, 2).
So, number of favourable outcomes = 25
∴ P(E2) ![]()
(iii) Let E3 be the event of obtaining a doublet of odd numbers.
Then, the favourable outcomes are as follows:
(1, 1), (3, 3), (5, 5)
So, number of favourable outcomes = 3
∴ P(E2) ![]()
Solution 34
When two dice are thrown by Peter, the outcomes are as follows:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6).
So, total number of outcomes = 36
Let E1 be the event of obtaining numbers having product as 25.
Then, the favourable outcome is (5, 5).
So, number of favourable outcomes = 1
∴ P(E1) ![]()
When a die is thrown by Rina, the outcomes are as follows:
1, 2, 3, 4, 5, 6
When these numbers are squared, we have
1, 4, 9, 16, 25, 36
⇒ Total number of outcomes = 6
Let E2 be the event of obtaining a number 25.
Then, the favourable outcome is 25.
So, number of favourable outcomes = 1
∴ P(E2) ![]()
Since ![]()
⇒ P(E2) > P(E1)
Hence, we conclude that Rina has better chance than Peter to get the number 25.
Solution 35
When a pair of distinct dice is thrown, the outcomes are as follows:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6).
So, total number of outcomes = 36
Let E be the event of getting the sum of numbers either less than 3 or more than 11.
Then, the favourable outcome are (1, 1) and (6, 6).
So, number of favourable outcomes = 2
∴ P(E) ![]()
Solution 36
Total number of apples = 900
Let E be the event of selecting a rotten apple from a heap.
∴ P(E) = 0.18

Hence, the number of rotten apples in the heap is 162.
Solution 37
An ordinary year has 365 days which means 52 complete weeks and one day.
That means, there are 52 Sundays in 52 weeks.
This 'one day' can be either Sunday, Monday, Tuesday, Wednesday, Thursday, Friday or Saturday.
So, we have
Total number of outcomes = 7
Number of favourable outcomes = 1
∴ Probability that an ordinary
year has 53 Sundays ![]()
Solution 38
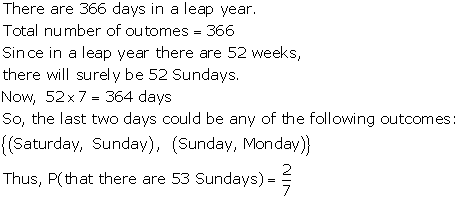
Solution 39

Solution 40
When a coin is tossed three times, the possible outcomes are as follows:
HHH, HTH, HHT, THH, THT, TTH, HTT, TTT
So, we have
Total number of outcomes = 8
Getting the same result in all the tosses is a success.
And, not getting the same result in all the tosses is losing the game.
So, favourable outcomes are HTH, HHT, THH, THT, TTH, HTT.
⇒ Number of favourable outcomes = 6
∴ Probability of losing the game
![]()
Solution 41
Total number of cards in a pack after losing cards of king, jack and 10 of spades = 52 - 3 = 49
(i) Let E1 be the event of drawing a red card.
Number of red cards in a pack = 26
∴ P(E1) ![]()
(ii) Let E2 be the event of drawing a black jack.
Number of black jack cards in a pack after losing a jack of spades = 2 - 1 = 1
∴ P(E2) ![]()
(iii) Let E3 be the event of drawing a red king.
Number of red king cards in a pack = 2
∴ P(E3) ![]()
(iv) Let E4 be the event of drawing a 10 of hearts card.
Number of 10 of heart cards in a pack = 1
∴ P(E4) ![]()
Solution 42

Solution 43

Solution 44
There are 26 red cards containing a 2
queensand 2 more black queens are there in a pack of cards
![]() P(getting a red card or a queen)
P(getting a red card or a queen) ![]()
![]() P(getting neither a red card nor a queen) =
P(getting neither a red card nor a queen) =
![]()
Solution 45

Solution 46
Total number of cards = 52
(i)There
are 13 cards of spade (including 1 ace) and 3 more ace cards are there in a pack
of cards
![]() P(getting a card of spades or an ace) =
P(getting a card of spades or an ace) = ![]()
(ii)There are 2 red kings in a pack of cards
![]() P(getting a red king) =
P(getting a red king) = ![]()
(iii)There are 4 kings and 4 queens in a pack of cards
![]() P(getting either a king or a queen) =
P(getting either a king or a queen) = ![]()
(iv)P(getting
neither a king nor a queen) = ![]()
Solution 47
Total numbers = 10
Sum of given numbers = 3 + 4 + 4 + 4 + 5 + 5 + 6 + 6 + 6 + 7 = 50
∴ Mean ![]()
Let E be the event of selecting a number 5.
So, number of favourable outcomes = 2
∴ P(E) ![]()
Solution 48
Let E be the event that it will rain tomorrow.
∴ P(E) = 0.85
⇒ Probability that it will not rain tomorrow = P(not E) = 1 - P(E) = 1 - 0.85 = 0.15
Solution 49
A leap year has 366 days which means 52 complete weeks and 2 days.
That means, there are 52 Sundays and 52 Mondays in 52 weeks.
These '2 days' can be (Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday)
So, we have
Total number of outcomes = 7
Number of favourable outcomes (Sunday, Monday) = 1
∴ Probability that a leap year
has 53 Sundays and 53 Mondays ![]()
Probability Exercise MCQ
Solution 1

Solution 2
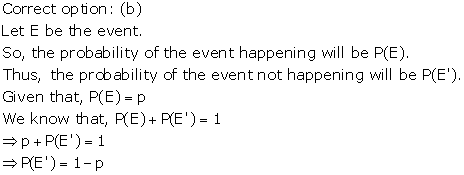
Solution 3
![]()
Solution 4
![]()
Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
Correct option: (a)
Numbers on cards are 2, 3, 4, ….., 11
∴ Total number of cards = 10
Let E be the event of getting a card with a prime number.
Prime numbers are 2, 3, 5, 7, 11.
Then, number of cards with prime numbers = 5
![]()
Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17
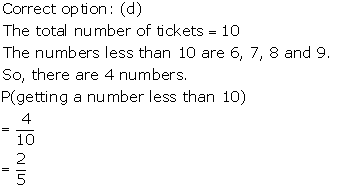
Solution 18

Solution 19
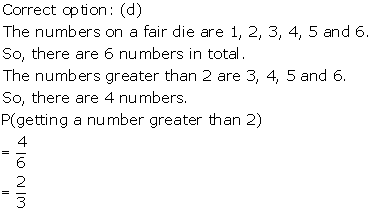
Solution 20
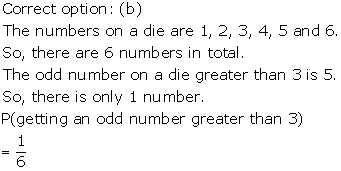
Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27
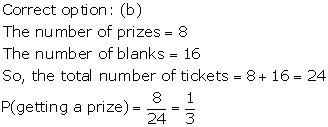
Solution 28
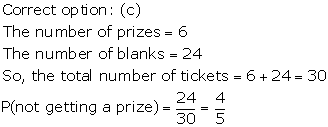
Solution 29

Solution 30

Solution 31

Solution 32

Solution 33

Solution 34

Solution 35

Solution 36

Solution 37
