ROUTERA

Chapter 17 Volume and Surface Areas of Solids

Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution

Exercise Test Yourself

Solution 2

Let space the space radius space and space height space of space one space cylinder space be space straight r space and space straight h space respectively. space And space the space radius space and space height space of space other space cylinder space be space straight R space and space straight H space respectively. Hence comma space straight H over straight h equals 1 half Also space we space have comma therefore πr squared straight h equals πR squared straight H therefore straight r squared over straight R squared equals straight H over straight h therefore straight r squared over straight R squared equals 1 half therefore straight r over straight R equals fraction numerator 1 over denominator square root of 2 end fraction

Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Volume space of space cylinder space equals space πr squared straight h equals 22 over 7 cross times 1.4 cross times 1.4 cross times straight h equals 6.16 straight h space cm cubed Now comma Volume space of space cylindrical space wire space equals space volume space of space sphere 6.16 straight h space equals space 38808 straight h space equals space fraction numerator 38808 over denominator 6.16 end fraction equals 6300 space cm straight h equals 63 space straight m Thus comma space length space of space wire space is space 63 space straight m.





Solution 9

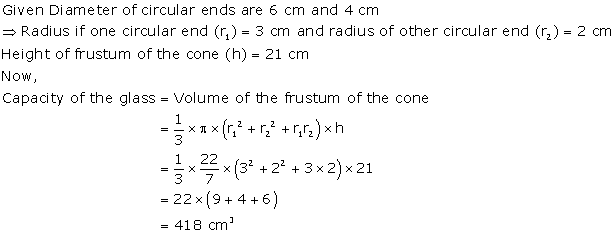
Solution 10

 

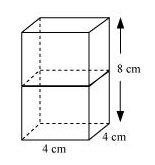
Solution 11

Solution 12

 

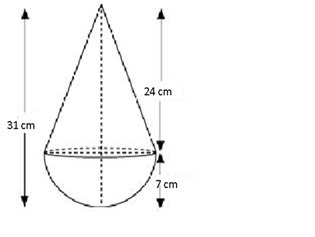
Solution 13

Solution 14

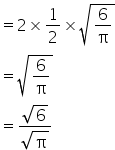
                                        equals 2 cross times 1 half cross times square root of 6 over straight pi end root equals square root of 6 over straight pi end root equals fraction numerator square root of 6 over denominator square root of straight pi end fraction

Solution 15

 

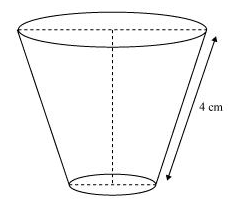
Note: Answer is incorrect in the textbook

Solution 16

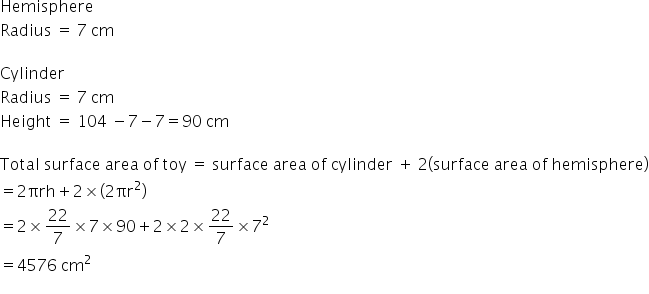
Hemisphere Radius space equals space 7 space cm Cylinder Radius space equals space 7 space cm Height space equals space 104 space minus 7 minus 7 equals 90 space cm Total space surface space area space of space toy space equals space surface space area space of space cylinder space plus space 2 left parenthesis surface space area space of space hemisphere right parenthesis equals 2 πrh plus 2 cross times open parentheses 2 πr squared close parentheses equals 2 cross times 22 over 7 cross times 7 cross times 90 plus 2 cross times 2 cross times 22 over 7 cross times 7 squared equals 4576 space cm squared

Solution 17

 

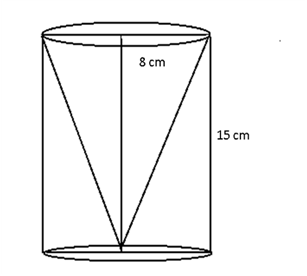
Solution 18

Solution 19

Solution 20

Volume and Surface Areas of Solids Exercise Ex. 17A

Solution 1

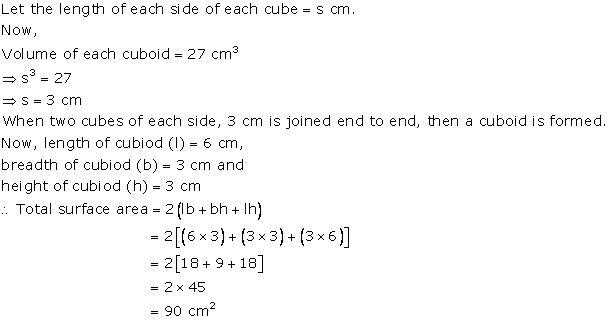
Solution 2

Solution 3

Solution 4(i)

Solution 5

Solution 6

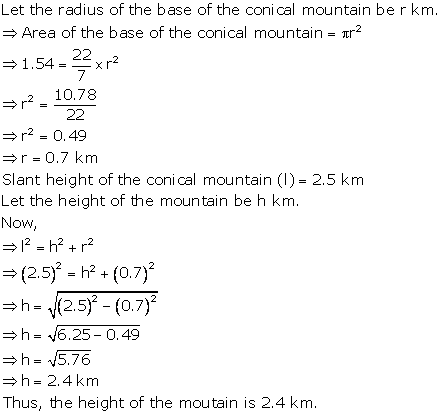
Solution 7

Solution 8

Solution 9

s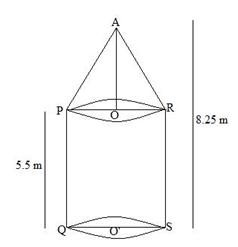  

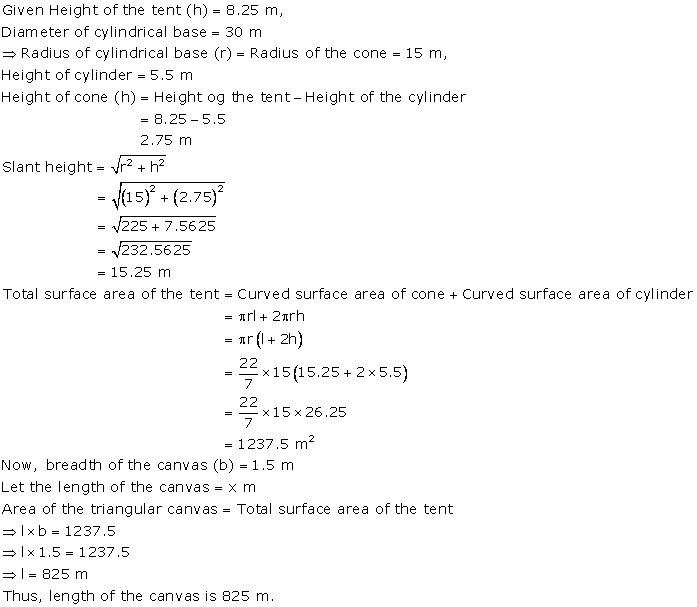
Solution 10

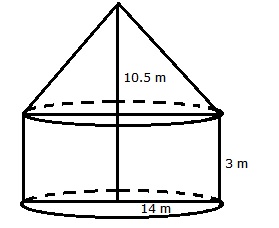
Radius of the cylinder = 14 m

And its height = 3 m

Radius of cone = 14 m

And its height = 10.5 m

Let l be the slant height

Curved surface area of tent

                    = (curved area of cylinder + curved surface area of cone)

                  

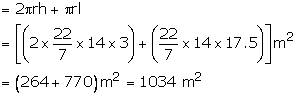
Hence, the curved surface area of the tent = 1034

Cost of canvas = Rs.(1034 × 80) = Rs. 82720

Solution 11

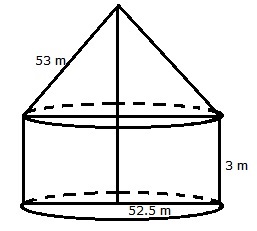
For the cylindrical portion, we have radius = 52.5 m and height = 3 m

For the conical portion, we have radius = 52.5 m

And slant height = 53 m

Area of canvas = 2rh + rl = r(2h + l)

                                

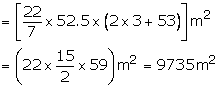
Solution 12

Radius o f cylinder = 2.5 m

Height of cylinder = 21 m

Slant height of cone = 8 m

Radius of cone = 2.5 m

Total surface area of the rocket = (curved surface area of cone

                                                              + curved surface area of cylinder + area of base)

                                                          

                                        

Solution 13

 

 

 

Solution 14

 

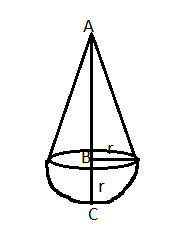
Radius = BO = r = 3.5 cm

Height of toy = AC = 15.5 cm

Height of cone = AO = h = AC - OC = 12 cm

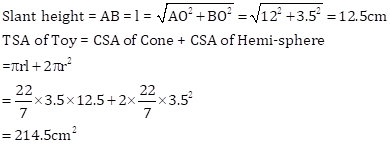
Solution 15

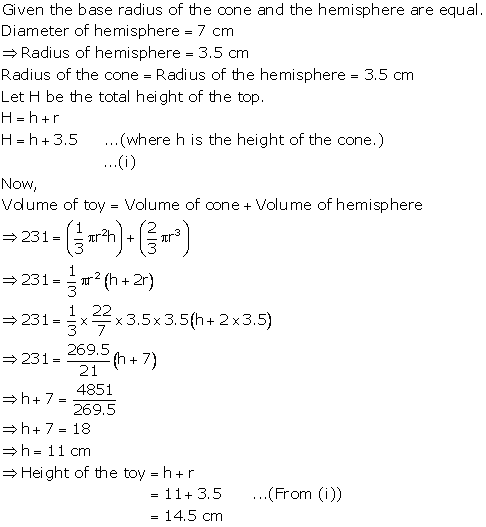
Solution 16

Solution 17

Radius of hemisphere = 10.5 cm

Height of cylinder = (14.5 - 10.5) cm = 4 cm

Radius of cylinder = 10.5 cm

Capacity = Volume of cylinder + Volume of hemisphere

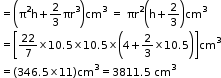
             begin mathsize 11px style equals open parentheses straight pi squared straight h plus 2 over 3 πr cubed close parentheses cm cubed space equals space πr squared open parentheses straight h plus 2 over 3 close parentheses cm cubed equals open square brackets 22 over 7 cross times 10.5 cross times 10.5 cross times open parentheses 4 plus 2 over 3 cross times 10.5 close parentheses close square brackets cm cubed equals open parentheses 346.5 cross times 11 close parentheses cm cubed equals 3811.5 space cm cubed end style

Solution 18

Solution 19

 

Solution 20

                    

Height of cylinder = 20 cm

And diameter = 7 cm and then radius = 3.5 cm

Total surface area of article

               = (lateral surface of cylinder with r = 3.5 cm and h = 20 cm)

                          

Solution 21

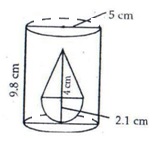
Radius of cylinder

And height of cylinder

Radius of cone r = 2.1 cm

And height of cone

Volume of water left in tub

              = (volume of cylindrical tub – volume of solid)

                        

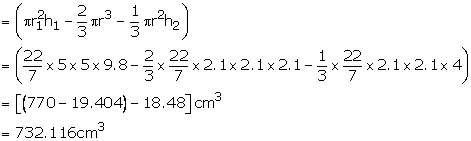
Solution 22

(i)Radius of cylinder = 6 cm

Height of cylinder = 8 cm

 

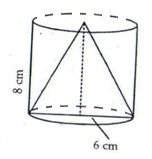
Volume of cylinder

             

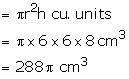
Volume of cone removed

             

The volume of remaining solid

equals space 288 straight pi space minus space 96 straight pi equals 192 straight pi equals 602.88 space cm cubed

 

(ii)Surface area of cylinder = 2 = 2× 6 × 8

Solution 23

Solution 24

Solution 25

Solution 26

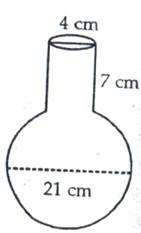
Diameter of spherical part of vessel = 21 cm

Solution 27

 

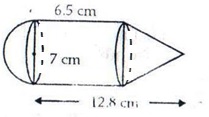
Height of cylinder = 6.5 cm

Height of cone =

Radius of cylinder = radius of cone

                          = radius of hemisphere

                         =

Volume of solid = Volume of cylinder + Volume of cone

+ Volume of hemisphere

                      

Solution 28

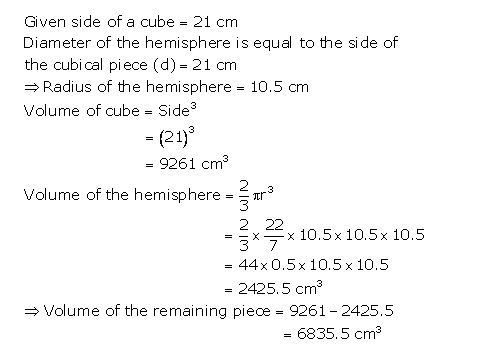
Total surface area of cube = 6(side)2

=6×212

=2646

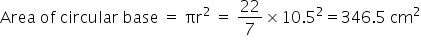
Area space of space circular space base space equals space πr squared space equals space 22 over 7 cross times 10.5 squared equals 346.5 space cm squared

Now the surface area of the remaining solid = Total surface area of the cube + curved surface area of the hemisphere - Area of the circular base of the hemisphere

=2646 + 693 - 346.5

=2992.5 cm2


Solution 29 (i)

 

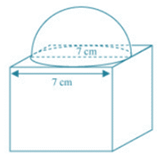
Note: In the question, cuboid is printed, but as the given data is insufficient, we are considering the shape as cube.

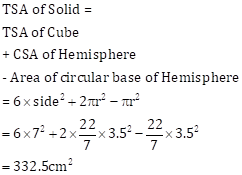
Solution 29(ii)

Solution 30

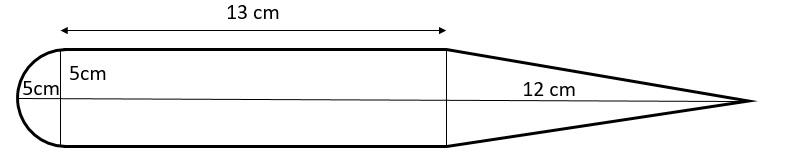
Cylinder space space straight r space equals space 5 space cm space space straight h equals space 13 space cm space space space space Hemisphere space space straight r space equals space 5 space cm space space space space Cone space space straight r space equals space 5 space cm space space straight h space equals space 12 space cm space space straight l space equals space square root of 12 squared plus 5 squared end root equals 13 space cm

 

 

Solution 31

Solution 32

 

 

Curved space surface space area space of space cylinder space equals space 2 πrh equals 2 cross times 22 over 7 cross times 2 cross times 20 equals 251.43 space cm squared So space the space area space painted space white space equals space 251.43 space plus space 88 over 7 space equals space 264 space cm squared

 


Solution 33

Volume displaced by 1 person = 0.04m3

∴ Volume displaced by 500 persons = 0.04×500 = 20m3

Now,

Volume displaced = Area of tank × height of displacement

Also,

Area of tank = 80×50 m2

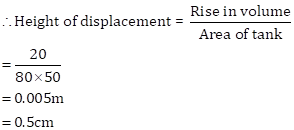
Solution 34

Canal is shaped like a cuboid,

Hence

Volume of water = lbh

Given,

b = 6 m

h = 1.5 m

l = 10 km per hour

 = 10000 m per 60 min.

 = 5000 m per 30 min.

Hence, volume of water for 30 min.

= 6×1.5×5000

= 45000

Now,

Volume of water = Volume of Area irrigated

45000 = Area irrigated × Height of standing water

Height of standing water required = 8cm = 0.08m

∴ Area irrigated = 45000/0.08

= 562500 m2

Solution 4 (ii)

Let the radius and height be 5x and 12x respectively

Hence

Volume of cone = 314cm3

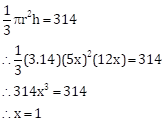
Hence,

Radius = 5cm

Height = 11cm

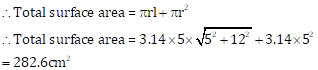
Volume and Surface Areas of Solids Exercise Ex. 17B

Solution 1

Solid cuboid

l = 9m

b = 8m

h = 2m

Volume = 9×8×2

 

Solid cube

S = 2m

Volume = s3 = 2×2×2

Solution 2

Solution 3

Solution 4

Radius of the cone = 12 cm and its height = 24 cm

Volume of cone =

                     

Solution 5

Solution 6

Internal radius = 3 cm and external radius = 5 cm

Hence, height of the cone = 4 cm

Solution 7

Solution 8

Inner radius of the bowl = 15 cm

Volume of liquid in it =

Radius of each cylindrical bottle = 2.5 cm and its height = 6 cm

Volume of each cylindrical bottle

                                      

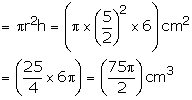
Required number of bottles =

                                      

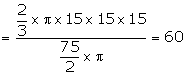
   Hence, bottles required = 60

Solution 9

Radius of the sphere=

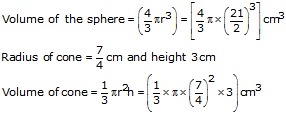
Let the number of cones formed be n, then

              

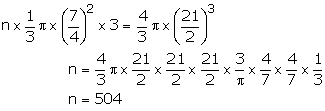
            Hence, number of cones formed = 504

Solution 10

Radius of the cannon ball = 14 cm

Volume of cannon ball =

Radius of the cone =

Let the height of cone be h cm

Volume of cone =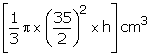

           

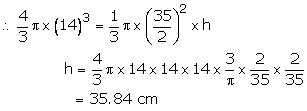
            Hence, height of the cone = 35.84 cm

Solution 11

Let the radius of the third ball be r cm, then,

           Volume of third ball = Volume of spherical ball volume of 2 small balls

          

Solution 12

External radius of shell = 12 cm and internal radius = 9 cm

Volume of lead in the shell =

Let the radius of the cylinder be r cm

Its height = 37 cm

Volume of cylinder =

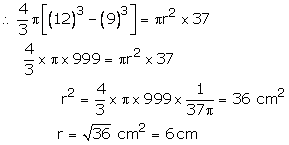
Hence diameter of the base of the cylinder = 12 cm

Solution 13

Volume of hemisphere of radius 9 cm

                                       

Volume of circular cone (height = 72 cm)

                                      

Volume of cone = Volume of hemisphere

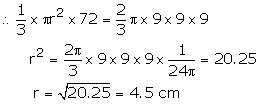
Hence radius of the base of the cone = 4.5 cm

Solution 14

Diameter of sphere = 21 cm

Hence, radius of sphere =

Volume of sphere =  =

Volume of cube = a3 = (1×1×1)

Let number of cubes formed be n

Volume of sphere = n Volume of cube

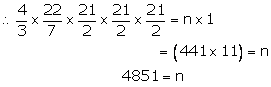
Hence, number of cubes is 4851.

Solution 15

Volume of sphere (when r = 1 cm) =  =

Volume of sphere (when r = 8 cm) =  =

Let the number of balls = n

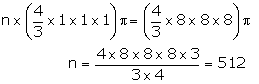
Solution 16

Radius of sphere = 3 cm

Volume of sphere =

Radius of small sphere =

Volume of small sphere =

                                

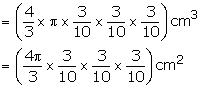
Let number of small balls be n

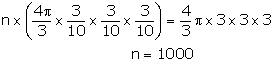
Hence, the number of small balls = 1000.

Solution 17

Diameter of sphere = 42 cm

Radius of sphere =

Volume of sphere =

Diameter of cylindrical wire = 2.8 cm

Radius of cylindrical wire =

Volume of cylindrical wire =

                                  

Volume of cylindrical wire = volume of sphere

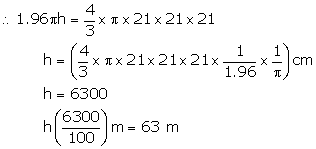
Hence length of the wire 63 m.

Solution 18

Diameter of sphere = 18 cm

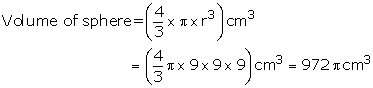
Length of wire = 108 m = 10800 cm

Let the radius of wire be r cm

                         

But the volume of wire = Volume of sphere

        

Hence the diameter = 2r = (0.3 ×  2) cm = 0.6 cm

Solution 19

Solution 20

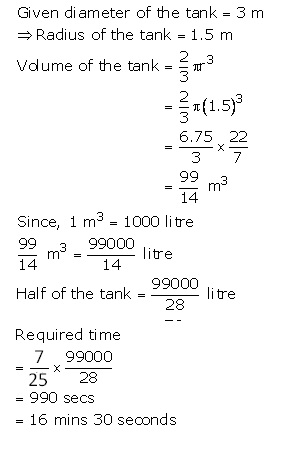
Solution 21

Solution 22

Solution 23

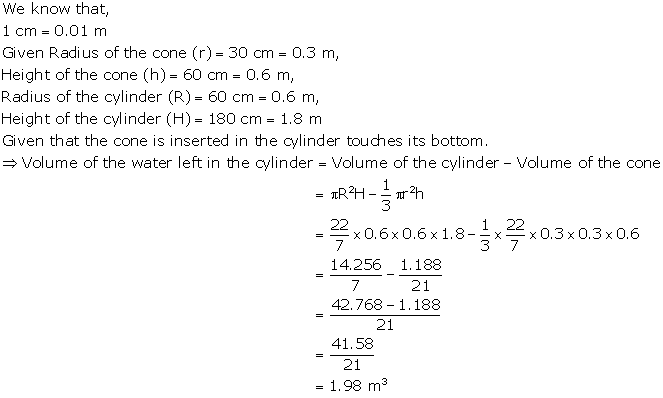
Solution 24

Solution 25

Solution 26

Canal is shaped like a cuboid,

Hence

Volume of water = lbh

Given,

b = 5.4 m

h = 1.8 m

l = 25 km per hour

 = 25000 m per 60 min.

 =  m per 40 min.

 

Hence, volume of water for 30 min.

 

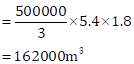
Now,

Volume of water = Volume of Area irrigated

162000 = Area irrigated × Height of standing water

Height of standing water required = 10cm = 0.1m

∴ Area irrigated = 162000/0.1

= 1620000 m2

Solution 27

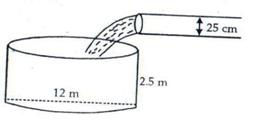
Height of cylindrical tank = 2.5 m

Its diameter = 12 m, Radius = 6 m

Volume of tank =

Water is flowing at the rate of 3.6 km/ hr = 3600 m/hr

Diameter of pipe = 25 cm, radius = 0.125 m

Volume of water flowing per hour

                         


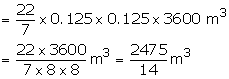
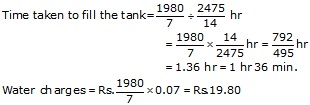
Solution 28

Solution 29

Solution 30

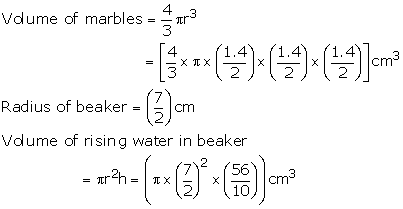
Let the number of marbles be n

n volume of marble = volume of rising water in beaker

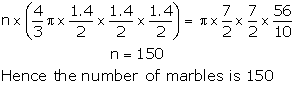
Solution 31


Solution 32

Solution 33

Solution 34

 

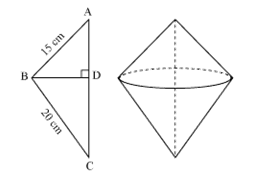
Solution 35

Cylindrical tank

d = 2 m

r = 1 m

h = 5 m

 

Volume of water for irrigation = Area of park × Standing water height

 

Recycling of water is a need of hour, since the reserves of fresh water are depleting very fast due to increase in population, manufacturing, production etc. We should keep the wastage of water minimum and recycle them as much as we can.

Volume and Surface Areas of Solids Exercise Ex. 17C

Solution 1

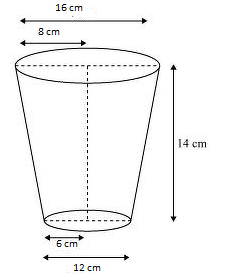
Solution 2

Solution 3

 

Solution 4

Solution 5

(i)


(ii)

Volume space of space container space equals space volume space of space frustum equals 1 third straight pi left parenthesis straight R squared plus straight r squared plus rR right parenthesis straight h equals 1 third cross times 22 over 7 cross times left parenthesis 20 squared plus 8 squared plus 20 cross times 8 right parenthesis cross times 16 equals 10459.43 space cm cubed equals 10.459 space liter Now comma space cost space of space milk space that space can space fill space the space container space at space Rs.35 space per space liter space rate space equals space Rs. space 366.08

Solution 6

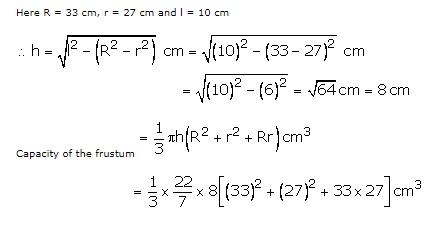
                                     = 22704 cm3

Total surface area = 

                        

Solution 7

Height = 15 cm, R = and 

Capacity of the bucket =

                              

Quantity of water in bucket = 28.49 litres

Solution 8

R = 20 cm, r = 8 cm and h = 16 cm

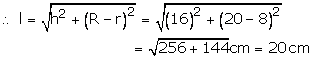
Total surface area of container =

                                         

Cost of metal sheet used =

Solution 9

R = 15 cm, r = 5 cm and h = 24 cm

 

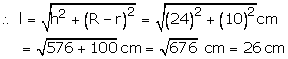
(i)Volume of bucket =

          

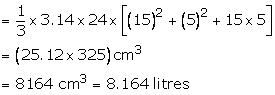
Cost of milk = Rs. (8.164 20) = Rs. 163.28

 

(ii)Total surface area of the bucket

         

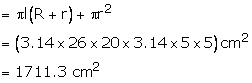
Cost of sheet =

Solution 10

= 13970g

= 13.97kg

The total cost of the oil in the container = 13.97×40 = Rs. 558.80


Solution 11

Solution 12

Solution 13

Solution 14

           

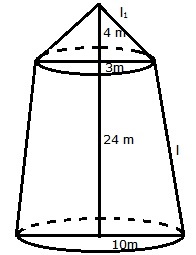
R = 10cm, r = 3 m and h = 24 m

Let l be the slant height of the frustum, then

    

Quantity of canvas = (Lateral surface area of the frustum)

                                + (lateral surface area of the cone)

                          

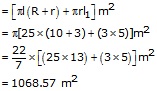
Solution 15

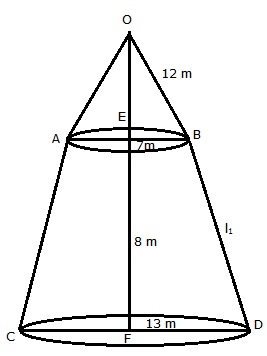
ABCD is the frustum in which upper and lower radii are EB = 7 m and FD = 13 m

Height of frustum= 8 m

Slant height of frustum

            

Radius of the cone = EB = 7 m

Slant height of cone = 12 m

Surface area of canvas required

             

Solution 16

Solution 17

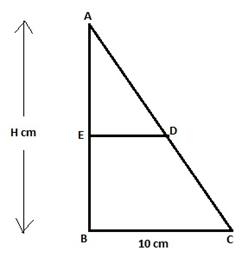
Solution 18

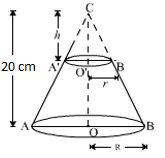
Solution 19

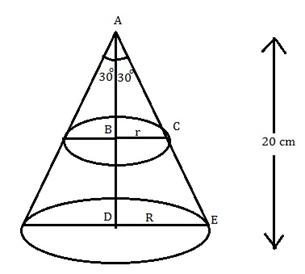
Solution 20

Solution 21




Solution 22

 

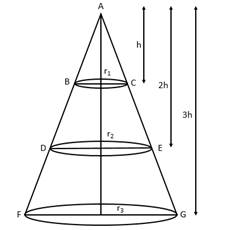
We have,

cone ABC with radius 'r1' and height 'h'

cone ADE with radius 'r2' and height '2h'

cone AFG with radius 'r3' and height '3h'

Now,

∆ABC ~ ∆ADE,

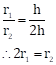
∆ABC ~ ∆AFG,

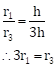
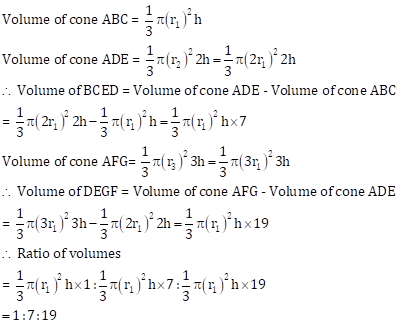
Volume and Surface Areas of Solids Exercise Ex. 17D

Solution 1

Solution 2

Solution 3

Solution 4

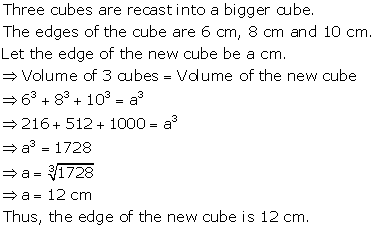
Solution 5

Solution 6

Solution 7

Solution 8

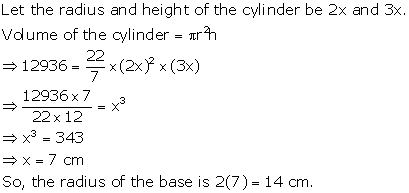
Solution 9

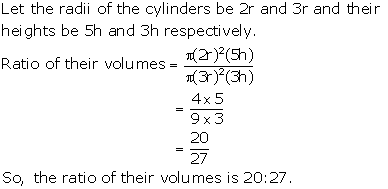
Solution 10

Solution 11

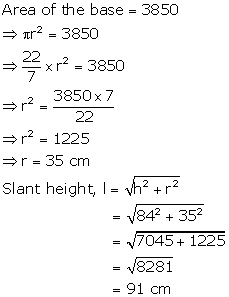
Solution 12

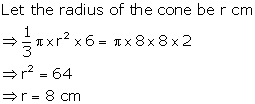
Solution 13

Solution 14

Solution 15

Solution 16

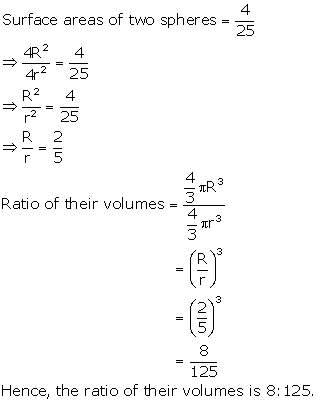
Solution 17

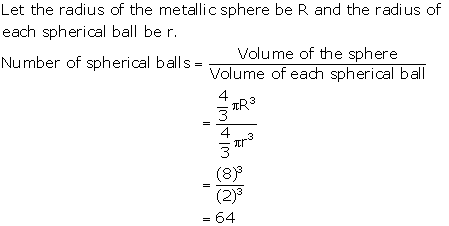
Solution 18

Solution 19

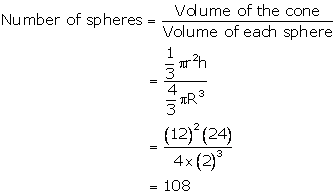
Solution 20

Solution 21

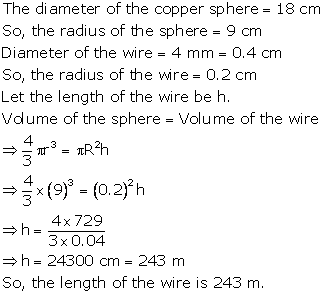
Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27

Solution 28

Solution 29

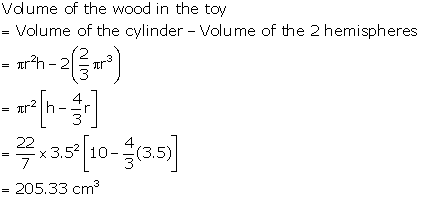
Solution 30

Solution 31

Solution 32

Solution 33

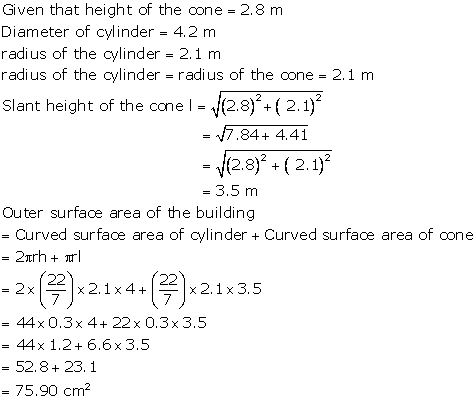
Solution 34

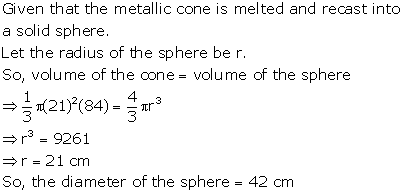
Solution 35

ch17/17.17.jpg



Solution 36

Solution 37

Solution 38

Solution 39

Solution 40

Volume and Surface Areas of Solids Exercise MCQ

Solution 1

Correct option: (a)

 

A cylindrical pencil sharpened at one edge is the combination of a cylinder and a cone. Observe the figure, the lower portion is a cylinder and the upper tapering portion is a cone.

Solution 2

Correct option: (b)

A shuttlecock used for playing badminton is the combination of a frustum of a cone and a hemisphere, the lower portion being the hemisphere and the portion above that being the frustum of the cone.

Solution 3

Correct option: (c)

A funnel is the combination of a cylinder and frustum of a cone. The lower portion is cylindrical and the upper portion is a frustum of a cone.

Solution 4

Correct option: (a)

A surahi is a combination of a sphere and a cylinder, the lower portion is the sphere and the upper portion is the cylinder.

Solution 5

Correct option: (b)

The shape of a glass (tumbler) is usually in the form of a frustum of a cone.

Solution 6

Correct option: (c)

The shape of a gill in the gilli-danda game is a combination of two cones and a cylinder. The cones at either ends with the cylinder in the middle.

Solution 7

Correct option: (a)

A plumbline (sahul) is the combination of a hemisphere and a cone, the hemisphere being on top and the lower portion being the cone.

Solution 8

Correct option: (d)

A cone is cut by a plane parallel to its base and the upper part is removed. The part that is left over is called the frustum of a cone.

Solution 9

Correct option: (c)

During conversion of a solid from one shape to another, the volume of the new shape will remain altered.

Solution 10

Correct option: (c)

In a right circular cone, the cross section made by a plane parallel to the base is a circle.

Solution 11

Solution 12

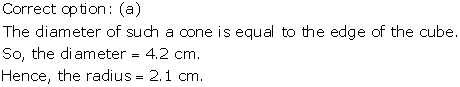
Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

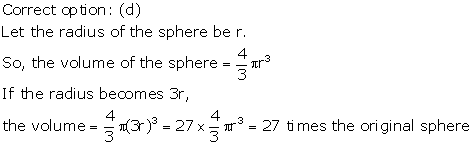
Solution 19

Solution 20

Solution 21

 

 

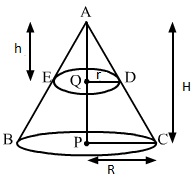
Solution 22

Solution 23

Solution 24

Correct option: (c)

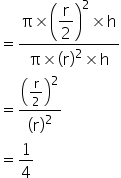
equals fraction numerator straight pi cross times open parentheses begin display style straight r over 2 end style close parentheses squared cross times straight h over denominator straight pi cross times open parentheses straight r close parentheses squared cross times straight h end fraction equals open parentheses straight r over 2 close parentheses squared over open parentheses straight r close parentheses squared equals 1 fourth

Solution 25

Solution 26

Solution 27

Solution 28

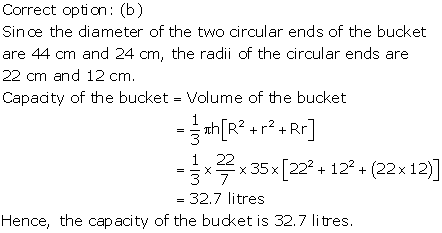
Solution 29

Solution 30

Solution 31

Solution 32

Solution 33

Solution 34

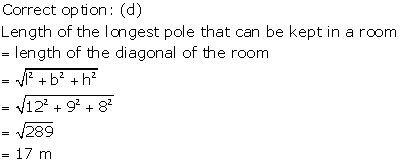
Solution 35

Solution 36

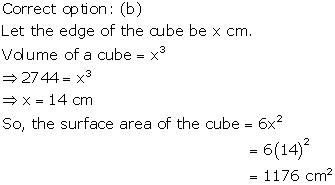
Solution 37

Solution 38

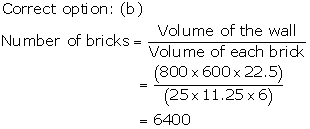
Solution 39

Solution 40

 

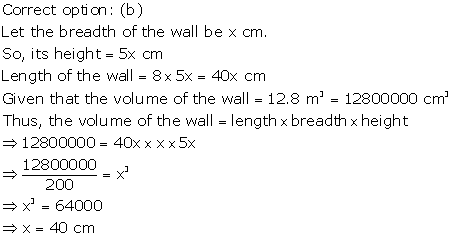
Solution 41

Solution 42

Solution 43

Solution 44

Solution 45

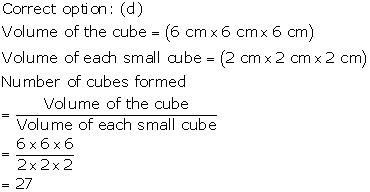
Solution 46

Solution 47

Solution 48

Solution 49

Solution 50

Solution 51

Solution 52

Solution 53

Solution 54

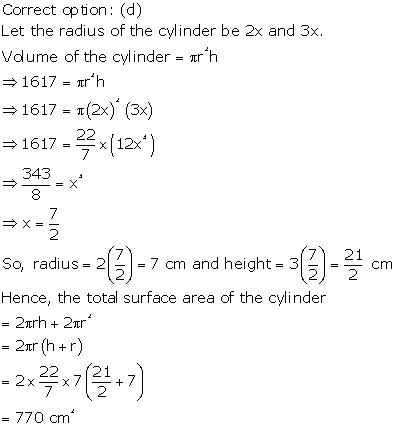
Solution 55

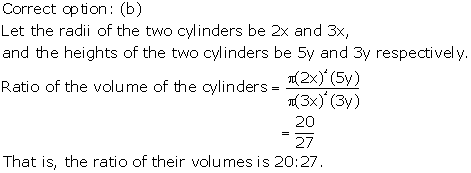
Solution 56

Solution 57

Solution 58

Solution 59

Solution 60

Solution 61

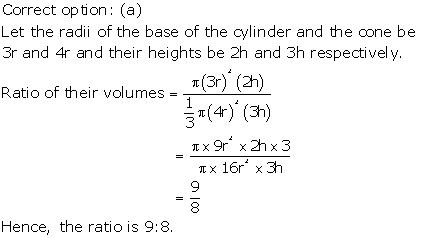
Solution 62

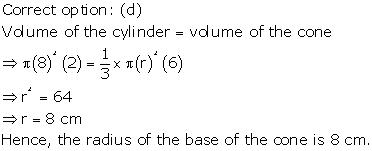
Solution 63

Solution 64

Solution 65

Solution 66

Solution 67

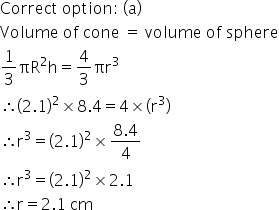
 Correct space option colon space left parenthesis straight a right parenthesis Volume space of space cone space equals space volume space of space sphere 1 third πR squared straight h equals 4 over 3 πr cubed therefore open parentheses 2.1 close parentheses squared cross times 8.4 equals 4 cross times open parentheses straight r cubed close parentheses therefore straight r cubed equals open parentheses 2.1 close parentheses squared cross times fraction numerator 8.4 over denominator 4 end fraction therefore straight r cubed equals open parentheses 2.1 close parentheses squared cross times 2.1 therefore straight r equals 2.1 space cm

Solution 68

Correct option: (a)

 

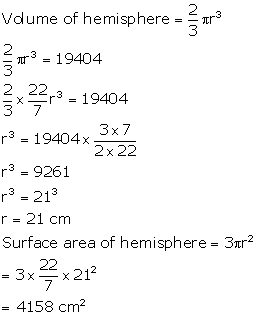
Solution 69

Correct option: (a)

 

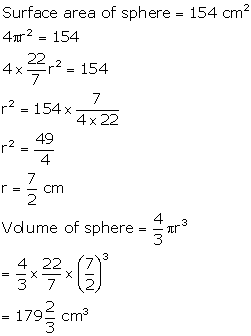
Solution 70

Solution 71

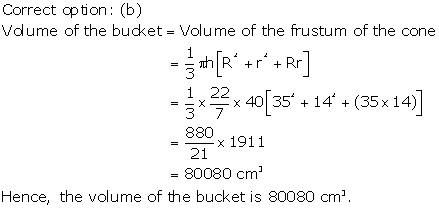
Solution 72

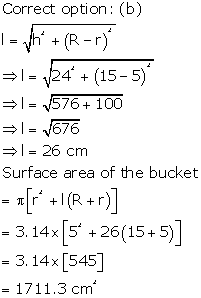
Solution 73

Solution 74

Solution 75

Solution 76

Solution 77

Solution 78

Solution 79

Solution 80