Chapter 16 Area of Circle, Sector and Segment
Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution
Area of Circle, Sector and Segment Exercise Ex. 16A
Solution 1
Circumference of circle = 2
r
= 39.6 cm
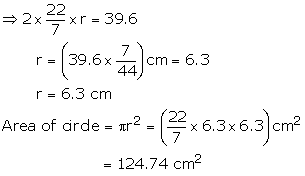
Solution 2
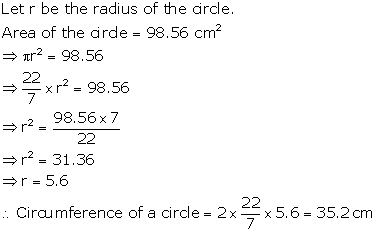
Solution 3
Solution 4
Area of square = 
Perimeter of square = 4 side = 4 22 = 88 cm
Circumference of circle = Perimeter of square
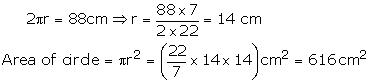
Solution 5
Area of equilateral = 
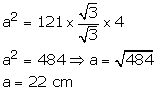
Perimeter of equilateral triangle = 3a = (3 22) cm
= 66 cm
Circumference of circle = Perimeter of circle
2
r
= 66 
r
= 
Area of circle = 
= 
Solution 6
Solution 7
Let the radii of circles be x cm and (7 - x) cm
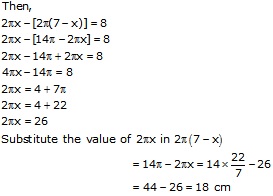
Circumference of the circles are 26 cm and 18 cm
Solution 8
Area of outer circle = 
= 1662.5 
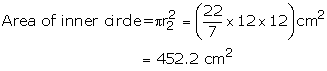
Area of ring = Outer area - inner area
= (1662.5 - 452.5) 
Solution 9
(i)
Inner radius of the circular park = 17 m
Width of the path = 8 m
Outer radius of the circular park = (17 + 8)m = 25 m
Area of path = 
(ii)
Diameter of park = 7 m
Radius r1 = 3.5 m
Width of park = 0.7 m
Bigger radius = r2 = 0.7 + 3.4 = 4.2 m
Now,
Area of path = Area of the bigger circle - Area of the smaller circle
Solution 10
Let r m and R m be the radii of inner circle and outer boundaries
respectively.
Then, 2
r
= 352 and 2R
= 396
Width of the track = (R - r) m
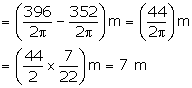
Area the track = 
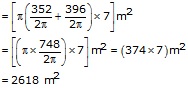
Solution 11
Length of the arc 
Length of arc = 
Area of the sector = 
Solution 12
We know that the area of a minor segment of angle θo in a circle of radius r is given by
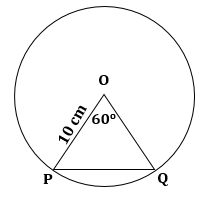
So, we have
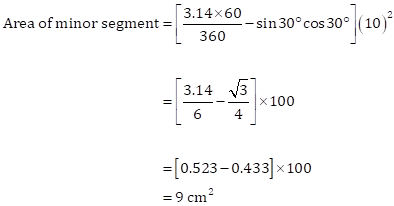
Area of a circle = pr2 = 3.14 × 10 × 10 = 314 cm2
Therefore, area of major segment
= Area of a circle - Area of minor segment
= (314 - 9) cm2
= 305 cm2
Solution 13
Length of arc = 
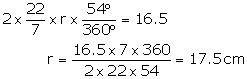
Circumference of circle = 2 
r
Area of circle = 
Solution 14
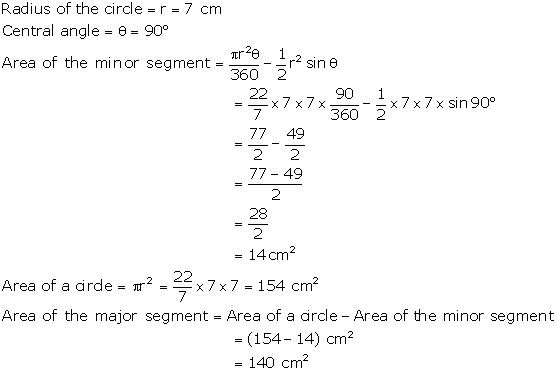
Solution 15
OAB
is equilateral.
So, 
AOB
= 60
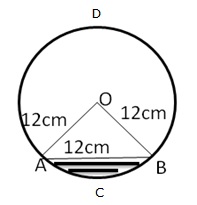
Length of arc BDA = (2
12 - arc ACB) cm
= (24
- 4)
cm = (20)
cm
= (20 3.14) cm = 62.8 cm
Area of the minor segment ACBA
Solution 16
Let OA = 
,
OB =
And AB = 10 cm
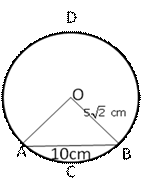
Area of 
AOB
= 
Area of minor segment = (area of sector OACBO) - (area of 
OAB)
= 
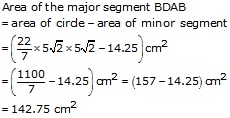
Solution 17
Area of sector OACBO
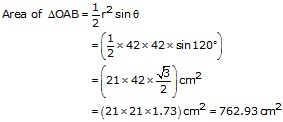
Area of minor segment ACBA
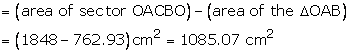
Area of major segment BADB
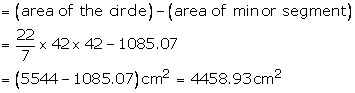
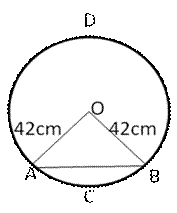
Solution 18
Let AB be the chord of the circle of centre O and radius = 30 cm such
that 
AOB
= 60°
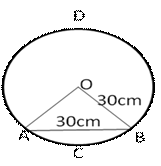
Area of the sector OACBO
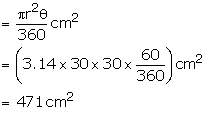
Area of 
OAB
=
=225 × 1.73 = 389.7 cm2
Area of the minor segment ACBA
= (area of the sector OACBO) - (area of the OAB)
=(471 - 389.7) 
=
81.3
Area of the major segment BADB
= (area of circle) - (area of the minor segment)
= [(3.14 × 30 × 30)
- 81.3)] =
2744.7
Solution 19
Let the major arc be x cm long
Then, length of the minor arc = 
Circumference = 
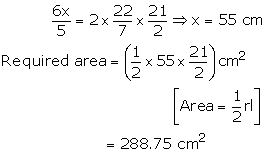
Solution 20
In 2 days, the short hand will complete 4 rounds
Distance
travelled by its tip in 2 days
=4(circumference of the circle with r = 4 cm)
= (4 × 2
× 4) cm = 32
cm
In 2 days, the long hand will complete 48 rounds
length
moved by its tip
= 48(circumference of the circle with r = 6cm)
= (48 × 2
× 6) cm = 576
cm
Sum
of the lengths moved
= (32
+ 576)
= 608
cm
= (608 × 3.14) cm = 1909.12 cm
Solution 21
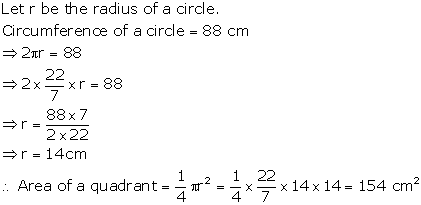
Solution 22
Area of plot which cow can graze when r = 16 m is 
= 804.5 m2
Area of plot which cow can graze when radius is increased to 23 m
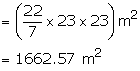
Additional ground = Area covered by increased rope - old area
= (1662.57 - 804.5) 
=
858
Solution 23
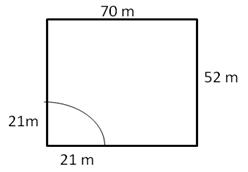
Area which the horse can graze = Area of the quadrant of radius 21 m
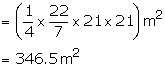
Area ungrazed = 
Solution 24
Each angle of an equilateral triangle is 60
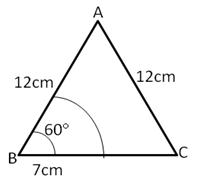
=62.352 - 25.67
=36.69 m2
Solution 25
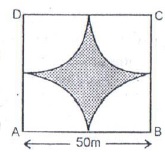
Ungrazed area
Solution 26
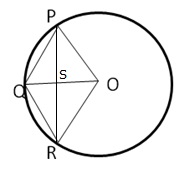
OP = OR = OQ = r
Let OQ and PR intersect at S
We know the diagonals of a rhombus bisect each other at right angle.
Therefore we have
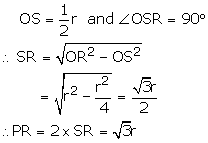
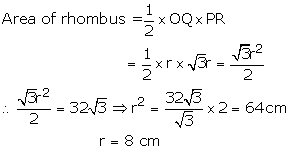
Solution 27
Diameter of the inscribed circle = Side of the square = 10 cm
Radius
of the inscribed circle = 5 cm
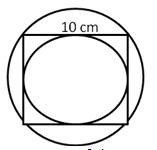
Diameter of the circumscribed circle
= Diagonal of the square
Radius of circumscribed circle = 
(i)Area of inscribed circle = 
(ii)Area of the circumscribed circle
Solution 28
Let the radius of circle be r cm
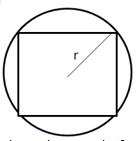
Then diagonal of square = diameter of circle = 2r cm
Area of the circle = 
Solution 29
Let the radius of circle be r cm
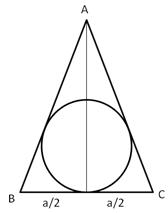
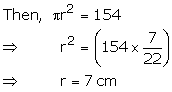
Let each side of the triangle be a cm
And height be h cm
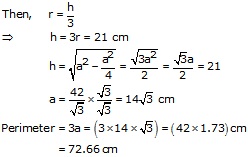
Solution 30
Radius of the wheel = 42 cm
Circumference of wheel =2
r
= 
Distance travelled = 19.8 km = 1980000 cm
Number of revolutions = 
Solution 31
Radius of wheel = 2.1 m
Circumference of wheel = 
Distance covered in one revolution = 13.2 m
Distance covered in 75 revolutions = (13.2 75) m = 990 m
= 
Distance a covered in 1 minute = 
Distance covered in 1 hour = 
Solution 32
Distance covered by the wheel in 1 revolution
The
circumference of the wheel = 198 cm
Let the diameter of the wheel be d cm
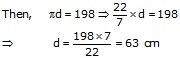
Hence diameter of the wheel is 63 cm
Solution 33
Radius of the wheel 
Circumference of the wheel = 2
r
= 
Distance covered in 140 revolution
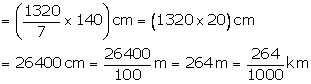
Distance covered in one hour = 
Solution 34
Radius of the wheel = r = 35 cm
Let the wheel of a motorcycle makes 'n' revolutions per minute to keep a speed of 66 km/hr.
Then, distance covered by the wheel in one revolution
= Circumference of the wheel
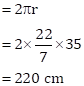
⇒ Distance covered by the wheel in 'n' revolutions = (220 × n) cm
⇒ Distance covered by the wheel in one minute = (220 × n) cm
Given, speed of the motorcycle = 66 km/hr
⇒ Wheel covers 66 km in one hour.
⇒ Distance covered by the wheel in one minute 
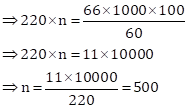
Hence, the wheel makes 500 revolutions per minute.
Solution 35
Radius of the front wheel = 40 cm = 
Circumference of the front wheel= 
Distance moved by it in 800 revolution
Circumference of rear wheel = (2
1)m = (2)
m
Required number of revolutions = 
Solution 36
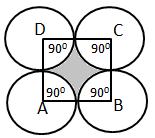
Each side of the square is 14 cm
Then, area of square = (14 × 14) 
= 196
Thus, radius of each circle 7 cm
Required area = area of square ABCD
-4 (area of sector with r = 7 cm, 
= 90°)
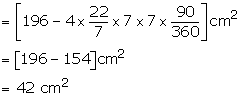
Area of the shaded region = 42
Solution 37
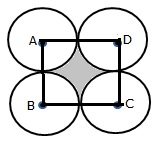
Let A, B, C, D be the centres of these circles
Join AB, BC, CD and DA
Side of square = 10 cm
Area of square ABCD
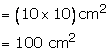
Area of each sector = 
= 19.625 
Required area = [area of sq. ABCD - 4(area of each sector)]
= (100 - 4 19.625)
= (100 - 78.5) =
21.5
Solution 38
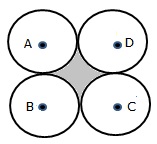
Required area = [area of square - areas of quadrants of circles]
Let the side = 2a unit and radius = a units
Area of square = (side side) = (2a 2a) sq. units
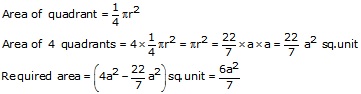
Solution 39
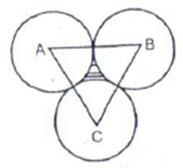
Let A, B, C be the centres of these circles. Joint AB, BC, CA
Required area=(area of 
ABC
with each side a = 12 cm)
-3(area of sector with r = 6, 
=
60°)
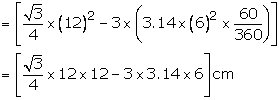
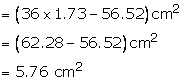
The area enclosed = 5.76 cm2
Solution 40
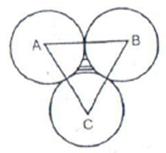
Let A, B, C be the centers of these circles. Join AB, BC, CA
Required area= (area of 
ABC
with each side 2)
-3[area of sector with r = a cm, 
=
60°]
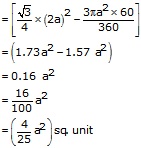
Solution 41
Solution 42
Solution 43
Solution 44
Solution 45
Solution 46
Solution 47
Solution 48
Solution 49
Solution 50
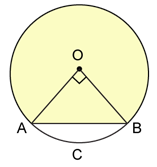
Solution 51
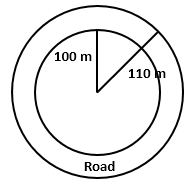
=6594 m2
cost of levelling per m2 = Rs. 20
Hence, the cost of levelling 6594 m2 = Rs. 20 × 6594 = Rs. 1,31,880
Solution 52
Area of equilateral triangle ABC = 49
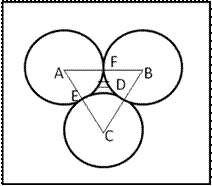
Let a be its side
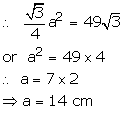
Area of sector BDF = 
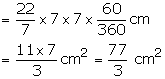
Area of sector BDF = Area of sector CDE = Area of sector AEF
Sum of area of all the sectors
Shaded
area = Area of 
ABC
- sum of area of all sectors
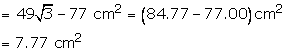
Solution 53
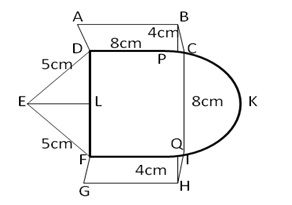
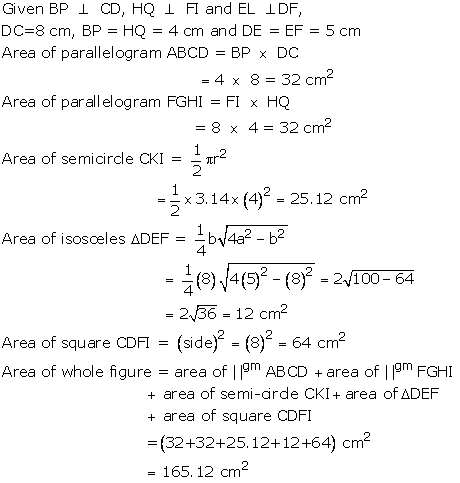
Solution 54
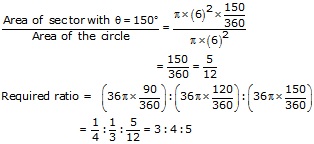
Solution 55
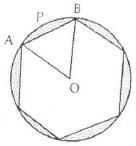
ABCDEF is a hexagon
AOB
= 60, Radius = 35 cm
Area of sector AOB
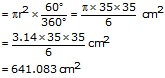
Area of 
AOB
= 
Area of segment APB = (641.083 = 530.425)
=
110.658
Area of design (shaded area) = 6 110.658=
663.948
= 663.95
Solution 56
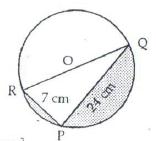
In 
PQR,
P
= 90, PQ = 24 cm, PR = 7 cm
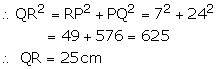
Area of semicircle
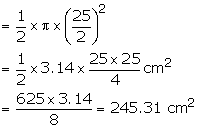
Area of PQR
= 
Shaded
area = 245.31 - 84 = 161.31 
Solution 57
In 
ABC,
A
= 90°, AB =
6cm, BC = 10 cm
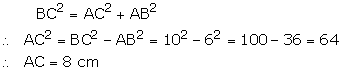
Area of ABC = 
Let r be the radius of circle of centre O
Solution 58
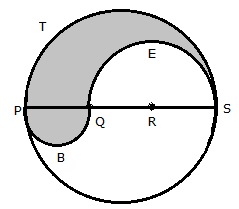
PS = 12 cm
PQ = QR = RS = 4 cm, QS = 8 cm
Perimeter = arc PTS + arc PBQ + arc QES
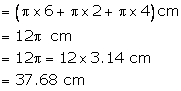
Area of shaded region = (area of the semicircle PBQ)
+ (area of semicircle PTS)-(Area of semicircle QES)
Solution 59
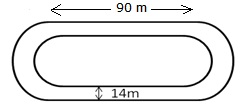
Length of the inner curved portion
= (400 - 2 90) m
= 220 m
Let the radius of each inner curved part be r
Inner radius = 35 m, outer radius = (35 + 14) = 49 m
Area
of the track = (area of 2 rectangles each 90 m 14 m)
+ (area of circular ring with R = 49 m, r = 35 m
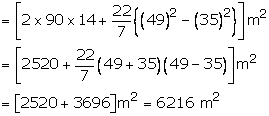
Length of outer boundary of the track
Solution 60
Area of rectangle ABCD = 21 cm × 14 cm = 294 cm2
Diameter of a semicircle = BC = 14 cm
⇒ Radius of a semicircle = 7 cm
Then, area of a semicircle 
cm2
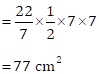
Therefore, area of shaded region
= Area of rectangle ABCD - Area of semicircle
= (294 - 77) cm2
= 217 cm2
Now, perimeter of the shaded region
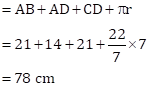
Solution 61
Area of the region ABDC = Area of sector AOB - Area of sector COD
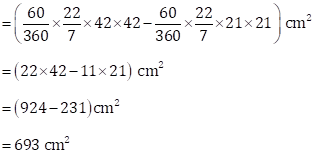
Area of the circular ring 
= (5544 - 1386) cm2
= 4158 cm2
Therefore, area of the shaded region
= Area of the circular ring - Area of the region ABDC
= (4158 - 693) cm2
= 3465 cm2
Solution 62
Area of each semicircle of diameter 3 cm
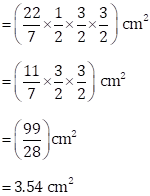
Area of the circle of diameter 4.5 cm 
Area of the semicircle of radius 4.5 cm 
Now, area of the shaded region
= Area of the semicircle of radius 4.5 cm - Area of the circle - 2(area of semicircle of diameter 3 cm) + Area of semicircle of diameter 3 cm
= Area of the semicircle of radius 4.5 cm - Area of the circle -Area of semicircle of diameter 3 cm
= (31.82 - 15.92 - 3.54) cm2
= 12.36 cm2
Solution 63
Area of a square = (28 cm)2 = 784 cm2
Radius of each circle = 
Then, area of each circle = 
Now, area of each quadrant of circle = 
Therefore, area of the shaded region
= Area of a square + Area of two circles - Area of two quadrants
= [784 + 2(616) - 2(154)] cm2
= [784 + 1232 - 308] cm2
= 1708 cm2
Solution 64
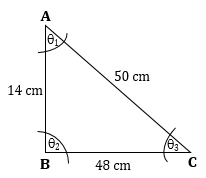
Let ∠A = q1, ∠B = q2, and ∠C = q3.
Now, area of three sectors with central angles q1, q2 and q3 and each with radius 5 cm
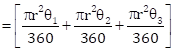
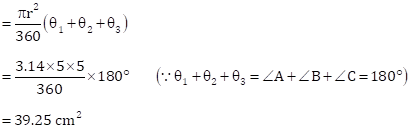
Sides of triangle ABC are as follows:
a = AB = 14 cm
b = BC = 48
c = CA = 50 cm
Then,
(s - a) = (56 - 14) = 42 cm
(s - b) = (56 - 48) = 8 cm
(s - c) = (56 - 50) = 6 cm
Therefore, area of triangle ABC
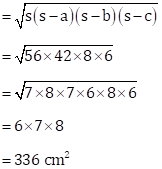
Hence, area of the shaded region
= Area of triangle ABC - Area of three sectors
= 336 - 39.25
= 296.75 cm2
Solution 65
Let the diameters of the given concentric circles be x, 2x and 3x respectively.
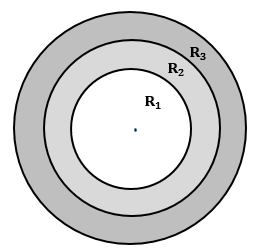
So, we have
Area of R1 = Area of circle
with radius x units
Area of R2 = Area of circle
with radius 2x units - Area of circle with radius x units
Area of R3 = Area of circle
with radius 3x units - Area of circle with radius 2x units
Therefore, ratio of the areas of three regions
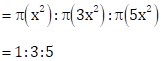
Solution 66
Let the radius of a circular playground = r
Now, area of a circular playground = 22176 cm2
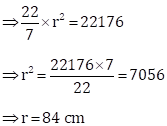
Then, circumference of a circular playground 
Cost of fencing per metre ground = Rs. 50
So, cost of fencing 5.28 m ground = Rs. 50 × 5.28 = Rs. 264
Area of Circle, Sector and Segment Exercise Ex. 16B
Solution 1
Solution 2
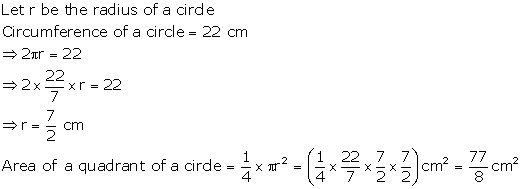
Solution 3
Solution 4
Solution 5
Since square circumscribes a circle of radius a cm, we have
Side of the square = 2 ⨯ radius of circle = 2a cm
Then, Perimeter of the square = (4 ⨯ 2a) = 8a cm
Solution 6
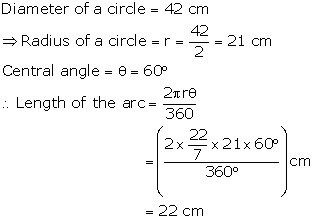
Solution 7
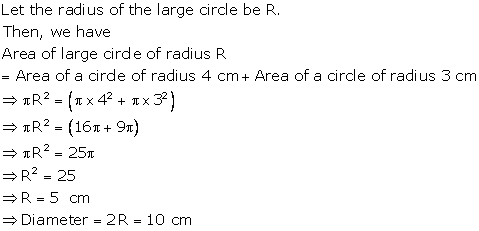
Solution 8
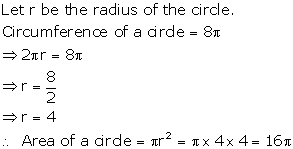
Solution 9
Solution 10
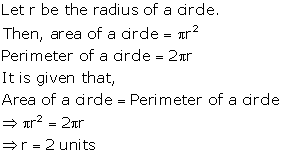
Solution 11
Solution 12
Solution 13
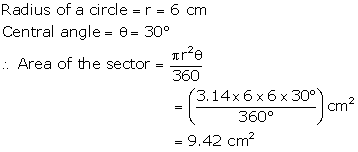
Solution 14
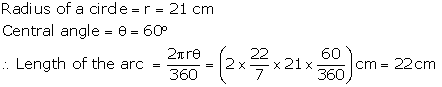
Solution 15
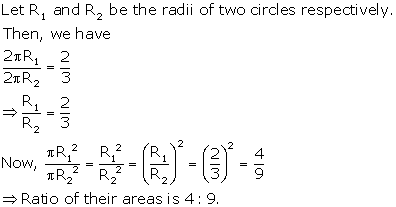
Solution 16
Solution 17
Solution 18
Solution 19
Length of the pendulum = radius of sector = r cm
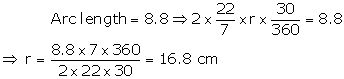
Solution 20
Angle described by the minute hand in 60 minutes = 360°
Angle described by minute hand in 20 minutes
Required area swept by the minute hand in 20 minutes
=Area of the sector(with r = 15 cm and 
= 120°)
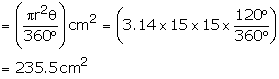
Solution 21
=
56o and let radius is r cm
Area of sector = 
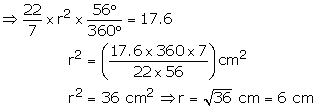
Hence radius= 6cm
Solution 22
Area of the sector of circle = 
Radius = 10.5 cm
Solution 23
Let sector of circle is OAB
Perimeter of a sector of circle =31 cm
OA + OB + length of arc AB = 31 cm
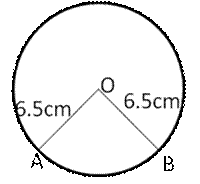
6.5 + 6.5 + arc AB = 31 cm
arc AB = 31 - 13
= 18 cm
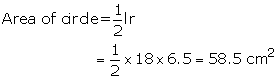
Solution 24
Length of arc of circle = 44 cm
Radius of circle = 17.5 cm
Area of sector = 
Solution 25
Solution 26
Solution 27
Solution 28
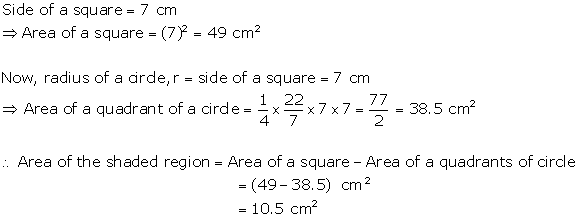
Solution 29
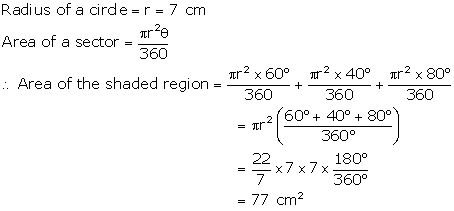
Solution 30
Solution 31
Solution 32
Solution 33
Solution 34
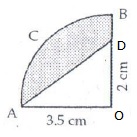
Shaded area = (area of quadrant) - (area of DAOD)
Solution 35
Solution 36
Solution 37
Solution 38
Solution 39
Solution 40
Solution 41
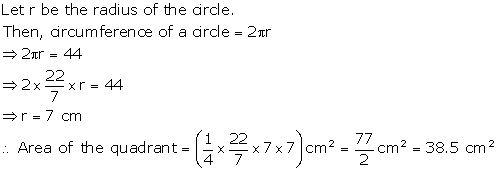
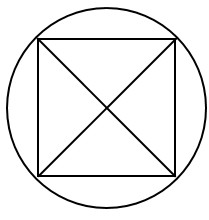
Solution 42
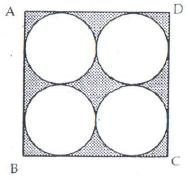
Side of the square ABCD = 14 cm
Area of square ABCD = 14 14 = 196 
Radius of each circle = 
Area of the circles = 4 area of one circle
Area of shaded region = Area of square - area of 4 circles
= 196 - 154 = 42
Solution 43
Solution 44
Solution 45
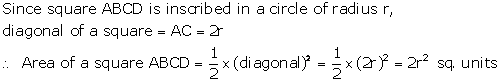
Solution 46
Solution 47
Area of rectangle = (120 × 90) 
= 10800
Area of circular lawn = [Area of rectangle - Area of park excluding circular lawn]
= [10800 - 2950] =
7850
Area of circular lawn = 7850 
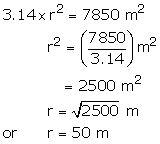
Hence, radius of the circular lawn = 50 m
Solution 48
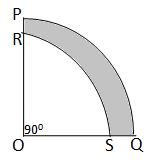
Area of flower bed = (area of quadrant OPQ)
-(area of the quadrant ORS)
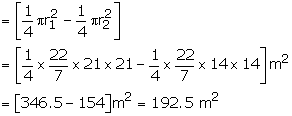
Solution 49
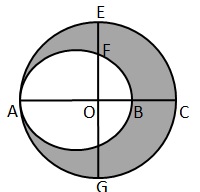
Diameter of bigger circle = AC = 54 cm
Radius of bigger circle = 
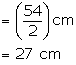
Diameter AB of smaller circle
Radius of smaller circle = 
Area of bigger circle = 
= 2291. 14 
Area of smaller circle = 
= 1521. 11
Area of shaded region = area of bigger circle - area of smaller circle
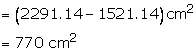
Solution 50
Solution 51
Area of Circle, Sector and Segment Exercise MCQ
Solution 1
Solution 2
Solution 3
Solution 4
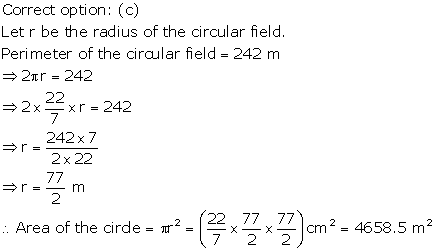
Solution 5
Solution 6
Solution 7
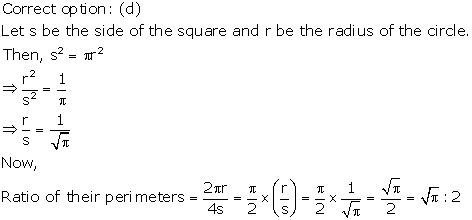
Solution 8
Solution 9
Solution 10
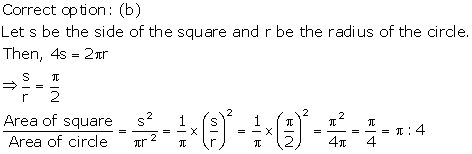
Solution 11
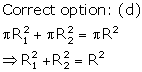
Solution 12
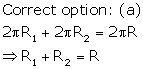
Solution 13
Solution 14
Solution 15
Solution 16
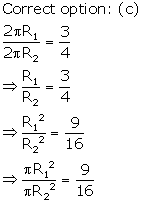
Solution 17
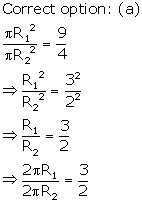
Solution 18
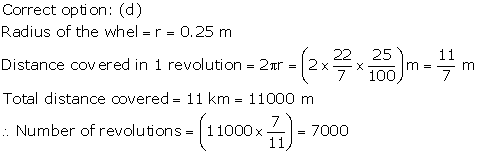
Solution 19
Solution 20
Solution 21
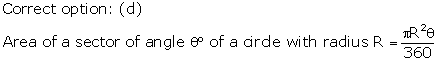
Solution 22
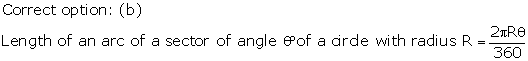
Solution 23
Solution 24
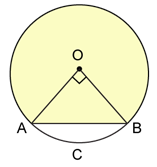
Solution 25
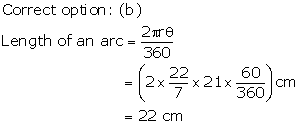
Solution 26
Area of Circle, Sector and Segment Exercise Test Yourself
Solution 1
Solution 2
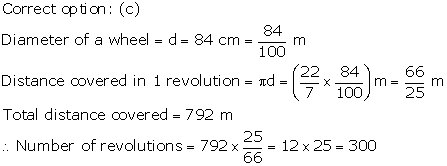
Solution 3
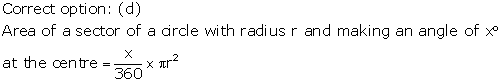
Solution 4
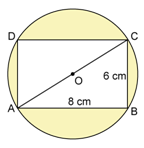
Solution 5
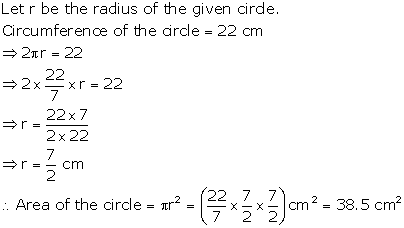
Solution 6
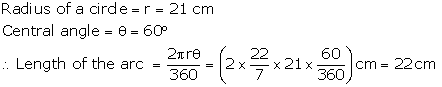
Solution 7
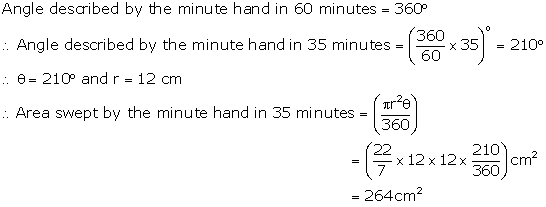
Solution 8
Solution 9
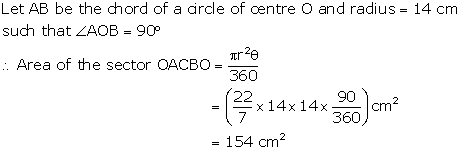
Solution 10
Solution 11
Solution 12
Solution 13
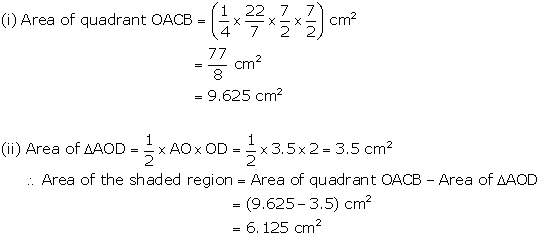
Solution 14
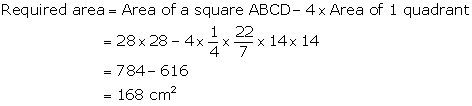
Solution 15
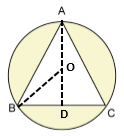
Solution 16
Solution 17
Solution 18
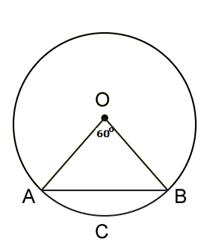
Solution 19
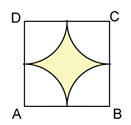
Solution 20
