Chapter 15 Perimeter and Area of Plane Figures
Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution
Perimeter and Area of Plane Figures Exercise Ex. 15A
Solution 1
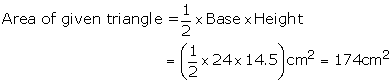
Solution 2
Let a = 42 cm, b = 34 cm and c = 20 cm
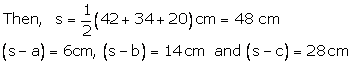
(i)Area of triangle = 
(ii)Let base = 42 cm and corresponding height = h cm
Then area of
triangle = 
Hence, the height corresponding to the longest side = 16 cm
Solution 3
Let a = 18 cm, b = 24 cm, c = 30 cm
Then,2s = (18 + 24 + 30) cm = 72 cm
s = 36 cm
(s a) = 18cm, (s b) = 12 cm and (s c) = 6 cm
(i)Area of triangle = 
(ii)Let base = 18 cm and altitude = x cm
Then, area of
triangle = 
Hence, altitude corresponding to the smallest side = 24 cm
Solution 4
On dividing 150 m in the ratio 5 : 12 : 13, we get
Length of one side = 
Length of the second side = 
Length of third side = 
Let a = 25 m, b = 60 m, c = 65 m
(s a) = 50 cm, (s b) = 15 cm, and (s c) = 10 cm
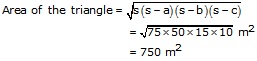
Hence, area of the triangle = 750 m2
Solution 5
On dividing 540 m in the ratio 25 : 17 : 12, we get
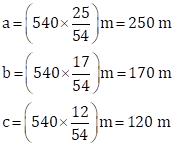
Then,
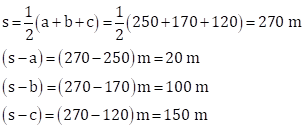
Therefore, area of triangular field
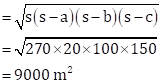
Cost of ploughing 100 m2 field = Rs. 40
Then, cost of ploughing 9000 m2 field 
Solution 6
Let the length of one side be x cm
Then the length of other side = {40 (17 + x)} cm = (23 - x)
cm
Hypotenuse = 17 cm
Applying Pythagoras theorem, we get
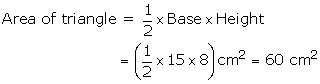
Hence, area of the triangle = 60 cm2
Solution 7
Let the sides containing the right - angle be x cm and (x - 7) cm
One side = 15 cm and other = (15 - 7) cm = 8 cm
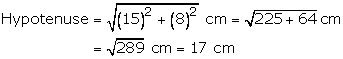
perimeter
of triangle (15 + 8 + 17) cm = 40 cm
Solution 8
Let the sides containing the right angle be x and (x-2) cm
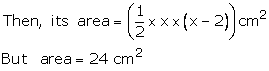
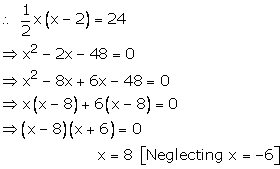
One side = 8 cm, and other (8-2) cm = 6 cm
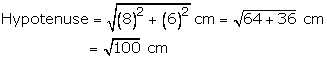
= 10 cm
Therefore, perimeter of the triangle = 8 + 6 + 10 = 24 cm
Solution 9
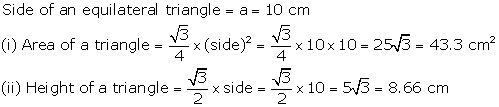
Solution 10
Let each side of an equilateral triangle = 
cm
Then,
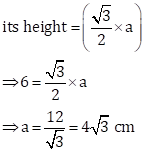
Therefore, area of an equilateral triangle
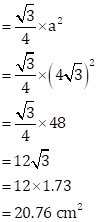
Solution 11
Let each side of the equilateral triangle be a cm
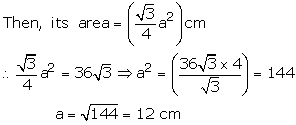
Perimeter of equilateral triangle = 3a = (3x12) cm = 36 cm
Solution 12
Let each side of the equilateral triangle be a cm
area
of equilateral triangle =
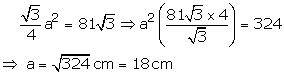
Height of equilateral triangle
Solution 13
Base of right angled triangle = 48 cm
Height of the right angled triangle =
Solution 14
Let the hypotenuse of right - angle triangle = 65cm
Base = 60 m
Hence, perpendicular = 25 cm and area of the triangle =750 cm2
Solution 15
The circumcentre of a right - triangle is the midpoint of the hypotenuse
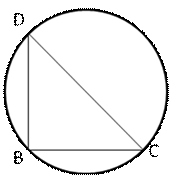
Hypotenuse = 2 × (radius of circumcircle)
= (2 × 8) cm = 16 cm
Base = 16 cm, height = 6 cm
Area of right angled triangle
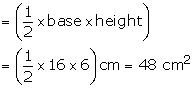
Hence, area of the triangle= 48 cm2
Solution 16
Let each equal side be a cm in length.
Then,
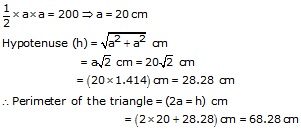
Hence, hypotenuse = 28.28 cm and perimeter = 68.28 cm
Solution 17
Let each equal side be a cm and base = 80 cm
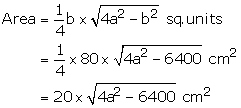
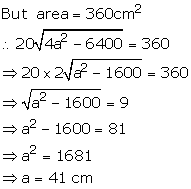
perimeter
of triangle = (2a + b) cm
= (2 41 + 80) cm
= (82 + 80) cm = 162 cm
Hence, perimeter of the triangle = 162 cm
Solution 18
Let the height be h cm, then a= (h + 2) cm and b = 12 cm
Squaring both sides,
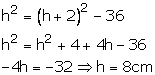
Therefore, a = h + 2 = (8 + 2)cm = 10 cm
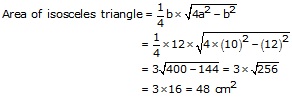
Hence, area of the triangle = 48 cm2.
Solution 19
Let 
ABC
is a isosceles triangle. Let AC, BC be the equal sides
Then AC = BC = 10cm. Let AB be the base of ABC
right angle at C.
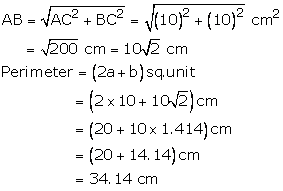
Area of right isosceles triangle ABC
Hence, area = 50 cm2 and perimeter = 34.14 cm
Solution 20
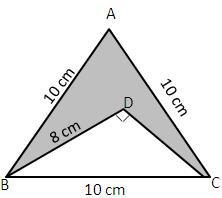
Area of shaded region = Area of 
ABC
– Area of DBC
First we find area of ABC
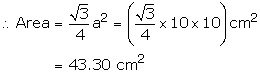
Second we find area of DBC
which is right angled
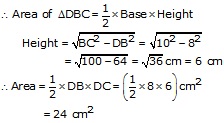
Area of shaded region = Area of ABC
– Area of DBC
= (43.30 - 24) 
=
19. 30
Area of shaded region = 19.3
Perimeter and Area of Plane Figures Exercise Ex. 15B
Solution 1
Let the length of a rectangular plot = L m
Given, perimeter = 80 m and breadth = 16 m
Now,
Perimeter of a rectangular plot = 2(Length + Breadth)
⇒ 80 = 2(L + 16)
⇒ 40 = L + 16
⇒ L = 24 m
Therefore, area of the plot = Length × Breadth
= 24 m × 16 m
= 384 m2
Solution 2
Solution 3
Let the other side of a rectangle = 
cm
Then, by Pythagoras theorem,
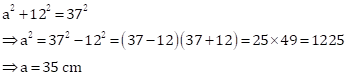
And, area of a rectangle = 35 cm × 12 cm = 420 cm2
Solution 4
Let the breadth of a rectangular plot = 
m
Given, area of the rectangular plot = 462 m2
⇒ Length × Breadth = 462
⇒ 28 × =
462
⇒ =
16.5 cm
Now, perimeter of a rectangular plot = 2(Length + Breadth)
= 2(28 + 16.5)
= 2(44.5)
= 89 m
Solution 5
Solution 6
Solution 7
Area of floor = Length Breadth
Area of carpet = Length Breadth
= 
Number of carpets =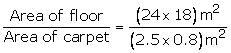 
= 216
Hence the number of carpet pieces required = 216
Solution 8
Area of verandah = (36 × 15) 
=
540
Area of stone = (0.6 × 0.5) [10
dm = 1 m]
Number of stones required = 
Hence, 1800 stones are required to pave the verandah.
Solution 9
Perimeter of rectangle = 2(l + b)
2(l
+ b) = 56 Þ
l + b = 28 cm
b = (28 l) cm
Area of rectangle = 192
l (28 l) = 192
28l - 
=
192
-
28l + 192 = 0
-
16l 12l + 192 = 0
l(l 16) 12(l 16) = 0
(l 16) (l 12) = 0
l = 16 or l = 12
Therefore, length = 16 cm and breadth = 12 cm
Solution 10
Length of the park = 35 m
Breadth of the park = 18 m
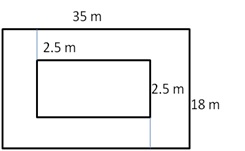
Area of the park = (35 18) 
=
630
Length of the park with grass =(35 5) = 30 m
Breadth of the park with grass = (18- 5) m = 13 m
Area of park with grass = (30 13) =
390
Area of path without grass = Area of the whole park area of park with grass
= 630 -
390 =
240
Hence, area of the park to be laid with grass = 240 m2
Solution 11
Length of the plot = 125 m
Breadth of the plot = 78 m
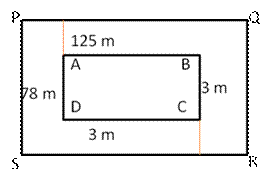
Area of plot ABCD = (125 78) 
=
9750
Length of the plot including the path= (125 + 3 + 3) m = 131 m
Breadth of the plot including the path = (78 + 3 + 3) m = 84 m
Area of plot PQRS including the path
= (131 84) =
11004
Area of path = Area of plot PQRS Area of plot ABCD
= (11004 9750)
= 1254
Cost of gravelling = Rs 75 per m2
Cost
of gravelling the whole path = Rs. (1254 75) = Rs.
94050
Hence, cost of gravelling the path = Rs 94050
Solution 12(i)
Area of rectangular field including the foot path = (54
35) 
Let the width of the path be x m
Then, area of rectangle plot excluding the path = (54 2x) (35 2x)
Area of path = (54 35) (54 2x) (35 2x)
(54 35) (54 2x) (35 2x) = 420
1890 1890 + 108x + 70x - 4
= 420
178x - 4
= 420
4
- 178x + 420 = 0
2
- 89x + 210 = 0
2
- 84x 5x + 210 = 0
2x(x 42) 5(x 42) = 0
(x 42) (2x 5) = 0
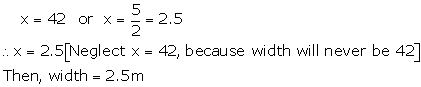
Solution 12(ii)
Let the width of the border = b m
Then, the length of a carpet = (8 - b - b) = (8 - 2b) m
And, the breadth of a carpet = (5 - b - b) = (5 - 2b) m
∴ Area of a carpet = (8 - 2b) × (5 - 2b) = (40 - 26b + 4b2) m2
Length of a room = 8 m
Breadth of a room = 5 m
∴ Area of a room = 8 × 5 = 40 m2
Given, area of border = 12 m2
Now,
Area of a carpet = Area of a room - Area of a border
⇒ (40 - 26b + 4b2) = 40 - 12
⇒ 4b2 - 26b + 12 = 0
⇒ 2b2 - 13b + 6 = 0
⇒ 2b2 - 12b - b + 6 = 0
⇒ 2b(b - 6) - (b - 6) = 0
⇒ (b - 6)(2b - 1) = 0
⇒ b - 6 = 0 or 2b - 1 = 0
⇒ b = 6 or b = ½
b ≠ 6 as width of the border cannot be greater than width of the room.
⇒ b = ½ = 0.5 m = 50 cm
Hence, the width of the carpet is 50 cm.
Solution 13
Let the length and breadth of a rectangular garden be 9x and 5x.
Then, area of garden = (9x 5x)m = 45
Length of park excluding the path = (9x 7) m
Breadth of the park excluding the path = (5x 7) m
Area of the park excluding the path = (9x 7)(5x 7) 
Area
of the path = 
(98x
49) = 1911
98x = 1911 + 49
Length = 9x = 9 20 = 180 m
Breadth = 5x = 5 20 = 100 m
Hence, length = 180 m and breadth = 100 m
Solution 14
Solution 15
Let the width of the grass strip = b m
Then, the length of the pond = (50 - b - b) = (50 - 2b) m
And, the breadth of the pond = (40 - b - b) = (40 - 2b) m
∴ Area of the pond = (50 - 2b) × (40 - 2b) = (2000 - 180b + 4b2) m2
Length of a park = 50 m
Breadth of a park = 40 m
∴ Area of a park = 50 × 40 = 2000 m2
Given, area of the grass strip = 1184 m2
Now,
Area of the pond = Area of a park - Area of the grass strip
⇒ (2000 - 180b + 4b2) = 2000 - 1184
⇒ 4b2 - 180b + 1184 = 0
⇒ b2 - 45b + 296 = 0
⇒ b2 - 37b - 8b + 296 = 0
⇒ b(b - 37) - 8(b - 37) = 0
⇒ (b - 37)(b - 8) = 0
⇒ b - 37 = 0 or b - 8 = 0
⇒ b = 37 or b = 8
b ≠ 37 as width of the grass strip at both ends is exceeding 50 m.
⇒ b = 8 m
⇒ Length of the pond = 50 - 2(8) = 34 m and breadth of the pond = 40 - 2(8) = 24 m.
Solution 16
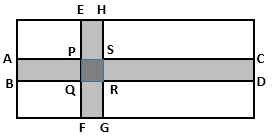
Solution 17
Solution 18
Solution 19
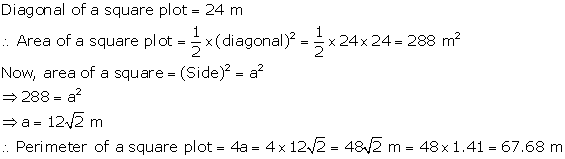
Solution 20
Area of the square = 
Let diagonal of square be x
Length of diagonal = 16 cm
Side of square = 
Perimeter of square = [4 side] sq. units
=[ 4 11.31] cm = 45.24 cm
Solution 21
Let d meter be the length of diagonal
Area of square field = 
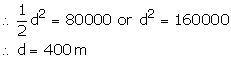
Time taken to cross the field along the diagonal
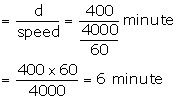
Hence, man will take 6 min to cross the field diagonally.
Solution 22
Solution 23
Rs. 14 is the cost of fencing a length = 1m
Rs. 28000 is the cost of fencing the length= 
Perimeter = 4 side = 2000
side
= 500 m
Area of a square = 
= 250000 
Cost of mowing the lawn =
Solution 24
Solution 25
ABCD be the given quadrilateral in which AD = 24 cm, BD = 26 cm, DC = 26 cm and BC = 26 cm
By Pythagoras theorem
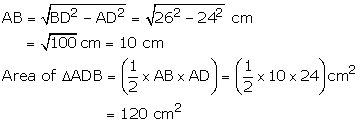
For area of equilateral 
DBC,
we have
a = 26 cm
Area of quad. ABCD = Area of ABD
+ Area of DBC
= (120 + 292.37) 
=
412.37
Perimeter ABCD = AD + AB + BC + CD
= 24 cm + 10 cm + 26 cm + 26 cm
= 86 cm
Solution 26
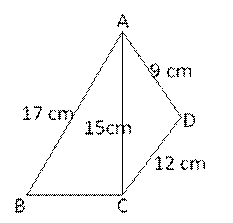
Area of quad. ABCD = Area of 
ABC
+ Area of ACD
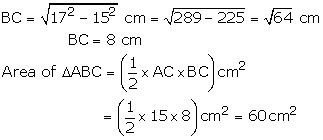
Now, we find area of a ACD
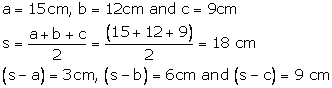
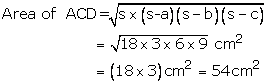
Area of quad. ABCD = Area of ABC
+ Area of ACD
Perimeter of quad. ABCD = AB + BC + CD + AD
=(17 + 8 + 12 + 9) cm
= 46 cm
Perimeter
of quad. ABCD = 46 cm
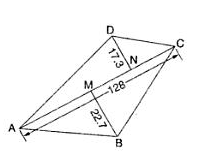
Solution 27
Area of quad. ABCD = Area of 
ABD
+ Area ofDBC
For area of ABD
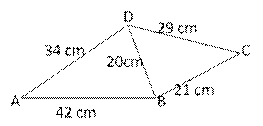
Let a = 42 cm, b = 34 cm, and c = 20 cm
For area of DBC
a = 29 cm, b = 21 cm, c = 20 cm
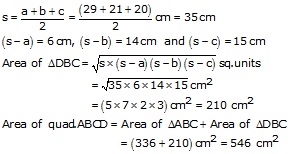
Solution 28
Area of the ||gm = (base height) sq. unit
= (25 16.8) 
Solution 29
Longer side = 32 cm, shorter side = 24 cm
Distance between longer sides = 17.4 cm
Let the distance between the shorter sides be x cm
Area of ||gm = (longer side distance between longer sides)
= (shorter side distance between the short sides)
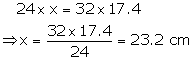
distance
between the shorter side = 23.2 cm
Solution 30
Solution 31
Area ofparallelogram = 2 area of DABC
Opposite sides of parallelogram are equal
AD = BC = 20 cm
And AB = DC = 34 cm
In 
ABC
we have
a = AC = 42 cm
b = AB = 34 cm
c = BC = 20 cm
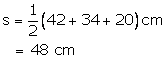
Then, (s a) = 6 cm, (s b) = 14 cm and (s c) = 28 cm
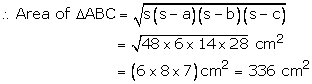
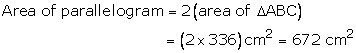
Solution 32
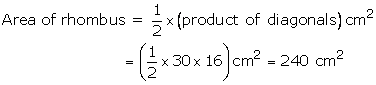
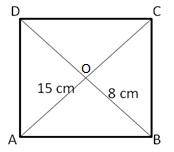
We know that the diagonals of a rhombus, bisect each other at right angles
OA = OC = 15 cm,
And OB = OD = 8 cm
And 
AOB
= 90
By
Pythagoras theorem, we have
Solution 33
(i)Perimeter of rhombus = 4 side
4
side = 60 cm
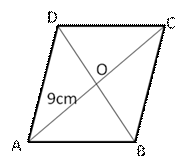
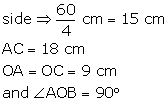
By Pythagoras theorem
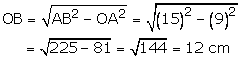
OB = 12 cm
OB = OD = 12 cm
BD
= OB + OD = 12 cm + 12 cm = 24 cm
Length of second diagonal is 24 cm
(ii) Area of rhombus = 
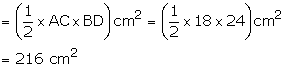
Solution 34
(i)Area of rhombus = 480 
One of its diagonals = 48 cm
Let the second diagonal =x cm
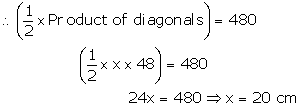
Hence the length of second diagonal 20 cm
(ii)We know that the diagonals of a rhombus bisect each other at right angles
AC
= 48, BD = 20 cm
OA
= OC = 24 cm and OB = OD = 10 cm
By Pythagoras theorem , we have
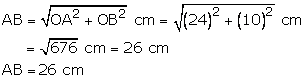
(iii)Perimeter
of the rhombus = (4 26) cm = 104 cm
Solution 35
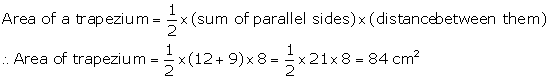
Solution 36
Areaof cross section = 
Solution 37
Let ABCD be a given trapezium in which
AB = 25, CD = 11
BC = 15, AD = 13
Draw CE || AD
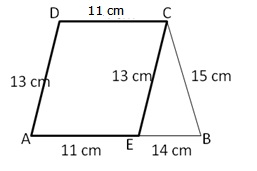
In ||gm ADCE, AD || CE and AE || CD
AE = CD = 11 cm,
And BE = AB BE
= 25 11 = 14 cm
In 
BEC,
Area of BEC
= 
Let height of 
BEC
is h
Area of BEC
= 
From (1) and (2), we get
7h = 84 
h
= 12 m
Area of trapezium ABCD
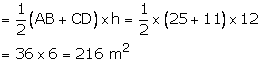
Perimeter and Area of Plane Figures Exercise MCQ
Solution 1
Solution 2
Solution 3
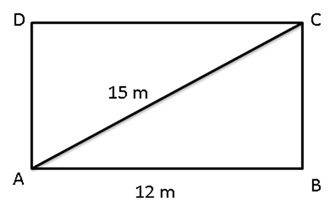
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
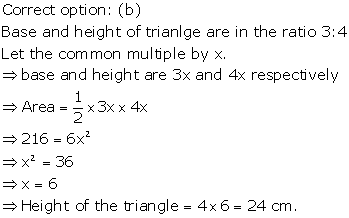
Solution 16
Solution 17
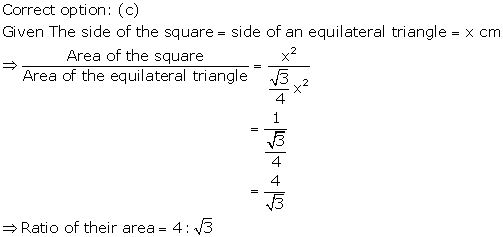
Solution 18
Solution 19
Solution 20
Perimeter and Area of Plane Figures Exercise Test Yourself
Solution 1
Solution 2
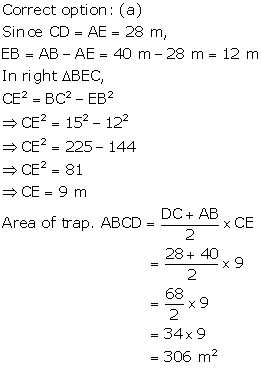
Solution 3
Solution 4
Solution 5
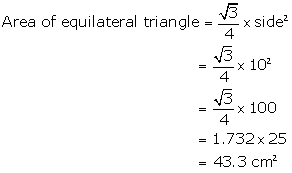
Solution 6
Solution 7
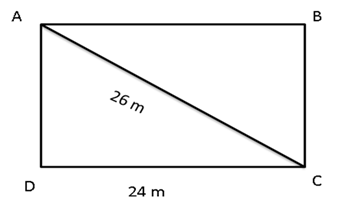
Solution 8
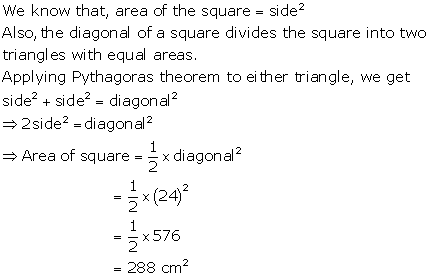
Solution 9
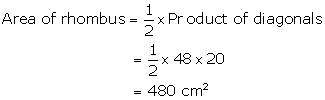
Solution 10
Solution 11
Solution 12
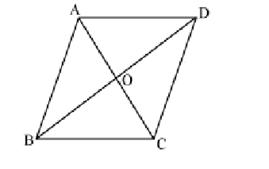
Solution 13
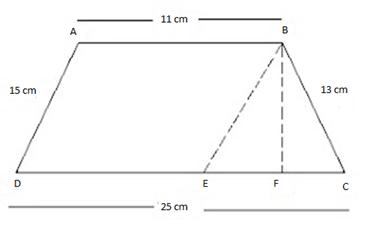
Solution 14
Solution 15
Let the side of a square lawn = S metre
Then,
4S × 14 = 2800
⇒ 4S = 200
⇒ S = 50 m
⇒ Area of a square lawn = (50 m)2 = 2500 m2
Now,
cost of mowing 100 m2 lawn = Rs. 54
Then, cost of mowing 2500 m2 lawn 
Therefore, the cost of mowing the lawn is Rs. 1350.
Solution 16
Solution 17
Solution 18
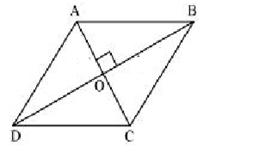
Solution 19
Solution 20
